УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ

П 34. Умножение десятичных дробей на натуральные числа

Пусть поле имеет форму квадрата со стороной 1,83 км. Найдем периметр поля: 1,85+1,85+1,85+1,85=7,32 км. Для решения задачи мы нашли сумму четырех слагаемых, каждое из которых равно 1,83. Такую сумму называют произведением числа 1, 83 и натурального числа 4 и обозначают 1,83∙4.

Произведением десятичной дроби и натурального числа называют сумму слагаемых, каждое из которых равно этой дроби, а количество слагаемых равно этому натуральному числу.

Значение 7,32 для произведения 1,83∙4 можно получить иначе: умножить 1,83 на 4, не обращая внимание на запятую, а в полученном произведении 732 отделить запятой столько цифр справа, сколько их после запятой в дроби 1,83:

Чтобы умножить десятичную дробь на натуральное число, надо:
1) умножить её на это число, не обращая внимания на запятую;
2) в полученном произведении отделить запятой столько цифр справа, сколько их отделена запятой в десятичной дроби.

Найдем произведение 9,865∙10. По правилу сначала умножаем 9865 на 10, получим 9865∙10=9865. Теперь отделяем запятой три цифры справа и получаем:

9,865∙10=98,650=98,65

Таким образом при умножении 9,865 на 10 мы переносим запятую через одну цифру вправо. Если умножить 9,865 на 100, то получим 986,5, то есть запятую перенесли через две цифры вправо.

Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, надо в этой дроби перенести запятую на столько цифр право, сколько нулей стоит в множителе после единицы.

П.35 Деление десятичных дробей на натуральные числа

Задача. Кусок ленты длиной 19,2 м разрезали на 8 равных частей. Найдите длину каждой части.

Решение. Чтобы решить задачу, выразим длину ленты в дециметрах: 19,2 м = 192 дм. Но 192 : 8 = 24. Значит, длина каждой части равна 24 дм, то есть 2,4 м. Если умножить 2,4 на 8, получим 19,2. Значит, 2,4 является частным от деления 19,2 на 8.

Пишут: 19,2 : 8 = 2,4.
Тот же ответ можно получить, не переводя метры в дециметры. Для этого надо разделить 19,2 на 8, не обращая внимания на запятую, и поставить в частном запятую, когда кончится деление целой части:

Разделить десятичную дробь на натуральное число — значит найти такую дробь, которая при умножении на это натуральное число дает делимое.

Чтобы разделить десятичную дробь на натуральное число, надо:
1) разделить дробь на это число, не обращай внимания на запятую;
2) поставить в частном запятую, когда кончится деление целой части.

Если целая часть меньше делителя, то частное начинается с нуля целых:

Разделим 96,1 на 10. Если частное умножить на 10, должно получиться снова 96,1.

Но при умножении десятичной дроби на 10 запятую переносят на одну цифру вправо. Значит, при делении на 10 запятую надо переносить на одну цифру влево: 96,1 : 10 = 9,61.
Проверка: 9,61 . 10 = 96,1.
При делении на 100 запятую переносят на две цифры влево.

Чтобы разделить десятичную дробь на 10, 100, 1000 и так далее, надо в этой дроби перенести запятую на столько цифр влево, сколько нулей стоит в делителе после единицы.
При этом иногда приходится написать перед целой частью нуль или несколько нулей.
Например: 8,765 : 100 = 008,765 : 100 = 0,08765.
С помощью деления находят десятичную дробь, равную данной обыкновенной дроби.
Другими словами, с помощью деления обращают обыкновенную дробь в
десятичную.

Пример. Обратим дробь  в десятичную.

Решение.

Дробь  является частным от деления 3 на 4. Деля 3 на 4, получаем десятичную дробь 0,75. Значит, 

Как умножить число на десятичную дробь?

Как умножить число на десятичную дробь?

Чтобы умножить десятичную дробь на натуральное число, надо: 1) умножить её на это число, не обращая внимания на запятую; 2) в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.

Как правильно умножать числа с запятой?

Умножение десятичных дробей

1. Десятичные дроби записывают в столбик и умножают как обыкновенные числа.
2. Считаем количество знаков после запятой у первой десятичной дроби и у второй. Их количество складываем.
3. В полученном результате отсчитываем справа налево столько же цифр, сколько получилось их в пункте выше и ставим запятую.

Как умножить десятичную дробь на десятичную дробь?

Чтобы перемножить две десятичные дроби, надо: 1) умножить дроби, не обращая внимания на запятые; 2) посчитать общее количесво цифр после запятой в обеих дробях и столько цифр справа в полученном числе отделить запятой.

Как умножить десятичную дробь на смешанное число?

Для умножения конечной десятичной дроби или бесконечной периодической десятичной дроби на обыкновенную дробь или смешанное число, нужно десятичную дробь представить в виде обыкновенной дроби, после чего провести умножение. Проведите умножение десятичной дроби 0,4 на смешанное число . Так как 0,4=4/10=2/5 и , то .

Как умножить дробь на целое число?

Чтобы дробь умножить на натуральное число нужно числитель дроби умножить на это число, а знаменатель дроби оставить без изменения. Если в результате умножения получилась неправильная дробь, не забудьте превратить её в смешанное число, то есть выделить целую часть.

Как решать целые числа с дробями?

Алгоритм расчета:

1. Приводим дроби к общему знаменателю.
2. Складываем дроби
3. Если есть возможность, то сокращаем полученную дробь.
4. Если же получилась неправильная дробь, то вычисляем из нее целую часть.

Как найти одну десятую часть от числа?

Чтобы найти десятую часть числа, надо число разделить на 10 и умножить на 1.

Чему равна три четверти часа?

Три четверти часа — 45 минут.

Как пишется рукав три четверти?

Очень мучает вопрос, как правильно писать такие слова и как объяснить их написание: платок каре (или платок-каре?), карман-кенгуру, рукав три четверти, рукав реглан, рукав летучая мышь, воротник-лодочка,трусы-бразилиана, жакет «Бар», трусы-слипы, ботинки монки, воротник-апаш, воротник-стойка.

Сколько в мл 3 4 стакана?

Три четверти стакана (3/4 стакана объемом 200 мл) это 150 грамм воды.

Сколько это три четверти стакана?

Три четвёртых стандартного стакана – это 150 мл.

Преобразование десятичных дробей в дроби

Чтобы преобразовать десятичную дробь в дробь, выполните следующие действия:

• Шаг 1: Запишите десятичную дробь, деленную на 1, например: десятичный 1
• Шаг 2: Умножьте верхнее и нижнее число на 10 для каждого числа после запятой. (Например, если после запятой два числа, используйте 100, если их три, используйте 1000 и т.  д.)
• Шаг 3: Упростите (или уменьшите) дробь

Пример: преобразование 0,75 в дробь

Шаг 1: Запишите 0,75, деленное на 1:

0,75 1

Шаг 2: Умножьте верхнее и нижнее число на 100 (поскольку после запятой 2 цифры, то есть 10×10=100):

× 100
0,75 1	=	75 100
× 100

(Видите, как это превращает верхнее число
в целое число?)

Шаг 3: Упростите дробь (это заняло у меня два шага):

	÷5		÷ 5
75 100	=	15 20	=	3 4
	÷5		÷ 5

 

Ответ =

3 4

 

Примечание.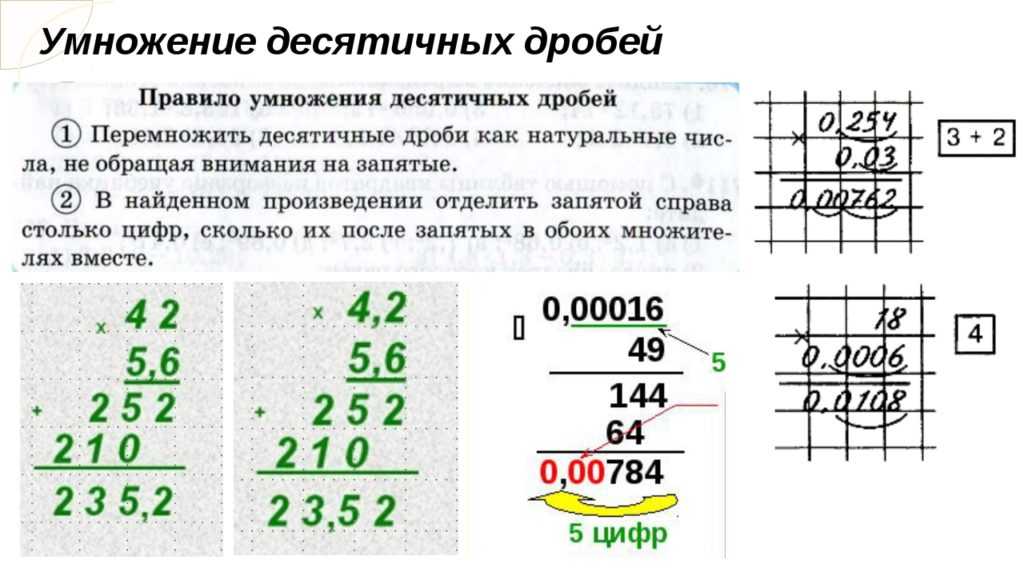 75/100 называется десятичной дробью , а 3/4 называется обыкновенной дробью !

Пример: преобразование 0,625 в дробь

Шаг 1: запишите:

0,625 1

Шаг 2: умножьте верхнее и нижнее число на 1000 (3 цифры после запятой, поэтому 10×10×10=1000)

625 1000

Шаг 3: Упростите дробь (здесь мне потребовалось два шага):

	÷ 25		÷ 5
625 1000	=	25 40	=	5 8
	÷ 25		÷ 5

 

Ответ =

5 8

Когда есть целая часть числа, отложите целое число и верните его в конец:

Пример: преобразование 2,35 в дробь

Отложите 2 и просто поработайте над 0,35

Шаг 1: запишите:

0,35 1

Шаг 2: умножить верх и низ на 100 (2 цифры после запятой, так что 10×10=100):

35 100

Шаг 3: Упростить дробь:

÷ 5
35 100	=	7 20
÷ 5

Верните 2 (для получения смешанной дроби):

Ответ = 2

7 20

Пример: преобразование 0,333 в дробь

Шаг 1:

Запишите:

0,333 1

Шаг 2: Умножьте верхнее и нижнее число на 1000 (3 знака после запятой, так что 10×10×10=1000)

333 1000

Шаг 3: Упростить дробь:

Проще не бывает!

 

Ответ =

333 1000

Если вы действительно имели в виду 0,333. .. (другими словами, 3 с, повторяющихся вечно, что называется 3 повторяющихся ), то нам нужно следовать специальному аргументу. В таком случае запишем:

0,333… 1

Затем умножьте верх и низ на 3:

× 3
0,333… 1	=	0,999… 3
× 3

А 0,999… = 1 (Так ли это? — см. 9 Повторяющееся обсуждение для получения дополнительной информации, если вам интересно), поэтому:

Ответ = 1 3

Инструмент преобразования 

Вы также можете попробовать калькулятор десятичных дробей

 

944, 1358, 945, 1359, 3483, 3484, 3485, 3486, 946, 1360

Калькулятор десятичной дроби

Использование калькулятора

Этот калькулятор преобразует десятичное число в дробное или десятичное число в смешанное число.

Для повторяющихся десятичных знаков введите, сколько знаков после запятой повторяется в вашем десятичном числе.

Ввод повторяющихся десятичных знаков

• Для повторяющихся десятичных знаков, таких как 0,66666… ​​где 6 повторяется вечно, введите 0,6, а поскольку 6 является единственным повторяющимся десятичным знаком после запятой, введите 1, чтобы десятичные разряды повторялись. Ответ 2/3
• Для повторяющихся десятичных знаков, таких как 0,363636…, где 36 повторяются вечно, введите 0,36, а поскольку 36 являются единственными двумя повторяющимися десятичными знаками в конце, введите 2, чтобы десятичные знаки повторялись. Ответ 4/11
• Для повторяющегося десятичного знака, такого как 1,8333… где 3 повторяется вечно, введите 1,83, а поскольку 3 является единственным повторяющимся десятичным знаком после запятой, введите 1, чтобы десятичные знаки повторялись. Ответ 1 5/6
• Для повторяющегося десятичного числа 0,857142857142857142….., где 857142 повторяется вечно, введите 0,857142, а поскольку 857142 — это 6 повторяющихся десятичных знаков в конце, введите 6, чтобы десятичные знаки повторялись. Ответ 6/7

Как преобразовать отрицательное десятичное число в дробь

1. Удалить отрицательный знак из десятичного числа
2. Выполнить преобразование положительного значения
3. Применить знак минус к ответу дроби

Если a = b, то верно, что -a = -b.

Как преобразовать десятичную дробь в дробь

1. Шаг 1: Составьте дробь, используя десятичное число в качестве числителя (верхнее число) и 1 в качестве знаменателя (нижнее число).
2. Шаг 2: Удалить десятичные разряды путем умножения. Во-первых, подсчитайте, сколько знаков справа от десятичной запятой. Далее, учитывая, что у вас есть x знаков после запятой, умножьте числитель и знаменатель на 10 ^x .
3. Шаг 3: Уменьшите дробь. Найдите наибольший общий делитель (GCF) числителя и знаменателя и разделите числитель и знаменатель на GCF.
4. Шаг 4: Упростите оставшуюся дробь до дроби смешанного числа, если это возможно.

Пример: преобразовать 2,625 в дробь

1. Переписать десятичное число как дробь (больше 1)

\( 2,625 = \dfrac{2,625}{1} \)

2. Умножить числитель и знаменатель на на 10 ³ = 1000, чтобы убрать 3 знака после запятой

\( \dfrac{2.625}{1}\times \dfrac{1000}{1000}= \dfrac{2625}{1000} \)

3. Найдите наибольший общий делитель (НОД) чисел 2625 и 1000 и сократите дробь, разделив числитель и знаменатель на НОД = 125.

\( \dfrac{2625 \div 125}{1000 \div 125}= \dfrac{21}{8} \)

4. Упростите неправильную дробь

\( = 2 \dfrac{5}{8} \)

Следовательно,

\( 2,625 = 2 \dfrac{5}{8} \)

Десятичная дробь

• Для другого примера, конвертировать 0,625 до дроби.
• Умножьте 0,625/1 на 1000/1000, чтобы получить 625/1000.
• Уменьшая получаем 5/8.

Преобразование повторяющейся десятичной дроби в дробь

1. Составьте уравнение, в котором x равно десятичному числу.
2. Подсчитать количество знаков после запятой, y. Создайте второе уравнение, умножив обе части первого уравнения на 10 ^y .
3. Вычесть второе уравнение из первого уравнения.
4. Найти х
5. Уменьшить дробь.

Пример: преобразование повторяющегося десятичного числа 2,666 в дробь

1. Составьте уравнение, в котором x равно десятичному числу
Уравнение 1:

\( x = 2.\overline{666} \)

2. Подсчитайте количество знаков после запятой, y. В повторяющейся десятичной группе 3 цифры, поэтому y = 3. Составьте второе уравнение, умножив обе части первого уравнения на 10 ³ = 1000.
Уравнение 2:

\( 1000 x = 2666.\overline{666} \)

3. Вычесть уравнение (1) из уравнения (2)

\( \eqalign{1000 x &= &\hfill2666.666…\ cr x &= &\hfill2.666…\cr \hline 999x &= &2664\cr} \)

Получаем

\( 999 x = 2664 \)

4. Находим x

\( x = \dfrac{2664}{999} \)

5. Сократите дробь. Найдите наибольший общий делитель (НОД) чисел 2664 и 999 и сократите дробь, разделив числитель и знаменатель на НОД = 333.

\( \dfrac{2664 \div 333}{999 \div 333}= \dfrac{8}{3} \)

Упростите неправильную дробь

\( = 2 \dfrac{2}{3} \)

Следовательно,

\( 2.