Умножение десятичных дробей — примеры, правила как умножать в 5 классе

Поможем понять и полюбить математику

Начать учиться

163.8K

Десятичные дроби — хитрый зверек, но только не для нас. В этой статье научимся умножать десятичные дроби, чтобы решать задачки на контрольной в 5 классе и старше легко и быстро.

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,

• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути,

десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,8

• 7,42

• 9,932

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

• 0,600 = 0,6;

• 21,10200000 = 21,102.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то она равна нулю.

• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т.

  д.

• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь в десятичную.

Как решаем:

1. Знаменатель равен 10 — это один ноль.

2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.

3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Ответ:

Пример 2. Перевести в десятичную дробь.

Как решаем:

1. Знаменатель равен 1000 — это три нуля.

2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.

3. Так как в числителе только две цифры, то на пустующие места пишем нули.

4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ:

Как читать десятичную дробь

Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:

Сколько цифр после запятой?	Читается, как
одна цифра — десятых;	1,3 — одна целая, три десятых;
две цифры — сотых	2,22 — две целых, двадцать две сотых;
три цифры — тысячных;	23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных;
четыре цифры — десятитысячных;	0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных;
и т. д.

Сохраняй наглядную картинку, чтобы быстрее запомнить.

Свойства умножения

С десятичными дробями можно производить те же действия, что и с любыми другими числами: складывать и вычитать, делить и умножать. В этом блоке узнаем, как умножать дроби.

Свойства умножения десятичных дробей

Переместительное свойство умножения — от перестановки мест множителей произведение не изменяется. ab = ba Сочетательное свойство умножения — чтобы умножить число на произведение двух чисел, нужно сначала умножить его на первый множитель, затем полученное произведение умножить на второй множитель. (ab)c = a(bc) Распределительное свойство умножения относительно сложения — чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить. a(b + c) = ab + ac Распределительное свойство умножения относительно вычитания — чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе. a(b — c) = ab — ac

Умножение десятичных дробей друг на друга можно упростить и просто умножить натуральные числа. Главное — правильно поставить запятую в ответе.

Если в задаче даны десятичные дроби с разными знаками — используем правило умножения отрицательных чисел. Как быстро запомнить:

«−−»	минус на минус дает плюс
«−+»	минус на плюс дает минус
«+−»	плюс на минус дает минус
«++»	плюс на плюс дает плюс

Числа с единицей и нулями (10, 100, 1000 и т.  д.) называются разрядными единицами, так как цифра 1 — единственная значимая цифра в числе и от ее местоположения зависит количественное значение числа. Важно запомнить правила для умножения и деления на разрядную единицу:

• Чтобы умножить число на разрядную единицу, достаточно к числу справа дописать столько нулей, сколько их содержит разрядная единица.

• Чтобы разделить число на разрядную единицу, достаточно от числа справа отбросить столько нулей, сколько их содержит разрядная единица.

Как умножать десятичные дроби в столбик

Чтобы перемножить десятичные дроби нужно сделать три шага:

1. Записать десятичные дроби в столбик и умножить друг на друга, как обыкновенные числа.

2. Посчитать количество знаков после запятой у каждой дроби. Сложить их количество.

3. Полученное количество знаков отсчитать справа налево и поставить запятую.

Пример: умножить 3, 11 на 0,01.

Как решаем:

1. Запишем дроби в столбик и умножим их, как будто у нас нет никаких запятых:

   Получаем: 311 ∗ 001 = 311.

2. Считаем общее количество цифр после запятой у обеих дробей — в нашем примере их четыре (по две на каждую).

3. Берем число, которое получилось после умножения и отсчитываем справа налево 4 знака. Но у нас получилось всего три цифры, а не четыре. Значит добавляем перед ними один ноль и вуаля — четыре цифры после запятой готовы

Ответ: 3,11 ∗ 0,01 = 0,0311.

Примеры умножения десятичных дробей столбиком:

Как умножать десятичные дроби на натуральные числа

Умножение десятичных дробей на обычные числа происходит так же, как и умножение между десятичными дробями.

Чтобы считать быстрее, умножайте их в столбик по правилам выше. А вот и примерчики!

Пример 1. Умножить десятичную дробь 2,27 на целое число 15.

Как решаем:

умножить столбиком данные числа и отделить два знака запятой.

Ответ: 15 ∗ 2,27 = 34,05.

Пример 2. Умножить 11 на 0,005.

Как решаем:

умножить столбиком данные числа и отделить три знака запятой.

Ответ: 11 ∗ 0,005 = 0,055.

Пример 3. Умножить 0,1557.. на 3.

Как решаем:

1. Округлить бесконечную дробь:

   0,1557..≈ 0,156

2. 0,156 * 3 ≈ 0,468.

Ответ: 0,1557.. ∗ 3 ≈ 0,468.

Как умножать десятичные дроби на 10, 100, 1000

Чтобы умножить десятичную дробь на 10, 100, 1000, нужно просто перенести запятую в дроби вправо на столько знаков, сколько нулей стоит во втором множителе. Лишние нули слева можно отбросить. А если цифр не хватает — дописываем нули.

Примеры:

• 1,15 ∗ 10 = 11,5;

• 22,345 ∗ 100 = 2 234,5;

• 8,99 ∗ 1 000 = 8 990;

• 0,54678 ∗ 10 000 = 5467,8;

• 0,07 ∗ 1 000 = 70;

• 0,00033 ∗ 100 = 0,033.

Как умножать десятичные дроби на 0,1, 0,01, 0,001

Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, нужно перенести запятую в дроби влево на столько знаков, сколько нулей стоит перед единицей. Ноль целых — тоже считаем. Если цифр не хватает — просто дописываем дополнительный ноль — один или несколько — после запятой.

Примеры:

• 34,9 ∗ 0,1 = 3,49;

• 1,8 ∗ 0,1 = 0,18;

• 145,7 ∗ 0,01 = 1,457;

• 9655,1 ∗ 0,001 = 9,6551;

• 11,9 ∗ 0,0001 = 0,00119.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить  на 0,9.

Как решаем:

1. Записать 0,9 в виде обыкновенной дроби:

2. Умножить числа по правилам

Ответ:

Пример 2. Умножить 0,18 на .

Как решаем:

1. Записать в виде десятичной дроби:

2. Произвести умножение в столбик или при помощи калькулятора:

Ответ:

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

Десятичные дроби

К следующей статье

477.1K

Решение уравнений с дробями

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Умножение дробей.

Умножение дробей.

Навигация по странице:

• Умножение дроби на натуральное число
• Умножение обыкновенных дробей
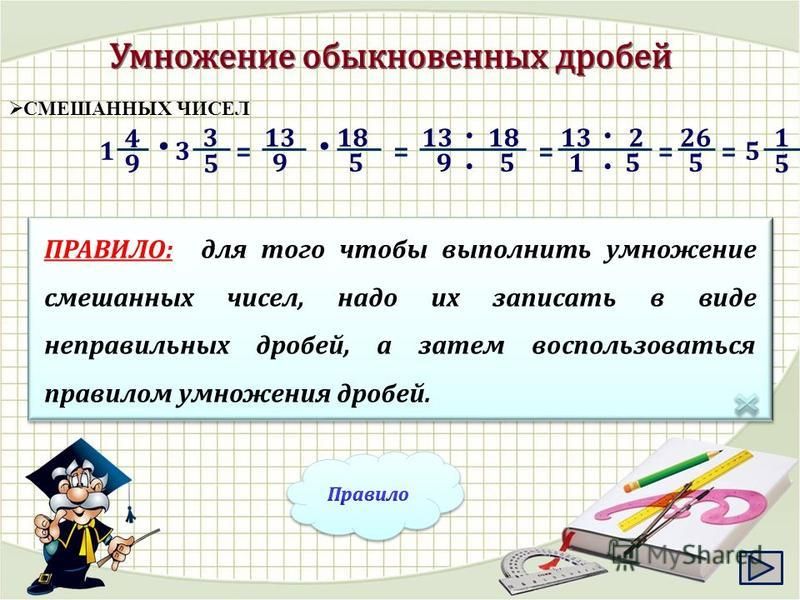
• Умножение смешанных чисел

Умножение дроби на натуральное число.

Определение.

Чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же.

Примеры умножения дроби на натуральное число

Пример 1.

Найти произведение дроби и натурального числа:

3	· 2	=	3 · 2	=	6
7			7		7

Пример 2.

Найти произведение дроби и натурального числа:

1	· 4	=	4	=	2·2	=	2
2			2		2

Умножение обыкновенных дробей.

Определение.

Чтобы умножить две обыкновенные дроби, надо
• перемножить числители и знаменатели дробей;
• сократить полученную дробь.

Примеры умножения обыкновенных дробей

Пример 3.

Найти произведение двух дробей:

3	·	2	=	3 · 2	=	6
7		5		7 · 5		35

Пример 4.

Найти произведение двух дробей:

10	·	3	=	10 · 3	=	2 · 5 · 3	=	5	=	5
9		4		9 · 4		2 · 2 · 3 · 3		2 · 3		6

Онлайн калькулятор дробей

Упражнения на тему умножение двух обыкновенных дробей

Умножение смешанных чисел.

Примеры умножения смешанных чисел

Пример 5.

Найти произведение двух смешанных чисел:

212 · 123 = 2 · 2 + 12 · 1 · 3 + 23 = 52 · 53 = 5 · 52 · 3 = 256 = 6 · 4 + 16 = 416

Пример 6.

Найти произведение смешанного числа и целого числа:

4	1	·	6	=	4 · 3 + 1	·	6	=	13 · 6	=	26
	3				3				3

Пример 7.

Найти произведение смешаного числа и обыкновенной дроби:

217 · 35 = 2 · 7 + 17 · 35 = 157 · 35 = 15 · 37 · 5 = 3 · 37 = 97 = 7 + 27 = 127

Онлайн калькулятор дробей

Упражнения на тему умножение двух смешанных чисел

Дроби Виды дробей (обыкновенная правильная, неправильная, смешанная, десятичная) Основное свойство дроби Сокращение дроби Приведение дробей к общему знаменателю Преобразование неправильной дроби в смешанное число Преобразование смешанного числа в неправильную дробь Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичной дроби в обыкновенную дробь

Онлайн калькуляторы дробей

Онлайн упражнения с дробями

Умножение дроби на целые числа? Определение, примеры

Что такое целые числа?

Целые числа — это набор чисел, включающий все натуральные числа, а также 0. Например, 10, 18, 200 и т. д. 

Связанные игры

Что такое дробь?

Дроби часто называют числом между числами. Дроби — это числовые значения, которые представляют собой часть или часть целого. Например, посмотрите на пиццу ниже.

Эта пицца разрезана на 4 равные части. Таким образом, каждый кусок пиццы представляет собой 1 из 4 равных частей. Таким образом, математически мы можем представить каждую часть как $\frac{1}{4}$. Это число называется дробью.

В общем, когда целое разделено на равные части, каждая часть представляет собой часть целого, и мы записываем дроби как $\frac{a}{b}$, где a и b — действительные числа, а b не может быть равно нулю .

Число под чертой, представляющее общее количество равных частей, на которые делится целое, называется знаменателем. А число сверху, которое представляет количество рассматриваемых нами равных частей, называется числителем.

Связанные рабочие листы

Умножение дробей на целые числа

Умножение двух чисел аналогично многократному сложению. Например,

2 раза по 4 или $2 \times 4$ равносильно добавлению числа «4» 2 раза.

Таким образом, умножение дробей на целые числа — это то же самое, что многократное сложение, когда дробь складывается столько же раз, сколько и целое число.

Например: попробуем перемножить 3 и $\frac{1}{4}$.

3 раза $\frac{1}{4}$ означает сложение дроби $\frac{1}{4}3$ раза.

Алгебраически это означает,

Мы можем решить это выражение визуально,

Источник

И наш ответ будет:

Но теперь давайте посмотрим, как мы можем обобщить это, не создавая модель каждый раз, когда мы хотим умножить целое число и дробь.

Умножение дробей с целыми числами

Сделаем это с помощью примера,

Умножим 5 и $\frac{3}{4}$.

Шаг 1: Преобразуйте 5 в дробную форму, применив 1 к знаменателю.

Шаг 2: Умножьте числитель на числитель и знаменатель на знаменатель.

И вуаля, у нас есть ответ.
В качестве дополнительного шага, если вы получили неправильную дробь, вы можете преобразовать ее в смешанное число.

Умножение смешанных дробей на целые числа

Умножение смешанных чисел на целые числа следует той же процедуре, только с дополнительным шагом.

Сделаем это на примере.

Как умножить 3 на $2\frac{1}{5}$?

Шаг 1: Преобразуйте смешанное число в неправильную дробь.

Шаг 2: Преобразуйте 3 в дробную форму, применив 1 к знаменателю.

Шаг 2: Умножьте числитель на числитель и знаменатель на знаменатель.

И после преобразования в неправильную дробь

Получим ответ:

Решенные примеры

Пример 1: Кэтрин готовит торт, для которого ей нужно три четверти чашки масла . Если она решит испечь три лепешки, сколько потребуется масла?

Решение : 

Количество пирожных $= 3$ 

Масло, необходимое для 1 пирожного $= \frac{3}{4}$ чашек

Общее количество требуемого масла $= 3 \times { 3}{4} = \frac{9}{4} = 2\frac{1}{4}$ чашек

Пример 2. Найдите произведение целого числа 10 и смешанной дроби 523.  Решение : $10\times 5\frac{2}{3} = 10\times \frac{17}{3} = \frac{170}{3} = 56\frac{2}{3}$

Практические задачи

1

На вечеринке каждый человек выпивает $\frac{3}{5}$$l$ сока. Если вы пригласите на свою вечеринку 15 человек, сколько сока вам понадобится?

$8$$l$

$10$$l$

$9$$l$

$15$$l$

Правильный ответ: $9$$l$
Необходимое количество сока $= 15 \times \ frac{3}{5} = \frac{45}{5} = $$9$$l$

2

Clove ежедневно проезжает $\frac{1}{4}$ миль. Сколько она проедет за 10 дней?

$2\frac{2}{4}$ миль

$\frac{2}{5}$ миль

$2$ миль

$1\frac{1}{4}$ миль

Правильный ответ: $2\frac{2}{4}$ миль
Пройденное расстояние за 10 дней $= 10 \times$ расстояние, пройденное за один день
$= 10 \times \frac{1}{4} = \frac{10}{4} = 2\frac{2}{4}$ миль

3

Джейн купила в магазине 20 яблок, из которых $\frac{1}{5}$ яблок были гнилыми.

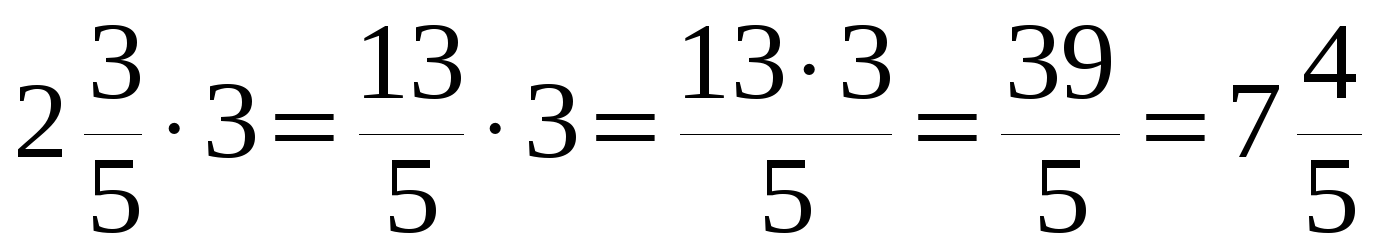Сколько яблок было гнилым?

5

10

2

4

Правильный ответ: 4
Общее количество яблок $= 20$
Доля гнилых яблок $= \frac{1}{5}$
Количество гнилых яблок $= 20 \times \frac{1}{5} = \frac{20}{ 5} = 4 яблока

Часто задаваемые вопросы

Как умножить дробь на целое число, используя числовую прямую?

Сначала мы отмечаем дробь на числовой прямой, а затем, чтобы умножить ее на целое число, прибавляем к той же дроби столько раз, сколько этого требует умножение.

Чему равно произведение умножения целого числа на смешанную дробь?

Произведением целого числа и смешанной дроби может быть смешанная дробь, неправильная дробь, правильная дробь или целое число.

Какое целое число дает тот же продукт, что и исходная дробь?

Число «1» при умножении на любую дробь дает ту же дробь, что и ответ. Например, $1 \times \frac{3}{5} = \frac{3}{5}$.

Полное руководство — Mashup Math

Ключевой вопрос: Как умножать дроби и целые числа?

Узнайте, как решать подобные проблемы.

Добро пожаловать в этот бесплатный урок, в котором вы изучите простой двухэтапный процесс умножения дробей на целые числа И умножения целых чисел на дроби.

Это полное руководство по умножению дробей на целые числа включает в себя несколько примеров, мини-урок с анимированным видео, а также бесплатный рабочий лист и ключ к ответу.

Начнем!

Прежде чем мы изучим, как умножать дроби, давайте быстро рассмотрим, как умножать дробь на дробь (понимание того, как применять приведенное ниже правило, значительно облегчит вам умножение дробей и целых чисел!)

Правило умножения дробей: При перемножении дробей умножайте числители вместе, затем умножайте знаменатели вместе следующим образом…

Пример правила:

Сколько будет (3/4) x (1/2) ?

Обратите внимание, что дробь (3/8) не может быть упрощена (так как 8 и 3 не имеют общего делителя)

Ответ: (3/4) x (1/2) = 1/8

Ищете дополнительную помощь по умножению дроби на дробь? Ознакомьтесь с этим бесплатным руководством

Как умножить дробь на целое число (и наоборот)

Теперь, когда вы знакомы с правилом умножения дроби на дробь, вы можете использовать его, чтобы легко умножать дробь на целое число.

Начнем с примера:

Умножение дробей на целые числа: Пример 1

Пример 1: Сколько будет (2/7) x 3 ?

Начните с перезаписи целого числа (3 в данном примере) в виде дроби (3/1) следующим образом…

(Вы можете сделать это, потому что любое число, деленное на единицу, всегда равно самому себе)

Теперь, поскольку вы умножаете дробь на дробь, вы можете применить правило и решить следующим образом…

А так как (6/7) не может быть упрощено, то можно сделать вывод, что:

Ответ: (2/7) x 3 = (6/7)

Подождите! Что произошло бы, если бы ответ можно было упростить? Давайте рассмотрим ситуацию в следующем примере…

Умножение дробей на целые числа: Пример 2

Пример 1: Сколько будет 5 x (9/10) ?

Начните с перезаписи целого числа (5 в этом примере) в виде дроби (5/1)…

Затем примените правило следующим образом…

В этом примере (45/10) не является окончательный ответ, потому что его можно упростить.