«Умножение двузначного числа на однозначное в столбик» | План-конспект занятия по математике (3 класс):

Урок математики  в 3 классе

 Тема: «Умножение двузначного числа на однозначное в столбик»

Цель урока: познакомить с алгоритмом умножения двузначного числа на однозначное в столбик; повторить распределительное свойство умножения и свойство умножения суммы на число; закреплять умения решать задачи, находить площадь прямоугольника.

Задачи урока:

Личностные:

— прививать интерес к математике;

— уметь находить выход из спорных ситуаций при объяснении алгоритма умножения двузначного числа на однозначное в столбик;

— развитие способности к рефлексивной оценке собственных действий.

Предметные:

— уметь пользоваться: устной и письменной речью при объяснении алгоритма умножения двузначного числа на однозначное в столбик, основами логического мышления, исполнения алгоритмов при вычислении выражений;

— составлять последовательности (цепочки) предметов, чисел, фигур по заданному правилу;

— выполнять перебор всех возможных вариантов объектов и комбинаций, удовлетворяющих заданным условиям.

Метапредметные:

— умение выполнять заданное учебное действие, в случае неуспеха грамотно фиксировать своё затруднение, анализировать ситуацию, устранять причины затруднения;

— формирование специфических для математики логических операций (сравнение, анализ, аналогия).

Ход урока

I. Организационный момент.

— Здравствуйте, дети! Я очень рада вас видеть, начинаем наш урок!

Математика – королева наук!

Без нее не летят корабли,

Без нее не поделишь ни акра земли,

Даже хлеба не купишь, рубля не сочтешь,

Что почем, не узнаешь,

А узнав, не поймешь!

II. Устный счет, актуализация знаний:

— умножьте 78 на 8;

— умножьте 32 на 3;

— умножьте 14 на 6;

— умножьте 28 на 2.

— Удобно ли было умножать устно?

— Что нужно помнить, когда мы устно умножаем двузначное число на однозначное?

III. Открытие новых знаний. (Презентация.)

— Рассмотрим графическую модель распределительного свойства умножения – нахождение площади прямоугольника по известным его сторонам:

(a + b) ∙ c = a ∙ c + b ∙ c

— Как же можно выполнить умножение 24 на 8?

(Дети решают. Ответы фиксируются на доске.)

24 х 8 = (20+4) х 8 = 20 х 8 + 4 х 8 = 160 + 32 = 192

Постановка проблемы:

— Запись решения громоздкая, неудобная. Существует ли другой способ умножения таких чисел? Сформулируйте задачи урока: (придумать более компактную, удобную запись по аналогии записи сложения в столбик).

Логика рассуждений:

— Произведение 24 и 8 равно площади прямоугольника со сторонами 24 ед. и 8 ед. Разбив большую сторону на части 20 ед. и 4 ед., видим, что вся площадь равна сумме площадей получившихся прямоугольников: 32 и 160 кв. ед. Записав сумму в столбик, приходим к более удобной записи умножения:

 24  

   8

  32

 160

 192

— Эту запись можно еще упростить, вычисляя число десятков «в уме». Тогда число десятков первого произведения удобно писать для памяти над числом десятков первого множителя.

   3

   24

     8

 192

Знакомство с алгоритмом:

— Чему мы будем учиться на уроке? (Выполнять умножение, записывая числа в столбик).

IV. Первичное закрепление знаний.

Работа по учебнику —  № 2- 3 на странице 36.

(Коллективное выполнение с комментированием у доски).

14х2        21х4        32х3

11х9        13х3        42х3

VI. Самостоятельная работа.

Решение примеров:

26 х 3        44 х 5    73 х 4

(Самопроверка по образцу).

VII. Физкультминутка.

VIII. Закрепление изученного материала.

Работа по учебнику — №4, с.36 (самопроверка),     №6, с.37 (работа в парах).

IX. Подведение итогов урока.

— Все ли было понятно сегодня на уроке?

— Кому  было трудно?

— Расскажите алгоритм умножения двузначного числа на однозначное в столбик.

— Где можно применить полученные знания?

Х. Рефлексия.

— Кто доволен своей работой?

— Кому еще нужна помощь?

XI. Домашнее задание

№9, с.37, №15, 16, с.38

Выучить алгоритм умножения в столбик.

— Спасибо за работу! До свидания!

3 класс. Математика.

Умножение на однозначное число — Умножение двузначного числа на однозначное

Комментарии преподавателя

Умножить многозначное число на однозначное можно с помощью правила умножения суммы на число, разложив при этом многозначное число на разрядные слагаемые. Но такой способ не всегда удобен.

При умножении многозначного числа на однозначное можно делать запись столбиком, как при сложении и вычитании. Такой способ очень помогает при умножении многозначных чисел. В этом уроке научимся находить значение произведения многозначного и однозначного чисел, выполняя запись столбиком.

Найдем значение произведения: 32 ∙ 2.

Запишем произведение столбиком.

Первый множитель 32 имеет два разряда: 3 десятка, 2 единицы.

 

Второй множитель 2 имеет один разряд – 2 единицы.

 

При записи в столбик записываем множители поразрядно: единицы под единицами.

При умножении столбиком знак умножения записываем крестиком «х».

Вместо знака равно проводим черту под вторым множителем.

 

Заметим, что при умножении многозначного числа на однозначное число умножаем  число каждого разряда первого множителя на второй множитель.

Умножать начинаем с единиц: 2 умножить на 2 – равно 4.

4 единицы записываем под единицами.

Потом умножаем десятки первого множителя, 3 десятка умножить на 2 – равно 6 десятков.

6 записываем под десятками.

Читаем результат 64.

 

Аналогично можно умножить любое многозначное число на однозначное.

Например, 4211 умножить на 2.

Начинаем с единиц:

1 умножить на 2 – равно 2, 2 единицы записываем под единицами.

1 десяток умножить на 2 – равно 2 десятка, 2 записываем под десятками.

2 сотни умножить на 2 – равно 4 сотни, 4 записываем под сотнями.

4 единицы тысяч умножить на 2 – равно 8 единиц тысяч, 8 записываем под единицами тысяч.

Читаем результат: 8422.

 

А теперь рассмотрим произведения, в которых при умножении чисел разрядов получается двузначное число.

 

Например, 547 умножить на 4.

 

Начинаем умножать с единиц:

7 умножить на 4 – равно 28.

28 – это двузначное число, в нем 2 десятка и 8 единиц.

8 единиц записываем под единицами, 2 десятка запомним и прибавим к десяткам.

4 десятка первого множителя умножаем на 4 – равно 16, добавим 2 десятка, полученных при умножении единиц, получится 18 десятков.

8 записываем под десятками, а 1 запомним и прибавим к сотням.

Умножим 5 сотен на 4 – равно 20 сотен, прибавим 1 сотню от умножения десятков, получится 21.

1 записываем под сотнями, 2 являются единицами тысяч.

Читаем результат: 2 188.

 

Подведем итоги.

1. При умножении столбиком записываем множители друг под другом поразрядно: единицы пишем под единицами.
2. Умножать начинаем с разряда единиц.
3. Если при умножении однозначного числа на значение разряда многозначного числа получается двузначное число, количество единиц этого двузначного числа записываем в разряд, который умножали, а количество десятков прибавляем к результату умножения однозначного числа на значение следующего разряда многозначного числа.

ИСТОЧНИКИ

http://znaika.ru/catalog/3-klass/matematika/Umnozhenie-na-odnoznachnoe-chislo-stolbikom

Файлы

Нет дополнительных материалов для этого занятия.

Случайные математические трюки в уме (Часть 1): Умножение двузначных чисел | Тайсон Ву

Фото: Unsplash

Умственная математика относится к вычислению простых арифметических выражений в уме без использования бумаги, карандашей и калькуляторов. Мы часто сталкиваемся с некоторыми простыми арифметическими задачами в нашей повседневной жизни — рассчитать стоимость проезда на автобусе, внести изменения, разделить счет между группой друзей и т. д. Этот навык всегда полезно приобрести, чтобы сделать свою жизнь более удобно или, что более важно, произвести впечатление на своих друзей, дав арифметический ответ, прежде чем они переключатся на приложение-калькулятор в своих телефонах.

С другой стороны, это важный навык для тех, кто работает в количественной области. Трейдеры, торгующие на финансовом рынке, должны быть очень чувствительны к цифрам, и поэтому сеанс ментальной математики иногда включается в процедуры собеседования для количественных позиций трейдера.

В этой серии статей я поделюсь некоторыми быстрыми математическими приемами и советами, которые я усвоил за годы учебы. Чтобы продемонстрировать эти приемы и советы, я собираюсь представить несколько примеров арифметических выражений и показать вам, как я обрабатываю вопрос.

Фото: Unsplash

Пример 1

45 * 63 = ?

Прежде чем искать лучший способ решения таких задач на умножение, давайте посмотрим, как подойдет к этому вопросу обычный способ, которому обучают в начальной школе:

Вертикальная форма

Когда нам нужно умножить два двузначных числа в, мы можем интуитивно разделить их на две задачи умножения двузначного и однозначного числа. В приведенном выше примере обычный способ выполнить математику — разбить его на 45*60+45*3.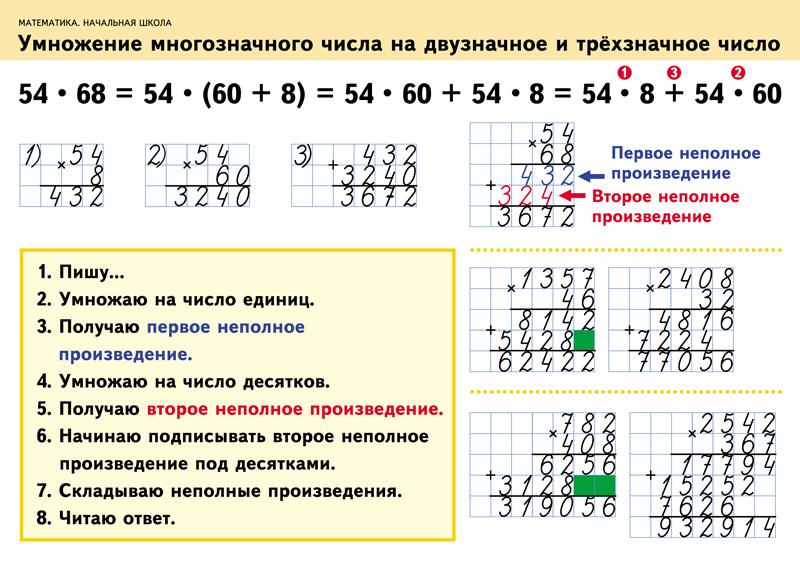

Проблема возникает при обычной практике

Однако, когда нам приходится делать математику без карандаша и бумаги, мы не можем отметить какие-либо промежуточные результаты и мы часто забываем результат 45*60, когда переходим к вычислению 45*3. Не говоря уже о том, что мы должны сложить два результата, чтобы получить окончательный ответ. Мы должны найти лучший способ, который меньше полагался бы на запоминание промежуточных результатов.

Метод

Практическое правило выглядит так:

«Внешние * Внутренние, Десятки * Десятки, Единицы * Единицы»

Вот объяснение:

• Умножьте две «внешние» цифры (4 и 3) и две «внутренние» цифры (5 и 6), затем добавьте их вверх: 4*3+5*6 = 42. Это первый промежуточный результат из . Чтобы промежуточный результат не занимал ваши драгоценные слоты памяти, вы можете напомнить себе число 42, используя жест рукой, так что 4 на левой руке и 2 на правой руке.

Ваша рука должна выглядеть так.

• Идем дальше, смотрим на две цифры десятков и перемножаем их. 4*6=24. Снова посмотрите на свою руку и представьте число 24. Совместите крайнюю правую цифру с десяткой на руке и сложите их, как показано ниже. Вы должны получить число 282 , и это число, которое нужно запомнить сейчас:

Посмотрите на свою руку и представьте, что эти числа парят в воздухе

• Наконец, мы смотрим на две цифры на единицах и умножаем их. 5*3=15. Помните промежуточный результат 282 ? Совместите крайнюю левую цифру числа 15 с самой правой цифрой промежуточного результата и сложите их. И это окончательный ответ: 2835.

Это считается улучшенным способом умножения двузначных чисел, так как нам нужно только запомнить не более двух простых промежуточных результатов в любом случае. Кроме того, мы могли меньше запоминать с помощью жестов рук.

Пример 2

Давайте сделаем еще один пример:

79 * 23 = ?

Число, которое проходит через вашу руку и голову, следует отметить следующим образом:

• Первый промежуточный результат от «Внешние * Внутренние» должен быть 39 .
• «Добавить» 14 к первому промежуточному результату и получить 179.
• «Добавить» 27 к 179, чтобы получить 1817.
• Готово!

Это то, что вы сделали в своем уме?

79 * 23 = ?

Поначалу ваша скорость вычислений с помощью этого трюка может быть немного медленной, но я могу гарантировать, что после небольшой практики вы сможете найти ответ быстрее, чем ваш друг, который пытается ввести числа в калькулятор. чтобы получить результат. Это трюк, который определенно стоит немного попрактиковать!

Это небольшой трюк, который помог мне посчитать в уме немного на быстрее, чем средний человек. Помните: практика делает совершенным. Меньшая зависимость от калькулятора в повседневной жизни может значительно сократить время вычислений, когда вы сталкиваетесь с ним посреди сложной математической задачи. Далее мы рассмотрим другие маленькие хитрости для других типов вопросов!

Часть 1: Умножение двузначных чисел [Эта статья]

Часть 2: Специальные операции умножения

арифметика — Как быстрее всего умножать двузначные числа?

спросил 10 лет, 11 месяцев назад

Изменено 6 лет, 5 месяцев назад

Просмотрено 53 тысячи раз

$\begingroup$

В последнее время я играю в различные математические игры на своем Android (например, Math Cruncher).

Я заметил, что не могу быстро (менее 7-8 секунд) умножать двузначные числа (например, $ 18 * 17 $). Итак, мой вопрос: как быстрее всего умножать двузначные числа?

• арифметика
• ментальная арифметика

$\endgroup$

12

$\begingroup$

Как я это выучил:

$$\begin{array}{rrl} & 18 & \\ \раз & 17 & \\ \hline & 156 & (10\умножить на 10 + 8\умножить на 7) \\ + & 70 & (10\умножить на 7) \\ + & 80 & (10\умножить на 8) \\ \hline = & 306 &\\ \hline \end{массив}$$

Обычно:

$$\begin{array}{rrl} & {\гм АВ} & \\ \times & {\rm CD} & \\ \hline & {\rm ACBD} & \text{(добавить 0, если необходимо)} \\ + & {\ гм до н.э.} 0 & \\ + & {\ rm AD} 0 & \\ \hline \end{array}$$

Это просто деление на многочлен: $(10+7)\times (10+8)$. И это позволяет мне визуализировать легче, чем традиционный метод.

$\endgroup$

1

$\begingroup$

Самый быстрый способ умножать двузначные числа — это заранее знать результат, выучив таблицу умножения двузначных чисел точно так же, как вы выучили таблицу умножения однозначных чисел. Конечно, это означает много работы впереди.

$\endgroup$

$\begingroup$

Мой метод умножения некоторых двузначных чисел не будет работать хорошо во всех случаях, и его недостатком является то, что вы должны запомнить все квадраты. Но я представляю это просто как еще один трюк, которому вы можете научиться. Я добавил +1 к ответу FiniteA, так как это кажется хорошим способом, который хорошо работает практически в любом случае и требует очень небольшого запоминания или навыков, т. Е. Он сводит его к простейшим частям. 92=2500$ и, следовательно, 50*42=2500-400$.

(2) Как правило, округляйте в большую или меньшую сторону до ближайшего числа, кратного 10$, а затем исправьте: например, вычислите 93*42=100*42-7*42$. Это особенно полезно, если вам не нужно точное значение — тогда вы очень быстро получите хорошее приближение. Единственный выбор, который вам нужно сделать здесь, — это округлить одно из двух чисел, и вы должны сделать это, чтобы максимизировать результирующее упрощение. В выбранном мной примере лучше округлить 93$ до 100$, так как умножить на 100$ немного проще, чем умножить на 40$.

(3) Когда вы начнете считать в уме с большими числами, вы поймете, что главное препятствие — не скорость, а пространство: вы столкнетесь с проблемой, что не можете надежно хранить в голове больше нескольких цифр за раз . Чтобы преодолеть это, вам понадобится мнемоника. Один относительно безболезненный способ описан в книге Арта Бенджамина «Секреты ментальной математики: руководство математика по молниеносным вычислениям и удивительным математическим трюкам»: превращайте числа в фразы, стихи, рассказы или песни!

$\endgroup$

1

$\begingroup$

Уловка калькулятора в уме состоит в том, чтобы начать слева:

$$ \начать{массив}{г} 17\\ \ раз 18 \конец{массив} $$
$$ \begin{массив}{с л} \text{‘перекрестное’ вычисление} &\text{ частичный результат}\\ 1\cdot 1=1 и 1\\ 1\cdot 8+7\cdot 1=15 и 25\\ 7\cdot 8=56 &306 \конец{массив} $$

Другой пример $$ \начать{массив}{г} 237\\ \ раз 543 \конец{массив} $$
$$ \begin{массив}{с л} \text{‘перекрестное’ вычисление} &\text{ частичный результат}\\ 2\cdot 5=10 и 10\\ 2\cdot 4+3\cdot 5=23 и 123\\ 2\cdot 3+3\cdot 4 +7\cdot5=53 &1283\\ 3\cdot 3+7\cdot 4=37 и 12867\\ 7\cdot 3=21 и 128691\\ \конец{массив} $$

Тот же трюк (работа слева направо) используется для других операций. Аккуратно и быстро!

$\endgroup$

$\begingroup$

Я разбиваю одно из чисел на 10, так что это разбивается на 3 простых умножения.

$$\begin{выравнивание} &18 \умножить на 17 = 18 \умножить на 10 + 18 \умножить на 7\\ &18 х 7 = 7 х 10 + 7 х 8. \end{align}$$

По этой логике $$ 18 х 17 = 18 х 10 + 7 х 10 + 8 х 7. $$

Потребуется несколько попыток, чтобы уложить шаблон в голове, но у меня работает!

$\endgroup$

$\begingroup$

Ребята, вы слишком усердствуете. Просто выучите один раз две цифры внутри и снаружи, а затем сделайте это. 69 * 89. Получаем 6*89 = 534. Прибавляем это к первым двум цифрам 9*89 = 801. Делаем так: 534 + 80 = 614. Приклеиваем 1 к концу. Получаем 6141. Это должен быть лучший способ, так как я химик с низким уровнем жизни, но могу сделать это за секунды (без карандаша или ручки).