Умножение дробей: простая инструкция — Лайфхакер

15 января 2021ЛикбезОбразование

Простая шпаргалка для тех, кто подзабыл школьную программу по математике.

Поделиться

0

Умножение дробей друг на друга

Обыкновенные дроби

Всё просто: числитель умножьте на числитель, а знаменатель на знаменатель. Потом проверьте, можно ли сократить дробь. Например:

Правило работает для дробей и с разными, и с одинаковыми знаменателями. Если дробь большая, допустим ²⁴/₃₅, постарайтесь сразу сократить её — так будет легче вести подсчёты.

Если в примере есть смешанное число, сначала преобразуйте его в неправильную дробь, а потом умножайте способом, описанным выше. Полученный результат переведите обратно в смешанное число.

Вспомните основы 💡

• Какие бывают дроби и как их складывать

Десятичные дроби

Процесс умножения происходит в три шага:

1. Запишите дроби в столбик и умножьте как натуральные числа, пока не думая о запятых.
2. Посмотрите, сколько знаков после запятой было в каждой дроби, и сложите их количество.
3. Двигаясь справа налево, отсчитайте в результате умножения столько же цифр, сколько получилось в предыдущем шаге. Поставьте там запятую. Это и есть ответ. Например:

Если умножаете на 0,1, 0,01, 0,001 и так далее, то переместите запятую влево на столько знаков, сколько их после запятой в множителе: 0,18 × 0,1 = 0,018; 0,5 × 0,001 = 0,0005.

Освежите знания 👈

• Как перевести обычную дробь в десятичную

Умножение дробей на натуральные числа

Обыкновенные дроби

Нужно умножить только числитель, а знаменатель оставить без изменений. Если результат — неправильная дробь, выделите из неё целую часть, чтобы получить смешанное число. Например:

Если нужно умножить смешанное число, переведите его в неправильную дробь и умножайте по тому же принципу. То есть:

Есть и второй способ: разделить знаменатель на данное вам натуральное число, а числитель не трогать. Этот способ удобнее применять, когда знаменатель делится на это натуральное число без остатка. Например:

Сравните этот метод с первым — результат одинаковый.

Десятичные дроби

В этом случае используйте такой же способ, как для умножения дроби на дробь. Перемножьте числа столбиком, потом отсчитайте столько цифр, сколько их было после запятой в десятичной дроби, и там поставьте запятую. То есть:

Если нужно умножить десятичную дробь на 10, 100, 1 000 и так далее, просто переместите запятую вправо на столько знаков, сколько нулей после единицы. Например: 0,045 × 10 = 0,45; 0,045 × 100 = 4,5.

Читайте также 🧮👌🤓

• Умножать, делить, складывать как Шелдон Купер? Математические хаки…
• Как научить ребёнка считать играючи
• 6 способов посчитать проценты от суммы с калькулятором и без
• Как выучить таблицу умножения легко и быстро
• Как освоить устный счёт школьникам и взрослым

Как умножить обыкновенную дробь на десятичную дробь

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Алгебра Умножение обыкновенной дроби на десятичную: правило, примеры

В данной публикации мы рассмотрим, каким образом обыкновенную (простую) дробь можно умножить на десятичную. Также разберем примеры для закрепления теоретического материала.

• Произведение обыкновенной и десятичной дробей
• Примеры

Произведение обыкновенной и десятичной дробей

Чтобы умножить обыкновенную дробь на десятичную (и наоборот, т.к. от перестановки множителей результат не меняется), необходимо одну из дробей представить в виде другой.

Примечания:

1. Бесконечные десятичные дроби сначала требуется округлить, т.е. оставить конечное количество цифр после запятой.
2. Смешанные обыкновенные дроби сперва необходимо превратить в неправильные.

Примеры

Пример 1

Давайте найдем результат произведения дроби 

3/20

 и 2,19.

 
Решение 1

Переведем обыкновенную дробь в десятичную:

3/20

=

3⋅5/20⋅5

=

15/100

= 0,15

 
Теперь выполним умножение десятичных дробей:

0,15 ⋅ 2,19 = 0,3285.

Решение 2

Преобразуем десятичную дробь в обыкновенную:

2,19 = 2

19/100

=

2 ⋅ 100 + 19/100

=

219/100

 
Остается только найти произведение двух обыкновенных дробей:

219/100

⋅

3/20

=

219 ⋅ 3/100 ⋅ 20

=

657/2000

 
Пример 2

Умножим 6,24 на дробь 2

4/9

.

 
Решение

Преобразуем заданную смешанную дробь в неправильную:

2

4/9

=

2 ⋅ 9 + 4/9

=

22/9

 
Далее у нас есть выбор: либо мы переводим десятичную дробь в обыкновенную, либо наоборот. Выберем первый вариант.

6,24 = 6

24/100

=

6 ⋅ 100 + 24/100

=

624/100

 
Теперь разделим одну простую дробь на другую:

624/100

:

22/9

=

624/100

⋅

9/22

=

624 ⋅ 9/100 ⋅ 22

=

5616/2200

= 2

1216/2200

= 2

152/275

≈ 2,5528

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Как умножать дроби за 3 шага [обновлено]

Как умножать дроби

Умножение дробей можно обсуждать в рамках трех основных категорий.

1. Умножение правильных дробей
2. Умножение неправильных дробей
3. Умножение смешанных чисел

Умножение правильных дробей

Правильная дробь – это дробь меньше единицы, у которой числитель меньше знаменателя.

Пример:

Чтобы умножить правильные дроби, вам нужно выполнить всего три простых шага

Шаг 1  – Умножить числители
Шаг 2 – Умножить знаменатели
Шаг 3 – Простейшая форма должны следовать этому шагу, только когда у нас есть общие множители для числителя и знаменателя. В противном случае оставьте все как есть.)

Теперь давайте обсудим несколько простых примеров

Пример 01 :

Теперь давайте решим это, выполнив три простых шага, описанных выше.

Шаг 01  и  Шаг 02 (если вам трудно умножать, вы можете использовать таблицу умножения)

Шаг 03 –

Следуя шагу 01 и шагу 02, мы получили ответ 9005 На шаге 03 мы должны упростить дробь. Но в приведенном выше ответе мы видим, что нет общих множителей (число, которое делит и 2, и 15).

Таким образом, окончательный ответ будет

Пример 02 :

Шаг 01 и Шаг 02

Шаг 03

Теперь мы получили

в качестве ответа. Мы видим, что и 15, и 24 могут

разделить на 3 (3 — общий множитель)

Окончательный ответ будет

Пример 03 :

Шаг 01 и Шаг 02

Шаг 03 –

Для этого числителя и знаменателя у нас есть несколько общих делителей, таких как 2,3 и 6.

из этих делителей вы должны выбрать наибольший общий делитель (он также называется Наибольшим общим делителем — HCF)

Таким образом, окончательный ответ будет

Думайте, что вы не можете найти наибольший общий делитель,
, который равен 6 в приведенном выше примере. Не запутайтесь. Вы можете продолжить упрощать дробь с любым общим множителем, который вы помните.

Предположим, вы смогли найти только 2 в качестве общего множителя. Просто продолжайте с 2.

В нашей новой дроби

снова, мы можем видеть, что 3 является общим делителем.

Умножение неправильных дробей

Неправильная дробь — это дробь, у которой числитель больше знаменателя

Пример:

Чтобы умножить неправильную дробь, нужно выполнить всего три простых шага

Шаг 1 – Умножить числители
Шаг 2 – Умножить знаменатель в неправильную дробь
1 Шаг 3 смешанный номер

Теперь давайте обсудим несколько простых примеров

Пример 1 :

Шаг 01 и Шаг 02

Шаг 03 –

смешанное число. Существует несколько методов преобразования.

Позвольте мне объяснить вам простой метод.

В этом методе Вы должны использовать длинное деление. Разделить числитель на знаменатель.

Таким образом, окончательный ответ равен 9.0005

Пример 02 :

Шаг 01 и Шаг 02

Шаг 03 –

Разделите 63 на 12, тогда частное равно 5, а остаток равен 3.

Ответ

Умножение смешанных чисел

Число, представляющее собой сумму целого числа и правильной дроби, записанной таким образом, определяется как смешанные числа

Примеры:

Чтобы умножить смешанные числа, необходимо выполнить четыре простых шага.

Шаг 1

– Преобразуйте смешанное число в неправильную дробь
Шаг 2 – Умножьте числители
Шаг 3 – Умножьте знаменатели
Шаг 4 – Выразите ответ в виде смешанного числа

Пример 01 :

Шаг 01

Запишите каждое смешанное число в виде неправильной дроби.

Шаг 02 и Шаг 03

Умножить числитель на числитель и знаменатель на знаменатель

Шаг 04

Преобразование неправильной дроби в смешанное число

Пример 02 :

Общие множители можно удалить следующим образом.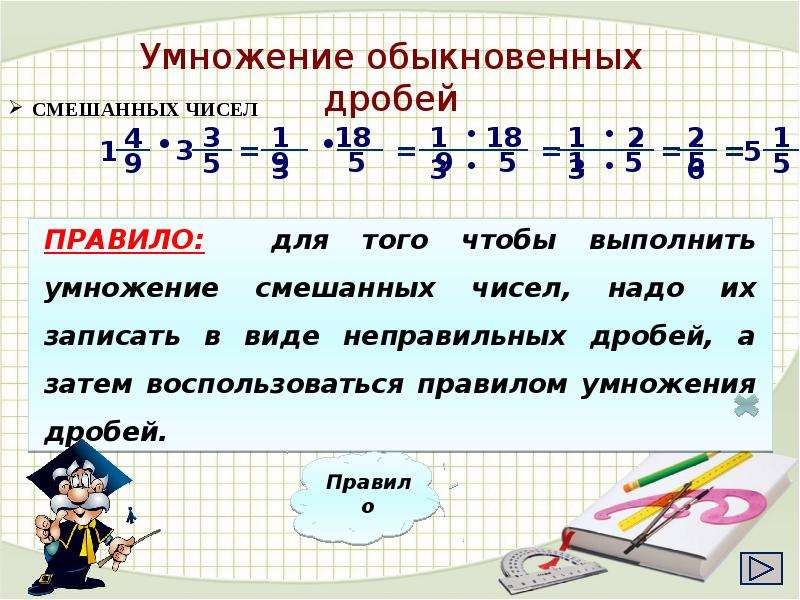

Пример 03 :

Теперь вы знаете, как умножать дроби. Также вам нужно потренироваться,

• как умножать смешанные дроби с разными знаменателями
• как умножать дроби на дроби
• как делить и умножать дроби
• как умножить две дроби

Если у вас возникли трудности с умножением двух дробей, оставьте комментарий ниже.

Умножение дробей – методы и примеры

Как умножать дроби?

В этой статье рассматриваются все шаги, которые необходимо знать при умножении дробей, в том числе умножение правильных и неправильных дробей, смешанная дробь и умножение дроби на целое число. Вот шаги для умножения дробей:

• Перемножьте числители и поместите произведение в верхнюю часть полученной дроби
• Перемножьте знаменатели и запишите результат в конец новой дроби
• Если возможно, сократите или упростите результат

Пример 1:

1/2 × 2/5

Шаг 1. Умножьте числители:

1/2 × 2/5 = 1 × 2 = 2

Шаг 2. Умножьте знаменатели:

5

2 5 = 10

Шаг 3. Упростите фракцию:

2/10 = 1/5

Пример 2:

1/3 × 9/16

Шаг 1. Умножение Числова:

1. /3 × 9/16 = 1 × 9 = 9

Шаг 2. Умножьте знаменатели:

3 × 16 = 48 
Шаг 3. Упростите дробь:

9/48 = 3/16

0 Пример 3:

Умножить: 4/5 x 7/9

Сначала умножьте числители, чтобы получить: 4 × 7 = 28,

Затем умножьте знаменатели, чтобы получить: 5 × 9 = 45.

Результат = 28/45

Поскольку у 28 и 45 нет общих делителей, эта дробь уже находится в наименьшем значении. Окончательный ответ 28/45.

Пример 4:

Умножить: 9/4 x 14/15

Вы можете решить все операции в одной строке математики. Помните, что числитель должен оставаться сверху, а знаменатель — внизу.

9/4 x 14/15 = (9 x 14)/(4 x 15) = 126/60

Умножение более чем двух дробей

Отмена — отличный способ сократить число умножений, включающих более двух множителей.

Пример 5:

Умножьте (1/2) × (2/3) × (3/4) × (4/5).

Начните с исключения общих множителей.

(1/2) × (2/3) × (3/4) × (4/5).

= 1/5

Как умножать дроби с целыми числами?

Дроби можно умножать на целые числа точно так же, как умножаются другие дроби. Самая важная процедура — переписать целое число в виде дроби, введя в знаменателе 1. Затем можно применить те же методы умножения дроби.

Целое число N можно преобразовать в дробь со знаменателем, равным 1, следующим образом:

N = N/1

Пример 6:

Умножить:3/5 × 60. 60 = 3/5 x 60/1

Умножьте числители:

3 x 60 = 180

Умножьте знаменатели:

1 x 5 = 5

Результат 180/5, Упростите ответ до наименьшего возможного условия.

180/5 = 36.

Как умножать смешанные дроби?

Смешанная фракция – это фракция, состоящая из целой и дробной частей. Например, 7½ — это смешанная дробь, состоящая из целого числа 7 и дробной части ½.