Дроби — как объяснить ребенку действия с дробями

Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.

Как объяснить суть дробей ребенку?

Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.

Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.

Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.

Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.

Что нужно знать о дробях?

1. Дробь — число нецелое, оно обозначает количество долей целого.

2. Дробь меньше целого.

3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.

Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.

Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.

Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.

Что такое смешанные дроби?

В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.

У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.

Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть.

А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.

Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.

Примеры:

• 14/5 = (5*2+4) / 5 = 2 4/5
• 21/6 = (6*3+ 3) / 6 = 3 3/6

Задание:

Выделите целую часть из неправильных дробей:

• 15/4,
• 22/12,
• 30/7.

Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.

Примеры:

• 3 1/8 = (3*8+1) / 8 = 25/8
• 7 4/9 = (7*9+4) / 9 = 67/9

Задание:

1.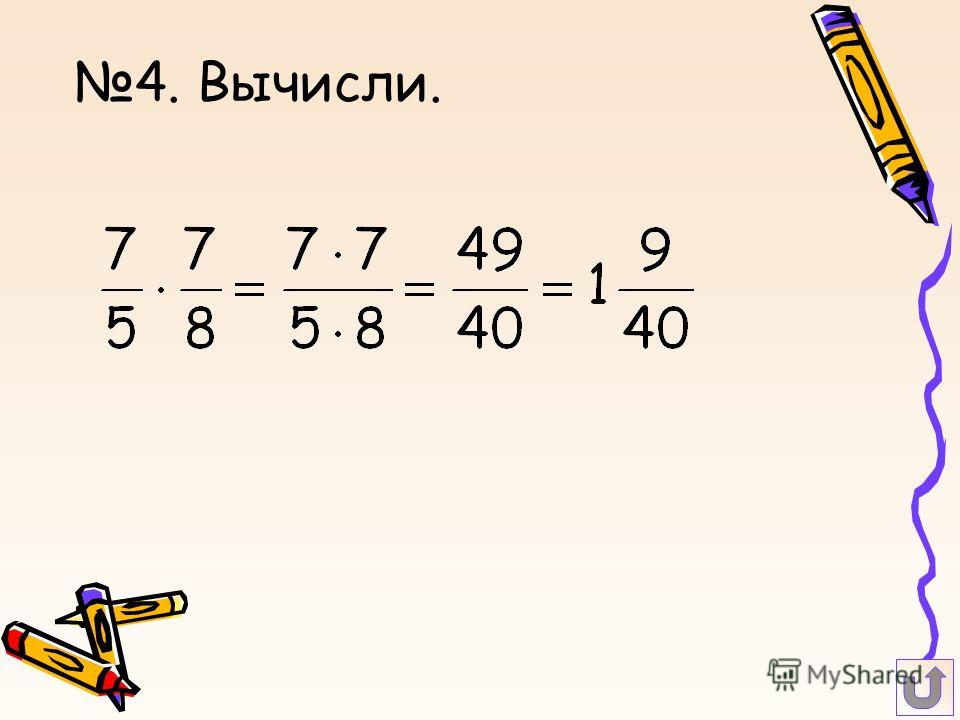 Преобразовать в смешанное число неправильную дробь:

• 27/4,
• 18/5,
• 45/7.

2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:

• 3 4/5;
• 12 7/11.

Десятичные дроби

Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.

Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.

Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».

Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления  применяется человечеством с самых древних времен. Она интуитивна понятна и проста.

Задание:

Преобразовать следующие дроби в десятичные:

• 8/10,
• 4/100,
• 7/1000.

Сокращение дробей

Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.

Пример 1. Сократить дробь 8/12

Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:

8/12 = 8:4 / 12:4 = 2/3

Пример 2.

Сократить дробь 10/25

Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:

10/25 = 10:5 / 25:5 = 2/5

Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.

Задание:

Сократите следующие дроби:

• 6/18,
• 20/40;
• 7/21.

Сложение дробей

Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.

Примеры:

• 1/7 + 2/7 = 3/7
• 3/8 + 5/8 = 8/8 = 1

Задание:

Выполни сложение дробей с одинаковыми знаменателями:

Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например:

3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.

Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:

• 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
• 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.

Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:

• 3*6 / 7*6 = 18/42;
• 2*7 / 6*7 = 14/42.

Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:

• 18/42 + 14/42 = 32/42

Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.

Задание:

Выполни сложение дробей с разными знаменателями:

 

Вычитание дробей

Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.

Пример:

7/9 — 2/9 = (7-2) / 9 = 5/9

Задание:

Выполни вычитание дробей с одинаковыми знаменателями:

Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.

Пример:

6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70

Задание:

Выполни вычитание дробей с разными знаменателями:

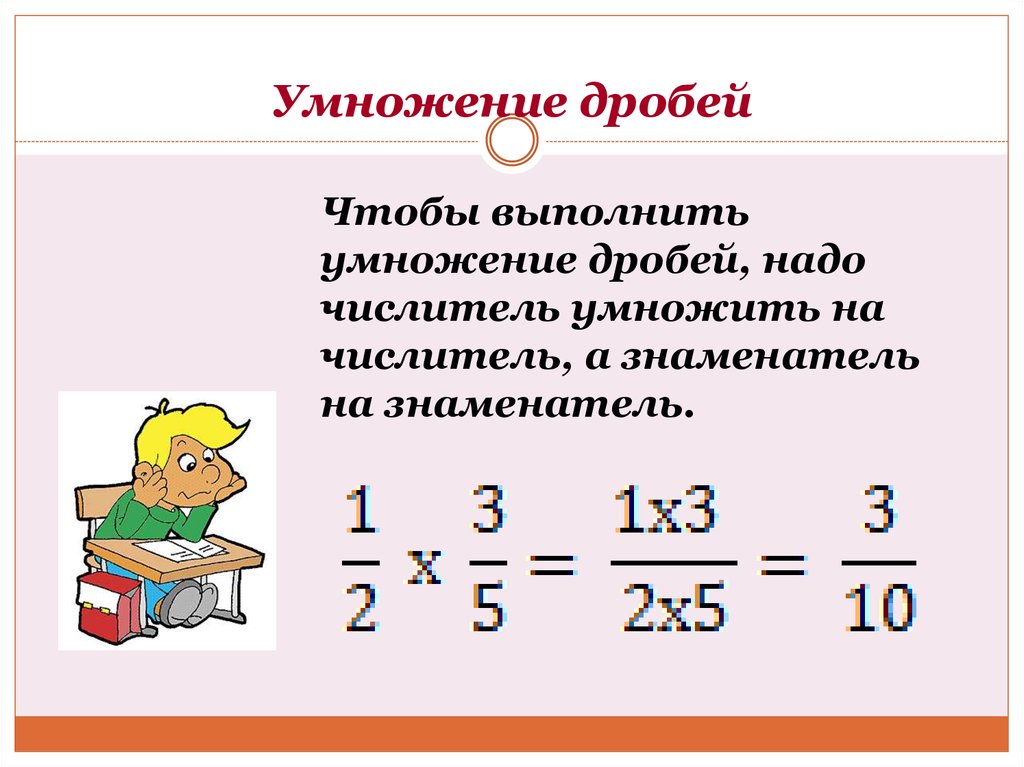
Умножение дробей

Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.

Умножение обыкновенных дробей

В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.

Пример:

2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10

Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.

Пример:

24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21

Умножение смешанных дробей

Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.

Пример:

4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24

Задание:

Выполните умножение дробей:

• 5/7 * 6/8;
• 6/11 * 2/3;
• 2 3/7 * 4 5/9;
• 4 6/7 * 7 9/10.

Деление дробей

Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый  знаменатель).

Пример:

4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7

Бывают ситуации, когда дробь нужно разделить на целое число.

В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.

Пример:

5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18

Задание:

Выполните деление дробей:

• 6/11 : 3;
• 7/15 : 2;
• 9/12 : 4.

Сравнение дробей

Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.

Пример:

1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.

Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.

Пример:

1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.

Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби.

Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.

Пример:

Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.

Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно.  Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.

Задание:

Определите, какие дроби изображены на рисунке, и сравните их:

Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.

Математика и логика для детей 7-13 лет

Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате

узнать подробнее

---

Читайте также:

• Таблица умножения для детей
• Как объяснить ребенку состав числа?

---

 

Умножение дробей через калькулятор онлайн

Дроби – это определенная форма исчисления, которая часто используется для выполнения различных математических операций. Дроби, как правило, используются для умножения, деления, вычитания или прибавления. Дробная черта обычно используется для того, чтобы разделить разные части дроби. Например, верхнюю часть обычно называют числителем, а нижнюю – знаменателем.

Все дроби могут отличаться своими особенностями и характеристиками. Например, бывают такие дроби, в которых числитель обычно больше знаменателя. В некоторых случаях бывают обратные ситуации. Такие дроби считаются неправильными, поэтому для работы с ними применяются некоторые другие правила, которые позволяют пользователю выполнить определенные операции. Бывают также смешанные дроби, которые представляют собой целое число и дробную часть. С ними можно также выполнять операции умножения по определенным правилам. Для этого нужно внимательно изучить алгоритм, чтобы предпринять соответствующие действия.

Умножение дробей – это классическая операция, которая используется для того, чтобы умножить одну дробь на другое. Для выполнения поставленной задачи следует знать определенные правила. Если следовать всем рекомендациям, можно легко выполнить все процедуры с минимальными затратами. Также можно воспользоваться специальными онлайн-калькуляторами, которые помогут решить задачу намного быстрее. При этом важно понимать базовые принципы выполнения операции, чтобы вникнуть в механику действий.

Как умножить дробь на дробь?

Это классический пример, который часто используется в математике для выполнения соответствующих действий. Чтобы выполнить подобную операцию, достаточно выполнить некоторые базовые рекомендации. Умножить дроби можно следующим образом. Для этого необходимо отдельно выполнить операцию умножения числителей и знаменателей. В результате должно получится новое число, которое будет результатом умножения числителя и знаменателя.

Часто в результате умножения простых дробей может возникнуть такая ситуация, когда дробь можно сократить. В таком случае значения действительно можно сократить для того, чтобы получить более общее значение. Также можно привести дроби к общему знаменателю, что поможет уменьшить полученное значение, а также упростить дальнейшие математические манипуляции. В качестве примера можно рассмотреть такие дроби:

7/15 х 10/9 = (7 х 10)/(15 х 9) = 70/135 = 14/27.

Как видно из описанного выше примера, сначала были выполнены операции отдельного умножения числителя и знаменателя. После этого Полученный результат был сокращен для получения более аккуратного и чистого результата, который можно использовать для выполнения дальнейших математических исчислений любой сложности. Если воспользоваться калькулятором умножения дробей, можно существенно упростить выполнение операции, минимизировав затраты.

Как умножить смешанные дроби?

Для выполнения операции со смешанными дробями, необходимо знать определенные правила. Для этого следует обратить внимание на следующие базовые правила:

• для начала необходимо смешанную дробь преобразовать в неправильную – для этих целей нужно выполнить несколько простых манипуляций;
• далее необходимо обязательно умножить отдельно числители и знаменатели, как это было выполнено в наиболее простом случае с обычными дробями;
• при необходимости полученный результат сокращают на определенное значение;
• если получена неправильная дробь в результате выполнения соответствующих манипуляций, тогда необходимо преобразовать его в смешанный – обычно эта процедура не требует много времени и усилий.

Если следовать всем перечисленным рекомендациям, получится быстро решить задачу с минимальными усилиями. Для большего понимания особенностей операции следует внимательно изучить пример:

2 1/2 х 1 2/3 = (2 х 2 + 1) / 2 х (1 х 3 + 2) / 3 = 5/2 х 5/3 = 25/6 = 4 1/6.

Как видно, операция умножения смешанных дробей выполняется по формуле, поэтому вы можете более подробно рассмотреть данный пример. Можно легко выполнить умножение дробей онлайн с помощью специального калькулятора, что позволит избежать наиболее распространенных ошибок, а также снизить риски получения неправильных результатов, что может оказать неприятные последствия в более сложных задачах.

Как умножить дробь на число?

Как правило, умножение дробей на целые числа практически ничем не отличается от обычной процедуры умножения дробей. Для выполнения операции необходимо преобразовать обычное число в дробь, приведя все к общему знаменателю для того, чтобы было проще выполнения операцию умножения. Для лучшего понимания данного примера необходимо обратить внимание на такой простой пример:

5 х 1 1/2 = 10/2 х 1 1/2 = 10/2 х 3/2 = (10 х 3)/2 = 30/2 = 15.

Если говорить проще, то в данном случае необходимо привести все к общему знаменателю для того, чтобы выполнить дальнейшие действия умножения дробей. Если возникают какие-либо трудности с самостоятельным решением подобных примеров, тогда лучше воспользоваться онлайн-калькулятором, что позволит существенно упростить операцию, а также уменьшить временные затраты при решении более сложных и трудоемких примеров.

Как умножать 3 и более дробей?

Если необходимо умножить три и более дробей, можно воспользоваться соответствующим правилом. Числитель будет равен произведению этих чисел, а знаменатель – произведению соответствующих знаменателей дробей. Умножение можно выполнить по формуле, поэтому достаточно следовать указанным правилам. В качестве примера можно рассмотреть следующее:

2/3 х 1/5 х 3/7 = (2 х 1 х 3)/(3 х 5 х 7) = 2/35.

Как видно, умножение такого рода достаточно простое, поэтому не требует никакого труда и усилий. Также можно легко воспользоваться специальным калькулятором для того, чтобы провести расчеты. Это поможет упростить задачу максимально и снизить временные затраты.

Правила умножения дробей обычно простые, поэтому каждый сможет с ними справиться. Для выполнения операции достаточно понимать базовые принципы выполнения транзакции. Также можно воспользоваться калькулятором для получения результатов и выполнения более простых математических вычислений.

Онлайн-калькулятор умножения дробей поможет существенно упростить многие задачи для любого студента, ученика или преподавателя, которому нужно быстро проверить тот или иной пример. Теперь больше не нужно задумываться о сложных операциях или самостоятельно придумывать какие-либо правила. Можно быстро воспользоваться всеми преимуществами, которые предлагаются.

Как умножать дроби — лучшие классы GED

Умножать дроби относительно легко. Если вы хотите умножить две дроби, вам просто нужно умножить и числители, и знаменатели.

Умножать дроби совсем не сложно. Это всего лишь два умножения, а затем, может быть, некоторое упрощение. Если вы будете умножать вершины и основания, все готово. Думаю, здесь у вас не возникнет проблем.

Онлайн-курсы GED — быстро и просто

Учитесь всего 1 час в день, чтобы получить диплом за 2 месяца .

Быстро подготовьтесь к сдаче теста GED.

Начало работы

Этот урок предоставлен Onsego GED Prep.

Следующий урок: Деление дробей

Транскрипция видео

Умножение простых дробей — Здесь мы начнем с некоторых простых дробей, которые имеют небольшие числа. Я думаю, вы помните таблицу умножения до \(10\) (десять).

Во-первых, давайте начнем с однозначных цифр. Вы можете заметить, что мы больше не беспокоимся об общих знаменателях. Как сказано, просто умножьте верхние числа, а затем умножьте нижние числа.

\(\frac{2}{5}* \frac{2}{3}\) равно ?

Онлайн-курсы GED от Onsego

Онлайн-курсы GED от Onsego. Просто, быстро и Просто.
Получите Onsego и сдайте GED в этом году.

Начало работы

• Сначала умножьте два числителя, чтобы получить новый числитель произведения. Итак: \(2 * 2 = 4\)

• Затем умножьте два знаменателя, чтобы получить новый знаменатель произведения. Итак: \(5 * 3 = 15\)

• Затем сложите вместе новый числитель и новый знаменатель. Итак: \(\frac{4}{15}\)

• Тогда упрости. Упрощение этой дроби невозможно.

Ответ: \(\frac{2}{5}* \frac{2}{3}\) равно \(\frac{4}{15}\)

Можем ли мы сделать три дроби таким же образом? Конечно вещь.

\(\frac{1}{2}* \frac{3}{4}* \frac{2}{5}\) равно ?

• Сначала умножьте три числителя, чтобы получить новый числитель произведения. Итак, \(1*3*2 = 6\)

• Затем умножьте три знаменателя, чтобы получить новый знаменатель произведения. Значит \(2*4*5 = 40\)

• Затем сложите вместе новый числитель и новый знаменатель. Итак, \(\frac{6}{40}\)

• Тогда упрости. \(6\) и \(40\) имеют общий делитель, равный двум \((2)\). Итак, разделите верх и низ на \(2\) (два), чтобы получить упрощенную дробь \(\frac{3}{20}\).

Ответ: \(\frac{1}{2}* \frac{3}{4}* \frac{2}{5}\) равно \(\frac{3}{20}\)

Умножение сложных дробей — Будут времена, когда вы застрянете с более сложными дробями. Итак, давайте попробуем один пример с более сложным умножением:

. \(\frac{5}{12}* \frac{5}{6}\) равно ?

• Сначала умножьте оба числителя, чтобы получить новый числитель. Итак, \(5 * 5 = 25\)

• Затем умножьте оба знаменателя, чтобы получить новый знаменатель. Итак, \(12 * 6 = 72\)

• Затем сложите вместе новый числитель и новый знаменатель. Итак, \(\frac{25}{72}\)

• Тогда, если возможно, упростите. Ну, для этой дроби нет возможности упростить.

Ответ: \(\frac{5}{12}* \frac{5}{6}\) равно \(\frac{25}{72}\)

Видишь? Мы используем тот же процесс. Даже когда у нас есть большие числа для умножения.

Умножение смешанных чисел — Вы помните, когда мы вычитали смешанные числа? Затем мы сначала составили неправильные дроби, прежде чем приступить к решению задачи. В этом первом примере мы будем использовать тот же процесс.

\(5\,\frac{1}{3} * 2\,\frac{4}{9}\) равно ?

• Сначала преобразуйте все множители в неправильные дроби:

Итак, \(5\,\frac{1}{3} = 5\,+\frac{1}{3} = \frac{15}{3} + \frac{1}{3} = \frac{16}{3}\)

И \(2\,\frac{4}{9} = 2\,+\frac{4}{9} = \frac{18}{9}+ \frac{4}{9} = \frac {22}{9}\)

• Затем умножьте два числителя. Итак, \(16 * 22 = 352\)

• Затем умножьте два знаменателя. Итак, \(3 * 9 = 27\)

• Затем запишите необработанный продукт, используя новый числитель и новый знаменатель. Итак, \(\frac{352}{27}\)

• Затем преобразуйте эту неправильную дробь в целое число.

Итак, \(\frac{352}{27} = 352 \div 27 = 13r1 = 13\, \frac{1}{27}\)

• Затем, если возможно, упростите дробь. Здесь упрощение невозможно.

Ответ: \(5\,\frac{1}{3} * 2\,\frac{4}{9} \) равно \(13\, \frac{1}{27}\)

Имейте в виду, что знаменатели не имеют значения, когда мы умножаем дроби. Эти три шага единственные:

1. Сначала умножьте все числители и получите новый числитель.
2. Затем умножьте знаменатели и получите новый знаменатель.
3. Затем просто ответьте, если необходимо.

 

Как умножать дроби. Полное руководство от Prep Expert

Независимо от того, сдаете ли вы SAT или ACT, вам нужно научиться умножать дроби.

Вы увидите множество вопросов, которые потребуют от вас не только понимания того, как работают дроби, но и умения умножать эти дроби за ограниченное время.

В разделах SAT Math у вас будет 75 секунд на вопрос в разделе Math (без калькулятора) и 87 секунд на вопрос в разделе Math (Calculator). В разделе ACT Math вы получаете 1 минуту на каждый вопрос.

Это означает, что вам нужно будет уметь быстро умножать дроби во время теста.

Хотя умножение дробей может показаться сложным, эту концепцию освоить намного проще, чем может показаться. Фактически, вы можете умножать дроби всего за четыре простых шага.

Это руководство поможет вам понять дроби и проведет вас через четыре шага, которые вам необходимо знать, чтобы умножить дроби.

Что такое дроби?

Проще говоря, дроби являются частью целого. Например, если вы съели половину пиццы, вы съели часть всей пиццы.

Когда вы видите определенные дроби, такие как ¾, ⅚ или ⅞, эти дроби означают, какая часть целого не была «потреблена». В приведенном выше примере, если вы съели половину пиццы, вы съели ½ пиццы, потому что есть две половинки, и вы съели одну из них. Это означает, что осталось ½ пиццы.

Дроби разбиваются на числители и знаменатели.

Числители — это числа в верхней половине дроби, которые представляют количество неиспользованного целого.

Например, в приведенной ниже дроби числитель равен 7.

Знаменатель числа представляет целое или сумму. В приведенном выше примере знаменатель равен 8.

Глядя на это через призму потребления пиццы, дробь ⅞ будет означать, что осталось семь кусков пиццы из пиццы, которая изначально состояла из восьми кусков.

Как только вы поймете, что обозначают числители и знаменатели, вам будет легче понимать дроби.

Если вы съедите 3 куска пирога, разрезанного на четыре части, у вас останется ¼ этого пирога. Если у вас есть целое число, например 1, и вы вычтете из него ⅓, то у вас останется ⅔ (⅔ + ⅓ = 1).

Благодаря этим знаниям у вас будет все необходимое, чтобы уметь умножать дроби, когда вы сталкиваетесь с такими задачами в разделах SAT или ACT по математике.

Умножение дробей

Умножение дробей требует четырех шагов:

1. Умножение числителей

Первое, что вам нужно сделать при умножении двух дробей, это умножить два числителя.

Например, если вы умножаете ⅔ и ⅞ , вам сначала нужно умножить 2 и 7, что даст вам 14 для вашего нового числителя.

2. Умножьте знаменатели

Затем вам нужно будет умножить два знаменателя. В этом случае вы должны умножить 3 на 8, что даст вам 24 в качестве нового знаменателя.

3. Создайте новую дробь

Теперь, когда у вас есть новый числитель и новый знаменатель, вам нужно создать новую дробь. Поместите новый числитель и знаменатель в формат дроби, как я сделал ниже.

2	*	7	=	14
3	8	24

4. Reduce your fraction

If possible, reduce your fraction to наименьшая возможная дробь, которая по-прежнему представляет то же количество целого.

Найдите наибольший общий делитель числителя и знаменателя новой дроби. В этом случае вам нужен наибольший общий множитель 14 и 24, который равен 2.

Получив этот множитель, разделите числитель и знаменатель на этот множитель. В случае приведенного выше примера у вас есть 14, деленное на 2, что равно 7 для вашего конечного числителя, и 24, деленное на 2, что составляет 12 для вашего окончательного знаменателя.

14	→	7
24	12

Это означает, что после сокращения вашей дроби ваш окончательный ответ после умножения ⅔ и ⅞ будет 7/12.

Выполнив четыре описанных выше шага, вы сможете легко умножать дроби.

Попробуйте выполнить эти шаги на нескольких примерах (мы дадим вам ответы, чтобы вы могли проверить свою работу).0010

Умножение ¾ и ⅚ 

Умножение ½ и ⅗ 

Когда вы закончите, проверьте свою работу ниже. У вас должны быть следующие ответы:

1. Ответ= ⅕ . После выполнения шагов 1-3 у вас должно было получиться 4/20, которое можно уменьшить до ⅕, используя наибольший общий делитель 4.
2. Ответ = ⅝ . После выполнения шагов 1-3 у вас должно было получиться 15/24, что можно уменьшить до ⅝, используя наибольший общий делитель 3.
3. Ответ = 3/10. После выполнения шагов 1-3 у вас должно получиться 3/10, которое нельзя уменьшить.

Умножение смешанных дробей

Иногда на SAT или ACT можно увидеть смешанные дроби.

Смешанные дроби имеют целое число с дробью.

Например, 7 ⅔ — это смешанная дробь.

При умножении смешанных дробей сначала нужно преобразовать смешанную дробь в обыкновенную.

Для этого нужно выполнить пару шагов:

1. Умножьте целое число на знаменатель

В приведенном выше примере 7 ⅔  вы умножите 7 и 3, что равно 21.

2. Добавьте ответ из шага 1 к числителю

, вы должны добавить 21 к 2, чтобы получить новый числитель 23. Это сделает вашу новую дробь такой:

3. Используйте эту новую дробь, чтобы умножить

Если бы вас попросили умножить 7 ⅔ и ¼, вы бы сначала преобразуйте 7 ⅔ в 23/3, а затем вы можете использовать шаги, упомянутые ранее, чтобы умножить эту дробь на ¼. (Кстати, вы должны получить 23/12 или 1 11/12).

Изучение SAT и ACT Советы по математике

Если вы хотите узнать о сложении, вычитании или делении дробей, а также о других математических понятиях, которые вы увидите в математических разделах SAT или ACT, я настоятельно рекомендую записаться на ACT или Курс подготовки к SAT или работа с частным репетитором.