Как умножить смешанное число на натуральное. Дробь. Умножение дробей обыкновенных, десятичных, смешанных
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Запишем сначала основное правило:
Определение 1
Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a / b и c / d это можно выразить как a b · c d = a · c b · d .
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 1 4 и 1 8 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8 · 4 = 32).
У нас получился закрашенный фрагмент со сторонами, равными 5 8 числовой единицы и 3 4 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 5 8 · 3 4 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15 , значит, общая площадь составляет 15 32 квадратных единиц.
Поскольку 5 · 3 = 15 и 8 · 4 = 32 , мы можем записать следующее равенство:
5 8 · 3 4 = 5 · 3 8 · 4 = 15 32
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как a b · c d = a · c b · d . Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Пример 1
Умножьте 7 11 на 9 8 .
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9 . У нас получилось 63 . Затем вычислим произведение знаменателей и получим: 11 · 8 = 88 . Составим их двух чисел ответ: 63 88 .
Все решение можно записать так:
7 11 · 9 8 = 7 · 9 11 · 8 = 63 88
Ответ: 7 11 · 9 8 = 63 88 .
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Пример 2
Вычислите произведение дробей 4 15 и 55 6 .
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10 .
Выполним сокращение дроби: 220 90 НОД (220 , 90) = 10 , 220 90 = 220: 10 90: 10 = 22 9 . В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 22 9 = 2 4 9 .
В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 22 9 = 2 4 9 .
Ответ: 4 15 · 55 6 = 2 4 9 .
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a · c b · d . Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Пример 3
Вычислите произведение 4 15 · 55 6 .
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
4 15 · 55 6 = 4 · 55 15 · 6
Поскольку как 4 = 2 · 2 , 55 = 5 · 11 , 15 = 3 · 5 и 6 = 2 · 3 , значит, 4 · 55 15 · 6 = 2 · 2 · 5 · 11 3 · 5 · 2 · 3 .
2 · 11 3 · 3 = 22 9 = 2 4 9
Ответ : 4 15 · 55 6 = 2 4 9 .
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
a b · c d = c d · a b = a · c b · d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Определение 2
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби a b на натуральное число n можно записать в виде формулы a b · n = a · n b .
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
a b · n = a b · n 1 = a · n b · 1 = a · n b
Поясним нашу мысль конкретными примерами.
Пример 4
Вычислите произведение 2 27 на 5 .
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10 . В силу правила, указанного выше, мы получим в результате 10 27 . Все решение приведено в этой записи:
2 27 · 5 = 2 · 5 27 = 10 27
Ответ: 2 27 · 5 = 10 27
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.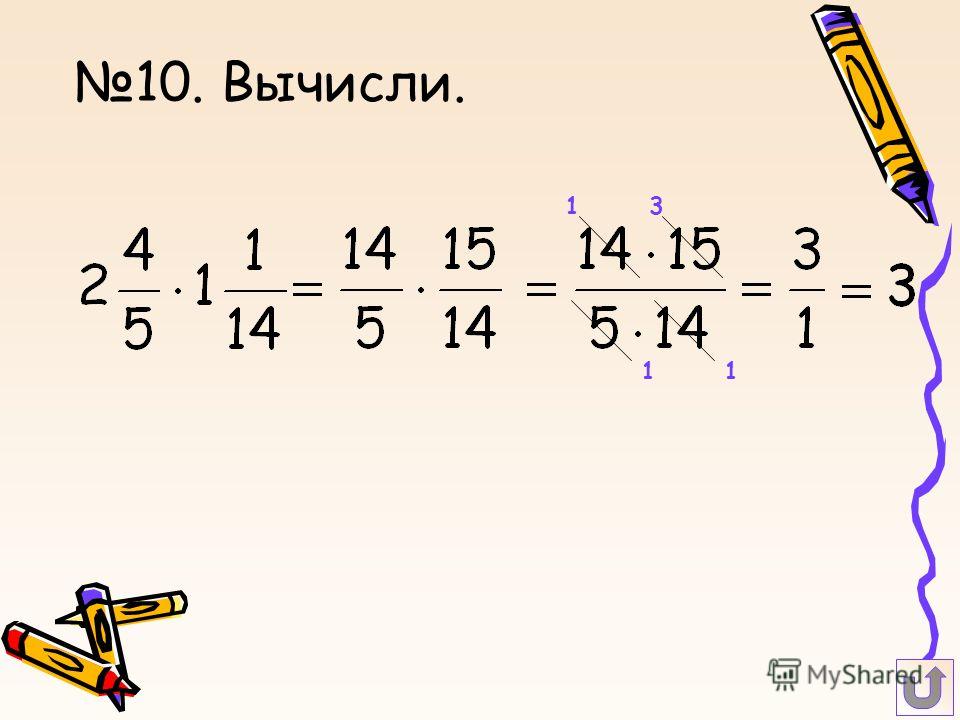
Пример 5
Условие: вычислите произведение 8 на 5 12 .
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 5 12 · 8 = 5 · 8 12 = 40 12 . Итоговая дробь имеет признаки делимости на 2 , поэтому нам нужно выполнить ее сокращение:
НОК (40 , 12) = 4 , значит, 40 12 = 40: 4 12: 4 = 10 3
Теперь нам осталось только выделить целую часть и записать готовый ответ: 10 3 = 3 1 3 .
В этой записи можно видеть все решение целиком: 5 12 · 8 = 5 · 8 12 = 40 12 = 10 3 = 3 1 3 .
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 5 12 · 8 = 3 1 3 .
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
a b · n = n · a b = a · n b
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Пример 6
Умножьте четыре обыкновенные дроби 1 20 , 12 5 , 3 7 и 5 8 .
Решение: для начала сделаем запись произведения. У нас получится 1 20 · 12 5 · 3 7 · 5 8 . Нам надо перемножить между собой все числители и все знаменатели: 1 20 · 12 5 · 3 7 · 5 8 = 1 · 12 · 3 · 5 20 · 5 · 7 · 8 .
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 1 · (2 · 2 · 3) · 3 · 5 2 · 2 · 5 · 5 · 7 (2 · 2 · 2) = 3 · 3 5 · 7 · 2 · 2 · 2 = 9 280
Ответ: 1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 9 280 .
Пример 7
Перемножьте 5 чисел 7 8 · 12 · 8 · 5 36 · 10 .
Решение
Для удобства мы можем сгруппировать дробь 7 8 с числом 8 , а число 12 с дробью 5 36 , поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
7 8 · 12 · 8 · 5 36 · 10 = 7 8 · 8 · 12 · 5 36 · 10 = 7 · 8 8 · 12 · 5 36 · 10 = 7 1 · 2 · 2 · 3 · 5 2 · 2 · 3 · 3 · 10 = = 7 · 5 3 · 10 = 7 · 5 · 10 3 = 350 3 = 116 2 3
Ответ: 7 8 · 12 · 8 · 5 36 · 10 = 116 2 3 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Умножение целого числа на дробь – несложная задача. Но есть тонкости, в которых вы, наверняка, разбирались в школе, но с тех пор забыли.
Как умножить целое число на дробь – немного терминов
Если вы помните, что такое числитель, знаменатель и чем отличается правильная дробь от неправильной – пропустите этот абзац. Он для тех, кто совсем забыл теорию.
Числитель – это верхняя часть дроби – то, что делим. Знаменатель – нижняя. Это то, на что делим.
Знаменатель – нижняя. Это то, на что делим.
Правильная дробь та, у которой числитель меньше знаменателя. Неправильной называется дробь, у которой числитель больше или равен знаменателю.
Как умножить целое число на дробь
Правило умножения целого числа на дробь очень простое – умножаем числитель на целое, а знаменатель не трогаем. Например: два умножить на одну пятую – получаем две пятых. Четыре умножить на три шестнадцатых – получится двенадцать шестнадцатых.
Сокращение
Во втором примере полученную дробь можно сократить.
Что это значит? Обратите внимание – и числитель, и знаменатель этой дроби делятся на четыре. Разделить оба числа на общий делитель и называется – сократить дробь. Получим три четвертых.
Неправильные дроби
Но, предположим, мы умножили четыре на две пятых. Получилось восемь пятых. Это неправильная дробь.
Её обязательно нужно привести к правильному виду. Для это нужно выделить из нее целую часть.
Здесь нужно использовать деление с остатком. Получаем единицу и три в остатке.
Одна целая и три пятых и есть наша правильная дробь.
Привести к правильному виду тридцать пять восьмых – задача чуть посложнее.Самое близкое к тридцати семи число, которое делится на восемь – это тридцать два. При делении получим четыре. Отнимем от тридцати пяти тридцать два – получим три. Итог: четыре целых и три восьмых.
Равенство числителя и знаменателя. А тут все очень просто и красиво. При равенстве числителя и знаменателя получается просто единица.
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
- Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Например:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.
Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.
В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример . Представить дробь 7 21 / 1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное — целое;
- и остаток — числитель дробной части, причем знаменатель остается неизменным.
Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .
Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.
Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.
Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.
Пример . Найти произведение 4½ и 6 2 / 5.
Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример . Вычислить произведение 5 / 8 и 12.
Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Ответ : 7 1 / 2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример . Найти произведение 9 5 / 6 и 9.
Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Ответ : 88 1 / 2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1 . Найти произведение 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2 . Найти произведение 3,9 и 1000.
Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ : 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1 . Найти произведение 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2 . Найти произведение 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.
Урок 17. Умножение дробей | Уроки математики и физики для школьников и родителей
ВИДЕО УРОК
Здесь многое придётся делать по–новому, потому что действие умножение дробей во многом отличается от умножения над натуральными числами.
Умножение обыкновенной дроби на обыкновенную дробь.
ПРИМЕР:
Найти значение выражения:
Получили ответ. Сокращаем данную дробь. Дробь можно сократить на 2. Тогда окончательное
решение примет следующий вид:
Сокращаем данную дробь. Дробь можно сократить на 2. Тогда окончательное
решение примет следующий вид:
Это действие можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть а пиццы:
Как взять от этой половины две третьих ?
Сначала нужно поделить эту половину на три равные части:
И взять от этих трёх кусочков два:
У нас получится одна треть всей пиццы. Вспомните как выглядит пицца, разделённая на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идёт об одном и том же размере пиццы. Поэтому значение выражения равно:
Произведением дробей называют такую дробь, числитель которой равен произведению числителей данных дробей, а знаменатель – произведению их знаменателей.
Чтобы умножить дробь на дробь, нужно умножить числитель на числитель, а знаменатель на знаменатель и первое произведение сделать числителем, а второе – знаменателем произведения.
При умножении следует делать (если возможно) сокращение.
ПРИМЕР:
Приведём пример, иллюстрирующий правило умножения обыкновенных дробей.
ПРИМЕР:
Рассмотрим квадрат со стороной 1 ед., при этом его площадь равна 1 ед2.
Разделим этот квадрат на равные прямоугольники со сторонами 1/4 ед. и 1/8 ед., при этом исходный квадрат будет состоять из
4 ∙ 8 = 32
прямоугольников. Следовательно, площадь каждого прямоугольника составляет 1/32 долю площади исходного квадрата, то есть она равна 1/32 ед2. Теперь закрасим часть исходного квадрата.
Следовательно, площадь каждого прямоугольника составляет 1/32 долю площади исходного квадрата, то есть она равна 1/32 ед2. Теперь закрасим часть исходного квадрата.
Стороны закрашенного прямоугольника равны 5/8 ед. и 3/4 ед., значит, его площадь равна произведению дробей 5/8 и 3/4, то есть,
Но закрашенный прямоугольник состоит из 15 маленьких прямоугольников, значит его площадь равна 15/32 ед2. Следовательно,
Так как
5 ∙ 3 = 15
8 ∙ 4 = 32,
то последнее равенство можно переписать как
что подтверждает формулу умножения обыкновенных дробей.
С помощь этого правила умножения можно умножать и правильные и неправильные дроби, и дроби с одинаковыми знаменателями, и дроби с разными знаменателями.
ПРИМЕР:
Выполните умножение обыкновенной дроби 7/11 на обыкновенную дробь 9/8.
РЕШЕНИЕ:
Произведение числителей умножаемых дробей 7 и 9 равно 63, а произведение знаменателей 11 и 8 равно 88. Таким образом, умножение обыкновенных дробей 7/11 и 9/8 даёт дробь 63/88.
Краткая запись решения:
ОТВЕТ: 63/88
Помните про сокращение полученной дроби, если в результате умножения получается сократимая дробь, и при выделении целой части из неправильной дроби.
ПРИМЕР:
Выполните умножение обыкновенной дроби 4/15 на обыкновенную дробь 55/6.
РЕШЕНИЕ:
Применим правило умножения обыкновенных дробей:
Очевидно, что полученная дробь сократима. Выполним сокращение дроби.
НОД (220; 90) = 10.
Осталось выделить целую часть из полученной неправильной дроби:
Краткая запись решения:
ОТВЕТ: 24/9
Сокращение дроби можно проводить до вычисления произведений числителей и произведений знаменателей умножаемых дробей, то есть когда дробь имеет вид
Для этого числа
a, b, c, d
заменяют их разложениями на простые множители, после чего сокращаются одинаковые множители числителя и знаменателя.
Решим предыдущий пример другим способом.
ПРИМЕР:
Выполните умножение обыкновенной дроби 4/15 на обыкновенную дробь 55/6.
РЕШЕНИЕ:
Применим правило умножения обыкновенных дробей:
Так как
4 = 2 ∙ 2,
55 = 11 ∙ 5,
15 = 5 ∙ 3,
6 = 2 ∙ 3, то
Теперь сокращаем общие простые множители:
Вычислим произведения в числителе и знаменателе дроби, после чего выделим целую часть из неправильной дроби.
Краткая запись решения:
ОТВЕТ: 24/9
Для умножения дробей характерно переместительное свойство, то есть умножаемые дроби можно менять местами:
Умножение обыкновенной дроби на натуральное число.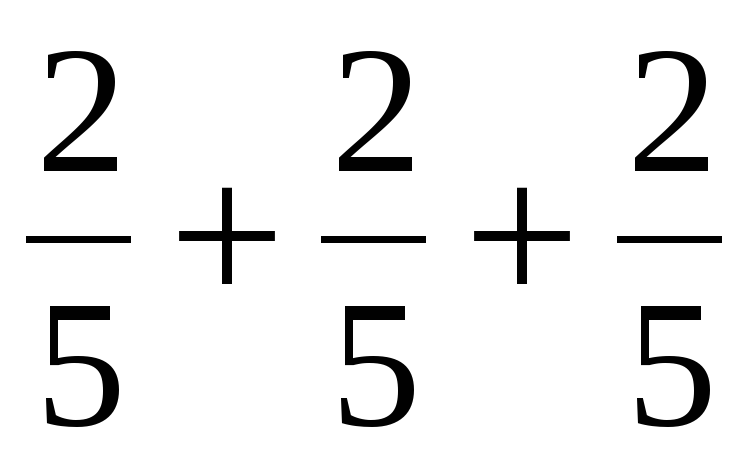
Смысл умножения обыкновенной дроби на натуральное число выясняется из следующего определения: умножить обыкновенную дробь (множимое) на натуральное число (множитель) – значит найти эту дробь множимого.
Чтобы умножить натуральное число на дробь, надо умножить натуральное число на числитель дроби и это произведение сделать числителем, а знаменателем подписать знаменатель данной дроби.
С помощью букв правило умножение дроби a/b на натуральное число n имеет вид:
Эта формула следует из формулы умножения двух обыкновенных дробей:
Представив натуральное число как дробь со знаменателем 1, получим:
Если учесть, что целое число представляет собой дробь со знаменателем 1, то умножение дроби на целое число и целого числа на дробь можно выполнить по этому же правилу.
ПРИМЕР:
ПРИМЕР:
ПРИМЕР:
Выполните умножение дроби 2/27 на 5.
РЕШЕНИЕ:
Умножение числителя 2 на число 5 даёт 10, поэтому в силу правила умножения дроби на натуральное число, произведение 2/27 на 5 равно дроби 10/27.
ОТВЕТ: 10/27
При умножении дроби на натуральное число полученную дробь часто приходится сокращать, а если она ещё и неправильная, то представить её в виде смешанной дроби.
ПРИМЕР:
Выполните умножение дроби 5/12 на 8.
РЕШЕНИЕ:
По формуле умножения дроби на натуральное число имеем:
Полученная дробь сократима. Выполним сокращение дроби. Так как
НОК (40: 12) = 4, то
Осталось выделить целую часть:
Краткое решение примера:
Сокращение можно было провести, заменив числа в числителе и знаменателе их разложением на простые множители. В этом случае решение выглядело бы так:
ОТВЕТ: 31/3
Умножение дроби на натуральное число обладает переместительным свойством, то есть произведение дроби на натуральное число, равно произведению этого натурального числа на дробь.
Умножение смешанных чисел.
Чтобы перемножить смешанные числа, нужно предварительно обратить их в неправильные дроби и потом перемножить по правилу умножения дроби на дробь.
ПРИМЕР:
Если же перемножают смешанное число на целое, то проще множить отдельно целую и дробную части.
ПРИМЕР:
Законы и правила умножения натуральных чисел справедливы и для дробей. Их использование упрощает устные и письменные вычисления.
Произведение дробных чисел подчиняется переместительному, сочетательному и распределительному закону.
Если один из сомножителей – целое число, то умножение может быть выполнено на основании распределительного закона.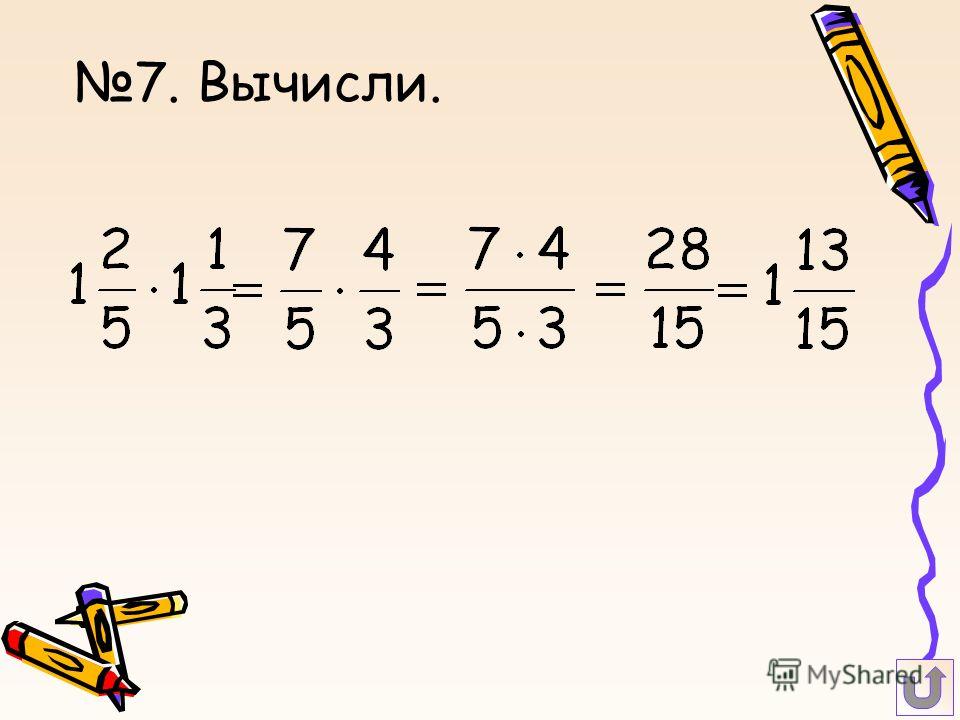
ПРИМЕР:
42/5 ∙ 3 = (4 + 2/5) ∙ 3
= 4 ∙ 3 + 2/5 ∙ 3
= 12 + 6/5 = 131/5.
ПРИМЕР:
97/8 ∙ 8 = 9 ∙ 8 + 7/8 ∙ 8
= 72 + 7 = 79.
Если один из двух сомножителей увеличим в несколько раз, а другой оставим без изменения, то произведение увеличится во столько же раз.
Если один из сомножителей уменьшим в несколько раз, а другой оставим без изменения, то произведение уменьшится во столько же раз.
Умножение трёх и большего количества дробей.
Свойства умножения натуральных чисел распространяются и на умножение дробей.
Переместительное и сочетательное свойства умножения позволяют однозначно определить умножение трёх и большего количества дробей. При этом всё происходит по аналогии с умножением трёх и большего количества натуральных чисел. В частности, дроби и натуральные числа в произведении можно для удобства вычисления переставлять местами, а при отсутствии скобок, указывающих порядок выполнения действий, можно самим расставить скобки любым из доступных способов.
ПРИМЕР:
3/4 ∙ (79/31 ∙ 11/3) =
(3/4 ∙ 4/3) ∙ 79/31 =
1 ∙ 79/31 = 79/31.
ПРИМЕР:
(122/5 ∙ 435/17) ∙ 5/31 =
(122/5 ∙ 5/31) ∙ 435/17
= 2 ∙ 435/17 = 8610/17.
ПРИМЕР:
Выполните умножение четырёх обыкновенных дробей:
1/20, 12/5, 3/7, 5/8.
РЕШЕНИЕ:
Запишем произведение, которое нам нужно вычислить:
В силу правила умножения дробей записанное произведение равно дроби, числитель которой равен произведению числителей всех дробей, а знаменатель – произведению знаменателей.
Прежде чем вычислить произведения в числителе и знаменателе, целесообразно заменить все множители их разложениями на простые множители и провести сокращение:
ОТВЕТ: 9/280
ПРИМЕР:
Выполните умножение пяти чисел:
РЕШЕНИЕ:
В этом произведении удобно сгруппировать дробь 7/8 с числом 8, а число 12 с дробью 5/36, это позволит упростить вычисления, так как при такой группировке очевидно сокращение. Имеем
ОТВЕТ: 116 2/3
Умножение 0,125. Умножение дроби на натуральное число. Умножение десятичных дробей на натуральное число.
- Альфашкола
- Статьи
- Как легко умножить на 0,125
В этой статье ты узнаешь как легко умножить любое число на \(0,125\), для этого тебе даже не понадобится калькулятор. \(0,125-\) это десятичная дробь, приведём её к виду обыкновенной дроби:
При умножении на \(0,125\) можно заменить умножением на \(\frac{1}{8}\). Обратная дробь одной восьмой \(-8\) То есть для того чтобы умножить на \(0,125\) надо разделить на \(8.\) Легко не так ли?
Пример 1. Умножьте \(16\) на \(0,125\).
Решение: \(16*0,125=16*\frac{1}{8}=16:8=2\)
Ответ: \(2\).
Пример 2. Умножьте \(32\) на \(0,125\).
Решение: \(32*0,125=32*\frac{1}{8}=32:8=4\)
Ответ: \(4\).
Пример 2. Умножьте \(72\) на \(0,125\).
Решение: \(72*0,125=72*\frac{1}{8}=72:8=9\)
Ответ: \(9\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Севиль Эннановна Калафатова
Репетитор по математике
Стаж (лет)
Образование:
Крымский федеральный университет им. Вернадского
Вернадского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 классов. Развитие логического и аналитического мышления, дисциплина ума — следствия изучения математики. Буду рада помочь успешно усвоить материал школьной программы. Стану другом и наставником для вашего ребёнка! Приглашаю каждого на занятия!
Анастасия Александровна Чарута
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный педагогический университет им. М. Танка
М. Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-4 классов. Математика — отличный тренажер! Только тренирует он не мышцы, а наш ум! А я могу Вам помочь с тренировками, ведь изучать математику не всегда бывает легко. На занятиях будем развивать память и мышление, используя различные интересные задания и игры!
Людмила Иннокентьевна Пьянкова
Репетитор по математике
Стаж (лет)
Образование:
Пермский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 4 -7 классов. Хочу, чтобы математика стала вашим любимым предметом! А нравиться она начинает, когда становится понятной. Помогу понять!
Хочу, чтобы математика стала вашим любимым предметом! А нравиться она начинает, когда становится понятной. Помогу понять!
Похожие статьи
- Периметр ромба
- ИВТ (Информатика и Вычислительная Техника): МФТИ
- РУДН (Архитектура): проходной балл
- ОГЭ по математике, базовый уровень. Простейшие уравнения
- ЕГЭ по математике, базовый уровень. Планиметрия. Равнобедренный треугольник (вариант 1)
- Задачи на исследование функций
- 10 способов помириться с другом/подругой
- Маленькие герои Великой Отечественной войны
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Умножение дробей, нахождение дроби от числа
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Умножение обыкновенных дробей
Умножение обыкновенных дробей
2. Нахождение дроби от числа
Умножение обыкновенных дробей
Правило умножения обыкновенных дробей: При умножении двух дробей получается дробь, в числителе которой записывается произведение числителей данных дробей, а в знаменателе – произведение знаменателей:
$\frac{a}{b}\cdot\frac{c}{d}=\frac{a\cdot c}{b\cdot d}$
Замечание 1
Данное правило можно использовать для умножения правильных и неправильных дробей, дробей с одинаковыми и разными знаменателями.
Пример 1
Умножить обыкновенную дробь $\frac{12}{23}$ на обыкновенную дробь $\frac{4}{5}$.
Решение.
Произведение числителей данных дробей равно $12\cdot 4=48$.
Произведение знаменателей равно $23\cdot 5=115$.
Найдем произведение дробей $\frac{12}{23}$ и $\frac{4}{5}$:
$\frac{12}{23}\cdot \frac{4}{5}=\frac{12\cdot 4}{23\cdot 5}=\frac{48}{115}$.
Ответ: $\frac{48}{115}$.
Замечание 2
Если в результате умножения дробей получают сократимую дробь или неправильную дробь, необходимо сократить дробь или выделить целую часть.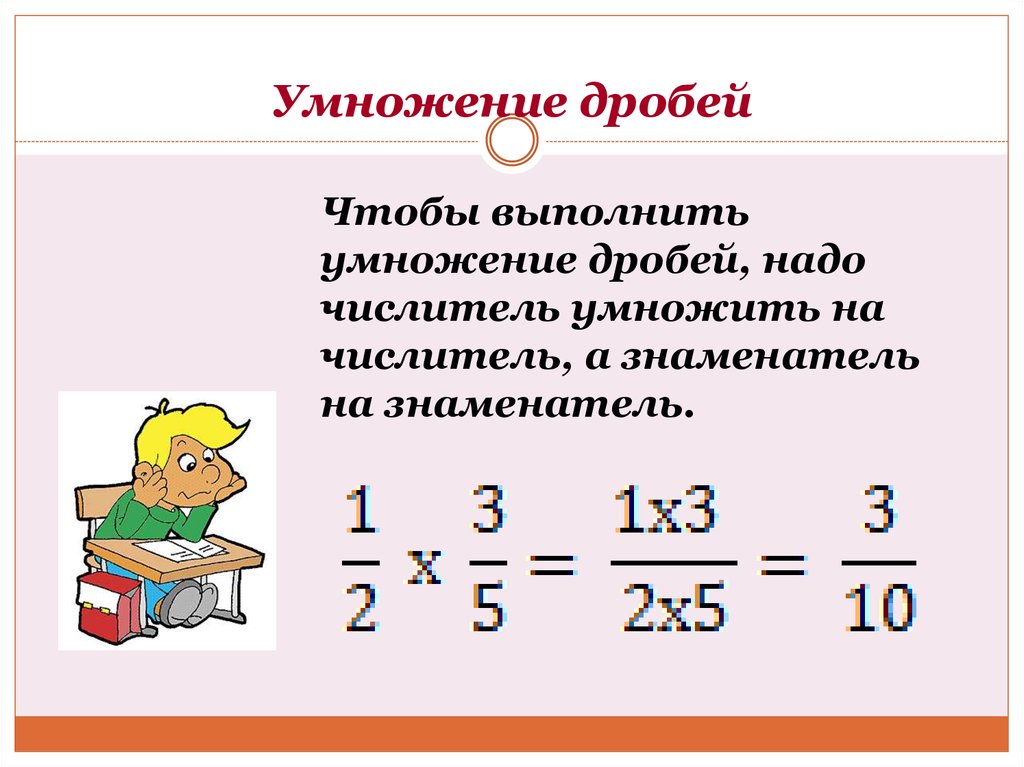
Пример 2
Выполнить умножение дробей $\frac{5}{17}$ и $\frac{43}{4}$.
Решение.
По правилу умножения обыкновенных дробей получим:
$\frac{5}{17}\cdot \frac{43}{4}=\frac{5\cdot 43}{17\cdot 4}=\frac{215}{68}$
Получили неправильную дробь, из которой выделим целую часть:
$\frac{215}{68}=\frac{3 \ 11}{68}$
Ответ: $\frac{3 \ 11}{68}$.
Замечание 3
Если хотя бы одна из умножаемых дробей сократима, можно выполнить ее сокращение до умножения. Для этого числители и знаменатели раскладывают на простые множители и сокращают одинаковые множители числителя и знаменателя.
Пример 3
Вычислить произведение дробей $\frac{6}{42}\cdot {49}{9}$.
Решение.
Используя правило умножения обыкновенных дробей, найдем:
$\frac{6}{42}\cdot \frac{49}{9}=\frac{6\cdot 49}{42\cdot 9}$.
Разложим числитель и знаменатель дроби на простые множители:
$\frac{6\cdot 49}{42\cot 9}=\frac{2\cdot 3\cdot 7\cdot 7}{2\cdot 3\cdot 7\cdot 3\cdot 3}$.
Сократим одинаковые множители в числителе и знаменателе:
$\frac{2\cdot 3\cdot 7\cdot 7}{2\cdot 3\cdot 7\cdot 3\cdot 3}=\frac{7}{9}$.
Ответ: $\frac{7}{9}$.
При умножении дробей можно использовать переместительное свойство умножения:
Замечание 4
При изменении мест множителей их произведение не изменится:
$\frac{a}{b}\cdot {c}{d}=\frac{c}{d}\cdot {a}{b}=\frac{a\cdot c}{b\cdot d}$
Нахождение дроби от числа
Замечание 5
Чтобы найти дробь от числа, нужно умножить число на эту дробь.
Правило умножения обыкновенной дроби на натуральное число:
В результате умножения дроби на натуральное число получают дробь, у которой числитель равен произведению числителя дроби и натурального числа, а знаменатель остается неизменным:
$\frac{a}{b}\cdot n=\frac{a\cdot n}{b}$
Если представить натуральное число $n$ в виде неправильной дроби $\frac{n}{1}$ и применить правило умножения двух дробей, получим:
$\frac{a}{b}\cdot n=\frac{a}{b}\cdot \frac{n}{1}=\frac{a\cdot n}{b\cdot 1}=\frac{a\cdot n}{b}$
Пример 4
Выполнить умножение обыкновенной дроби $\frac{7}{13}$ на натуральное число $8$.
Решение.
При умножении числителя дроби $7$ на натуральное число $8$ получим $56$. Воспользуемся правилом умножения дроби на число:
$\frac{7}{13}\cdot 8=\frac{56}{13}$
Т.к. полученная дробь – неправильная, выделим целую часть:
$\frac{56}{13}=4 \frac{4}{13}$
Ответ: $\frac{7}{13}\cdot 8=4 \frac{4}{13}$.
Замечание 6
Если в результате умножения дроби на число получают сократимую дробь или неправильную дробь, необходимо сократить дробь или выделить целую часть.
Пример 5
Умножить обыкновенную дробь $\frac{4}{25}$ на натуральное число $5$.
Решение.
Используя правило умножения обыкновенной дроби на натуральное число, получим:
$\frac{4}{25}\cdot 5=\frac{4\cdot 5}{25}=\frac{20}{25}$.
В результате умножения получили сократимую дробь $\frac{20}{25}$ (признак делимости на $5$). Выполним ее сокращение:
$\frac{20}{25}=\frac{20\div 5}{25\div 5}=\frac{4}{5}$.
Краткая запись решения:
$\frac{4}{25}\cdot 5=\frac{4\cdot 5}{25}=\frac{20}{25}=\frac{4}{5}$.
Ответ: $\frac{4}{25}\cdot 5=\frac{4}{5}$.
Замечание 7
Если умножаемая дробь сократима или натуральное число и знаменатель дроби имеют общий делитель, можно выполнить сокращение дроби, разложив ее числитель и знаменатель на простые множители и сократив одинаковые множители числителя и знаменателя.
Пример 6
Вычислить произведение $\frac{6}{42}\cdot 49$.
Решение.
Используя правило умножения дроби на число, найдем:
$\frac{6}{42}\cdot 49=\frac{6\cdot 49}{42}$.
Разложим числитель и знаменатель дроби на простые множители:
$\frac{6\cdot 49}{42\cdot 9}=\frac{2\cdot 3\cdot 7\cdot 7}{2\cdot 3\cdot 7}$.
Сократим одинаковые множители в числителе и знаменателе:
$\frac{2\cdot 3\cdot 7\cdot 7}{2\cdot 3\cdot 7}=\frac{7}{1}=7$.
Ответ: $1$.
При умножении дроби на натуральное число можно использовать переместительное свойство:
Замечание 8
При изменении мест множителей их произведение не изменится:
$\frac{a}{b}\cdot n=n\cdot \frac{a}{b}=\frac{a\cdot n}{b}$.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 08.06.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
| Табличка на двери |
Конспект урока по математике «Умножение дробей» 6 класс
Урок математики по теме: «Умножение дробей». 6-й класс
Цели урока:
Обучающие: 1)сформулировать правило умножения обыкновенной дроби на натуральное число, правило умножения обыкновенных дробей;
2)вырабатывать у учащихся навыки применения правил при выполнении действий.
Развивающие:
1)развитие аналитического мышления учащихся;
2)формирование умения выделять главное и обобщать.
Воспитывающие:
формирование умения организовать свою деятельность.
Тип урока: изучение нового материала.
Задачи урока:
настроить детей на рабочий лад;
повторить правила сложения, вычитания дробей; сложения и вычитания смешанных чисел;
проверить умение детей выполнять сложение и вычитание дробей;
сформулировать правило умножения обыкновенной дроби на натуральное число; правило умножения обыкновенных дробей;
отрабатывать навыки умножения дроби на натуральное число, дроби на дробь;
проверить уровень усвоения материала.
По завершении урока учащийся должен:
Знать: правило умножения дроби на натуральное число; дроби на дробь.
Уметь: умножать дробь на натуральное число, дробь на дробь.
Методы организации учебной деятельности: проблемный, объяснительно-иллюстративный, использование ИКТ.
Оборудование: учебник математики 6-й класс, автор Н. Л. Виленкин; сборник математических диктантов; мультимедийный проектор.
ХОД УРОКА
1. Организационный момент (2 мин.) (Приложение. Слайд 2)
Учитель. Эпиграф нашего урока “О, сколько нам открытий чудных готовит просвещенья дух…”. А были ли открытия в вашей жизни? Что значат слова “Я сделал открытие”? Если человек своим трудолюбием, упорством достигает истины в чем-либо, то это и есть его открытие. По этому поводу Борис Пастернак сказал:
Во всем мне хочется дойти
До самой сути.
В работе, в поисках пути,
В сердечной смуте.
До сущности истекших дней
До их причины,
До оснований, до корней,
До сердцевины
Всё время схватывая нить
Судеб, событий,
Жить, думать, чувствовать, любить
Свершать открытья.
– На сегодняшнем уроке мы тоже попытаемся совершить маленькое, но самостоятельное открытие. Для этого надо быть настойчивым и внимательным.
2. Вводный контроль (3 мин.)
Учитель. Начнём урок с повторения. (Приложение. Слайд 3)
Слайд 3)
1 вариант 2 вариант
1) 2-2/3 =1 1/3 п 1)5-7/12 =4 5/12 л
2) 2 ½-1/3 =2 1/6 л 2) 3 1/5-1/7=3 2/35 о
3) 3 1/4+4 1/5 =7 9/20 а 3) 2 1/8+3 1/3=5 11/24 м
4) 2/5-1/3 =1/15 н 4) 2/3+1/9 =7/9 а
5) 1/6+5/12=7/12 у 5) 5-3 5/6=1 1/6 т
6) 2-1 11/12 =1/12 д 6) 3/5+6/25 =21/25 ь
ПЛАНУД ЛОМАТЬ
Сначала на слайде видны примеры и таблицы ответов, затем ответы и слова.
Рассказывает учащийся, подготовленный дома.
Первое понятие дроби появилось в древнем Египте много веков назад. У многих народов дроби называли ломаными числами. Этим названием пользуется и автор первого русского учебника по математике Л.Ф.Магницкий. В русском языке слово «дробь» появилось лишь в VIII веке.
Происходит слово “дробь” от слова “дробить, разбивать, ломать на части”. Современное обозначение дробей берет своё начало в древней Индии; дробная черта появилась в записи дробей лишь около 300 лет назад. Название “числитель” и “знаменатель” ввёл в употребление греческий монах учёный-математик Максим Плануд. Для запоминания: “Человек стоит на земле”. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка “попасть в дроби”, что означает попасть в трудное положение.
Для запоминания: “Человек стоит на земле”. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка “попасть в дроби”, что означает попасть в трудное положение.
Учитель: задача сегодняшнего урока – доказать, что дроби не смогут поставить вас в трудное положение.
Какие правила вы применяли?
Как читается правило сложения, сравнения, вычитания дробей с разными знаменателями?
Как выполнить сложение смешанных чисел?
Как выполнить вычитание смешанных чисел?
Повторяем правила сложения, сравнения, вычитания дробей с разными знаменателями. Учащиеся формулируют правила.
3. Сообщение темы урока (4 мин.)
Учитель. Какие действия вы умеете выполнять и знаете правило, как это сделать? Какие действия с обыкновенными дробями нам предстоит научиться выполнять?
Дети. Действия с дробями. Мы умеем сравнивать, складывать, вычитать дроби с разными знаменателями и эти же действия со смешанными числами.
Учитель. Сегодня на уроке будем работать над темой:
«Умножение дробей». Сформулируем правило умножения дробей, научимся его применять.
Подготовительная работа (Приложение. Слайд 4)
Замените сумму произведением:
5 + 5 + 5 = 5 • 3
2 + 2 + 2 + 2 + 2 + 2 + 2 = 2 • 7
а + а + а + а + а + а = а•6
Замените произведение суммой (Приложение. Слайд 5):
3 • 5 = 3 + 3 + 3 + 3 + 3
8 • 2 = 8 + 8
b • 3 = b + b + b
4. Изучение нового материала (10 мин.)
Задача. (Приложение. Слайд 6)
Скорость улитки 2/3 см /мин. Какое расстояние проползёт улитка за 4 минуты?
– Что неизвестно в задаче?
– Как найти расстояние, зная скорость и время? (Скорость умножить на время)
– Мы умножать не умеем, а только складывать и вычитать.
– Как быть?
– Как быстрее получить? (Заменить произведение суммой одинаковых слагаемых).
2/3• 4 =2/3 +2/3+2/3+2/3 =8/3 = 2 2/3 см.
Что значит умножить 2/3 на 4? (Найти сумму четырёх слагаемых каждое из которых равно 2/3).
Сравните 2/3 • 4 и 8/3 , что интересного заметили? (Числитель дроби 8/3 равен произведению числителя дроби 2/3 и числа 4, а знаменатель остался без изменения.)
Попробуем сформулировать правило умножения дроби на натуральное число.
Дети выдвигают версии правила умножения дроби на натуральное число. (Приложение. Слайд 7)
– Чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменений.
Записывают в буклет правило умножения дроби на число (начало правила уже вписано, нужно только закончить).
5. Закрепление новых знаний (10 мин.)
Задача: отработать навыки умножения дроби на натуральное число и дроби на дробь. (Приложение. Слайд 8)
№ 427 б, в – на доске, г – с комментированием на месте, ж, з – самостоятельно.
б) 5/18*12=5*12/18=10/3=3 1/3
в) 7/15*40=7*40/15=56/3=18 2/3
г) 7/8*24=7*24/8=21
ж) 2/3*1=2/3
з)19/20*0=0 .
Физкультминутка (3 мин. )
)
Сокращение дробей. Если верно – поднимаем руки вверх, неверно – делаем круговые движения головой. (Приложение. Слайд 9)
6/8 = 1/3; 21/49 = 3/8; 15/20 = 3/4; 16/32 = 1/3.
6. Работа с учебником (5 мин.)
Цель: научиться умножать дробь на дробь.
– Самостоятельно рассмотрите по учебнику задачу 2 на стр 71. Попробуйте сформулировать правило умножения дроби на дробь.
Дети формулируют правило, оно появляется на слайде. (Приложение. Слайд 10)
Чтобы умножить дробь на дробь, надо:
1) найти произведение числителей и произведение знаменателей этих дробей;
2) первое произведение записать числителем, а второе – знаменателем.
– Выполните умножение дробей (учащиеся проговаривают правило): № 433 (в; е – на доске; з; и – с комментированием с места; к; л – сам-но, 2 человека за доской).
в)4/7*5/6=10/21
е)11/12*8/9=11/27
з)11/15*3/5=11/25
и)15/16*5/9=25/48
к)12/25*9/16=27/100
л)14/17*34/63=4/9
– Нужно ли в данном случае находить отдельно произведение числителей и произведение знаменателей? (Нет, нужно сначала сократить дробь, а затем умножить оставшиеся множители. )
)
– Прочитайте текст в учебнике на стр71 под рубрикой «Говори правильно».
– Выполните умножение дробей (на доске):
а) 4/7*14/25*5/16=4*14*5 /7*25*16=3/10
б) 24/7*21/15*35/36=24*21*35 /7*15*36=14/9=1 5/9
– Составьте алгоритм умножения трёх и более дробей (Приложение. Слайд 11)
При умножении и трёх и более дробей:
Удобнее сначала в числителе записать произведение всех числителей, в знаменателе – произведение всех знаменателей.
Сократить получившуюся дробь.
Выполнить умножение оставшихся множителей.
Если надо, выделить целую часть.
7. Рефлексия (1 мин.) (Приложение. Слайд 12)
Я хорошо понял, как умножать дроби (приклеить на круг зелёную полоску).
Я не всё понял, у меня были ошибки (приклеить на круг жёлтую полоску).
Я не понял, как умножать дроби (приклеить на круг красную полоску).
Приклеивают полоски на круг и показывают.
8. Домашнее задание (1 мин.) (Приложение. Слайд 13)
п. 13 (1, 2), № 472 (а, б, ж, з), № 478 (а, б), дополнительное задание в буклете.
13 (1, 2), № 472 (а, б, ж, з), № 478 (а, б), дополнительное задание в буклете.
9. Итог урока (2 мин.)
Учитель. Какое открытие вы сделали для себя сегодня на уроке? Как умножить дробь на натуральное число? Как умножить дробь на дробь?
Дети. Научились умножать дробь на натуральное число, дробь на дробь. Учащиеся отвечают правило.
Урок разработали
учителя математики
Гарайшина Г.Р.
Закирова Н.И.
Нуриахметов А.Р.
Дробное Выражение
Дробь
Знаменатель
Частное
Числитель
Так как дробь равна частному 2 : 3, то и частное от деления одного выражения на другое можно записать с помощью черты. Например, выражние (41,3 — 4,4) : (15,3 + 33,9) можно записать так: . Выполнив указанные действия, найдем значение этого выражения: 0,75 или .
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
Например, − дробные выражения.
Выражение, стоящее над чертой, называют числителем, а выражение, стоящее под чертой, — знаменателем дробного выражения. Числителем и знаменателем дробного выражения могут быть любые числа, а также числовые или буквенные выражения.
С дробными выражениями можно выполнять действия по тем же правилам, что и с обыкновенными дробями.
Пример 1. Найдем значение выражения .
Решение. Умножив числитель и знаменатель этого дробного выражения на 6, получим:
Пример 2. Найдем произведение и .
Решение.
Пример 3. Найдем сумму .
Решение. .
При сложении дробных выражений удобнее сначала представить их в виде обыкновенных дробей, а потом уже выполнять сложение:
.
1.1 Что такое числа? Рациональные числа
У нас есть много видов чисел, но все они начинаются с натуральных чисел , которые
\(1, 2, 3\) и так далее.
Если вы посчитаете свои цифры и пальцы ног, вы придете к \(20\) (большинство из вас), и это натуральное число. Мы можем в нашем воображении считать, что эти натуральные числа продолжаются вечно, после миллиона, миллиарда, триллион и так далее.
В начальной школе вы изучали не только эти числа, но и то, как над ними можно производить действия.
Какие операции?
Есть сложения, вычитания, умножения и деления .
Вы можете сложить два натуральных числа вместе, и вы всегда получите еще одно натуральное число, как в известный факт, что один и один два.
С вычитанием дело обстоит сложнее. Если вычесть число, например число \(5\), из
само по себе, вы получаете что-то новое, что-то, что вовсе не является натуральным числом. Мы называем это числом \(0\) или ноль . И если вы вычтете число, снова скажем \(5\), из меньшего числа, скажем \(3\), тогда
вы получаете нечто новое, а именно отрицательное целое число, которое в данном случае равно \(-2\), называемое «минус два» .
Мы называем это числом \(0\) или ноль . И если вы вычтете число, снова скажем \(5\), из меньшего числа, скажем \(3\), тогда
вы получаете нечто новое, а именно отрицательное целое число, которое в данном случае равно \(-2\), называемое «минус два» .
Вы можете использовать числа, чтобы подсчитать количество копеек, которые у вас есть в кармане. Таким образом, у вас может быть пять пенни в твой карман. Ноль — это количество пенни, которое у вас было бы, если бы в вашем кармане была дырка, а все те, что вы положили в сразу выпал снова.
Теперь предположим, что вы идете в магазин, и владелец магазина достаточно глуп, чтобы отдать вам должное. Предположим далее, что
у вас было пять копеек, и вы купили какую-то дорогую вещь стоимостью 11 копеек. Тогда отрицательное целое, \(-6\),
представляет собой тот факт, что у вас не только нет пенни, но если бы вы получили еще шесть, вы были бы обязаны
сдайте их, чтобы заплатить за этот предмет. Шесть – это количество пенни, которое вы должны были бы своему кредитору, если бы
заплатить ему ваши \(5\) пенни, и он отдал вам предмет, а остальные деньги одолжил вам.
Шесть – это количество пенни, которое вы должны были бы своему кредитору, если бы
заплатить ему ваши \(5\) пенни, и он отдал вам предмет, а остальные деньги одолжил вам.
Таким образом, чтобы приспособиться к вычитанию и иметь возможность представлять «сумму долга» числами, мы расширяем естественный числа, включающие числа \(0\) и отрицательные значения натуральных чисел. Весь этот набор цифр, положительные натуральные числа, их отрицательные значения и 0 называется набором из целых чисел и обозначается буквой \(Z\).
Мы можем взять любые два члена \(Z\) и добавить их или вычесть их и в любом случае получить еще один член \(З\).
Я все это знаю, но я очень заржавел в реальных сложениях и вычитаниях. Я ошибаюсь в большинстве время я пытаюсь сделать их.
Большинство людей делают ошибку примерно один раз из десяти сложений или вычитаний однозначных цифр, которые они совершают. выполнять. Это означает, что если они добавляют или вычитают многозначные числа, например \(1234123\) и \(5432121\),
у них есть отличный шанс получить неправильный ответ.
выполнять. Это означает, что если они добавляют или вычитают многозначные числа, например \(1234123\) и \(5432121\),
у них есть отличный шанс получить неправильный ответ.
К счастью, сегодня это не имеет значения. Вы можете легко проверить сложения и вычитания на калькуляторе или в электронной таблице и посмотрите, получите ли вы один и тот же ответ несколько раз. К сожалению, я обычно делаю ошибка при вводе чисел для сложения или вычитания, или сложения вместо вычитания, или выполнения чего-либо еще в равной степени абсурд. Все, что это означает сегодня, это то, что я должен сделать каждый расчет по крайней мере три раза, чтобы иметь разумное шанс на правильность. Правда, количество моих усилий в три раза больше, чем могло бы быть, но в три раза очень мало усилия по-прежнему очень мало усилий.
Если у вас есть эта проблема, вам лучше всего добавлять или вычитать в электронной таблице. Тогда вы можете посмотреть на свой
вычисления и использовать свое суждение относительно того, имеет ли это смысл. Вот несколько правил проверки на смысл.
Тогда вы можете посмотреть на свой
вычисления и использовать свое суждение относительно того, имеет ли это смысл. Вот несколько правил проверки на смысл.
Когда вы добавляете положительные числа, результат должен быть больше, чем оба из двух «сумм» , которые вы добавили. Если одно из чисел положительное, а другое отрицательное, величина (значение, если вы игнорируете любое знак минус) суммы должен быть меньше, чем величина большего из двух, а знак должен быть то из слагаемого с большей величиной.
Кроме того, младшие значащие цифры ваших чисел должны правильно складываться или вычитаться, если вы игнорируете остальные. За например, если вы вычтете \(431\) из \(512\), то последняя цифра ответа должна быть \(1\), что равно \(2\) минус \(1\).
Если ваша проверка выдает что-то подозрительное, попробуйте еще раз вычислить, будучи более осторожным, особенно
с входными данными.
Операция вычитания 5 из другого числа, отменяет операцию добавления \(5\) к другой номер. Таким образом, если вы выполняете обе операции, прибавляете пять, а затем вычитаете пять или наоборот, вы снова откуда вы начали: \(3 + 5 — 5 = 3\).
Сложение \(5\) и вычитание \(5\) считаются обратными операциями друг к другу из-за this property: Выполнение их одно за другим равносильно бездействию.
Кстати, почему \(0\) не является натуральным числом?
Я понятия не имею. Так люди определяли натуральные числа давным-давно, и никто особо не заботился об их изменении. это определение.
Еще в начальной школе вы также столкнулись с понятием умножения на . Это что-то
вы можете сделать с двумя целыми числами, которые дадут третье, называемое их произведением . Ты был (я
надеюсь) вынужден выучить таблицу умножения, которая дает произведение каждой пары однозначных чисел и
затем научился использовать эту таблицу для умножения чисел с большим количеством цифр.
Ты был (я
надеюсь) вынужден выучить таблицу умножения, которая дает произведение каждой пары однозначных чисел и
затем научился использовать эту таблицу для умножения чисел с большим количеством цифр.
Я никогда не был хорош в этом .
В старину нужно было уметь делать эти вещи, сложения и умножения, хотя бы для того, чтобы уметь обращаться с деньги и совершать обычные покупки, не подвергаясь мошенничеству.
Теперь вы можете использовать калькулятор или компьютерную электронную таблицу, чтобы сделать эти вещи, если вы знаете, как вводить целые числа и , чтобы нажать кнопки \(+\) или \(-\) или \(*\) и = соответственно.
( К сожалению, этот факт заставил педагогов поверить, что им не нужно заставлять учеников проходить нудное изучение таблицы умножения.
Это наносит большой вред тем, кто этого не делает, из-за того, как работает наш мозг. оказывается
что чем больше времени мы тратим на любую деятельность в детстве и даже во взрослом возрасте, тем больше площадь мозга
получает то, что посвящено этой деятельности, и чем больше она становится, тем лучше мы справимся с этой деятельностью.
оказывается
что чем больше времени мы тратим на любую деятельность в детстве и даже во взрослом возрасте, тем больше площадь мозга
получает то, что посвящено этой деятельности, и чем больше она становится, тем лучше мы справимся с этой деятельностью.
Таким образом, вы тратите меньше времени на изучение таблицы умножения, что приводит к уменьшению площади вашего мозг посвящен вычислениям, что препятствует вашему дальнейшему математическому развитию.
Ваши математические способности будут прямо пропорциональны количеству времени, которое вы посвящаете математике. думаю об этом. И это зависит от вас. )
Как только мы познакомимся с умножением, возникает естественный вопрос: как мы можем отменить умножение? Что это
обратная операция, скажем, к умножению на \(5\), так что умножение, а затем выполнение этого равносильно выполнению
ничего такого? Эта операция называется деление. Итак, вы научились делить целые числа. операция, обратная умножению на \(x\) — это деление на \(x\) , (если только \(x\) не равно \(0\)).
Итак, вы научились делить целые числа. операция, обратная умножению на \(x\) — это деление на \(x\) , (если только \(x\) не равно \(0\)).
Теперь возникает проблема: если мы попытаемся разделить \(5\) на \(3\), мы не получим целое число. Итак, как мы и должны были расширить натуральные числа до целых, чтобы приспособить операцию вычитания, мы должны расширить наши числа из целых чисел включают также соотношения целых чисел , например \(\frac{5}{3}\), если мы хотим сделать деление определено для каждой пары ненулевых целых чисел. И мы хотим иметь возможность определять разделение, где бы мы ни находились. Можно.
Отношения целых чисел называются рациональными числами, и вы получаете единицу для любой пары целых чисел, если второе
целое число, называемое знаменателем, не равно нулю. Соотношения типа \(\frac{5}{3}\), которые сами по себе не являются целыми числами,
называется дроби.
После того, как мы ввели дроби, мы хотим предоставить правила их сложения и вычитания, а также правила умножения. и разделив их. Это начинает усложняться, но, к счастью для нас, у нас есть калькуляторы и электронные таблицы. которые могут делать все это без каких-либо жалоб, если у нас хватит ума ввести то, что мы хотим сделать.
Есть одна вещь, которую мы не можем делать с нашими рациональными числами, — делить на \(0\). Дивизия, в конце концов, является действием отмены умножения. Но умножение любого числа на 0 дает результат \(0\). Нет способа верни из этого произведения \(0\) то, на что ты умножил \(0\), чтобы получить его.
Конечно, складывать и умножать (а также вычитать и делить) дроби сложнее, чем делать это для
целые числа. Чтобы умножить, скажем, \(\frac{a}{b}\) на \(\frac{c}{d}\), новый числитель является произведением старого
единицы (а именно \(ac\)) и новый знаменатель является произведением старых (\(bd\)), поэтому произведение равно
\(\frac{ac}{bd}\): \(\frac{a}{b}*\frac{c}{d} = \frac{ac}{bd}\).
Обратная операция умножения на \(\frac{c}{d}\) — это умножение на \(\frac{d}{c}\), и эта обратная операция по определению операция деления на \(\frac{c}{d}\). Произведение любого числа на обратное всегда равно \(1\). Это означает, что \(\frac{d}{d}\) всегда \(1\) для любого \(d\), отличного от \(0\).
Таким образом, \(\frac{a}{b}\), деленное на \(\frac{c}{d}\), равно \(\frac{a}{b}\), умноженному на величину, обратную \(\frac{ CD}\) что равно \(\frac{a}{b}\), умноженному на \(\frac{d}{c}\). Ответ: \(\frac{ad}{bc}\).
Добавление немного сложнее. Понятие сложения можно применять как к объектам, так и к числам в
следующий смысл. Мы знаем, например, что \(3+5\) равно \(8\). Значит, если у нас есть 3 редиски и выкопаем
\(5\) больше, у нас будет \(8\) редиски (при условии, что никто не ел первую \(3\)). И то же самое верно для
любые другие предметы вместо редиски. Это говорит нам, как складывать дроби с одинаковыми знаменателями. Таким образом
\(\frac{3}{a} + \frac{5}{a}\) — это \(\frac{8}{a}\), в котором \(\frac{1}{a}\) заменено редька. Мы применяем
общее правило добавления подобных вещей к объекту \(\frac{1}{a}\).
Это говорит нам, как складывать дроби с одинаковыми знаменателями. Таким образом
\(\frac{3}{a} + \frac{5}{a}\) — это \(\frac{8}{a}\), в котором \(\frac{1}{a}\) заменено редька. Мы применяем
общее правило добавления подобных вещей к объекту \(\frac{1}{a}\).
Чтобы сложить дроби с разными знаменателями, нужно сначала изменить их так, чтобы знаменатели были одинаковыми, затем добавьте числители, как вы добавляли числа. Самый простой способ сделать это — сделать новый знаменатель продукт старых. Таким образом, чтобы найти \(\frac{a}{b} + \frac{c}{d}\), вы сначала умножаете первый член на \(\frac{d}{d}\), а второй на \(\frac{b}{b}\), получив \(\frac{ad}{bd} + \frac{cb}{bd} \) и ответ \(\frac{ad+cb}{bd}\). Вы можете сделать то же самое для вычитания.
Вас, вероятно, заставляли выносить за скобки общие члены в числителе и знаменателе в этом ответе в школе,
но вам не нужно делать это при вводе ответа в электронную таблицу, что значительно усложняет сложение дробей
легче, когда вы используете электронные таблицы.
NumberNut.com: дроби и десятичные дроби: типы чисел
Мы говорили о числах на всех других страницах. Ваша голова сейчас забита цифрами. Поскольку область математики росла, математикам требовалось классифицировать эти числа, чтобы с ними было легче работать. Сначала они классифицировали самые простые числа. Это похоже на то, как вы начинаете с самых простых чисел в своих задачах. Эта страница даст вам краткий обзор чисел. У нас есть более подробная информация о многих из этих типов чисел на следующих нескольких страницах.
Натуральные числа — это числа, которые вы используете каждый день. Эти числа включают значения от единицы до бесконечности. Все числа, которые вы можете сосчитать пальцами рук и ног, являются натуральными числами.
Натуральные числа Примеры: 1, 2, 5, 18, 150, 1 586, 258 569.
Целые числа такие же, как и натуральные, за исключением того, что они также включают 0. Знаете ли вы, что древние математики работали задолго до того, как использовали понятие 0? В конце концов они поняли, что им нужно значение, которое не представляет собой сумму.
Знаете ли вы, что древние математики работали задолго до того, как использовали понятие 0? В конце концов они поняли, что им нужно значение, которое не представляет собой сумму.
Целое число Примеры: 0, 1, 2, 5, 18, 150, 1 586, 258 569.
Вы заметили, что все эти числовые строки начинались с 0? Числовые строки с целыми числами могут содержать все положительные и отрицательные числа. Подставив отрицательные числа, мы получили набор целых чисел. Целые числа включают в себя все числа от отрицательной бесконечности до положительной бесконечности.
Целое число Примеры: -258 589, -1 586, -150, -18, -5, -2, -1, 0, 1, 2, 5, 18, 150, 1 586, 258 569.
Мы разбрасывались словом « бесконечность «, но так и не объяснили этот термин. Бесконечность представляет значение, которое слишком велико или слишком мало для подсчета. Это номер, который длится вечно. Если у вас есть число с пятью миллионами цифр, у бесконечности их больше. Это бесконечное значение. Когда вы увидите выписанную бесконечность, она будет выглядеть как цифра 8 на боку, вот так: ∞.
Это бесконечное значение. Когда вы увидите выписанную бесконечность, она будет выглядеть как цифра 8 на боку, вот так: ∞.
Возможно, мы говорили о них раньше, но мы собираемся напомнить вам о четных и нечетных числах. Четные числа делятся на два и не имеют остатка. Нечетные числа дают в остатке 1 при делении на 2. Неважно, положительные они или отрицательные.
Примеры четных чисел: -18, -6, 2, 8, 256
Примеры нечетных чисел: -55, -47, -5, 3, 453, 1 536 859
Мы рассмотрим дроби в другом разделе. Вы, наверное, слышали о них раньше. Другой термин для дроби — рациональное число. Слово рациональный происходит от слова отношение . В случае рациональных чисел это отношение двух целых чисел. Целое число сверху называется « числитель », а целое число снизу называется « знаменатель ». Есть дополнительное правило, которое вы должны помнить. Нижнее число никогда не может быть 0. Если внизу стоит 0, деление не работает. Мы рассмотрим математику дробей и десятичных знаков в других разделах. Просто знайте, что рациональное число — это одно целое поверх другого в виде дроби.
Если внизу стоит 0, деление не работает. Мы рассмотрим математику дробей и десятичных знаков в других разделах. Просто знайте, что рациональное число — это одно целое поверх другого в виде дроби.
Рациональное число Примеры: 16/5 = 3,2, 1/5 = 0,2
16 и 5 являются целыми числами.
Возможно, вы слышали о простых числах. Простые числа особенные, потому что их можно разделить без остатка только на 1 и на самих себя. Такое число, как шесть, можно разделить на 1, 6, 2 и 3. При делении на эти числа остатка не будет. Простое число, такое как 7, можно разделить только на 1 и 7 без остатка. Чуть позже мы еще поговорим о простых числах. Вот список простых.
Примеры простых чисел: 2, 3, 5, 7, 11, 13, 17, 19.
Противоположное простому числу составное число. Мы говорили о том, как шесть можно разделить на 1, 6, 2 и 3. Шесть — составное число, потому что оно делится на множество различных чисел и не имеет остатка. Все четные числа после 2 являются составными числами, потому что все они имеют множитель 2 (дополнительную информацию см. в разделе о факторинге).
в разделе о факторинге).
Составной номер Примеры: 4 (2*2), 6 (2*3), 8 (4*2), 15 (3*5), 33 (11*3)
ПРИМЕЧАНИЕ. Помните, что звездочка или звездочка означают умножение.
Настоящей математической категории для -совместимых чисел не существует, но вы можете о них слышать. Эти числа совместимы с вами. Это числа, которые вы можете легко умножать и делить. Для большинства из нас это такие числа, как пять, десять и двадцать пять. Мы постоянно используем эти числа для обозначения стоимости денег (пятаков, десятицентовиков и четвертаков). Мы очень быстро думаем с этими цифрами. Если бы вы заставили нас попытаться умножить 17 на 23, это заняло бы у нас намного больше времени. Совместимые числа различны для каждого человека. Вы можете умножить на 17.
Давайте закончим с одним последним термином. Противоположности — довольно простая тема. Вы знаете об отрицательных и положительных числах. Противоположным положительному числу является отрицательное. Противоположностью негативу является позитив. Как только вы измените знак исходного числа, вы получите противоположное значение.
Противоположным положительному числу является отрицательное. Противоположностью негативу является позитив. Как только вы измените знак исходного числа, вы получите противоположное значение.
Противоположные числа Примеры: -2 и 2, -589 и 589, -4 587 и 4 587.
► СЛЕДУЮЩАЯ СТРАНИЦА ПО ДРОБЯМ И ДЕСЯТИЧНЫМ ЗНАКАМ
► СЛЕДУЮЩАЯ ОСТАНОВКА НА ОБЪЕКТЕ ПО ОБЪЕКТУ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ
► Или поищите на сайтах…
Как умножать дроби с помощью простых шагов и 7 увлекательных заданий
Вы уже преуспели в обучении умножению, но теперь предстоит, казалось бы, сложная задача — научить их умножать дроби.
Глубокий вдох.
Учителя и ученики могут утверждать, что эта концепция более сложна, чем переход от вычитания и сложения к умножению.
К счастью, существуют стратегии, которые значительно облегчат понимание процесса умножения дробей, и мы собрали их для вас в четком руководстве.
Простой способ умножить фракции
Существует три простых шага, которые должны следовать вашим ученикам, чтобы следовать, как умножить фракции:
- Умножьте числители ( Верхние числа )
- Умножение деноминаторы 9004)
- . нижние числа )
- При необходимости упростите или уменьшите дробь
0097 может умножить две дроби с различными знаменателями.
Давайте рассмотрим пример вместе!
Пример умножения дробей
Понимание трех типов дробей и способов их умножения
Прежде чем мы углубимся в эту концепцию и объясним умножение дробей, мы подумали, что имеет смысл понять различные типы дробей.
Хорошо бы начать с простой терминологии о том, как состоит дробь:
- Числитель — верхнее число, указывающее, сколько частей (целого) у вас есть.
- Знаменатель — нижнее число, которое относится к общему количеству частей, составляющих целое.

Авторы и права: Бретт Берри
Теперь мы рассмотрим три типа дробей и способы их умножения.
1. Умножение правильных дробей
У правильной дроби числитель на меньше знаменателя . Это самое простое место для начала умножения дробей. Пример, который мы использовали выше, идеально подходит для умножения этого типа дроби.
Например: ½, ⅔, ¾, ⅘, ⅚
2. Умножение неправильных дробей
Неправильная дробь похожа по структуре, но имеет числитель больше знаменателя на .
Примечание : Когда числитель равен знаменателю, это считается «неправильным», потому что вы можете преобразовать его в целое число. То же правило применяется к неправильным дробям, таким как ²⁶⁄₁₃, которые при уменьшении становятся целыми (т. Е. Двойками).
Например: ³⁄₂, ⁵⁄₃, ⁷⁄₆, ¹¹⁄₁₀, ⁸⁄₈
Credit: Miranda Weenusk
Неправильные дроби умножаются точно так же. Однако иногда учащиеся могут столкнуться с неправильными дробями.
Однако иногда учащиеся могут столкнуться с неправильными дробями.
Возьмите эту проблему в качестве примера:
Решение : ⁵⁄₃ × ⁷⁄₆ Умножение числителей : 5 × 7 = 35 Умножаемые знаменатели : 3 × 6 = 18 Новая фракция : ³⁵₁₈₁₈.
Если учащиеся знакомы со смешанными дробями, они могут заменить неправильную дробь на смешанную. В этом случае это смешанное число будет 1 ¹⁷⁄₁₈.
Но вы можете узнать больше о смешанных числах ниже!
3. Умножение смешанных дробей
Прежде чем учить учащихся умножать дроби со смешанными числами, они должны знать три шага:
- Преобразование любых смешанных дробей в неправильные дроби
- Умножение неправильных дробей
- Преобразование конечного произведения обратно в смешанное число
Чтобы выполнить первый шаг, научите своих учеников составлять смешанное число «MAD» .
Кредит: Fabulous Finch Facts
Помните: смешанное число состоит из целого числа и правильной дроби. Чтобы выполнить первый шаг и преобразовать смешанную дробь в неправильную, вам необходимо:
Чтобы выполнить первый шаг и преобразовать смешанную дробь в неправильную, вам необходимо:
- Найти новый числитель — Умножить целое число на знаменатель, а затем прибавить к нему исходный числитель.
- Сохранить тот же знаменатель — Знаменатель не изменить.
Отсюда и полезная аббревиатура:
M умножить A dd D знаменатель
Шаг второй: умножьте неправильные дроби, как мы показали в этом разделе.
Шаг третий, превратите эту неправильную дробь обратно в смешанное число. Вот небольшой стишок, который поможет вашим учащимся запомнить, как это делать:
С неправильной дробью деление — это действие!
Кредит: Хизер «Покажи и расскажи»
Давайте воспользуемся показанным ранее примером: ¹⁶⁄₅.
Если деление — это действие, то нужно разделить числитель (16) на знаменатель (5) и посмотреть, есть ли остаток.
Пять входит в число 16 трижды равномерно , всего 15. Это означает, что целая часть смешанного числа будет три .
Но он не разделился идеально, что вы можете видеть по остатку на . Итак, дробная часть смешанного числа — это остаток от знаменателя исходной дроби (⅕).
В виде смешанной дроби это выглядит так: 3 ⅕ .
Чтобы получить более наглядное представление о том, как умножать смешанные числа, посмотрите этот четырехминутный видеоролик от Академии Хана:
И это то, что вам нужно знать при умножении дробей и смешанных чисел.
Как насчет умножения дробей на целые числа?
Кредит: Эрика Наджера
Умножение целых чисел и дробей может поставить ваших учеников в тупик. Почему? Потому что кажется, что дробь одна, а не две.
Но, изучая, как умножать дроби на целые числа, учащиеся могут переписать их как дроби. Вместо 4, например, превратите его в дробь ⁴⁄₁.
Теперь умножать стало проще и понятнее. Например, они могут переписать 2 × ⁵⁄₁₃:
Решение : 2 × ⁵⁄₁₃ Перепишите целое число в виде фракции : ²⁄₁ × ⁵⁄₁₃ Умножаемые числовые число : 2 × 5 = 10 0003 Умножить знаменатели : 1 × 13 = 13 Новая дробь : ¹⁰⁄₁₃
Примечание . Если учащиеся испытывают затруднения с целыми числами, объясните, что они могут думать о целом числе как о верхнем числе, при этом нижнее число всегда равно единице.
Модели площадей для умножения дробей
Идеально подходит для визуалов в вашем классе, модель площади эффективно иллюстрирует, как одна дробь умножается на другую.
Как видно из рисунка ниже, создать модель площади при умножении дробей очень просто:
- Нарисуйте дроби, которые вы умножаете, в отдельных коробках, используя разные цвета
- Объедините рисунки в одну рамку, используя новый цвет для перекрывающихся частей
- Чтобы написать произведение, задайте себе два вопроса:
Сколько коробок имеют оба цвета? Это будет ваш числитель
Сколько всего коробок? Это будет ваш знаменатель
Кредит: миссис Коггинс
Броское напоминание0250
О! А если ваши ученики когда-нибудь забудут шаги, просто напомните им спеть эту песенку:
Умножение дробей? Это не большая проблема. Делайте верхние разы верхние над нижним временами нижние. И прежде чем попрощаться, не забудьте упростить!
Делайте верхние разы верхние над нижним временами нижние. И прежде чем попрощаться, не забудьте упростить!
2 Основные ошибки, которые учащиеся допускают при умножении дробей
Хотя некоторые ученики быстро усвоят ваши уроки умножения дробей, другие могут испытывать трудности с этими новыми понятиями.
Чем раньше учителя уловят эти заблуждения, тем быстрее ученики смогут извлечь уроки из своих ошибок и исправить их.
Согласно практическому руководству What Works Clearinghouse Института педагогических наук «Разработка эффективных инструкций по дробям для детского сада до 8-го класса», это одни из наиболее распространенных заблуждений в отношении обучения тому, как умножать дроби.
1. Вера в то, что целые числа имеют тот же знаменатель, что и дробь в задаче
Группа из восьми экспертов признала, что это заблуждение может привести к тому, что учащиеся возьмут такую задачу, как 4 – ⅜, и перепишут ее как ⁴⁄₈ – ⅜, для неверный ответ ⅛.
При представлении смешанного числа учащиеся с таким неправильным представлением могут добавить целое число к числителю, как в ³¹⁄₃ × ⁶⁄₇ = (³⁄₃ + ⅓) × ⁶⁄₇ = ⁴⁄₃ × ⁶ ⁄₇ = ²⁴⁄₂₁.
Помощь учащимся в понимании взаимосвязи между смешанными числами и неправильными дробями, а также в том, как перевести одно в другое, имеет решающее значение для работы с дробями.
Как помочь своим ученикам
Не поддавайтесь искушению взорвать фундаментальные уроки.
Уделите время своим ученикам, чтобы помочь им понять взаимосвязь между неправильными дробями и смешанными числами, а также способы их преобразования из одних в другие.
Кредит: Однажды в творческом классе
2. Оставить знаменатель без изменений
Учащиеся могут совершить ошибку, забыв умножить равные знаменатели. Вероятно, это связано с тем, что вам не нужно касаться равных знаменателей при сложении дробей.
Например, они могут увидеть ⅔ × ⅓ и неправильно ответить ⅔ вместо ²⁄₉.
Как помочь учащимся
В практическом руководстве эксперты-эксперты предлагают «объяснить концептуальную основу умножения дробей с помощью единичных дробей (например, ½ × ½ = половина половины = ¼)».
В частности, учителя могут показать, что задача ½ × ½ на самом деле спрашивает, какова ½ от ½, что подразумевает, что произведение должно быть меньше любой умножаемой дроби.
Вербализация этого заблуждения полезна, но визуализация особенно эффективна. Войдите в стену фракции !
Дробные стены — отличный способ помочь учащимся увидеть, как в данном случае выглядит абстрактная половина одной половины (т. е. одна четверть).
Теперь вы знаете о болевых точках многих студентов, изучающих умножение дробей, что дальше? Давайте рассмотрим, как закрепить уроки дробей и почему рабочие листы могут быть не лучшей стратегией.
Помогают ли рабочие листы умножать дроби?
Доктор Стивен Камарата, специалист по детскому развитию и порокам развития, считает, что природное любопытство детей рушится.
В эссе для Psychology Today он выразил недовольство предположением, что заполнение рабочих листов напрямую связано с улучшением обучения.
Но данные о количестве успеваемости в США по сравнению с остальным миром говорят об обратном. По иронии судьбы, по мере того, как все больше и больше рабочих листов выдвигают в более ранние классы и все больше механических и скучных домашних заданий навязывают развивающимся умам, успеваемость учащихся в США продолжает снижаться.
Источник: Источник: NAEP Data Explorer, Национальный центр статистики образования
В отчете исследовательского центра Pew указывается на снижение и без того удручающих показателей успеваемости в США. Д-р Камарата подчеркнул:
В 2011 г. только 34% четвероклассников и 27% восьмиклассников были оценены как хорошо владеющие математикой, и этот показатель снизился до 33% для четвероклассников и 25% для восьмиклассников в 2015 г. данные доступны). Невозможно оценить эти результаты положительно: в настоящее время 9 0003 более двух третей четвероклассников и трое из четырех восьмиклассников не владеют математикой . Это 38-е место в мире.
Это 38-е место в мире.
Означает ли это, что школы должны отказаться от рабочих листов? Не обязательно.
Корреляция не является причинно-следственной связью. На самом деле, многие учителя и ученики добились успеха с рабочими листами.
Однако преподаватели должны осознавать, что образование быстро меняется, начиная с рабочих листов и заканчивая классными технологиями.
Итак, вот несколько творческих способов научить умножению дробей — без рабочих листов!
7 Увлекательные занятия для обучения учащихся умножению дробей
1. Prodigy
Prodigy — это математическая онлайн-игра, адаптированная к учебной программе, которая предлагает материалы по всем основным математическим темам с 1 по 8 класс.
Наряду со многими другими навыками и стандартами Prodigy может помочь учащимся научиться:
- Умножать две дроби
- Умножать дробь на целое число
- Умножать две дроби с помощью текстовых задач
- Умножение целого числа на недостающую дробь
И многое другое!
Играя в Prodigy, вы можете отправить своих учеников в увлекательное и познавательное путешествие, вдохновленное фэнтези. Кроме того, вы получите данные об их успехах, чтобы использовать их в своих повседневных стратегиях обучения.
Кроме того, вы получите данные об их успехах, чтобы использовать их в своих повседневных стратегиях обучения.
Готовы начать?
Зарегистрируйтесь сейчас!2. Переверните дроби
Кредит: MathFileFolderGames
Для этого задания разделите учащихся на группы по четыре человека. Затем они делятся на команды по два человека, одна из которых является игроком А, а другая — игроком Б.
Дайте каждой группе по колоде перетасованных карт (тузы = 1, валеты = 10, дамы = 11 и короли = 12).
Как показано на рисунке выше, каждый учащийся вытягивает карту числителя (над карандашом) и карту знаменателя (под карандашом).
Оба игрока А перепишут и умножат дроби на бумаге, а затем, если возможно, упростят произведение. Как только они ответят, игрок Б сделает то же самое.
В зависимости от вашего расписания вы можете назначить всю колоду или дать учащимся таймер, чтобы заполнить столько, сколько они могут.
Предложите учащимся сдать листы для ответов после выполнения упражнения, чтобы вы могли отметить их, или вместе ответьте на 10+ вопросов всем классом.
Примечание : Вы также можете назвать эту игру «Slam-it дроби», заменив карты и карандаши домино.
3. Умножение дробей БИНГО
Кредит: jimmiehomeschoolmom
Каждый ученик получает карточку бинго с заполненными дробями вместе с небольшими листами бумаги (или «фишками бинго»), на которых находятся соответствующие задачи на умножение дробей.
Когда вы говорите «ВПЕРЕД», они могут начать решать каждую задачу одну за другой, кладя фишку поверх правильной дроби.
Вам решать, хотите ли вы, чтобы они завершили линию или всю карту бинго. Вы также можете выбрать, будут ли упрощены ответы на карты бинго.
Для простоты вы можете дать всем одну и ту же карточку бинго с одинаковыми вопросами. Таким образом, вы сможете потом пройтись по каждой проблеме и вместе решить, как их решить.
Примечание : Вы можете использовать этот и последующие примеры в качестве формативного оценивания для оценки знаний учащихся и выявления неправильных представлений на раннем этапе
4.
 Словесные задачи
Словесные задачиСловесные задачи — прекрасный способ сделать уроки математики актуальными для ваших учеников ‘ жизни.
Умение умножать дроби может показаться им чуждым, но простая история может полностью изменить их представление не только о дробях, но и о математике в целом.
Вот пример словесной задачи:
У вас есть ½ пакета чипсов в шкафу, но вы съели ½ после ужина. Сколько всего пакета ты съел? (Не сокращайте свой ответ до минимума.)
Конечно, это простой пример. Но секунду назад эта дробь была просто числом над и под короткой чертой. Однако теперь эта «повседневная» проблема со словами сделала умножение дробей применимым к реальной жизни.
5. Война фракций
Кредит: Шерри Фишер
Это занятие для двух человек взято из карточной игры «Война».
Примечание : Многие учителя отказываются от быстрого решения задач, потому что это не обязательно демонстрирует понимание учеником. У вас также могут быть дети в вашем классе, которые беспокоятся из-за необходимости быстро решать математику и поэтому не успевают. Поэтому лучше всего оценить свой класс, прежде чем играть в эту версию.
У вас также могут быть дети в вашем классе, которые беспокоятся из-за необходимости быстро решать математику и поэтому не успевают. Поэтому лучше всего оценить свой класс, прежде чем играть в эту версию.
У каждого ученика, сидящего рядом, будет половина колоды карт фракций (которую вы можете скачать здесь).
Положив стопку карт лицевой стороной вниз, каждый учащийся вытянет карту одновременно .
Первый учащийся, правильно умноживший две дроби, добавит эти карты в свою колоду.
Учащийся выигрывает, если у него в руке оказывается вся колода карт фракций или у него больше карт по истечении, например, 20 минут.
Более того, быстрое мышление на месте этого дробного задания может помочь улучшить навыки ментальной математики ваших учеников.
Кроме того, вы можете запустить версию этой игры, позволяющую всем играть против вас.
Кто не любит шанс перехитрить своего учителя!?
Разделите свой класс на пять групп.
Вы попадете в первую группу и ответите на один вопрос, прежде чем перейти во вторую группу и так далее. Помните: цель этой версии не в том, чтобы ответить перед вашими учениками, а в том, чтобы помочь улучшить их математические способности в уме.
Это позволяет учащимся отвечать коллективно, чтобы не выделять детей, у которых могут возникнуть проблемы с ментальной арифметикой.
6. Пищевые фракции
Дети любят поесть – это не секрет! Так почему бы не включить его в свой план урока?
Учитель в твите выше заставил своих детей попрактиковаться в умножении дробей путем преобразования рецептов вкусных блюд.
Каждый ученик может выбрать свою любимую еду и увеличить количество ингредиентов, чтобы накормить весь класс.
Поощрение тоже может помочь! Например, после того, как все переделают свою любимую еду, выберите безопасную закуску, которая понравится классу.
Откройте исходный рецепт. Теперь пусть ваши ученики поработают вместе, чтобы умножить ингредиенты, и, если они сделают это правильно, весь класс получит домашнюю (или купленную в магазине) выпечку!
7.
 Вымпел с умноженной дробью
Вымпел с умноженной дробьюКредит: Scaffolded Math
Вырежьте листы бумаги в форме ленты или треугольника для каждого учащегося. Вверху напишите «Я могу умножать…»
Ниже вы включите:
- Модель площади, иллюстрирующая дроби, которые они умножают
- Сама задача на умножение (с местом для демонстрации своей работы)
- Место внизу с надписью «Мой продукт сводится к…»
После того, как каждый учащийся заполнит и украсит свой вымпел на умножение дроби, клей или лента их в нитку!
Эта активная учебная деятельность не только поможет усвоить, как умножать дроби, но и придаст уверенности вашим ученикам. Это их работают на стене, проблема они решен, а каждый может это увидеть.
Хотите научить своих учеников умножать дроби прямо сейчас?
Надеемся!
Умножение дробей может оказаться непростой задачей — выучить и научить.
Надеемся, что подробный разбор различных типов дробей, способов их умножения и того, как сделать их обучение увлекательным, поможет вам и вашим ученикам обогатить опыт преподавания и обучения.
Читать дальше: Как разделить дробь за 3 простых шага
Это не повторяющееся дополнение
Это не повторяющееся дополнение Если когда-либо и требовался веский аргумент в пользу того, что профессиональные математики должны заинтересоваться математическим образованием K-12 и принять в нем участие, то один только этот пример должен предоставить его. Учителя, которые связываются со мной, делают это, потому что они искренне хотят знать, что я имею в виду, поскольку сами учились, предположительно, либо в педагогических школах, либо еще из школьных учебников, что умножение есть многократное сложение.
Учителя, которые связываются со мной, делают это, потому что они искренне хотят знать, что я имею в виду, поскольку сами учились, предположительно, либо в педагогических школах, либо еще из школьных учебников, что умножение есть многократное сложение.
Начнем с основного факта. Умножение просто не является повторным сложением, и рассказывая младшим школьникам об этом, неизбежно возникают проблемы, когда они впоследствии узнают, что это не так. Умножение натуральных чисел непременно дает тот же результат, что и , как многократное сложение, но это не делает его таким же. На велосипеде я добираюсь до офиса примерно за то же время, что и на машине, но эти два процесса очень разные. Рассказывать ученикам неправду, предполагая, что ее можно исправить позже, редко бывает хорошей идеей. И сказать им, что умножение — это многократное сложение, безусловно, потребует отмены позже.
Насколько позже? Как только ребенок перейдет от умножения целых чисел к умножению на дроби (или произвольные действительные числа). В этот момент вы должны рассказать другую историю.
В этот момент вы должны рассказать другую историю.
«О, значит, умножение дробей — это ДРУГОЙ вид умножения, не так ли?» — скажет сообразительный ребенок, задаваясь вопросом, сколько еще раз ты собираешься менять правила. Неудивительно, что так много людей в конечном итоге думают, что математика — это просто набор произвольных, нелогичных правил, которые нельзя вычислить, а просто нужно выучить — только для того, чтобы у них выдернули ковер из-под них, когда правило, которое они только что выучили, заменяется другим. какое-то другое (на первый взгляд) произвольное, нелогичное правило.
Представление о том, что существует только одна базовая операция над числами (будь то целые числа, дроби или что-то еще), наверняка приведет к тому, что ученики будут считать числа просто аддитивной системой и не более того. Почему бы не сделать это правильно с самого начала?
Почему бы не сказать, что есть (по крайней мере) две основные вещи, которые вы можете делать с числами: вы можете складывать их и вы можете их умножать. (Здесь я не учитываю вычитание и деление, так как они являются просто операциями, обратными сложению и умножению, и, следовательно, не являются «базовыми» операциями. Это не означает, что их обучение несложно; сделать с номерами — они идут в комплекте. Мы включаем их, потому что есть много полезных вещей, которые мы можем сделать, когда мы можем складывать и умножать числа. Например, добавление чисел говорит вам, сколько вещей (или частей вещей) у вас есть при объединении коллекций.
Умножение полезно, если вы хотите узнать результат масштабирования некоторой величины.
(Здесь я не учитываю вычитание и деление, так как они являются просто операциями, обратными сложению и умножению, и, следовательно, не являются «базовыми» операциями. Это не означает, что их обучение несложно; сделать с номерами — они идут в комплекте. Мы включаем их, потому что есть много полезных вещей, которые мы можем сделать, когда мы можем складывать и умножать числа. Например, добавление чисел говорит вам, сколько вещей (или частей вещей) у вас есть при объединении коллекций.
Умножение полезно, если вы хотите узнать результат масштабирования некоторой величины.
Вам не обязательно использовать эти приложения, но оба они просты и знакомы, и, на мой взгляд, они настолько хороши, насколько это возможно с точки зрения уместности. (Я думаю, что вам нужно представить простые повседневные примеры приложений.
Обучать класс учащихся начальной школы аксиоматической области целочисленности, вероятно, не очень хорошая идея!
Эта колонка не является разглагольствованием в пользу «Новой математики» — термина, который я использую здесь для обозначения популярной концепции давно прерванной реформы образования, которая носит это название. )
)
Как только вы установили, что существует две 90 733 различных 90 734 (я не говорю несвязанных) полезных операций с числами, то, несомненно, самоочевидно, что многократное сложение не есть умножение, а просто сложение. — повторил!
Но теперь вы подготовили почву для того прекрасного момента, когда вы можете рассказать детям, или, что еще лучше, может быть, они могут открыть для себя этот замечательный трюк, что умножение дает вам супер быстрый способ вычислить повторяющуюся сумму сложения. Зачем лишать детей этого чудесного волшебства?
[Конечно, любой фокус многое теряет, если заглянуть за кулисы. В самые ранние дни развития концепции числа, около 10 000 лет назад, существовали только целые числа, и, возможно, самым ранним предшественником того, что сейчас называется умножением, действительно было многократное сложение. Но все это было 10 000 лет назад, и с тех пор многое изменилось. Мы не пытаемся понять, как работает iPod с точки зрения счетов, и мы не должны основывать нашу систему образования на том, что люди знали и делали в 8000 г. до н.э.]
до н.э.]
Математика полна примеров, когда то, что касается А, оказывается полезным для выполнения Б.
Возведение в степень обеспечивает быстрый способ многократного умножения — вау, это снова случилось! Это математика классная или что!
Антидифференцирование оказывается быстрым способом вычисления интеграла. Мальчик, это глубоко!
Я просто слышу, как некоторые ученики недоумевают: «Эй, сколько еще таких примеров? Это очень, очень интригует. Кажется, все сходится. Здесь должно быть что-то глубокое. Я должен узнать больше.»
Я предполагаю, что причина нынешнего положения дел в том, что учителя (что на самом деле означает их инструкторы или составители учебников, которыми должны пользоваться эти учителя) считают, что дети не смогут справиться с тем фактом, что существует две основных операции. вы можете выполнять на числах.
И поэтому они говорят им, что на самом деле есть только один, а другой — просто его вариант. Но действительно ли мы верим, что с двумя операциями труднее смириться, чем с одной? Огромный скачок к абстракции связан с идеей абстрактных чисел, с которыми можно что-то делать. Как только вы преодолели эту поистине удивительную когнитивную пропасть, уже не имеет большого значения, можете ли вы сделать одну абстрактную вещь с числами или дюжину или больше.
Как только вы преодолели эту поистине удивительную когнитивную пропасть, уже не имеет большого значения, можете ли вы сделать одну абстрактную вещь с числами или дюжину или больше.
Конечно, с числами можно выполнять не только две основные операции. Я только что упомянул третью базовую операцию: возведение в степень. Университетские профессора математики доблестно борются за то, чтобы избавить студентов от ложного убеждения, что возведение в степень — это «повторное умножение». Эй, если вы можете однажды запутать учеников ложью, почему бы не провернуть тот же трюк снова? Я дразню здесь. Но из лучших побуждений привлечь внимание к тому, что, как мне кажется, нужно исправить.
И способ исправить это — убедиться, что когда мы готовим будущих учителей, когда авторы пишут или государство принимает учебники, мы все делаем это правильно. Мы, математики, несем здесь окончательную ответственность. Мы являемся признанными мировыми экспертами в области математических структур, включая различные системы счисления. («Системы» здесь включают в себя операции, которые можно над ними выполнять.) Наши профессиональные предшественники построили эти структуры. Они являются частью нашего мировоззрения, вещами, которые мы освоили так давно в нашем образовательном путешествии, что они стали второй натурой. Слишком долго мы молчаливо предполагали, что наши знания и понимание этих систем разделяют и другие. Но это не так. У меня есть досье озадаченных электронных писем от квалифицированных учителей, свидетельствующих о пробеле.
(«Системы» здесь включают в себя операции, которые можно над ними выполнять.) Наши профессиональные предшественники построили эти структуры. Они являются частью нашего мировоззрения, вещами, которые мы освоили так давно в нашем образовательном путешествии, что они стали второй натурой. Слишком долго мы молчаливо предполагали, что наши знания и понимание этих систем разделяют и другие. Но это не так. У меня есть досье озадаченных электронных писем от квалифицированных учителей, свидетельствующих о пробеле.
В заключение я должен отметить, что я не пытался предписывать , как учителя должны преподавать арифметику. Я не являюсь обученным учителем K-12, и у меня нет личного опыта, на который можно было бы опереться. Но термин «преподавание математики» состоит из двух слов, и у меня есть опыт в первом. Это мое внимание здесь, и я уступаю другим, у которых есть опыт в преподавании. Наилучший путь вперед, безусловно, состоит в том, чтобы две группы специалистов, математики и учителя, регулярно и часто вели диалог.
А пока, учителя, пожалуйста, перестаньте говорить своим ученикам, что умножение — это многократное сложение.
Угол Девлина обновляется в начале каждого месяца.
Математик Кит Девлин (email: [электронная почта защищена]) исполнительный директор Центра изучения языка и информации Стэнфордского университета и Математик в выпуске выходного дня NPR. Последняя книга Девлина, Раскрытие преступлений с помощью математики: ЦИФРЫ ЗА NUMB3RS, книга-компаньон к хиту телевизионный криминальный сериал NUMB3RS, и написана в соавторстве с профессором Гэри Лорденом из Калифорнийского технологического института, ведущим консультантом по математике в этой серии. Он был опубликован в сентябре прошлого года издательством Plume.
Умножение дробей.
Умножение дробей.Навигация по страницам:
- Умножение дроби на целое число
- Умножение дробей
- Умножение смешанных чисел
Умножение дроби на целое число.

Определение.
Чтобы умножить дробь на целое число, необходимо числитель умножить на целое число, а знаменатель оставить без изменений. При необходимости упростите дробь.
Примеры умножения дроби и целого числа
Пример 1.
Найдите произведение дроби и натурального числа:
| 3 | · 2 | = | 3 · 2 | = | 6 |
| 7 | 7 | 7 |
Example 2.
Find the product of дробь и натуральное число:
| 1 | · 4 | = | 4 | = | 2·2 | = | 2 |
| 2 | 2 | 2 |
Multiplication of fractions.

Примеры умножения дробей
Пример 3.
Найдите произведение двух дробей:
| 3 | · | 2 | = | 3 · 2 | = | 8 |
| 7 | 5 | 7 · 5 | 35 |
| 10 | · | 3 | = | 10 · 3 | = | 2 · 5 · 3 | = | 5 | = | 5 |
| 9 | 4 | 9 · 4 | 2 · 2 · 3 · 3 | 2 · 3 | 6 |
Онлайн-калькулятор дробей
Упражнения. Умножение двух дробей.
Умножение смешанных чисел.
Определение.
- Чтобы умножить смешанные числа:
- преобразование смешанных чисел в неправильные дроби;
- умножить числители и умножить знаменатели;
- упростить дробь;
- если эта дробь неправильная, то преобразовать дробь в смешанное число.

Примеры умножения смешанных чисел
Пример 5.
Найдите произведение двух смешанных чисел:
| 2 | 1 | · | 1 | 2 | = | 2 · 2 + 1 | · | 1 · 3 + 2 | = | 5 | · | 5 | = | 5 · 5 | = | 25 | = | 6 · 4 + 1 | = 4 | 1 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 · 3 | 6 | 6 | 6 |
Example 6.
Найдите произведение смешанного числа и целого числа:
| 4 | 1 | · | 6 | = | 4 · 3 + 1 | · | 6 9078 9078 9078 9078 9078 9078 9078 9078 9078 9. 9078 9078 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9078 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. 9078 9. | .0728= | 26 |
| 3 | 3 | 3 |
Найдите произведение 4:9002
| 2 | 1 | · | 3 | = | 2 · 7 + 1 | · | 3 | = | 15 | · | 3 | = | 15 · 3 | = | 3 · 3 | = | 9 | = | 7 + 2 | = 1 | 2 |
| 7 | 5 | 7 | 5 | 7 | 5 | 7 · 5 | 7 | 7 | 7 | 7 |
Онлайн-калькулятор дробей
Упражнения. Умножение двух смешанных чисел.
Умножение двух смешанных чисел.
Фракция Формы дробей (простая дробь, правильная дробь, неправильная дробь, смешанные числа, десятичные) Основное свойство дроби Упрощение дробей Наименьший общий знаменатель дробей Преобразование неправильных дробей (составных дробей) в смешанные числа Преобразование смешанных чисел в неправильные дроби (составные дроби) Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичных дробей в обыкновенные дроби
Калькулятор дробей онлайн
Задачи и упражнения с дробями
4.6: Умножение дробей — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 9847
- Мишель Манес
- Гавайский университет
Модель площади
Одной из наших моделей умножения целых чисел была модель площади. Например, произведение \(23 \times 37\) равно площади (количество квадратов 1 × 1) прямоугольника размером 23 на 37:
Например, произведение \(23 \times 37\) равно площади (количество квадратов 1 × 1) прямоугольника размером 23 на 37:
Таким образом, произведение двух дробей, скажем, \(\frac {4}{7} \times \frac{2}{3}\) также должны соответствовать задаче площади.
Пример: (4/7 × 2/3)
Начнем с отрезка некоторой длины, который мы называем 1 единицей:
Теперь постройте квадрат с одной единицей на каждой стороне:
Площадь квадрата, конечно же, равна \(1 \times 1 = 1\) квадратной единицы.
Теперь разделим верхний отрезок на три равные части. (Так что каждая часть равна \(\frac{1}{3}\).) И мы разделим отрезок на стороне на семь частей одинакового размера. (Так что каждая часть равна \(\frac{1}{7}\).)
Мы можем использовать эти метки, чтобы разделить весь квадрат на маленькие прямоугольники одинакового размера. (У каждого прямоугольника одна сторона равна \(\frac{1}{3}\), а другая сторона равна \(\frac{1}{7}\).)
Теперь мы можем отметить четыре седьмых с одной стороны и две трети с другой стороны.
Результатом умножения должна быть площадь прямоугольника с \(\frac{4}{7}\) с одной стороны и \(\frac{2}{3}\) с другой. Что это за район?
Помните, весь квадрат был одной единицей. Этот одноэлементный квадрат разделен на 21 часть одинакового размера, а наш прямоугольник (тот, у которого стороны \(\frac{4}{7}\) и \(\frac{2}{3}\)) содержит восемь из этих прямоугольников. Поскольку заштрихованная область является ответом на нашу задачу на умножение, мы заключаем, что
\[\frac{4}{7} \times \frac{2}{3} = \frac{8}{21} \ldotp \nonumber \]
Think / Pair / Share
- Использование модели для вычисления каждого из следующих продуктов. Нарисуйте картинку, чтобы ясно увидеть ответ. $$\frac{3}{4} \times \frac{5}{6}, \qquad \frac{3}{8} \times \frac{4}{5}, \qquad \frac{5}{ 8} \times \frac{3}{7} \ldotp$$
- Задача о площади \(\frac{4}{7} \times \frac{2}{3}\) дала диаграмму с общим числом из 21 маленького прямоугольника.
 Объясните, почему 21 появляется как общее количество прямоугольников одинакового размера.
Объясните, почему 21 появляется как общее количество прямоугольников одинакового размера. - Задача о площади \(\frac{4}{7} \times \frac{2}{3}\) дала диаграмму с 8 маленькими заштрихованными прямоугольниками. Объясните, почему 8 отображается как количество заштрихованных прямоугольников.
Задача 5
Как можно расширить модель площади для дробей больше 1? Попробуйте нарисовать картинку для каждого из них: \[\frac{3}{4} \cdot \frac{3}{2}, \qquad \frac{2}{5} \cdot \frac{4}{3 }, \qquad \frac{3}{10} \cdot \frac{5}{4}, \qquad \frac{5}{2} \cdot \frac{7}{4} \ldotp \nonumber \]
Самостоятельно
Выполните следующие упражнения самостоятельно или с партнером.
- Вычислите следующие произведения, максимально упростив каждый из ответов. Вам не нужно рисовать картинки, но вы, безусловно, можете сделать это, если это поможет! $$\frac{5}{11} \times \frac{7}{12}, \qquad \frac{4}{7} \times \frac{4}{8}, \qquad \frac{1}{ 2} \times \frac{1}{3}, \qquad \frac{2}{1} \times \frac{3}{1}, \qquad \frac{1}{5} \times \frac{5 {1}\ldotp$$
- Вычислите следующие произведения.
 (Не переусердствуйте!) $$\frac{3}{4} \times \frac{1}{3} \times \frac{2}{5}, \qquad \frac{5}{5} \ раз \frac{7}{8}, \qquad \frac{88}{88} \times \frac{541}{788}, \qquad \frac{77876}{311} \times \frac{311}{77876 } \ldotp$$
(Не переусердствуйте!) $$\frac{3}{4} \times \frac{1}{3} \times \frac{2}{5}, \qquad \frac{5}{5} \ раз \frac{7}{8}, \qquad \frac{88}{88} \times \frac{541}{788}, \qquad \frac{77876}{311} \times \frac{311}{77876 } \ldotp$$ - Попробуйте этот. Можете ли вы использовать правило дробей \(\frac{xa}{xb} = \frac{a}{b}\) для помощи в вычислениях? Как? $$\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} \times \frac{4}{5} \times \frac{5}{6} \times \frac{6}{7} \times \frac{7}{8} \times \frac{8}{9} \times \frac{9}{10} \ldotp$$
Подумай / Соедини / Поделись
Чем отличаются эти две проблемы? Нарисуйте изображение каждого.
- У Пэм в холодильнике было \(\frac{2}{3}\) торта, и она съела его \(\frac{1}{2}\). Сколько всего торта она съела?
- В понедельник Пэм съела \(\frac{2}{3}\) торта. Во вторник Пэм съела \(\frac{1}{2}\) торта. Оба торта были одинакового размера. Сколько всего торта она съела?
Если задача включает в себя такую фразу, как «\(\frac{2}{3}\) of…», учащихся учат рассматривать «of» как умножение и использовать это для решения задачи. Как показывают приведенные выше проблемы, в некоторых случаях это имеет смысл, а в некоторых нет. Важно внимательно читать и понимать, о чем задача, а не запоминать правила «перевода» текстовых задач.
Как показывают приведенные выше проблемы, в некоторых случаях это имеет смысл, а в некоторых нет. Важно внимательно читать и понимать, о чем задача, а не запоминать правила «перевода» текстовых задач.
Объяснение правила
Вероятно, вы упростили свою работу в приведенных выше упражнениях, используя следующее правило умножения.
Умножение дробей\[\frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \ldotp \nonumber \]
Конечно, вы можете затем упростить окончательный ответ, но ответ всегда будет эквивалентным этому. Почему? Модель области может помочь нам объяснить, что происходит.
Во-первых, давайте четко запишем, как модель площади говорит умножать \(\frac{a}{b} \cdot \frac{c}{d}\). Мы хотим построить прямоугольник, у которого одна сторона имеет длину \(\frac{a}{b}\), а другая сторона имеет длину \(\frac{c}{d}\). Начинаем с квадрата, по одной единице с каждой стороны.
- Разделите верхний сегмент на части одинакового размера.
 Тень этих частей. (Это будет сторона прямоугольника с длиной \(\frac{a}{b}\).)
Тень этих частей. (Это будет сторона прямоугольника с длиной \(\frac{a}{b}\).) - Разделите левый сегмент на равные части. Тень этих частей. (Это будет сторона прямоугольника с длиной \(\frac{c}{d}\).)
- Разделите весь прямоугольник по отметкам на сторонах, сделав прямоугольники одинакового размера.
- Закрасьте прямоугольник, ограниченный заштрихованными сегментами.
Если ответ \(\frac{a \cdot c}{b \cdot d}\), это означает, что в квадрате всего \(b \cdot d\) фигур одинакового размера, и \ (a \cdot c\) из них заштрихованы. Из модели видно, почему это так:
- Верхний сегмент был разделен на части одинакового размера. Итак, в прямоугольнике есть столбцы.
- Боковой сегмент был разделен на части одинакового размера. Итак, в прямоугольнике есть ряды.
- Прямоугольник со столбцами и строками состоит из \(b \cdot d\) частей.
 (Модель площади для умножения целых чисел!)
(Модель площади для умножения целых чисел!)
Подумай / Соедини / Поделись
Придерживайтесь общего правила умножения
\[\frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \ldotp \nonumber \]
Напишите ясное объяснение, почему \(a \cdot c\) маленьких прямоугольников будет затенено.
Умножение дробей на целые числа
Часто учащихся начальной школы учат умножать дроби на целые числа, используя правило дробей.
Пример: умножение дробей
Например, чтобы умножить \(2 \cdot \frac{3}{7}\), мы думаем о «2» как \(\frac{2}{1}\) и вычисляем таким образом \[2 \cdot \frac{3}{7} = \frac{2}{1} \cdot \frac{3}{7} = \frac{2 \cdot 3}{1 \cdot 7} = \frac{6} {7} \ldotp \nonumber \]
Мы также можем думать с точки зрения нашей исходной модели «Пирогов на ребенка», чтобы отвечать на подобные вопросы.
Пример: пирогов на ребенка
Мы знаем, что \(\frac{3}{7}\) означает количество пирога, которое получит каждый ребенок, когда 7 детей поровну поделят 3 пирога .
Если мы вычислим \(2 \cdot \frac{3}{7}\), это означает, что мы удвоим количество пирога, которое получит каждый ребенок. Мы можем сделать это, удвоив количество пирогов. Таким образом, ответ такой же, как \(\frac{6}{7}\): количество пирога, которое получает каждый ребенок, когда 7 детей поровну делят 6 пирогов.
Наконец, мы можем мыслить в терминах единиц и объединения.
Пример: Единицы
Дробь \(\frac{3}{7}\) означает, что у меня есть 7 равных частей (от до ), и я беру 3 из них.
Итак, \(2 \cdot \frac{3}{7}\) означает сделать это дважды. Если я возьму 3 штуки, а потом еще 3 штуки, то в сумме получится 6 штук. Всего осталось 7 равных частей, поэтому ответ равен \(\frac{6}{7}\).
Подумай / Соедини / Поделись
- Используйте все три метода, чтобы объяснить, как найти каждый продукт: $$3 \cdot \frac{2}{5}, \qquad 4 \cdot \frac{3}{8}, \ qquad 6 \cdot \frac{1}{5} \ldotp$$
- Сравните эти разные способы умножения дробей.
 Какие из них более естественны для вас? Один имеет больше смысла, чем другие? Влияют ли конкретные числа в задаче на ваш ответ? Ваш партнер согласен?
Какие из них более естественны для вас? Один имеет больше смысла, чем другие? Влияют ли конкретные числа в задаче на ваш ответ? Ваш партнер согласен?
Объяснение правила ключевой дроби
Рой говорит, что правило дроби
\[\frac{xa}{xb} = \frac{a}{b} \nonumber \]
«очевидно», если подумать Условия умножения дробей. Он рассуждает следующим образом:
Мы знаем, что умножение чего-либо на 1 не меняет числа:
\[\begin{split} 1 \cdot 4 &= 4 \\ 1 \cdot 2014 &= 2014 \\ 1 \ cdot \frac{5}{7} &= \frac{5}{7} \end{split} \nonumber \]
Итак, в общем,
\[1 \cdot \frac{a}{b} = \frac{a}{b} \ldotp \nonumber \]
Теперь \(\frac{ 2}{2} = 1\) , так что это означает, что
\[\frac{2}{2} \cdot \frac{a}{b} = 1 \cdot \frac{a}{b} = \frac{a}{b}, \nonumber \]
, что означает
\[\frac{2a}{2b} = \frac{a}{b} \ldotp \nonumber \]
По тем же соображениям \(\frac{3}{3} = 1\) , так что это означает, что
\[\frac{3}{3} \cdot \frac{a}{b} = 1 \cdot \frac{a}{b} = \frac{a}{b}, \nonumber \]
что означает
\[\frac{3a}{3b} = \frac{a}{b} \ldotp \nonumber \]
Think / Pair / Share
Что вы думаете о рассуждениях Роя? Имеет ли это смысл? Как бы Рой объяснил общее правило для положительных целых чисел:
\[\frac{xa}{xb} = \frac{a}{b} ? \номер\]
Эта страница под названием 4.


 Умножение обыкновенных дробей: правила, примеры, решения
Умножение обыкновенных дробей: правила, примеры, решения .. к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
.. к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху». Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения. На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
 Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
 Математики эту задачу решить не могут, а вот шаманы — элементарно.
Математики эту задачу решить не могут, а вот шаманы — элементарно. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
 И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.
И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.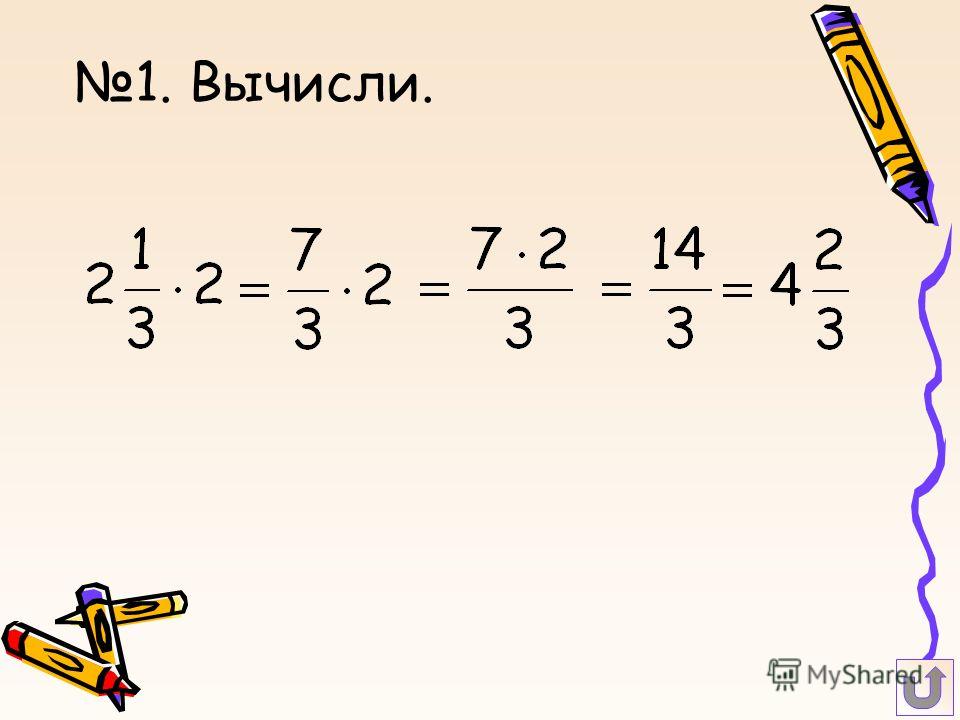 Если к пиццы прибавить пиццы, то получится пиццы:
Если к пиццы прибавить пиццы, то получится пиццы: Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1
целая и ещё пиццы.
Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1
целая и ещё пиццы.
 Делим 6 на 3, получаем 2.
Делим 6 на 3, получаем 2. К прибавить получается .
К прибавить получается .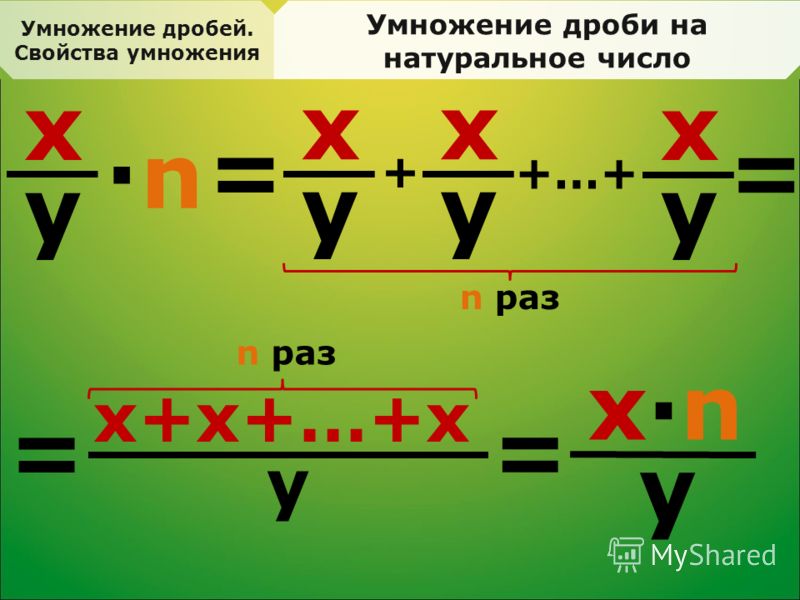 Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Находясь в школе, данный пример нам пришлось бы записать следующим образом: Знаменатели дробей это числа 2, 3 и 4
Знаменатели дробей это числа 2, 3 и 4 Осталось сложить эти дроби. Складываем:
Осталось сложить эти дроби. Складываем: Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним. Достаточно понимать следующие правила:
Достаточно понимать следующие правила:
 Записываем тройку над второй дробью:
Записываем тройку над второй дробью: Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
 Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц: Поэтому значение выражения равно
Поэтому значение выражения равно Она называется «обратные числа».
Она называется «обратные числа».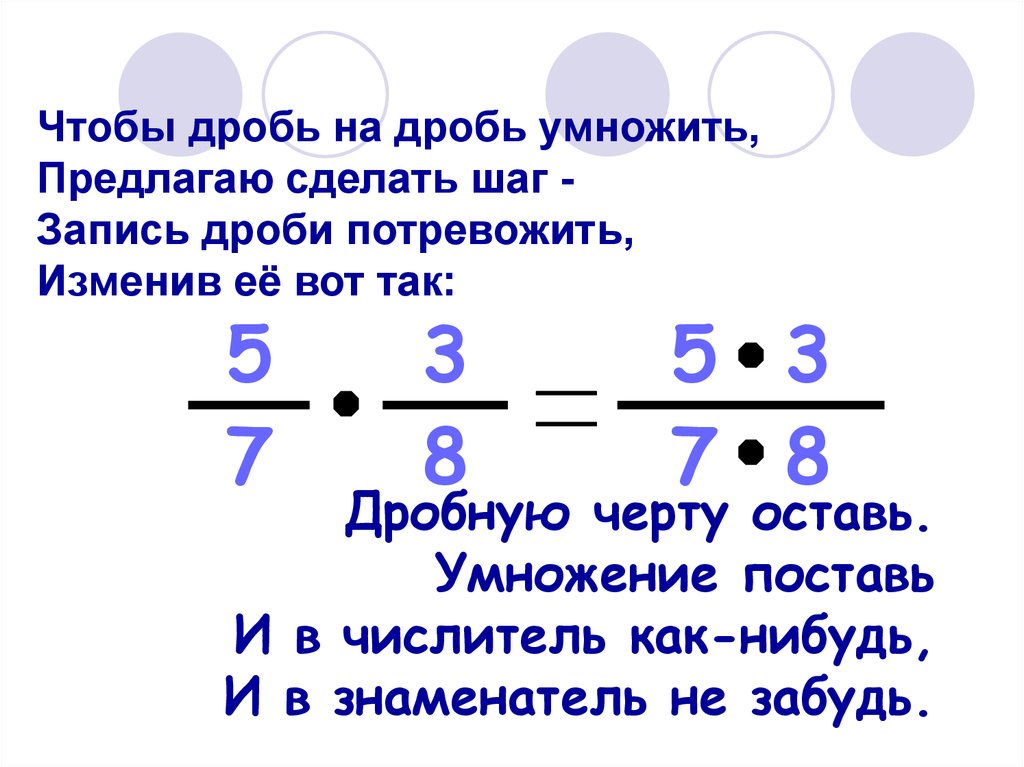 Для этого достаточно перевернуть её.
Для этого достаточно перевернуть её.

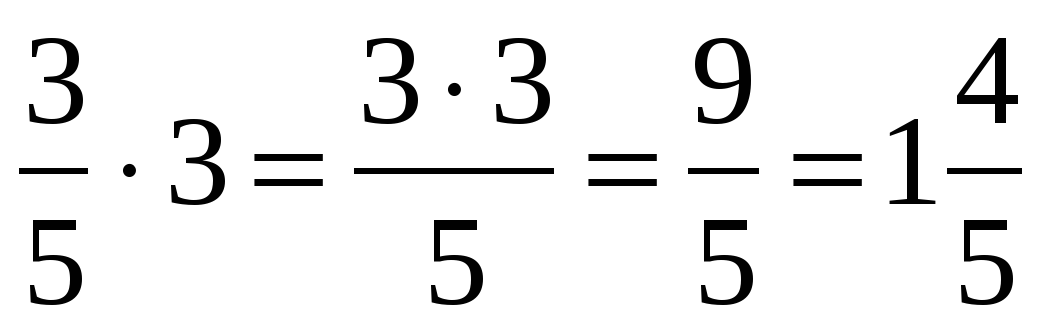 Получится отрицательная дробь.
Получится отрицательная дробь. Найдите значение выражения:
Найдите значение выражения: В общем, будьте внимательны.
В общем, будьте внимательны.
 Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме. Сокращение дробей при расчётах значительно облегчит ваши вычисления.
Сокращение дробей при расчётах значительно облегчит ваши вычисления.
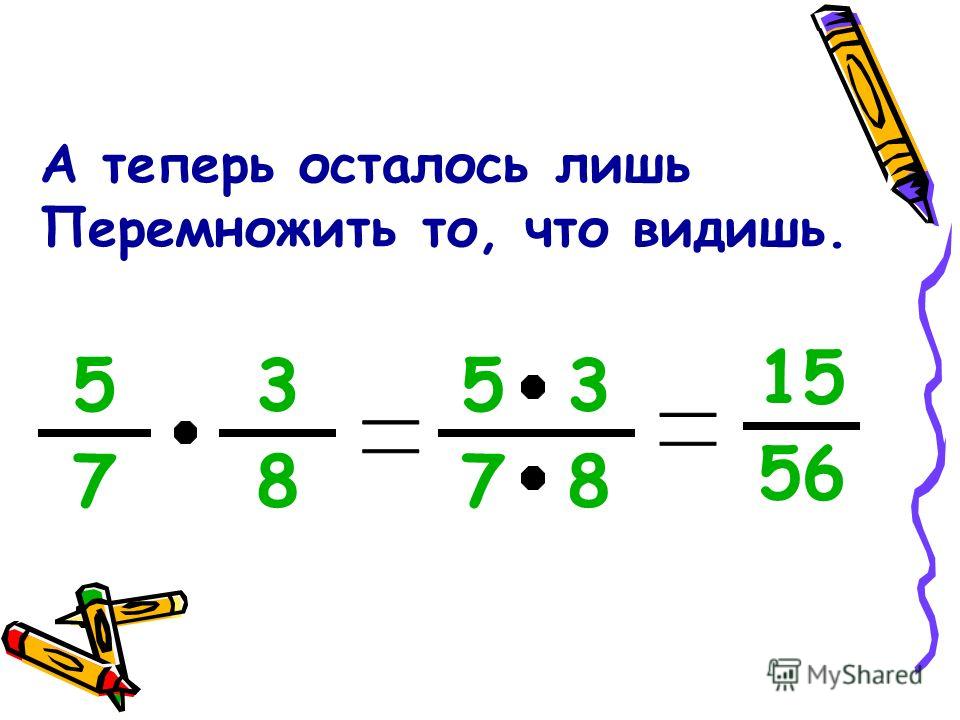 В нашем случае целая часть выделяется легко — два разделить на два равно единице:
В нашем случае целая часть выделяется легко — два разделить на два равно единице:

 Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
 Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Получили первый дополнительный множитель 6. Записываем его над первой дробью: Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке. Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним. Так и сделаем:
Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним. Так и сделаем: Достаточно понимать следующие правила:
Достаточно понимать следующие правила:
 Осталось умножить дроби на свои дополнительные множители:
Осталось умножить дроби на свои дополнительные множители: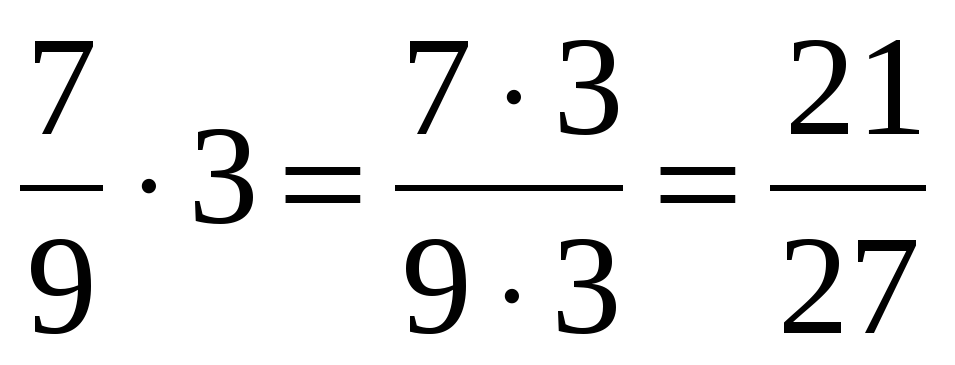 Дробь и описывает эти пять кусочков.
Дробь и описывает эти пять кусочков. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
 Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби: Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид: Чтобы сократить эту дробь, её нужно разделить на НОД числителя и знаменателя. Итак, найдём НОД чисел 105 и 450:
Чтобы сократить эту дробь, её нужно разделить на НОД числителя и знаменателя. Итак, найдём НОД чисел 105 и 450: