Умножение дробей: простая инструкция — Лайфхакер
Умножение дробей друг на друга
Обыкновенные дроби
Всё просто: числитель умножьте на числитель, а знаменатель на знаменатель. Потом проверьте, можно ли сократить дробь. Например:
Правило работает для дробей и с разными, и с одинаковыми знаменателями. Если дробь большая, допустим 24/35, постарайтесь сразу сократить её — так будет легче вести подсчёты.
Если в примере есть смешанное число, сначала преобразуйте его в неправильную дробь, а потом умножайте способом, описанным выше. Полученный результат переведите обратно в смешанное число.
Вспомните основы 💡
Десятичные дроби
Процесс умножения происходит в три шага:
- Запишите дроби в столбик и умножьте как натуральные числа, пока не думая о запятых.
- Посмотрите, сколько знаков после запятой было в каждой дроби, и сложите их количество.
- Двигаясь справа налево, отсчитайте в результате умножения столько же цифр, сколько получилось в предыдущем шаге. Поставьте там запятую. Это и есть ответ. Например:
Если умножаете на 0,1, 0,01, 0,001 и так далее, то переместите запятую влево на столько знаков, сколько их после запятой в множителе: 0,18 × 0,1 = 0,018; 0,5 × 0,001 = 0,0005.
Освежите знания 👈
Умножение дробей на натуральные числа
Обыкновенные дроби
Нужно умножить только числитель, а знаменатель оставить без изменений. Если результат — неправильная дробь, выделите из неё целую часть, чтобы получить смешанное число. Например:
Если нужно умножить смешанное число, переведите его в неправильную дробь и умножайте по тому же принципу. То есть:
Есть и второй способ: разделить знаменатель на данное вам натуральное число, а числитель не трогать. Этот способ удобнее применять, когда знаменатель делится на это натуральное число без остатка. Например:
Этот способ удобнее применять, когда знаменатель делится на это натуральное число без остатка. Например:
Сравните этот метод с первым — результат одинаковый.
Десятичные дроби
В этом случае используйте такой же способ, как для умножения дроби на дробь. Перемножьте числа столбиком, потом отсчитайте столько цифр, сколько их было после запятой в десятичной дроби, и там поставьте запятую. То есть:
Если нужно умножить десятичную дробь на 10, 100, 1 000 и так далее, просто переместите запятую вправо на столько знаков, сколько нулей после единицы. Например: 0,045 × 10 = 0,45; 0,045 × 100 = 4,5.
Читайте также 🧮👌🤓
Урок 75. умножение смешанных дробей — Математика — 5 класс
Математика
5 класс
Урок № 75
Умножение смешанных дробей
Перечень рассматриваемых вопросов:
– умножение смешанной дроби на натуральное число;
– возведение смешанной дроби в степень;
– умножение смешанных дробей.
Тезаурус
Распределительный закон умножения – чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Переместительный закон умножения – от перестановки множителей произведение не меняется.
Площадь прямоугольника – произведение длины на ширину.
Порядок убывания – расположение элементов от большего к меньшему.
Порядок возрастания – расположение элементов от меньшего к большему.
Обязательная литература
- Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О.
 Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
Ф. Зарапина. — М.: Просвещение, 2009. — 142 с. - Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
На предыдущих уроках вы научились умножать обыкновенные дроби и записывать смешанные дроби в виде неправильных.
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Чтобы записать смешанную дробь неправильной дробью, надо знаменатель дробной части умножить на целую часть, прибавить числитель дробной части и полученное число записать в числитель, а знаменатель оставить прежним.
Этих умений достаточно, чтобы сегодня научиться умножать смешанные дроби.
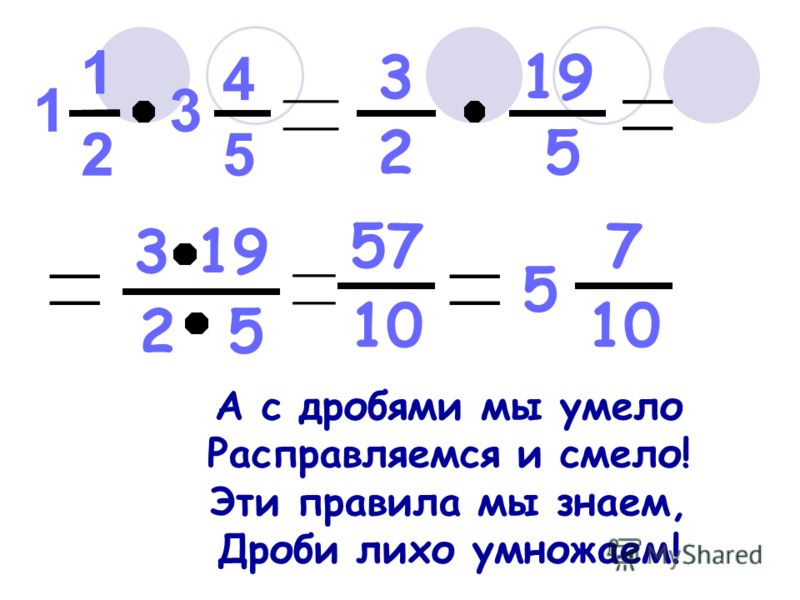
Правило умножения смешанных дробей звучит так: чтобы умножить смешанные дроби, нужно записать их в виде неправильных дробей и выполнить умножение с обыкновенными дробями.
Результат получился тот же, что и при умножении.
Рассмотрим ещё один случай применения распределительного закона умножения для упрощения вычислений.
Найдём сумму произведения трёх целых четырёх пятых и пяти восьмых с произведением четырёх целых одной пятой и пяти восьмых.
В этих произведениях есть одинаковый множитель – пять восьмых. Его по распределительному закону вынесем за скобки, в которых останется сумма трёх целых четырёх пятых и четырёх целых одной пятой. Найдём значение суммы в скобках. Складываем отдельно целые части – три и четыре – это будет семь, и дробные части – четыре пятых и одну пятую – это будет пять пятых.
Сумму целой и дробной части записываем смешанной дробью – семь целых пять пятых и умножаем на пять восьмых. Так как дробная часть получившейся смешанной дроби – неправильная дробь, равная одному, то смешанную дробь заменяем на восемь целых. Умножаем восемь на пять восьмых – это пять.
Расставим порядок действий. Сначала выполняются действия в скобках. В скобках есть умножение и сложение. Умножение выполняется в первую очередь, затем сложение. Четвёртым действием будет вычитание из числа суммы в скобках. Пятое действие – нахождение частного в знаменателе. Шестое действие – деление числителя исходной дроби на знаменатель. Деление заменяется умножением, а умножать мы научились:
Сначала выполняются действия в скобках. В скобках есть умножение и сложение. Умножение выполняется в первую очередь, затем сложение. Четвёртым действием будет вычитание из числа суммы в скобках. Пятое действие – нахождение частного в знаменателе. Шестое действие – деление числителя исходной дроби на знаменатель. Деление заменяется умножением, а умножать мы научились:
Итак, чтобы умножить смешанные дроби необходимо:
• представить эти смешанные дроби неправильными дробями;
• выполнить умножение неправильных дробей;
• сократить, если возможно;
• представить неправильную дробь, полученную в результате умножения, смешанной дробью.
При возведении смешанной дроби в степень нужно:
• представить эту смешанную дробь неправильной дробью;
• возвести полученную неправильную дробь в нужную степень.
Тренировочные задания
№ 1. Поставьте на места пропусков числа так, чтобы вычисления были верными.
Умножение и деление дробей
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:Задача. Найдите значение выражения:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
- Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).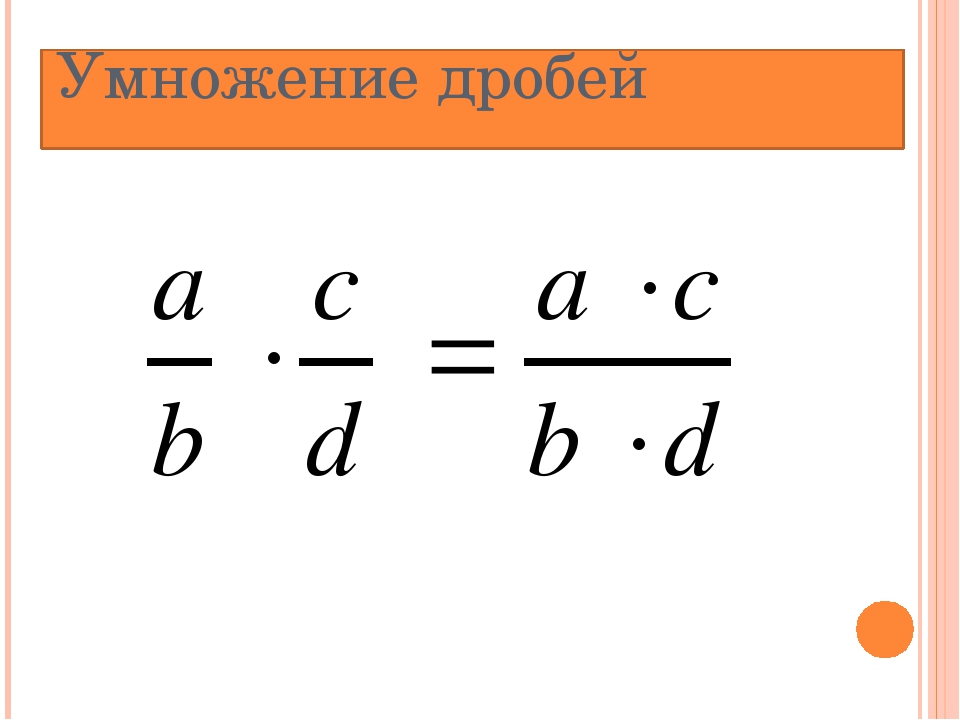
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения. Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
Смотрите также:
- Сложные выражения с дробями. Порядок действий
- Тест к уроку «Сложение и вычитание дробей» (средний)
- Тест к уроку «Площади многоугольников на координатной сетке» (средний)
- Площади многоугольников на координатной сетке
- Сводный тест по задачам B15 (2 вариант)
- Как решать задачи про летающие камни?
Деление дробей друг на друга.
 Деление дроби на натуральное число
Деление дроби на натуральное числоОбыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей
- правильные;
- неправильные;
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
Рано или поздно, все дети в школе начинают изучать дроби: их сложение, деление, умножение и все возможные действия, которые только возможно выполнять с дробями. Чтобы оказать должную помощь ребенку, родителям самим не стоит забывать, как происходит деление целых чисел на дроби, иначе, вы не сможете ему ничем помочь, а лишь запутаете. Если вам понадобилось вспомнить данное действие, но вы никак не можете свести всю информацию в голове в единое правило, то данная статья вам поможет: вы научитесь делить число на дробь и увидите наглядные примеры.
Как разделить число на дробь
Запишите свой пример на черновик, чтобы у вас была возможность делать заметки и помарки. Помните, что целое число записывается между клеток, прямо на их пересечении, а дробные числа – каждая в своей клетке.
- В данном способе вам нужно перевернуть дробь вверх ногами, то есть, знаменатель записать в числитель, а числитель – в знаменатель.
- Знак деления нужно поменять на умножение.
- Теперь вам осталось выполнить умножение по уже изученным правилам: числитель умножается на целое число, а знаменатель не трогаете.

Конечно, в результате такого действия у вас получится очень большое число в числителе. В таком состоянии оставлять дробь нельзя – учитель попросту не примет этот ответ. Сократите дробь, разделив числитель на знаменатель. Целое число, которое получится в результате, запишите слева от дроби посередине клеток, а остаток и будет новым числителем. Знаменатель остается неизменным.
Этот алгоритм довольно прост, даже для ребенка. Выполнив его пять-шесть раз, малыш запомнит порядок действия и сможет применять его к любым дробям.
Как разделить число на десятичную дробь
Бывают дроби другого вида – десятичные. Деление на них происходит по совсем другому алгоритму. Если вы столкнулись с таким примером, то придерживайтесь инструкции:
- Для начала, превратите оба числа в десятичные дроби. Сделать это просто: делитель у вас и так представлен в виде дроби, а делимое натуральное число вы отделяете запятой, получая десятичную дробь. То есть, если делимое было числом 5, вы получаете дробь 5,0. Отделять число нужно на столько цифр, сколько стоит после запятой и делителя.
- После этого, обе десятичные дроби вы должны сделать натуральными числами. Сперва, вам покажется это немного запутанным, но это самый быстрый способ деления, который будет занимать у вас секунды, после нескольких тренировок. Дробь 5,0 станет числом 50, дробь 6,23 будет 623.
- Выполните деление. Если числа получились большие, либо деление будет происходить с остатком, выполните его в столбик. Так вы наглядно увидите все действия данного примера. Вам не нужно специально ставить запятую, так как она сама появится в процессе деления в столбик.
Данный вид деления изначально кажется слишком запутанным, так как вам нужно превратить делимое и делитель в дробь, а потом снова в натуральные числа. Но после недолгой тренировки, вы сразу станете видеть те числа, которые нужно просто разделить друг на друга.
Помните, что умение правильно делить дроби и целые числа на них могут ни раз пригодиться в жизни, поэтому, знать эти правила и простые принципы ребенку нужно идеально, чтобы в более старших классах они не стали камнем преткновения, из-за которого ребенок не может решать более сложные задачи.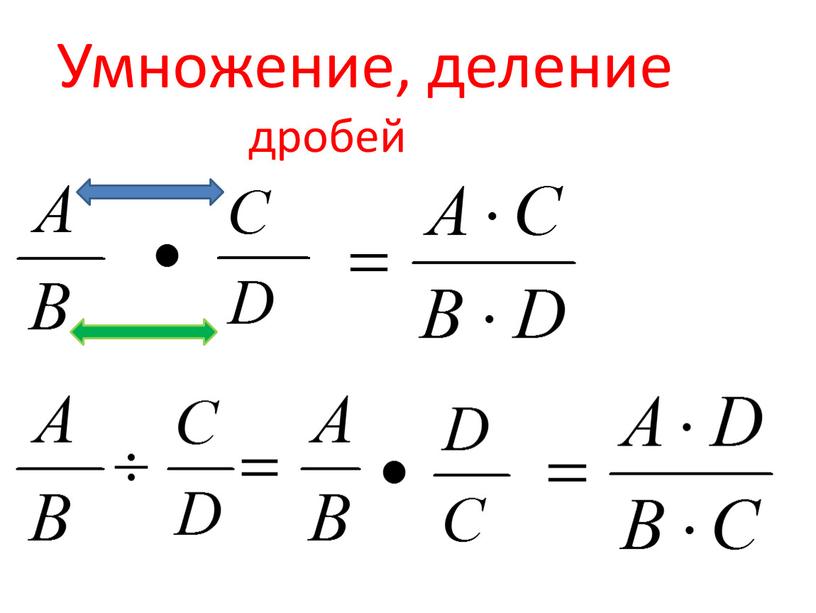
) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Например:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.
Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.
С дробями можно выполнять все действия, в том числе и деление. Данная статья показывает деление обыкновенных дробей. Будут даны определения, рассмотрены примеры. Подробно остановимся на делении дробей на натуральные числа и наоборот. Будет рассмотрено деление обыкновенной дроби на смешанное число.
Деление обыкновенных дробей
Деления является обратным умножению. При делении неизвестный множитель находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.
Если необходимо произвести деление обыкновенной дроби a b на c d , тогда для определения такого числа нужно произвести умножение на делитель c d , это даст в итоге делимое a b . Получим число и запишем его a b · d c , где d c является обратным c d числу. Равенства можно записать при помощи свойств умножения, а именно: a b · d c · c d = a b · d c · c d = a b · 1 = a b , где выражение a b · d c является частным от деления a b на c d .
Отсюда получим и сформулируем правило деления обыкновенных дробей:
Определение 1
Чтобы разделить обыкновенную дробь a b на c d , необходимо делимое умножить на число, обратное делителю.
Запишем правило в виде выражения: a b: c d = a b · d c
Правила деления сводятся к умножению. Чтобы придерживаться его, нужно хорошо разбираться в выполнении умножения обыкновенных дробей.
Перейдем к рассмотрению деления обыкновенных дробей.
Пример 1
Выполнить деление 9 7 на 5 3 . Результат записать в виде дроби.
Решение
Число 5 3 – это обратная дробь 3 5 . Необходимо использовать правило деления обыкновенных дробей. Это выражение запишем так: 9 7: 5 3 = 9 7 · 3 5 = 9 · 3 7 · 5 = 27 35 .
Ответ: 9 7: 5 3 = 27 35 .
При сокращении дробей следует выделять целую часть, если числитель больше знаменателя.
Пример 2
Разделить 8 15: 24 65 . Ответ записать в виде дроби.
Решение
Для решения нужно перейти от деления к умножению. Запишем это в такой форме: 8 15: 24 65 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Необходимо произвести сокращение, а это выполняется следующим образом: 8 · 65 15 · 24 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Выделяем целую часть и получаем 13 9 = 1 4 9 .
Ответ: 8 15: 24 65 = 1 4 9 .
Деление необыкновенной дроби на натуральное число
Используем правило деления дроби на натуральное число:чтобы разделить a b на натуральное число n , необходимо умножить только знаменатель на n . Отсюда получим выражение: a b: n = a b · n .
Правило деления является следствием правила умножения. Поэтому представление натурального числа в виде дроби даст равенство такого типа: a b: n = a b: n 1 = a b · 1 n = a b · n .
Рассмотрим данное деление дроби на число.
Пример 3
Произвести деление дроби 16 45 на число 12 .
Решение
Применим правило деления дроби на число. Получим выражение вида 16 45: 12 = 16 45 · 12 .
Произведем сокращение дроби. Получим 16 45 · 12 = 2 · 2 · 2 · 2 (3 · 3 · 5) · (2 · 2 · 3) = 2 · 2 3 · 3 · 3 · 5 = 4 135 .
Ответ: 16 45: 12 = 4 135 .
Деление натурального числа на обыкновенную дробь
Правило деления аналогично правилу деления натурального числа на обыкновенную дробь: чтобы разделить натуральное число n на обыкновенную a b , необходимо произвести умножение числа n на обратное дроби a b .
Исходя из правила, имеем n: a b = n · b a , а благодаря правилу умножения натурального числа на обыкновенную дробь, получим наше выражение в виде n: a b = n · b a . Необходимо рассмотреть данное деление на примере.
Пример 4
Делить 25 на 15 28 .
Решение
Нам необходимо переходить от деления к умножению. Запишем в виде выражения 25: 15 28 = 25 · 28 15 = 25 · 28 15 . Сократим дробь и получим результат в виде дроби 46 2 3 .
Ответ: 25: 15 28 = 46 2 3 .
Деление обыкновенной дроби на смешанное число
При делении обыкновенной дроби на смешанное числолегко можно свети к делению обыкновенных дробей. Нужно совершить перевод смешанного числа в неправильную дробь.
Пример 5
Разделить дробь 35 16 на 3 1 8 .
Решение
Так как 3 1 8 — смешанное число, представим его в виде неправильной дроби. Тогда получим 3 1 8 = 3 · 8 + 1 8 = 25 8 . Теперь произведем деление дробей. Получим 35 16: 3 1 8 = 35 16: 25 8 = 35 16 · 8 25 = 35 · 8 16 · 25 = 5 · 7 · 2 · 2 · 2 2 · 2 · 2 · 2 · (5 · 5) = 7 10
Ответ: 35 16: 3 1 8 = 7 10 .
Деление смешанного числа производится таким же образом, как и обыкновенных.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
- Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
правила, примеры, решения, как умножать десятичные дроби
В этой статье мы рассмотрим такое действие, как умножение десятичных дробей. Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)
Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)
В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.
Умножение десятичных дробей: общие принципы
Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.
Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.
Посмотрим, как решаются такие задачи.
Пример 1Вычислите произведение 1,5 и 0,75.
Решение: для начала заменим десятичные дроби на обыкновенные. Мы знаем, что 0,75 – это 75/100, а 1,5 – это 1510. Мы можем сократить дробь и произвести выделение целой части. Полученный результат 1251000 мы запишем как 1,125.
Ответ: 1,125.
Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.
Пример 2Умножьте одну периодическую дробь 0,(3) на другую 2,(36).
Решение
Для начала приведем исходные дроби к обыкновенным. У нас получится:
0,(3)=0,3+0,03+0,003+0,003+…=0,31-0,1=0,39=39=132,(36)=2+0,36+0,0036+…=2+0,361-0,01=2+3699=2+411=2411=2611
Следовательно, 0,(3)·2,(36)=13·2611=2633.
Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:
Ответ: 0,(3)·2,(36)=0,(78).
Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см. статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.
Пример 3Вычислите произведение 5,382… и 0,2.
Решение
У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5,382…≈5,38. Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5,38·0,2=538100·210=1 0761000=1,076.
Ответ: 5,382…·0,2≈1,076.
Как умножать десятичные дроби столбиком
Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:
Определение 1Умножение десятичных дробей столбиком выполняется в 2 шага:
1. Выполняем умножение столбиком, не обращая внимание на запятые.
2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.
Разберем примеры таких расчетов на практике.
Пример 4Умножьте десятичные дроби 63,37 и 0,12 столбиком.
Решение
Первым делом выполним умножение чисел, игнорируя десятичные запятые.
Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4. Дописывать нули не придется, т.к. знаков достаточно:
Ответ: 3,37·0,12=7,6044.
Пример 5Подсчитайте, сколько будет 3,2601 умножить на 0,0254.
Решение
Считаем без учета запятых. Получаем следующее число:
Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:
Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:
Ответ: 3,2601·0,0254=0,08280654.
Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д
Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:
Определение 2Если мы умножим десятичную дробь на 0,1, 0,01 и т.д., в итоге получится число, похожее на исходную дробь, запятая которого перенесена влево на нужное количество знаков. При нехватке цифр для переноса нужно дописывать нули слева.
Так, для умножения 45,34 на 0,1 надо перенести в исходной десятичной дроби запятую на один знак. У нас получится в итоге 4,534.
Пример 6Умножьте 9,4 на 0,0001.
Решение
Нам придется переносить запятую на четыре знака по количеству нулей во втором множителе, но цифр в первом для этого не хватит. Приписываем необходимые нули и получаем, что 9,4·0,0001=0,00094.
Ответ: 0,00094.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеДля бесконечных десятичных дробей мы пользуемся тем же правилом. Так, к примеру, 0,(18)·0,01=0,00(18) или 94,938…·0,1=9,4938…. и др.
Как перемножить десятичную дробь с натуральным числом
Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.
Пример 7Подсчитайте, сколько будет 15·2,27.
Решение
Умножим столбиком исходные числа и отделим два знака запятой.
Ответ: 15·2,27=34,05.
Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.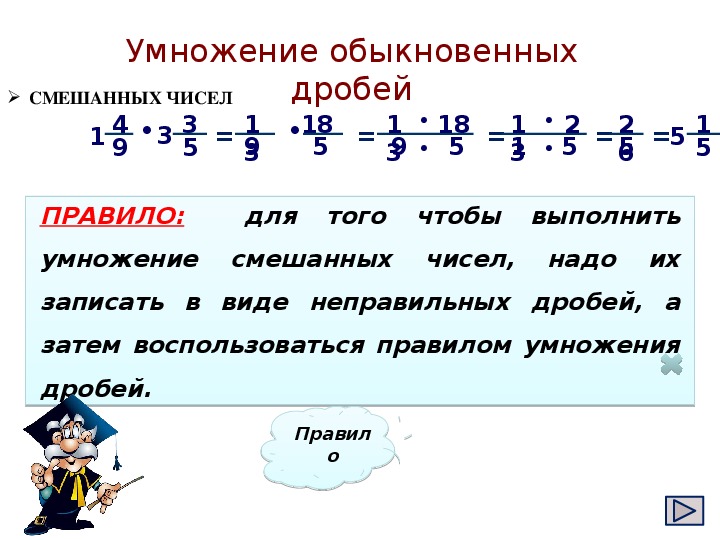
Вычислите произведение 0,(42) и 22.
Решение
Приведем периодическую дробь к виду обыкновенной.
0,(42)=0,42+0,0042+0,000042+…=0,421-0,01=0,420,99=4299=1433
Далее умножаем:
0,42·22=1433·22=14·223=283=913
Итоговый результат можем записать в виде периодической десятичной дроби как 9,(3).
Ответ: 0,(42)·22=9,(3).
Бесконечные дроби перед подсчетами надо предварительно округлить.
Пример 9Вычислите, сколько будет 4·2,145….
Решение
Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:
4·2,145…≈4·2,15=8,60.
Ответ: 4·2,145…≈8,60.
Как умножить десятичную дробь на 1000, 100, 10 и др
Умножение десятичной дроби на 10, 100 и др. часто встречается в задачах, поэтому мы разберем этот случай отдельно. Основное правило умножения звучит так:
Определение 3Чтобы умножить десятичную дробь на 1000, 100, 10 и др., нужно перенести ее запятую на 3, 2,1 цифры в зависимости от множителя и отбросить слева лишние нули. Если цифр для переноса запятой недостаточно, дописываем справа столько нулей, сколько нам нужно.
Покажем на примере, как именно это делать.
Пример 10Выполните умножение 100 и 0,0783.
Решение
Для этого нам надо перенести в десятичной дроби запятую на 2 цифры в правую сторону. Мы получим в итоге 007,83Нули, стоящие слева, можно отбросить и записать результат как 7,38.
Ответ: 0,0783·100=7,83.
Пример 11Умножьте 0,02 на 10 тысяч.
Решение: мы будем переносить запятую на четыре цифры вправо. В исходной десятичной дроби нам не хватит для этого знаков, поэтому придется дописывать нули. В этом случае будет достаточно трех 0. В итоге получилось 0,02000,перенесем запятую и получим 00200,0. Игнорируя нули слева, можем записать ответ как 200.
Ответ: 0,02·10 000=200.
Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.
Пример 12Вычислите произведение 5,32(672) на 1 000.
Решение: первым делом мы запишем периодическую дробь как 5,32672672672…, так вероятность ошибиться будет меньше. После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726).
Ответ: 5,32(672)·1 000=5 326,(726).
Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.
Как перемножить десятичную дробь с обыкновенной или со смешанным числом
Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.
Пример 13Умножьте 0,4 на 356
Решение
Cначала переведем десятичную дробь в обыкновенную. Имеем: 0,4=410=25.
Далее считаем: 0,4·356=25·236=2315=1815.
Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1,5(3).
Ответ: 1,5(3).
Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.
Пример 14Вычислите произведение 3,5678…·23
Решение
Второй множитель мы можем представить как 23=0,6666…. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3,568 и 0,667. Посчитаем столбиком и получим ответ:
Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2,379856≈2,380.
Ответ: 3,5678…·23≈2,380
Дробь. Умножение дробей обыкновенных, десятичных, смешанных. Умножение простых и смешанных дробей с разными знаменателями
В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа.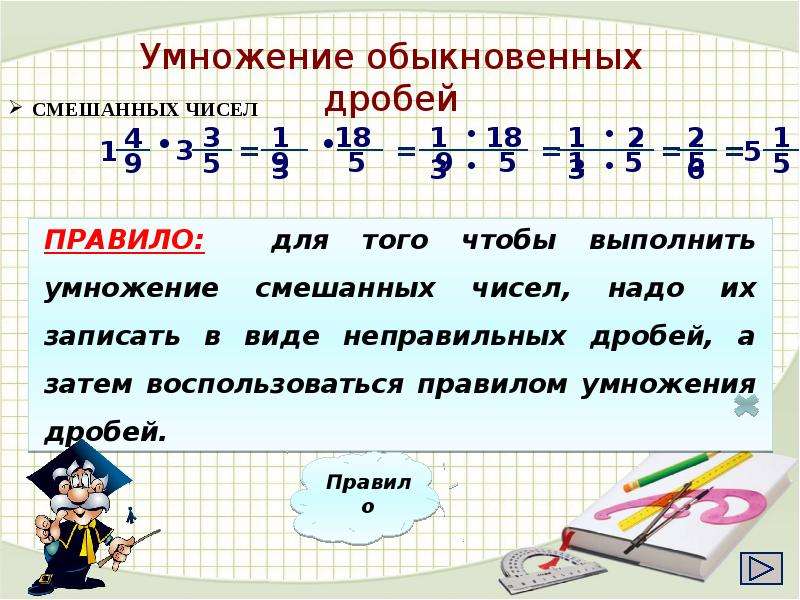 Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример . Представить дробь 7 21 / 1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное — целое;
- и остаток — числитель дробной части, причем знаменатель остается неизменным.
Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .
Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.

Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.
Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.
Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.
Пример . Найти произведение 4½ и 6 2 / 5.
Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.
Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример . Вычислить произведение 5 / 8 и 12.
Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Ответ : 7 1 / 2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример . Найти произведение 9 5 / 6 и 9.
Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Ответ : 88 1 / 2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1 . Найти произведение 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2 . Найти произведение 3,9 и 1000.
Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ : 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1 . Найти произведение 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2 . Найти произведение 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.
) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Например:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
Вызов 0-7 | 1) Организационный момент. Психологический настрой на урок. Чтоб урок наш стал светлее, Мы поделимся добром. Вы ладони протяните, В них любовь свою вложите, Ей с друзьями поделитесь И друг другу улыбнитесь. 2) Определение темы урока и постановка цели урока. Проблемный вопрос. Задача. Длина прямоугольника равна дм, ширина — дм. Найдите периметр и площадь прямоугольника? a — дм b — дм P — ? дм S — ? дм2 — Как найти периметр и площадь прямоугольника? (P = 2(a + b) S = ab) — Как найти периметр и площадь данного прямоугольника? P = 2 · = 2 · = 2 · = 2 · = — Чему мы должны научиться, чтобы решить данную задачу? (Умножать обыкновенные дроби, дробь на натуральное число, смешанные числа) — Какова тема сегодняшнего урока? (Умножение обыкновенных дробей) — Давайте её запишем в тетрадь. — Ребята, мы можем с вами умножать дроби друг на друга или дробь на натуральное число? (Нет) — Чему мы должны научиться за 45 минут? (Умножать обыкновенные дроби, смешанные числа, дробь на натуральное число) | Задача на доске, рабочая тетрадь. | Осмысление 8-40
|
Чтобы умножить дробь на дробь, надо умножить их числители и записать числителем, умножить их знаменатели и записать знаменателем. — Теперь мы можем найти площадь нашего прямоугольника? (Да) — Давайте найдём. дм2
Чтобы умножить обыкновенную дробь на натуральное число, надо числитель дроби умножить на это натуральное число и записать числитель, а знаменатель оставить тот же. — Теперь мы можем найти периметр нашего прямоугольника? (Да) — Давайте найдём. P = 2 · = 2 · = 2 · = 2 · = дм Ответ: P = 3 дм, S = дм2. 3. Как умножить смешанные числа? Чтобы умножить смешанное число на смешанное число, надо:
3) Взаимообучение. Работа в парах сменного состава. Приём «Велосипедная цепь». Учащиеся должны за 1 минуту объяснить друг другу выполнение примеров: 4) Проверочная работа по вариантам. Взаимопроверка. №№1077 (1-6), 1078 (1-6), 1079 (1-6)
| Видеоролик «Умножение дробей». Учебник «Математика-5» Алдамуратовой Т.А., часть 2 рабочая тетрадь. Примеры на доске, рабочая тетрадь, песочные часы. Карточки с заданием, лист с ответами (Приложение 1). |
Перекрестное умножение дробей — не бойтесь дробей
Перекрестное умножение дробей
Привет, ребята! Добро пожаловать в это видео о том, как скрестить дробей .
При перекрестном умножении дробей название как бы намекает на то, как это делается на самом деле.
Вы буквально умножаете на по горизонтали. Допустим, у вас есть две равные друг другу дроби. Итак, скажем, \ (\ frac {a} {b} = \ frac {c} {d} \).
Ну, чтобы перемножить их, вы умножаете числитель первой дроби на знаменатель второй дроби, а затем записываете это число.Затем вы умножаете числитель второй дроби на число в знаменателе вашей первой дроби и записываете это число.
Причина, по которой мы скрещиваем дроби умножения, заключается в их сравнении. Перекрестное умножение дробей говорит нам, равны ли две дроби или какая из них больше. Это особенно полезно, когда вы работаете с более крупными дробями, которые вы не знаете, как уменьшить.
Давайте взглянем на несколько числовых примеров.
Найдите наибольшую из двух дробей.
\ (\ frac {4} {26} = \ frac {7} {32} \).
Итак, когда мы перемножаем его, когда мы устанавливаем его равным, а затем перемножаем эти две дроби вместе, мы получаем 128. Итак, \ (4 \ times 32 = 128 \). И когда мы скрестим, умножим эти два, мы получим \ (7 \ times 26 = 182 \). Итак, мы знаем, что \ (\ frac {7} {32} \) больше, чем \ (\ frac {4} {26} \), потому что 182 больше 128.
Мы всегда должны помнить, что число, которое мы умноженный на наш числитель, представляет соответствующую дробь. Итак, это число (128) представляет эту дробь \ ((\ frac {4} {26}) \), а это число (182) представляет эту дробь \ ((\ frac {7} {32}) \).Я упоминаю об этом, потому что может быть немного запутанным видеть, как числа, взятые из двух разных дробей, умножаются вместе, но произведение представляет только одну из дробей, а не другую. 128 идет слева, чтобы представить \ (\ frac {4} {26} \), а \ (7 \ times 26 = 182 \) идет справа, чтобы представить эту дробь прямо здесь \ ((\ frac {7} {32}) \).
Перекрестное умножение дробей помогает нам увидеть, равны ли числа, а если нет, какие из них больше, а какие меньше. Но это не единственное его применение.Перекрестное умножение дробей может помочь нам найти неизвестные переменные в дробях.
Допустим, у нас есть две дроби \ (\ frac {9} {16} = \ frac {x} {27} \). Мы можем пересечь умножение в любое время, когда у нас есть дробь, равная другой дроби. Теперь, чтобы пересечь умножение, мы делаем то же самое, что и в нашем последнем примере. Мы берем числитель одной стороны и умножаем его на знаменатель другой стороны, и делаем то же самое с числителем другой стороны. В этом случае мы умножаем \ (9 \ times 27 \) и \ (16 \ times x \).Это даст нам \ (243 = 16x \). Теперь все, что нам нужно сделать, чтобы получить x сам по себе, — это разделить обе части на 16. Это сокращает, и это дает нам \ (x = \ frac {243} {16} \), и вы можете упростить это еще больше. Мы бы сделали то же самое, даже если в знаменателе стоит x , это не имеет значения.
Я надеюсь, что это видео о перекрестном умножении дробей было для вас полезным. Если это было полезно, и вы хотели бы получить дополнительную помощь, вы можете подписаться на наш канал, нажав ниже.
Увидимся в следующий раз!
Как умножать и делить дроби [Видео]
Умножение и деление дробей
Многие студенты по-настоящему боятся дробей. Однако, если вы помните, что представляет собой дробь , и несколько математических правил того, как работать с ними алгебраически, вы сможете уверенно обращаться с дробями. В этом видео мы рассмотрим, как умножать и делить дроби. Давайте начнем.
Мы должны начать с определения того, что такое дробь.Дробь представляет собой отношение «части» к «целому» или части к целому. Значение над линией деления называется числителем , а значение под линией деления — знаменателем .
Чтобы умножить дроби, просто умножьте «прямо поперек», то есть «числитель умноженный на числитель», разделенный на «знаменатель умноженный на знаменатель». Давайте посмотрим на пару быстрых примеров:
Здесь мы хотим умножить две трети на две пятых.Как мы уже говорили ранее, мы будем размножаться прямо поперек. Итак, у нас будет 2 умножить на 2, больше, 3 умножить на 5. Что равно четырем на пятнадцать. Итак, наш ответ — четыре пятнадцатых.
А теперь попробуем еще. Мы попробуем четыре седьмых раза три одиннадцатых.
Опять та же концепция. Мы собираемся умножить 4 на 3, разделить на 7 умножить на 11. Что дает нам 12 на 77, то есть двенадцать семьдесят седьмых.
Довольно просто, правда? Теперь давайте посмотрим на деление дробей.
Процесс деления на дроби немного отличается. Прежде чем мы перейдем к механике этого процесса, давайте рассмотрим интуитивно понятный пример деления дроби на два. Результат деления на 2 — это просто разрезание дроби пополам или простое умножение дроби на 1.
Итак, четыре пятых, разделенные на 2, на самом деле то же самое, что сказать четыре пятых, умноженные на половину. Затем он будет умножен, как мы это делали раньше. Итак, у нас 4 умножить на 1 равно четырем, более 5 умножить на два будет десять.Что затем упрощается до 2 вместо 5.
Другими словами, две пятых — это половина размера четырех пятых.
Точно так же деление дроби на 3 приведет к дроби, которая составляет одну треть размера оригинала:
Две пятых разделить на то же самое, что сказать две пятых, умноженные на одну треть, что дает вам два — пятнадцатые.
Итак, две пятых — это одна треть размера двух пятых.
Прежде чем обобщать этот процесс, давайте рассмотрим некоторые важные термины.Рассмотрим соотношение между 2 и половиной. Эти числа называются обратными друг другу, что означает, что числитель одного числа является знаменателем другого, и наоборот. Помните, что «2» можно записать в виде дроби, написав ее над «1», например: 2 на 1. Следовательно, 2 на 1 и половину являются обратными. То же самое верно для 3 и одной трети, потому что 3 можно записать как 3 на 1. Следовательно, 3 и одна треть являются обратными.
Имея это в виду, какую закономерность вы видите в процессе деления дробей?
Процесс деления дробей такой же, как умножение первой дроби на обратную величину второй. «сокращенная» версия этого многословного объяснения , которая может помочь вам запомнить процесс деления: «Сохранить, изменить, перевернуть»:
Вы «Сохраняете» первую дробь как есть;
Затем вы «меняете» операцию с деления на умножение;
И вы «переверните» (или возьмете обратную величину) вторую дробь.
После того, как эта корректировка сделана, просто следуйте правилам умножения дробей путем умножения числителей и деления на произведение знаменателей.
Вот пример использования процесса «сохранить, изменить, перевернуть»:
Допустим, мы хотим разделить три пятых на семь пятых. Мы оставим первую дробь как есть, изменим операцию с деления на умножение и перевернем второе число. Теперь мы просто умножаем наши числители, 3 умножить на 5 будет пятнадцать, больше, 5 умножить на 7 будет тридцать пять. А затем мы упрощаемся до трех седьмых.
Надеюсь, это видео было полезным! Спасибо за просмотр и удачной учебы!
Умножение и деление дробей — Предалгебра
Цели обучения
К концу этого раздела вы сможете:
- Упростить дроби
- Умножение дробей
- Найти обратные
- Разделить на дроби
Перед тем, как начать, пройдите тест на готовность.
- Найдите разложение на простые множители
Если вы пропустили эту задачу, просмотрите (рисунок). - Нарисуйте модель дроби
Если вы пропустили эту задачу, просмотрите (рисунок). - Найдите две дроби, эквивалентные
. Ответы могут отличаться. Допустимые ответы: и т. Д.
Если вы пропустили эту проблему, просмотрите (рисунок).
Упростите дроби
При работе с эквивалентными дробями вы увидели, что есть много способов записать дроби, которые имеют одинаковое значение или представляют одну и ту же часть целого.Как узнать, какой из них использовать? Часто мы будем использовать дробь в упрощенной форме .
Дробь считается упрощенной, если нет общих множителей, кроме числителя и знаменателя. Если у дроби есть общие множители в числителе и знаменателе, мы можем привести дробь к ее упрощенной форме, удалив общие множители.
Упрощенная дробь
Дробь считается упрощенной, если в числителе и знаменателе нет общих множителей.
Например,
Процесс упрощения дроби часто называют уменьшением дроби . В предыдущем разделе мы использовали свойство Equivalent Fractions Property, чтобы найти эквивалентные дроби. Мы также можем использовать свойство Equivalent Fractions в обратном порядке, чтобы упростить дроби. Мы переписываем свойство, чтобы отображать обе формы вместе.
Эквивалентные дроби Свойство
Если это числа, то где
Обратите внимание, что это общий множитель в числителе и знаменателе.Каждый раз, когда у нас есть общий множитель в числителе и знаменателе, его можно убрать.
Упростите дробь.
- Перепишите числитель и знаменатель, чтобы показать общие множители. При необходимости разложите числитель и знаменатель на простые числа.
- Упростите, используя свойство эквивалентных дробей, удалив общие множители.
- Умножьте оставшиеся множители.
Упростить:.
Упростить:.
Чтобы упростить отрицательную дробь, мы используем тот же процесс, что и на (рисунок). Не забывайте сохранять отрицательный знак.
Упростить:
Упростить:
После упрощения дроби всегда важно проверять результат, чтобы убедиться, что у числителя и знаменателя больше нет общих множителей. Помните, что определение упрощенной дроби: дробь считается упрощенной, если в числителе и знаменателе нет общих множителей.
Когда мы упрощаем неправильную дробь, нет необходимости заменять ее смешанным числом.
Упростить:
Упростить:
Упростите дробь.
- Перепишите числитель и знаменатель, чтобы показать общие множители. При необходимости разложите числитель и знаменатель на простые числа.
- Упростите, используя свойство эквивалентных дробей, удалив общие множители.
- Умножьте оставшиеся множители
Иногда бывает непросто найти общие множители числителя и знаменателя.Тогда хорошая идея — разложить числитель и знаменатель на простые числа. (Вы можете использовать метод факторного дерева для определения простых множителей.) Затем разделите общие множители, используя свойство Equivalent Fractions Property.
Упростить:
Упростить:
Упростить:
Мы также можем упростить дроби, содержащие переменные. Если переменная является общим множителем в числителе и знаменателе, мы удаляем ее так же, как и целочисленный множитель.
Упростить:
Упростить:
Умножение дробей
Модель может помочь вам понять умножение дробей. Мы будем использовать плитки с дробями для моделирования. Чтобы умножить и подумайте о
.Начните с дробных плиток на три четверти. Чтобы найти половину из трех четвертей, нам нужно разделить их на две равные группы. Поскольку мы не можем разделить три плитки равномерно на две части, мы меняем их на более мелкие плитки.
Мы видим, что взятие половины из шести плиток дает нам три плитки, что составляет
.Следовательно,
Выполнение задания по манипуляции с математикой «Модельное умножение дробей» поможет вам лучше понять, как умножать дроби.
Используйте схему для модели
Используйте схему для модели:
Используйте схему для модели:
Посмотрите на результат, который мы получили от модели на (Рисунок).Мы обнаружили, что вы заметили, что мы могли бы получить тот же ответ, умножив числители и умножив знаменатели?
| Умножьте числители и знаменатели. | |
| Упростить. |
Это приводит к определению умножения дроби. Чтобы умножить дроби, умножаем числители и умножаем знаменатели.Затем запишем дробь в упрощенном виде.
Умножение дробей
Если это числа, то где
Умножьте и запишите ответ в упрощенном виде:
Решение
| Умножаем числители; умножьте знаменатели. | |
| Упростить. |
Общих множителей нет, поэтому дробь упрощена.
Умножьте и запишите ответ в упрощенном виде:
Умножьте и запишите ответ в упрощенном виде:
При умножении дробей по-прежнему применяются свойства положительных и отрицательных чисел. В качестве первого шага рекомендуется определить знак продукта. В примере 4.26 мы умножим два отрицательных числа, так что произведение будет положительным.
Умножьте и запишите ответ в упрощенном виде:
Умножьте и запишите ответ в упрощенном виде:
Умножьте и запишите ответ в упрощенном виде:
Умножьте и запишите ответ в упрощенном виде:
Умножьте и запишите ответ в упрощенном виде:
При умножении дроби на целое число может оказаться полезным записать целое число в виде дроби.Любое целое число может быть записано, например, как So.
Умножьте и запишите ответ в упрощенном виде:
ⓐ
ⓑ
Умножьте и запишите ответ в упрощенном виде:
- ⓐ
- ⓑ
Умножьте и запишите ответ в упрощенном виде:
- ⓐ
- ⓑ
- ⓐ
- ⓑ
Найти взаимные значения
Дроби и связаны друг с другом особым образом.Итак, и вы видите, как? Помимо того, что они выглядят как перевернутые версии друг друга, если бы мы умножили эти пары дробей, произведение было бы
.Такие пары чисел называются обратными.
Чтобы найти величину, обратную дроби, мы инвертируем дробь. Это означает, что мы помещаем числитель в знаменатель, а знаменатель в числитель.
Чтобы получить положительный результат при умножении двух чисел, числа должны иметь одинаковый знак. Значит, у взаимных знаков должен быть один и тот же знак.
Чтобы найти обратную величину, сохраните тот же знак и инвертируйте дробь. Число ноль не имеет обратного значения. Почему? Число и его обратная величина умножаются на. Есть ли такое число, что нет. Итак, у числа нет обратной величины.
Решение
Чтобы найти обратные, мы сохраняем знак и инвертируем дроби.
Найдите обратное:
- ⓐ
- ⓑ
- ⓒ
- ⓓ
Найдите обратное:
- ⓐ
- ⓑ
- ⓒ
- ⓓ
В предыдущей главе мы работали с противоположностями и абсолютными значениями.(Рисунок) сравнивает противоположности, абсолютные значения и обратные.
| напротив | Абсолютное значение | Взаимный |
|---|---|---|
| имеет противоположный знак | никогда не бывает отрицательным | имеет тот же знак, дробь инвертирует |
Заполните таблицу для каждой дроби в левом столбце:
| Номер | напротив | Абсолютное значение | Взаимный |
|---|---|---|---|
Решение
Чтобы найти обратное, измените знак.Чтобы найти абсолютное значение, оставьте положительные числа такими же, но возьмите противоположные числа. Чтобы найти обратную величину, оставьте знак прежним и инвертируйте дробь.
Заполните таблицу для каждого указанного числа:
| Номер | напротив | Абсолютное значение | Взаимное |
|---|---|---|---|
Разделить на дроби
Почему это Мы ранее смоделировали это с помощью счетчиков.Сколько групп счетчиков можно составить из группы счетчиков?
Есть группы счетчиков. Другими словами, в Итак,
их четыре.А как насчет деления на дроби? Предположим, мы хотим найти частное: нам нужно выяснить, сколько их в. Мы можем использовать дробные плитки для моделирования этого деления. Начнем с того, что выстроим плитки половинной и шестой фракций, как показано на (Рисунок). Обратите внимание, в нем три плитки, поэтому
Выполнение задания по манипуляции с математикой «Модельное деление на дроби» поможет вам лучше понять деление дробей.
Модель:
Модель:
Модель:
Модель:
Модель:
Модель:
Давайте использовать деньги, чтобы моделировать по-другому. Мы часто читаем как «четверть», и мы знаем, что четверть доллара, как показано на (Рисунок). Итак, мы можем думать так: «Сколько четвертей в двух долларах?» Один доллар — это четверти, поэтому доллары будут четвертями.Итак, снова
Монета США, называемая четвертью, стоит четверть доллара.
Используя плитки с дробями, мы показали это. Обратите внимание и на это. Как связаны и связаны? Они взаимны. Это подводит нас к процедуре дробного деления.
Фракционный дивизион
Если это числа, то где
Чтобы разделить дроби, умножьте первую дробь на обратную величину второй.
Нам нужно сказать, чтобы убедиться, что мы не делим на ноль.
Разделите и запишите ответ в упрощенном виде:
Решение
| Умножьте первую дробь на обратную величину второй. | |
| Умножить. Товар отрицательный. |
Разделите и запишите ответ в упрощенном виде:
Разделите и запишите ответ в упрощенном виде:
Разделите и запишите ответ в упрощенном виде:
Решение
| Умножьте первую дробь на обратную величину второй. | |
| Умножить. |
Разделите и запишите ответ в упрощенном виде:
Разделите и запишите ответ в упрощенном виде:
Разделите и запишите ответ в упрощенном виде:
Разделите и запишите ответ в упрощенном виде:
Разделите и запишите ответ в упрощенном виде:
Разделите и запишите ответ в упрощенном виде:
Разделите и запишите ответ в упрощенном виде:
Разделите и запишите ответ в упрощенном виде:
Ключевые концепции
- Эквивалентные дроби Свойство
- Упростите дробь.
- Перепишите числитель и знаменатель, чтобы показать общие множители. При необходимости разложите числитель и знаменатель на простые числа.
- Упростите, используя свойство эквивалентных дробей, удалив общие множители.
- Умножьте оставшиеся множители.
- Умножение дробей
- Взаимный
- Число и его обратная величина имеют произведение.
Напротив Абсолютное значение Взаимное имеет противоположный знак никогда не бывает отрицательным имеет тот же знак, дробь инвертирует
- Фракционное подразделение
Практика ведет к совершенству
Упростить дроби
В следующих упражнениях упростите каждую дробь.Не переводите неправильные дроби в смешанные числа.
Умножение дробей
В следующих упражнениях используйте диаграмму для моделирования.
В следующих упражнениях умножьте и запишите ответ в упрощенной форме.
Найти обратные
В следующих упражнениях найдите обратное.
Заполните таблицу.
| напротив | Абсолютное значение | Взаимное | |
|---|---|---|---|
Разделить на дроби
В следующих упражнениях смоделируйте каждое дробное деление.
В следующих упражнениях разделите и запишите ответ в упрощенной форме.
Письменные упражнения
Объясните, как найти величину, обратную дроби.
Объясните, как найти обратную величину отрицательной дроби.
Приведите пример из повседневной жизни, демонстрирующий, как
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
Глоссарий
- обратная
- Обратное значение дроби — где и.
- упрощенная дробь
- Дробь считается упрощенной, если в числителе и знаменателе нет общих множителей.
операций над дробями | Колледж алгебры Corequisite
Результаты обучения
- Сложить или вычесть дроби.
- Упростите дроби.
- Умножение дробей.
- Разделить дроби.
Студенты-математики и работающие взрослые часто обнаруживают, что их знания о том, как складывать, вычитать, умножать и делить дроби, заржавели из-за неиспользования.Мы склонны полагаться на калькуляторы, которые делают за нас большую часть работы с дробями. Тем не менее, College Algebra разрабатывает некоторые важные методы работы с выражениями и уравнениями, основанными на операциях с дробями. Поэтому важно заново познакомиться с этими навыками. Этот раздел напомнит вам, как делать операции с дробями. По мере прохождения оставшейся части курса вы можете вернуть этот раздел по мере необходимости для быстрого напоминания об операциях с дробями.
Прежде чем мы начнем, давайте определимся с терминологией.
- произведение: результат умножения
- Коэффициент : что-то перемножаемое — для [латекс] 3 \ cdot 2 = 6 [/ latex] оба [latex] 3 [/ latex] и [latex] 2 [/ latex] являются факторами [latex] 6 [ / латекс]
- числитель: верхняя часть дроби — числитель дроби [латекс] \ Large \ frac {2} {3} [/ latex] равен [latex] 2 [/ latex]
- знаменатель : нижняя часть дроби — знаменатель дроби [латекс] \ Large \ frac {2} {3} [/ latex] равен [latex] 3 [/ latex]
Примечание к инструкциям
Определенные слова используются в учебниках математики и учителями, чтобы дать учащимся инструкции о том, что делать с той или иной задачей.Например, вы можете увидеть такие инструкции, как find или simpleify. Важно понимать, что означают эти слова, чтобы вы могли успешно решать задачи этого курса. Вот краткий список некоторых инструкций по проблемам вместе с их описаниями, поскольку они будут использоваться в этом модуле.
| Инструкция | Интерпретация |
|---|---|
| Найти | Выполните указанные математические операции, которые могут включать в себя сложение, вычитание, умножение, деление (позже использование слова найти будет расширено до решения уравнений, как в найти значение переменной). |
| Упростить | 1) Выполните указанные математические операции, включая сложение, вычитание, умножение, деление. 2) Напишите математическое утверждение в кратчайшие сроки, чтобы не было никаких других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями и порядком операций |
| Оценить | 1) Выполните указанные математические операции, включая сложение, вычитание, умножение, деление. 2) Заменить заданное значение переменной в выражении, а затем выполнить указанные математические операции |
| Уменьшить | Напишите математическое утверждение в наименьшем или наименьшем значении, чтобы не было никаких других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями или делением. |
Сложить дроби
Когда вам нужно сложить или вычесть дроби, вам нужно сначала убедиться, что дроби имеют одинаковый знаменатель.Знаменатель сообщает вам, на сколько частей было разбито целое, а числитель говорит вам, сколько из этих частей вы используете.
Концепцию «частей целого» можно смоделировать с помощью пиццы и кусочков пиццы. Например, представьте, что пицца разрезана на [латекс] 4 [/ latex] куска, и кто-то берет [латекс] 1 [/ latex] кусок. Теперь [латекс] \ Large \ frac {1} {4} [/ latex] пиццы исчез, а [latex] \ Large \ frac {3} {4} [/ latex] остается. Обратите внимание, что обе эти фракции имеют знаменатель [латекс] 4 [/ латекс], который относится к количеству ломтиков, на которые была нарезана вся пицца.Что делать, если у вас есть другая пицца, которая была разрезана на [латекс] 8 [/ latex] равных частей, а [латекс] 3 [/ latex] из этих частей исчезли, оставив [латекс] \ Large \ frac {5} {8} [/латекс]?
Как вы можете описать общее количество пиццы, которое осталось, одним числом, а не двумя разными дробями? Вам нужен общий знаменатель, технически называемый наименьшим общим кратным . Помните, что если одно число кратно другому, вы можете разделить их и не иметь остатка.
Один из способов найти наименьшее общее кратное двух или более чисел — сначала умножить каждое на [латекс] 1, 2, 3, 4 [/ латекс] и т. Д.Например, найдите наименьшее общее кратное для [латекс] 2 [/ латекс] и [латекс] 5 [/ латекс].
| Сначала перечислите все кратные [latex] 2 [/ latex]: | Затем перечислите все числа, кратные 5: |
| [латекс] 2 \ cdot 1 = 2 [/ латекс] | [латекс] 5 \ cdot 1 = 5 [/ латекс] |
| [латекс] 2 \ cdot 2 = 4 [/ латекс] | [латекс] 5 \ cdot 2 = 10 [/ латекс] |
| [латекс] 2 \ cdot 3 = 6 [/ латекс] | [латекс] 5 \ cdot 3 = 15 [/ латекс] |
| [латекс] 2 \ cdot 4 = 8 [/ латекс] | [латекс] 5 \ cdot 4 = 20 [/ латекс] |
| [латекс] 2 \ cdot 5 = 10 [/ латекс] | [латекс] 5 \ cdot 5 = 25 [/ латекс] |
Наименьшее кратное, которое у них есть общее, будет общим знаменателем, используемым для преобразования каждой дроби в эквивалентные дроби.См. Пример ниже для демонстрации нашей задачи с пиццей.
Пример
В одной пицце, разрезанной на четыре части, отсутствует одна. Еще одна пицца того же размера была разрезана на восемь частей, из которых три были удалены. Опишите общее количество пиццы, оставшееся в двух пиццах, используя общие термины.
Показать решение Перепишите дроби [latex] \ dfrac {3} {4} [/ latex] и [latex] \ dfrac {5} {8} [/ latex] как дроби с наименьшим общим знаменателем.Найдите наименьшее общее кратное знаменателей.Это наименьший общий знаменатель.
Кратные [latex] 4: 4, \ textbf {8}, 12,16, \ textbf {24} [/ latex]
Кратные [latex] 8: \ textbf {8}, 16, \ textbf {24} [/ latex]
Наименьший общий знаменатель [латекс] 8 [/ латекс] — наименьшее общее кратное.
Перепишите [латекс] \ dfrac {3} {4} [/ latex] со знаменателем [латекс] 8 [/ latex]. Вам нужно умножить верхнюю и нижнюю части на [latex] 2 [/ latex], чтобы не менять отношения между ними.
[латекс] \ dfrac {3} {4} \ cdot \ dfrac {2} {2} = \ dfrac {6} {8} [/ латекс]
Нам не нужно перезаписывать [latex] \ dfrac {5} {8} [/ latex], поскольку у него уже есть общий знаменатель.
Ответ
И [latex] \ dfrac {6} {8} [/ latex], и [latex] \ dfrac {5} {8} [/ latex] имеют одинаковый знаменатель, и вы можете описать, сколько пиццы осталось, с помощью общих терминов. . Сложите числители и поставьте их над общим знаменателем.
У нас остался [latex] \ dfrac {6} {8} [/ latex] из первой пиццы и [latex] \ dfrac {5} {8} [/ latex] из второй пиццы. Это [латекс] \ dfrac {11} {8} [/ latex] пиццы одинакового размера или [latex] 1 [/ latex] и [latex] \ dfrac {3} {8} [/ latex], пицца еще на столе.
Чтобы сложить дроби с разными знаменателями, сначала перепишите их с одинаковыми знаменателями. Затем сложите или вычтите числители над общим знаменателем.
Сложение дробей с разными знаменателями
- Найдите общий знаменатель.
- Записываем каждую дробь как эквивалентную дробь, используя общий знаменатель.
- Теперь, когда дроби имеют общий знаменатель, можно складывать числители.
- Упростите, отбросив все общие множители в числителе и знаменателе.
Упростите дробь
В математике принято представлять дроби в наименьших числах. Мы называем эту практику упрощением или сокращением дроби, и это может быть достигнуто путем отмены (деления) общих множителей в числителе и знаменателе дроби. Мы можем это сделать, потому что дробь представляет собой деление, и для любого числа [латекс] a [/ latex], [latex] \ dfrac {a} {a} = 1 [/ latex].
Например, чтобы упростить [latex] \ dfrac {6} {9} [/ latex], вы можете переписать [latex] 6 [/ latex] и [latex] 9 [/ latex], используя наименьшие возможные коэффициенты:
[латекс] \ dfrac {6} {9} = \ dfrac {2 \ cdot3} {3 \ cdot3} [/ латекс]
Поскольку и в числителе, и в знаменателе есть [латекс] 3 [/ латекс], а дроби можно считать делением, мы можем разделить [латекс] 3 [/ латекс] в верхней части на [латекс] 3 [/ латекс] внизу уменьшить до [латекс] 1 [/ латекс].
[латекс] \ dfrac {6} {9} = \ dfrac {2 \ cdot \ cancel {3}} {3 \ cdot \ cancel {3}} = \ dfrac {2 \ cdot1} {3} = \ dfrac { 2} {3} [/ латекс]
В следующем примере вам показано, как сложить две дроби с разными знаменателями, а затем упростить ответ.
Пример
Добавьте [латекс] \ Large \ frac {2} {3} + \ Large \ frac {1} {5} [/ latex]. Упростите ответ.
Показать решение Поскольку знаменатели не похожи, найдите общий знаменатель, умножив знаменатели.[латекс] 3 \ cdot5 = 15 [/ латекс]
Запишите каждую дробь со знаменателем [латекс] 15 [/ латекс].
[латекс] \ begin {array} {c} \ Large \ frac {2} {3} \ cdot \ Large \ frac {5} {5} = \ Large \ frac {10} {15} \\\\\ Большой \ frac {1} {5} \ cdot \ Large \ frac {3} {3} = \ Large \ frac {3} {15} \ end {array} [/ latex]
Сложите дроби, сложив числители и сохранив знаменатель прежним. Убедитесь, что дробь нельзя упростить.
[латекс] \ Large \ frac {10} {15} + \ Large \ frac {3} {15} = \ Large \ frac {13} {15} [/ latex]
Ответ
[латекс] \ Large \ frac {2} {3} + \ Large \ frac {1} {5} = \ Large \ frac {13} {15} [/ latex]
Вы можете найти общий знаменатель, найдя общие кратные знаменателей.Наименьшее общее кратное — самый простой в использовании.
Пример
Добавьте [латекс] \ Large \ frac {3} {7} + \ Large \ frac {2} {21} [/ latex]. Упростите ответ.
Показать решение Поскольку знаменатели не одинаковы, найдите наименьший общий знаменатель, найдя наименьшее общее кратное (НОК) 7 и 21.Кратные [latex] 7: 7, 14, \ textbf {21} [/ latex]
Множество [latex] 21: \ textbf {21} [/ latex]
Запишите каждую дробь со знаменателем [латекс] 21 [/ латекс].
[латекс] \ begin {array} {c} \ Large \ frac {3} {7} \ cdot \ Large \ frac {3} {3} = \ Large \ frac {9} {21} \\\\\ Большой \ frac {2} {21} \ end {array} [/ latex]
Сложите дроби, сложив числители и сохранив знаменатель прежним. Убедитесь, что дробь нельзя упростить.
[латекс] \ Large \ frac {9} {21} + \ Large \ frac {2} {21} = \ Large \ frac {11} {21} [/ latex]
Ответ
[латекс] \ Large \ frac {3} {7} + \ Large \ frac {2} {21} = \ Large \ frac {11} {21} [/ latex]
В следующем видео вы увидите пример того, как сложить две дроби с разными знаменателями.
Вы также можете сложить более двух дробей, если сначала найдете для них общий знаменатель. Пример суммы трех дробей показан ниже. В этом примере вы будете использовать метод простой факторизации, чтобы найти НОК.
Подумай об этом
Добавьте [latex] \ Large \ frac {3} {4} + \ Large \ frac {1} {6} + \ Large \ frac {5} {8} [/ latex]. Упростите ответ и напишите смешанное число.
Чем этот пример отличается от предыдущих? Воспользуйтесь рамкой ниже, чтобы записать несколько мыслей о том, как сложить три дроби с разными знаменателями.
Показать решение Поскольку знаменатели не похожи, найдите наименьший общий знаменатель, найдя наименьшее общее кратное (НОК) [латекс] 4, 6 [/ латекс] и [латекс] 8 [/ латекс].[латекс] 4 = 2 \ cdot2 \\ 6 = 3 \ cdot2 \\ 8 = 2 \ cdot2 \ cdot2 \\\ текст {LCM}: \, \, 2 \ cdot2 \ cdot2 \ cdot3 = 24 [/ латекс]
Запишите каждую дробь со знаменателем [латекс] 24 [/ латекс].
[латекс] \ begin {array} {c} \ Large \ frac {3} {4} \ cdot \ Large \ frac {6} {6} = \ Large \ frac {18} {24} \\\\\ Большой \ frac {1} {6} \ cdot \ Large \ frac {4} {4} = \ Large \ frac {4} {24} \\\\\ Large \ frac {5} {8} \ cdot \ Large \ frac {3} {3} = \ Large \ frac {15} {24} \ end {array} [/ latex]
Сложите дроби, сложив числители и сохранив знаменатель прежним.
[латекс] \ Large \ frac {18} {24} + \ Large \ frac {4} {24} + \ Large \ frac {15} {24} = \ Large \ frac {37} {24} [/ латекс ]
Запишите неправильную дробь как смешанное число и упростите дробь.
[латекс] \ Large \ frac {37} {24} = \ normalsize 1 \, \, \ Large \ frac {13} {24} [/ latex]
Ответ
[латекс] \ Large \ frac {3} {4} + \ Large \ frac {1} {6} + \ Large \ frac {5} {8} = \ normalsize 1 \ Large \ frac {13} {24} [/ латекс]
Вычесть дроби
Вычитание дробей происходит по той же технике, что и их сложение.Во-первых, определите, одинаковы ли знаменатели. Если нет, перепишите каждую дробь как эквивалентную дробь с одинаковым знаменателем. Ниже приведены несколько примеров вычитания дробей, знаменатели которых не совпадают.
Пример
Вычтите [латекс] \ Large \ frac {1} {5} — \ Large \ frac {1} {6} [/ latex]. Упростите ответ.
Показать решение У дробей разные знаменатели, поэтому вам нужно найти общий знаменатель. Напомним, что общий знаменатель можно найти, умножив два знаменателя вместе.[латекс] 5 \ cdot6 = 30 [/ латекс]
Перепишем каждую дробь как эквивалентную дробь со знаменателем [латекс] 30 [/ латекс].
[латекс] \ begin {array} {c} \ Large \ frac {1} {5} \ cdot \ Large \ frac {6} {6} = \ Large \ frac {6} {30} \\\\\ Большой \ frac {1} {6} \ cdot \ Large \ frac {5} {5} = \ Large \ frac {5} {30} \ end {array} [/ latex]
Вычтите числители. При необходимости упростите ответ.
[латекс] \ Large \ frac {6} {30} — \ Large \ frac {5} {30} = \ Large \ frac {1} {30} [/ latex]
Ответ
[латекс] \ Large \ frac {1} {5} — \ Large \ frac {1} {6} = \ Large \ frac {1} {30} [/ latex]
Пример ниже показывает, как использовать кратные для нахождения наименьшего общего кратного, который будет наименьшим общим знаменателем.
Пример
Вычтите [латекс] \ Large \ frac {5} {6} — \ Large \ frac {1} {4} [/ latex]. Упростите ответ.
Показать решение Найдите наименьшее общее кратное знаменателей — это наименьший общий знаменатель.Кратное [латекс] 6: 6, \ textbf {12}, 18, 24 [/ latex]
Кратные [latex] 4: 4, 8, \ textbf {12}, 16, 20 [/ latex]
[латекс] 12 [/ латекс] является наименее распространенным кратным [латекса] 6 [/ латекса] и [латекса] 4 [/ латекса].
Запишите каждую дробь со знаменателем [латекс] 12 [/ латекс].
[латекс] \ begin {array} {c} \ Large \ frac {5} {6} \ cdot \ Large \ frac {2} {2} = \ Large \ frac {10} {12} \\\\\ Большой \ frac {1} {4} \ cdot \ Large \ frac {3} {3} = \ Large \ frac {3} {12} \ end {array} [/ latex]
Вычтите дроби. При необходимости упростите ответ.
[латекс] \ Large \ frac {10} {12} — \ Large \ frac {3} {12} = \ Large \ frac {7} {12} [/ latex]
Ответ
[латекс] \ Large \ frac {5} {6} — \ Large \ frac {1} {4} = \ Large \ frac {7} {12} [/ latex]
В следующем видео вы увидите пример вычитания дробей с разными знаменателями.
Умножение дробей
Подобно тому, как вы складываете, вычитаете, умножаете и делите при работе с целыми числами, вы также используете эти операции при работе с дробями. Часто бывает необходимо умножать дроби. Модель может помочь вам понять умножение дробей.
Когда вы умножаете дробь на дробь, вы получаете «дробь дроби». Предположим, у вас есть [latex] \ Large \ frac {3} {4} [/ latex] шоколадного батончика, и вы хотите найти [latex] \ Large \ frac {1} {2} [/ latex] [latex] ] \ Large \ frac {3} {4} [/ latex]:
Разделив каждую четвертую пополам, вы можете разделить моноблок на восьмые.
Затем выберите половину из них, чтобы получить [latex] \ Large \ frac {3} {8} [/ latex].
В обоих вышеупомянутых случаях, чтобы найти ответ, вы можете перемножить числители и знаменатели.
Умножение двух дробей
[латекс] \ Large \ frac {a} {b} \ cdot \ Large \ frac {c} {d} = \ Large \ frac {a \ cdot c} {b \ cdot d} = \ Large \ frac {\ text {произведение числителей}} {\ text {произведение знаменателей}} [/ латекс]
Умножение более двух дробей
[латекс] \ Large \ frac {a} {b} \ cdot \ Large \ frac {c} {d} \ cdot \ Large \ frac {e} {f} = \ Large \ frac {a \ cdot c \ cdot e} {b \ cdot d \ cdot f} [/ латекс]
Пример
Умножьте [латекс] \ Large \ frac {2} {3} \ cdot \ Large \ frac {4} {5} [/ latex]
Показать решение Умножьте числители и знаменатели.[латекс] \ Large \ frac {2 \ cdot 4} {3 \ cdot 5} [/ латекс]
Упростите, если возможно. Эта доля уже на самом низком уровне.
[латекс] \ Large \ frac {8} {15} [/ латекс]
Ответ
[латекс] \ Large \ frac {8} {15} [/ латекс]
Чтобы проверить: если дробь имеет общие делители в числителе и знаменателе, мы можем уменьшить дробь до ее упрощенной формы, удалив общие множители.
Например,
- Учитывая [латекс] \ Large \ frac {8} {15} [/ latex], коэффициенты [latex] 8 [/ latex] таковы: [latex] 1, 2, 4, 8 [/ latex] и Факторами [латекс] 15 [/ латекс] являются: [латекс] 1, 3, 5, 15 [/ латекс].[latex] \ Large \ frac {8} {15} [/ latex] упрощен, потому что нет общих факторов [latex] 8 [/ latex] и [latex] 15 [/ latex].
- Учитывая [латекс] \ Large \ frac {10} {15} [/ latex], коэффициенты [latex] 10 [/ latex] равны: [latex] 1, 2, 5, 10 [/ latex] и коэффициенты из [латекса] 15 [/ латекса] являются: [латекс] 1, 3, 5, 15 [/ латекс]. [latex] \ Large \ frac {10} {15} [/ latex] не упрощается, потому что [latex] 5 [/ latex] является общим фактором [latex] 10 [/ latex] и [latex] 15 [/ latex] ].
Вы можете сначала упростить, прежде чем умножать две дроби, чтобы облегчить вашу работу.Это позволяет вам работать с меньшими числами при умножении.
В следующем видео вы увидите пример того, как умножить две дроби, а затем упростить ответ.
Подумай об этом
Умножьте [латекс] \ Large \ frac {2} {3} \ cdot \ Large \ frac {1} {4} \ cdot \ Large \ frac {3} {5} [/ latex]. Упростите ответ.
Чем этот пример отличается от предыдущих? Воспользуйтесь рамкой ниже, чтобы записать несколько мыслей о том, как бы вы умножили три дроби вместе.
Показать решение Умножьте числители и знаменатели.[латекс] \ Large \ frac {2 \ cdot 1 \ cdot 3} {3 \ cdot 4 \ cdot 5} [/ латекс]
Сначала упростите, исключив (разделив) общие множители [латекс] 3 [/ латекс] и [латекс] 2 [/ латекс]. [латекс] 3 [/ латекс] разделить на [латекс] 3 [/ латекс] равно [латекс] 1 [/ латекс], а [латекс] 2 [/ латекс] разделить на [латекс] 2 [/ латекс] будет [латекс] ] 1 [/ латекс].
[латекс] \ begin {array} {c} \ Large \ frac {2 \ cdot 1 \ cdot3} {3 \ cdot (2 \ cdot 2) \ cdot 5} \\\ Large \ frac {\ cancel {2} \ cdot 1 \ cdot \ cancel {3}} {\ cancel {3} \ cdot (\ cancel {2} \ cdot 2) \ cdot 5} \\\ Large \ frac {1} {10} \ end {array} [/ латекс]
Ответ
[латекс] \ Large \ frac {2} {3} \ cdot \ Large \ frac {1} {4} \ cdot \ Large \ frac {3} {5} [/ latex] = [латекс] \ Large \ frac {1} {10} [/ латекс]
Разделить на дроби
Бывают случаи, когда вам нужно использовать деление для решения проблемы.Например, если для нанесения одного слоя краски на стены комнаты требуется [латекс] 3 [/ латекс] кварты краски, и у вас есть ведро, содержащее [латекс] 6 [/ латекс] квартов краски, сколько слоев краски краска ты можешь рисовать на стенах? Вы разделите [латекс] 6 [/ латекс] на [латекс] 3 [/ латекс] и получите ответ в размере [латекс] 2 [/ латекс] пальто. Также будут моменты, когда вам нужно будет разделить на дробь. Предположим, для покраски туалета в один слой требуется только [латекс] \ Large \ frac {1} {2} [/ latex] литр краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить [latex] 2 [/ latex] на дробь, [latex] \ Large \ frac {1} {2} [/ latex].
Прежде чем мы начнем делить дроби, давайте рассмотрим некоторые важные термины.
- обратное: две дроби являются обратными, если их продукт [латекс] 1 [/ латекс] (не волнуйтесь, мы покажем вам примеры того, что это означает.)
- частное: результат деления
Для деления дробей необходимо использовать обратную величину числа или дроби. Если вы умножите два числа и в результате получите [latex] 1 [/ latex], то эти два числа будут обратными.Вот несколько примеров обратных:
| Оригинальный номер | Взаимное | Товар |
|---|---|---|
| [латекс] \ Large \ frac {3} {4} [/ латекс] | [латекс] \ Large \ frac {4} {3} [/ латекс] | [латекс] \ Large \ frac {3} {4} \ cdot \ Large \ frac {4} {3} = \ Large \ frac {3 \ cdot 4} {4 \ cdot 3} = \ Large \ frac {12 } {12} = 1 [/ латекс] |
| [латекс] \ Large \ frac {1} {2} [/ латекс] | [латекс] \ Large \ frac {2} {1} [/ латекс] | [латекс] \ Large \ frac {1} {2} \ cdot \ Large \ frac {2} {1} = \ Large \ frac {1 \ cdot2} {2 \ cdot1} = \ Large \ frac {2} { 2} = 1 [/ латекс] |
| [латекс] 3 = \ Large \ frac {3} {1} [/ latex] | [латекс] \ Large \ frac {1} {3} [/ латекс] | [латекс] \ Large \ frac {3} {1} \ cdot \ Large \ frac {1} {3} = \ Large \ frac {3 \ cdot 1} {1 \ cdot 3} = \ Large \ frac {3 } {3} = 1 [/ латекс] |
| [латекс] 2 \ Large \ frac {1} {3} = \ Large \ frac {7} {3} [/ latex] | [латекс] \ Large \ frac {3} {7} [/ латекс] | [латекс] \ Large \ frac {7} {3} \ cdot \ Large \ frac {3} {7} = \ Large \ frac {7 \ cdot3} {3 \ cdot7} = \ Large \ frac {21} { 21} = \ normalsize 1 [/ latex] |
Иногда мы называем обратное «переворотом» другого числа: flip [latex] \ Large \ frac {2} {5} [/ latex], чтобы получить обратное [latex] \ Large \ frac {5} {2} [/ латекс].
Дивизион по нулю
Вы знаете, что значит разделить на [латекс] 2 [/ латекс] или разделить на [латекс] 10 [/ латекс], но что значит разделить количество на [латекс] 0 [/ латекс]? Это вообще возможно? Можете ли вы разделить [латекс] 0 [/ латекс] на число? Рассмотрим дробь
[латекс] \ Large \ frac {0} {8} [/ латекс]
Мы можем читать это как «ноль, деленный на восемь». Поскольку умножение — это обратное деление, мы могли бы переписать это как задачу умножения.
[латекс] \ text {?} \ Cdot {8} = 0 [/ латекс].
Мы можем сделать вывод, что неизвестное должно быть [латекс] 0 [/ латекс], поскольку это единственное число, которое даст результат [латекс] 0 [/ латекс] при умножении на [латекс] 8 [/ латекс] .
Теперь давайте рассмотрим обратную величину [latex] \ Large \ frac {0} {8} [/ latex], которая будет [latex] \ Large \ frac {8} {0} [/ latex]. Если мы перепишем это как задачу умножения, у нас будет
[латекс] \ text {?} \ Cdot {0} = 8 [/ латекс].
В этом нет никакого смысла. Нет чисел, которые можно умножить на ноль, чтобы получить результат 8.Обратное значение [latex] \ Large \ frac {8} {0} [/ latex] не определено, и фактически все деление на ноль не определено.
Осторожность! Деление на ноль не определено, равно как и обратная величина для любой дроби, числитель которой равен нулю. Для любого действительного числа a [latex] \ Large \ frac {a} {0} [/ latex] не определено. Кроме того, значение, обратное [latex] \ Large \ frac {0} {a} [/ latex], всегда будет неопределенным.Разделить дробь на целое число
Когда вы делите на целое число, вы умножаете на обратное.В примере с покраской, где вам нужно [латекс] 3 [/ латекс] кварты краски для покрытия и у вас есть [латекс] 6 [/ латекс] квартов краски, вы можете найти общее количество слоев, которые можно покрасить, разделив [ латекс] 6 [/ латекс] by [латекс] 3 [/ латекс], [латекс] 6 \ div3 = 2 [/ латекс]. Вы также можете умножить [латекс] 6 [/ latex] на обратное значение [latex] 3 [/ latex], то есть [latex] \ Large \ frac {1} {3} [/ latex], так что проблема умножения станет
[латекс] \ Large \ frac {6} {1} \ cdot \ Large \ frac {1} {3} = \ Large \ frac {6} {3} = \ normalsize2 [/ latex]
Деление — это умножение на обратное
Для любого деления вы можете превратить операцию в умножение, используя обратную величину.Деление аналогично умножению на обратное.
Та же идея будет работать, когда делитель (то, что делится) является дробью. Если у вас есть [латекс] \ Large \ frac {3} {4} [/ latex] шоколадного батончика и вам нужно разделить его между [latex] 5 [/ latex] людьми, каждый человек получит [latex] \ Large \ frac {1} {5} [/ latex] из имеющихся конфет:
[латекс] \ Large \ frac {1} {5} \ normalsize \ text {of} \ Large \ frac {3} {4} = \ Large \ frac {1} {5} \ cdot \ Large \ frac {3 } {4} = \ Large \ frac {3} {20} [/ latex]
Каждый человек получает [латекс] \ Large \ frac {3} {20} [/ latex] целого шоколадного батончика.
Если у вас есть рецепт, который нужно разделить пополам, вы можете разделить каждый ингредиент на [латекс] 2 [/ latex], или вы можете умножить каждый ингредиент на [латекс] \ Large \ frac {1} {2} [ / latex], чтобы найти новое количество.
Например, деление на [латекс] 6 [/ латекс] аналогично умножению на обратную величину [латекс] 6 [/ латекс], то есть [латекс] \ Large \ frac {1} {6} [/ latex ]. Посмотрите на схему двух пицц ниже. Как можно справедливо разделить то, что осталось (заштрихованная красным область) среди [латексных] 6 [/ латексных] людей?
Каждый человек получает один кусок, поэтому каждый получает [латекс] \ Large \ frac {1} {4} [/ latex] пиццы.
Деление дроби на целое число аналогично умножению на обратную, поэтому вы всегда можете использовать умножение дробей для решения задач деления.
Пример
Найдите [латекс] \ Large \ frac {2} {3} \ div \ normalsize 4 [/ latex]
Показать решение Напишите свой ответ самым простым языком.Деление на [латекс] 4 [/ латекс] или [латекс] \ Large \ frac {4} {1} [/ latex] аналогично умножению на обратную величину [латекс] 4 [/ латекс], то есть [ латекс] \ Large \ frac {1} {4} [/ latex].
[латекс] \ Large \ frac {2} {3} \ normalsize \ div 4 = \ Large \ frac {2} {3} \ cdot \ Large \ frac {1} {4} [/ latex]
Умножение числителей и знаменателей.
[латекс] \ Large \ frac {2 \ cdot 1} {3 \ cdot 4} = \ Large \ frac {2} {12} [/ latex]
Упростите до наименьших значений, разделив числитель и знаменатель на общий коэффициент [латекс] 4 [/ латекс].
[латекс] \ Large \ frac {1} {6} [/ латекс]
Ответ
[латекс] \ Large \ frac {2} {3} \ normalsize \ div4 = \ Large \ frac {1} {6} [/ latex]
Пример
Разделить.[латекс] 9 \ div \ Large \ frac {1} {2} [/ латекс]
Показать решение Напишите свой ответ самым простым языком.Деление на [латекс] \ Large \ frac {1} {2} [/ latex] аналогично умножению на обратную величину [latex] \ Large \ frac {1} {2} [/ latex], то есть [ латекс] \ Large \ frac {2} {1} [/ latex].
[латекс] 9 \ div \ Large \ frac {1} {2} = \ Large \ frac {9} {1} \ cdot \ Large \ frac {2} {1} [/ latex]
Умножение числителей и знаменателей.
[латекс] \ Large \ frac {9 \ cdot 2} {1 \ cdot 1} = \ Large \ frac {18} {1} = \ normalsize 18 [/ latex]
Этот ответ уже упрощен до минимума.
Ответ
[латекс] 9 \ div \ Large \ frac {1} {2} = \ normalsize 18 [/ latex]
Разделить дробь на дробь
Иногда нужно решить задачу, требующую деления на дробь. Предположим, у вас есть пицца, которая уже нарезана [латексными] 4 [/ латексными] ломтиками. Сколько там кусочков [latex] \ Large \ frac {1} {2} [/ latex]?
Есть [латексные] 8 [/ латексные] ломтики. Вы можете видеть, что деление [latex] 4 [/ latex] на [latex] \ Large \ frac {1} {2} [/ latex] дает тот же результат, что и умножение [latex] 4 [/ latex] на [latex] 2 [/латекс].
Что бы произошло, если бы вам нужно было разделить каждый кусок на три части?
У вас будет [latex] 12 [/ latex] срезов, что эквивалентно умножению [latex] 4 [/ latex] на [latex] 3 [/ latex].
Деление на дроби
- Найдите обратное число после символа деления.
- Умножьте первое число (число перед символом деления) на величину, обратную второму числу (число после символа деления).
Любой простой способ запомнить, как делить дроби, — это фраза «сохранить, изменить, перевернуть.Это означает: СОХРАНИТЬ первое число, ИЗМЕНИТЬ знак деления для умножения, а затем FLIP (использовать обратную величину) второго числа.
Пример
Разделить [латекс] \ Large \ frac {2} {3} \ div \ Large \ frac {1} {6} [/ latex]
Показать решение Умножьте на обратное.KEEP [латекс] \ Large \ frac {2} {3} [/ latex]
ИЗМЕНИТЬ [латекс] \ div [/ latex] на [латекс] \ cdot [/ latex]
FLIP [латекс] \ Large \ frac {1} {6} [/ латекс]
[латекс] \ Large \ frac {2} {3} \ cdot \ Large \ frac {6} {1} [/ latex]
Умножение числителей и знаменателей.
[латекс] \ Large \ frac {2 \ cdot6} {3 \ cdot1} = \ Large \ frac {12} {3} [/ latex]
Упростить.
[латекс] \ Large \ frac {12} {3} = \ normalsize 4 [/ latex]
Ответ
[латекс] \ Large \ frac {2} {3} \ div \ Large \ frac {1} {6} = \ normalsize 4 [/ latex]
Пример
Разделить [латекс] \ Large \ frac {3} {5} \ div \ Large \ frac {2} {3} [/ latex]
Показать решение Умножьте на обратное. Сохраните [латекс] \ Large \ frac {3} {5} [/ latex], замените [latex] \ div [/ latex] на [latex] \ cdot [/ latex] и переверните [латекс] \ Large \ frac { 2} {3} [/ латекс].[латекс] \ Large \ frac {3} {5} \ cdot \ Large \ frac {3} {2} [/ latex]
Умножение числителей и знаменателей.
[латекс] \ Large \ frac {3 \ cdot 3} {5 \ cdot 2} = \ Large \ frac {9} {10} [/ latex]
Ответ
[латекс] \ Large \ frac {3} {5} \ div \ Large \ frac {2} {3} = \ Large \ frac {9} {10} [/ latex]
При решении задачи деления умножением на обратную не забудьте записать все целые и смешанные числа как неправильные дроби. Окончательный ответ следует упростить и записать смешанным числом.
В следующем видео вы увидите пример того, как разделить целое число на дробь, а также пример того, как разделить дробь на другую дробь.
% PDF-1.5 % 1 0 obj> эндобдж 2 0 obj> эндобдж 3 0 obj> эндобдж 5 0 obj> / Font> / ProcSet [/ PDF / Text] >> / Group 20 0 R / PieceInfo> / LastModified (D: 20050415105228-07’00 ‘) >> эндобдж 7 0 obj> эндобдж 8 0 obj> эндобдж 9 0 obj> поток %! PS-Adobe-3.0 %% Создатель: Adobe Illustrator (R) 10.0 %% AI8_CreatorVersion: 10.0 %% Для: (\ 712) () %% Заголовок: (Div. Of Fractions.pdf) %% CreationDate: 15.04.05, 10:52 %% BoundingBox: 31 28 592 923 %% HiResBoundingBox: 31,3223 28,9854 591,8838 922,8579 %% DocumentProcessColors: голубой, пурпурный, желтый, черный % AI5_FileFormat 6.0 % AI3_ColorUsage: Цвет % AI7_ImageSettings: 0 %% CMYKProcessColor: 1 1 1 1 ([Регистрация]) %% AI6_ColorSeparationSet: 1 1 (набор цветоделения AI6 по умолчанию) %% + Варианты: 1 16 0 1 0 1 0 0 0 0 1 1 1 18 0 0 0 0 0 0 0 -1-1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 2 3 4 %% + PPD: 1 21 0 0 60 45 2 2 1 0 0 1 0 0 0 0 0 0 0 0 0 0 () % AI3_TemplateBox: 306.5 395,5 306,5 395,5 % AI3_TileBox: 13 11 601 779 % AI3_DocumentPreview: Нет % AI5_ArtSize: 612 792 % AI5_RulerUnits: 0 % AI9_ColorModel: 2 % AI5_ArtFlags: 1 0 0 1 0 0 1 0 0 % AI5_TargetResolution: 800 % AI5_NumLayers: 1 % AI9_OpenToView: -342 892 1 1268 972 26 1 1 6 42 0 0 1 1 1 0 % AI5_OpenViewLayers: 7 %% PageOrigin: 13 11 %% AI3_PaperRect: -12 780 600 -12 %% AI3_Margin: 12-12-12 12 % AI7_GridSettings: 72 8 72 8 1 0 0 0 0 0,5 0,5 0,5 % AI9_Flatten: 0 %% EndComments конечный поток эндобдж 10 0 объект / DeviceGray эндобдж 11 0 объект / DeviceCMYK эндобдж 12 0 obj> эндобдж 13 0 obj> эндобдж 14 0 obj> эндобдж 15 0 obj> эндобдж 16 0 obj> эндобдж 17 0 obj> эндобдж 18 0 obj> эндобдж 19 0 obj> эндобдж 20 0 obj> эндобдж 21 0 obj> поток HkY ?.XiHaP
Калькулятор умножения дробей. Смешанные / целые числа
С помощью этого калькулятора умножения дробей вы быстро научитесь выполнять умножение дробей, будь то простые дроби , неправильные дроби или смешанные числа . Кроме того, вы узнаете, как умножить дроби на целые числа , и даже умножение трех дробей больше не будет препятствием. Помните, что в нашем инструменте вы можете умножать до пяти дробей — круто, не правда ли? 😍
Если вы хотите проверить, как работают другие операции с дробями, взгляните на наш универсальный калькулятор дробей.
Как умножать дроби?
Умножение дробей — это не ракетостроение, поверьте нам. Вам нужно только уметь умножать числа и упрощать дроби!
Допустим, у вас есть две дроби: 3/5 и 5/8. Как умножить эти дроби?
3 / 5 * 5 / 8 =?
- Умножить числитель на другой числитель, а знаменатель на другой знаменатель :
3 / 5 * 5 / 8 = (3 * 5) / (5 * 8) = 15 / 40
Если бы у вас было больше дробей, чем две, процесс был бы аналогичным: умножьте все числители вместе, чтобы получить новый числитель, и проделайте то же самое со знаменателями, чтобы получить новый знаменатель.
- При необходимости упрощаем дробь :
15 / 40 = 3 / 8
Для уменьшения найдите наибольший общий делитель числителя и знаменателя и разделите их на это значение.
Если вы хотите получить некоторое представление о том, как работает умножение дробей, взгляните на этот рисунок:
Как умножить дробь на целые числа?
Когда дело доходит до умножения дробей на целые числа, это еще проще! Почему? Помните, что вы можете записать каждое целое число в виде дроби , что равно , превышающему 1 .
В качестве проблемы со словами вы можете представить ее, как семь человек, пришедших на вашу вечеринку в честь Хэллоуина 🎃👻🕷️. Вы купили три тыквенных пирога и разрезали каждый пирог на шесть равных ломтиков. Теперь вам интересно, хватит ли всем, если каждый из ваших гостей захочет съесть два ломтика тыквенного пирога
- Подумайте о проблеме: как записать один кусок пирога дробью? Вы разрезаете каждый пирог на шесть частей и вынимаете из него одну часть. Так будет:
1 / 6
- Вы знаете, что каждый гость хочет съесть два ломтика.У вас будет семь гостей (допустим, вы не едите, потому что вы не большой поклонник тыквенного пирога). Итак, вам нужно 7 (гости) умножить на 2/6 (2 части из 6):
7 * 2 / 6 🥧
7 * 2 / 6
- Умножая дробь на целое число, мы выполняем ту же операцию, что и при умножении простых дробей: мы умножаем числители на числители и знаменатели на знаменатели.Как мы писали ранее, вы всегда можете написать целое число вместо одного:
7 = 7 / 1
Наконец:
7 * 2 / 6 = 7 / 1 * 2 / 6 = (7 * 2) / (1 * 6) = 14 / 6 = 2 2 / 6 = 2 1 / 3
Итак, удачи! 🍀 Вы можете накормить всех своих голодных гостей тремя пирожками 🥧🥧🥧! Проверьте результат с помощью нашего калькулятора умножения дробей и посмотрите пошаговое решение, если у вас есть какие-либо сомнения.
Как умножить смешанные дроби? Умножение смешанных чисел
Умножение смешанных чисел также несложно, если вы знаете, как умножать простые дроби. Для этого нужен только один дополнительный шаг в начале — изменение с смешанной дроби на неправильную дробь :
. Допустим, мы хотим перемножить смешанные числа 2 3 / 5 и 1 1 / 6
Для начала превратите смешанную дробь 2 3 / 5 в неправильную дробь:
- Умножьте знаменатель на целое число:
2 * 5 = 10
- Добавьте к результату числитель :
10 + 3 = 13
Это числитель вашей неправильной дроби.
- Знаменатель остается тем же , что и в исходном смешанном числе. В нашем примере это
5:
13 / 5
Повторите процедуру для 1 1 / 6 . Вы получите эквивалент смешанного числа в неправильной дробной форме:
1 1 / 6 = ((6 * 1) + 1) / 6 = 7 / 6
Затем умножьте дроби как обычно:
13 / 5 * 7 / 6 = (13 * 7) / (5 * 6) = 91 / 30
Вы также можете изменить результат обратно с неправильной дроби на смешанное число:
91 / 30 = 3 1 / 30
Умножение дробей на смешанные числа
Задача умножения дробей на смешанные числа очень похожа на проблему, с которой мы только что имели дело — умножение смешанных чисел.На этот раз одна ваша дробь представлена в простой форме, а другая — в форме смешанной дроби.
Решение простое: вам нужно оставить вашу простую дробь в ее текущей форме , и, опять же, изменить смешанную дробь на неправильную форму . Затем, следуя стандартной процедуре, вы получите результат умножения дробей на смешанные числа.
Пример 1: умножение трех дробей
После такого тщательного прочтения мы уверены, что вы знаете все об умножении дробей: как умножать простые дроби, как умножать дроби на целые числа и как умножать смешанные дроби.Итак, самое время проверить , как работает наш калькулятор умножающих дробей!
Давайте выберем сценарий, о котором раньше не говорили — попробуем умножить на три дроби : 3 / 4 , 1 5 / 6 и - 2 / 7 . Обратите внимание, что мы также умножаем дроби на смешанные числа, так как у нас есть одна дробь в смешанной форме. Итак, как рассчитать это с помощью нашего инструмента?
- Выберите вид дроби. Так как у вас есть одна дробь в смешанной форме, выберите этот вариант.
- Введите данные :
- Для первой дроби оставьте поле целое число пустым (или введите 0), введите 3 в поле числителя и 4 в знаменатель один;
- Для второй дроби введите 1 как целое число, 5 в качестве числителя и 6 в качестве знаменателя; и
- Для третьей дроби оставьте поле целое число снова пустым, введите -2 в поле числителя и 7 в поле знаменателя.
- И все, калькулятор умножения дробей покажет вам результат умножения трех дробей! Это — 11 / 28 .
- Чтобы понять процесс, ознакомьтесь с пошаговым решением .
Пример 2: умножение дроби на целое число
Давайте проанализируем другой пример: умножение дроби 7 / 8 на 13 , которое, конечно же, является целым числом.
Выберите тип дроби из раскрывающегося списка. Выберите смешанную форму, так как вам понадобится целая дробная часть.
Введите дроби :
- Первый числитель 7, а знаменатель 8 (вся часть остается пустой)
- В целой части второй дроби введите 13, а дробную часть оставьте пустой
- Калькулятор умножения дробей отображает результат:
91 / 8, что составляет11 3 / 8в смешанной числовой форме.Очень просто!
Вы также можете использовать форму простой дроби, изменив целое число на 13 / 1 😎
Сложение, вычитание, разделение и умножение дробей
Инструкции по эксплуатации
- Введите дроби в калькулятор выше.
- Выберите математическую операцию, которую вы хотите выполнить (сложение, вычитание, умножение, деление), используя серое раскрывающееся поле выбора между двумя дробями.
- Результаты будут обновляться автоматически при изменении любого значения в калькуляторе.
- Флажок под калькулятором позволяет выбрать между уменьшением дроби до эквивалента наименьшего общего знаменателя (если установлен) или отказом от уменьшения (если флажок не установлен).
Как вычислить дроби вручную
Как складывать дроби
- Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
- Умножьте каждый числитель на те же числа, на которые были умножены знаменатели.
- Сложите числители.
- Уменьшить результат до наиболее упрощенного числа.
Как вычесть дроби
- Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
- Умножьте каждый числитель на те же числа, на которые были умножены знаменатели.
- Складываем второй числитель с первого.
- Уменьшить результат до наиболее упрощенного числа.
Как умножать дроби
- Умножьте числа сверху вместе.
- Умножьте числа внизу вместе.
- Уменьшить результат до наиболее упрощенного числа.
Как разделить дроби
- Переверните вторую дробь вверх дном, чтобы получить обратное число.
- Умножьте дроби вместе (как в разделе умножения выше).
- Уменьшить результат до наиболее упрощенного числа.
Дроби: история, актуальность и популярное использование
— Руководство Автор: Корин Б. Аренас , опубликовано 22 октября 2019 г.
Практически каждый день мы имеем дело с дробями. Подумай об этом. Независимо от того, получаете ли вы четвертинки для разнообразия, покупаете одежду со скидкой 75% или готовите с половиной стакана масла, вы используете дроби.
В этом разделе мы поговорим о происхождении дробей, их важности при передаче информации и золотом сечении.
Что такое дроби?
Дроби представляют части целого числа или любое количество равных частей. Он функционирует чтобы описать, как части соотносятся с целым числом.
Для иллюстрации представьте целое число как торт. Если вы разрежете торт на 4 равные части, один кусок будет частью этого торта. В данном случае это 1/4 часть всего торта.
- 1 представляет один фрагмент или часть целого числа, которое называется числителем .
- 4 представляет, сколько всего частей содержится в целом числе, которое называется знаменателем .
Краткая история дробей
Слово Происхождение: Термин дробь происходит от латинского слово fractio что означает «сломать». В раннем английском языке это означает «сломанный кусок или фрагмент ». Английское слово« разрушение »также имеет то же происхождение слова.
Концепция дробей существует более 4000 лет.Но у разных цивилизаций есть свой способ стандартизации дробей для универсального использования.
Египтяне
Согласно Математика на протяжении веков : Мягкая история для учителей и других, египтяне были одними из первых, кто придумал форму дроби еще в 1800 году до нашей эры. Их концепция в основном ограничивалась частями, иначе известными как единичные дроби. Дроби единиц используют 1 в качестве числителя.
Египетские математики создали систему с основанием 10. идея, которая похожа на системы счисления, которые мы используем сегодня.Цифра иероглифы представляли их числа, что означает символы, соответствующие определенное значение.
Поскольку числитель всегда равен 1, они должны были указать только знаменатель. Египтяне отметили знаменатель овалом или точкой над значением. Вот несколько примеров из книги «Математика сквозь века» :
.Части были выражены как суммы долей единиц. Однако система не позволяла повторять дроби единиц в этой последовательности, что затрудняло выполнение расчетов.Чтобы решить эту проблему, египтяне создали обширные списки таблиц, в которых указаны двойные значения различных частей.
Вавилоняне
Другая цивилизация, создавшая сложную систему для По словам преподавателя математики и автора Лиз Памфри, фракции принадлежали вавилонянам.
вавилоняне организовали фракции в группы по 60 человек (основание 60). Сегодня мы обычно группируем числа в группы по 10. Но для вычислений, таких как углы и минуты для времени, мы также используем основание 60.Система сгруппировала дроби по 10 и использовала два символа, один для единицы, а другой для 10.
Ниже приведены символы, представляющие вавилонскую систему счисления от 1 до 20:
.Однако у них не было символа нуля (который они позже добавили около 311 года до н.э.) или знака, который функционировал как десятичная точка для обозначения дробей целого числа. Это затрудняло интерпретацию чисел.
Например, цифры ниже читаются как 12 и 15.
По словам Памфри, символы также могут читаться как разные значения:
| х60 | Единицы измерения | Шестидесятые | Число |
|---|---|---|---|
| 12 | 15 | ||
| 12 | 15 | 720 + 15 |
- 12 и 15 как отдельные номера
- 15/12
- 12 15/60
- 720 + 15
Как видите, отсутствие индикатора дроби делает его трудно отделить целые числа от дробей.Скорее всего, они полагались на контекст, чтобы разобраться в числовых значениях.
Как египетская, так и вавилонская системы были переданы позже людям в Греции, а затем и к средиземноморской цивилизации.
Греки
В Греции практика использования дробных величин в качестве сумм единицы дроби были довольно распространены до средневековья. Например, Liber Abbaci итальянского математика Фибоначчи — это примечательный текст 13 века. В нем широко использовались дроби, описывающие различные способы преобразования других дробей в суммы единичных дробей.
Чтобы лучше понять, ниже приводится таблица греческого языка. цифровые символы. Обратите внимание, что они такие же, как буквы в греческом алфавит:
| Значение | Единицы измерения | Десятки | Сотни |
|---|---|---|---|
| 1 | α | ι | ρ |
| 2 | β | κ | σ |
| 3 | γ | λ | τ |
| 4 | δ | µ | υ |
| 5 | ε | ν | φ |
| 6 | ϝ | ξ | χ |
| 7 | ζ | ο | ψ |
| 8 | η | π | ω |
| 9 | θ | ϙ | ϡ |
греческий запись дробей требует от читателя понимания контекста для правильного интерпретация.Чтобы выделить дробь, они ставят диакритический знак знак (‘) после знаменателя дроби.
Например, число β (2) становится ½ при записи с диакритический знак, β ’.
Аналогично, µβ (42) становится 1/42 при записи в µβ ’.
Однако здесь возникает путаница: µβ ’может также означать 40 ½. Вот почему понимание контекста имеет решающее значение при интерпретации греческих дробей.
Римлянам
У римлян дроби выражались только словами, которые усложняли любые вычисления.
Их система была основана на единице веса, называемой «as». При таком подходе 1 «as» равнялось 12 унций (римский базовая единица измерения, основа современной унции). Таким образом, дроби имеют знаменатели со значениями кратными 12.
В таблице ниже указаны римские дроби. с соответствующими условиями:
| Дробь | Римский термин |
|---|---|
| 11/12 | deunx для de uncia, забрал 1/12 |
| 10/12 | декстанов для декстанов, отнято 1/6 |
| 9/12 | dodrans for de quadrans, 1/4 отнято |
| 8/12 | bes — bi as for duae partes, 2/3 |
| 7/12 | перегородка для septem unciae |
| 6/12 | полуфабрикаты |
| 5/12 | quincunx для quinque unciae |
| 4/12 | триенс |
| 3/12 | квадранты |
| 2/12 | секстан |
| 1/12 | UNCIA |
| 1/24 | semuncia |
| 1/48 | сицилийский |
| 1/72 | сценарий |
| 1/144 | сценарий |
| 1/288 | scrupulum |
китайский
Китайцы написали Девять Главы по математическому искусству , датируемые примерно 100 годом до н. Э.С. Он включает текст о дробях, аналогичный тем, которые мы используем сегодня.
Согласно Math Through the Ages , он содержал большинство обычных правил вычисления с дробями, например, как складывать, делить и умножать дроби, а также сокращать дробь до наименьшего значения.
Однако в их системе не использовались неправильные дроби. Например, вместо неправильной дроби 9/4 они использовали бы ее эквивалентную смешанную дробь 2 1/4.
В отличие от западной математики, китайцы сосредоточились на практических приложениях, а не на теоретических рассуждениях и геометрии.
Индейцы
Индейцы разработали способ записи дробей, ближе к тому, что мы используем сегодня.
До 1000 г. до н.э. индуистские мантры в ранний ведический период вызывали силы от десяти до сотни, даже до триллиона, согласно сайту The Story of Mathematics. Это свидетельство того, что ранняя индийская цивилизация использовала сложные математические операции, включая дроби, квадраты, кубы и корни.
Около 500 г. до н. Э. Они изобрели систему письма, называемую брахми, которая состояла из 9 цифровых символов и нуля. Учитель математики и писатель Лиз Памфри отмечает, что эти числа во многом повлияли на современные числа, которые мы используем сегодня. См. Изображение ниже.
Индийская система записывала дроби, помещая одно значение поверх другого, точно так же, как сегодня числитель пишется над знаменателем. Однако они не поставили между ними черту. Например, дробь 4/5 будет выглядеть так:
Позже эту систему использовали арабы при торговле с индейцами.Именно арабы нарисовали черту, чтобы отличить верхнее число от нижнего числа в дроби. В конечном итоге это привело к тому, что в современную эпоху мы пишем дроби.
Как дроби улучшают способ передачи информации
Согласно доктору Петерсону из MathForum.org: «дроби были изобретены, чтобы обеспечить способ работы с величинами меньше единицы».
Если люди использовали только целые числа, единственный способ сослаться на меньшие количества — использовать меньшие единицы.Это то, что сделали римляне — они использовали целые числа при измерении футов и использовали дюймы, когда им нужно было учитывать меньшие единицы.
Например, вместо 1/12 фута они будут обозначать длину как 1 дюйм, а 1/4 фута будет 3 дюйма. Но что, если вы имеете в виду 2 с половиной фута? Как насчет 1 и 3/4 фута?
Если вы выбираете стандартную длину в соответствии с футами, это сбивает с толку одновременное упоминание футов и дюймов. По сути, фракции позволяют проводить измерения без необходимости создания новые юниты.Было бы лучше учесть измерения в последовательная мода.
США, как правило, больше используют дроби (английское измерение), поскольку они используют чашки, а не весы для измерения при приготовлении пищи и выпечке.
американца еще не приняли метрическую систему, которая является десятичная система, в которой используются единицы, относящиеся к десятичному коэффициенту. Метрическая система обычно использует граммы и литры вместо американских единиц измерения. за унции, чашки, пинты и так далее.
В таблице ниже показано преобразование объема из английской единицы измерения в ее метрический эквивалент:
США в метрические единицы преобразования объема
| Стандартное количество в США (на английском языке) | Метрический эквивалент |
|---|---|
| 1 чайная ложка | 5 мл |
| 1 столовая ложка 608259 | |
| 1/4 стакана или 2 жидких унции | 60 мл |
| 1/3 стакана | 80 мл |
| 1/2 стакана или 4 жидких унции | 125 мл |
| 2/3 стакана | 160 мл |
| 3/4 стакана или 6 жидких унций | 180 мл |
| 1 стакан или 8 жидких унций или 1/2 пинты | 250 мл |
| 1 ½ стакана или 12 жидких унций | 375 мл |
| 2 чашки или 1 пинта или 16 жидких унций | 500 мл |
| 3 чашки или 1 ½ пинты | 700 мл |
| 4 чашки или 2 пинты или 2 пинты 1 кварта | 950 мл |
| 4 кварты или 1 галлон | 3.8 л |
| 1 унция | 28 граммов |
| 1/4 фунта (4 унции) | 112 граммов |
| 1/2 фунта (8 унций) | 225 граммов |
| 337 грамм | |
| 1 фунт (16 унций) | 450 грамм |
Более того, сохранение измерений в одной единице позволяет нам складывать, вычитать, умножать и легко делить дроби.Это устраняет проблему преобразования, которая невозможна при измерении между двумя разными единицами.
Чтобы упростить вычисление дробей, воспользуйтесь калькулятором в верхней части этой страницы.
В то время как десятичные дроби предоставляют альтернативный способ обозначения дроби (и более простой способ вычисления дробей с помощью калькулятора), это необходимо понимать традиционные дроби и то, как их значения влияют на целое число.
По данным Thoughtco.com, студенты, которые не осваивают дроби в ранние годы, имеют тенденцию запутаться и испытать математическое беспокойство.Они также упомянули половину американской восьмерки. грейдеры не могут расположить дроби по значению.
Интуитивное обучение дробям помогает детям развить более широкое понимание теоретических математических концепций, позволяя им использовать их в реальной жизни. Это намного лучше, чем запоминать таблицы с единицами измерения или символами.
Золотое сечение и последовательность Фибоначчи
В математике соотношение — это, по сути, сравнение двух числа, которые зависят от типа сравниваемых чисел.
Вы можете встретить такой пример: 1: 3 или 1 из 3. Например, бутылка концентрата апельсинового сока состоит из 1 части апельсина. сок и 3 части воды. Это также можно записать в виде дроби, 1/3.
Коэффициенты относятся к дробям, потому что они сравнивают разные ценности, которые могут представлять собой целое. В этом примере бутылка целиком апельсинового сока.
Золотое сечение — специальное число, представленное греческим символом фи ( φ ) с приблизительным значением 1.618.
Получается путем разделения линии на 2 части, так что длинный отрезок (а) деленная на короткую часть (б) равна всей длине, разделенной на длинный раздел.
Чтобы лучше понять, вот иллюстрация со стандартным уравнением:
Исторически сложилось так, что соотношение соблюдалось в древних такие сооружения, как Парфенон и пирамиды Египта. В Великой пирамиде Гизы отношение основания к высоте примерно 1.5717, что является близко к золотому сечению. Он также встречается в повторяющихся закономерностях в природе, таких как как лепестки цветов, ракушки, ветви деревьев и спиральные галактики.
С другой стороны, Фибоначчи последовательность — еще одна известная математическая формула. Последовательность получена из сумма двух предшествующих чисел. Многие источники говорят, что Леонардо Фибоначчи (Леонардо Пизанский) популяризировал его в своей книге Liber Abacci .
Но согласно Live Science, математик Кейт Девлин, автор книги Finding Fibonacci: The Quest to «Откройте для себя заново забытого математического гения, который изменил мир », — говорится в сообщении. что Леонардо Фибоначчи на самом деле не «открыл» последовательность.
Древние санскритские письма, в которых использовались индуистско-арабские цифры системы были первыми, кто обсудил это за столетия до Леонардо Фибоначчи.
Последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811 и так далее…
Когда математики создают квадраты на основе этой последовательности, они могут нарисовать спираль.
Как золотое сечение связано с последовательностью Фибоначчи?
Исследователи заметили, что когда вы берете любые два последовательных числа Фибоначчи, их отношение очень близко к золотому сечению.Таким образом, φ составляет примерно 1,618. Чтобы дать вам представление, см. Таблицу ниже.
| A | B | B / A |
|---|---|---|
| 2 | 3 | 1,5 |
| 3 | ||
| 3 | 8 | 1,6 |
| 8 | 13 | 1,625 |
Нижняя линия
Понятие дроби разработали разные древние цивилизации.Одними из первых, кто изобрели дробную систему с обширными таблицами, были египтяне. Другие древние общества, такие как вавилоняне, греки, римляне и китайцы, также внесли свой вклад в его улучшение. Но на современные цифры и то, как мы пишем дроби, в основном повлияли индейцы, которые ввели индуистско-арабскую систему счисления.
Использование дробей помогает нам легко передавать информацию об измерениях. Это не позволяет людям использовать разные единицы измерения, что упрощает их расчет.
Наконец, дроби связаны со знаменитым золотым рационом и последовательностью Фибоначчи, которая во многом повлияла на то, как мы проектируем все виды структур.
Об авторе
Корин — страстный исследователь и автор финансовых тем, изучающий экономические тенденции, их влияние на население, а также то, как помочь потребителям принимать более мудрые финансовые решения. Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма в Филиппинском университете, одном из ведущих учебных заведений в мире, и степень бакалавра коммуникационных искусств в колледже Мириам.
 Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.