5.4.2. Примеры сокращения обыкновенных дробей.

Главная » 5 класс. Математика. » 5.4.2. Примеры сокращения обыкновенных дробей

Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 15.5k. Опубликовано 3 июня 2012

Деление и числителя и знаменателя дроби на их общий делитель, отличный от единицы, называют сокращением дроби.

Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число.

Это число является наибольшим общим делителем числителя и знаменателя данной дроби.

Возможны следующие формы записи решения примеров на сокращение обыкновенных дробей.

Учащийся вправе выбрать любую форму записи.

 

Примеры. Упростить дроби.

Сократим дробь на 3 (делим числитель на 3;

делим знаменатель на 3).

 

 

Сокращаем дробь на 7.

 

 

 

Выполняем указанные действия в числителе и знаменателе дроби.

Полученную дробь сокращаем на 5.

 

 

Сократим данную дробь 4) на 5·7³ — наибольший общий делитель (НОД) числителя и знаменателя, который состоит из общих множителей числителя и знаменателя, взятых в степени с наименьшим показателем.

 

 

Разложим числитель и знаменатель этой дроби на простые множители.

 

Получаем: 756=2²·3³·7 и 1176=2³·3·7².

Определяем НОД (наибольший общий делитель) числителя и знаменателя дроби 5).

Это произведение общих множителей, взятых с наименьшими показателями.

НОД(756; 1176)=2²·3·7.

 

 

Делим числитель и знаменатель данной дроби на их НОД, т. е. на 2²·3·7 получаем несократимую дробь 9/14.

А можно было записать разложения числителя и знаменателя  в виде произведения простых множителей, не применяя понятие степени, а затем произвести сокращение дроби, зачеркивая одинаковые множители в числителе и знаменателе. Когда одинаковых множителей не останется — перемножаем оставшиеся множители отдельно в числителе и отдельно в знаменателе и выписываем получившуюся дробь 9/14.

И, наконец, можно было сокращать данную дробь 5) постепенно, применяя признаки деления чисел и к числителю и к знаменателю дроби. Рассуждаем так: числа 756 и 1176 оканчиваются четной цифрой, значит, оба делятся на 2. Сокращаем дробь на 2. Числитель и знаменатель новой дроби — числа 378 и 588 также делятся на 2. Сокращаем дробь на 2. Замечаем, что число 294 — четное, а 189 — нечетное, и сокращение на 2 уже невозможно. Проверим признак делимости чисел 189 и 294 на 3.

(1+8+9)=18 делится на 3 и (2+9+4)=15 делится на 3, следовательно, и сами числа 189 и 294 делятся на 3. Сокращаем дробь на 3.  Далее, 63 делится на 3, а 98 — нет. Перебираем другие простые множители. Оба числа делятся на 7. Сокращаем дробь на 7 и получаем несократимую дробь 9/14.

сокращение обыкновенной дроби

( 4 оценки, среднее 4.75 из 5 )

VI. Основное свойство дроби.

Теорема 4. Числитель и знаменатель дроби можно разделить и умножить на одно и то же натуральное число. В результате получим дробь, равную данной.

Доказательство. Возьмем дробь . Пусть m=km₁

n=kn₁

Докажем, что

По теореме 1:

Домножим:

Левые и правые части равны, т.е. дроби .

Теорема доказана

VII.

Использование основного свойства дроби

Основное свойство дроби используется при сокращении дробей и приведении их к общему знаменателю.

Сократить дробь – это значит заменить дробь равной ей дробью, но с меньшим числителем и знаменателем. Существует 2 приема сокращения дробей:

1. Последовательное сокращение на небольшие числа, которые являются общими делителями числителя и знаменателя.

2. Сокращение числителя и знаменателя на них НОД.

Привести дроби к общему знаменателю – значит заменить данные дроби равными им дробями, имеющие одинаковые знаменатели. Общий знаменатель двух дробей является их НОК.

и

НОК(28; 42)=

Таким образом, можно сформулировать следующий алгоритм приведения чисел к наименьшему общему знаменателю:

1. Найти НОК знаменателей данный дробей.

2. Найти дополнительные множители для каждой дроби путем деления НОК на соответствующий знаменатель.

3. Умножение числителя и знаменателя каждой дроби на соответствующий дополнительный множитель.

VIII. Действия над рациональными числами

1. Сумма положительных рациональных чисел.

Определение. Суммой 2х положительных рациональных чисел с одинаковыми знаменателями и называется рациональное число с тем же знаменателем и числителем, равным сумме числителей слагаемых .

Теорема 5. Сумма рациональных чисел не зависит от выбора представителей из классов равных дробей.

Доказательство. Пусть даны рациональные числа и . Возьмем для каждой из данных дробей еще по одному представителю из их классов, т.е. и .

Докажем, что .

По определению суммы: ,

Из равенств и следует:

Сложим эти равенства почленно:

Теорема доказана.

IX. Свойства сложения рациональных чисел

Свойство 1. Сложение целых неотрицательных чисел является частными случаем сложения дробей с одинаковыми знаменателями.

Свойство 2. Сумма двух положительных рациональных чисел всегда существует.

Доказательство основано на том, что любые две дроби можно привести к общему знаменателю.

Свойство 3. Сумма двух рациональных положительных чисел единственна.

Доказательство этого факта вытекает из того, что нахождение суммы двух рациональных чисел сводится к действиям над натуральными числами m, n, p, q.

Свойство 4. Сложение чисел на Q₊ коммутативно.

Доказательство.

Свойство 5. Сложение на Q₊ ассоциативно.

Пусть все дроби приведены к одному знаменателю:

X. Разность положительных рациональных чисел

Разность во множестве положительных рациональных чисел определяется аналогично разности во множестве целых неотрицательных чисел, т.е. как операция, обратная сложению.

Определение. Разностью положительных рациональных чисел и называется такая дробь , что .

Выведем из этого определения правило вычитания дробей (положительных рациональных чисел). Будем считать, что данные дроби уже имеют одинаковые знаменатели (или уже приведены к общему знаменателю).

Разделив обе части этого равенства на n, получим:

p+r=m, где

Таким образом, вычитание положительных рациональных чисел сводится к вычитанию натуральных чисел, а значит, обладает всеми свойствами вычитания натуральных чисел.

1. Если разность существует (при условии, что ), то она единственна.

2. Правило вычитания числа из суммы. Для любых чисел можно записать:

3. Правило вычитания суммы из числа. Для любых положительных рациональных чисел a, b и c можно записать:

XI. Умножение на Q₊

Определение. Произведением положительных рациональных чисел и называется рациональное число .

Теорема 6. Произведение рациональных чисел не зависит от выбора дробей, которые их представляют.

Доказательство. Возьмем ,

Предположим, что . Тогда по теореме 1: .

Поскольку и равные дроби, то применим к ним критерий равенства дробей: .

Домножим первое равенство на pq₁:

Домножим первое равенство на nm₁:

Отсюда по критерию равенства дробей:

Теорема доказана.

Т.к. умножение на множестве Q₊ сводится к действиям над натуральными числами, то свойства умножения на множествах Q₊

и N совпадают.

:

1. Коммутативность: ab=ba

2. Ассоциативность: a(bc)=(ab)c

3. Дистрибутивность:

XII. Деление на Q₊

Определение. Частным двух положительных рациональных чисел a и b называется такое положительное рациональное число с, для которого выполняется .

Выведем правило деления дробей:

Пусть

– по определению

– по критерию равенства дробей

Воспользуемся коммутативностью умножения положительных рациональных чисел:

Чтобы найти частное двух дробей, нужно первую дробь умножить на дробь, обратную второй. (Две дроби взаимно обратны, если их произведение равно 1).

Таким образом, чтобы разделить 2 дроби, необходимо делимое умножить на дробь, обратную делителю:

При делении смешанных дробей их сначала переводят в неправильные дроби, а затем деление заменяют умножением делимого на дробь, обратную делителю.

Свойства деления:

1. Для любых положительных рациональных чисел всегда существует их частное, причем оно единственно.

2. Деление натуральных чисел – частный случай деления рациональных чисел.

3. Деление суммы на число:

4. Деление произведения на число:

5. Деление числа на произведение:

XIII. Отношение «меньше» на Q₊

Определение. Пусть имеется 2 положительных рациональных числа a и b. Число a будет называться меньшим числа b, если существует такое положительное рациональное число с, которое, будучи сложено с a, дает b.

Практические приемы установления отношения «меньше»:

1. Относится к дробям с одинаковыми знаменателями

, т.к.

2. Для дробей с разными знаменателями:

или

Свойства отношения «меньше» на Q₊:

1.

Рефлексивность – не является

– ложно

2. Симметричность – не является

– ложно

– свойство асимметричности

3. Транзитивность — является

– истинно

Таким образом, отношение «меньше» на Q₊ обладает свойствами асимметричности и транзитивности, т.е. является отношением строгого порядка.

XIV.Свойства множества Q₊

1. Q₊ – упорядоченное множество.

Доказательство (см. выше).

2. Множество N – подмножество Q₊.

Каждое натуральное число можно представить в виде , т.е. каждое натуральное число является рациональным.

3. В множестве Q₊ нет наименьшего числа.

Доказательство (методом от противного)

Предположим, что – наименьшее положительное рациональное число. Но всегда можно образовать число . Значит, наше предположение неверно.

4. Множество Q₊ плотно в себе. Т.е. между любыми двумя положительными рациональными числами заключено бесконечное число чисел из Q₊ .

Доказательство.

Возьмем две дроби: и .

Найдем дроби, которые находятся между ними. Для этого найдем среднее арифметическое этих дробей:

Этот процесс можно продолжать бесконечно.

XV.Множество Q₊ счетно

Определение.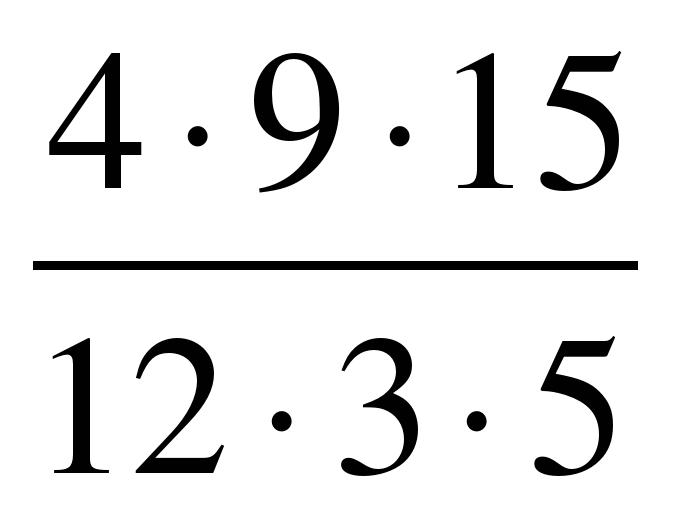 Множество называется счетным, если между ним и множеством N можно установить взаимно однозначное соответствие.

Доказательство.

Представим каждое рациональное число в виде дроби. Назовем высотой рационального числа сумму его числителя и знаменателя.

– числа, которые имеют высоту 5.

Расположим все рациональные числа в порядке возрастания высоты, а числа одинаковой высоты — в порядке возрастания числителя. Установим отображение множества Q₊ на множество N.

Таким образом каждому числу из Q₊ мы поставили в соответствие единственное N число. И наоборот: каждому натуральному числу соответствует одно и только одно рациональное число. Т.е. устанавливаемое соответствие является взаимно однозначным или биективным, а множество Q₊ – счетным.

Упрощение дробей и сложные дроби

Освойте 7 столпов успеха в школе

Улучшите свои оценки и снизьте стресс дробь, которую необходимо упростить или уменьшить.

• Этот метод упрощения дроби  включает использование дерева факторов для уменьшения дроби.
  

• Вот шаги по уменьшению или упрощению дроби с помощью дерева множителей.
  

Факторное дерево  – это диаграмма, помогающая находить простые делители числа. Вы находите множитель числа, а затем множители этого числа до тех пор, пока вы больше не сможете множить. Конечным результатом дерева множителей являются все простые множители исходного числа.

Шаг 1.  Составьте дерево множителей для верхнего числа (числитель) и нижнего числа (знаменатель).

Шаг 2.  Подчеркните простые числа в дереве множителей.

Шаг 3.  Составьте список простых чисел для числителя и знаменателя.

Шаг 4.  Отменить найденные общие множители в числителе и знаменателе

Шаг 5.  Перемножить оставшиеся множители.

Рассмотрим пример из видео:

Упростим или Уменьшим дробь     16

120

Вы также можете насладиться . …..

РЕЗЕМЕНТА 1. Настройте дерево множителей для вашего числителя и вашего знаменателя Ваш числитель — это верхнее число вашей дроби, а знаменатель — нижнее число

Шаг 2. Подчеркните простые числа на обоих деревьях факторов. Простые числа делятся только на себя и на 1

Шаг 3. Составьте список простых чисел для вашего числителя и знаменателя

Шаг 5. Умножьте любые оставшиеся множители, найденные в числителе и знаменателе.

Шаг 4. Вычеркните общие множители. В числителе нет ни 5, ни 3, поэтому они не вычеркиваются.

Как упростить дроби?

Упростить фракцию = снижение добычи до самых низких терминов

Связанные сайты

СОС РЕЗЕМЕННЫЕ Фракции

ДЛЯ Фракции

комплексные фракции/Purple Math

9000 2 9012 212222222222222222222222222222222222222222222222222222н.

Определение сложной дроби

Сложная дробь — это дробь с дробью внутри дроби. Другими словами, знаменатель, числитель или оба содержат дробь.

Как упростить сложную дробь?

Я считаю, что самый простой способ упростить сложную дробь  – это переписать дробь как задачу на деление, используя Изменить,Сохранить,Перевернуть

Пример 1. Упростить следующую сложную дробь

этой сложной дроби

Числитель

Винкулум можно представить как знак деления

Знаменатель

Шаг 1  Упростите числители, если можете. В этой задаче сложите 5+7=12, а затем превратите дробь в задачу на деление. См. шаг 2.

Шаг 2   Перепишите задачу на деление в задачу на умножение, используя метод «Сохранить, изменить, перевернуть».

Перевернуть последнюю дробь/ Создать обратную

Шаг 3 Умножение прямо, чтобы получить комплексную фракцию в самой простой форме

Упростить комплексную фракцию, которая включает переменную

Шаг 1.

Шаг 2.

Шаг 3.   

Упростите эту сложную дробь с показателем степени

Упростите числитель, используя общий знаменатель 2×0005

Сохранить Первая фракция той же

Изменение Знак

Flip самая простая форма

Ответы на вопросы в этом видео…

Как упростить сложный вопрос?

Что такое сложная дробь?
92 +2x?

Упрощение сложных дробей

Общий базовый стандарт: 4.NF.1

К  упростить дробь  означает сократить дробь до наименьшего ее значения.

Дробь является наименьшей, если числитель и знаменатель не имеют общего делителя, кроме единицы.

Расширение и сокращение дробей — Уроки Wyzant

Вас могут попросить сделать две вещи: увеличить и уменьшить (или упростить) дроби. Расширение фракции
означает сделать его «больше», а сокращение дроби означает сделать его «меньше».

Расширяющиеся дроби

Расширение дробей означает их «увеличение». Например, предположим, что вы съели 3/8
этой пиццы, но ваш друг хотел знать, сколько шестнадцатых вы съели. Вам нужно было бы
расширить 3/8, чтобы дать ему ответ. Расширение дроби НЕ меняет
того, сколько вы съели (или съели), оно просто меняет то, как вы говорите человеку
что ты съел. Вы бы расширили дробь следующим образом:

Посмотрите на знаменатели. На что нужно умножить 8, чтобы получить 16? Подумайте о своих
таблицах умножения на 8. 8 раз что дает вам 16? Ну, мы знаем, что 8 х 2 = 16. Это означает
, что мы увеличиваем дробь на 2. У вас уже есть расширенный знаменатель,
, а значит, вам нужно еще расширить вершину. Для этого вы берете то же число
, которое вы использовали для нижнего умножения (в данном случае 2), и умножаете это число на 9. 0005 по верхнему числу (числителю). Он сказал бы: 3 x 2 = ? Что такое 3 х 2? Мы знаем, что
ответ на этот вопрос равен 6, поэтому 6 теперь наш новый числитель. Когда мы сложим вместе
, мы получим 6/16, поэтому мы знаем, что 3/8 в расширенном виде равно 6/16. Затем вы можете
сказать своему другу, что съели 6/16 пиццы. Это то же самое, что вы изначально считали
, 3/8, но это другой способ сказать ему.

Позвольте мне показать вам еще раз. На этот раз я дам вам дробь, и
число, на которое мы расширяемся, и вы получите новую фракцию самостоятельно.

Расширить 3/4 на 5.

Подумайте: расширьте числитель (верхнее число). 3 х 5 = ? Мы знаем, что 3 x 5 = 15, поэтому
наш новый числитель равен 15. Затем расширьте знаменатель. 4 х 5 = ? Мы знаем, что 4
х 5 = 20, поэтому 20 — наш новый знаменатель. Итак, вся наша расширенная дробь равна 15/20.
15/20 по-прежнему означает то же самое, что и 3/4, просто это другой способ написания.

Сокращение (упрощение) дробей

Теперь поговорим о сокращении дробей. Сокращение дробей (также известное как упрощение дробей
) противоположно их расширению. Иногда мы видим действительно большие дроби
, которые можно записать (или произнести) проще. Например, вы не стали бы говорить кому-то
, что съели 75/200 пиццы, вы бы сказали проще, чтобы он
или она могли вас понять. Для этого вам нужно будет уменьшить (упростить)
дробь. Есть два разных способа сделать это, я покажу вам оба из них.

Первый способ — попытаться вычислить наибольшее число, которое делится как на
, так и на числитель и знаменатель вашей дроби. Я собираюсь использовать 5/20 для моего примера.
Я хочу придумать число, которое можно разделить и на 5, и на 20. Я могу положить 5 в число
и на 5, и на 20. Затем я беру задуманное число (5) и делю числитель
и знаменатель на это количество. В этом примере 5 ÷ 5 = 1, а 20 ÷ 5 = 4. Итак, теперь
мой новый числитель равен 1, а мой новый знаменатель равен 4, что делает мою дробь 1/4.

Это будет выглядеть так:

Сейчас я покажу вам второй способ. Для второго способа вам нужно перечислить простые множители
каждого числа. В этом случае простые множители числа 5 равны 1 и 5. Простые множители
числа 20 равны 2 x 2 x 5. Вы бы поместили их туда, где они принадлежат частям дроби
бар, так что 1 x 5 будет продолжаться. сверху (куда идет числитель) и 2 x 2 x 5 будет
внизу (куда идет знаменатель). Это будет выглядеть так:

Теперь вы должны искать какие-либо общие факторы между двумя числами. В этом примере
5 является общим множителем, поэтому мы вычеркнем 5 как сверху, так и снизу.

Теперь вы должны посмотреть на числа, которые у вас остались, 1 вверху и 2 x 2 внизу
.