Как сокращать дроби с умножением 6 класс: Сокращение дробей – примеры, правила, формулы (6 класс, математика)

Содержание

Как сокращать дроби | Математика

Чтобы понять, как сокращать дроби, сначала рассмотрим один пример.

Сократить дробь — значит, разделить числитель и знаменатель на одно и то же натуральное число. И 360, и 420 оканчиваются на четную цифру, поэтому можем сократить эту дробь на 2. В новой дроби и 180, и 210 тоже делятся на 2, сокращаем и эту дробь на 2. В числах 90 и 105 сумма цифр делится на 3, поэтому оба эти числа делятся на 3, сокращаем дробь на 3. В новой дроби 30 и 35 оканчиваются на 0 и 5, значит, оба числа делятся на 5, поэтому сокращаем дробь на 5. Получившаяся дробь шесть седьмых — несократимая. Это — окончательный ответ.

К этому же ответу можем прийти другим путем.

И 360, и 420 оканчиваются нулем, значит, они делятся на 10. Сокращаем дробь на 10. В новой дроби и числитель 36, и знаменатель 42 делятся на 2. Сокращаем дробь на 2. В следующей дроби и числитель 18, и знаменатель 21 делятся на 3, значит, сокращаем дробь на 3.

Пришли к результату — шесть седьмых.

И еще один вариант решения.

Сначала сокращаем дробь на 10, поскольку запись числителя и знаменателя оканчиваются на нуль. Затем новую дробь сокращаем на 6. В результате приходим все к тому же ответу — шесть седьмых — но уже гораздо быстрее.

Как сокращать дроби удобнее? Разумеется, так, чтобы как можно быстрее получить окончательный ответ — несократимую дробь. Как научиться сокращать дроби таким образом? В этом нам поможет следующий план решения.

Чтобы сократить дробь:

1) Проверяем, а не делится ли бо́льшее число на меньшее (числитель на знаменатель или знаменатель на числитель). Если делится, то дробь сокращаем на меньшее из чисел.

2) Если и числитель, и знаменатель оканчиваются на нуль, можно сократить дробь на 10; если и числитель, и знаменатель оканчиваются двумя нулями — на 100 и т.д.

3) При сокращении дробей удобно использовать таблицу умножения. Если и числитель, и знаменатель есть в одной колонке (то есть делятся на одно и то же число), то сокращаем дробь на это число.

При этом, если числитель и знаменатель присутствуют в двух или трех колонках, выбираем из чисел, на которые можно сократить, наибольшее.

4) Используем признаки делимости чисел.

В следующий раз рассмотрим примеры сокращения дробей.

Презентация «Сокращение дробей» — математика, презентации

библиотека
материалов

Содержание слайдов

Номер слайда 1

Первый урок по теме «Основное свойство дроби»Презентацию подготовила учитель математики МБОУ Жирятинская СОШ им. А. Ф. Возликова Григорьева Л.

И.

Номер слайда 2

Основное свойство дробислова помощники Повторять Делать открытия и изучать новое Решать

Номер слайда 3

В пакете имеется некоторое количество конфет. Вам предлагают взять из пакета или 12/20 или 3/5 конфет, чтобы угостить своих друзей. Что вы выберете? Почему?Задача

Номер слайда 4

Исследуем

Номер слайда 5

Исследуем

Номер слайда 6

=Исследуем

Номер слайда 7

Основное свойство дроби. Сокращение дроби. Приведение дроби к нужному знаменателюstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Номер слайда 8

Из истории. Фрактура – это слово означает дробь. Русский термин дробь, как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять.

Номер слайда 9

Номер слайда 10

Номер слайда 11

Номер слайда 12

Номер слайда 13

Номер слайда 14

Основное свойство дроби=:5:5=????

Номер слайда 15

Основное свойство дроби=:2:2=????

Номер слайда 16

Основное свойство дроби. Сокращение дроби. Приведение дроби к нужному знаменателюstyle.colorr

Номер слайда 17

=:n:n??Сокращение дроби. Говорят, что дробь сократили на nstyle.colorfillcolorfill.type

Номер слайда 18

=Сокращение дроби=Если числитель и знаменатель дроби разделили на одно и то же , не равное нулю число n, то говорят, что дробь сократили на n. style.colorfillcolorfill.type

Номер слайда 19

=========Подробная запись. Краткая записьstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Номер слайда 20

Основное свойство дроби. Сокращение дроби. Приведение дроби к нужному знаменателюstyle.colorfillcolorfill.typer

Номер слайда 21

=Приведение дроби к нужному знаменателю. Если числитель и знаменатель дроби умножили на одно и то же , не равное нулю число n, то говорят, что дробь привели к знаменателю k.=Число n называется дополнительным множителем.style.colorfillcolorfill.typestyle.colorfillcolorfill.type

Номер слайда 22

2======362===36 Подробная запись. Краткая записьstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Номер слайда 23

Спасибо за внимание.

Конспект урока по математике » Сокращение дробей» 6 класс

Государственное образовательное учреждение
высшего образования
«Государственный социально-гуманитарный университет»
(ГОУ ВПО «ГСГУ»)

Факультет повышения квалификации и профессиональной переподготовки

Практико-значимая работа по теме

«КОНСПЕКТ УРОКА ПО МАТЕМАТИКЕ В 6 КЛАССЕ»

Выполнил:

слушатель гр. АИ 13-16

Петрова Т.С.

Проверил: к.пед.н., доцент

Яковлева Т.В.

Коломна 2016

Конспект урока математики в 6 классе по теме:

«Сокращение дробей».

Данная работа представляет собой методическую разработку, рассчитанную на учащихся 6 класса первого урока по теме «Сокращение дробей».

Задачи урока: проверка знаний учащимися фактического материала, умений применять знания при решении поставленных задач, совершенствование вычислительных навыков; развитие навыков самостоятельности, самоконтроля, самооценки.

Каждый ученик в ходе урока выполняет определенные задания, самостоятельно оценивает себя за каждое задание и выставляет отметку в индивидуальный оценочный лист. По итогам занятия по сумме набранных баллов учащиеся оценивают свою работу и анализируют, насколько успешной была его деятельность на уроке.

На уроке формируются УУД учащихся: коммуникативные, регулятивные, познавательные, личностные.

Технологическая карта урока математики в 6 классе по теме «Сокращение дробей»

по учебнику Виленкина Н.Я.

Ввести понятие сокращения дробей и познакомиться с понятием «несократимая дробь».

Научиться сокращать дроби, используя основное свойство дроби и применять признаки делимости чисел.

Вывести алгоритм сокращения дробей и научиться применять его на практике.

Регулятивные – развивать умение видеть математическую задачу в контексте проблемной ситуации в окружающей жизни; совершенствовать критерии оценки и использовать их в ходе оценки и самооценки.

Познавательные – понимать сущность составления алгоритма, действовать по алгоритму, проговаривать выводы в виде правил «если …, то …».

Коммуникативные – уметь оформлять свои мысли в устной и письменной речи с учётом речевых ситуаций;

уметь слушать собеседника и вести диалог, работать в паре.

Личностные —

адекватно оценивать результаты своей учебной деятельности, осозновать и принимать социальную роль ученика, объяснять свои достижения, понимать причины успеха в учебной деятельности.

Ход урока

Этап урока: создание проблемной ситуации (используя материал домашнего задания) и формирование проблемы (формулировка темы и постановка задач).

Мотивация к учебной деятельности, вхождение каждого учащегося в пространство учебной деятельности на уроке, создание условий для возникновения внутренней потребности включения в деятельность на основе практического применения материала данного урока.

Целеполагания: планирование учащимися способов достижения намеченной цели.

Деятельность учителя

Деятельность учащихся

Применяемые учебные действия

Результаты

Примечание

При выполнении, какого задания домашней работы у вас возникли затруднения? (Приложение 3)
Какая возникла проблема, а кто смог отметить на координатном луче эти дроби.

Давайте проверим это задание?
А почему эти дроби на координатной прямой выражены одной точкой?
А что вы для этого применили?
14/21; 20/30; 16/24 Что связывает эти дроби?
А как по вашему мнению можно назвать эту операцию?
Формулируем тему урока.
Цель урока.
А зачем нужно уметь сокращать дроби, где нам может пригодится?

Отвечают на вопросы

Применяли основное свойство дробей, делили числитель и знаменатель на одно и тоже число.

Формулируют тему урока, ставят цель урока. Записывают тему урока:

«Сокращение дробей».

1 ученик называет свои группы.

В 1 группе числитель и знаменатель дроби взаимно простые числа (НОД=1)

Сократимые и несократимые дроби.

Применить основное свойство дроби: разделить числитель и знаменатель дроби на их общий делитель.

Формирование познавательной мотивации.

Актуализация.

Смыслообразование. (зачем?)

Актуализация внутренней потребностей в деятельности.

Применяют знания по аналогии.

Л: Умение обосновывать и выражать свое мнение.

Р: Формулировка темы и цели урока.

Р: Умение анализировать,

проводить аналогию, делать выводы

Р: Умение ставить цели и задачи.

П :Уметь достаточно точно и полно выражать свои мысли.

Умение формулировать понятия.

Слайд №2 с проверкой координатной прямой.

На доске 14/21; 20/30; 16/24.

Слайд №3.

Этап урока: актуализация имеющихся знаний и поиск решения проблемы: Как сократить дробь?

Планирование учащимися способов достижения намеченной цели.

Деятельность учителя

Деятельность учащихся

Применяемые учебные действия

Результаты

Примечание

Учитель организует выявление учащимися места и причин затруднения (возвращаемся к заданию5)

На какие группы вы разбили дроби?

— как называются числа, у которых НОД = 1.

-попробуем дать название этим группам; (Выход на сократимые и несократимые дроби)

Как объединить данные группы в одну.

Что мы для этого должны сделать?

Сформулируем алгоритм сокращения дробей (работа в группах)

Знаем основное свойство дробей

Признаки делимости

Нахождение НОД

Умеем выполнять разложение числа на простые множители.

Планирование сотрудничества.

Построение проекта выхода из затруднения.

Выдвижение гипотез.

К: Умение корректно возражать другим.

Умение контролировать, оценивать собственную деятельность.

Проверим алгоритм.

Работа в группах

1) найти НОД числителя и знаменателя

2) разделить на это число числитель и знаменатель дроби

3) записать получившуюся дробь.

Поиск оптимального варианта решения проблемы.

К: Умение слушать, договариваться.

П: Умение работать с информацией, текстом.

П: Понимать связь между основным свойством дроби и сокращением дробей.

Слайд №4 сверка с эталоном.

Образец оформления сокращения дробей:

39/65, (8*9)/ (6*24), (3*а)/(5*а)

Всегда можно сократить?

А когда невозможно?

Образец оформления сокращения дробей учащиеся записывают в тетрадь.

На доске 39/65, (8*9)/ (6*24), (3*а)/(5*а) (при а не равном 0)

Этап урока: открытие и применение новых знаний.

Самоконтроль, взаимоконтроль: организация, по возможности, для каждого ученика ситуации успеха, мотивирующей его к включению в дальнейшую познавательную деятельность.

Деятельность учителя

Деятельность учащихся

Применяемые учебные действия

Результаты

Примечание

Работа в мобильных группах

Сократить дроби, используя различные приемы сокращения

(заслушиваются представители всех групп, дополняя друг друга)

1, 2, 3 группа: выписать №243- -а 5 дробей, №244 – б – 2 дроби

4, 5, 6 группа: №243 – б – 5 дробей, №244 – а – 2 дроби.

Ребята обсуждают приемы сокращения и договариваются, кто из группы будет представлять приемы.

Формирование коммуникативных универсальных учебных действий.

К: Культура общения со сверстниками.

Р: Умение контролировать свое поведение и эмоциональное состояние.

П: Уметь применять различные приемы при сокращении дробей.

К: Умение организовать сотрудничество со сверстниками.

Задание на слайде №5.

Самостоятельная работа по карточкам. (Приложение 1)

Выполнить задания и оцените количеством баллов свою работу.

Оцените количество правильных ответов (1 балл за правильный ответ) поставив себе от 1 до 9 баллов на полях в тетради

Выполняют в тетради.

а) Сократите дробь:

;(1 балл)

б) Найти х:

(2 балла)

Ответы:

a)
;

б)

X = 4

X = 36

Выполняют самостоятельную работу.

Самооценка.

Р: Умение выстраивать последовательности необходимых операций (алгоритма).

Р: Уметь удерживать цель до получения ее результатов; определять последовательность промежуточных действий с учетом конечного результата.

Задания на карточках, ответы, самопроверка и самооценка на слайдах №6 и №7.

Этап урока: рефлексивно-оценочная деятельность, домашнее задание.

Рефлексия: оценка учащимися своей деятельности по ее результатам, запись домашнего задания.

Деятельность учителя

Деятельность учащихся

Применяемые учебные действия

Результаты

Примечание

— удалось ли решить проблему урока

— чему мы сегодня с вами научились.

Ответы на поставленные вопросы.

Ведение диалога.

Соотношение цели учебной деятельности и её результатов.

Р: Аргументация своего мнения.

Адекватное понимание причин успеха/неуспеха в учебной деятельности.

Заполните оценочные листы, применяя цветовую оценку проанализировав свою деятельность.

Заполнение оценочных листов.(Приложение 2)

Анализ полученных оценочных листов. Выявление проблем.

Р: Анализ и оценка результатов своей деятельности.

Запишите домашнее задание:

№246 – 248 – практическое применение сокращения дробей.

№268,269,270.

Запись домашнего задания.

Дифференцированное домашнее задание.

Слайд №8: Большое спасибо за урок!

Самоанализ урока математики в 6 классе

по теме «Сокращение дробей»

Учитель математики Петрова Т.С.

Стаж работы в должности учителя 21 год

Урок проводился в 6 классе. В классе обучается 17 учащихся. Работаем вместе второй год. Дети по уровню развития способные и творческие. Из них 70 % учатся на 4 и 5, но есть и слабые ученики, которые не усваивают материал.

Учащиеся 6 класса работоспособные, активные.

Цель: Сформулировать правило сокращения дробей. Научить учащихся сокращать дроби.

Задачи урока:

обучающие: подвести учащихся к «открытию» способа сокращения дробей, разработать алгоритм действий и научиться пользоваться им;
развивающие: развивать логическое мышление, внимательность, самостоятельность, умение рассуждать, делать выводы;
воспитательные: воспитывать умение сотрудничать в паре.

Тип урока: урок «открытия нового знания»

Оборудование: экран, мультимедийный проектор, ноутбук, презентация по теме урока, карточки для самостоятельной работы

Свой урок я строила в соответствии с ФГОС, используя информационно-коммуникативные технологии.

Данный урок представлен по ходу изучения раздела «Сложение и вычитание дробей с разными знаменателями».

На уроке были учтены возрастные и психологические особенности учащихся.

В содержание урока я включила элементы обучения школьников универсальным учебным действиям: цели урока определяли сами ученики, исходя из соответствующей проблемной ситуации.

На данном уроке применялся деятельностный метод обучения, который был реализован в следующих видах деятельности: учебной и учебно-исследовательской.

Любой процесс познания начинается с импульса, побуждающего к действию. Необходима мотивация, побуждающая ученика к вступлению к деятельности. Помня об этом, я тщательно продумывала каждый этап урока, составляла задания, подбирала вопросы, использовала различные приёмы активизации учеников.

На всех этапах урока ученики были вовлечены в активную мыслительную и практическую деятельность исследовательского характера, детям надо было не только использовать уже имеющиеся знания, но и найти новый способ выполнения уже известного им действия.

Этапы урока были тесно взаимосвязаны между собой, чередовались различные виды деятельности. Умственные действия опирались и подкреплялись практическими действиями. Учебный материал на протяжении всего урока работал на организацию посильного поиска и исследования шестиклассников, соответствовал их жизненному опыту.

Для каждого ученика была создана ситуация успеха, что также способствовало повышению мотивации и поддержанию познавательного интереса к учению.

Учебный материал урока соответствовал принципу научности, доступности и был посилен для учащихся шестого класса. Учебная информация была привлекательна для детей. За счёт привлекательности содержания заданий и подачи учебного материала, повысились возможности учеников в достижении поставленных целей на уроке.

Я считаю, что учебное время на уроке использовалось эффективно, запланированный объём урока выполнен. Интенсивность урока была оптимальной с учётом физических и психологических особенностей учащихся.

На уроке наблюдалось рациональное использование времени, предупреждение перегрузки детей обеспечивалось за счёт быстрой смены видов деятельности. На уроке применялись здоровье сберегающие технологии (физминутка общего воздействия). Применялись задания, направленные именно на развитие детей. При проведении урока были использованы различные формы обучения: индивидуальная и фронтальная работа, детям оказывалась индивидуальная помощь. При проведении урока была использована презентация, как компьютерная поддержка. При подведении итогов и рефлексии был применен самоанализ деятельности учеников и схема — кластер. Урок проведён в доброжелательной рабочей обстановке.

Я считаю, что на уроке поставленная цель была достигнута.

Приложение 1

Карточки для самостоятельной работы

Карточка.

а) Сократите дробь и соотнесите с правильным ответом:

;

Ответы: а) , в) , с) , д) , е) , ж)

б) Найти х:

Ответы:

а) х=, в) х= 4, с) х= 36, д) х=28, е) х= 30

Внесите ответы в таблицу:

1 балл

2 балла

6) ___

7) ___

Карточка.

а) Сократите дробь и соотнесите с правильным ответом:

;

Ответы: а) , в) , с) , д) , е) , ж)

б) Найти х:

Ответы:

а) х=, в) х= 4, с) х= 36, д) х=28, е) х= 30

Внесите ответы в таблицу:

1 балл

2 балла

6) ___

7) ___

Карточка.

а) Сократите дробь и соотнесите с правильным ответом:

;

Ответы: а) , в) , с) , д) , е) , ж)

б) Найти х:

Ответы:

а) х=, в) х= 4, с) х= 36, д) х=28, е) х= 30

Внесите ответы в таблицу:

1 балл

2 балла

6) ___

7) ___

Карточка.

а) Сократите дробь и соотнесите с правильным ответом:

;

Ответы: а) , в) , с) , д) , е) , ж)

б) Найти х:

Ответы:

а) х=, в) х= 4, с) х= 36, д) х=28, е) х= 30

Внесите ответы в таблицу:

1 балл

2 балла

6) ___

7) ___

Приложение 2

Оценочный лист

Фамилия Имя _______________________________ Класс _______

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Оценочный лист

Фамилия Имя _______________________________ Класс _______

________________________________________________________________________________________________________________________________________________________________

Домашнее задание Приложение 3

Разложите на простые множители числа:

75; 100; 4; 64; 96; 120; 360; 12; 48; 126; 198; 210; 450; 630; 936.

Используя основное свойство дроби, разделите числитель и знаменатель каждой дроби на НОД этих чисел, стоящих в числителе и знаменателе: ;.
Найдите НОД: НОД(75;100) НОД(2;3) НОД(3;12) НОД(48:64)

НОД(64;96) НОД(120;360) НОД(75;120)

НОД(1;3) НОД(3;4) НОД(5;6)

Отметьте на координатном луче дроби (если единичный отрезок равен 12 клеткам):

Разбейте дроби (из пункта 4) на группы.

Напишите, по какому общему признаку вы их разбили?

____________________________________________________________________________________________________________

Какие полученные ранее знания вам пригодились при выполнении Домашнего задания?
1. ______________________________________________________________________________________________________
2. ______________________________________________________________________________________________________
3. ______________________________________________________________________________________________________
4. ______________________________________________________________________________________________________
Какие трудности вы испытывали при выполнении Домашнего задания?
1. ______________________________________________________________________________________________________
2. ______________________________________________________________________________________________________
3. ______________________________________________________________________________________________________
4. ______________________________________________________________________________________________________

Конспект урока.

Сокращение дробей. 6 класс | План-конспект урока по математике (6 класс) на тему:

Урок математики в общеобразовательной школе по теме

«Сокращение дробей» 6 класс

Михайлова Вера Ивановна

учитель математики
ЧОУ «Школа экономики и права»

г. С-Петербург Красносельский район.

Тема урока: Сокращение дробей

Цель: вывести правило сокращения дробей, используя признаки делимости чисел и основного свойства дроби, и уметь применять его на практике.

Задачи:

1. Сформулировать правило сокращения дробей

2. Ввести понятие несократимой дроби

3. Научиться применять эти правила на практике

4. Формировать умение работать индивидуально, в парах, аргументировать и отстаивать свое мнение

Ход урока

I Организационный момент

— Доброе утро, ребята! Я рада вас видеть в хорошем настроении. У нас сегодня много гостей. Постараемся показать наши знания и умения.

II Актуализация знаний

1.Что называется делителем числа a?

2. Что называется НОД чисел a и b?

3. Какие числа называются взаимно простыми?

5. Признаки делимости на 2, 5, 10, 3, 9.

6. Сформулируйте основное свойство дроби.

7. Назовите несколько дробей, равных данным:

Используя основное свойство дроби выполните графический диктант.

Ответ «да» соответствует +, ответ «нет» соответствует — .

+ — — + + + + — — +

Взаимопроверка

Критерии

9-10 заданий 3 балла

8-7 заданий 2 балла

4,5,6 заданий 1 балла

менее 5 заданий 0 балла

III Первичное восприятие учебного материала

Решение задачи

А теперь откроем учебник, стр. 40, задача № 250.

Прочтите, пожалуйста, вслух задачу.

О чем задача?

Сколько было рабочих?

Что говорится в задаче об этих рабочих?

Что нужно найти?

Что для этого нужно знать?

Я даю вам 2-3 минутки, чтобы вы в парах обсудили решение данной задачи.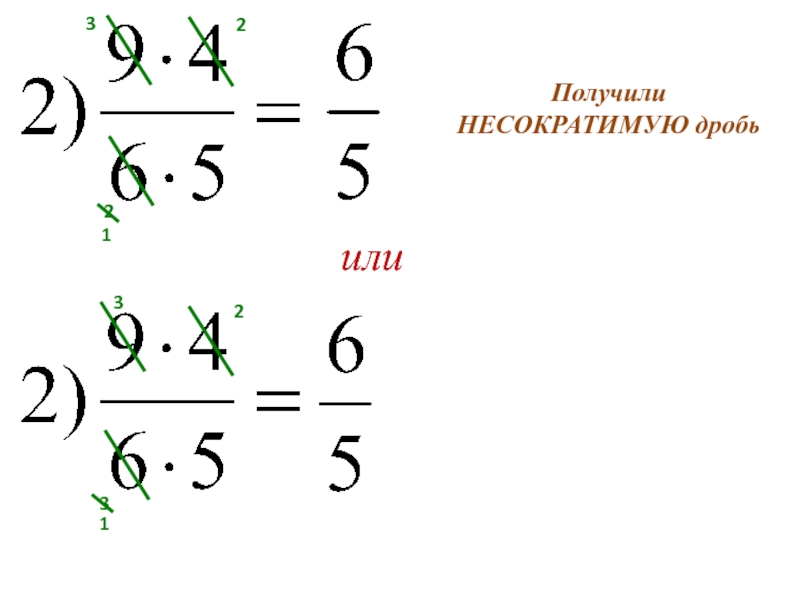

Выслушать мнения учащихся, записать решение на доске:

1) 6 : 16 = (ч) затратил первый рабочий

2) 15 : 24 = (ч) затратил второй рабочий

– Как выяснить, кто из них затратил времени больше?

– Умеем ли мы сравнивать дроби с разными знаменателями?

– А с одинаковыми знаменателями?

– Можем ли мы из этих дробей получить равные им дроби, но с другими знаменателями?

– Какое свойство мы для этого используем?

IV Определение темы урока

– Итак, мы с вами применили основное свойство дроби, заменили дроби на равные им путём деления числителя и знаменателя на одно и то же число.

Получилась дробь, значение которой равно данной дроби, но с меньшим числителем и знаменателем

Такое преобразование называют …. СОКРАЩЕНИЕМ ДРОБЕЙ

– Тема нашего урока «Сокращение дробей». Запишите её в тетрадь.

– Рассказ о применении понятия «сокращение».

V Постановка цели урока

– А теперь попробуйте сформулировать цель нашего урока, с чем мы должны познакомиться и чему научиться на уроке.

Ставим перед собой цель:

Учится сокращать дроби, используя признаки делимости чисел и основного свойства дроби.

Задачи

1. Сформулировать правило сокращения дробей

2. Ввести понятие несократимой дроби

3. Научиться применять эти правила на практике

– Как получили ответ?

– Давайте вместе попробуем сформулировать правило, что такое сокращение дробей и как сократить дробь.

– Молодцы!

– Теперь откройте учебник на стр. 39, прочитайте правило (запишите его в тетрадь)

VI Проверка понимания учащимися нового материала

– А теперь применим наши новые знания на практике. Сократить дроби, комментируя:

– Задание решать будем самостоятельно, к доске пойдут два человека и будут выполнять задание на доске, потом мы вместе все проверим.

____________________________________________________________________________

– Посмотрите на слайд, сократите дробь, если это возможно:

– В каких из этих дробей числитель и знаменатель дроби – взаимно простые числа?

– Чему равен в этом случае НОД числителя и знаменателя?

– Правильно, 1. Значит, общих делителей, кроме 1, у этих чисел нет, и такую дробь сократить нельзя. Она так и называется – несократимая.

– Попробуйте сформулировать определение несократимой дроби.

(Если числитель и знаменатель дроби взаимно простые числа, то их НОД равен 1 и такая дробь несократима.)

VII Включение нового материала в систему ранее усвоенных знаний

12/16 рассмотрим дробь

— используя определение сокращения дробей, на какое число можно разделить числитель и знаменатель?

Например на 2, получаем 6/8

— а еще можем разделить на какое-нибудь число? Можем, на 2. Получаем ¾

— какую дробь получили? Несократимую, дальше сокращать нельзя.

— т.е. мы постепенно делили на 2, потом еще на два, а насколько мы в итоге раздели ? на 4

— чем является 4 для чисел 12 и 16? НОД

— рассмотрим еще одну дробь

18/30 = 9/15 = 3/5

VIII Закрепление

Тест

Самооценка

IX Подведение итогов урока

-Подходит к завершению наш урок, пора подвести итоги.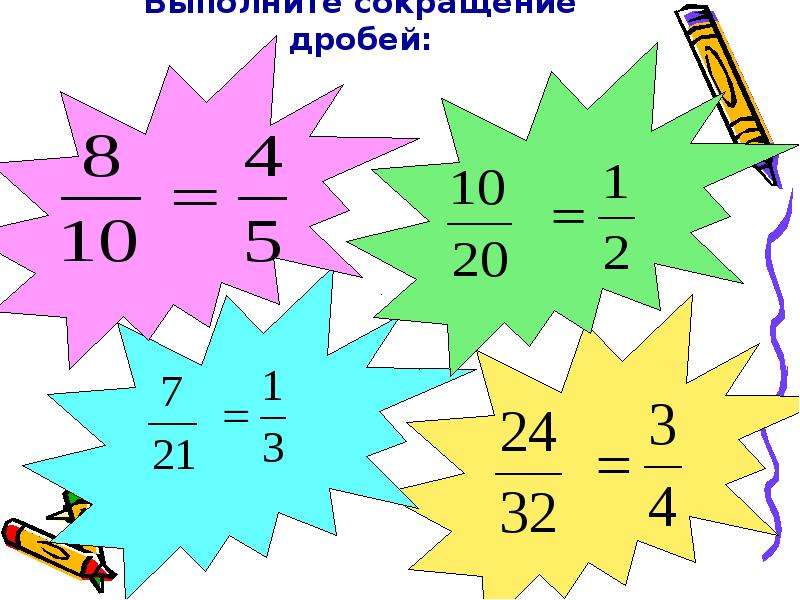

-Запишите домашнее задание:

– Что значит сократить дробь?

– Что меняется при сокращении дроби?

– Какая дробь называется несократимой?

– Поставьте себе оценку за урок.

Х Рефлексия

О чем мы сегодня говорили?

Какую цель мы поставили сегодня?

Достигли ли мы этой цели?

Все ли было понятно?

Урок окончен! Вы все молодцы! Спасибо за работу!

Тренинг по математике «Сокращение дробей» 6 класс

Макарова Т.П., ГБОУ СОШ № 618

Макарова Татьяна Павловна,

Учитель ГБОУ СОШ №618 г. Москвы

Контингент: 6 класс

Тема: Сокращение дробей.

Вид работы: Тренинг

Тренинг направлен на проверку знаний и умений учеников по теме «Сокращение дробей». Тренинг предназначен для учащихся 6 класса к учебнику Н.Я. Виленкин, В.И. Жохова и др. Учебник для 6 класса. – М.: Мнемозина, 2013. – 288с.

Цели: отработать умения и навыки по применению сокращения дробей для решения задач; развивать воображение, логическое мышление, внимание, навыки умственной и практической деятельности, самоконтроля, содействовать воспитанию интереса к предмету.

Тренинг содержит четыре варианта по восемь заданий в каждом. Полностью соответствует программным требованиям, может быть использован при проведении классно-урочного контроля.

Тренинг по теме «Сокращение дробей»

Вариант 1

Вариант 3

Урок 46. умножение и деление смешанных дробей произвольного знака — Математика — 6 класс

Математика

6 класс

Урок № 46

Умножение и деление смешанных дробей произвольного знака

Перечень рассматриваемых вопросов:

умножение смешанных дробей произвольного знака;
деление смешанных дробей произвольного знака.

Тезаурус

Натуральные числа – это числа, которые используются при подсчёте предметов.

Правильная дробь – это дробь, у которой числитель меньше знаменателя.

Положительная смешанная дробь есть сумма натурального числа и правильной дроби.

Обязательная литература:

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

«Математика – царица наук, арифметика – царица математики», – сказал К. Ф. Гаусс. Следуя за царицей математики, продолжим изучать арифметические действия со смешанными дробями. И сегодня поговорим об умножении и делении смешанных чисел любого знака.

Как выделять целую часть из положительной неправильной дроби и как приводить положительную смешанную дробь к виду неправильной мы вспоминали на прошлом уроке. Поэтому сразу переходим к алгоритму умножения смешанных чисел:

Чтобы найти произведение смешанных дробей произвольного знака, их выражают в виде неправильных дробей и применяют правила умножения дробей. При необходимости результат упрощают (сокращают и выражают в виде смешанной дроби).

Найдём произведение

Количество отрицательных множителей нечётное, значит, произведение будет отрицательным.

Приведём смешанные дроби к виду неправильных.

Представим данную неправильную дробь в виде смешанного числа.

Чтобы найти частное смешанных дробей произвольного знака, их выражают в виде неправильных дробей и применяют правила деления дробей. При необходимости результат упрощают (сокращают и выражают в виде смешанной дроби).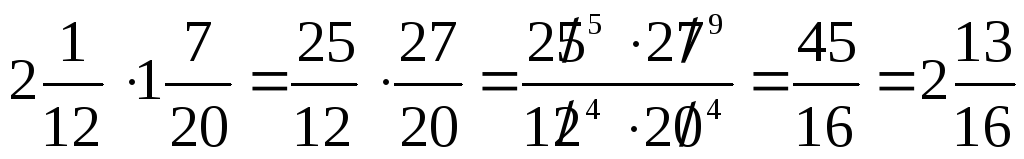

Найдём частное

Количество отрицательных дробей в выражении нечётное, значит, частное будет отрицательным.

Приведём смешанные дроби к виду неправильных.

Перемножим отдельно числитель и знаменатель.

Сравнение значений выражений.

Сравним значения выражений, не вычисляя их.

Решение

Для сравнения достаточно посмотреть на знаки, которые будут получаться при вычислениях. Так как в первом выражении две отрицательные дроби, то произведение будет положительным.

Во втором выражении две дроби с разными знаками, следовательно, частное будет отрицательным. Значит, значение первого выражения больше, чем второго.

Разбор заданий тренировочного модуля

№ 1. Какой знак имеет выражение?

Решение

Так как числа в выражении имеют разные знаки, то знак частного будет отрицательным.

Ответ: знак «».

№ 2. Выберите число x, для которого верно равенство.

Решение

Чтобы определить значение х, нужно выполнить арифметические действия в правой части равенства. Но для начала приведём дроби к общему знаменателю 15.

Далее применим правило сложения и вычитания смешанных дробей.

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Ответ:

Конспект урока по математике 6 класс «Сокращение дробей»

Урок–путешествие к острову Сокращение дробей.

6 класс.

Тема урока. Сокращение дробей.

Цель. Способствовать созданию условий для самостоятельного открытия учащимися правила сокращения обыкновенных дробей.

Задачи:

Обучающая: подвести учащихся к «открытию» способа сокращения дробей, разработать алгоритм действий и научиться пользоваться им;

Развивающая: развивать логическое мышление, внимательность, самостоятельность, умение рассуждать, делать выводы;

Воспитывающая: продолжить работу по воспитанию любви к предмету, любознательности, чувства сопереживания и уважительного отношения к мнению одноклассников, культуры общения. воспитывать умение сотрудничать в паре.

Тип урока: урок изучения и первичного закрепления новых знаний.

Методы и приёмы: словесный, наглядный, исследовательский, проблемно-поисковый.

Формы организации познавательной деятельности: индивидуальная, работа в парах.

Средства обучения: учебник, мультимедийная доска (проектор)

Место урока в учебном плане. На изучение математики в 6 классе отводится 5 уроков в неделю. Данный урок стоит первым уроком в теме «Сокращение дробей». Всего отводится 3 урока на данную тему.

Ход урока

I. Орг. момент.

Учитель: Ребята, сегодня мы отправляемся в путешествие на корабле в неизведанную вами страну.

Все задания должны быть выполнены в судовых журналах (судовые журналы – это ваши тетради). За каждое правильно выполненное задание на полях ставьте звездочку.

Учитель: Откройте свои судовые журналы и поставьте в них дату отплытия (На доске записано).

II Актуализация

(Музыка) Учитель: На море поднимается шторм. Чтобы проверить вашу готовность к путешествию, необходимо ответить на вопросы.

Что показывает дробь?

Что вы знаете о дробях? (Из каких частей состоят дроби?)

Какие действия мы умеем выполнять с дробями? (Сложение и вычитание дробей с одинаковыми знаменателями, сравнение дробей).

Как называют дробь ½? ¼? (половина, четверть).

Что такое наибольший общий делитель? Как его найти?

Одну долю или несколько равных долей единицы называют дробью или дробным числом.

В дроби число, стоящее над чертой, называют числителем дроби, а число, стоящее под чертой, называют знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей разделена единица, а числитель дроби показывает, сколько таких частей взято.

Учитель: Молодцы. Команда готова к отправке!

В гавани находятся 2 корабля «Дроби» и «Делитель». Необходимо проверить исправность кораблей и устранить все неполадки.

На экране записано шесть примеров. В некоторых их них имеются ошибки. Необходимо эти ошибки выявить и исправить, тем самым будет устранена неисправность корабля.

8/10=4/5; 24/32=3/4; 4/8=12/32; 10/20=1/2; 7/21=1/7; 12/36=60/144.

Каким правилом вы воспользовались, для решения этой задачи? Как звучит основное свойство дроби?

Учитель: Итак, неисправности устранены, корабли к выходу из гавани готовы.

III. Изучение

Давайте решим, на каком корабле нам путешествовать?

Корабль «Делитель» проплывает 6 км за 16 минут, а корабль «Дроби» 15 км за 24 минуты. Какой из кораблей быстрее доберется до цели?

Поставьте вопросы на которые вам надо ответить, что бы решить задачу. (Какая скорость кораблей?)

Обсудите с соседом по парте решение данной задачи в течении 2 минут.

Выслушать мнения учащихся, записать решение на доске:

1) 6 : 15 = (км/мин) – скорость корабля «Делитель».

2) 15 : 24 = (км/мин) – скорость корабля «Дроби».

Получилось две дроби. Можете ли сравнить полученные дроби? (Нет)

Какое свойство дробей вам известно? Давайте используем его.

В учебники найдите как называется такое действие с дробями? Стр.39. В какую страну мы с вами отправимся? (Сокращение дробей).

Запишите её название в судовых журналах.

Как думаете, для чего мы с вами отправимся в путешествие в страну «Сокращение дробей».

Корабль мы с вами назвали, но известно ли вам история возникновения нашего корабля под названием «дробь»?

Об этом нам с вами расскажет один из матросов Ассев Дмитрий. Слушайте внимательнее, после доклада вам предстоит ответить на вопросы.

История возникновения обыкновенных дробей.

Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.

В самых древних дошедших до нас письменных источниках – вавилонских глиняных табличках и египетских папирусах встречаются не только натуральные числа, но и дроби.

Дроби были нужны, чтобы выразить результат измерения длины, массы, площади в случаях, когда единица измерения не укладывалась в измеряемой величине целое число раз.

Тогда вводили новую, меньшую единицу измерения. Названия этих новых единиц измерения и стали первыми названиями дробей. Например, дробь до сих пор называется «половина»; у римлян слово «унция» сначала было названием двенадцатой доли единицы массы, но потом унция стала обозначать одну двенадцатую долю любой величины.

В русском языке слово «дробь» появилось в VIII веке, оно происходило от глагола «дробить» — разбивать, ломать на части. В первых учебниках математики (в XVII веке) дроби так и назывались – «ломаные числа». У других народов называние дроби также связано с глаголами «ломать», «разбивать».

Современное обозначение дробей берет своё начало в Древней Индии; его стали использовать и арабы, а от них в ХII – XIV веках было заимствовано европейцами. В начале в записи дробей не использовалась дробная черта, черта дроби стала постоянно использоваться лишь около 300 лет назад. Первым европейским ученым, который стал использовать и распространять современную запись дробей, был итальянский купец и путешественник, сын городского писаря Фибоначчи (Леонардо Пизанский). В 1202 году он ввёл слово «дробь». Названия «числитель» и «знаменатель» ввёл в ХIII веке Максим Плануд – греческий монах, ученый – математик.

Вопросы:

Для чего нужны дроби?

От какого глагола произошло слово «дробь»?

Кто ввёл понятия «числитель» и «знаменатель»?

Учитель: Итак, мы отплыли. Внимание! В море появились гигантские акулы, которые могут перевернуть корабль. Необходимо срочно сократить дроби и отогнать акул.

Для этого откройте учебник на стр. 39 №243(а).

IV. Физ.минутка

Ребята, вы, наверное, уже устали. Давайте выйдем на палубу и разомнемся.

Встаньте, пожалуйста, все из-за парт. Сейчас я проверю на сколько вы внимательны и всё ли вы знаете. Я говорю утверждение, если вы с ним согласны вы хлопаете в ладоши 3 раза, если я не права вы топаете ногами 2.

1. Если площадь квадрата равна 36 см², то сторона квадрата равна 6 см. (Да)

2. Если сумма цифр в составе числа делиться на 2, то и число делить на 2. (Нет)

3. Делить на ноль нельзя. (Да)

4. Дробь состоит из числителя и знаменателя. (Да)

5. Числитель показывает, насколько частей разделили целое. (Нет)

6. Если число делиться на 2, то оно четное. (Да)

7. Площадь – это сумма длин всех сторон. (Нет)

8. Число 3 является делителем 6. (Да)

9. Число 2 является кратным числа 10. (Нет).

Отдохнули? Присаживайтесь на свои места и продолжим путешествие.

V. Закрепление полученных знаний

Учитель: Командам кораблей приготовиться к прохождению трудного участка пути, впереди подводные рифы. Чтобы благополучно их обойти, нужно самостоятельно решить уравнения.

Решите уравнения:

Высадка на остров.

Учитель: Итак, путешествие наше подходит к концу. Мы подплываем к суше.

Рефлексия

Учитель:

Посмотрите какое дерево нас встретило на суше. Чего же ему не хватает? Правильно, листочков. Давайте вместе нарядим его. Выберете листочек, который соответствует вашему ощущению сегодняшнего урока.

Урок полезен, все понятно (зеленый)

Лишь кое-что чуть-чуть неясно. (желтый)

Еще придется потрудиться (оранжевый)

Да, трудно все-таки учиться (красный).

_______пожалуйста соберите листочки с вашего ряда и повесьте их на дерево.

Смотрите какое красивое дерево у нас получилось. Но все же не все листья зеленые, значит еще есть над чем поработать.

Путешествие завершено. Оно прошло благополучно. Благодарю за хорошую службу.

Закройте судовые журналы.

X. Домашнее задание.

П.9, №243(б), 257(а,б).

Творческое задание: Составить задачу на сокращение дробей.

Удачного дня!

Рабочий лист упрощения дробей

Добро пожаловать на нашу страницу рабочего листа упрощения дробей.

Здесь вы найдете широкий спектр рабочих листов градуированных фракций для печати. который поможет вашему ребенку попрактиковаться в преобразовании дробей в их простейшую форму.

У нас есть подборка разработанных рабочих листов чтобы помочь вашему ребенку понять, как упростить дроби.

Листы отсортированы таким образом, чтобы более легкие находились вверху.

Поддерживается первый лист в разделе, и уже указан наивысший общий коэффициент.

Последний лист самый сложный и представляет собой серьезную проблему для более способных математиков.

Использование этих листов поможет вашему ребенку:

практика упрощения ряда фракций;
применяют свои знания таблицы умножения.

Упрощение дробей также иногда называют приведением дробей к их простейшей (или наименьшей) форме.

Это предполагает деление числителя и знаменателя на общий коэффициент для уменьшения дроби до эквивалентной дроби с наименьший возможный числитель и знаменатель.

На приведенной ниже странице дроби для печати содержится дополнительная информация, примеры и практика по упрощению дробей.

Калькулятор упрощающих дробей также покажет вам, как работают примеры того, как упростить дроби, если вы действительно застряли!

Взгляните на еще несколько наших рабочих листов и ресурсов, похожих на эти.

Здесь вы найдете бесплатную онлайн-справку по математике Math Salamanders о дробях.

Существует широкий спектр справочных страниц, в том числе справка по следующим вопросам:

;
эквивалентных фракций;
преобразование неправильных дробей;
как складывать и вычитать дроби;
как переводить дроби в десятичные и проценты;
как упростить дроби.

Вот наша коллекция математических игр с дробями.

Эти игры подходят для детей от 3-го класса и старше.

Игра в игры — отличный способ развить навыки дроби в увлекательной игровой форме.

Эквивалентность дробей, преобразование дробей в десятичные и свойства дробей — все это исследуется в наших забавных играх.

Саламандры по математике надеются, что вам понравятся эти бесплатные распечатанные рабочие листы по математике. и все другие наши математические игры и ресурсы.

Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.

Упрощение сложных дробей — ChiliMath

Когда «нормальная» дробь содержит дроби либо в числителе, либо в знаменателе, либо в обоих, мы считаем ее сложной дробью. Этот тип фракции также известен как составная фракция.

Существует два метода , используемых для упрощения такого вида дроби.

Метод 1

Ключевые шаги :

Создайте единую дробь в числителе и знаменателе.
Примените правило деления дробей, умножив числитель на величину, обратную или обратную знаменателю.
При необходимости упростите.

Метод 2

Ключевые шаги :

Найдите наименьший общий знаменатель (LCD) всех знаменателей в комплексных дробях.
Умножьте этот ЖК-дисплей на числитель и знаменатель комплексной дроби.
При необходимости упростите.

Рассмотрев несколько примеров, вы должны понять, что Method 2 намного лучше, чем Method 1 , потому что почти всегда требуется меньше шагов, чтобы добраться до окончательного ответа.

Примеры упрощения сложных дробей

Пример 1: Упростите приведенную ниже сложную дробь.

И числитель, и знаменатель комплексной дроби уже выражены как отдельные дроби.Это здорово!

Следующий шаг — применить правило деления, умножив числитель на обратную величину знаменателя. Закончите, исключив общие факторы, чтобы получить окончательный ответ.

Найдите ЖК-дисплей всей проблемы, то есть ЖК-дисплей верхнего и нижнего знаменателей.

Поскольку ЖК-дисплей 3y и 6y — это просто \ textbf {6y}, теперь мы умножим комплексный числитель и знаменатель на этот ЖК-дисплей. После этого мы можем ожидать, что проблема будет сведена к одной дроби, которую можно упростить, как обычно.2} Умножьте верх и низ на этот ЖК-дисплей.

Пример 3: Упростите приведенную ниже сложную дробь.

Создайте отдельные дроби в числителе и знаменателе, затем разделите дроби.

Общий ЖК-дисплей знаменателей равен \ color {red} 6x. Используйте это, чтобы перемножить верхнее и нижнее выражения.

Пример 4: Упростите приведенную ниже сложную дробь.

Для этой задачи мы будем использовать Method 1 только .

Задача требует, чтобы вы применили метод FOIL (умножение двух биномов) и простую факторизацию трехчлена. Поначалу это может показаться немного устрашающим; однако, если вы обратите внимание на детали, гарантирую, что все не так уж и плохо.

Если вы заметили, комплексный знаменатель уже находится в желаемой форме — с одним дробным символом. Это означает, что нам нужно немного поработать над сложным числителем. Нашим следующим шагом будет преобразование сложного числителя в «простую» или одинарную дробь.

Пример 5: Упростите приведенную ниже сложную дробь.

Для этой задачи мы будем использовать Method 2 только .

Обратите внимание, что ЖК-дисплей всех знаменателей равен \ color {red} 12x. Используйте это как общий множитель как для верхних, так и для нижних выражений.

Практика с рабочими листами

Возможно, вас заинтересует:

Умножение комплексных дробей

Разделение комплексных чисел

Что делать, когда студенты борются с дробными операциями

Вы умнее пятиклассника? Когда дело доходит до операций с дробями, для многих взрослых ответ — нет.’

Если вы не преподаете математику, вы можете быть удивлены тем, чего мы ожидаем от пятиклассников. Вот пример вопроса для 5-го класса от Министерства образования Луизианы.

Не знаю, как вы, но из-за этой проблемы я почесал затылок. Я почти уверен, что ответ — D. Но я определенно не мог решить эту проблему, когда мне было 10.

Итак, если ваши ученики испытывают трудности с операциями с дробями, вы не одиноки. Многие полагаются на такие уловки, как «сохранить, изменить, перевернуть», , но никогда не развивают концептуального понимания.

Этим студентам трудно применять свое понимание к проблемам реального мира. И они гораздо быстрее забывают то, чему учатся.

Обеспечение беглого владения учащимися дробями имеет важное значение для их общего успеха в математике. Понимание дробей обеспечивает основу для десятичных дробей, процентов и соотношений. Они также позволяют учащимся понимать пропорции, наклон и рациональные числа.

Когда ученики не усваивают дроби в начальной школе, они с трудом справляются с обучением в средней школе, алгебре, статистике и даже математике (если они их добиваются).

Чтобы помочь своим ученикам, сначала вы захотите узнать , почему у них возникают проблемы с операциями с дробями. Затем убедитесь, что у вас есть инструменты и стратегии для устранения их заблуждений.

Почему студенты борются с дробными операциями?

Чрезмерная зависимость от «уловок» не является уникальной особенностью операций с дробями. На протяжении всего обучения в K-12 (и за его пределами) ученики часто учатся считать, но не учатся рассуждать.

Так почему остро стоит проблема с дробями? Отчасти причина в том, что фракциям труднее подключиться к их жизненному опыту.

Дроби также требуют, чтобы учащиеся основывали свои предыдущие знания на операциях с целыми числами. Поэтому, когда ученикам не хватает этих основ, дроби становятся вдвое сложнее (или ½ легче).

Фактический ответ для каждого ученика индивидуален. Но вот распространенные ошибки, на которые следует обратить внимание.

Дроби не интуитивно понятны

Одна из причин, по которой учащиеся борются с операциями с дробями, заключается в том, что дроби менее интуитивно понятны, чем целые числа. Студенты постоянно складывают и вычитают целые числа в своей повседневной жизни, даже не осознавая этого.Иногда они даже размножаются и делятся.

И хотя они знают, что значит съесть половину печенья или отмерить ½ стакана муки, они обычно не оперируют с дробями. Многие думают, что «половина» — это , а именно половина , а не число, у которого единица в числителе и два — в знаменателе.

Многим студентам не хватает основополагающих концепций
Еще одна причина, по которой учащиеся борются, заключается в том, что они не усвоили базовые концепции. А именно значение дробей и целочисленных операций.
Если вы попросите своих учеников умножить 3 на 13, представят ли они себе массив? Модель площади? Пропустить счет по 10 три раза, а затем пропустить счет по три раза? Или они просто складываются и просчитывают?
3 на 13 Массив
Учащиеся, которые могут визуализировать операции с целыми числами, могут, основываясь на своем понимании деления, представить себе целое, разрезанное на четыре части. Они могут расширить эту идею, добавив одну четвертую к другой четверти. Или пятую часть умножить на три.
Но поскольку у многих студентов нет этих концептуальных основ, они просто видят дроби как одно число, сложенное поверх другого.Чем больше приемов и процедур они узнают, тем больше вероятность, что они забудут их или воспользуются неправильным приемом для решения неправильной задачи.
Но есть еще большая проблема с алгоритмами без концепций . Учащиеся не развивают способность видеть математику, которая их окружает. Они не признают математику как язык или изучение пространства и количества. Они не видят красоты и искусства в математике.
Вместо этого он становится набором «математических фактов», случайных правил и секретных символов.
Операции с дробями противоречат правилам целых чисел
Даже учащиеся, которые понимают концепции целых чисел, могут столкнуться с проблемами с дробями.
В начальной школе ученики сосредотачиваются на освоении системы Base-10. Они считают десятками, объединяют десятки и единицы и разбивают числа по разрядам, чтобы действовать. Все дело в том, чтобы сделать десятки, разбить десятки и использовать ноль в качестве заполнителя.
Но дроби не строятся на десятках. Дроби можно разделить на 3, 7 или 45-е.И при изменении знаменателя изменяется размер «единицы». Как и единицы, необходимые для создания группы (одного целого).
Дроби также противоречат «правилам», которые студенты изучают для целых чисел. Когда вы умножаете 3 на 5, результат будет больше обоих. Но умножая дроби, мало ли. Произведение ⅓ и ¼ меньше обоих. Но умножение ⅕ на 4 дает произведение между двумя факторами.
Когда учащиеся имеют прочную концептуальную основу, они могут обобщать то, что они знают о целых числах, чтобы понимать дроби.Но без этого понимания им может показаться, что они начинают все сначала, с совершенно новым набором правил!
Три совета по обучению дробным операциям
Первый шаг к тому, чтобы помочь своим ученикам с операциями с дробями, — это понять, почему они борются.
Следующее — это конкретные действенные шаги для решения этих проблем.
Во-первых, убедитесь, что ваши ученики действительно понимают значение дроби. Затем свяжите это с тем, что они уже знают об операциях с целыми числами.
И то, и другое можно выполнить с помощью модели The Three Vehicles — моделей уроков на основе запросов, которые могут поддерживать практически любую математическую концепцию.
1. Обзор и оценка дробных оснований
Проще говоря, знаменатель говорит нам, на сколько частей делится целое. Числитель говорит нам, сколько таких фигур у нас есть. Хотя числитель сверху , он мало что значит, если вы не знаете знаменатель. Вот почему я учу дроби снизу вверх.
В какой-то момент (обычно около 5 класса) ученики узнают, что дробь также можно рассматривать как частное. Результат деления числителя на знаменатель. Итак, 3 ÷ 4 это то же самое, что ¾. Визуально это можно представить в виде 3 целых, каждая из которых разделена на 4 равные части, причем части перегруппированы в одну фракцию.
Чтобы оценить свое понимание, учащиеся должны уметь это без направления . Если вам нужно сказать им, чтобы они стригли или заштриховывали, они не понимают концепции.Они просто рисуют.
2. Соедините операции дроби с операциями целых чисел
Когда учащиеся поймут дроби, они смогут работать с дробями так же, как с целыми числами. Если, конечно, они понимают смысл операций.
Сложение и вычитание
Когда учащиеся поймут значение, они могут начать счет вверх и вниз, чтобы складывать и вычитать дроби с одинаковыми знаменателями.
Следующий шаг — составить целое, например, счет до четвертых или прибавление ⅓ к ⅔.Затем они могут вычесть, чтобы разбить целое (1 — ⅙).
Подсчитав из , они могут начать работать со смешанными числами (⅔ + ⅔ = 1 ⅓).
Сложить и вычесть дроби с разными знаменателями сложнее. Учащимся необходимо преобразовать в эквивалентные дроби, что зависит от навыков, полученных путем умножения дробей. Таким образом, студенты сначала изучают эти концепции, прежде чем вернуться к сложению и вычитанию с разными знаменателями.
Дробные упражнения для вашего класса
Умножение дробей
После того, как учащиеся научатся складывать дроби, достаточно просто умножить дробь на целое число.Просто представьте ¼ x 3 как ¼ + ¼ + ¼.
Затем замените знак умножения словом «of». Таким образом, ¼ x 3 становится «одна четвертая из трех». Это связывает умножение дроби с умножением целых чисел. 3 x 2 означает три (группы) из двух. Таким образом, имеет смысл для ⅓ x 4 равняться одной трети (группы) 4.
Он также расширяет концепцию умножения на дроби до умножения на дроби, что позволяет учащимся решать, когда оба множителя являются дробями.
В этом упражнении «Google Презентации» используются визуальные представления, чтобы продемонстрировать значение умножения дробей: учащиеся скользят по моделям дробей, чтобы увидеть, что происходит при умножении.
Помимо поддержки концептуального понимания, модели умножения дробей показывают учащимся, почему мы умножаем числители и знаменатели в алгоритме.
Чтобы узнать больше о том, как связать дробное умножение с целыми числами, просмотрите пять значений умножения.
На дроби
Деление на дроби также может быть связано с тем, что учащиеся знают о целых числах.
Начните с деления дроби на ее числитель, например, деление на 3. Это включает дробное деление, при котором делитель определяет количество групп .
Затем разделите целое число на дробь. Здесь мы используем кавычки , , в котором делитель определяет размер каждой группы .При делении 2 на обе целые разделяются на трети (делитель = размер группы) и подсчитывается общее количество групп (частное = количество групп). Это показывает, почему мы умножаем на знаменатель при делении на дробь.
Котативное деление также полезно для деления дроби на дробь, но только в некоторых случаях. Чтобы разделить ⅔ на ⅓, просто создайте 2 группы по в каждой.
А как насчет ⅓, разделенного на ¼? Можно представить себе разделение трети на группы размером в четверть… но это не очень интуитивно понятно.В этом случае я возвращаюсь к разделению на части и использую то, что я называю стратегией «копии-призрака».
Если бы я разделил 8 на 2 частично, я бы преобразовал одну группу из 8 на две новые группы, по четыре в каждой группе. Если вместо этого я делю 8 на ½, я превращаю одну группу из 8 в , половину группы . Чтобы создать одну целую группу, мне нужно сделать призрачную копию моего начального значения (делимого).
Стратегия фантомных копий может быть расширена для таких коэффициентов, как ½ ÷ ⅓.Рассматривайте ½ как полной группы . Таким образом, мы добавляем две копии-призраки ½, чтобы образовать одну целую группу, в результате получилась 1½.
Пять значений умножения также полезно для студентов с дробным делением. И наоборот, каждое значение умножения применимо к делению.
Эквивалентные дроби
Эквивалентные дроби могут быть самым сложным аспектом операций с дробями. Трудно связать это с целыми числами, поскольку нет другого эквивалента целых чисел: восемь — это всего лишь восемь, нет целого числа, эквивалентного 8.
Но дробь, такая как ⅓, также может быть записана как 2/6 или 10/30, и при этом иметь то же значение. Фактически, вы можете возразить, что эквивалент , почему мы в первую очередь используем дроби .
Когда студенты спрашивают, «зачем нам и дроби, и десятичные дроби», отличный ответ заключается в том, что дроби позволяют нам делить целые числа на части любого размера, которые мы хотим. В десятичных дробях мы ограничены десятичными множителями.
Но я включаю здесь эквивалентность по двум причинам. Во-первых, это очень важно для многих последующих применений дробей.Для упрощения дробей и сложения различных знаменателей требуется преобразование эквивалентных дробей. Как и десятичные и процентные преобразования, работа с пропорциями и нахождение наклона. Этот список можно продолжить.
Вторая причина заключается в том, что умножение дробей может использоваться для обучения эквивалентным дробям.
Я учу преобразование дроби как умножение на единицу . Чтобы найти эквивалент для ½, я могу умножить на 3/3 (он же один), получив 3/6.
Студенты, которые могут использовать модели площадей для умножения дробей, должны связать идею умножения на с идеей умножения на 3/3.Как визуально, так и с алгоритмом «умножения по горизонтали».
3. Используйте
Три машины для обучения дробным операциям
Три машины — это модели уроков, основанные на запросах, которые способствуют концептуальному пониманию. Их можно использовать для обучения практически любой математической концепции на любом уровне обучения.
Транспортные средства построены на теории множественных представлений , идее о том, что любое математическое понятие может быть представлено пятью различными способами: физически, визуально, символически, концептуально и вербально.
Мы можем определить беглость как способность переводить математическую идею во все пять представлений. Это включает перевод выражения в визуальную модель. Или объяснить на словах, как работает манипулятивное средство.
Пять представлений определяют, как могут быть представлены математические идеи. И машины учат студентов, как переводить среди них.
Масштабные модели
Первая машина — это масштабная модель. Он сочетает в себе физические и визуальные представления (также известные как конкретные и графические), поскольку оба служат одной цели.Они представляют размер чисел и значение операций.
Масштабные модели полезны для построения и оценки концептуального понимания. Чтобы использовать масштабные модели в качестве учебного пособия, сначала научите принципам чтения и создания масштабных моделей. Затем используйте модели как инструменты, помогающие учащимся учиться через вопросы.
Например, если учащиеся понимают дроби и умножение целых чисел, они могут использовать свои навыки моделирования, чтобы «обнаружить» умножение дробей, даже без прямых инструкций.
Для учащихся важно создавать свои собственные модели, а не просто интерпретировать модели из учебников или созданные учителями. Чтение моделей полезно, но недостаточно для беглости речи.
Три моста Интернет-семинары для преподавателей
Число предложений
Следующее транспортное средство — это числовое предложение. Числовые предложения (уравнения и неравенства) основаны на концепциях, разработанных с помощью визуальных моделей, для поддержки развития абстрактного понимания.
Числовые предложения позволяют студентам манипулировать выражениями и работать в несколько этапов, что делает их гораздо более полезными, чем вычисления с помощью алгоритмов.
Я использую доказательства числовых предложений, чтобы помочь студентам выучить числовые предложения и связать их с другими представлениями.
История проблем
Третий автомобиль, сюжетные задачи, помощь с прикладными навыками и математическим языком.
Я учу студентов использовать процесс Polya для решения словесных задач.Этот подход подчеркивает важность использования нескольких представлений для решения текстовых задач.
Этот автомобиль идет последним, потому что учащиеся могут использовать масштабные модели и числовые предложения в качестве инструментов для решения словесных задач.
Обучение дробным операциям в классе
Я надеюсь, что эта статья предложила полезный обзор основных концепций, необходимых для успеха операций с дробями.
Ресурсы для обучения дробям на всех трех автомобилях можно найти в нашем интернет-магазине.
Или повысьте свои математические навыки на основе запросов, записавшись на онлайн-семинар. Это занятия в реальном времени, проводимые ведущим в реальном времени. Мы предлагаем отдельные занятия по каждому транспортному средству для учителей начальной и средней школы, чтобы вы могли сосредоточиться на методах и стандартах, которые наиболее важны для ваших учеников.
Наконец, если вы хотите сразу же включить этот тип обучения, загрузите наш пакет Fractions Essentials Bundle. В нем есть все необходимое для начала работы, от интерактивных занятий Google Slides до планов уроков, ключей ответов и многого другого!
Получите копию FRACTION ESSENTIALS
Об авторе
Джефф Лисиандрелло — основатель Room to Discover и консультант по образованию, специализирующийся на обучении, ориентированном на учащихся.Его 3-мостовой дизайн обучения помогает школам изучать инновационные методы в традиционных условиях. Ему нравится помогать педагогам применять индивидуальный подход к обучению, основанный на запросах. Вы можете связаться с ним через Twitter @EdTechJeff
Что такое упрощающие дроби? — Определение, факты и примеры
Упрощающие дроби
Дробь — это часть целого. У него есть числитель и знаменатель.
Например: 12 здесь 1 — числитель, а 2 — знаменатель.Он представлен цифрой, приведенной ниже:
Здесь фигура разделена на 2 равные части, поэтому знаменатель равен 2, а 1 из 2 частей заштрихована, поэтому числитель равен 1.
Простейшая форма дроби
Дробь называется простейшей формой, если 1 является единственным общим делителем ее числителя и знаменателя. Например, 89, потому что 1 — единственный общий делитель 8 и 9 в этой дроби.
Мы упрощаем дроби, потому что всегда нужно работать или вычислять, когда дроби представлены в простейшей форме.
Упрощение правильных и неправильных дробей
Шагов:
Найдите наибольший общий множитель числителя и знаменателя.
Разделите числитель и знаменатель на HCF.
Пример 1 : Проверить, находится ли дробь 715 в простейшей форме?
Решение: Коэффициенты числителя 7 = 1, 7
Множители знаменателя 15 = 1, 3, 5, 15
Мы видим, что 1 является единственным общим делителем 7 и 15
Следовательно, 715 в простейшем виде.
Пример 2: Уменьшите 1218 в простейшей форме.
Решение: Факторы 12 = 1, 2, 3, 4, 6, 12
Факторы 18 = 1, 2, 3, 6, 9, 18
Наивысший общий множитель (HCF) 12 и 18 = 6
Разделив числитель и знаменатель на 6 (HCF), получим
12 ÷ 6 18 ÷ 6 = 2 3
Следовательно, 23 — это простейшая форма дроби 1218.
Упрощение смешанной фракции
Шагов:
Найдите наибольший общий множитель числителя и знаменателя дроби.
Разделите числитель и знаменатель на HCF, чтобы получить упрощенную дробь.
Запишите целое и упрощенную дробь вместе.
Пример 4: У Мэтью 31216 мороженого. Сколько у него мороженого в простейшем виде?
Решение: Коэффициенты 3 12 16 = 1 4 12 = 1, 2, 3, 4, 6, 12
Множители 16 = 1, 2, 4, 8, 16
Наивысший общий множитель (HCF) 12 и 16 = 4
Разделив числитель и знаменатель на 4 (HCF), получим
12 ÷ 4 16 ÷ 4 = 3 4
Следовательно, у Мэтью есть 31216 мороженого в его простейшем виде.
Интересные факты:
Слово «дробь» происходит от латинского слова «Fractio», что означает «ломать».
Каждое целое число можно записать в виде дроби. Например, 2 можно записать как 21
БЕСПЛАТНЫЕ настольные игры с дробями
Одна математическая концепция, которая может заставить многих учеников споткнуться, — это дробей . Понимание того, что они представляют, использование их в расчетах и упрощение может вызвать такое беспокойство.Но с небольшой практикой , упрощающей дроби , это не должно быть так пугающе. Эта супер милая, красочная математическая игра Fraction Race — отличный способ попрактиковаться для учеников третьего, четвертого и пятого классов. Наши настольные игры с дробями — это простая игра с небольшой подготовительной дробью, которая помогает упростить дроби.
Фракция настольных игр
Гонка за сокращением дробей продолжается с этой веселой бесплатной распечаткой Настольные игры на дроби ! Учащиеся 3-го, 4-го, 5-го и 6-го классов получат удовольствие от этой игры с дробями, поскольку они получат практику упрощения дробей.Нам нравится делать обучение увлекательным, а подобные обучающие математические игры — отличный способ заинтересовать детей и сделать изучение математики увлекательным!
Являетесь ли вы родителем или школьником на дому, который хочет дополнительно попрактиковаться в математике дома, чтобы закрепить математические навыки, или потихоньку поучиться летом; или учитель хочет попробовать веселую математическую игру или добавить эту игру с дробями в математический центр.
Фракционные настольные игры для печати
Начните с прокрутки сообщения до конца в соответствии с условиями использования и щелкните текстовую ссылку с надписью >> Загрузить <<.PDF-файл откроется в новом окне, где вы сможете сохранить халяву и загрузить шаблон. Распечатайте PDF-файл в цвете на карточках. Вам также нужно будет захватить игровые фишки (мы используем минифигурки Lego)
Игра на дроби для печати
Цель этой игры — записать дроби в их низшей форме . Уменьшая дроби, дети работают над , распознавая факторы и находя наибольший общий фактор .
Кроме того, постоянно наблюдая за дробями, которые сводятся к одной и той же дроби, ваши дети начнут узнавать эквивалентные дроби .
Хотя я не рекомендую запоминать все дроби, включенные в эту игру, возможность легко распознать общие эквивалентные дроби очень полезна. Многие из них станут узнаваемы, если сыграют в эту игру вместе .
Это также поможет вашим детям отработать навыки деления , поскольку они делят на упрощают дроби .
Упростить дроби
Полные инструкции по игре включены в загрузку, но основная идея игры проста и похожа на Candyland.
Самый молодой игрок начинает с , выбирая карту дроби .
Они уменьшают дробь до самого низкого значения (все дроби уменьшаются до 1/2, 1/3, 1/4, 1/5 или 1/6).
Затем они переходят к ближайшей дроби на доске дробей , соответствующей их решению.
Например, если их доля уменьшается до 1/2, они перемещают свою игровую фишку на следующую 1/2 на доске.
Игра переходит к следующему игроку, который выбирает карту и играет таким же образом.
Эквивалентные дроби
Если игрок выбирает карту с надписью «Ой, спустило колесо» или «Пора сделать пит-стоп», игрок теряет ход и игра переходит к следующему игроку.
Игрок , первым добравшийся до финиша (для чего требуется решение 1/6), выигрывает игру !
Надеюсь, эта увлекательная игра с дробями даст вам увлекательный способ практиковать важные математические навыки и повысит уверенность ваших детей с помощью дробей.
Дроби Игры
Ищете больше удовольствия игры дроби для детей ? Вам понравятся эти бесплатные распечатанные дроби для детей всех возрастов.
Знаете ли вы, что у нас есть более 1 миллиона страниц бесплатных распечатываемых рабочих листов для детей, в том числе математические задания для дошкольников, математика для детского сада, математика для первого класса, математика для 2-го класса и рабочие листы с алфавитом, которые помогут сделать обучение УДОВОЛЬСТВИЕМ. А также наши уроки истории и удивительные простые научные эксперименты для детей
Предпочитаете просто взглянуть на наши математические игры по классам? Вам понравится этот пост!
Скачать Настольная игра Fractions
Перед загрузкой бесплатного пакета вы соглашаетесь со следующим:
Этот набор предназначен только для личного и учебного использования.
Запрещается продавать, размещать, воспроизводить или хранить этот набор для печати на каких-либо других веб-сайтах или в электронных поисковых системах.
Графика Приобретается и используется с разрешения
Все загружаемые материалы в этом блоге защищены авторским правом.
>> Скачать Fraction Board Game
<<
Визуализируйте дроби — Элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
Найти эквивалентные дроби
Упростить дроби
Умножение дробей
Разделить на дроби
Упростить выражения, написанные дробной чертой
Перевести фразы в выражения с дробями
Более подробное введение в темы, затронутые в этом разделе, можно найти в главе Prealgebra , Fractions .
Найти эквивалентные дроби
Дроби — это способ представления частей целого. Дробь означает, что одно целое было разделено на 3 равные части, и каждая часть является одной из трех равных частей. См. (Рисунок). Дробь представляет собой две из трех равных частей. В дроби 2 называется числителем, а 3 — знаменателем.
Круг слева разделен на 3 равные части. Каждая часть состоит из 3 равных частей. В круге справа заштрихованы части круга (2 из 3-х равных частей).
Выполнение задания по манипуляции математикой «Модель дробей» поможет вам лучше понять дроби, их числители и знаменатели.
Дробь
А дробь пишется где и
a — это числитель , а b — знаменатель .
Дробь представляет собой части целого. Знаменатель b — это количество равных частей, на которые было разделено все целое, а числитель a указывает, сколько частей включено.
Если весь пирог был разрезан на 6 частей, и мы съели все 6 частей, мы съели кусочки или, другими словами, один целый пирог.
Итак, это приводит нас к свойству единицы, которое говорит нам, что любое число, кроме нуля, деленное само на себя, равно 1.
Собственность одного человека
Любое число, кроме нуля, деленное само на себя, равно единице.
Выполнение задания по манипуляции с математикой «Дроби, эквивалентные единице», поможет вам лучше понять дроби, эквивалентные единице.
Если пирог разрезали на части и мы съели все 6, мы съели кусочки, или, другими словами, один целый пирог. Если пирог был разрезан на 8 частей, и мы съели все 8, мы съели кусочки или один целый пирог. Съели столько же — целый пирог.
Дроби и имеют одинаковое значение 1, поэтому они называются эквивалентными дробями. Эквивалентные дроби — это дроби с одинаковым значением.
Давайте на этот раз подумаем о пицце. (Рисунок) показывает два изображения: одну пиццу слева, разрезанную на две равные части, и вторую пиццу того же размера, разрезанную на восемь частей справа.Это способ показать, что эквивалентно. Другими словами, это эквивалентные дроби.
Поскольку одинаковое количество каждой пиццы закрашено, мы видим, что это эквивалентные дроби.
Эквивалентные дроби
Эквивалентные дроби — это дроби с одинаковым значением.
Как мы можем использовать математику для преобразования в Как мы можем взять пиццу, разрезанную на 2 части, и разрезать ее на 8 частей? Мы могли бы разрезать каждую из 2 больших частей на 4 меньших! Тогда вся пицца будет разрезана на кусочки, а не на 2.Математически то, что мы описали, можно было бы записать следующим образом: См. (Рисунок).
Разрезав каждую половину пиццы на кусочки, мы получим пиццу, разрезанную на 8 частей:
Эта модель приводит к следующему свойству:
Эквивалентные дроби Свойство
Если это числа, то где
Если бы мы по-другому нарезали пиццу, то получили бы
Итак, мы говорим, что дроби эквивалентны.
Выполнение задания по манипуляции с математикой «Эквивалентные дроби» поможет вам лучше понять, что означает, когда две дроби эквивалентны.
Найдите три дроби, эквивалентные
Решение
Чтобы найти дробь, эквивалентную, умножим числитель и знаменатель на то же число. Мы можем выбрать любое число, кроме нуля. Умножим их на 2, 3, а затем на 5.

Итак, эквивалентны
Найдите три дроби, эквивалентные
ответы могут отличаться
Найдите три дроби, эквивалентные
ответы могут отличаться
Упростить дроби
Дробь считается упрощенной , если в ее числителе и знаменателе нет общих множителей, кроме 1.
Например,
упрощен, потому что нет общих множителей 2 и 3.
не упрощается, потому что это общий множитель 10 и 15.
Упрощенная дробь
Дробь считается упрощенной, если в ее числителе и знаменателе нет общих множителей.
Фраза сократить дробь означает упростить дробь. Мы упрощаем или сокращаем дробь, удаляя общие множители числителя и знаменателя.Дробь не упрощается, пока не будут удалены все общие множители. Если в выражении есть дроби, оно не будет полностью упрощено, пока дроби не будут упрощены.
В (рисунок) мы использовали свойство эквивалентных дробей, чтобы найти эквивалентные дроби. Теперь мы воспользуемся свойством эквивалентных дробей в обратном порядке, чтобы упростить дроби. Мы можем переписать свойство, чтобы отображать обе формы вместе.
Эквивалентные дроби Свойство
Если это числа, где
Упростить:
Упростить:
Иногда бывает непросто найти общие множители числителя и знаменателя.Когда это происходит, хорошей идеей будет разложить числитель и знаменатель на простые числа. Затем разделите общие множители, используя свойство эквивалентных дробей.
Как упростить дробь
Упростить:
Упростить:
Упростить:
Теперь мы суммируем шаги, которые вы должны выполнить, чтобы упростить дроби.
Упростите дробь.
Перепишите числитель и знаменатель, чтобы показать общие множители.
Если необходимо, сначала разложите числитель и знаменатель на простые числа.
Упростите использование свойства эквивалентных дробей, разделив общие множители.
При необходимости умножьте оставшиеся множители.
Упростить:
Решение
Перепишите общие множители, затем разделите общие множители.
Упростить.
Упростить:
Упростить:
Умножение дробей
Многим людям проще умножать и делить дроби, чем складывать и вычитать дроби.Итак, начнем с умножения дробей.
Выполнение задания по манипуляциям с математикой «Модельное умножение дробей» поможет вам лучше понять умножение дробей.
Мы будем использовать модель, чтобы показать вам, как умножить две дроби, и помочь вам запомнить процедуру. Начнем с
Теперь возьмем
Обратите внимание, что теперь целое разделено на 8 равных частей. Итак
Для умножения дробей умножаем числители и знаменатели.
Умножение дробей
Если это числа, то где
Чтобы умножить дроби, умножьте числители и знаменатели.
При умножении дробей, конечно, все еще применяются свойства положительных и отрицательных чисел. В качестве первого шага рекомендуется определить знак продукта. В (Рисунок) мы умножим отрицательное и положительное, так что произведение будет отрицательным.
Умножить:
Решение
Первый шаг — найти знак товара.Поскольку знаки разные, товар отрицательный.
Определить знак товара; умножить.
Есть ли общие множители в числителе и демонинаторе? №
Умножить:
Умножить:
При умножении дроби на целое число может оказаться полезным записать целое число в виде дроби.Любое целое число, a , можно записать как So, например,
Умножить:
Решение
Определите знак товара. Знаки такие же, значит, товар положительный.
Умножить:
Умножить:
Разделить дроби
Теперь, когда мы знаем, как умножать дроби, мы почти готовы к делению. Прежде чем мы сможем это сделать, нам понадобится словарный запас.
Обратное значение дроби находится путем инвертирования дроби, помещения числителя в знаменатель и знаменателя в числитель.Обратное значение равно
.
Обратите внимание, что число A и его обратная величина умножаются на 1.
Чтобы получить произведение положительной единицы при умножении двух чисел, числа должны иметь одинаковый знак. Значит, у взаимных знаков должен быть один и тот же знак.
Обратное значение с
Взаимный
, обратное от
Число и его обратное умножение на единицу
Выполнение задания по манипуляции математикой «Модельное деление на дроби» поможет вам лучше понять деление дробей.
Чтобы разделить дроби, мы умножаем первую дробь на величину, обратную второй.
Фракционное подразделение
Если это числа, то где
Чтобы разделить дроби, мы умножаем первую дробь на величину, обратную второй.
Нам нужно сказать, чтобы убедиться, что мы не делим на ноль!
Разделить:
Решение
Чтобы разделить, умножьте первую дробь на обратную величину второй.
Умножить.
Разделить:
Разделить:
Найдите частное:
Найдите частное:
Найдите частное:
Есть несколько способов запомнить, какие шаги нужно предпринять для умножения или деления дробей. Один из способов — повторить призыв про себя. Если вы будете делать это каждый раз, когда выполняете упражнение, вы запомните шаги.
«Чтобы умножить дроби, умножьте числители и умножьте знаменатели».
«Чтобы разделить дроби, умножьте первую дробь на величину, обратную второй».
Другой способ — запомнить два примера:
Числители или знаменатели некоторых дробей сами содержат дроби. Дробь, в которой числитель или знаменатель является дробью, называется комплексной дробью .
Комплексная фракция
Комплексная дробь — это дробь, в числителе или знаменателе которой содержится дробь.
Примеры сложных дробей:
Чтобы упростить сложную дробь, мы помним, что черта дроби означает деление. Например, сложная дробь означает
Упростить:
Упростить:
Упростить:
Упростить:
Упростить:
Упростить:
Упростите выражения с помощью дроби
Линия, отделяющая числитель от знаменателя дроби, называется чертой дроби.Полоса дроби действует как символ группировки. Затем порядок действий подсказывает нам упростить числитель, а затем знаменатель. Потом делим.
Чтобы упростить выражение, сначала упростим числитель и знаменатель по отдельности. Потом делим.
Упростите выражение с помощью дроби.
Упростите выражение в числителе. Упростите выражение в знаменателе.
Упростим дробь.
Упростить:
Упростить:
Где идет знак минус в дроби? Обычно перед дробью стоит отрицательный знак, но иногда вы можете увидеть дробь с отрицательным числителем, а иногда и с отрицательным знаменателем.Помните, что дроби представляют собой деление. Когда числитель и знаменатель имеют разные знаки, частное отрицательное.
Размещение отрицательного знака в дроби
Для любых положительных чисел a и b ,
Упростить:
Упростить:
Практика ведет к совершенству
Найти эквивалентные дроби
В следующих упражнениях найдите три дроби, эквивалентные данной дроби.Покажите свою работу, используя цифры или алгебру.
ответы могут отличаться
ответы могут отличаться
Упростить дроби
Упростите следующие упражнения.
Умножение дробей
В следующих упражнениях умножьте.
Разделить на дроби
В следующих упражнениях разделите.
Упростите следующие упражнения.
Упростите выражения, написанные с помощью дроби
Упростите следующие упражнения.
Перевод фраз в выражения с дробями
В следующих упражнениях переведите каждую английскую фразу в алгебраическое выражение.
частное r и сумма s и 10
частное A и разница 3 и B
частное от разницы
частное от суммы
Письменные упражнения
Рафаэль хотел заказать половину средней пиццы в ресторане. Официант сказал ему, что пиццу среднего размера можно разрезать на 6 или 8 ломтиков. Он предпочел бы 3 ломтика из 6 или 4 из 8? Рафаэль ответил, что, поскольку он не очень голоден, он предпочел бы 3 ломтика из 6.Объясните, что неверно в рассуждениях Рафаэля.
Приведите пример из повседневной жизни, демонстрирующий, как
Объясните, как найти величину, обратную дроби.
Объясните, как найти обратную величину отрицательного числа.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ После просмотра контрольного списка, думаете ли вы, что хорошо подготовились к следующему разделу? Почему или почему нет?
Решение уравнений с очисткой дробей
Результаты обучения
Используйте наименьший общий знаменатель, чтобы исключить дроби из линейного уравнения перед его решением
Решите уравнения с дробями, которые требуют нескольких шагов
Вы можете быть ошеломлены, когда видите дроби в уравнении, поэтому мы собираемся показать метод решения уравнений с дробями, в котором вы используете общий знаменатель, чтобы исключить дроби из уравнения.Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей.
Обратите внимание на то, что каждый член в уравнении умножается на наименьший общий знаменатель. Вот что отличает его от оригинала!
ПРИМЕР
Решение: [латекс] \ frac {1} {8} x + \ frac {1} {2} = \ frac {1} {4} [/ latex].
Решение:
[латекс] \ frac {1} {8} x + \ frac {1} {2} = \ frac {1} {4} \ quad {LCD = 8} [/ latex]
Умножьте обе части уравнения на этот ЖК-дисплей, [латекс] 8 [/ латекс].Это очищает фракции. [латекс] \ color {красный} {8 (} \ frac {1} {8} x + \ frac {1} {2} \ color {red} {)} = \ color {red} {8 (} \ frac {1} {4} \ color {red} {)} [/ latex]
Используйте свойство распределения. [латекс] 8 \ cdot \ frac {1} {8} x + 8 \ cdot \ frac {1} {2} = 8 \ cdot \ frac {1} {4} [/ latex]
Упростите — и заметьте, никаких дробей! [латекс] x + 4 = 2 [/ латекс]
Решите, используя общую стратегию решения линейных уравнений. [латекс] x + 4 \ color {red} {- 4} = 2 \ color {red} {- 4} [/ latex]
Упростить. [латекс] x = -2 [/ латекс]
Проверить: Пусть [латекс] x = -2 [/ латекс]
[латекс] \ frac {1} {8} x + \ frac {1} {2} = \ frac {1} {4} [/ latex]
[латекс] \ frac {1} {8} (\ color {red} {- 2}) + \ frac {1} {2} \ stackrel {\ text {?}} {=} \ Frac {1} { 4} [/ латекс]
[латекс] \ frac {-2} {8} + \ frac {1} {2} \ stackrel {\ text {?}} {=} \ Frac {1} {4} [/ latex]
[латекс] \ frac {-2} {8} + \ frac {4} {8} \ stackrel {\ text {?}} {=} \ Frac {1} {4} [/ latex]
[латекс] \ frac {2} {8} \ stackrel {\ text {?}} {=} \ Frac {1} {4} [/ latex]
[латекс] \ frac {1} {4} = \ frac {1} {4} \ quad \ checkmark [/ latex]
В последнем примере наименьший общий знаменатель был [латекс] 8 [/ латекс].Теперь ваша очередь найти ЖК-дисплей и очистить дроби, прежде чем решать эти линейные уравнения.
Обратите внимание, что после того, как мы очистили уравнение дробей, оно было похоже на те, которые мы решали ранее в этой главе. Мы изменили проблему на ту, которую уже знали, как решить!
Решите уравнения, очистив знаменатели
Найдите наименьший общий знаменатель для всех дробей в уравнении.
Умножьте обе части уравнения на этот ЖК-дисплей.Это очищает фракции.
Выделите переменные члены с одной стороны и постоянные члены с другой.
Упростите обе стороны.
Используйте свойство умножения или деления, чтобы коэффициент переменной был равен [latex] 1 [/ latex].
Вот пример с тремя переменными членами. После того, как вы очистите дроби с помощью ЖК-дисплея, вы упростите три члена переменной, а затем выделите переменную.
Пример
Решение: [латекс] 7 = \ frac {1} {2} x + \ frac {3} {4} x- \ frac {2} {3} x [/ latex].
Показать решение
Решение:
Мы хотим очистить дроби, умножив обе части уравнения на ЖК-дисплей всех дробей в уравнении.
Найдите наименьший общий знаменатель всех дробей в уравнении. [латекс] 7 = \ frac {1} {2} x + \ frac {3} {4} x- \ frac {2} {3} x \ quad {LCD = 12} [/ latex]
Умножьте обе части уравнения на [латекс] 12 [/ латекс]. [латекс] \ color {red} {12} (7) = \ color {red} {12} \ cdot (\ frac {1} {2} x + \ frac {3} {4} x- \ frac {2 } {3} x) [/ латекс]
Распространить. [латекс] 12 (7) = 12 \ cdot \ frac {1} {2} x + 12 \ cdot \ frac {3} {4} x-12 \ cdot \ frac {2} {3} x [/ латекс ]
Упростите — и заметьте, никаких дробей! [латекс] 84 = 6x + 9x-8x [/ латекс]
Объедините похожие термины. [латекс] 84 = 7x [/ латекс]
Разделить на [латекс] 7 [/ латекс]. [латекс] \ frac {84} {\ color {red} {7}} = \ frac {7x} {\ color {red} {7}} [/ latex]
Упростить. [латекс] 12 = x [/ латекс]
Проверить: Пусть [латекс] x = 12 [/ латекс].
[латекс] 7 = \ frac {1} {2} x + \ frac {3} {4} x- \ frac {2} {3} x [/ latex]
[латекс] 7 \ stackrel {\ text {?}} {=} \ Frac {1} {2} (\ color {red} {12}) + \ frac {3} {4} (\ color {red} {12}) — \ frac {2} {3} (\ color {red} {12}) [/ latex]
[латекс] 7 \ stackrel {\ text {?}} {=} 6 + 9-8 [/ латекс]
[латекс] 7 = 7 \ четырехугольник \ галочка [/ латекс]
А теперь попробуйте аналогичную задачу. Очистите дроби, упростите и решите.
Внимание!
Одна из наиболее распространенных ошибок при очистке дробей — это забвение умножения ОБЕИХ частей уравнения на ЖК-дисплей. Если ваш ответ не проходит, убедитесь, что вы умножили обе части уравнения на ЖК-дисплей.
В следующем примере у нас будут переменные и дроби с обеих сторон уравнения. После того, как вы очистите дроби с помощью ЖК-дисплея, вы увидите, что это уравнение похоже на уравнения с переменными с обеих сторон, которые мы решили ранее.Не забудьте выбрать переменную сторону и постоянную сторону, чтобы помочь вам организовать свою работу.
Пример
Решение: [латекс] x + \ frac {1} {3} = \ frac {1} {6} x- \ frac {1} {2} [/ latex].
Показать решение
Решение:
Найдите на ЖК-дисплее все дроби в уравнении. [латекс] x + \ frac {1} {3} = \ frac {1} {6} x- \ frac {1} {2}, \ quad {LCD = 6} [/ latex]
Умножьте обе стороны на ЖК-дисплей. [латекс] \ color {red} {6} (x + \ frac {1} {3}) = \ color {red} {6} (\ frac {1} {6} x- \ frac {1} {2 }) [/ latex]
Распространить. [латекс] 6 \ cdot {x} +6 \ cdot \ frac {1} {3} = 6 \ cdot \ frac {1} {6} x-6 \ cdot \ frac {1} {2} [/ латекс ]
Упростите — больше никаких дробей! [латекс] 6x + 2 = x-3 [/ латекс]
Вычтите [латекс] x [/ латекс] с обеих сторон. [латекс] 6x- \ color {красный} {x} + 2 = x- \ color {красный} {x} -3 [/ latex]
Упростить. [латекс] 5x + 2 = -3 [/ латекс]
Вычтите 2 с обеих сторон. [латекс] 5x + 2 \ color {red} {- 2} = — 3 \ color {red} {- 2} [/ latex]
Упростить. [латекс] 5x = -5 [/ латекс]
Разделить на [латекс] 5 [/ латекс]. [латекс] \ frac {5x} {\ color {red} {5}} = \ frac {-5} {\ color {red} {5}} [/ latex]
Упростить. [латекс] x = -1 [/ латекс]
Проверка: Заменить [латекс] x = -1 [/ латекс].
[латекс] x + \ frac {1} {3} = \ frac {1} {6} x- \ frac {1} {2} [/ latex]
[латекс] (\ color {red} {- 1}) + \ frac {1} {3} \ stackrel {\ text {?}} {=} \ Frac {1} {6} (\ color {red} {-1}) — \ frac {1} {2} [/ latex]
[латекс] (- 1) + \ frac {1} {3} \ stackrel {\ text {?}} {=} — \ frac {1} {6} — \ frac {1} {2} [/ латекс ]
[латекс] — \ frac {3} {3} + \ frac {1} {3} \ stackrel {\ text {?}} {=} — \ frac {1} {6} — \ frac {3} { 6} [/ латекс]
[латекс] — \ frac {2} {3} \ stackrel {\ text {?}} {=} — \ frac {4} {6} [/ latex]
[латекс] — \ frac {2} {3} = — \ frac {2} {3} \ quad \ checkmark [/ latex]
Теперь вы можете попробовать решить уравнение с дробями, в котором переменные находятся по обе стороны от знака равенства.Ответ может быть дробным.
В следующем видео мы показываем еще один пример решения уравнения, которое содержит дроби и переменные по обе стороны от знака равенства.

В следующем примере мы начнем с уравнения, в котором переменный член заключен в скобки и умножен на дробь. Вы можете очистить дробь, или, если вы используете свойство распределения, оно удалит дробь. Вы понимаете почему?
ПРИМЕР
Решение: [латекс] 1 = \ frac {1} {2} \ left (4x + 2 \ right) [/ latex].
Показать решение
Решение:
[латекс] 1 = \ frac {1} {2} (4x + 2) [/ латекс]
Распространить. [латекс] 1 = \ frac {1} {2} \ cdot4x + \ frac {1} {2} \ cdot2 [/ latex]
Упростить. Теперь дробей нет! [латекс] 1 = 2x + 1 [/ латекс]
Вычтите 1 с обеих сторон. [латекс] 1 \ color {red} {- 1} = 2x + 1 \ color {red} {- 1} [/ latex]
Упростить. [латекс] 0 = 2x [/ латекс]
Разделить на [латекс] 2 [/ латекс]. [латекс] \ frac {0} {\ color {red} {2}} = \ frac {2x} {\ color {red} {2}} [/ latex]
Упростить. [латекс] 0 = x [/ латекс]
Проверка: пусть [latex] x = 0 [/ latex].
[латекс] 1 = \ frac {1} {2} (4x + 2) [/ латекс]
[латекс] 1 \ stackrel {\ text {?}} {=} \ Frac {1} {2} (4 (\ color {red} {0}) + 2) [/ latex]
[латекс] 1 \ stackrel {\ text {?}} {=} \ Frac {1} {2} (2) [/ латекс]
[латекс] 1 \ stackrel {\ text {?}} {=} \ Frac {2} {2} [/ latex]
[латекс] 1 = 1 \ квадратик \ галочка [/ латекс]
Теперь вы можете попробовать решить уравнение, в котором переменный член в скобках умножен на дробь.

Вариант 2
1.Выберете те из дробей , которые являются несократимыми	1.Выберете те из дробей , которые являются несократимыми.
2. Сократите дробь: а) б) в) г)	2. Сократите дробь: а) б) в) г)
3. Выполните действия, сократив, полученную дробь: а) б)	3. Выполните действия, сократив, полученную дробь: а) б)
4. Сократите дробь и исключите из каждой из них целую часть:	4. Сократите дробь и исключите из каждой из них целую часть: .
5.Какую часть развернутого угла составляет угол, градусная мера которого равна 84⁰.	5. Какую часть прямого угла составляет угол, градусная мера которого равна 48⁰
6. Сократите:	6. Сократите:
7. Какую часть часа составляют 50 минут ?	7. Какую часть минуты составляют 48 секунд ?
8. Запишите десятичную дробь в виде обыкновенной дроби и результат сократите 0,456.	8. Запишите десятичную дробь в виде обыкновенной дроби и результат сократите 0,425.
Вариант 4
1. Выберете те из дробей , которые являются несократимыми	1.Выберете те из дробей , которые являются несократимыми.
2. Сократите дробь: а) б) в) г) .	2. Сократите дробь: а) б) в) г) .
3. Выполните действия, сократив, полученную дробь: а) б)	3. Выполните действия, сократив, полученную дробь: а) б)
4. Сократите дробь и исключите из каждой из них целую часть:	4. Сократите дробь и исключите из каждой из них целую часть:
5.Какую часть развернутого угла составляет угол, градусная мера которого равна 27⁰.	5. Какую часть прямого угла составляет угол, градусная мера которого равна 72⁰
6. Сократите:	6. Сократите:
7. Какую часть часа составляют 45 минут ?	7. Какую часть минуты составляют 28 секунд ?
8. Запишите десятичную дробь в виде обыкновенной дроби и результат сократите 0,256.	8. Запишите десятичную дробь в виде обыкновенной дроби и результат сократите 0,632.


Перепишите общие множители, затем разделите общие множители.
Упростить.


Определить знак товара; умножить.
Есть ли общие множители в числителе и демонинаторе? №


Чтобы разделить, умножьте первую дробь на обратную величину второй.
Умножить.

	[латекс] \ frac {1} {8} x + \ frac {1} {2} = \ frac {1} {4} \ quad {LCD = 8} [/ latex]
Умножьте обе части уравнения на этот ЖК-дисплей, [латекс] 8 [/ латекс].Это очищает фракции.	[латекс] \ color {красный} {8 (} \ frac {1} {8} x + \ frac {1} {2} \ color {red} {)} = \ color {red} {8 (} \ frac {1} {4} \ color {red} {)} [/ latex]
Используйте свойство распределения.	[латекс] 8 \ cdot \ frac {1} {8} x + 8 \ cdot \ frac {1} {2} = 8 \ cdot \ frac {1} {4} [/ latex]
Упростите — и заметьте, никаких дробей!	[латекс] x + 4 = 2 [/ латекс]
Решите, используя общую стратегию решения линейных уравнений.	[латекс] x + 4 \ color {red} {- 4} = 2 \ color {red} {- 4} [/ latex]
Упростить.	[латекс] x = -2 [/ латекс]
Проверить: Пусть [латекс] x = -2 [/ латекс] [латекс] \ frac {1} {8} x + \ frac {1} {2} = \ frac {1} {4} [/ latex] [латекс] \ frac {1} {8} (\ color {red} {- 2}) + \ frac {1} {2} \ stackrel {\ text {?}} {=} \ Frac {1} { 4} [/ латекс] [латекс] \ frac {-2} {8} + \ frac {1} {2} \ stackrel {\ text {?}} {=} \ Frac {1} {4} [/ latex] [латекс] \ frac {-2} {8} + \ frac {4} {8} \ stackrel {\ text {?}} {=} \ Frac {1} {4} [/ latex] [латекс] \ frac {2} {8} \ stackrel {\ text {?}} {=} \ Frac {1} {4} [/ latex] [латекс] \ frac {1} {4} = \ frac {1} {4} \ quad \ checkmark [/ latex]

Найдите наименьший общий знаменатель всех дробей в уравнении.	[латекс] 7 = \ frac {1} {2} x + \ frac {3} {4} x- \ frac {2} {3} x \ quad {LCD = 12} [/ latex]
Умножьте обе части уравнения на [латекс] 12 [/ латекс].	[латекс] \ color {red} {12} (7) = \ color {red} {12} \ cdot (\ frac {1} {2} x + \ frac {3} {4} x- \ frac {2 } {3} x) [/ латекс]
Распространить.	[латекс] 12 (7) = 12 \ cdot \ frac {1} {2} x + 12 \ cdot \ frac {3} {4} x-12 \ cdot \ frac {2} {3} x [/ латекс ]
Упростите — и заметьте, никаких дробей!	[латекс] 84 = 6x + 9x-8x [/ латекс]
Объедините похожие термины.	[латекс] 84 = 7x [/ латекс]
Разделить на [латекс] 7 [/ латекс].	[латекс] \ frac {84} {\ color {red} {7}} = \ frac {7x} {\ color {red} {7}} [/ latex]
Упростить.	[латекс] 12 = x [/ латекс]
Проверить: Пусть [латекс] x = 12 [/ латекс].
[латекс] 7 = \ frac {1} {2} x + \ frac {3} {4} x- \ frac {2} {3} x [/ latex] [латекс] 7 \ stackrel {\ text {?}} {=} \ Frac {1} {2} (\ color {red} {12}) + \ frac {3} {4} (\ color {red} {12}) — \ frac {2} {3} (\ color {red} {12}) [/ latex] [латекс] 7 \ stackrel {\ text {?}} {=} 6 + 9-8 [/ латекс] [латекс] 7 = 7 \ четырехугольник \ галочка [/ латекс]

Найдите на ЖК-дисплее все дроби в уравнении.	[латекс] x + \ frac {1} {3} = \ frac {1} {6} x- \ frac {1} {2}, \ quad {LCD = 6} [/ latex]
Умножьте обе стороны на ЖК-дисплей.	[латекс] \ color {red} {6} (x + \ frac {1} {3}) = \ color {red} {6} (\ frac {1} {6} x- \ frac {1} {2 }) [/ latex]
Распространить.	[латекс] 6 \ cdot {x} +6 \ cdot \ frac {1} {3} = 6 \ cdot \ frac {1} {6} x-6 \ cdot \ frac {1} {2} [/ латекс ]
Упростите — больше никаких дробей!	[латекс] 6x + 2 = x-3 [/ латекс]
Вычтите [латекс] x [/ латекс] с обеих сторон.	[латекс] 6x- \ color {красный} {x} + 2 = x- \ color {красный} {x} -3 [/ latex]
Упростить.	[латекс] 5x + 2 = -3 [/ латекс]
Вычтите 2 с обеих сторон.	[латекс] 5x + 2 \ color {red} {- 2} = — 3 \ color {red} {- 2} [/ latex]
Упростить.	[латекс] 5x = -5 [/ латекс]
Разделить на [латекс] 5 [/ латекс].	[латекс] \ frac {5x} {\ color {red} {5}} = \ frac {-5} {\ color {red} {5}} [/ latex]
Упростить.	[латекс] x = -1 [/ латекс]
Проверка: Заменить [латекс] x = -1 [/ латекс].
[латекс] x + \ frac {1} {3} = \ frac {1} {6} x- \ frac {1} {2} [/ latex] [латекс] (\ color {red} {- 1}) + \ frac {1} {3} \ stackrel {\ text {?}} {=} \ Frac {1} {6} (\ color {red} {-1}) — \ frac {1} {2} [/ latex] [латекс] (- 1) + \ frac {1} {3} \ stackrel {\ text {?}} {=} — \ frac {1} {6} — \ frac {1} {2} [/ латекс ] [латекс] — \ frac {3} {3} + \ frac {1} {3} \ stackrel {\ text {?}} {=} — \ frac {1} {6} — \ frac {3} { 6} [/ латекс] [латекс] — \ frac {2} {3} \ stackrel {\ text {?}} {=} — \ frac {4} {6} [/ latex] [латекс] — \ frac {2} {3} = — \ frac {2} {3} \ quad \ checkmark [/ latex]

	[латекс] 1 = \ frac {1} {2} (4x + 2) [/ латекс]
Распространить.	[латекс] 1 = \ frac {1} {2} \ cdot4x + \ frac {1} {2} \ cdot2 [/ latex]
Упростить. Теперь дробей нет!	[латекс] 1 = 2x + 1 [/ латекс]
Вычтите 1 с обеих сторон.	[латекс] 1 \ color {red} {- 1} = 2x + 1 \ color {red} {- 1} [/ latex]
Упростить.	[латекс] 0 = 2x [/ латекс]
Разделить на [латекс] 2 [/ латекс].	[латекс] \ frac {0} {\ color {red} {2}} = \ frac {2x} {\ color {red} {2}} [/ latex]
Упростить.	[латекс] 0 = x [/ латекс]
Проверка: пусть [latex] x = 0 [/ latex].
[латекс] 1 = \ frac {1} {2} (4x + 2) [/ латекс] [латекс] 1 \ stackrel {\ text {?}} {=} \ Frac {1} {2} (4 (\ color {red} {0}) + 2) [/ latex] [латекс] 1 \ stackrel {\ text {?}} {=} \ Frac {1} {2} (2) [/ латекс] [латекс] 1 \ stackrel {\ text {?}} {=} \ Frac {2} {2} [/ latex] [латекс] 1 = 1 \ квадратик \ галочка [/ латекс]

Как сокращать дроби | Математика

Презентация «Сокращение дробей» — математика, презентации

Конспект урока по математике » Сокращение дробей» 6 класс

Практико-значимая работа по теме

«КОНСПЕКТ УРОКА ПО МАТЕМАТИКЕ В 6 КЛАССЕ»

Конспект урока.

Тренинг по математике «Сокращение дробей» 6 класс

Урок 46. умножение и деление смешанных дробей произвольного знака — Математика — 6 класс

Конспект урока по математике 6 класс «Сокращение дробей»

Рабочий лист упрощения дробей

Упрощение сложных дробей — ChiliMath

Метод 1

Метод 2

Примеры упрощения сложных дробей

Что делать, когда студенты борются с дробными операциями

Почему студенты борются с дробными операциями?

Три совета по обучению дробным операциям

1. Обзор и оценка дробных оснований

2. Соедините операции дроби с операциями целых чисел

Дробные упражнения для вашего класса

3. Используйте

Обучение дробным операциям в классе

Что такое упрощающие дроби? — Определение, факты и примеры

БЕСПЛАТНЫЕ настольные игры с дробями

Фракция настольных игр

Фракционные настольные игры для печати

Игра на дроби для печати

Эквивалентные дроби

Скачать Настольная игра Fractions

>> Скачать Fraction Board Game

Визуализируйте дроби — Элементарная алгебра

Цели обучения

Найти эквивалентные дроби

Упростить дроби

Умножение дробей

Разделить дроби

Упростите выражения с помощью дроби

Практика ведет к совершенству

Письменные упражнения

Самопроверка

Решение уравнений с очисткой дробей

Результаты обучения

ПРИМЕР

Решите уравнения, очистив знаменатели

Пример

Внимание!

Пример

ПРИМЕР

Добавить комментарий Отменить ответ