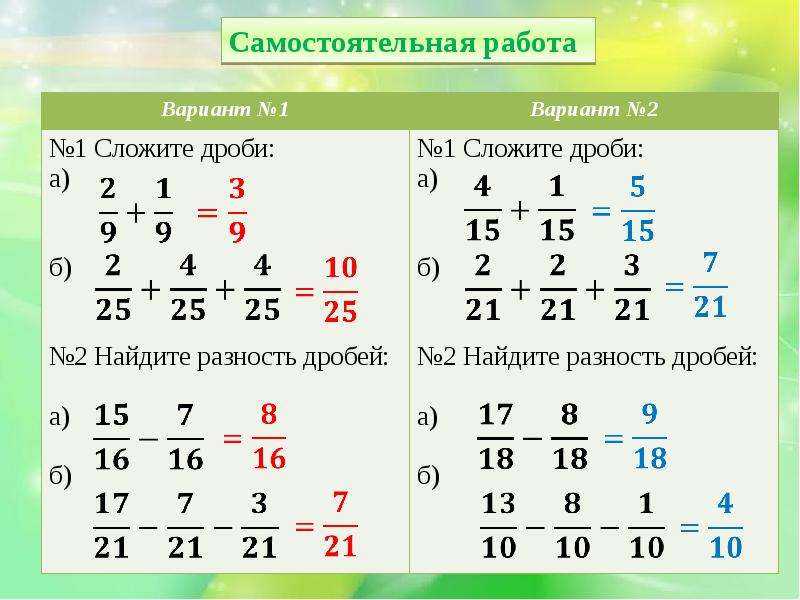
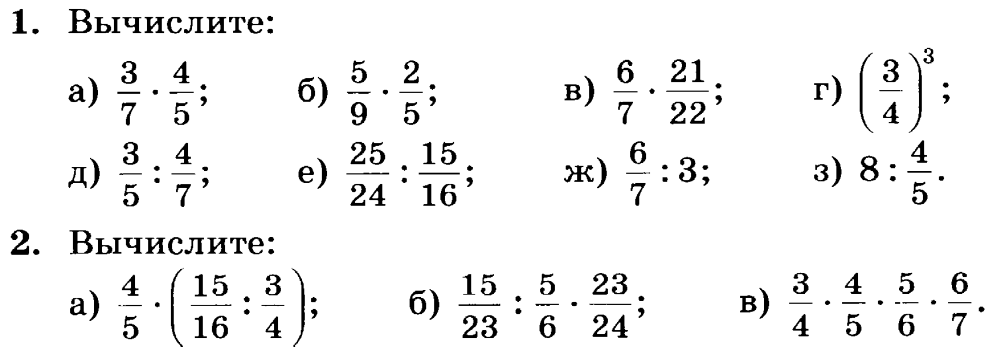Как складывать дроби с разными знаменателями — Математика для школьников
16 комментариев / От Светлана Михайловна / 27.01.2013 18.03.2018
Чтобы понять, как складывать дроби с разными знаменателями, сначала изучим правило, а затем рассмотрим конкретные примеры.
Чтобы сложить или вычесть дроби с разными знаменателями, надо:
1) Найти наименьший общий знаменатель (НОЗ) данных дробей.
2) Найти дополнительный множитель к каждой дроби. Для этого новый знаменатель нужно разделить на старый.
3) Умножить числитель и знаменатель каждой дроби на дополнительный множитель и сложить или вычесть дроби с одинаковыми знаменателями.
4) Проверить, является ли полученная в результате дробь правильной и несократимой.
В следующих примерах надо сложить или вычесть дроби с разными знаменателями:
Решение:
1) Чтобы вычесть дроби с разными знаменателями, сначала ищем наименьший общий знаменатель данных дробей.
2) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 100:25=4, 100:20=5. Соответственно, к первой дроби дополнительный множитель 4, ко второй — 5.
3) Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем дроби по правилу вычитания дробей с одинаковыми знаменателями.
4) Полученная дробь — правильная и несократимая. Значит, это — ответ.
1) Чтобы сложить дроби с разными знаменателями, сначала ищем наименьший общий знаменатель. 16 на 12 не делится. 16∙2=32 на 12 не делится. 16∙3=48 на 12 делится. Значит, 48 — НОЗ.
2) 48:16=3, 48:12=4. Это — дополнительные множители к каждой дроби.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем новые дроби.
4)Полученная в результате дробь — правильная и несократимая.
1) 30 на 20 не делится. 30∙2=60 на 20 делится. Значит, 60 — наименьший общий знаменатель этих дробей.
2) чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель поделить на старый: 60:20=3, 60:30=2.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем новые дроби.
4) полученную дробь надо сократить на 5.
1) 8 на 6 не делится. 8∙2=16 на 6 не делится. 8∙3=24 делится и на 4, и на 6. Значит, 24 — это и есть НОЗ.
2) чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый. 24:8=3, 24:4=6, 24:6=4. Значит, 3, 6 и 4 — дополнительные множители к первой, второй и третьей дроби.
3) умножаем числитель и знаменатель каждой долби на дополнительный множитель. Складываем и вычитаем. Полученная дробь — неправильная, поэтому необходимо выделить целую часть.
С разными знаменателями.
Сложение и вычитание обыкновенных дробейНа данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с разными знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с разными знаменателями. Для этого дроби необходимо привести к общему знаменателю. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. При этом мы уже умеем приводить алгебраические дроби к общему знаменателю. Сложение и вычитание дробей с разными знаменателями — одна из наиболее важных и сложных тем в курсе 8 класса. При этом данная тема будет встречаться во многих темах курса алгебры, которые вы будете изучать в дальнейшем. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с разными знаменателями, а также разберём целый ряд типовых примеров.
Рассмотрим простейший пример для обыкновенных дробей.
Пример 1. Сложить дроби: .
Решение:
Вспомним правило сложения дробей. Для начала дроби необходимо привести к общему знаменателю.
В роли общего знаменателя для обыкновенных дробей выступает наименьшее общее кратное (НОК) исходных знаменателей.
Определение
Наименьшее натуральное число, которое делится одновременно на числа и .
Для нахождения НОК необходимо разложить знаменатели на простые множители, а затем выбрать все простые множители, которые входят в разложение обоих знаменателей.
; . Тогда в НОК чисел должны входить две двойки и две тройки: .
После нахождения общего знаменателя, необходимо для каждой из дробей найти дополнительный множитель (фактически, поделить общий знаменатель на знаменатель соответствующей дроби).
Затем каждая дробь умножается на полученный дополнительный множитель. Получаются дроби с одинаковыми знаменателями, складывать и вычитать которые мы научились на прошлых уроках.
Получаем: .
Ответ: .
Рассмотрим теперь сложение алгебраических дробей с разными знаменателями. Сначала рассмотрим дроби, знаменатели которых являются числами.
Пример 2. Сложить дроби: .
Решение:
Алгоритм решения абсолютно аналогичен предыдущему примеру. Легко подобрать общий знаменатель данных дробей: и дополнительные множители для каждой из них.
.
Ответ: .
Итак, сформулируем алгоритм сложения и вычитания алгебраических дробей с разными знаменателями
1. Найти наименьший общий знаменатель дробей.
2. Найти дополнительные множители для каждой из дробей (поделив общий знаменатель на знаменатель данной дроби).
3. Домножить числители на соответствующие дополнительные множители.
4. Сложить или вычесть дроби, пользуясь правилами сложения и вычитания дробей с одинаковыми знаменателями.
Рассмотрим теперь пример с дробями, в знаменателе которых присутствуют буквенные выражения.
Пример 3. Сложить дроби: .
Решение:
Поскольку буквенные выражения в обоих знаменателях одинаковы, то следует найти общий знаменатель для чисел .
Итоговый общий знаменатель будет иметь вид: . Таким образом, решение данного примера имеет вид:.
Ответ: .
Пример 4. Вычесть дроби: .
Решение:
Если «схитрить» при подборе общего знаменателя не удаётся (нельзя разложить на множители или воспользоваться формулами сокращённого умножения), то в качестве общего знаменателя приходится брать произведение знаменателей обеих дробей.Ответ: .
Вообще, при решении подобных примеров, наиболее сложным заданием является нахождение общего знаменателя.
Рассмотрим более сложный пример.
Пример 5. Упростить: .
Решение:
При нахождении общего знаменателя необходимо прежде всего попытаться разложить знаменатели исходных дробей на множители (чтобы упростить общий знаменатель).
В данном конкретном случае:
Тогда легко определить общий знаменатель: .
Определяем дополнительные множители и решаем данный пример:
Ответ: .
Теперь закрепим правила сложения и вычитания дробей с разными знаменателями.
Пример 6.
Решение:
Ответ: .
Пример 7. Упростить: .
Решение:
.
Ответ: .
Рассмотрим теперь пример, в котором складываются не две, а три дроби (ведь правила сложения и вычитания для большего количества дробей остаются такими же).
Пример 8. Упростить: .
Следующее действие, которое можно выполнять с обыкновенными дробями, — вычитание. В рамках этого материала мы рассмотрим, как правильно вычислить разность дробей с одинаковыми и разными знаменателями, как вычесть дробь из натурального числа и наоборот. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.
Yandex.RTB R-A-339285-1
Как найти разность дробей с одинаковыми знаменателями
Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них.
В итоге у нас осталось 3 восьмых доли, поскольку 5 − 2 = 3 . Получается, что 5 8 — 2 8 = 3 8 .
Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.
Определение 1
Чтобы найти разность дробей с одинаковыми знаменателями, нужно из числителя одной вычесть числитель другой, а знаменатель оставить прежним. Это правило можно записать в виде a b — c b = a — c b .
Такую формулу мы будем использовать и в дальнейшем.
Возьмем конкретные примеры.
Пример 1
Вычтите из дроби 24 15 обыкновенную дробь 17 15 .
Решение
Мы видим, что эти дроби имеют одинаковые знаменатели. Поэтому все, что нам нужно сделать, – это вычесть 17 из 24 . Мы получаем 7 и дописываем к ней знаменатель, получаем 7 15 .
Наши подсчеты можно записать так: 24 15 — 17 15 = 24 — 17 15 = 7 15
Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.
Пример 2
Найдите разность 37 12 — 15 12 .
Решение
Воспользуемся описанной выше формулой и подсчитаем: 37 12 — 15 12 = 37 — 15 12 = 22 12
Легко заметить, что числитель и знаменатель можно разделить на 2 (об этом мы уже говорили ранее, когда разбирали признаки делимости). Сократив ответ, получим 11 6 . Это неправильная дробь, из которой мы выделим целую часть: 11 6 = 1 5 6 .
Как найти разность дробей с разными знаменателями
Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:
Определение 2
Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.
Рассмотрим на примере, как это делается.
Пример 3
Вычтите из 2 9 дробь 1 15 .
Решение
Знаменатели разные, и нужно привести их к наименьшему общему значению.
В данном случае НОК равно 45 . Для первой дроби необходим дополнительный множитель 5 , а для второй – 3 .
Подсчитаем: 2 9 = 2 · 5 9 · 5 = 10 45 1 15 = 1 · 3 15 · 3 = 3 45
У нас получились две дроби с одинаковым знаменателем, и теперь мы легко можем найти их разность по описанному ранее алгоритму: 10 45 — 3 45 = 10 — 3 45 = 7 45
Краткая запись решения выглядит так: 2 9 — 1 15 = 10 45 — 3 45 = 10 — 3 45 = 7 45 .
Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.
Пример 4
Найдите разность 19 9 — 7 36 .
Решение
Приведем указанные в условии дроби к наименьшему общему знаменателю 36 и получим соответственно 76 9 и 7 36 .
Считаем ответ: 76 36 — 7 36 = 76 — 7 36 = 69 36
Результат можно сократить на 3 и получить 23 12 . Числитель больше знаменателя, а значит, мы можем выделить целую часть. Итоговый ответ — 1 11 12 .
Краткая запись всего решения — 19 9 — 7 36 = 1 11 12 .
Как вычесть из обыкновенной дроби натуральное число
Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.
Пример 5
Найдите разность 83 21 – 3 .
Решение
3 – то же самое, что и 3 1 . Тогда можно подсчитать так: 83 21 — 3 = 20 21 .
Если в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа. Тогда предыдущий пример можно решить иначе.
Из дроби 83 21 при выделении целой части получится 83 21 = 3 20 21 .
Теперь просто вычтем 3 из него: 3 20 21 — 3 = 20 21 .
Как вычесть обыкновенную дробь из натурального числа
Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.
Пример 6
Найдите разность: 7 — 5 3 .
Решение
Сделаем 7 дробью 7 1 . Делаем вычитание и преобразуем конечный результат, выделяя из него целую часть: 7 — 5 3 = 5 1 3 .
Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.
Определение 3
Если та дробь, которую нужно вычесть, является правильной, то натуральное число, из которого мы вычитаем, нужно представить в виде суммы двух чисел, одно из которых равно 1 . После этого нужно вычесть нужную дробь из единицы и получить ответ.
Пример 7
Вычислите разность 1 065 — 13 62 .
Решение
Дробь, которую нужно вычесть – правильная, ведь ее числитель меньше знаменателя. Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065 — 13 62 = (1064 + 1) — 13 62
Теперь нам нужно найти ответ. Используя свойства вычитания, полученное выражение можно записать как 1064 + 1 — 13 62 .
Подсчитаем разность в скобках. Для этого единицу представим как дробь 1 1 .
Получается, что 1 — 13 62 = 1 1 — 13 62 = 62 62 — 13 62 = 49 62 .
Теперь вспомним про 1064 и сформулируем ответ: 1064 49 62 .
Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:
1065 — 13 62 = 1065 1 — 13 62 = 1065 · 62 1 · 62 — 13 62 = 66030 62 — 13 62 = = 66030 — 13 62 = 66017 62 = 1064 4 6
Ответ тот же, но подсчеты, очевидно, более громоздкие.
Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.
Пример 8
Вычислите разность 644 — 73 5 .
Решение
Вторая дробь – неправильная, и от нее надо отделить целую часть.
Теперь вычисляем аналогично предыдущему примеру: 630 — 3 5 = (629 + 1) — 3 5 = 629 + 1 — 3 5 = 629 + 2 5 = 629 2 5
Свойства вычитания при работе с дробями
Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей.
Рассмотрим, как использовать их при решении примеров.
Пример 9
Найдите разность 24 4 — 3 2 — 5 6 .
Решение
Схожие примеры мы уже решали, когда разбирали вычитание суммы из числа, поэтому действуем по уже известному алгоритму. Сначала подсчитаем разность 25 4 — 3 2 , а потом отнимем от нее последнюю дробь:
25 4 — 3 2 = 24 4 — 6 4 = 19 4 19 4 — 5 6 = 57 12 — 10 12 = 47 12
Преобразуем ответ, выделив из него целую часть. Итог — 3 11 12 .
Краткая запись всего решения:
25 4 — 3 2 — 5 6 = 25 4 — 3 2 — 5 6 = 25 4 — 6 4 — 5 6 = = 19 4 — 5 6 = 57 12 — 10 12 = 47 12 = 3 11 12
Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.
Пример 10
Н айдите разность 98 + 17 20 — 5 + 3 5 .
Решение
Зная основные свойства вычитания и сложения, мы можем сгруппировать числа следующим образом: 98 + 17 20 — 5 + 3 5 = 98 + 17 20 — 5 — 3 5 = 98 — 5 + 17 20 — 3 5
Завершим расчеты: 98 — 5 + 17 20 — 3 5 = 93 + 17 20 — 12 20 = 93 + 5 20 = 93 + 1 4 = 93 1 4
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Ваш ребенок принес домашнее задание из школы, и вы не знаете как его решить? Тогда этот мини урок для вас!
Как складывать десятичные дроби
Десятичные дроби удобнее складывать в столбик.
Чтобы выполнить сложение десятичных дробей, надо придерживаться одного простого правила:
- Разряд должен находиться под разрядом, запятая под запятой.
Как вы видите на примере, целые единицы находятся друг под другом, разряд десятых и сотых находится друг под другом. Теперь складываем числа, не обращая внимания на запятую. Что же делать с запятой? Запятая переносится на то место, где стояла в разряде целых.
Сложение дробей с равными знаменателями
Чтобы выполнить сложение с общим знаменателем, надо сохранить знаменатель без изменения, найти сумму числителей и получим дробь, которая будет являться общей суммой.
Сложение дробей с разными знаменателями методом нахождения общего кратного
Первое, на что надо обратить внимание – это на знаменатели. Знаменатели разные, не делятся ли одно на другое, являются ли простыми числами. Для начала надо привести к одному общему знаменателю, для этого существует несколько способов:
- 1/3 + 3/4 = 13/12, для решения этого примера нам надо найти наименьшее общее кратное число (НОК), которое будет делиться на 2 знаменателя.
Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3. - Перемножаем множители и выполняем сложение полученных чисел, получаем 13/12 – неправильную дробь.
Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3.- Для того чтобы перевести неправильную дробь в правильную, разделим числитель на знаменатель, получим целое число 1, остаток 1 – числитель и 12 – знаменатель.
Сложение дробей методом умножения крест на крест
Для складывания дробей с разными знаменателями существует еще один способ по формуле “крест на крест”. Это гарантированный способ уровнять знаменатели, для этого вам надо числители перемножить со знаменателем одной дроби и обратно. Если вы только на начальном этапе изучения дробей, то этот способ самый простой и точный, как получить верный результат при сложении дробей с разными знаменателями.
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с разными знаменателями
Понятие о НОК
Приведение дробей к одному знаменателю
Как сложить целое число и дробь
1 Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2 Сложение и вычитание дробей с разными знаменателями
Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3 Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
- Перемножить все числа в произведении, это и будет НОК.
Например, найдем НОК чисел 28 и 21:
4Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например.
В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей !
Понятие дроби вводится в курс математики начиная с 6 класса средней школы.
Дроби имеют вид: ±X/Y, где Y — знаменатель, он сообщает на сколько частей разделили целое, а X — числитель, он сообщает, сколько таких частей взяли. Для наглядности возьмем пример с тортом:
В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.
Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.
Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.
Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.
Если числитель меньше знаменателя — дробь является правильной, если наоборот — неправильной.
В состав дроби может входить целое число.
Например, 5 целых 3/4.
Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.
Если вы хотите запомнить, как решать дроби за 6 класс , вам надо понять, что решение дробей , в основном, сводится к понимаю нескольких простых вещей.
- Дробь по сути это выражение доли. То есть числовое выражение того, какую часть составляет данное значение от одного целого. К примеру дробь 3/5 выражает, что, если мы поделили что то целое на 5 частей и количество долей или частей это этого целого — три.
- Дробь может быть меньше 1, например 1/2(или по сути половина), тогда она правильная. Если дробь больше 1, к примеру 3/2(три половины или один с половиной), то она неправильная и для упрощения решения, нам лучше выделить целую часть 3/2= 1 целая 1/2.
- Дроби это такие же числа, как 1, 3, 10, и даже 100, только числа это не целые а дробные. С ними можно выполнять все те же операции, что с числами. Считать дроби не сложнее, и далее на конкретных примерах мы это покажем.
Считать дроби не сложнее, и далее на конкретных примерах мы это покажем.Как решать дроби. Примеры.
К дробям применимы самые разные арифметические операции.
Приведение дроби к общему знаменателю
Например, необходимо сравнить дроби 3/4 и 4/5.
Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т.е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей
Наименьший общий знаменатель(4,5) = 20
Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю
Ответ: 15/20
Сложение и вычитание дробей
Если необходимо посчитать сумму двух дробей, их сначала приводят к общему знаменателю, затем складывают числители, при этом знаменатель останется без изменений. Разность дробей считается аналогичным образом, различие лишь в том, что числители вычитаются.
Например, необходимо найти сумму дробей 1/2 и 1/3
Теперь найдем разность дробей 1/2 и 1/4
Умножение и деление дробей
Тут решение дробей несложное, здесь все достаточно просто:
- Умножение — числители и знаменатели дробей перемножаются между собой;
- Деление — сперва получаем дробь, обратную второй дроби, т. е. меняем местами ее числитель и знаменатель, после чего полученные дроби перемножаем.
е. меняем местами ее числитель и знаменатель, после чего полученные дроби перемножаем.Например:
На этом о том, как решать дроби , всё. Если у вас остались какие то вопросы по решению дробей , что то непонятно, то пишите в комментарии и мы обязательно вам ответим.
Если вы учитель, то возможно скачать презентацию для начальной школы (http://school-box.ru/nachalnaya-shkola/prezentazii-po-matematike.html) будет вам кстати.
Интерактивный урок математики | Сложение дробей с отличием в знаменателях
Извините, вы использовали все доступные подсказки для этого урока.
Достигнут предел практики
Вы достигли ежедневного лимита практики в 12 вопросов.
Когда вы зарегистрируете бесплатную учетную запись и войдете в нее, вы сможете играть во все, что захотите.
(Для регистрации вам должно исполниться 18 лет.)
Математическая онлайн-игра: сложение дробей с разными знаменателями
Складывайте дроби с разными знаменателями в этой интерактивной математической игре для детей.
Студенты будут иметь возможность попрактиковаться в сложении дробей, у которых разные знаменатели. Чтобы сложить дроби, учащиеся должны найти общий знаменатель. Им будет предложено упростить дроби, если это возможно. Вот типы вопросов, с которыми учащиеся могут столкнуться на этом онлайн-уроке математики:
* Решите текстовую задачу, содержащую дроби с разными знаменателями.
* Решайте задачи на сложение дробей в вертикальном формате.
* Решение задач на сложение дробей в горизонтальном формате. Используйте полоски дробей, чтобы визуализировать математическую задачу.
Математическая практика в форме игры
Учащимся начальных классов нравятся уроки математики на iKnowit.com, потому что каждый урок похож на захватывающую математическую игру. Интерактивные занятия по математике представлены в динамичном, удобном для детей формате. Дети находят наши математические игры веселыми и интересными.
Каждый раз, когда учащийся правильно отвечает на вопрос, симпатичный анимированный персонаж отправляет положительный отзыв, выполняя забавный трюк с танцем.
Когда учащийся отвечает на вопрос неправильно, всплывает страница объяснения с легко читаемой графикой, которая разбивает этапы решения проблемы, чтобы учащийся мог извлечь уроки из своей ошибки.
Если ученик считает, что его или ее нужно подтолкнуть в правильном направлении, в левом нижнем углу экрана есть кнопка «Подсказка», к которой можно обратиться по желанию учителя или родителей. Когда учащийся нажимает значок «Подсказка», ему или ей будет дана подсказка, которая поможет решить математическую задачу. Учителя или родители могут решить, сколько подсказок за урок должен получить ученик.
Зарегистрируйтесь, чтобы получить доступ ко всем функциям
Пользователи iKnowit.com, имеющие у нас учетную запись, будут иметь неограниченный доступ ко всем полезным административным функциям на iKnowit.com. Учителя могут создавать список классов, добавлять в него учеников, назначать уроки отдельным учащимся и отслеживать оценки своих учеников.
Каждый раз, когда учащийся входит в систему iKnowit.
com, вы сможете отслеживать его успехи и наблюдать, какие задачи для этого учащегося являются более сложными. Страница входа студента «удобна для детей». Студенты легко найдут вкладку «Задания от учителя» в верхней части страницы. Им также будут показаны различные предлагаемые математические темы для изучения.
Учащиеся не смогут видеть уровень оценки заданий, которые им дает учитель, поэтому преподаватели могут назначить более высокий или более низкий уровень обучения по мере необходимости.
Другие административные функции включают возможность включать и выключать анимированных персонажей и режим подсказки. Учителя также могут выбрать, хотят ли они, чтобы учащиеся использовали опцию чтения вслух.
iKnowit.com постоянно растет! У нас есть сотни уроков по математике на сайте, и мы регулярно добавляем новые! Просмотрите нашу коллекцию математических игр для детей и найдите множество тем для всех ваших потребностей в обучении математике! Чтобы увидеть больше игр для четвертого класса, посетите нашу страницу Математика для четвертого класса.
Уровень
Этот урок обозначен как Уровень D и предназначен для четвероклассников.
Common Core Standard Alignment
5.NF.2
Числа и операции — дроби
Использование эквивалентных дробей в качестве стратегии для вычитания и сложения дробей: Учащиеся должны уметь решать текстовые задачи, требующие сложения или вычитания дробей, относящихся к одно и то же целое, включая сложение и вычитание дробей с разными знаменателями. Учащиеся будут использовать наглядные пособия, такие как полоски дробей, чтобы помочь им решить математические задачи.
Вас также может заинтересовать…
Площадь прямоугольников (уровень D)
Используйте формулу A=lw, чтобы найти площадь прямоугольника.
Периметр (уровень D)
Нахождение периметра многоугольника путем сложения сторон. Найдите длину недостающей стороны, если известны периметр и другие стороны.
| You are here: Home → Рабочие листы → Сложение дробей Создавайте неограниченное количество рабочих листов для сложения дробей и смешанных чисел (4-7 классы)! Рабочие листы могут быть сделаны в формате html или PDF — оба варианта легко распечатать. Сложение дробей обычно преподается, начиная с 4-го класса, с одинаковыми дробями (с одинаковым знаменателем, например, 3/8 + 2/8). Дети начинают с манипулятивных действий, чтобы понять концепцию, а затем могут переходить к абстрактным задачам. Затем, в 5-м классе, учащиеся учатся складывать в отличие от дробей (дроби с разными знаменателями, например 3/4 + 2/5) и смешанные числа с разными дробными частями. Процедура для этого включает преобразование дробей, которые должны быть добавлены, в эквивалентные дроби с общим знаменателем. После преобразования у вас есть как дроби (дроби с одинаковым знаменателем), которые вы можете легко складывать. Чтобы понять, как это делается, посмотрите это видео о добавлении непохожих дробей на другом моем сайте (MathMammoth.com) .В 6-м и 7-м классах учащиеся просто тренируются в сложении дробей с большими знаменателями и в более сложных задачах. Перейти к:
Основные инструкции к рабочим листам Каждый рабочий лист генерируется случайным образом и поэтому уникален. Вы можете создавать рабочие листы либо в формате html, либо в формате PDF — оба варианта легко распечатать. Чтобы получить рабочий лист PDF, просто нажмите кнопку под названием « Создать PDF » или « Создать рабочий лист PDF ». Чтобы получить рабочий лист в формате html, нажмите кнопку « Посмотреть в браузере » или « Сделать рабочий лист html 9».0066 «. Преимущество этого заключается в том, что вы можете сохранить рабочий лист прямо из браузера (выберите Файл → Сохранить), а затем отредактировать его в Word или другом текстовом редакторе. Иногда сгенерированный рабочий лист не совсем то, что вам нужно. Просто попробуйте еще раз! Чтобы получить другой рабочий лист с теми же параметрами:
Рабочие листы для сложения дробей: 4 классДроби в задачах на сложение 4 класса ограничены , как и дробей — дроби с одинаковым знаменателем.
Вот еще несколько рабочих листов с дробями, которые вы можете использовать в 4 классе.
Рабочие листы для сложения дробей: 5 класс В 5 классе учащиеся учатся складывать в отличие от дробей — дробей с разными знаменателями.
Вот еще несколько рабочих листов для 5 класса.
Рабочие листы для сложения дробей: 6-7 классы В 6-м и 7-м классах учащиеся просто практикуются в сложении дробей, знаменатель которых больше, чем в 5-м классе.
Вот еще несколько рабочих листов для 6-7 классов. 
Генератор таблиц дробейИспользуйте генератор для создания настраиваемых рабочих листов для операций с дробями. Генератор таблиц дробей
|
Вы также можете настроить их с помощью генератора ниже. 
Ключ ответа генерируется автоматически и помещается на вторую страницу файла.
В них также используются только дроби с одинаковым знаменателем (например, дроби).
