Сложение дробей, формулы и примеры решений
Содержание:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
- Сложение смешанных дробей
Сложение дробей с одинаковыми знаменателями
Определение
Суммой двух дробей с одинаковыми знаменателями называется дробь, числитель которой равен сумме числителей исходных дробей, а знаменатель — знаменателю дробей, то есть
$\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}$
Чтобы сложить две дроби с одинаковым знаменателем, надо сложить их числители и результат записать в числитель, а знаменатель оставить без изменения.
Пример
Задание. Найти сумму дробей $\frac{3}{11}$ и $\frac{7}{11}$
Решение. $\frac{3}{11}+\frac{7}{11}=\frac{3+7}{11}=\frac{10}{11}$
Ответ. $\frac{3}{11}+\frac{7}{11}=\frac{10}{11}$
Если в результате сложения получается дробь, числитель и знаменатель которой можно сократить,
то для конечного результата выполняем и сокращение дроби.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти сумму дробей $\frac{3}{14}$ и $\frac{11}{14}$
Решение. Складываются дроби с одинаковым знаменателем, поэтому просто складываем числитель, а знаменатель оставляем исходный:
$\frac{3}{14}+\frac{11}{14}=\frac{14}{14}$
Полученная дробь $\frac{14}{14}$ является неправильной, у которой числитель равен знаменателю, и такая дробь равна единице, то есть
$\frac{3}{14}+\frac{11}{14}=\frac{14}{14}=1$
Ответ. $\frac{3}{14}+\frac{11}{14}=1$
Сложение дробей с разными знаменателями
Определение
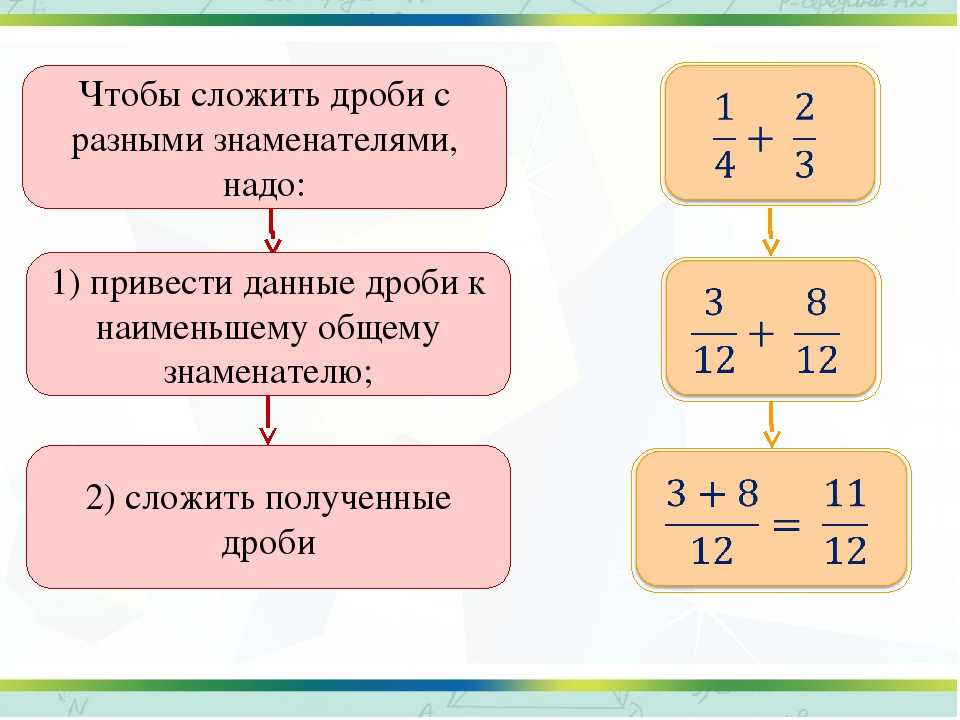
Чтобы сложить дроби с разными знаменателями, вначале надо привести их к общему знаменателю, а
далее складывать как дроби с общим знаменателем.
Ответ. $\frac{2}{3}+\frac{1}{8}=\frac{19}{24}$
Замечание. После первого знака равенства справа вверху у каждой дроби указан дополнительный множитель к ней.
Сложение смешанных дробей
Определение
Чтобы сложить смешанные дроби, надо отдельно найти сумму целых частей и отдельно сумму дробных частей.
Пример
Задание. Вычислить сумму дробей 3$\frac{2}{5}$ и 4$\frac{7}{10}$
Решение. В данном случае складываем отдельно целые и дробные части:
$3 \frac{2}{5}+4 \frac{7}{10}=(3+4)+\left(\frac{2}{5}+\frac{7}{10}\right)$
Так как знаменатели дробных частей разные, то приводим дроби к общему знаменателю, который равен 10, так как НОК знаменателей 5 и 10. Соответственно дополнительные множители, как частные общего знаменателя и знаменателей дробей, равны 2 и 1:
$3 \frac{2}{5}+4 \frac{7}{10}=7+\frac{2^{2}}{5}+\frac{7^{1}}{10}=7+\frac{2 \cdot 2+7 \cdot 1}{10}=7+\frac{11}{10}=7 \frac{11}{10}$
Так как дробная часть представляет собой неправильную дробь, то выделяем целую часть:
$3 \frac{2}{5}+4 \frac{7}{10}=7 \frac{11}{10}=7\left(1+\frac{1}{10}\right)=8 \frac{1}{10}$
Ответ. $3 \frac{2}{5}+4 \frac{7}{10}=8 \frac{1}{10}$
$3 \frac{2}{5}+4 \frac{7}{10}=8 \frac{1}{10}$
Читать следующую тему: вычитание дробей.
Сложение дробей. — tutomath.ru репетитор по математике
Разные действия с дробями можно выполнять, например, сложение дробей. Сложение дробей можно разделить на несколько видов. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.
Сложение дробей с одинаковыми знаменателями.
На примере посмотрим, как складывать дроби с общим знаменателем.
Туристы пошли в поход из точки A в точку E. В первый день они прошли от точки A до B или \(\frac{1}{5}\) от всего пути. Во второй день они прошли от точки B до D или \(\frac{2}{5}\) от всего пути. Какое расстояние они прошли от начала пути до точки D?
Решение:
Чтобы найти расстояние от точки A до точки D нужно сложить дроби \(\frac{1}{5} + \frac{2}{5}\).
Сложение дробей с одинаковыми знаменателями заключается в том, что нужно числители этих дробей сложить, а знаменатель останется прежний.
\(\frac{1}{5} + \frac{2}{5} = \frac{1 + 2}{5} = \frac{3}{5}\)
В буквенном виде сумма дробей с одинаковыми знаменателями будет выглядеть так:
\(\bf \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)
Ответ: туристы прошли \(\frac{3}{5}\) всего пути.
Сложение дробей с разными знаменателями.
Рассмотрим пример:
Нужно сложить две дроби \(\frac{3}{4}\) и \(\frac{2}{7}\).
Чтобы сложить дроби с разными знаменателями нужно сначала найти общий знаменатель, а потом воспользоваться правилом сложения дробей с одинаковыми знаменателями.
Как найти общий знаменатель можно посмотреть здесь, нажав на ссылку>>
Для знаменателей 4 и 7 общим знаменателем будет число 28. Первую дробь \(\frac{3}{4}\) нужно умножить на 7. Вторую дробь \(\frac{2}{7}\) нужно умножить на 4.
\(\frac{3}{4} + \frac{2}{7} = \frac{3 \times \color{red} {7} + 2 \times \color{red} {4}}{4 \times \color{red} {7}} = \frac{21 + 8}{28} = \frac{29}{28} = 1\frac{1}{28}\)
В буквенном виде получаем такую формулу:
\(\bf \frac{a}{b} + \frac{c}{d} = \frac{a \times d + c \times b}{b \times d}\)
Сложение смешанных чисел или смешанных дробей.
Сложение смешанных дробей происходит по закону сложения.
У смешанных дробей складываем целые части с целыми и дробные части с дробными.
Если дробные части смешанных чисел имеют одинаковые знаменатели, то числители складываем, а знаменатель остается тот же.
Сложим смешанные числа \(3\frac{6}{11}\) и \(1\frac{3}{11}\).
\(3\frac{6}{11} + 1\frac{3}{11} = (\color{red} {3} + \color{blue} {\frac{6}{11}}) + (\color{red} {1} + \color{blue} {\frac{3}{11}}) = (\color{red} {3} + \color{red} {1}) + (\color{blue} {\frac{6}{11}} + \color{blue} {\frac{3}{11}}) = \color{red}{4} + (\color{blue} {\frac{6 + 3}{11}}) = \color{red}{4} + \color{blue} {\frac{9}{11}} = \color{red}{4} \color{blue} {\frac{9}{11}}\)
Если дробные части смешанных чисел имею разные знаменатели, то находим общий знаменатель.
Выполним сложение смешанных чисел \(7\frac{1}{8}\) и \(2\frac{1}{6}\).
Знаменатель разный, поэтому нужно найти общий знаменатель, он равен 24. Умножим первую дробь \(7\frac{1}{8}\) на дополнительный множитель 3, а вторую дробь \(2\frac{1}{6}\) на 4.
Умножим первую дробь \(7\frac{1}{8}\) на дополнительный множитель 3, а вторую дробь \(2\frac{1}{6}\) на 4.
\(7\frac{1}{8} + 2\frac{1}{6} = 7\frac{1 \times \color{red} {3}}{8 \times \color{red} {3}} = 2\frac{1 \times \color{red} {4}}{6 \times \color{red} {4}} =7\frac{3}{24} + 2\frac{4}{24} = 9\frac{7}{24}\)
Вопросы по теме:
Как складывать дроби?
Ответ: сначала надо определиться к какому типу относиться выражение: у дробей одинаковые знаменатели, разные знаменатели или смешанные дроби. В зависимости от типа выражения переходим к алгоритму решения.
Как решать дроби с разными знаменателями?
Ответ: необходимо найти общий знаменатель, а дальше по правилу сложения дробей с одинаковыми знаменателями.
Как решать смешанные дроби?
Ответ: складываем целые части с целыми и дробные части с дробными.
Пример №1:
Может ли сумма двух правильных дробей в результате получить правильную дробь? Неправильную дробь? Приведите примеры.
Решение:
\(\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} = \frac{5}{7}\)
\(\frac{2}{5} + \frac{8}{9} = \frac{2 \times 9 + 8 \times 5}{5 \times 9} =\frac{18 + 40}{45} = \frac{58}{45}\)
Дробь \(\frac{58}{45}\) является неправильной дроби, она получилась в результате суммы правильных дробей \(\frac{2}{5}\) и \(\frac{8}{9}\).
Ответ: на оба вопроса ответ да.
Пример №2:
Сложите дроби: а) \(\frac{3}{11} + \frac{5}{11}\) б) \(\frac{1}{3} + \frac{2}{9}\).
а) \(\frac{3}{11} + \frac{5}{11} = \frac{3 + 5}{11} = \frac{8}{11}\)
б) \(\frac{1}{3} + \frac{2}{9} = \frac{1 \times \color{red} {3}}{3 \times \color{red} {3}} + \frac{2}{9} = \frac{3}{9} + \frac{2}{9} = \frac{5}{9}\)
Пример №3:
Запишите смешанную дробь в виде суммы натурального числа и правильной дроби: а) \(1\frac{9}{47}\) б) \(5\frac{1}{3}\)
а) \(1\frac{9}{47} = 1 + \frac{9}{47}\)
б) \(5\frac{1}{3} = 5 + \frac{1}{3}\)
Пример №4:
Вычислите сумму: а) \(8\frac{5}{7} + 2\frac{1}{7}\) б) \(2\frac{9}{13} + \frac{2}{13}\) в) \(7\frac{2}{5} + 3\frac{4}{15}\)
Решение:
а) \(8\frac{5}{7} + 2\frac{1}{7} = (8 + 2) + (\frac{5}{7} + \frac{1}{7}) = 10 + \frac{6}{7} = 10\frac{6}{7}\)
б) \(2\frac{9}{13} + \frac{2}{13} = 2 + (\frac{9}{13} + \frac{2}{13}) = 2\frac{11}{13} \)
в) \(7\frac{2}{5} + 3\frac{4}{15} = 7\frac{2 \times 3}{5 \times 3} + 3\frac{4}{15} = 7\frac{6}{15} + 3\frac{4}{15} = (7 + 3)+(\frac{6}{15} + \frac{4}{15}) = 10 + \frac{10}{15} = 10\frac{10}{15} = 10\frac{2}{3}\)
Задача №1:
За обедам съели \(\frac{8}{11}\) от торта, а вечером за ужином съели \(\frac{3}{11}\). Как вы думаете торт полностью съели или нет?
Как вы думаете торт полностью съели или нет?
Решение:
Знаменатель дроби равен 11, он указывает на сколько частей разделили торт. В обед съели 8 кусочков торта из 11. За ужином съели 3 кусочка торта из 11. Сложим 8 + 3 = 11, съели кусочков торта из 11, то есть весь торт.
\(\frac{8}{11} + \frac{3}{11} = \frac{11}{11} = 1\)
Ответ: весь торт съели.
Сложение и вычитание дробей с отрицательными числами
Горячая математикаКак только вы научились складывать и вычитать положительные дроби , вы можете расширить метод, включив в него отрицательные дроби.
Обратите внимание, что:
− 2 3 такой же как − 2 3 и 2 − 3
− 2 − 3 упрощает до 2 3
Когда вы добавляете или вычитаете отрицательную дробь, вы обычно хотите учитывать числитель как отрицательный. Метод точно такой же, за исключением того, что теперь вам может понадобиться добавить отрицательные или положительные числители.
Метод точно такой же, за исключением того, что теперь вам может понадобиться добавить отрицательные или положительные числители.Пример 1:
Найдите сумму.
9 5 + ( − 4 3 )
LCM 5 и 3 является 15 .
Чтобы сложить дроби с разными знаменателями, переименуйте дроби с общим знаменателем.
9 5 «=» 9 × 3 5 × 3 «=» 27 15 − 4 3 «=» − 4 × 5 3 × 5 «=» − 20 15
Так,
9 5 + ( − 4 3 ) «=» 27 15 + ( − 20 15 )
Так как знаменатели одинаковые, складываем числители.
«=» 27 + ( − 20 ) 15 «=» 7 15
Пример 2:
Найдите разницу.
− 7 10 − 2 15
LCM 10 и 15 является 30 .
Чтобы вычесть дроби с разными знаменателями, переименуйте дроби с общим знаменателем.
− 7 10 «=» − 7 10 × 3 3 «=» − 21 30 2 15 «=» 2 15 × 2 2 «=» 4 30
Так,
− 7 10 − 2 15 «=» − 21 30 − 4 30
Так как знаменатели одинаковые, вычтите числители.
− 21 30 − 4 30 «=» − 21 − 4 30
Упрощать. Мы получаем:
− 25 30 или − 5 6
Как складывать дроби с отрицательными числами?
Дробь — это числовое значение, определяющее часть целого. Оно происходит от слова «fractio» — ломать. Он используется для решения повседневных жизненных задач, таких как разделение продуктов питания, припасов, валюты и т. д. Число в форме a/b можно назвать дробью. Где а, b — любые числа. Например, 2/3, 12/4 и т. д. Рациональные, иррациональные числа, имеющие форму a/b, можно рассматривать как дроби.
Часть дроби
Дробь состоит из двух частей:
- Знаменатель: Наименьшая часть дроби называется знаменателем.
 Он показывает, на сколько частей будет делиться данное целое число. Например, 2/3, здесь 3 называется знаменателем.
Он показывает, на сколько частей будет делиться данное целое число. Например, 2/3, здесь 3 называется знаменателем. - Числитель: Верхняя часть дроби называется числителем. Он представляет, в каком количестве разделов дроби. Например, 2/3, здесь 3 называется числителем 9.0076
Тип дроби
Ниже приведены типы дробей:
- Правильная дробь: Правильные дроби — это те дроби, в которых числитель всегда меньше знаменателя. Например, 5/16, 1/4 и т. д.
- Неправильная дробь: Неправильные дроби — это те дроби, в которых числитель всегда больше или равен знаменателю. Например, 5/2, 11/4 и т. д.
- Дробная единица: Дробные единицы — это те дроби, у которых в числителе только 1. Например, 1/2, 1/14 и т. д.
- Смешанная фракция: Смешанные фракции — это те фракции, которые содержат смесь цельных и правильных фракций. Например, и т.
 д.
д. - Эквивалентная дробь: Эквивалентные дроби — это дроби, содержащие одинаковые значения. Например, 2/9 х 2/2 = 4/18.
- Подобная дробь: Подобные дроби — это те дроби, которые содержат одинаковые знаменатели. Например, 2/8, 4/8 и т. д.
- Отличие от дроби: Отличие от дроби — это те дроби, которые содержат разные знаменатели. Например, 2/9, 8/13 и т. д.
Сложение дробей с отрицательными числами
Как мы знаем, сложение — это основная операция математики. Он используется для нахождения суммы двух положительных или отрицательных чисел. Мы также можем складывать дроби с одинаковыми или разными знаменателями. Нам разрешено также добавлять дроби с отрицательными числами. Некоторые правила, которые нам нужно помнить, когда мы выполняем сложение или вычитание между любыми положительными или отрицательными числами. Они указаны ниже:
Правило 1: При умножении двух положительных чисел мы получаем положительный результат.
(+) x (+) = +
Пример: 5×2=10
Правило 2: Результат умножения отрицательный.
(-) x (-) = +
Пример: (-7)×(-2)= 14
Здесь два отрицательных символа сокращаются друг с другом.
Правило 3: При перемножении положительных и отрицательных целых чисел результирующее число будет отрицательным.
(-) x (+) = –
Пример: (-7) x 2 = -14 числа.
Шаги для сложения дробей с отрицательными числами:
У нас есть дробь a/b и отрицательное число -c. Теперь мы добавляем их, используя следующие шаги:
Шаг 1: Преобразуйте их символы в соответствии с приведенным выше правилом. Здесь a/b + (-c) = a/b – c
Шаг 2: a/b – c также можно записать как a/b -c/1
Шаг 3: Теперь возьмите LCM на b и 1
Шаг 4: Теперь окончательное уравнение (a – c)/b и решить это уравнение, чтобы получить окончательный результат.
Примеры вопросов
Вопрос 1: (1/2) + (-1) = ?
Решение:
Здесь у нас + операция перед отрицательным числом. По правилу-3 при умножении + на – получается отрицательный символ.
(1/2) + (-1) будет преобразовано в (1/2) – 1
Этот (1/2) – 1 можно переписать в (1/2) – (1/1)
НОК двух знаменателей 2,1 равно 2.
(1/2) – (1/1) = (1 – 2)/2
= -1/2
= -0,5
Вопрос 2: -(1/2) + (-1) = ?
Решение:
Здесь у нас операция + перед отрицательным числом. По правилу-3 при умножении + на – получается отрицательный символ.
-(1/2) + (-1) будет преобразовано в -(1/2) – 1
Это -(1/2) – 1 можно переписать в (-1/2) – (1/ 1)
НОК 2 знаменателя 2,1 равно 2.
(-1/2) – (1/1) = (-1 – 2)/2
= -3/2
= -1,5
Вопрос 3: -(1/3) + (3/6) = ?
Решение:
НОК двух знаменателей 3, 6 равно 6.
 Он показывает, на сколько частей будет делиться данное целое число. Например, 2/3, здесь 3 называется знаменателем.
Он показывает, на сколько частей будет делиться данное целое число. Например, 2/3, здесь 3 называется знаменателем.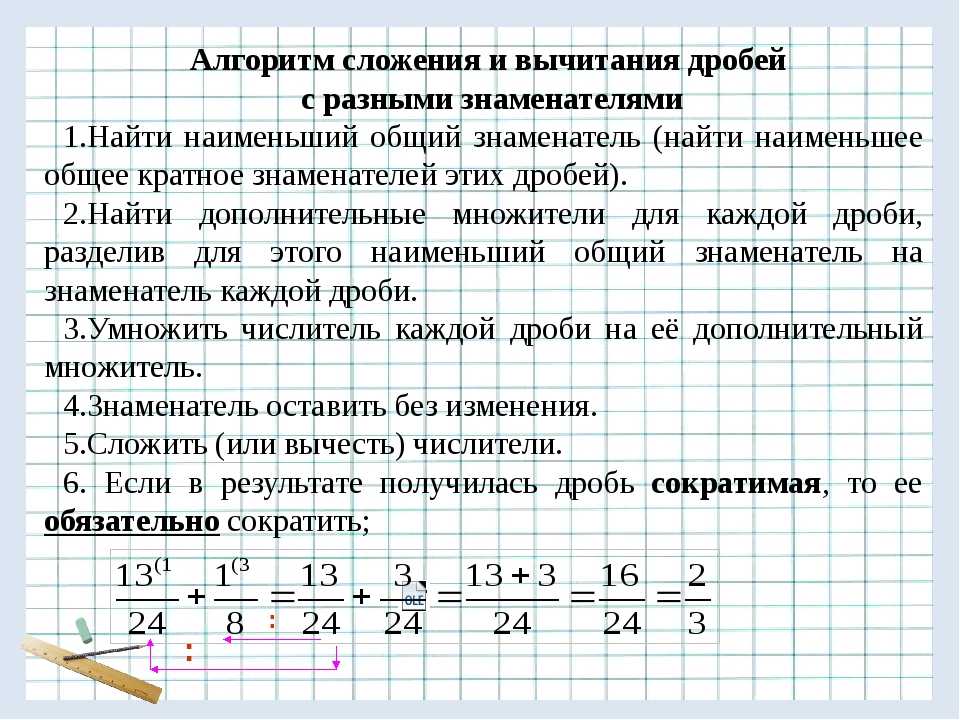 д.
д.

