Задача (условие, вопрос, схема, выражение, ответ). 1-й класс

Цели:

1. Закрепление навыков устного счёта в пределах 10.
2. Повторить составление выражений по рисункам, соотношение между целым и его частями.
3. Уточнить термины, связанные с понятием «задача»: условие, вопрос, выражение, решение, ответ.
4. Научить делать краткую запись в виде схем, познакомить с записью решения в тетради.
5. Учить составлять задачи по схемам и числовым выражениям.
6. Развивать мышление, речь, творческие способности.

Оборудование:

• наглядность к устному счёту: ромашки, поезд, зайчик, Великий Математик;
• иллюстрация к задаче;
• плакаты: условие, вопрос, схема, выражение, решение, ответ;
• схемы к задачам;
• плакат (проверка № 5 с. 45).

Ход урока

I. Организационный момент.

II. Вводная беседа.

— Ребята, сегодня на уроке мы отправляемся с вами путешествовать в страну Математики и нас будет сопровождать Великий Математик. Математика – это точная наука, требующая хороших знаний, чёткого выполнения всех арифметических действий.

— Какие действия мы с вами уже знаем? (Сложение и вычитание.)

— Во 2 классе мы познакомимся с умножением и делением.

— Сегодня на уроке мы будем заниматься наблюдениями, открывать математические закономерности, изучать новый материал.

III. Устный счёт.

1) Путешествовать мы с вами отправляемся на поезде, но прежде, чем наш поезд тронется, мы должны получить билеты. Для этого разделимся на команды и поиграем в игру «Кто быстрее?»

(Учащиеся выходят к доске и дописывают нужные числа.)

I ряд – 1 команда.

II ряд – 2 команда.

III ряд – 3 команда.

2) А теперь надо узнать № поезда.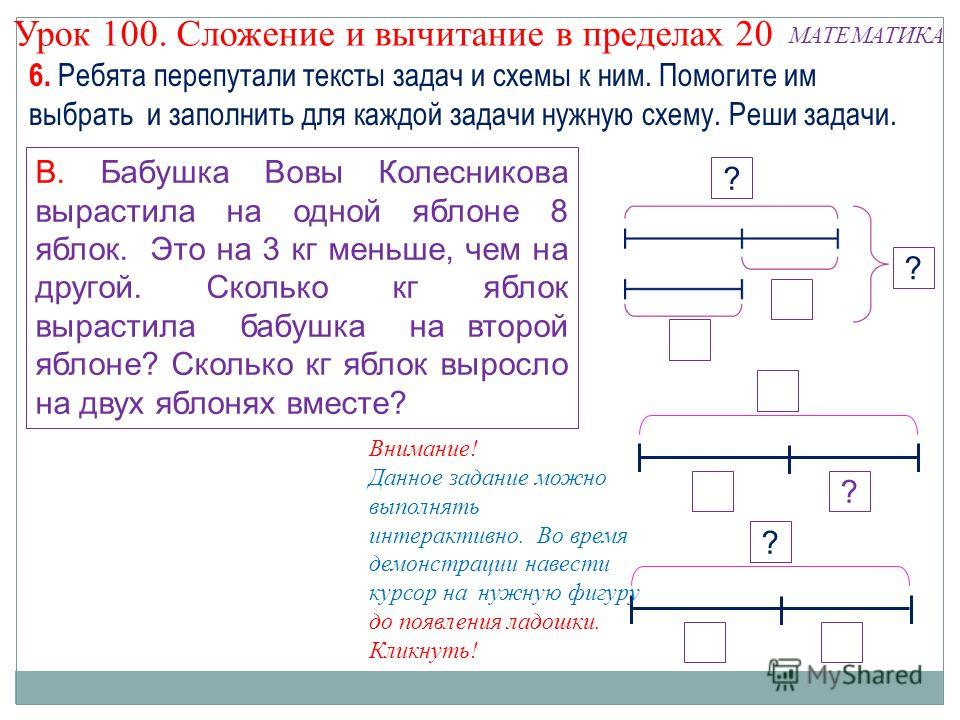

Для этого решим цепочку примеров:

Проверка (у каждого учащегося цифры, ответ показывает каждый с места).

(На доске картинка с зайчиком).

— Зайчик тоже хочет отправиться с нами путешествовать, но он не знает номер поезда, ему достался трудный пример. Он записан под цепочкой.

(Учащиеся записывают пример в тетради и решают.)

3 + 4 – 2 + 3 – 4 + 5 = ?

— Что вы заметили? (В примере выполнены те же действия, что и в цепочке. Значит ответ будет такой же 9.)

Значит Зайка едет в нашем поезде – берём его с собой.

Наш поезд отправился, давайте сосчитаем:

— Сколько пассажиров в каждом вагоне?

9-6	3	4+5	9	8-4	4
3+3	6	7-5	2	3+4	7

(Ответы в тетради. )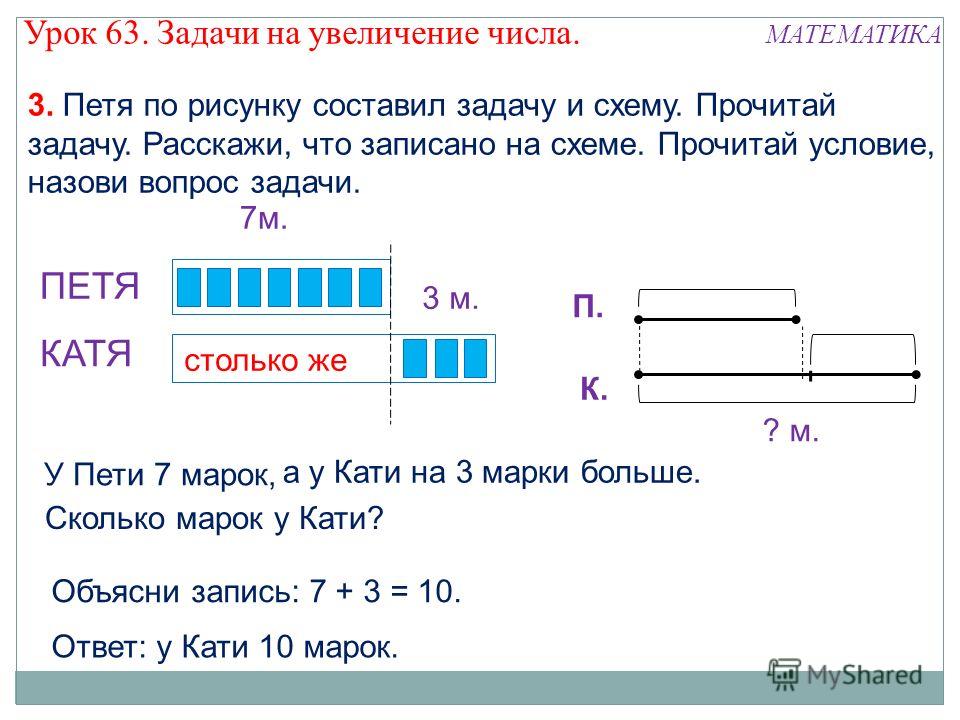

— Прочитаем ответы.

3

6

9

2

4

7

— Запишите их в порядке возрастания и вы отгадаете слово.

(На доске все картинки перемешаны, выходит ученик и располагает их в порядке возрастания.)

2	3	4	6	7	9
З	А	Д	А	Ч	А

— Какое слово получилось? (Дети отвечают хором. )

IV. Знакомство с новым материалом.

Тема сегодняшнего урока: Задача.

Наш поезд делает I остановку в лесу. Рассмотрите иллюстрацию. Составьте задачу про детей.

«Мальчик и девочка пошли в лес за грибами. Мальчик нашёл 2 гриба, а девочка 4.Сколько всего грибов нашли дети?»

— Правильно. Без чего нет задачи? (Без вопроса.)

— В задаче всегда о чём-то спрашивается, без вопроса нет задачи. Это нужно хорошо понять и запомнить.

— Задачу можно разбить на 2 части:

1. Условие – то, что известно.
2. Вопрос – то, что неизвестно.

(На доске постепенно открываются плакаты: условие, вопрос, схема, выражение, решение, ответ.)

— Давайте повторим условие нашей задачи, вопрос.

— А теперь запишем в тетради: Задача.

— Ниже запишите выражение: 4 + 2.

— Найдите его значение: 4 + 2 = 6(гр.)

— Полученное равенство называют решением задачи, а значение выражения 6 грибов – ответом задачи.

Ответ: 6 грибов. (На доске записан образец записи.)

— Разобраться в этом помогает рисунок, но если числа большие то делать рисунок неудобно – слишком много предметов надо рисовать. На помощь приходит схема-отрезок, разбитый на части. Разбивая отрезок на части, мы получаем те же самые соотношения между частью и целым, что и при разбиении совокупностей предметов.

(На доске схема.)

— Какой мы делаем вывод? (Наглядно представить содержание задачи можно сопоставив целое всему отрезку, а части – частям отрезка.)

— Что такое целое? (Отрезок.)

— Что обозначает весь отрезок? (Число грибов, собранных детьми.)

— Что такое части? (Части отрезка.)

— Что обозначают части отрезка? (Грибы, собранные мальчиком и девочкой.)

— Что показывает знак вопроса? (Находят целое.)

— Каким действием решаем задачу? (Сложением.)

— Почему? (Находим целое. )

V. Закрепление.

1) Следующая остановка нашего поезда «Поиграй-ка».

— А сейчас мы с вами немного поиграем.

— Великий Математик прислал конверты с задачами.

(Работа в группах).

— Каждой группе нужно определить, что относится к условию, вопросу, найти схему, записать выражение, решение, назвать ответ.

Проверка:

А) Условие. Во дворе играли 6 ребят. Двое ушли домой.

Вопрос. Сколько ребят осталось во дворе?

Схема:

На доске выражение: 6 – 2.

Решение: 6 – 2 = 4(р.)

Ответ: 4 ребят.

Б) Условие. В хоре пело 4 мальчика и 6 девочек.

Вопрос. Сколько детей пело в хоре?

Схема:

Выражение: 6 + 4.

Решение: 6 + 4 = 10(д.)

Ответ: 10 детей.

В) Условие. Из клетки улетело сначала 2 попугая, а потом ещё 3.

Вопрос. Сколько попугаев улетело из клетки?

Схема:

Выражение: 2 + 3.

Решение: 2 + 3 = 5(п.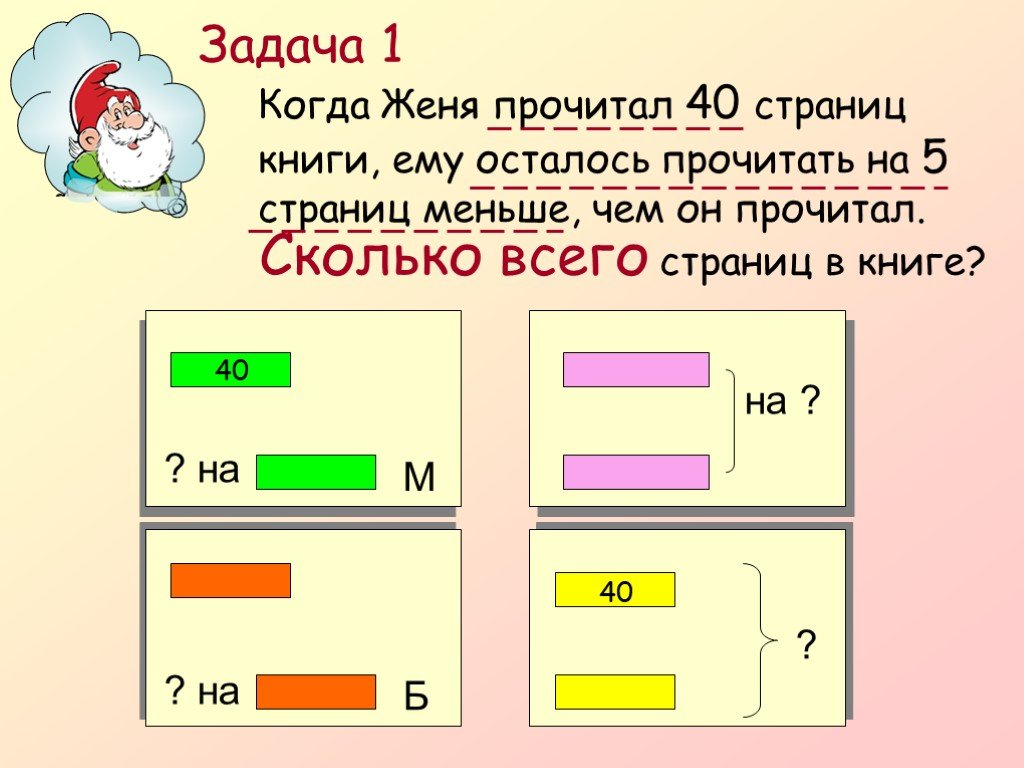

)

Ответ: 5 птиц.

Физкультурная минутка.

2) Наш поезд продолжает путешествие.

— Следующая остановка: «Объясни-ка».

— Откройте учебник с. 44 урок 23 № 2.

— Что нужно сделать? (Соотнести записи в рамках с соответствующими терминами.)

— Выполните самостоятельно.

— Назовите условие, вопрос, выражение, решение.

— Что обозначает весь отрезок? (Число конфет у девочки.)

— Его части? (Число конфет, которые она подарила и число конфет, которые у неё остались.)

— Почему задача решается вычитанием? (Ищем части.)

— Как найти часть? (Из целого вычитаем другую часть.)

3) Перейдём к №3. Составьте задачу по рисунку.

На столе лежали яблоки в 2-х вазах. В 1 вазе – 5 яблок, во 2 – 2 яблока.

— Сколько всего яблок лежало в двух вазах?

— Назовите условие, вопрос, выражение, решение.

— Что обозначает весь отрезок? (Все яблоки, лежащие на 1 и 2 вазе. )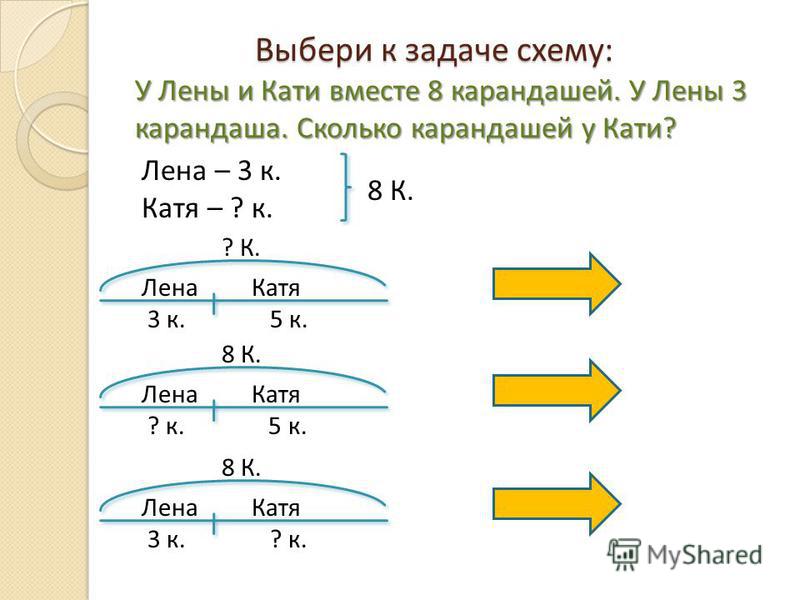

— Его части? (1 ваза с яблоками, 2 – с яблоками.)

— Почему задача решается сложением? (Находим целое.)

4) Путешествие наше продолжается, но нам надо забрать багаж в камере хранения ( №5).

Расшифруем записи – код ячеек.

— Что нужно выполнить? (Составить выражение с заданным числовым значением и дорисовать картинки.) Выполните самостоятельно.

Проверка (плакат на доске).

№ 6

— Наше путешествие подходит к концу.

— И в последнем задании Великий Математик зашифровал слово.

— Если вы правильно выполните действие и сосчитаете, то узнаете слово (умница).

— Великий Математик считает, что вы все умницы, так как хорошо работали на уроке и правильно отвечали на все вопросы, и выполнили все задания.

VI. Итог урока.

— Что нового узнали, чем занимались на уроке?

— Где можно использовать эти знания?

Реши задачу с помощью схемы.Язык и логика.ГДЗ.

Математика 5 класс.Дорофеев Г.В.Часть.1.Глава 1.Параграф 3.Задание 245 – Рамблер/класс Реши задачу с помощью схемы.Язык и логика.ГДЗ.Математика 5 класс.Дорофеев Г.В.Часть.1.Глава 1.Параграф 3.Задание 245 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Как это сделать ?
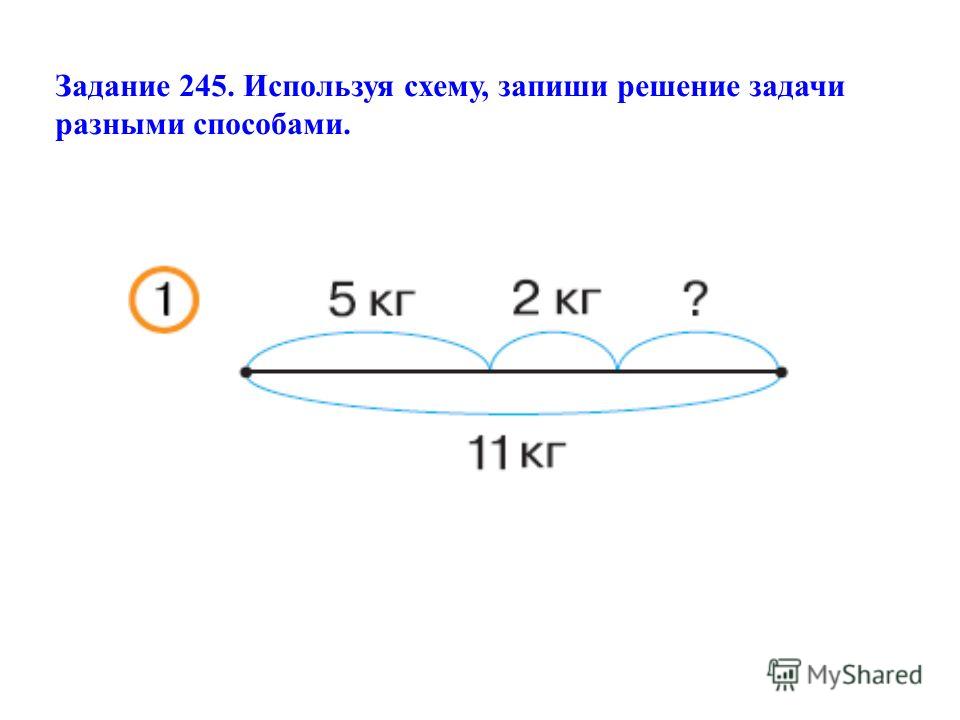
Реши задачу с помощью схемы:
 
1)  Число а составляет 4/5  числа b. Какую часть числа а составляет число 5?
2)   Число а меньше числа b на 1/5 часть b. Какую часть разность (b — a) составляет от а?
 

ответы

Надо сделать вот так:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

3 класс

Репетитор

Химия

Алгебра

похожие вопросы 5

Координатная прямая. Математика 5 класс.Зубарева И.И.Параграф 10, задание 191

Укажите начало отсчёта и координаты точек А, В, С, (Подробнее…)

ГДЗЗубарева И.И.Математика5 класс

Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.

   Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее. ..)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.

   Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Вырежи из бумаги № 694 ГДЗ Математика 6 класс Дорофеев Г.В. Часть3.

Вырежи из бумаги 20 одинаковых произвольных треугольников и составь
из них паркет. Всегда ли это можно сделать? Почему?

ГДЗМатематика6 классДорофеев Г. В.

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Помощь учащимся с ограниченными физическими возможностями научиться составлять математические задачи

Добавить в избранное

Джеффри МакКормак и Ян Мэтисон

Два поезда отправляются одновременно из городов, расстояние между которыми составляет 120 километров. Первый поезд едет со скоростью 40 км/ч, а второй поезд едет со скоростью 60 км/ч. Сколько минут до столкновения?

Если вам приходилось решать задачу со словами, подобную этой, возможно, вы чувствовали некоторую тревогу, пытаясь понять смысл вопроса и выбрать стратегию для его решения. Возможно, вас не удивит, что решение текстовых задач может оказаться сложной задачей для многих учащихся. Для учащихся с ограниченными возможностями обучения (LDs) текстовые задачи могут быть особенно сложными.

Учащиеся с LD чаще, чем обычно развивающиеся учащиеся, испытывают трудности с осмыслением и выбором подходящей стратегии при решении проблем (van Garderen, 2007). Кроме того, учащиеся с LD могут выбирать менее успешные «стратегии решения» (например, метод проб и ошибок), а не стратегии представления (например, построение диаграмм; van Garderen, Scheuermann, & Jackson, 2012). Для всех учащихся одной из наиболее эффективных стратегий решения текстовых задач является разработка диаграмм или, как они известны в литературе, представлений (van Garderen & Montague, 2003).

Щелкните здесь, чтобы получить доступ к статье на веб-сайте LD@school о визуальном представлении.

Часть 1: Чем могут помочь диаграммы

Создание диаграмм для решения математических задач может помочь учащимся во многих отношениях (Stylianou, 2010). В начале процесса диаграммы можно использовать как инструмент для записи информации о проблеме в процессе решения. Когда учащийся начинает концептуализировать проблему, диаграммы могут стать инструментом для изучения альтернативных способов понимания проблемы. Даже когда решение найдено, диаграммы можно использовать для мониторинга и оценки решения.

Несмотря на свою полезность, создание диаграмм может быть сложным процессом, состоящим из многих этапов (van Garderen, Scheuermann, & Poch, 2014). Студенты должны декодировать вербальную информацию и переводить ее в визуальную информацию — процесс, который требует, чтобы учащиеся идентифицировали и синтезировали информацию, прежде чем связать ее с предыдущими знаниями. Затем учащиеся должны определить подходящую форму диаграммы в зависимости от типа текстовой задачи. После выбора типа диаграммы, которая будет использоваться, учащиеся должны создать диаграммы, точно соответствующие содержанию словесной задачи. В более сложных текстовых задачах учащимся, возможно, даже придется изменить исходную диаграмму, чтобы включить новую информацию. Этот процесс может быть когнитивно утомительным и, следовательно, дополнительным испытанием для учащихся с LD, которые обладают когнитивным дефицитом (Rosenzweig, Krawec, & Montague, 2011).

Щелкните здесь, чтобы получить доступ к статьям LD@school об оперативной памяти и LD.

Нажмите здесь, чтобы получить доступ к статьям LD@school, посвященным исполнительным функциям и LD.

Умение работать с диаграммами требует навыков в пяти различных направлениях (van Garderen et al., 2014):

1. Концептуальное понимание предполагает понимание того, что такое диаграмма и как ее можно использовать.
2. Процедурная беглость включает в себя создание диаграммы, представляющей проблему.
3. Стратегическая компетентность предполагает использование диаграммы для представления, решения и отслеживания прогресса в решении проблемы.
4. Адаптивное рассуждение включает обоснование того, насколько диаграмма была полезна при решении проблемы.
5. Наконец, продуктивное расположение включает в себя признание ценности диаграмм для решения проблем и уверенность в их использовании, когда это уместно.

Учащиеся с LD и использование диаграмм

Учащиеся с LD используют диаграммы для решения текстовых задач по математике менее эффективно, чем их сверстники (van Garderen et al., 2012). Кроме того, диаграммы, создаваемые учащимися с LD, оказываются более низкого качества, чем у их сверстников, а учащиеся с LD используют диаграммы реже, чем их сверстники (van Garderen & Montague, 2003). К счастью, исследования показали, что, когда их специально обучают создавать и использовать их, учащиеся с LD способны изучать стратегии представления, такие как диаграммы (например, Hutchinson, 19). 86).

Хотя использование диаграмм является эффективной стратегией решения текстовых задач для учащихся с ограниченными возможностями, реализация этой стратегии сопряжена со своими проблемами. Если у учащихся плохие процедурные и концептуальные знания, им может быть сложнее создавать и использовать значимые диаграммы (van Garderen & Scheuermann, 2015). Кроме того, учащиеся должны использовать исполнительные функции, чтобы сосредоточить внимание и игнорировать посторонние детали при построении схемы (Uesaka & Manalo, 2012). Эти процессы требуют усилий, и, как и в случае со всеми стратегиями, если предполагаемая относительная выгода от диаграмм не стоит затрат, учащиеся будут избегать их использования (Uesaka & Manalo, 2012; van Garderen & Scheuermann, 2015).

Основная проблема для всех учащихся, особенно для тех, у кого LD, заключается в том, что создание эффективных диаграмм затруднено. Прежде чем учащиеся смогут разработать диаграмму, они должны уметь визуализировать проблему — навык, который обычно развивается в возрасте от 8 до 11 лет (van Garderen & Montague, 2003). Даже когда учащиеся могут визуализировать проблему, перевод этой визуализации во внешние образы (например, диаграммы на бумаге) проблематичен. Студенты также могут не записывать информацию эффективно, потому что они сосредотачиваются на посторонних деталях, неправильно обозначают диаграмму или исключают важную информацию. Наиболее проблематично то, что учащиеся могут думать, что диаграммы — это просто визуальное представление проблемы, и не понимать, что диаграммы отображают относительную и количественную информацию о проблеме.

Часть 2: Как научить учащихся использовать диаграммы для решения задач

Согласно van Garderen and Scheuermann (2015), обучение учащихся тому, как использовать диаграммы для решения текстовых задач, состоит из двух отдельных этапов. Прежде чем научиться использовать диаграммы для решения задач, учащиеся должны научиться создавать диаграммы. Учащиеся должны знать, что, как обсуждалось ранее, эффективные диаграммы требуют большего, чем визуальное представление объектов, присутствующих в словесной задаче. Без прямых инструкций по построению диаграмм учащиеся могут не полностью понять, как можно использовать диаграммы, и эта компетенция известна как метапредставление. Метарепрезентативная компетентность — это способность учащегося применять знания о диаграммах для надлежащего выбора, создания и использования диаграмм для решения математических задач (van Garderen, Scheuermann, & Jackson, 2012).

Чтобы помочь учащимся развить свою метарепрезентативную компетентность, учителя должны научить (а) что такое диаграммы, (б) почему диаграммы используются, (в) когда следует использовать диаграммы, (г) какой тип диаграмм подходит для математической задачи, (e) как создать диаграмму и (f) как использовать диаграмму. Для учащихся важно иметь широкое представление о диаграммах, потому что, хотя некоторые задачи естественным образом поддаются построению диаграмм, не все задачи подходят. Например, учащиеся чаще используют диаграммы при решении текстовых задач, связанных с длиной или расстоянием, чем при решении менее пространственных задач (Uesaka & Manalo, 2012). Прямые инструкции по построению диаграмм важны для учащихся с LD, потому что диаграммы должны быть неотъемлемым компонентом процесса решения проблемы, а не последним шагом (van Garderen, 2007).

Учащиеся должны понять, что диаграммы — это больше, чем просто рисунки. Неэффективные диаграммы, известные в литературе как графических диаграмм , изображают визуальное появление переменных в текстовой задаче (например, рисунок персонажа в текстовой задаче; например, van Garderen & Montague, 2003). Эффективные диаграммы (известные как схематические диаграммы ) выходят за рамки визуализации объектов в задаче; они представляют содержание проблемы и изображают реляционную информацию (ван Гардерен, 2007). Схематические диаграммы чрезвычайно полезны для текстовых задач по математике и могут быть перенесены из разных тем математики, включая геометрию и вероятность, а также из разных классов (Zahner & Corter, 2010).

Как только учащиеся поймут, что диаграммы являются когнитивными инструментами, заменяющими мыслительный процесс и отражающими его, им необходимо научиться использовать их для решения математических задач. На втором этапе учащиеся должны усвоить, что использование диаграмм требует трехэтапного процесса:

(a) Спросите: сосредоточьтесь на том, что нужно сделать,

(b) Сделайте: действуйте и/или производите и

(c) Проверьте: убедитесь, что диаграмма помогает решить проблему.

Хотя эти шаги кажутся линейными, учащиеся должны знать, что они повторяются (van Garderen & Scheuermann, 2015).

Часть 3: Примеры графических и схематических диаграмм

Следующие задачи из четырех слов включены для иллюстрации различий между графическими и схематическими диаграммами. Диаграммы ниже также демонстрируют, что диаграммы делают больше, чем просто визуализируют проблему; диаграммы являются инструментами для решения проблемы.

Магазин комиксов находится в 4,4 км к западу от дома Веры. Магазин видеоигр находится в 2,8 км к западу от дома Веры. Как далеко магазин комиксов от магазина видеоигр?

Иллюстрированный

Учащиеся с LD могут совершить ошибку, сосредоточив слишком много внимания на деталях рисунков.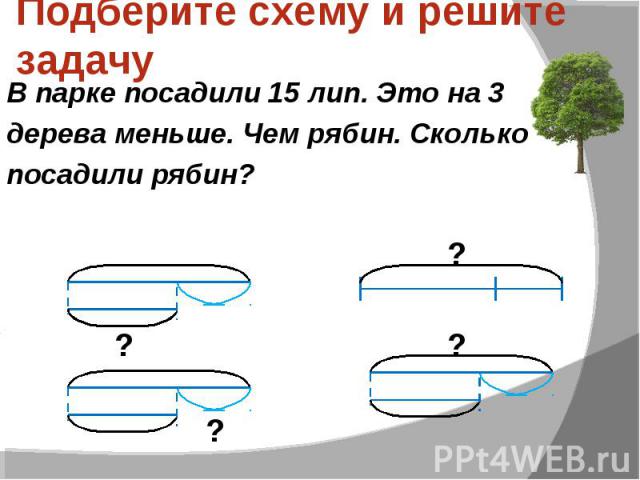 Этот студент, возможно, потратил слишком много времени на рисование зданий и добавление посторонней информации, такой как компас. Излишнее внимание к деталям могло быть причиной того, что студент неправильно обозначил расстояния.

Схема

Этот ученик использовал схему, которая включает меры длины. Включив реляционную информацию, такую ​​как расстояние на числовой прямой, этот студент смог лучше осмыслить и решить проблему.

Готовя пять рогаликов с пиццей для своих четырех друзей и себя, Лейла случайно сожгла два рогалика с пиццей. Теперь им предстоит разделить оставшуюся пиццу-бублики. Какое наибольшее количество пиццы-рогалика может съесть каждый человек, если у всех их одинаковое количество?

Иллюстрированный

Учащиеся более склонны интуитивно использовать диаграммы для решения определенных типов задач. Например, задачи со словами, связанные с расстоянием (см. предыдущую задачу со словами) и общими целыми (этот вопрос), легче представить, потому что они предполагают конкретные отношения и суммы. К сожалению, когда учащиеся с LD пытаются изобразить задачу в виде диаграммы, они, как правило, доходят только до рисования объектов задачи. Этот студент знал, что вопрос требует, чтобы он разделил три предмета между пятью людьми, но не знал, как использовать диаграмму, чтобы продвигать свои мысли.

Схема

Даже если учащиеся не в состоянии понять, что три рогалика можно разделить на пятые, они могут представить пятерых друзей, одновременно тянущих один и тот же рогалик. Используя диаграмму, иллюстрирующую, как друзья делят каждый рогалик, учащийся может понять, что при равном распределении каждый друг будет брать по одной пятой от каждого из трех рогаликов, всего три пятых. Также важно отметить, что, не рисуя лица Лейлы и ее друзей, студент смог исключить визуальную информацию, которая не была необходимой для решения задачи. Вместо того, чтобы рисовать лица, ученик использовал цифры (1-5) для обозначения друзей, тем самым упрощая визуализацию.

В прошлом месяце в зоомагазине было продано в четыре раза больше котят, чем ящериц. Если бы в прошлом месяце зоомагазин продал еще 18 ящериц, количество проданных котят и ящериц было бы равным. Сколько котят было продано в прошлом месяце?

Иллюстрированный

Составление диаграмм текстовых задач на отношения обычно более сложно для учащихся, чем словесных задач на расстояния. Не всегда может быть ясно, как включать реляционную информацию. Хотя этот студент смог визуализировать, что одна ящерица была продана на каждые четыре проданных котенка, он не смог определить, как эта информация связана с дополнительными 18 ящерицами, которые были бы равны количествам.

Одним из способов представления реляционной информации в виде диаграммы является использование столбцов, как показано здесь. На этом этапе учащийся может не знать количество каждого из столбцов, но использует столбцы для представления неизвестного количества. Ученик может представить себе, что было продано в четыре раза больше котят, чем ящериц, а разница между количествами составляет 18.

Схема

должны представлять шесть домашних животных. Диаграмма, которая теперь завершена, помогла учащемуся визуализировать вопрос, а также предоставила визуальную стратегию для решения вопроса.

Эти визуализации неизвестных величин могут стать первым шагом к пониманию алгебраических формулировок.

Ахмед участвует в 78-километровом триатлоне. Ему нужно проплыть 3 км. Ему нужно проехать на велосипеде в четыре раза больше расстояния, чем нужно пробежать. Какое расстояние он проедет на велосипеде в триатлоне?

Иллюстрированный

Для этой текстовой задачи учащийся нарисовал линию расстояния, потому что понял, что расстояние является релевантной переменной. К счастью, учащийся смог использовать линию для решения первого шага задачи (т. е. найти расстояние, которое не проплыл), но застрял на этом месте. Учащийся не смог использовать диаграмму для решения второго шага задачи (т. е. определить пройденное на велосипеде расстояние).

Схема

В этом примере учащийся использует два типа визуализации для решения задачи. Как и в приведенном выше ответе, этот ученик рисует линию, чтобы показать дистанцию ​​плавания и дистанции без плавания. Для второго шага задачи учащийся создает относительные столбцы (в нижней части диаграммы), чтобы показать, что спортсмен проехал на велосипеде в четыре раза больше, чем пробежал, а общее расстояние составило 75 километров. Опять же, диаграмма не просто визуализирует проблему; диаграмма представляет собой стратегию ее решения.

Диаграммы могут быть ценной стратегией при решении текстовых задач, но, что более важно, диаграммы позволяют учащимся думать и решать задачи по-новому. Учащимся с LD диаграммы могут помочь в организации информации, планировании решения и реализации решения — всех процессах, которые могут показаться им сложными! В качестве стратегии решения проблем использование диаграмм легко адаптируется и является динамичным, и это дает преподавателям прекрасную возможность следить за тем, как учащиеся думают, и при необходимости оказывать поддержку. В то время как обучение студентов эффективному использованию диаграмм займет некоторое время, успехи будут длительными, и стратегия может иметь решающее значение для некоторых студентов.

Ссылки

Hutchinson, NL (1986). Инструкция по представлению и решению алгебраических задач с подростками с ограниченными возможностями обучения (Неопубликованная докторская диссертация). Университет Саймона Фрейзера, Ванкувер, Британская Колумбия.

Розенцвейг, К., Кравец, Дж., и Монтегю, М. (2011). Использование метакогнитивной стратегии учащимися восьмого класса с нарушениями обучаемости и без них во время решения математических задач: анализ мыслей вслух. Журнал неспособности к обучению, 44 , 508-520. doi: 10.1177/0022219410378445

Стилианоу, Д. (2010). Представления учителей о репрезентации математики в средней школе. Журнал образования учителей математики, 13 , 325–434. doi: 10.1007/s10857-0109143-y.

Уэсака Ю. и Манало Э. (2012 г. ). Связанные с заданием факторы, влияющие на спонтанное использование диаграмм в математических задачах. Прикладная когнитивная психология, 26, 251–260. doi: 10.1002/acp.1816

ван Гардерен, Д. (2007). Обучение студентов с LD использовать диаграммы для решения математических текстовых задач. Journal of Learning Disability, 40, 540–553. doi: 10.1177/00222194070400060501

ван Гардерен, Д., и Монтегю, М. (2003). Визуально-пространственное представление, решение математических задач и учащиеся с разными способностями. Исследование и практика проблем с обучаемостью, 18 , 246–254. doi:10.1111/1540-5826.00079

ван Гардерен, Д., и Шойерманн, А. (2015). Диаграммы словесных задач: стратегический подход к обучению. Вмешательство в школу и поликлинику, 50 , 282–290. doi: 10.1177/1053451214560889

ван Гардерен Д., Шойерманн А. и Джексон К. (2012). Изучение того, как учащиеся с разными способностями используют диаграммы для решения математических задач. Ежеквартально по вопросам неспособности к обучению, 36 145–160. doi: 10.1177/0731948712438558

ван Гардерен Д., Шойерманн А. и Поч А. (2014). Ставит перед учащимися проблемы с обучаемостью и показывает высокий уровень успеваемости при использовании диаграмм в качестве инструмента визуализации для решения математических текстовых задач. ZDM Математическое образование, 46 , 135–149. doi: 10.1007/s11858-013-0519-1

Захнер, Д., и Кортер, Дж. Э. (2010). Процесс решения вероятностных задач: Использование внешних визуальных представлений. Математическое мышление и обучение, 12 , 177–204. doi: 10.1080/10986061003654240

Связанные ресурсы LD@school

Нажмите здесь, чтобы получить доступ к научно обоснованной статье «Визуальное представление в математике».

Нажмите здесь, чтобы получить доступ к видео «Использование совместного опроса учителей для поддержки учащихся с ограниченными возможностями по математике» и прилагаемому Руководству для зрителей.

Нажмите здесь, чтобы получить доступ к веб-семинару «Понимание дискалькулии развития: нарушение способности к обучению математике».

Нажмите здесь, чтобы получить доступ к статье, основанной на фактических данных, «Вмешательства, основанные на фактических данных, для учащихся с математическими отклонениями: один размер не подходит всем».

Нажмите здесь, чтобы получить доступ к статье, основанной на фактических данных, «Конкретные – репрезентативные – абстрактные: стратегия обучения математике».

Щелкните здесь, чтобы получить доступ к научно обоснованной статье «Математическая эвристика».

Нажмите здесь, чтобы получить доступ к статье, основанной на фактических данных, «Четкое обучение: стратегия обучения чтению, письму и математике для учащихся с ограниченными возможностями обучения».

Нажмите здесь, чтобы получить доступ к практической статье «Считаем до 99».

Джеффри — аспирант педагогического факультета Королевского университета, специализирующийся на познании.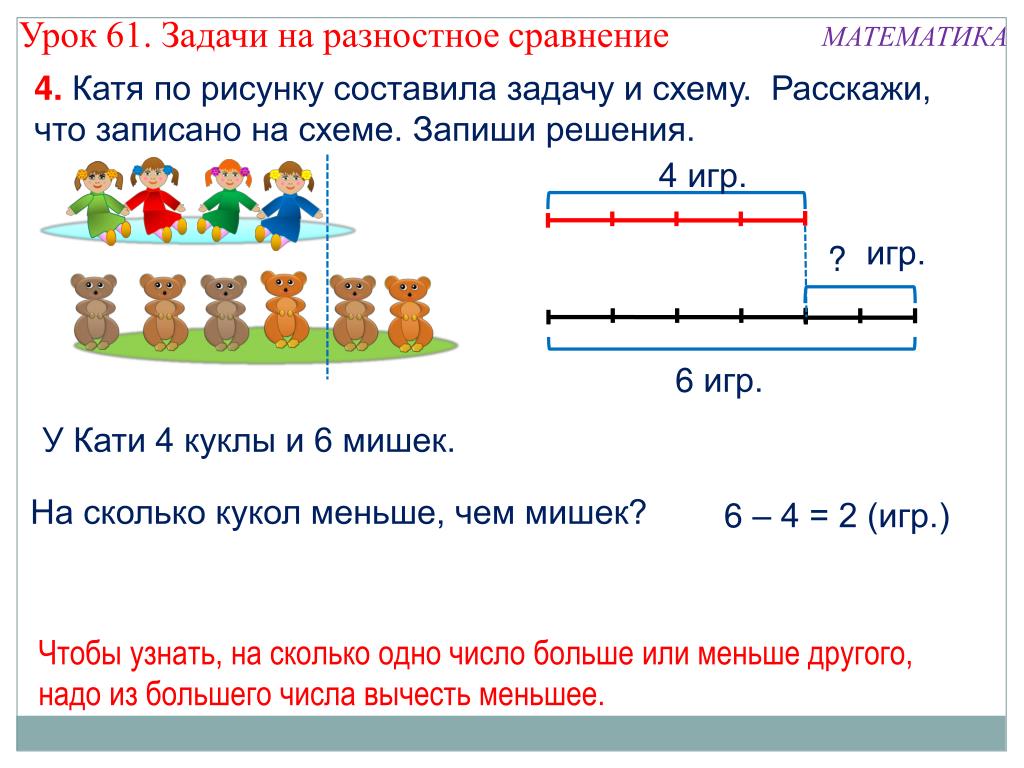 Он является учителем, сертифицированным Педагогическим колледжем Онтарио, с 9-летним опытом преподавания в начальной школе. Он работал инструктором в Королевском университете, преподавал и создавал онлайн-курсы для преподавателей. В настоящее время он проводит исследования по нескольким темам, включая проблемы с обучаемостью, аутизм, эмоциональное благополучие и развитие молодежи.

 

 

Ян Мэтисон является аспирантом программы докторантуры в области образования в Королевском университете, специализирующейся на обучении и познании. Наряду с преподавательским и исследовательским опытом в Королевском университете, Ян также имеет опыт работы учителем в начальной школе школьного совета округа Лаймстоун.

Общий тест GRE Quantitative Reasoning Обзор

 

Общий тест GRE ^®

Один тест для выпускников, бизнес- и юридических школ

Выберите шаг, чтобы узнать больше о своем пути к общему тесту GRE ^® .
 

Показатель количественного мышления общего теста GRE оценивает ваши:

• базовые математические навыки
• понимание элементарных математических понятий
• способность рассуждать количественно, а также моделировать и решать задачи количественными методами.
   

Охватываемые области содержания

Некоторые вопросы количественного мышления задаются в реальных условиях, тогда как другие задаются в чисто математических условиях. Многие из вопросов представляют собой «словные задачи», которые необходимо перевести и смоделировать математически. Навыки, концепции и способности оцениваются в четырех областях содержания, указанных ниже.

• Темы арифметики, в том числе:
  • свойства и типы целых чисел, такие как делимость, факторизация, простые числа, остатки, нечетные и четные целые числа
  • арифметические операции, показатели степени и корни
  • такие понятия, как оценка, процент, отношение, скорость, абсолютное значение, числовая линия, десятичное представление и последовательность чисел
• темы по алгебре, в том числе:
  • операции с показателями
  • факторизация и упрощение алгебраических выражений
  • отношения, функции, уравнения и неравенства
  • решение линейных и квадратных уравнений и неравенств
  • решение одновременных уравнений и неравенств
  • составление уравнений для решения текстовых задач
  • координатная геометрия, включая графики функций, уравнения и неравенства, точки пересечения и наклоны линий
• Темы по геометрии, в том числе:
  • параллельные и перпендикулярные линии
  • круга
  • треугольника, включая равнобедренные, равнобедренные и треугольники с углами 30°-60°-90°
  • четырехугольники
  • других полигонов
  • конгруэнтные и подобные фигуры
  • Объемные фигуры
  • район
  • периметр
  • том
  • теорема Пифагора
  • измерение угла в градусах

Способность конструировать доказательства не проверяется.

• Темы анализа данных , включая:
  • основные описательные статистические данные, такие как среднее значение, медиана, мода, диапазон, стандартное отклонение, межквартильный диапазон, квартили и процентили
  • интерпретация данных в таблицах и графиках, таких как линейные графики, гистограммы, круговые диаграммы, ящичные диаграммы, диаграммы рассеяния и частотные распределения
  • элементарная вероятность, такая как вероятности составных событий и независимых событий
  • условная вероятность
  • случайные величины и распределения вероятностей, включая нормальные распределения
  • методы подсчета, такие как комбинации, перестановки и диаграммы Венна

Эти темы обычно преподаются на курсах алгебры в средней школе или на вводных курсах статистики.

Логическая статистика не проверена.

Содержание в этих областях включает математику и статистику средней школы на уровне, который обычно не выше второго курса алгебры. Он не включает тригонометрию, исчисление или другую математику более высокого уровня. В Math Review (PDF) предоставляется подробная информация о содержании меры количественного рассуждения.

 

Символы, терминология, условные обозначения и допущения

Математические символы, терминология и условные обозначения, используемые в измерении количественного мышления, являются стандартными для старшей школы. Например, положительное направление числовой прямой — вправо, расстояния неотрицательны, а простые числа больше 1. Всякий раз, когда в вопросе используются нестандартные обозначения, они явно вводятся в вопросе.

Помимо условных обозначений, существуют некоторые важные предположения о числах и цифрах, которые перечислены в указаниях раздела «Количественное рассуждение»:

• Все используемые числа действительны.
• Предполагается, что все фигуры лежат в плоскости, если не указано иное.
• Геометрические фигуры, такие как линии, окружности, треугольники и четырехугольники, не обязательно изображаются в масштабе . Не предполагайте, что такие величины, как длины и угловые меры, представлены на рисунке. Однако следует исходить из того, что:
  • линии, показанные прямыми, на самом деле являются прямыми
  • точки на линии расположены в указанном порядке
  • все геометрические объекты находятся в показанных относительных позициях

Ответы на вопросы с геометрическими фигурами следует основывать на геометрических рассуждениях, а не на оценке или сравнении величин визуально или путем измерения.

• Следующие нарисованы в масштабе . Вы можете считывать, оценивать или сравнивать количества и значения данных визуально или путем измерения:
  • системы координат, такие как xy -плоскости и числовые линии
  • графические представления данных, такие как гистограммы, круговые диаграммы и линейные диаграммы

Чтобы узнать больше об соглашениях и допущениях, загрузите Математические соглашения (PDF).
 

Типы вопросов и наборы для интерпретации данных

Мера количественного рассуждения включает четыре типа вопросов:

• Вопросы количественного сравнения
• Вопросы с несколькими вариантами ответов — выберите один вариант ответа
• Вопросы с несколькими вариантами ответов — выберите один или несколько вариантов ответа
• Числовой ввод вопросов

Каждый вопрос появляется либо независимо как отдельный вопрос, либо как часть набора вопросов, который называется набором интерпретации данных. Все вопросы в наборе интерпретации данных основаны на одних и тех же данных, представленных в таблицах, графиках или других формах отображения данных.
 

В этих вопросах вам предлагается сравнить две величины — количество A и количество B — и затем определить, какое из следующих утверждений описывает сравнение.

• Количество A больше.
• Количество B больше.
• Обе величины равны.
• Отношение не может быть определено из предоставленной информации.

Советы по ответу

1. Ознакомьтесь с вариантами ответов . Вопросы количественного сравнения всегда имеют один и тот же вариант ответа, поэтому изучите их, особенно последний вариант: «Отношение нельзя определить на основе предоставленной информации». Никогда не выбирайте этот последний вариант, если ясно, что значения двух величин могут быть определены вычислением. Кроме того, если вы определили, что одно количество больше другого, убедитесь, что вы тщательно выбрали соответствующий вариант и не меняете местами первые два варианта.
2. Избегайте ненужных вычислений . Не тратьте время на ненужные вычисления для сравнения двух величин. Упростите, преобразуйте или оцените одну или обе заданные величины только по мере необходимости, чтобы сравнить их.
3. Помните, что геометрические фигуры не обязательно рисуются в масштабе . Если какой-либо аспект данной геометрической фигуры не определен полностью, попытайтесь перерисовать фигуру, оставив фиксированными те аспекты, которые полностью определяются данной информацией, но изменив аспекты фигуры, которые не определены. Изучите результаты. Какие вариации возможны в относительных длинах отрезков или мер углов?
4. Вставьте числа . Если одна или обе величины являются алгебраическими выражениями, вы можете заменить переменные простыми числами и сравнить полученные величины в своем анализе. Рассмотрите все виды подходящих чисел, прежде чем давать ответ: например, ноль, положительные и отрицательные числа, маленькие и большие числа, дроби и десятичные дроби. Если вы видите, что количество A больше количества B в одном случае, а количество B больше количества A в другом случае, выберите «Отношение не может быть определено на основе предоставленной информации».
5. Упростить сравнение . Если обе величины являются алгебраическими или арифметическими выражениями, и вы не можете легко увидеть взаимосвязь между ними, попробуйте упростить сравнение. Попробуйте выполнить пошаговое упрощение, аналогичное шагам, которые выполняются при решении уравнения для 90 401 x , или аналогичным шагам, которые необходимо выполнить, когда вы определяете, что неравенство  эквивалентно более простому неравенству. Начните с настройки сравнения, включающего два количества: 

, где  это заполнитель, который может обозначать отношение больше (>), меньше (<) или равно (=), либо может обозначать тот факт, что отношение невозможно определить на основе предоставленной информации. Затем попытайтесь упростить сравнение, шаг за шагом, пока не сможете определить взаимосвязь между упрощенными величинами. Например, вы можете сделать вывод после последнего шага, который представляет собой равенство (=). Основываясь на этом выводе, вы, возможно, сможете сравнить количества A и B. Чтобы лучше понять эту стратегию, см. примеры вопросов 6–9..

В этих вопросах с несколькими вариантами ответов вам предлагается выбрать только один вариант ответа из списка из пяти вариантов.
 

Советы по ответу

1. Используйте тот факт , что ответ есть . Если ваш ответ не входит ни в один из пяти предложенных вариантов ответа, предположите, что ваш ответ неверен, и сделайте следующее:
   • Внимательно перечитайте вопрос — возможно, вы упустили важную деталь или неверно истолковали какую-то информацию.
   • Проверьте свои вычисления — возможно, вы допустили ошибку, например, неправильно набрали число на калькуляторе.
   • Пересмотрите свой метод решения — у вас может быть изъян в рассуждениях.
2. Просмотрите варианты ответов . В некоторых вопросах вас прямо спрашивают, какой из вариантов имеет определенное свойство. Возможно, вам придется рассмотреть каждый вариант отдельно или вы сможете увидеть взаимосвязь между вариантами, что поможет вам быстрее найти ответ. В других вопросах может быть полезно работать в обратном направлении от вариантов, например, заменяя варианты в уравнении или неравенстве, чтобы увидеть, какой из них работает. Однако будьте осторожны, так как этот метод может занять больше времени, чем использование рассуждений.
3. Для вопросов, требующих приближения, просмотрите варианты ответов, чтобы увидеть, насколько близко требуется приближение . (Это может быть полезно и для других вопросов, так как поможет вам лучше понять, о чем идет речь. ) Для некоторых вопросов вам, возможно, придется выполнить все вычисления точно и округлить только ваш окончательный ответ, чтобы получить необходимая степень точности. В других случаях оценки достаточно, и это поможет вам не тратить время на долгие вычисления.

В этих вопросах с несколькими вариантами ответов вам предлагается выбрать один или несколько вариантов ответа из списка вариантов. Вопрос может указывать или не указывать количество вариантов для выбора.

Советы по ответу

1. Обратите внимание, просят ли вас указать конкретное количество вариантов ответа или все подходящие варианты . В последнем случае обязательно рассмотрите все варианты, определите, какие из них правильные, и выберите все эти и только эти варианты. Обратите внимание, что правильный выбор может быть только один.
2. В некоторых вопросах, которые включают условия, ограничивающие возможные значения числовых вариантов ответа, может оказаться эффективным определить наименьшее и/или максимально возможное значение . Зная наименьшее и/или максимально возможное значение, вы сможете быстро определить все правильные варианты.
3. Избегайте длинных вычислений, распознавая и продолжая числовые шаблоны .

Эти вопросы требуют, чтобы вы либо ввели свой ответ в виде целого числа или десятичной дроби в одно поле для ответа, либо в виде дроби в двух отдельных полях — одно для числителя и одно для знаменателя. Вы будете использовать компьютерную мышь и клавиатуру, чтобы ввести свой ответ.

Советы по ответу

1. Убедитесь, что вы ответили на заданный вопрос . Поскольку нет вариантов ответов, которые могли бы вам помочь, внимательно прочитайте вопрос и убедитесь, что вы даете требуемый тип ответа. Иногда перед или после поля для ответа будут метки, указывающие на соответствующий тип ответа. Обратите особое внимание на такие единицы, как футы или мили, на порядки величин, такие как миллионы или миллиарды, и на проценты по сравнению с десятичными дробями.
2. Если вас попросят округлить ответ, убедитесь, что округлили до требуемой степени точности . Например, если ответ 46,7 должен быть округлен до ближайшего целого числа, вам нужно ввести число 47. Если ваша стратегия решения включает промежуточные вычисления, выполните все вычисления точно и округлите только ваш окончательный ответ, чтобы получить требуемое степень точности. Если инструкции по округлению не указаны, введите точный ответ.
3. Изучите свой ответ, чтобы убедиться, что он разумен с учетом предоставленной информации . Вы можете использовать оценку или другой путь решения, чтобы перепроверить свой ответ.

Вопросы интерпретации данных сгруппированы вместе и относятся к одной и той же таблице, графику или другому представлению данных. Эти вопросы просят вас интерпретировать или анализировать данные. Типы вопросов могут быть с множественным выбором (оба типа) или числовым вводом.

Советы по ответу

1. Кратко просмотрите презентацию данных, чтобы понять, о чем она, но не тратьте время на подробное изучение всей информации . Сосредоточьтесь на тех аспектах данных, которые необходимы для ответа на вопросы. Обратите внимание на:
   • оси и шкалы графиков
   • единицы измерения или порядки величины (например, миллиарды), указанные в заголовках, метках и легендах
   • любые примечания, уточняющие данные
2. Когда графические представления данных, такие как гистограммы и линейные графики, отображаются с помощью масштабов, вы должны считывать, оценивать или сравнивать количества визуально или путем измерения в соответствии с соответствующими масштабами . Например, используйте относительные размеры столбцов или секторов для сравнения величин, которые они представляют, но помните о ломаных шкалах и столбцах, которые не начинаются с 0,
.
3. Отвечайте на вопросы только на основе представленных данных, повседневных фактов (таких как количество дней в году) и ваших знаний по математике . Не используйте специализированную информацию, которую вы можете вспомнить из других источников о конкретном контексте, на котором основаны вопросы, за исключением случаев, когда эта информация может быть получена из представленных данных.

Этапы решения проблем

В дополнение к советам по ответам в разделах типов вопросов выше, есть также некоторые общие шаги и стратегии решения проблем, которые вы можете использовать. Вопросы из измерения «Количественное мышление» требуют моделирования и решения проблем с использованием количественных или математических методов. Как правило, решение математических задач состоит из трех основных шагов:

Внимательно прочитайте формулировку задачи, чтобы убедиться, что вы понимаете предоставленную информацию и задачу, которую вам предстоит решить.

• Некоторая информация может описывать определенные количества.
• Количественная информация может быть представлена ​​словами или математическими выражениями, или их комбинацией.
• Вам может понадобиться читать и понимать количественную информацию в представлениях данных, геометрических фигурах или системах координат.
• Другая информация может иметь форму формул, определений или условий, которым должны удовлетворять величины. Например, условия могут быть уравнениями или неравенствами, или могут быть словами, которые можно перевести в уравнения или неравенства.

Помимо понимания предоставленной вам информации, убедитесь, что вы понимаете, что вам нужно сделать, чтобы решить проблему. Например, какие неизвестные величины необходимо найти? В какой форме они должны быть выражены?

Решение математической задачи требует большего, чем понимание описания задачи (количество, данные, условия, неизвестные и все другие математические факты, связанные с задачей). Это также требует определения какие математические факты использовать и когда и как использовать эти факты для разработки решения задачи. Это требует стратегии.

Математические задачи решаются с использованием самых разных стратегий, и могут быть разные способы решения данной задачи. Разработайте репертуар стратегий решения проблем и понимание того, какие стратегии, вероятно, будут работать лучше всего при решении конкретных проблем. Попытка решить проблему без стратегии может привести к большой работе без получения правильного решения.

После того, как вы определите стратегию, выполните ее. Если вы застряли, проверьте свою работу, чтобы увидеть, не допустили ли вы ошибку в своем решении. Сохраняйте гибкий и открытый образ мышления. Если вы проверяете свое решение и не можете найти ошибку, или если ваша стратегия решения просто не работает, поищите другую стратегию.

Когда вы получите ответ, убедитесь, что он разумен и корректен с точки зрения вычислений.

• Вы ответили на заданный вопрос?
• Является ли ваш ответ обоснованным в контексте вопроса? Проверить правильность ответа можно так же просто, как вспомнить основной математический факт и проверить, согласуется ли ваш ответ с этим фактом. Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. Возможно, вы сможете использовать оценку, чтобы проверить, является ли ваш ответ разумным. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть в диапазоне от 300 до 600.
• Вы допустили вычислительную ошибку при получении ответа или ошибку при вводе ключа с помощью калькулятора? Проверьте наличие ошибок на каждом этапе вашего решения. Или вы можете напрямую проверить правильность вашего решения. Например, если вы решаете уравнение относительно x, подставьте свой ответ в уравнение, чтобы убедиться, что он правильный.

Стратегии

Не существует установленных правил, применимых ко всем математическим задачам, для определения наилучшей стратегии. Способность определить стратегию, которая будет работать, растет по мере того, как вы решаете все больше и больше проблем. Загрузите примеры вопросов, чтобы получить список из 14 полезных стратегий, которые вы можете использовать, а также один или два примера вопросов, которые иллюстрируют, как использовать каждую стратегию.

Скачать PDF

Использование калькулятора

Вам предоставляется базовый экранный калькулятор для меры количественного рассуждения. Иногда вычисления, которые вам нужно сделать, чтобы ответить на вопрос в показателе количественного рассуждения, требуют много времени, например, деление в длину, или они включают квадратные корни. Хотя калькулятор может сократить время, необходимое для выполнения вычислений, имейте в виду, что калькулятор дает результаты, которые дополняют, но не заменяют ваши знания математики. Вам нужно будет использовать свои математические знания, чтобы определить, являются ли результаты калькулятора разумными и как результаты можно использовать для ответа на вопрос.

Вот некоторые общие рекомендации по использованию калькулятора в измерении количественного мышления:

• Большинство вопросов не требуют сложных вычислений, поэтому не используйте калькулятор только потому, что он доступен.
• Используйте его для вычислений, которые, как вы знаете, утомительны, таких как деление в длинную сторону, извлечение квадратных корней, а также сложение, вычитание или умножение чисел, состоящих из нескольких цифр.