Головоломки, сделанные своими руками — Блог идеальной жены — ЖЖ
Вообще, если спросить других людей, какое у меня хобби, большинство ответит — «Екатерина Георгиевна любит готовить».
Если у меня спросить, какое у меня хобби, ответ будет чуть-чуть другим, на самом деле гораздо более интересным — я люблю и собираю игрушки с математическим смыслом.
Я уже несколько раз писала про мои игрушки. Например, тут. Но это было уже давно. А с тех пор появилось новенькое.
Вообще, собирать математические игрушки сложно. Не всякая головоломка — хорошая математическая игрушка с глубоким математическим смыслом. Немножко выручает то, что математические игрушки можно делать самостоятельно.
Вот тут я писала про одну из самых моих любимых математических игрушек из детства — флексагон.
Сегодня расскажу, что еще есть в моем волшебном ящике такое, что мы смастерили самостоятельно.
Много математических игрушек дарит мне муж. (Он-то знает правильный ответ на вопрос про хобби!)
Самое простенькое — нестандартная игральная кость.
Деревянный кубик, углы скруглены, потом покрашен белой краской и маркером нарисованы числа от 0 до 5.
А вот — кубики, выигрывающие по кругу друг у друга. Я подробно про них писала. Каждый следующий кубик выигрывает у предыдущего с вероятностью 2/3, а у последнего первый выигрывает с вероятностью 2/3. Тогда в моей коллекции были мраморные кубики, сделанные мужем. И у них была чуть-чуть не равная вероятность выигрыша друг у друга.
Эти кубики — из стеариновых кубиков для охлаждения виски. Фрезой сделано углубление.
Использовать их в виски по-прежнему можно )
Одна из самых волшебных игрушек с математическим смыслом в мире, на мой взгляд — цепь Герона. Что это такое — можно получить представление по видео:
Герон (тот самый, который греческий математик, которого мы помним по «формуле Герона» для вычисления площади треугольника), согласно истории, зарабатывал себе на жизнь, показывая фокусы с этой цепью.
А сделать ее в домашних условиях легко из колечек для ключей. Тут — 50 штук. Очень рекомендую брать большое количество колечек, так интереснее.
Сама я делала себе игрушки по-проще. Например, вот игра «сет». Состоит из карточек с картинками. Фигурки 3 видов, покрашены 3 цветами, их на карточке 1, 2 или 3, и способы окраски: просто контур, заштриховано, или закрашено. (4 признака по 3 возможности = всего 81 карточка в наборе).
«Сет» — это комбинация из 3 карточек, в которых каждый признак либо на всех трех одинаковый, либо на всех трех разный. На картинке Денис показывает сет: количество одинаковое, формы все разные, цвета разные, способ закраски разный. На стол выкладывается 12 карточек и игроки находят сет. Кто первый нашел — забирает его себе, на пустые места выкладываются еще карточки. Очень азартная и интересная игра.
Для тренировки можно удалить один признак. Скажем, когда дети были в садике, мы брали только карточки, закрашенные сплошняком.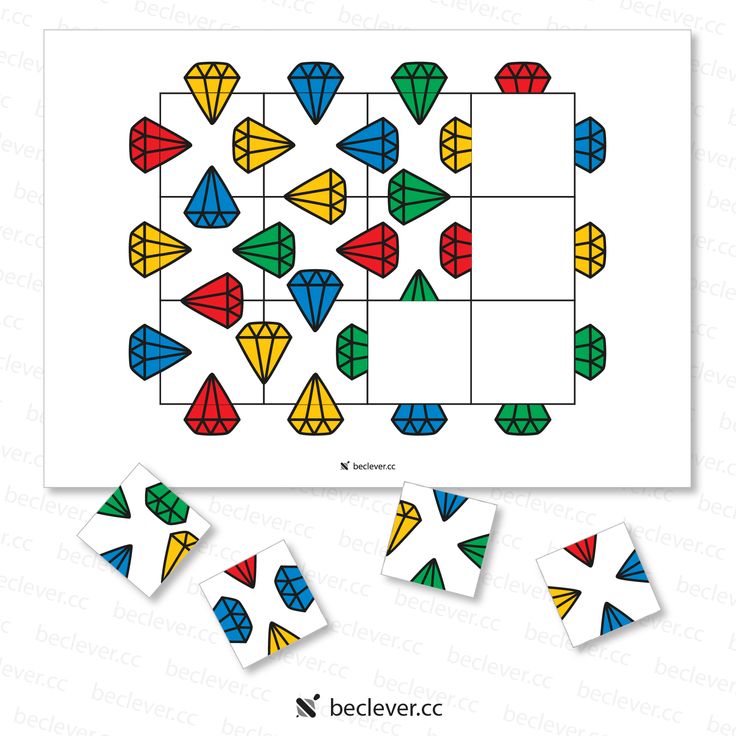
Сделаны просто: напечатаны на принетере (когда у нас еще не было даже цветного принтера), раскрашены фломастерами.
Магнитный танграм.
Одна из самых моих любимых головоломок — танграм. Можно вырезать танграм из картона, как мы и делали в детстве. А тут у меня вырезано из большого магнитного полотна. С танграмом из картона никто не играет обычно. А вот танграм из магнита висит на холодильнике постоянно и с ним всегда все играют. Приходишь — на холодильнике дети (или муж) собрали что-нибудь новенькое.
А вот как раз-таки из картона вырезанная головоломка — «Квадрат Пифагора». Первая задача — из 4 деталей сложить квадрат. А теперь добавить к этим деталям еще маленький квадрат и сложить новый квадрат уже из пяти деталей.
Недавно носила головоломки в универ. Почему-то студентам очень этот «квадрат» понравился.
А вот здесь — карточки со словами, имеющими отношение к математике.
Карточек много. Некоторые из какого-то раздела математики. Есть большой набор для школьников. Есть небольшой наборчик про наш ИМИТ.
Сделать, понятно, легко — напечатать на принтере. Чтобы не просвечивало — сзади рубашка с математическим смыслом.
Как играть? Ну, тут вариантов масса. Мне последнее время нравится такой.
Играющие делятся на пары. Первый круг. Карточки лежат стопкой. Берешь одну карточку — за отведенное время (скажем, за полминуты) объясняешь напарнику понятие на карточке, не используя однокоренных слов. Объяснил правильно — берешь следующую карточку. И т.д. Пропускать нельзя.
Второй круг — те же карточки, но объяснять без слов. Выручает то, что карточки те же и можно кое-что запомнить.
Третий круг — объяснение одним словом.
Ну, и выигрывает пара, набравшая в сумме больше всех.
Можно взять любые другие правила игр про объяснения слов (типа Активити). Один раз я даже так зачет принимала. И, конечно, тут особо специфического математического нет — можно и по химии такие карточки сделать, и по истории России )))
Вот. А недавно у нас появился 3д-принтер, и, конечно, возникла идея делать мне игрушки с помощью него ))
А недавно у нас появился 3д-принтер, и, конечно, возникла идея делать мне игрушки с помощью него ))
Например, появился у меня такой танграм.
Танграм можно сделать и из картона, но такой аккуратнее и интереснее. Вообще, я делала (ну, как я делала? Муж мне делал, конечно, на своем 3д-принтере) танграм (вот такой, с логотипом ИМИТ) как приз в одном из наших конкурсов. А этот получился как пробная (и немного неудачная) версия того. Зато тот, который приз — магнитный (а мой нет). Вот честное слово, магнитный танграм — вещь.
Вот такая вот штука: 3 одинаковых детали из которых собирается куб. Конечно, такой уже без 3д-принтера сделать очень сложно.
Но вещь очень классная. )
Мужа как инженера, а меня как математика буквально завораживают красивые шестереночные механизмы. Отсюда игрушки.
Например, вот такой куб, который можно крутить. Стоит у меня на кафедре и никогда не стоит. Постоянно находится у кого-нибудь в руках и его крутят.
Постоянно находится у кого-нибудь в руках и его крутят.
Оторваться практически невозможно.
Вот такие прикольные шестеренки.
А вот — несимметричные шестеренки. Такие можно увидеть в музеях типа «Эксперементариум» в Москве или «Джоуль-парк» в нашем Омске. А также у меня дома )))
Самое прикольное, что шестеренки вертятся и не заедают ))
Примерно из той же оперы — шкатулка-лабиринт. Закрыть ее не так трудно — вы видите линии лабиринта и двигаетесь к цели. А вот открыть! Надо пройти лабиринт, не видя его )))
Конечно, невозможно же не совместить 2 моих хобби: математические игрушки и готовку. Про формочки для математического печенья я недавно рассказывала. И вообще-то про месопатамскую печать с мозаиками Эшера тоже. Чудо-чудное. У меня таких несколько )
Мозаики Эшера? Да, они у меня есть не только в виде штук для готовки. А в виде мозаики тоже. Очень успокаивает нервы так раскладывать ящерок по плоскости.
А в виде мозаики тоже. Очень успокаивает нервы так раскладывать ящерок по плоскости.
А вот это — нерегулярная мозаика, известная под названием «Курицы Пенроуза» (ой, слово курицы перестало подчеркивать). Так вот, курицы Пенроуза, наоборот, раздражают )))
А вот самое последнее мое пополнение коллекции. Такое можно сделать запросто и из картона.
В английской версии называется «T-puzzle», в русской «Собери букву Т».
Есть детали (такие, как показано на картинке). Из них нужно собрать букву Т.
Почему на верхней картинке 2 набора? Потому что таких головоломок самых известных две. Одну приписывают Мартину Гарднеру (ту, что на картинке бледнее) и вторую приписывают японскому изобретателю головоломок Нобу (та, что темнее). Отличаются пропорциями буквы Т.
Говорят, что если дать детали и велеть составить букву Т, 80% людей сдаются, не решив задачу. Ну, а кроме буквы Т по типу танграма, можно собирать еще кучу интересных вещей.
Мне немного жалко, что букву Т нельзя сделать магнитной — тогда большую часть интересных картинок из нее будет не собрать. Но очень классная штука.
А! Вывод. Всегда у правильного поста должен быть вывод. Мужу bukov_ka респект и уважуха! А за кадром — безмерная любовь и поцелуи.
Ну, а второй вывод — вообще, конечно, круто, когда есть хорошие магазины, где продаются не «головоломки из гвоздей», а правильные математические игрушки. И, конечно, очень здорово, когда есть 3д-принтер, на котором можно что-нибудь сделать. Но вообще-то много математических развлечений можно сделать из простой бумаги подручными средствами.
Метки: игрушечное, математическое
в картинках и текстовые, для взрослых и детей
Занимательная математика и логика / Математические игры
Знакомим с популярными головоломками, увлекательными заданиями от ЛогикЛайк, которые
нравятся детям и их родителям. Разбираем решение известных числовых и логических
головоломок.
Разбираем решение известных числовых и логических
головоломок.
17 категорий числовых и логических математических головоломок
2 варианта занятий, выбор сложности
- Пройдите 3 стартовые главы курса логики – и откройте доступ к разным категориям. Попробуйте «Логические задачи», «Истина и ложь», «Умный счёт», «3D‑мышление».
-
Попробуйте задания разного уровня сложности:
«Новичок», «Опытный», «Эксперт».

Попробуйте курс ЛогикЛайк в игровой форме!
Выберите возраст для старта
4-6 лет1 класс
2 класс
3 класс
4-5 класс
старше
На платформе LogicLike.com дети и взрослые с удовольствием развивают логику и мышление. У нас 3500 занимательных заданий с ответами и пояснениями!
9 знаменитых математических головоломок, о которых будет интересно узнать вашим детям
Математические головоломки как способ помериться интеллектуальными силами всегда увлекали людей.
Разберите подборку головоломок вместе с детьми: «разомнете» мозги, весело проведете время и знание истории «прокачаете»! Мы выбрали интересные задачки, дошедшие до наших дней из «древности», и приближенные к «нашему» времени.
- Папирус Ахмеса
- Задача о переправе
- Печать царя Соломона
- Головоломка Фибоначчи о кроликах
- Задача Тартальи «Трудное наследство»
- Головоломка Льюиса Кэрролла
- «Безумный разрез» Мартина Гарднера
- Сингапурская головоломка
- Танграм
Папирус Ахмеса
Древние египтяне были не только опытными строителями пирамид, но и прекрасными математиками. Доказательством этому служит древнеегипетский папирус, автором которого был некий Ахмес. Как
выяснили исследователи-египтологи, папирус Ахмеса — копия очень древнего математического
сборника, составленного во времена фараона Аменемхета III (приблизительно 1853-1806 гг. до
н.э.). Задач в сборнике много — ниже одна из них.
Доказательством этому служит древнеегипетский папирус, автором которого был некий Ахмес. Как
выяснили исследователи-египтологи, папирус Ахмеса — копия очень древнего математического
сборника, составленного во времена фараона Аменемхета III (приблизительно 1853-1806 гг. до
н.э.). Задач в сборнике много — ниже одна из них.
Показать решение
Задача о переправе
Не только древние египтяне упражнялись в решении задач на сообразительность. Историки обнаружили
книгу, написанную на латыни, под названием «Задачи для развития молодого ума». Ирландский
богослов, ученый и просветитель Алкуин, живший в IX веке, собрал в книге 53 задачи. Предлагаем
одну из них — настолько «бородатую», что ее знают школьники во всем мире.
Ирландский
богослов, ученый и просветитель Алкуин, живший в IX веке, собрал в книге 53 задачи. Предлагаем
одну из них — настолько «бородатую», что ее знают школьники во всем мире.
Как крестьянину перевезти все в целости и сохранности?
Показать решение
Печать царя Соломона
На гробнице мудрого легендарного библейского царя Соломона потомки изобразили знаменитую печать правителя.
Попробуйте сосчитать, сколько равносторонних треугольников изображено на
печати.
Проверить себя
Попробуйте курс ЛогикЛайк «ВСЯ ЛОГИКА В ИГРОВОЙ ФОРМЕ»
- Развиваем мышление Решая задачи и головоломки дети развивают смекалку, а взрослые тренируют «извилины».
- Строим
фундамента успеха
Учим грамотно работать с информацией, тренируем память
и развиваем логико‑математический интеллект.
 Повышаем
познавательный интерес и уверенность в себе.
Повышаем
познавательный интерес и уверенность в себе. - Глоток «свежего воздуха» Можно потратить 20-30 минут на себя, пока ребёнок развивается. Заниматься на ЛогикЛайк одинаково интересно детям и взрослым.
Начать курс!
Задача Фибоначчи о размножении кроликов
Леонардо Пизанский (около 1170 г.р.), по прозвищу Фибоначчи, — один из первых именитых
математиков средневековой Европы. Он успешно участвовал в математических турнирах, а, создав
себе имя, придумывал для них занимательные задачи. Ниже одна из самых известных.
Ниже одна из самых известных.
«Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый
день января. Эта пара кроликов производит новую пару кроликов в первый день
февраля и затем в первый день каждого следующего месяца.
Каждая
новорожденная пара кроликов становится зрелой уже через месяц и затем через
месяц дает жизнь новой паре кроликов».
Сколько пар кроликов будет в огороженном месте через 12 месяцев с начала размножения?
Подсказка Вспомните последовательность Фибоначчи или запаситесь
терпением — и считайте.
Смотреть ответ
Задача Тартальи «Трудное наследство»
Никколо Тарталья (1499 г.р.), итальянский математик, обнаруживший общий алгоритм решения кубических уравнений. Описанный Никколо метод вошел в историю математики как Формула Кардано, по имени первого публикатора метода, до которого независимо друг от друга додумались Тарталья и Сципион дель Ферро.
Предлагаем решить ставшую известной задачу Тартальи о дележе лошадей.
Как выполнить завещание?
Показать решение
Головоломка Льюиса Кэрролла
Известный писатель Льюис Кэрролл, тот самый, который создал истории об Алисе и ее приключениях в
Стране Чудес и Зазеркалье, еще и очень любил придумывать головоломки и преподавал логику.
Своим маленьким поклонникам Кэрролл часто предлагал такую головоломку:
Задача усложняется особыми условиями ее выполнения:
- карандаш от бумаги отрывать нельзя;
- дважды проводить карандашом в одном месте нельзя;
- пересекать линии нельзя.
Показать решение
Отгадывайте головоломки
и решайте задания на логику от ЛогикЛайк!Классические логические вопросы и головоломки
Числовые ребусы, магические квадраты
Взвешивания и переливания
Комбинаторные задачи
Пространственные головоломки
Шестерёнки (вращение)
Алгоритмические задачи
Нестандартные шахматные задания
Начать занятия! Начать занятия!
«Безумный разрез» Мартина Гарднера
Мартин Гарднер — известный американский писатель, математик-любитель, автор множества статей и
книг по занимательной математике, научно-популярных этюдов, математических фокусов, головоломок
и задач на сообразительность и множества других публикаций.
Предлагаем решить одну из самых популярных головоломок Гарднера.
Сделайте один разрез (или нарисуйте одну линию) — не обязательно, прямую — чтобы разделить нарисованную фигуру на две одинаковые части.
Показать ответ
Сингапурская головоломка
Благодаря социальным сетям некоторые головоломки распространяются, как вирус, и становятся
известными. Так случилось с головоломкой, которую телеведущий Кеннет Конг из Сингапура разместил
на своей странице в фейсбуке, и вскоре ею поделились 4400 человек.
Альфред и Бернард только что познакомились с Шерил и хотят выяснить, когда у нее день рождения.
Шерил показала поклонникам 10 возможных дат:
Затем она показала Альфреду месяц своего рождения, а Бернарду — день.
Чтобы решить головоломку, друзья обменялись парой реплик:
Так когда же у Шерил день рождения?
Смотреть решение и ответ
Танграм
Согласно легенде, головоломка была создана несколько тысяч лет назад тремя древнекитайскими
мудрецами для сына императора. Правитель хотел чтобы через простую игру его сын постиг начала
математики, научился видеть окружающий мир глазами художника, стал терпеливым, как философ, и
осознал, что сложные вещи состоят из простых.
Правитель хотел чтобы через простую игру его сын постиг начала
математики, научился видеть окружающий мир глазами художника, стал терпеливым, как философ, и
осознал, что сложные вещи состоят из простых.
Так появился «Ши-Чао-Тю» — квадрат, разрезанный на семь частей:
5 треугольников (2 больших, 2 маленьких, 1 средний), квадрат и параллелограмм.
Суть «свободной» игры в танграм — собирать из имеющихся деталей по принципу мозаики всевозможные фигурки: животных, птиц, человека, что угодно. Младшим дошкольникам предлагают простой вариант развивающей игры, когда фигурки танграма нужно просто наложить на готовый образец-ответ.
Многие дети в 5-7 лет складывают модели из фигурок рядом с изображением-ответом, даже если
размеры вырезанных фигур и деталей на картинке отличаются.
Танграм как головоломка обычно по силам ребенку начиная с 6-7 лет. Все так же — из элементов танграма нужно сложить готовую модель, но на карточке изображен лишь силуэт фигуры.
Вырежьте элементы танграма из бумажного, картонного или другого квадрата, и для начала предлагаем собрать одну из популярных фигурок — бегущего человека, как на рисунке выше.
Помните 2 правила головоломки:
1) необходимо использовать все 7 фигурок головоломки;
2) фигуры не должны накладываться друг на друга.
Показать готовую фигурку
Среди поклонников танграма были Льюис Кэрролл и Наполеон Бонапарт. Считается, что именно
«танграмом» назвал игру американский шахматист, изобретатель «пятнашек» и многих других
головоломок, Самюэль Лойд.
В 21 веке самые интересные проявления танграма встречаются в дизайне мебели, одежды, ландшафтном
дизайне и архитектуре.
Ответы и решения к головоломкам
1. Папирус Ахмеса: решение
Пусть w — количество зерна для первого работника,
d — разница в количестве зерна между двумя работниками, следующими по порядку.
Составим два равенства.
5w + 10d = 100
7*(2w + d) = 3w + 9d
Остается только решить уравнение с двумя неизвестными.
Ответ:
1-ый работник = 10/6 мер зерна,
2-ой = 65/6 мер зерна,
3-ий = 120/6 (то есть 20) мер зерна,
4-ый = 175/6 мер зерна,
5-ый = 230/6 мер зерна.
Вернуться к условию.
2. Переправа: решение
Рассуждаем логически!
- Крестьянин перевозит козу (иначе потеряет часть имущества).
- Возвращается.

- Перевозит капусту (или волка), а козу увозит обратно.
- Козу оставляет на первом берегу.
- Перевозит волка (или капусту) на другой берег.
- Возвращается.
- Перевозит козу.
Вернуться к условию.
3. Печать царя Соломона: ответ
31 треугольник.
Вернуться к условию.
4. Задача Фибоначчи: решение
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …, …, …
Ответ:
233 пары.
Вернуться к условию.
5. Задача Тартальи: решение
Сам Тарталья предложил следующее решение.
Для раздела имеющихся лошадей необходимо
заимствовать еще одну, после чего их общее количество станет 18. Раздел этого количества даст 2,
6 и 9 лошадей, которых в сумме окажется 17.
Одна лошадь из 18 оказалась как бы «лишней» — это заимствованная лошадь, которую следует вернуть
владельцу после раздела имущества.
Можно решить головоломку и арифметическим способом:
пропорцию 1/2 : 1/3 : 1/9 достаточно
умножить на 18 и получится тот же результат.
Ответ:
2, 6 и 9 лошадей.
Вернуться к условию.
6. Головоломка Льюиса Кэрролла: ответ
Ниже мы изобразили 2 варианта решения. Возможно, вам удастся найти и другие.
Вернуться к условию.
7. «Безумный разрез» Гарднера: ответ
Намёк был верен. Линия действительно изогнутая.
Вернуться к условию.
8. Сингапурская головоломка: решение
Даты находятся в промежутке от 14 до 19. Числа 18 и 19 встречаются по разу. Если день рождения в
эти даты, то Бернард сразу бы сказал месяц.
Числа 18 и 19 встречаются по разу. Если день рождения в
эти даты, то Бернард сразу бы сказал месяц.
Если Шерил сказала Альфреду, что родилась в мае или июне, значит, день рождения может быть 19 мая или 18 июня. Раз Альфред точно знает, что Бернард не знает ответ, значит, речь не о мае или июне. Остаются июль или август.
В июле и августе остались даты в диапазоне от 15 до 17, а 14 встречается дважды. Если бы день рождения был 14-го, то Бернард после реплики Альфреда еще не мог бы дать точного ответа. Значит, речь не о 14-ом. Остаются 16 июля, 15 августа и 17 августа.
Если бы Шерил сказала Альфреду, что родилась в августе, то после ответа Бернарда, Альфред не мог
бы точно узнать дату рождения — ведь целых 2 даты приходятся на август.
Значит, Шерил родилась 16 июля.
Ответ:
16 июля.
Эту задачку Конгу показала племянница друга. Она же разыграла телеведущего, сказав, что головоломка предназначена для 10-летних школьников.
Дебаты о том, как решить «простую» задачку, развернулись нешуточные. Спустя 2 дня, когда большинство участников сдались, выяснилось, что задача — олимпиадная, для 14-летних школьников.
Вернуться к условию.
9. Танграм: ответ
Можно предварительно раскрасить элементы танграма и получится такой человечек:
Вернуться к условию.
Со всеми головоломками успешно справились? Великие математики и логики мира гордились бы вами!
IQ Puzzle — Фитнес для мозга! (официальный сайт производителя)
RU
Премиальные головоломки
разработка и производство головоломок
ФИТНЕС ДЛЯ МОЗГА
Премиальные головоломки
RU
IQ PUZZLE
разработка и производство головоломок
ФИТНЕС ДЛЯ МОЗГА
Премиальные головоломки
RU
IQ PUZZLE
разработка и производство головоломок
ФИТНЕС
ДЛЯ МОЗГА
Премиальные головоломки
RU
IQ PUZZLE
разработка и производство головоломок
Перейти
IQ Подписка
Закрытые продажи, решения, промокоды, скидка на пазлы 20%
Подписка на оптовые ценыЕсли у вас были планы создать головоломку из вашего логотипа, сегодня самое время!
Брендируем
Создать головоломки под заказ:
(на пример из вашего логотипа)
+7 (495) 374 97 14
brand@iqpuzzle. ru
ru
Производим
Запросить оптовые условия:
+7 (495) 374 97 14
[email protected]
Продаем
Оформить заказ по телефону:
+7 (495) 374 97 14
[email protected]
Примеры наших работ
accenture
Fujitsu & rrc
Lenovo
ЭЛТА
Росатом
Бахрушин
SWISSAM
JURO
АНТРАКС
AUTOMA
PSB
Lenovo
АЭРОДИСК
Репетиторская Империя
NORDBERG
SBI Bank
Аналитический центр Москвы
Консист
СПЕЦИАЛЬНЫЕ УСЛОВИЯ ДЛЯ РЕКЛАМНЫХ АГЕНСТВВстречайте!
Новая линейка головоломок
IQ Puzzle «Ракета»
Головоломка из 8 деталей
| Добавить в корзину |
IQ Puzzle «D»
Головоломка из 8 деталей
| Добавиьт в корзину |
IQ Puzzle «Автомобиль»
Головоломка из 6 деталей
| Добавить в корзину |
IQ Puzzle «Пьедестал»
Головоломка из 8 деталей
| Добавить в корзину |
IQ Puzzle «Тюльпан»
Головоломка из 6 деталей
| Добавить в корзину |
IQ Puzzle «К»
Головоломка из 8 деталей
| Добавить в корзину |
IQ Puzzle «Флаг»
Головоломка из 6 деталей
| Добавить в корзину |
IQ Puzzle «Луна» (коллекционный)
Головоломка из 7 деталей
| Добавить в корзину |
IQ Puzzle «С»
Головоломка из 8 деталей
| Добавить в корзину |
IQ Puzzle «Планетарий»
Головоломка из 9 деталей
| Добавить в корзину |
IQ Puzzle «N»
Головоломка из 6 деталей
| Добавить в корзину |
IQ Puzzle «Эверест»
Головоломка из 7 деталей
| Добавить в корзину |
IQ Puzzle «G»
Головоломка из 8 деталей
| Добавить в корзину |
IQ Puzzle «Джип»
Головоломка из 8 деталей
| Добавить в корзину |
IQ Puzzle «Чайник»
Головоломка из 7 деталей
| Добавить в корзину |
IQ Puzzle «Т»
Головоломка из 4 деталей
| Добавить в корзину |
IQ Puzzle «Щит»
Головоломка из 10 деталей
| Добавить в корзину |
IQ Puzzle «7»
Головоломка из 9 деталей
| Добавить в корзину |
IQ Puzzle «Корона»
Головоломка из 6 деталей
| Добавить в корзину |
Фитнес для мозга
Старая коллекция
Перейти
через ЛК дешевле
Купить IQ Puzzle
покупки через Личный Кабинет выгоднее
Бесплатная доставка
до ПВЗ
от 3000 ₽
Доставка
оперативно и в любую точку
Верхнелихоборская 8А — в день заказа.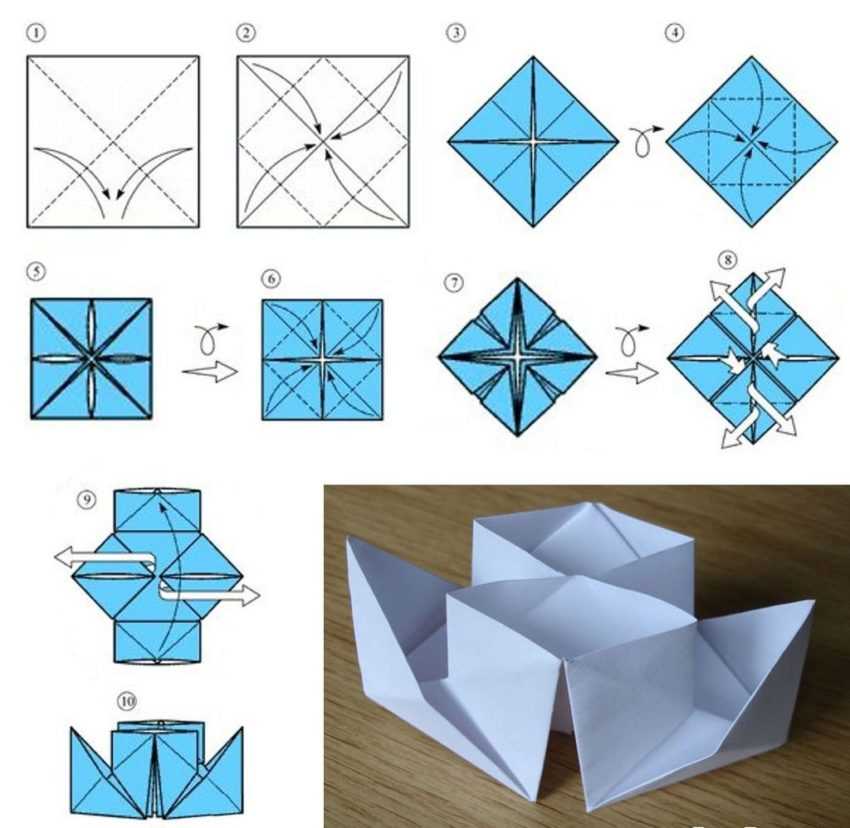
Моска/ МО/ Санкт-Петербург — на следующий день!
Остальные города России от 1 дня.
Стоимость
Самовывоз из офиса продаж, Верхнелихоборская 8А бесплатно — 0₽
Остальные ПВЗ — 199₽
Верхнелихоборская 8А — в день заказа.
Моска/ МО/ Санкт-Петербург — на следующий день!
Остальные города России от 1 дня.
Стоимость
Стандартная доставка курьером в большинство городов России — 349₽
Доставка за МКАД/ КАД — 499₽
По России от 1 дня
Международная от 6 дней
Стоимость
Быстрая доставка в любой населенный пункт. — 349₽
ТОЛЬКО ОПЛАЧЕННЫЕ ЗАКАЗЫ
Только Москва в пределах МКАД — от 2 часов
Стоимость
Доставка в течении нескольких часов — 599₽
В предпраздничные и праздничные дни — 999 ₽
Оплата
Как Вам удобно
Любым существующим способом дистанционной оплаты
Картой или наличными
(кроме доставки почтой и ПВЗ, такие заказы должны быть оплачены до отправки)
Для ИП и Юридических лиц (заказы от 5000₽)
Наши друзья
Хотим поделиться с Вами нашими фантастическим друзьями
Jooble
Агрегатор вакансий
@legkosnatali
ГУРУ ОТНОШЕНИЙ
Головоломки для детей ✅ Блог IQsha.
 ru
ruКак эффективно и без стресса обучать детей любого возраста? Конечно, с помощью игр! Всё, что проходит весело и увлекательно, даётся намного легче. Особенно это касается маленьких детей, которые не могут сосредоточиться и долго удерживать внимание, быстро устают и отвлекаются, а ещё их попросту сложно удержать на одном месте.
Поэтому для дошкольников важны не столько конкретные знания, сколько развитие познавательных процессов: памяти, внимания, воображения, мышления. Чем веселее ребёнку, тем легче и быстрее он будет развиваться!
Разнообразить обучение и сделать его увлекательным помогут головоломки! Они полезны не только для отработки нужных навыков, но и для умения находить нестандартные решения, проявлять смекалку и сообразительность.
Какие есть игры-головоломки?
Существует множество различных детских головоломок. Их можно поделить на 4 основные группы:
1. Предметные головоломки
Создаются из любых подручных средств: спичек, деревянных палочек, верёвок, пластиковых крышек и других материалов.
Дети очень любят такие игры, потому что предметы можно трогать, перекладывать в разные места, не боясь сломать или испортить, а ещё можно проявить фантазию и придумать новые правила и решения.
Самая популярная предметная головоломка — это игра со спичками. По правилам дети перекладывают спички так, чтобы получилась другая фигура, число или рисунок.
Также малышам нравятся верёвочные головоломки. Задача проста — распутать шнурок или ленточку, которые завязаны несколько раз, и “освободить” предмет. Ещё один вариант игры — завязать сложные узлы по схеме либо продеть шнурок через дырочки в картоне так, чтобы получилась новая фигура.
2. Механические головоломки
Их ещё часто называют “объёмными”. Такие головоломки не нужно делать самим. Но как и предметные, их можно трогать, переставлять, собирать или разъединять — всё зависит от задачи игры.
Самая известная механическая головоломка — это кубик Рубика. Услышав это название, большинство сразу представит себе объёмный квадратный предмет с разноцветными гранями. Эта головоломка учит просчитывать свои действия на несколько шагов вперёд, проявляя терпение и смекалку.
Услышав это название, большинство сразу представит себе объёмный квадратный предмет с разноцветными гранями. Эта головоломка учит просчитывать свои действия на несколько шагов вперёд, проявляя терпение и смекалку.
Головоломки-башни (Вавилонская башня, Варикон, Фонарик)
Эти игры-головоломки по своим задачам и оформлению очень похожи на кубик Рубика. В пластмассовом цилиндре или конусе составляется рисунок из разноцветных шариков. Вращая оси башни и перемещая шарики, нужно добиться одного цвета вдоль всего вертикального ряда.
«Змейка» — упрощённый вариант кубика Рубика. Это длинная пластиковая полоска с деталями, которые вращаются в разных направлениях, позволяя собрать множество разнообразных фигур. “Змейка” развивает воображение и пространственное мышление.
«Пятнашки» — не менее известная игра. Она состоит из квадратной коробочки, внутри которой находятся одинаковые квадратные костяшки с числами. Одно поле внутри коробки всегда остаётся пустым. Задача игрока — расставить кости по номерам, перемещая их по полю. Можно усложнить игру, сократив количество возможных перетаскиваний.
Задача игрока — расставить кости по номерам, перемещая их по полю. Можно усложнить игру, сократив количество возможных перетаскиваний.
Танграм. Цель игры — собрать из набора геометрических фигур разные картинки, выкладывая их рядом и не помещая друг на друга. Если нет готовых фигур, их можно сделать самим из картона, плотной цветной бумаги или фоамирана.
Пазлы. Это и обычные картонные пазлы, и 3D-пазлы — мелкие полупрозрачные детали, из которых можно собрать объёмную фигуру или предмет.
В последние годы особую популярность получил магнитный конструктор — набор деталей в форме шариков, квадратов, треугольников и многоугольников. Благодаря магнитам можно построить множество объёмных фигур. Такая игра развивает пространственное мышление, наблюдательность и воображение.
3. Печатные головоломки
К этой группе относятся кроссворды и сканворды, судоку, ребусы и другие игры, для решения которых нужно записывать буквы, цифры или нужные символы в подходящие ячейки и поля.
Головоломки-лабиринты любят многие дети. Ведь как интересно искать путь от точки А до точки Б по различным запутанным дорожкам и лабиринтам! Плюс таких головоломок в многообразии: они есть на любой возраст, степень сложности, размер и форму.
Ребусы — это загадки, в которых слова, которые нужно определить, даются в виде рисунков с отдельными буквами и знаками.
Ребусы можно использовать при обучении счёту, грамоте, кругозору и других предметов для закрепления знаний. Узнайте больше о математических ребусах в нашей статье «Математические ребусы с ответами».
Судоку популярны не менее ребусов. Что же это такое? Это головоломка-пазл, представляющая собой квадрат (9×9), который разделён на более мелкие ячейки. В игровом поле получается 81 клетка, внутри которых расставлены разные числа. Задача игрока — заполнить пустующие клетки числами так, чтобы каждое из них встречалось в строке и столбце один раз. Судоку отлично развивают навыки счёта, внимания и памяти и любимы не только детьми, но и взрослыми.
4. Устные головоломки
Сюда входят классические загадки, шарады и «да-нетки» — игры, в которых нужен словарный запас и эрудиция, но не требуются подручные материалы.
Выполните развивающие упражнения от Айкьюши
Не переживайте, если ребёнок не знает много слов, такие головоломки как раз тренируют слух, улучшают грамотность, развивают память и сообразительность.
Загадки — самые распространенные устные головоломки. Каждый ребёнок хоть раз слышал какую-нибудь загадку и пытался её решить. Устройте с малышом марафон по разгадыванию задачек от Айкьюши из нашей новой статьи «Логические загадки для детей».
Шарады — это разновидность загадок, в которых неизвестное слово разбивают на слоги и каждому из них придаётся собственное значение. Перед игроком ставится задача — отгадать целое слово с помощью слогов. Чаще всего шарады бывают в стихотворной форме.
Вот как много существует игр-головоломок для детей! Но как выбрать подходящую? Ориентируйтесь на возраст ребёнка и его знания. Вряд ли пятилетке будет под силу освоить судоку или проверить логику в шарадах.
Вряд ли пятилетке будет под силу освоить судоку или проверить логику в шарадах.
Головоломки для детей 2-4 лет
Для самых маленьких лучше всего подойдут крупные пазлы с домашними или дикими животными, как деревянные, так и картонные, кубики, и всевозможные пирамидки и сортеры.
Делайте упор на яркие и большие картинки, обилие цветов и деталей, которые хочется рассматривать и трогать — они привлекут внимание малыша и подогреют его интерес к игрушкам.
Головоломки для детей 5-6 лет
Эти головоломки уже сложнее, потому что дошкольники учатся анализировать и сравнивать предметы, становятся более усидчивыми и внимательными. Многие уже к этому возрасту умеют читать и считать.
Предложите более сложные пазлы, включая 3D-пазлы, различные головоломки-лабиринты, ребусы и шарады. Дети 5-6 лет с удовольствием играют с деревянными и магнитными конструкторами, прекрасно справляются с танграмом, дженгой (башня из деревянных брусочков) и схожими играми на баланс.
Головоломки для детей 7–8 лет
Школьники лучше анализируют и обобщают, строят логические цепочки, а значит, и более усидчивы. Дети 7-8 лет могут сохранять сосредоточенность намного дольше подготовишек, что позволяет им собирать пазлы из 1000 и более деталей.
Также в этом возрасте отлично подойдут кубик Рубика, “Змейка”, “Пятнашки”, головоломки-башни и игры со спичками.
Используйте и печатные головоломки: кроссворды, сложные запутанные лабиринты, ребусы, можно предложить судоку — все они будут полезны в развитии логического мышления, навыков счёта и расширении словарного запаса.
Головоломки для детей 10 лет
Детям этого возраста подойдут те же игры, что и для 7-8-летних, но с более высоким уровнем сложности.
Попробуйте популярные сейчас деревянные конструкторы-головоломки, лабиринты и тетрис со множеством деталей — так вы сможете надолго увлечь своих школьников.
Ученики 3–4 класса обладают более развитым абстрактным мышлением, поэтому легче и с интересом справляются с математическими ребусами и логическими задачками, 3D-головоломками.
Головоломки для детей 12 лет
Они отличаются ориентацией на общение. Подростки стараются постоянно быть в среде сверстников, поэтому в этом возрасте популярность набирают настольные и логические командные игры и увлекательные квесты и стратегии: “Морской бой”, “UNO”, “Activity”, “Крокодил”, “Мафия”, различные детективные головоломки и множество других.
Не менее интересны и лабиринты, пазлы, кроссворды, шарады, с которыми дети 12 лет так же легко справляются. Главное, найдите то, что сможет увлечь ребёнка — тогда успех будет гарантирован!
Выбирая подходящую головоломку, следует помнить золотое правило – задача для игрока должна быть немного сложнее, чем его возможности. Это условие обеспечивает постоянный интеллектуальный рост. Однако старайтесь не переусложнить, иначе интерес к игре может угаснуть вовсе.
И самое важное – головоломки должны в первую очередь приносить радость и положительные эмоции. Помните об этом и верьте в своих детей – у них обязательно всё получится.
Рекомендуем вам также нашу статью «Кроссворды для детей».
Екатерина Дорошина,
педагог, методист IQsha, автор статей и упражнений
Чествуем игривое волшебство Джона Хортона Конвея / Хабр
Всем привет. В преддверии старта продвинутого курса «Математика для Data Science», подготовили для вас перевод статьи, которая была написана в память о легендарном математике Джоне Хортоне Конвее.
Предлагаем вам развлечь себя, решая числовую головоломку, геометрический пазл, а также играя в игру со случайными узорами, вдохновленные игривым гением легендарного математика.
Легендарный математик Джон Хортон Конвей, умерший в апреле от COVID-19, по-детски искренне увлекался изобретением головоломок и игр. Он провел подробный анализ многих головоломок, таких как кубик Сома, пасьянс с колышками и солдаты Конвея. Он изобрел «алгоритм судного дня» (быстрый метод вычисления дня недели в вашей голове — Конвей мог сделать это менее чем за две секунды) и бесчисленное количество игр, в том числе игра ”Рассада” (Sprouts) и знаменитую игру “Жизнь”, которая положила начало изучению клеточных автоматов.
Большая часть серьезных математических работ Конвея также проистекает из его слабости к математическим играм. Он внес оригинальный вклад в теорию групп (Решётка Лича, гипотеза чудовищного вздора), многомерную геометрию, тесселяцию (мозаику), теорию узлов, теорию чисел (сюрреалистические числа), алгебру, математическую логику и анализ.
В этом месяце мы чествуем игривый гений известного британского математика двумя головоломками и исследовательской игрой. Сначала мы поиграем с числовой головоломкой, изобретенной Конвеем, которая без лишней скромности является воплощением самого совершенства. Затем насладимся геометрическим пазлом, относящимся к некоторым из его наиболее визуально доставляющих работ. И наконец, мы погрузимся в игру с открытым финалом, созданную читателем Quanta, которая напоминает культовую игру “Жизнь” Конвея.
Головоломка 1: Цифровое совершенство
Существует загадочное десятичное 10-значное число abcdefghij. Все его цифры разные, и они обладают следующими свойствами:
a делится на 1
ab делится на 2
abc делится на 3
abcd делится на 4
abcde делится на 5
abcdef делится на 6
abcdefg делится на 7
abcdefgh делится на 8
abcdefghi делится на 9
abcdefghij делится на 10
Какое это число?
Прежде чем приступить к решению этой головоломки, уделите минутку, чтобы полюбоваться абсолютным совершенством ее формы. Он излагается совершенно естественно, без малейших произвольностей или ухищрений. Прочитав первые два условия, вы точно знаете, в чем будет заключаться остальная часть головоломки. А когда этот естественный набор условий результирует в уникальном ответе, это просто восхитительно. Для меня, как создателя головоломок, эта головоломка с подстановкой цифр вызывает то же чувство, которое Моцарт внушал Эйнштейну, который сказал, что музыка Моцарта «была настолько чистой, что казалось, что она всегда присутствовала во Вселенной, ожидая, чтобы ее открыл мастер. » Только такой численно одаренный человек, как Конвей, мог уловить такую совершенную платоническую форму из райского сада головоломок!
Он излагается совершенно естественно, без малейших произвольностей или ухищрений. Прочитав первые два условия, вы точно знаете, в чем будет заключаться остальная часть головоломки. А когда этот естественный набор условий результирует в уникальном ответе, это просто восхитительно. Для меня, как создателя головоломок, эта головоломка с подстановкой цифр вызывает то же чувство, которое Моцарт внушал Эйнштейну, который сказал, что музыка Моцарта «была настолько чистой, что казалось, что она всегда присутствовала во Вселенной, ожидая, чтобы ее открыл мастер. » Только такой численно одаренный человек, как Конвей, мог уловить такую совершенную платоническую форму из райского сада головоломок!
Вы, конечно, можете решить эту головоломку, совершив поиск методом перебора с помощью компьютера, но это совсем не обязательно. Я призываю вас сделать это с помощью карандаша и бумаги. Все головоломки с подстановкой цифр такого типа могут быть решены с помощью двухэтапного процесса, знакомого тем, кто решал судоку: сначала вы устанавливаете отношения между цифрами, что сужает возможности, а затем вы проводите систематический поиск неизвестных цифр методом проб и ошибок. Здесь вам следует использовать уловки, которым вы научились в школе, чтобы определить, делится ли число на данную цифру. Если вы выжмите максимум из условий головоломки, у вас не останется слишком много кандидатов для поиска методом проб и ошибок.
Здесь вам следует использовать уловки, которым вы научились в школе, чтобы определить, делится ли число на данную цифру. Если вы выжмите максимум из условий головоломки, у вас не останется слишком много кандидатов для поиска методом проб и ошибок.
Если же вы хотите усложнить себе задачу, попробуйте решить эту головоломку полностью в своей голове. В конце концов, Конвей был известен тем, что решал математические задачи «голыми руками». Это требует большого внимания и терпения, но я уверяю вас, что это возможно.
Головоломка 2: Двойственные треугольники
Есть равнобедренный треугольник, который содержит угол равный x градусов. Отношение двух сторон разной длины равно y.
Оказывается, не один, а целых два разных треугольника имеют одинаковые значения x и y!
Каковы значения x и y для этих двух равнобедренных треугольников? Что особенного в этих треугольниках и какое отношение они имеют к творчеству Конвея?
Для нашей последней головоломки вам снова понадобятся бумага и карандаш. Будет даже лучше, если вы возьмете несколько листов в клетку. Это игра, которая погрузит вас в образ мышления Конвея — вы будете рисовать небольшие диаграммы и создавать различные структуры, как это делал он в своих играх “Рассада” и “Жизнь”. Наша игра, которая создает структуры, подобные полимино, была предоставлена Quanta читателем по имени Jona Raphael.
Будет даже лучше, если вы возьмете несколько листов в клетку. Это игра, которая погрузит вас в образ мышления Конвея — вы будете рисовать небольшие диаграммы и создавать различные структуры, как это делал он в своих играх “Рассада” и “Жизнь”. Наша игра, которая создает структуры, подобные полимино, была предоставлена Quanta читателем по имени Jona Raphael.
Головоломка 3: Случайные волосатые узоры
У вас есть бесконечная плоскость, на которой вы размещаете квадратные тайлы. Вы должны поочередно добавлять новые тайлы случайным образом, так чтобы каждый новый тайл имел по крайней мере одно общее ребро с ранее размещенным тайлом. Вероятность размещения тайла в любом конкретном месте пропорциональна количеству ребер ранее размещенных тайлов, которые граничат с этим местом.
Рассмотрим два примера:
Если у вас пока есть только один тайл, то второй тайл имеет равную вероятность оказаться на севере, юге, востоке или западе от исходного тайла.
Если у вас есть кольцо из восьми тайлов, то есть 12 позиций вокруг внешних сторон кольца и одна позиция в середине, и все они действительны для размещения следующего тайла.
 Для той, что посередине, вероятность получит тайл в четыре раза больше, чем для любой внешней подходящей позиции, потому что у нее четыре общих края с ранее размещенными тайлами, а не только одна.
Для той, что посередине, вероятность получит тайл в четыре раза больше, чем для любой внешней подходящей позиции, потому что у нее четыре общих края с ранее размещенными тайлами, а не только одна.
Мы оцениваем “волосатость” (H, потому что в оригинале используется “hairiness”) или “внешность” любой конфигурации как количество открытых ребер тайлов, деленное на количество тайлов. Например:
Для одного тайла на плоскости H = 4 ребра ÷ 1 тайл = 4.
Для кольца из восьми тайлов H = 16 ребер ÷ 8 тайлов = 2.
Для ряда из восьми тайлов H = 18 ребер ÷ 8 тайлов = 2,25.
Величину, обратную H, можно назвать “внутренностью” или компактностью конфигурации.
Цель этой игры — чистое исследование. В отличие от большинства игр, к которым мы привыкли, исключая игру «Жизнь» Конвея, это «бесконечная игра без игрока», как Конвей описывал свое творение. Для меня динамика нашей игры напоминает то, как взрослые дети уравновешивают свое желание оставаться рядом со своими родителями с желанием действовать самостоятельно. Параметр H является мерой того, насколько они расходятся, оставаясь при этом в минимальном контакте, в то время как его обратная величина, внутренность, является мерой того, насколько они сплачиваются.
Параметр H является мерой того, насколько они расходятся, оставаясь при этом в минимальном контакте, в то время как его обратная величина, внутренность, является мерой того, насколько они сплачиваются.
(В этом видео 2014 года Numberphile(числофил) Джон Конвей рассказывает, как он создавал игру “Жизнь”.)
Вот несколько вопросов, которые направят ваше исследование этого квадратного мира.
Новый тайл может быть помещен рядом с одним ребром (касаясь только одного другого тайла), в углу (касаясь двух), внутри буквы «U» (касаясь трех) или внутри отверстия (касаясь всех четырех). Как каждое размещение влияет на количество открытых ребер в новой конфигурации (узоре)?
Каковы минимальные и максимальные значения H и каким типам тайловых узоров они соответствуют? Можете ли вы придумать приблизительную или точную формулу для максимального и минимального значений H по мере увеличения количества тайлов (n)?
Какое ожидаемое значение H (приблизительное или точное) для данного значения n?
Найдите наименьший узор, которая является «сбалансированным», так что добавление следующего тайла с такой же вероятностью увеличивает количество открытых ребер, как и уменьшает его.
 Сможете ли вы найти симметричный узор, обладающую этим свойством?
Сможете ли вы найти симметричный узор, обладающую этим свойством?Найдите наименьший узор, для которой ожидаемое значение H остается неизменным после добавления еще одного тайла. Для какого следующего наименьшего по количеству тайлов узора справедливо это свойство?
Вот и все для начала. Теперь вы можете исследовать эту игру самостоятельно. Попробуйте найти ответы на несколько новых интересных вопросов. Может быть, вы найдете новую структуру (пожалуйста, поделитесь изображения интересных узоров!) Или даже докажете теорему. И пока вы это делаете, предложите название этой игре.
Играйте — подарите духу Конвея улыбку!
Узнать подробнее о курсе.
9 точек 4 линии
Если вы попали на эту страницу, то вы наверняка уже пытались решить «тест 9 точек», а именно соединить девять точек четырьмя прямыми линиями не отрывая ручки от листа бумаги. Если у вас не получилось разгадать эту головоломку, не отчаивайтесь. На этой странице вы сможете найти несколько решений этой знаменитой непростой задачи о девяти точках, которые напрягли умы уже многих тысяч, если не миллионов людей.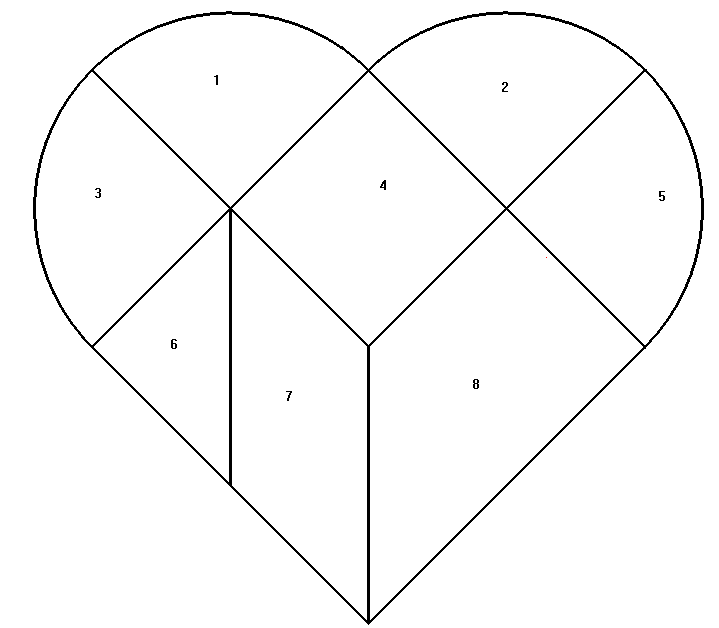
Оглавление:
- Условие задачи
- Верное решение
- Творческий подход к головоломке
- Другие решения
- Отзывы и комментарии
Условие задачи
Условие: нужно соединить нарисованные девять точек четырьмя прямыми линиями не отрывая ручки от листа бумаги.
ОБНОВИТЬ РИСУНОК
Условие: нужно соединить нарисованные девять точек четырьмя прямыми линиями не отрывая ручки от листа бумаги.
Эта задача является не такой уж простой, как может показаться. Чтобы ее решить нужно думать нестандартно и применить свое творческое мышление, иначе ничего не получится. Если пытаться действовать в лоб начать соединять все точки стандартными линиями, то вы можете потратить уйму времени и так и не решить задачу девяти точек. Наше стандартное мышление, которому нас учат в школе, направляет нас искать решение, опираясь лишь на шесть типичных линий: 4 стороны квадрата и 2 его диагонали. Большинству людей кажется, что решение головоломки о 9 точках должно лежать именно в этих рамках. Но его там нет. Его даже не найти если подключить еще 2 линии между центрами сторон квадрата:
Большинству людей кажется, что решение головоломки о 9 точках должно лежать именно в этих рамках. Но его там нет. Его даже не найти если подключить еще 2 линии между центрами сторон квадрата:
Вообще между всеми девятью точками можно провести всего 20 прямых линий: 4 стороны квадрата; 2 диагонали; 6 линий, соединяющих центры сторон большого квадрата; 8 линий соединяющих центры сторон большого квадрата с его углами. Как нарисовать все отрезки, соединяющие наши 9 точек, показано на рисунке ниже:
Но, даже используя эту схему, невозможно найти 4 линии, которыми можно было бы соединить все девять точек, не отрывая руки.
Верное решение «теста 9 точек»
Решение этой головоломки лежит несколько шире нашего стандартного восприятия задачи. Для того, чтобы самостоятельно найти верный подход вспомните, что:
- Через любые 2 точки можно провести только одну прямую линию.
- Прямая линия – это не отрезок и, следовательно, нам не обязательно ограничиваться при рисовании линий нашими девятью синими кружками.

Таким образом, давайте попробуем продолжить линии за пределы, ограничивающего нас до недавнего времени квадрата. Тут видно, что область нашего поиска значительно увеличилась. Потрудившись немного можно прийти к одному из правильных решений.
Последовательность соединений девяти точек четырьмя линиями:
- Для начала проведите линию, соединяющую точку №1 и точку №7, через точку №4. Не останавливайте движение и рисуйте дальше примерно столько, сколько от точки №4 до точки №7.
- Далее двигайтесь по диагонали направо-вверх, соединяя точки №8 и №6. Не останавливайтесь на точке №6 и продолжайте линию до мысленной прямой, проходящей через верхнюю сторону нашего квадрата.
- Нарисуйте линию справа налево последовательно через точки №3, №2 и №1. Остановитесь на точке №1.
- Теперь проведите финальный отрезок через точки №1, №5 и №9. Все 9 точек, и правда, соединены четырьмя линиями, как и требовалось в условии задачи.
Другие варианты. Этот способ не единственный, начинать можно от любого угла и двигаться одном из двух направлений. На сайте 4brain таких вариантов решения задачи «9 точек 4 линии» представлено минимум 12:
Этот способ не единственный, начинать можно от любого угла и двигаться одном из двух направлений. На сайте 4brain таких вариантов решения задачи «9 точек 4 линии» представлено минимум 12:
Только подумайте, задача, которую многие никак не могут решить, имеет 12 способов решения. Также смотрите упрощенный вариант этой задачи: как соединить 4 точки тремя линиями, чтобы линии замыкались в целую фигуру.
Творческий подход в этой головоломке
Большинство людей, которые решали эту задачу, так и не смогли выбраться за рамки стандартного мышления, которое в данном тесте выражено квадратом, образованным девятью точками. Нам комфортно смотреть на любую жизненную задачу прямо, наиболее просто. С другой стороны, человек может потратить много времени и сил для того, чтобы, используя стандартный подход, найти верное решение, когда это решение лучше искать, изначально подойдя к процессу творчески.
В нашей жизни мы часто сталкиваемся с такими задачами о «девяти точках и четырех линиях», и для того, чтобы их решать развивайте свое креативное мышление, в том числе и при помощи нашего тренинга. Ведь задача о 9 точках имеет и другие решения (об этом читайте дальше).
Ведь задача о 9 точках имеет и другие решения (об этом читайте дальше).
Другие способы решения
Изменив наш фрейм или применив латеральный разрыв можно найти и другие варианты решения этой задачи. Например, метод гиперболизации при создании латерального разрыва может нас привести к мысли, что никто не уточняет, что в задаче должны применяться стандартные условия геометрии (о бесконечной малости точек и бесконечной тонкости линий). Пусть наша линия будет настолько широкой, что сможет сразу пересекать несколько точек по своей ширине. Тогда мы не то что 4-мя линиями сможем соединить все 9 точек, а даже одной.
Кроме того, даже в нашем изображении 4-х точек, которое дано в нашем условии головоломки о 9 точках, сами точки-кружки достаточно большие, чтобы можно было их соединить 3-мя линиями вот так:
А может вообще не стоит ограничиваться двухмерным пространством или использовать концепцию искривления пространства. Также мы можем акцентировать внимание на фразу «не отрывая ручки от листа бумаги», и просто положив ручку на бок передвинуть ее и таким образом нарисовать просто 3 параллельных линии.
Евгений Буянов
← Творческие игры Друдлы →
Easy Paper Puzzle Game for kids
Если вам интересно, как сделать пазл с картинками для детей своими руками, вы обратились по адресу.
Здесь мы покажем вам, как сделать игру-головоломку из бумаги, которая займет ваших детей на несколько часов.
Это простая игра, которую можно сделать дома, используя бумагу и несколько основных материалов. Итак, давайте посмотрим, как вы можете сделать это дома.
Прежде чем приступить к уроку, я был бы очень признателен, если бы вы заглянули на наш канал на Youtube и подписались на него. Каждую неделю мы добавляем простые уроки по рукоделию.
Некоторые из ссылок в этом посте являются партнерскими ссылками, что просто означает, что если вы что-то купите, я получу небольшую комиссию БЕЗ дополнительных затрат для вас.
Необходимые материалы:
Для сборки этой бумажной головоломки вам понадобится
– Лист оригами ИЛИ любой квадратный лист размером 15 см
– Белая бумага
– Карандаш, линейка, ножницы и клей
– Черный маркер
– Масляная пастель или цветные маркеры
Как сделать игру-головоломку с картинками, шаг за шагом
Шаг 1: Складывание пазла
1a. Возьмите квадратный лист размером 15 см. Здесь мы используем лист оригами. Вы можете использовать цветную бумагу, используемую для поделок, или даже белую бумагу.
Возьмите квадратный лист размером 15 см. Здесь мы используем лист оригами. Вы можете использовать цветную бумагу, используемую для поделок, или даже белую бумагу.
1б. Сложите бумагу по диагонали (справа налево), чтобы соединить противоположные углы и сделать складку. Если вы используете лист оригами, убедитесь, что цветная часть бумаги находится внутри во время складывания.
1с. Развернуть.
1д. Теперь снова сложите бумагу по диагонали (слева направо), на этот раз, чтобы соединить два других угла. Сделайте складку.
1д. Сделав складку, разверните бумагу. Теперь нам нужно сложить каждый угол в центр бумаги, сделать складку и развернуть .
1ф-1ч. Здесь мы не показали складывание всех 4 углов, так как это полоскание и повторение. Но я надеюсь, что вы поняли идею. Опять же, вам нужно сделать следующее:
Сложите каждый угол к центру, сделайте складку, а затем разверните. Сделайте это со всеми 4 углами, а затем переходите к следующему шагу.
1и. На этом этапе мы складываем бумагу к центру по горизонтали. Имейте в виду, что бумага должна быть сложена точно по центру. Вы можете использовать складки, которые вы сделали ранее, в качестве эталона.
1к. Другой край также загибаем к центру.
1к. Разверните бумагу.
1л. Теперь повторите те же шаги (1i и 1j) с другой стороны.
1м. Согните параллельные края к центру и сделайте складку. Теперь держите бумажную головоломку вертикально, как показано на рисунке, и переходите к шагу 1n.
1н. После сгибания краев по горизонтали, нам нужно сделать следующее, чтобы сделать бумажную головоломку, — это сложить бумагу, сделав складки, которые мы сделали ранее в качестве ориентира.
1р. Начните с удержания бумаги на месте одной рукой и складывания другой рукой.
Медленно согните верхнюю часть бумаги к центру.
Проткните одним пальцем от середины задней стороны, направляя его к центру . Когда вы сделаете это, вы увидите, как бумага движется по складкам, которые мы сделали ранее.
1 шт. Середина верхнего края теперь согнута к центру. Вы можете видеть, как он касается центра.
1 кв. На рисунке 1q вы можете видеть две створки, направленные вверх. На следующем шаге мы собираемся сгладить их.
1р. Опустите обе створки, как показано на рисунке выше.
1с. Поверните бумажную головоломку на 180 градусов и повторите те же шаги (1n-1r) с другой стороны.
Шаг 2: Нарисуйте картинки
На втором этапе создания бумажной головоломки мы нарисуем 3 картинки, которые должны быть наклеены на бумажную головоломку.
Картинки могут быть любыми — мультяшными фигурками, животными, природой и т.д. Здесь мы нарисовали три кавайных фигурки.
2а. Возьмите лист белой бумаги. И держите квадратную фигуру бумажного пазла, которую мы только что сделали, поверх бумаги.
Обведите контур головоломки на белом листе. Это нужно, чтобы нарисовать картинки внутри квадратной формы и убедиться, что они вписываются в головоломку.
2б. Нарисуйте фигуры внутри квадрата, который мы только что взяли. Нарисуйте еще две фигуры такого же размера и раскрасьте их. Вырежьте фигурки.
Нарисуйте фигуры внутри квадрата, который мы только что взяли. Нарисуйте еще две фигуры такого же размера и раскрасьте их. Вырежьте фигурки.
Шаг 3. Создание бумажной головоломки
3a. На этом этапе мы приступаем к сборке головоломки.
Возьмите вырезанные фотографии. Возьмите первую картинку и приклейте ее на бумажный пазл.
При вставке изображения убедитесь, что отверстие бумаги проходит под ним вертикально.
Теперь будем резать отверстие. Убедитесь, что вы не отрезали слишком много. Режьте только до того момента, когда вы сможете полностью открыть створки.
3б. Откройте створки и вы увидите секцию с четырьмя отверстиями.
Теперь сделайте вторую картинку и приклейте ее на этот участок. Как мы сделали с последней картинкой, прорежьте отверстия.
3с. Помните, что есть четыре отверстия, так что разрежьте все четыре из них. После разрезания откройте все створки, и вы доберетесь до третьей секции.
3д. Наклейте третью и последнюю картинку на следующую секцию и сделайте два надреза вдоль отверстий.
Наклейте третью и последнюю картинку на следующую секцию и сделайте два надреза вдоль отверстий.
Вот и бумажная головоломка готова.
Открывайте створки по-разному и делайте из этого игру.
Надеюсь, вам понравится собирать эту бумажную головоломку своими руками. Дайте мне знать о вашем опыте в комментариях ниже.
Видеоурок по созданию бумажной головоломки
Если у вас есть какие-либо сомнения относительно какого-либо шага, посмотрите видеоурок по созданию бумажной головоломки на нашем канале Youtube. Каждую неделю мы добавляем новые и простые уроки по рукоделию.
Мы будем очень признательны, если вы подпишетесь и поможете нам расти. Заранее спасибо!
Еще уроки по изготовлению из бумаги для детей:
– Как сделать подсолнух из бумаги шаг за шагом
– Простые летние поделки из эскимо для дошкольников и старше (с бесплатным шаблоном)
– Простая прыгающая лягушка из бумаги шаг за шагом
Нравится этот пост? Сохраните на потом!
Как сделать пазл из бумаги, складывающийся гармошкой — Constructed Adventures
Всем привет! Crafter снова здесь, чтобы показать вам новый забавный гамбит, который вы можете использовать в своих приключениях! Я называю эту головоломку «Головоломка с аккордеоном». Это простая, но эффективная головоломка, которую можно включить в свои приключения, и она обязательно произведет впечатление на вашу семью и друзей!
Это простая, но эффективная головоломка, которую можно включить в свои приключения, и она обязательно произведет впечатление на вашу семью и друзей!
Недавно я сделал эту головоломку для друга, чтобы использовать его в своих приключениях. Игрокам нужно было дать актеру пароль, и они получили печатную версию следующей головоломки:
.Это похоже на случайный красивый узор, верно? Что ж, если бы игроки следовали подсказкам, они бы получили это!
Затем, если бы они повернули его на другую сторону, как подсказала им подсказка, они бы увидели это:
Дать им указание «Дай пять продавцу»!
Как я достиг этого волшебства? Это просто требует некоторого размышления и организации форм!
Как сделать пазл
Чтобы сделать пазл своими руками, вам понадобится компьютерная программа редактирования, например Photoshop или Adobe Illustrator, и принтер.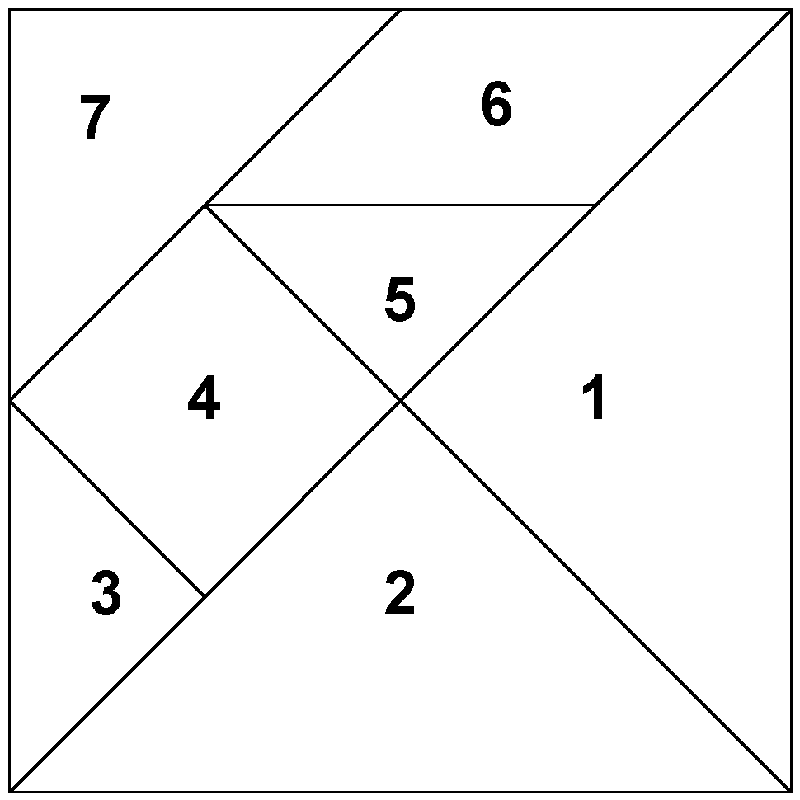 Для тех, кто не хочет тратить деньги, я настоятельно рекомендую версию этих программ с открытым исходным кодом; GIMP и Inkscape!
Для тех, кто не хочет тратить деньги, я настоятельно рекомендую версию этих программ с открытым исходным кодом; GIMP и Inkscape!
Для этой головоломки не нужно использовать треугольники; вы можете использовать практически любую форму, если они хорошо выстраиваются в линию/мозаику. Я видел этот эффект с кругами, квадратами и даже восьмиугольниками! Просто помните, чем больше ваши фигуры, тем сложнее сделать сообщение. Я использовал треугольники, потому что мог уместить их много на маленьком пространстве, и это было более тематическим для общего приключения.
Чтобы добиться этого эффекта, вам нужно представить свое сообщение в терминах пикселей; как в 8-битном. Сколько элементов каждой формы (пикселя) вам понадобится, чтобы написать свое сообщение? Какой длины должны быть ваши линии фигур? Не забудьте спланировать заранее, чтобы это могло поместиться на стандартном листе бумаги, чтобы его было легко распечатать.
Также имейте в виду, что эта головоломка работает, только если сообщение очень короткое; Я пропустил «gh» в «высоком», потому что это не подходило. Вам нужно будет оставить максимум 4-7 символов с каждой стороны.
Вам нужно будет оставить максимум 4-7 символов с каждой стороны.
Шаги к созданию головоломки
Зажим пустой головоломки «Гармошка».
Выясните, сколько фигур вам нужно в каждой строке и сколько строк вам понадобится, чтобы составить сообщение.
При работе в выбранной компьютерной программе убедитесь, что в настройках установлен размер стандартного листа бумаги (8,5 x 11 дюймов или 22 x 28 см).
Заполните свой лист выбранными контурами фигур, поместив линию между рядами (я использовал пунктирные линии, потому что они означают складывание), чтобы ваши игроки могли сгибаться, как показано в примере слева.
Это создаст строки для вашего сообщения. Ваше сообщение будет отображаться только при правильном складывании. Нужно спланировать так, чтобы «пикселей» для сообщения было помещается в каждую вторую строку .
 Это будет работать для одностороннего сообщения. Если вы хотите сделать двухстороннее сообщение (например, то, что было выше), вам нужно помнить, что вы собираетесь повернуть головоломку на 180 градусов (сообщение будет выглядеть вверх ногами по сравнению с первой частью) и что ваша вторая часть появится в строках, которые вы не использовали для первой части.
Это будет работать для одностороннего сообщения. Если вы хотите сделать двухстороннее сообщение (например, то, что было выше), вам нужно помнить, что вы собираетесь повернуть головоломку на 180 градусов (сообщение будет выглядеть вверх ногами по сравнению с первой частью) и что ваша вторая часть появится в строках, которые вы не использовали для первой части.
Раскрась пазл
Чистый лист, который я раскрасил вручную, чтобы выяснить, какие треугольники нужно заполнить.
Теперь пришло время выяснить, какие цвета вы хотите использовать; имейте в виду, что слишком много цветов будут слишком отвлекать, и ваше сообщение будет потеряно. Я выбрал цвета, чтобы соответствовать теме события, для которого использовалась эта головоломка. Вы хотите, чтобы один жирный цвет был вашим «цветом сообщения» , а затем другие цвета были цветом, который может легко исчезнуть на фоне. Как только вы разобрались с ними, пришло время заполнить ваши фигуры. Что сработало для меня, так это распечатать весь лист с пустыми контурами, сложить его, а затем раскрасить сообщение в том виде, в котором вы хотите. Как только вы это сделаете, вы можете раскрасить свое сообщение в программе. Я снял контуры, когда раскрашивал фигуры в своем пазле.
Как только вы разобрались с ними, пришло время заполнить ваши фигуры. Что сработало для меня, так это распечатать весь лист с пустыми контурами, сложить его, а затем раскрасить сообщение в том виде, в котором вы хотите. Как только вы это сделаете, вы можете раскрасить свое сообщение в программе. Я снял контуры, когда раскрашивал фигуры в своем пазле.
Зажим складного пазла частично заполнен. Четные строки — это место, где находится сообщение, и вы можете увидеть начало сообщения с заполненными строками (HI F из HI FIVE)
Маскировка сообщения
Теперь пришло время замаскировать ваше сообщение. Если вы делаете одностороннее сообщение, вы можете поместить часть «цвета сообщения» в ряды, которые вы не используете, потому что, когда они складывают пазл, они не увидят его. Это предотвратит легкое чтение сообщения и даст вам возможность создать интересный случайный узор. Если вы делаете двустороннее сообщение, просто убедитесь, что вы держите свои ряды прямыми (четные ряды — это первая часть, нечетные ряды — вторая часть или наоборот), чтобы сообщение не запуталось. Во всех неиспользуемых треугольниках для моего сообщения я решил сделать красивый узор, используя два цвета фона, и это помогло скрыть сообщение еще больше. Вы можете сделать то же самое со своей головоломкой.
Во всех неиспользуемых треугольниках для моего сообщения я решил сделать красивый узор, используя два цвета фона, и это помогло скрыть сообщение еще больше. Вы можете сделать то же самое со своей головоломкой.
В примере слева показан процесс сборки головоломки, которую я сделал выше.
Написание инструкций и подсказок
Пример решения этой головоломки
Теперь вам нужно написать ключи к этой головоломке. Я обнаружил, что с этим гамбитом вам нужно прямо сказать игрокам, что делать. Чтобы это сработало, вам нужно сложить бумагу веером, но вам нужно сложить ее определенным образом, иначе ваши сообщения будут перевернуты. Вот почему я включил в лист слово «ТОП». Они будут знать, что это верхняя часть листа, и когда они будут следовать указаниям сгиба на подсказке (справа), они смогут раскрыть сообщение. Чтобы прочитать сообщение, вы должны посмотреть на него определенным образом. Если смотреть прямо вниз, то ничего не увидишь. Но если вы немного откинетесь назад и проведете по нему взглядом, он будет выглядеть, как на картинках выше. В примере справа вы можете видеть, что я тоже понял, как читать сообщение. Помните, что эта головоломка должна быть умной и веселой, поэтому мы хотим помочь нашим игрокам, чем можем. Давать им инструкции — лучший способ убедиться, что они смогут решить эту проблему. Теперь вы можете распечатать головоломку и инструкции и перейти к следующему шагу!
Но если вы немного откинетесь назад и проведете по нему взглядом, он будет выглядеть, как на картинках выше. В примере справа вы можете видеть, что я тоже понял, как читать сообщение. Помните, что эта головоломка должна быть умной и веселой, поэтому мы хотим помочь нашим игрокам, чем можем. Давать им инструкции — лучший способ убедиться, что они смогут решить эту проблему. Теперь вы можете распечатать головоломку и инструкции и перейти к следующему шагу!
Тестирование головоломки
Последнее, что вам нужно сделать, это ТЕСТ! Вы всегда должны тестировать свои головоломки, чтобы убедиться, что они работают и доставляют удовольствие вашим игрокам! Дайте головоломку и инструкции другим и спросите их, ясны ли инструкции. Они раскрыли секретное сообщение? Наблюдайте за тем, как они пробуют это, и обратите внимание на то, что делают ваши тестировщики. Они могут сделать что-то, о чем вы даже не думали, и что вам нужно будет решить. Как только тестировщики смогут решить головоломку, используя только предоставленные инструкции, ваша головоломка готова!
Поздравляем! Вы сделали свой собственный складной аккордеон! Я надеюсь, что этот урок был полезен для создания ваших собственных складных пазлов для ваших приключений, и что вы получили удовольствие от процесса! Мы будем рады увидеть ваши пазлы, складывающие аккордеон, и любые другие пазлы, которые вы можете придумать! Пожалуйста, поделитесь своими приключениями и головоломками в сабреддите Constructed Adventures или отметьте нас в Instagram Constructed Adventures! Если вы хотите поболтать или получить помощь в решении головоломок от других создателей приключений, присоединяйтесь к нам на Discord-канале Constructed Adventures! Нам не терпится услышать от вас!
До новых встреч,
Счастливых приключений!
Комментарий
Foldology Origami Puzzles — игра-головоломка со 100 заданиями
Головоломка, не похожая ни на одну из тех, в которые вы когда-либо играли
Внимательное расслабление
Игра в фолдологию одновременно увлекает и успокаивает. Войдите в поток, погрузитесь в складывание и отпустите. Многие люди считают это медитативной деятельностью.
Войдите в поток, погрузитесь в складывание и отпустите. Многие люди считают это медитативной деятельностью.
Посмотрите, что говорят люди
Испытайте себя
Foldology с гордостью разработана для решения серьезных задач. Не торопитесь и пройдите через 100 испытаний. Не детская игрушка, но любознательным детям нравится.
ПЕЧАТЬ ОБРАЗЦА ЗАГАДКИ
Захватывающее развлечение
Разгадывать эти головоломки так приятно, что вы будете продолжать тянуться к следующей. Только не пропускайте вперед — головоломки постепенно усложняются, и по пути вы узнаете новые складки.
Вопросы? Читайте F.A.Q.
См. Как это работает
Buy Now на Amazon
Печатный образец.0274 №1 в Руководстве по праздничным подаркам Мела для детей и подростков Самые крутые чулки для подростков – в списке желаний №1 в Идеи дешевых рождественских подарков Майка (2019) ▶ Отзыв Origamieasy (2020, французский с английскими субтитрами) ▶ «Это так захватывает и определенно увеличивает сложность! … Я был почти в тупике, но так приятно продолжать пытаться и, наконец, решить их…» – Энджи «Так много способов сложить квадратный лист бумаги в меньший квадрат… Это здорово, просто весело. – Samantha Thompson «… отлично подходит для поездки (на машине или самолете), учебы или просто вечера дома. Каждую ночь мы делали несколько игр…» – D Lee «… здорово играть в интересную игру в одиночку, не глядя и не проводя пальцем по экран! …” – CC ПРОЧИТАТЬ ПОЛНЫЕ ОТЗЫВЫ НА AMAZON БЫСТРАЯ ДОСТАВКА КУПИТЬ НА AMAZON Видеообзоры на Youtube
Отзывы клиентов Amazon
«Отличные маленькие пазлы, берите их куда угодно!»
«Просто, но так весело!»
«Уникальная портативная игра/головоломка для складывания бумаги»  Любить это.»
Любить это.»
«Отличный перерыв для любителей головоломок» Яркие дизайны Напечатаны на бумаге из 100% эвкалиптового волокна, сделано в США
Инструкции

Ч.З.В.
Это выглядит потрясающе, где я могу это купить?
Foldology продается на Amazon, мы считаем, что это лучший способ совершения покупок для наших клиентов.
Чем Foldology отличается от распечатанных мною головоломок?
Хотя распечатанные головоломки дают приблизительное представление, они далеки от полного опыта.
- Высококачественная печать в ярких цветах
- Foldology напечатана на специальной бумаге, которая обладает повышенной прочностью и отлично подходит для складывания
- Каждая головоломка также имеет сетку на обратной стороне, которая помогает правильно складывать
- Всего 100 уникальные дизайны головоломок, тщательно отобранные в порядке возрастания сложности
Для какого возраста лучше всего подходит фолдология?
Мы рекомендуем его для подростков и взрослых, но он понравится и любознательным детям от 10 лет. Поскольку фолдология не стесняется предлагать задачи, детям младшего возраста может понадобиться помощь с более поздними головоломками. Но мы думаем, что это действительно хороший опыт обучения.
Поскольку фолдология не стесняется предлагать задачи, детям младшего возраста может понадобиться помощь с более поздними головоломками. Но мы думаем, что это действительно хороший опыт обучения.
Нужно ли мне знать Оригами, чтобы играть?
Опыт работы не требуется! Головоломки начинаются легко и усложняются, так что вы во всем разберетесь сами.
Это действительно научит меня оригами?
Да и нет…
- Да в том смысле, что: в процессе фолдологии вы узнаете много типов складок, с которыми вы также встретитесь в оригами.
- Нет в том смысле, что: в конечном итоге цель совсем другая. Все головоломки Foldology в конечном итоге складываются в плоский квадрат, тогда как Origami в первую очередь складывается из бумаги в различные трехмерные формы.
Есть ли пошаговые инструкции/решения?
Буклет содержит инструкции о том, как играть, но выяснение того, как складывать, остается на ваше усмотрение. Собственно, вот и вся задача!
Собственно, вот и вся задача!
Тем не менее, у нас также есть эта страница с некоторыми полезными советами по складыванию и видео-решениями, если вы застряли.
Каков размер и упаковка продукта?
Небольшой размер 5 x 5 x 0,35 дюйма предназначен для переноски и удобного использования в поездках. Продукт представляет собой небольшой буклет или блокнот, где каждый лист в буклете представляет собой одну из головоломок. Упакован он просто в пластиковую термоусадочную пленку.
Каковы правила доставки и возврата?
При покупке на Amazon или eBay ознакомьтесь с их соответствующими правилами.
Я хочу эту игру для своего магазина/школы/и т.д. Как заказать оптом?
Свяжитесь с нами напрямую, и мы все сделаем.
Как сделать пазл из фото на заказ
10,4 К акции
- Фейсбук
- Твиттер
- Электронная почта
Пазл с фотографиями на заказ станет отличным подарком, и это НАСТОЛЬКО просто ! Используйте фотографии детей, домашних животных или ваших любимых мест для этого проекта головоломки.
Требуемые навыки: Новичок. Чтобы собрать эту головоломку, вам не нужно много опыта в моддинге. Тем не менее, я призываю вас набраться терпения, особенно на шаге 3. Выждите необходимое время для высыхания, чтобы избежать образования складок.
Познакомьтесь со Стефани из довольно простого. Она будет вашим хозяином на весь день с нестандартной фото-головоломкой, а я сижу на пляже и пью май-таис. Шутя! Я только желаю.
Стефани — фантастический блогер, но ниже я позволю ей рассказать вам о себе. Сегодня мы поменялись местами, так что заходите к ней в блог, чтобы увидеть проект декупажа, который я сделал. Счастливой пятницы Поджеры!
Эй, мод-поджеры! Меня зовут Стефани, и я творческий человек и создатель несколько простых вещей.
Я так рада, что сегодня возглавила этот блог! Прошлым летом я начала вести блог — это мой маленький уголок вселенной, где я делюсь уроками по рукоделию и всем, что связано с творчеством.
Пазл «Сделай сам»
Все трое моих детей заболели на этой неделе (давай, пожалей меня!). В перерывах между обниманием больных и дезинфекцией моего дома снова и снова, я собрал этот забавный учебник по головоломке с картинками. Это для тех, кто хочет милый, простой проект, которым могут наслаждаться их дети (если они не больны, конечно!),
В перерывах между обниманием больных и дезинфекцией моего дома снова и снова, я собрал этот забавный учебник по головоломке с картинками. Это для тех, кто хочет милый, простой проект, которым могут наслаждаться их дети (если они не больны, конечно!),
Я называю это « Пазл с семейными картинками » (такой оригинальный, я знаю!) Каждый шаг учебника содержит изображение для тех из вас, кто учится визуально, как я.
Печать фотографий для фотопазла «Сделай сам»
Перед тем, как вы соберете фотопазл, вам нужно будет распечатать выбранное вами изображение. Я рекомендую отсканировать ваше изображение на компьютер — вы не захотите использовать для этого проекта оригинальные фотографии или фотобумагу.
Лучше всего распечатать изображение на принтере с сухим тонером или на лазерном струйном принтере, чтобы не было смазывания. Я обнаружил, что мой струйный принтер HP работает, хотя это и не лазерный принтер, потому что HP использует очень сухие чернила.
Когда я распечатываю свои изображения, я даю им высохнуть в течение нескольких часов перед использованием. Вы также можете пойти в Кинко или куда-нибудь с лазерным принтером.
Если у вас нет доступа к лазерному принтеру, я рекомендую распылить на обе стороны вашего струйного изображения прозрачный акриловый герметик перед модификацией.
Это поможет предотвратить смазывание изображения. Если вы собираетесь потратить время и силы на изготовление фотопазла на заказ, особенно если это подарок, вы не хотите, чтобы что-то пошло не так!
После того, как вы распечатали изображение, вы готовы начать. Узнайте, как сделать головоломку ниже.
Сделайте фото-пазл
Соберите эти материалы
- Изображение, напечатанное на бумаге для лазерной печати или сухого тонера
- Ножницы
- Нож X-Acto
- Бумага для вырезок – 1 лист хлопьев
- ДСП
- быть больше, чем ваше изображение.
- Mod Podge Gloss
- Губчатая кисть
- Вам также может понадобиться пакет Ziploc и транспортировочная этикетка (они не изображены, но я покажу вам, что я сделал с ними позже в этом руководстве)
Инструкции
Шаг 1. Отрежьте одну сторону коробки с хлопьями. Каждая коробка будет составлять две головоломки, так что спасите другую сторону!
Отрежьте одну сторону коробки с хлопьями. Каждая коробка будет составлять две головоломки, так что спасите другую сторону!
Шаг 2. Также сохраните Box Top для образования. Отправьте его в школу вместе с детьми (это не относится к учебнику, но я должен был добавить его туда!),
Шаг 3. Нанесите изображение на неузорчатую (коричневую) сторону хлопьев коробка с Mod Podge. Нанесите средний слой Mod Podge, поместите изображение вниз и тщательно разгладьте пальцами или брайером. Если какой-либо Mod Podge выдавливает бока, сотрите его щеткой.
Дайте высохнуть в течение 15–20 минут, затем нанесите сверху слой Mod Podge. Дайте высохнуть.
Шаг 4. Переверните картон и нанесите бумагу для вырезок на обратную сторону, нанеся больше Mod Podge. Это должен быть относительно толстый лист бумаги для вырезок, чтобы он закрывал рисунок коробки с хлопьями.
Если ваша бумага для вырезок тонкая, вы можете подумать о том, чтобы покрасить коробку с хлопьями в белый цвет, прежде чем приклеивать бумагу. Какой бы метод вы ни выбрали, дайте полностью высохнуть.
Какой бы метод вы ни выбрали, дайте полностью высохнуть.
Шаг 5. Обрежьте излишки картона и бумаги для вырезок по краям.
Шаг 6. С помощью маркера или другого предмета, который вы видите, обведите контуры кусочков пазла на картинке. Карандаш тоже подойдет.
Шаг 7. Вырежьте каждую часть ножом X-Acto. Ножницами проще, но не так точно — поэтому, если вы ленивы, как я, вы начнете с ножа X-Acto, но в конечном итоге будете использовать ножницы. Мне иногда не хватает терпения. . .
Шаг 8 (необязательно). Распечатайте ту же картинку меньшего размера на транспортной этикетке и прикрепите ее к передней части пакета Ziploc.
Шаг 9. Поместите все детали в пакет Ziploc для безопасного хранения. У меня есть коробка самодельных головоломок, которые мои дети любят собирать. Каждая головоломка находится в отдельной сумке, и это способствует спокойной игре!
Варианты пазла с картинками «Сделай сам»:
- Нарежьте кусочки больше или меньше в зависимости от возраста ваших детей.
 Для моего 3-летнего ребенка у меня есть пазлы, состоящие всего из 3-4 частей. Малыши тоже любят собирать пазлы.
Для моего 3-летнего ребенка у меня есть пазлы, состоящие всего из 3-4 частей. Малыши тоже любят собирать пазлы. - Вместо бумаги для вырезок вы можете оставить заднюю часть коробки с хлопьями открытой — моим детям нравится использовать коробку с хлопьями как пазл сам по себе.
- Накройте заднюю часть войлоком и используйте эту головоломку на фланелевой доске.
Ваш фотопазл своими руками готов! Супер просто, едва ли достойно быть в компании с другими замечательными проектами Эми. Если вы хотите увидеть, что я могу делать, когда я не жонглирую больными детьми, переходите к более простому. Я хотел бы тебя увидеть!
Время подготовки 5 минут
Активное время 10 минут
Время высыхания 20 минут
Общее время 35 минут
Сложность Easy
Ориентировочная стоимость $0
Материалы
- Изображение, напечатанное на сухом тонере или бумаге для лазерной печати
- Бумага для вырезок – 1 лист
- Чипборд (например, коробка из-под хлопьев) – должен быть больше вашего изображения
- Мод Podge Gloss
- Пакет Ziploc
- Транспортная этикетка
Инструменты
- Щетка-губка
- Ножницы
- Нож X-Acto
Инструкции
- Отрежьте одну сторону коробки с хлопьями.
 Каждая коробка будет составлять две головоломки, так что сохраните другую сторону.
Каждая коробка будет составлять две головоломки, так что сохраните другую сторону. - Нанесите изображение на неузорчатую (коричневую) сторону коробки с хлопьями с помощью Mod Podge. Нанесите средний слой Mod Podge, поместите изображение вниз и тщательно разгладьте пальцами или брайером. Если какой-либо Mod Podge выдавливает бока, сотрите его щеткой.
- Дайте высохнуть в течение 15–20 минут, затем нанесите сверху слой Mod Podge. Дайте высохнуть.
- Переверните картон и приклейте бумагу для вырезок на обратную сторону с большим количеством Mod Podge. Это должен быть относительно толстый лист бумаги для вырезок, чтобы он закрывал рисунок коробки с хлопьями. Если бумага для вырезок тонкая, вы можете подумать о том, чтобы покрасить коробку с хлопьями в белый цвет, прежде чем наклеивать бумагу. Какой бы метод вы ни выбрали, дайте полностью высохнуть.
- Обрежьте излишки картона и бумаги для вырезок по краям.
- С помощью маркера или другого предмета, который вы видите, обведите контуры кусочков пазла на картинке.
 Карандаш тоже подойдет.
Карандаш тоже подойдет. - Вырежьте каждую часть ножом X-Acto. Ножницами проще, но не так аккуратно.
- Распечатайте ту же картинку меньшего размера на транспортной этикетке и прикрепите ее к передней части пакета Ziploc.
- Поместите все детали в пакет Ziploc для безопасного хранения.
Примечания
У меня были все материалы под рукой, поэтому этот проект мне ничего не стоил.
Если вам или вашим детям понравилось собирать этот нестандартный фотопазл, попробуйте другие увлекательные занятия:
- Фоторамка из палочек для мороженого
- Шашки своими руками с липкой лентой
- Конфетти Mod Podge Slime
- Как сделать слизь
10,4 К акции
- Фейсбук
- Твиттер
- Электронная почта
пазлов «Сделай сам» — дом, который построил Ларс
Бумажный пазл Nufun
Бумажный пазл Nufun — отличный способ сделать пазл на заказ. Вот так! Используя подходящие материалы, вы можете выбрать изображение по своему выбору (в нашем магазине так много симпатичных принтов на выбор!), распечатать его и перенести на пустой пазл с помощью утюга или термопресса. Вы даже можете сделать соответствующую сумку, чтобы пойти с ним! Мне нравится, как удивительно легко это сделать. Это отличная поделка, которую вы можете сделать вместе со своими детьми, а затем она станет милым занятием, которое они смогут выполнять, чтобы развеять скуку.
Вот так! Используя подходящие материалы, вы можете выбрать изображение по своему выбору (в нашем магазине так много симпатичных принтов на выбор!), распечатать его и перенести на пустой пазл с помощью утюга или термопресса. Вы даже можете сделать соответствующую сумку, чтобы пойти с ним! Мне нравится, как удивительно легко это сделать. Это отличная поделка, которую вы можете сделать вместе со своими детьми, а затем она станет милым занятием, которое они смогут выполнять, чтобы развеять скуку.
Вот что нужно сделать:
Как сделать пазл на заказ
Печать вашего изображения
- Сначала выберите дизайн (отличные варианты можно найти в нашей типографии). Не забудьте отразить изображение перед печатью.
- Загрузите переводные листы в принтер так, чтобы изображение печаталось на неглянцевой (неразлинованной) стороне.
- Теперь распечатайте изображение! Используйте следующие настройки: HP: Утюг при переносе, обычный режим; Epson: обычная бумага, фоторежим; Canon: бумага для струйной печати, стандартная в высоком режиме.

Подготовка к переносу
- Сохраняя целостность пазла, соедините пазл и картонный лист. Слегка согните листы пазла, чтобы ослабить части, чтобы после глажки они легко ломались.
- Теперь отрежьте небольшой угол (около 1 см) от копировальной бумаги, чтобы облегчить процесс отделения.
Перенос вашего изображения
Есть два варианта переноса изображения вашего пользовательского пазла. Первый с термопрессом, второй с утюгом. Вот что нужно сделать для каждого:
Нагрев пресса
- Сначала нагрейте пресс до 350 градусов по Фаренгейту.
- Затем положите пазл тканевой стороной вверх на пресс.
- Теперь поместите распечатанное изображение на пазл лицевой стороной вниз (разлинованная сторона должна быть обращена вверх).
- Нажмите на 25 секунд.
- Для достижения наилучших результатов сразу снимите кожуру (пока она еще горячая).
 Подождите 5 секунд, затем плавным, равномерным движением снимите бумажную подложку с трансфера. Вот как можно сделать свою собственную головоломку с помощью термопресса!
Подождите 5 секунд, затем плавным, равномерным движением снимите бумажную подложку с трансфера. Вот как можно сделать свою собственную головоломку с помощью термопресса!
Утюг
- Сначала нагрейте утюг до максимальной температуры «Лен». Положите наволочку на гладильную поверхность. Мы не рекомендуем использовать для этого гладильную доску!
- Затем поместите распечатанный переводной лист лицевой стороной вниз на войлочную головоломку.
- С сильным, равномерным давлением держите утюг обеими руками и переносите вес своего тела. Гладить в общей сложности 2 минуты 45 секунд. Когда вы гладите, медленно скользите утюгом по пазлу слева направо. Поднимите утюг, чтобы вернуться к рисунку слева направо, и повторите, чтобы покрыть весь лист. Не забудьте также покрыть все края и углы.
- Как и в случае с термопрессом, подождите 5 секунд, затем плавным равномерным движением снимите бумажную подложку, пока она еще горячая.
 Теперь у вас есть собственная головоломка!
Теперь у вас есть собственная головоломка!
Разделение пазла
- Чтобы разделить кусочки пазла, держите лист пазла обеими руками. Аккуратно и осторожно разъедините крайние части со всех четырех сторон головоломки, пока граница не отделится. Откажитесь от границы. Совет: чтобы получить более четкий вид, используйте утюг, установленный на максимальную температуру, и прижмите пергаментной бумагой в течение 30 секунд таким же образом слева направо. Убедитесь, что граница удалена, а пергаментная бумага покрывает всю головоломку, так как прямое воздействие железа и перенос могут повредить ваш шедевр! Подождите, чтобы снять пергаментную бумагу, пока головоломка полностью не остынет.
- Теперь, один вертикальный ряд за раз, ослабьте и отделите остальную часть головоломки. Осторожно отделите каждую часть головоломки, осторожно потянув на себя. Повторяйте с каждым рядом, пока все части не будут разделены. Сделанный!
Как сделать подходящую сумку
- Чтобы напечатать изображение, выполните действия, описанные в разделе «Печать изображения» выше.

- После печати обрежьте изображение с трансферного листа, чтобы удалить лишнюю область. Скруглите все острые края. Это облегчит перенос изображения!
Перенос изображения
Как и в случае с головоломкой, для переноса изображения можно использовать термопресс или утюг. Вот как это сделать:
Термопресс
- Сначала нагрейте термопресс до 375 градусов по Фаренгейту.
- Теперь прогладьте ткань, чтобы выпустить влагу и разгладить складки.
- Затем положите распечатанное изображение на одежду лицевой стороной вниз на подкладке вверх. Установите на 40-60 фунтов на квадратный дюйм или используйте сильное давление для достижения наилучших результатов.
- Нажмите на 25 секунд, а затем сразу же снимите для достижения наилучших результатов. Подождите 3 секунды и снимите бумажную подложку с трансфера плавным, равномерным движением, пока трансфер еще горячий.

Утюг
- Сначала разогрейте утюг до максимальной настройки «Лен» для смесей с содержанием 50-100% хлопка и настройки «Хлопок» для тканей, содержащих менее 50% хлопка или эластичных тканей, таких как лайкра. Положите наволочку на гладильную поверхность. Помните, мы не рекомендуем использовать гладильную доску.
- Теперь предварительно прогладьте ткань, чтобы выпустить влагу и убрать складки.
- Затем положите распечатанное изображение на одежду лицевой стороной вниз (разлинованной стороной вверх).
- Теперь используйте твердое, постоянное давление, чтобы скользить утюгом круговыми движениями по всему переносу в течение следующих промежутков времени: ¼ листа: 1,5 минуты, ½ листа: 2,5 минуты, полный лист: 3,5 минуты.
- После проглаживания каждой части трансфера еще раз проведите утюгом по всей поверхности, чтобы равномерно нагреть.
- Как только это будет сделано, немедленно снимите кожуру для достижения наилучших результатов.
 Подождите 3 секунды и снимите бумажную подложку с трансфера плавным, равномерным движением, пока трансфер еще горячий.
Подождите 3 секунды и снимите бумажную подложку с трансфера плавным, равномерным движением, пока трансфер еще горячий. - Если во время отслаивания наблюдается какое-либо приподнимание изображения, немедленно остановитесь и проведите утюгом по переводу для равномерного нагрева, уделяя особое внимание участкам, которые приподнялись. Затем повторите шаг 6.
Инструкции по стирке
Выверните пакет наизнанку и постирайте в холодной воде отдельно от остальной одежды в деликатном режиме. Сушить при низкой температуре или сушить в подвешенном состоянии. Если сушите в сушилке, быстро достаньте ее, когда она будет готова.
Когда вы не используете свою головоломку, храните ее в очаровательной подходящей сумке, которую вы только что сделали!
Больше вдохновения
Понравился этот урок о том, как сделать пазл своими руками и подходящую сумку? Посмотрите этот пост, где мы собрали другие замечательные развлечения для детей, чтобы занять их все лето!
Актуальные статьи
Последние статьи
63 Отобранные вручную идеи квестов, создающие радость и тайну
Перейти к головоломкамИли, СКАЧАТЬ НАБОР ДЛЯ ПОБЕГА
Ищете идеи головоломок для квестов, чтобы создать удивительное приключение? Соберите лучшее из богатого урожая головоломок этого года ниже.
Итак, вы разрабатываете приключенческий побег своими руками, чтобы увлечь своих друзей , бросить вызов своим коллегам или порадовать своих детей.
Потрясающе!
Вы в правильном месте. (Вы читали наш пошаговый план дизайна квеста 9?0824?)
Эти идеи головоломок были отобраны самими Высшими Волшебниками. Они дешевы, легко изготавливаются и не требуют знания темной магии. Короче говоря, эти головоломки идеально подходят для начинающих дизайнеров-повелителей, таких как вы!
Здесь собрано огромное количество головоломок, так что, если у вас мало времени, , просто загрузите один из наших готовых к игре наборов для квестов.
Каждый полностью настраиваемый , так что вы можете стать дизайнером без всей рутинной работы .
Просто загрузите игру, распечатайте ее, и вы готовы к вечеринке!
ПОКАЖИТЕ МНЕ ГОТОВЫЕ НАБОРЫ ДЛЯ ИГРЫ
Самая большая ошибка дизайнеров квестов, которые делают самодельные.
 ..
..Самая важная часть вашего самодельного квеста — это не головоломки, не тема и даже не пицца.
Это весело.
В конце концов, никто не хочет идти к товарищам и заниматься математикой (кроме, может быть, наших бухгалтерских троллей).
Вместо этого они хотят оживиться. Они хотят немного посмеяться с друзьями. И да, они хотят пиццу…
Именно здесь ошибаются 99% дизайнеров квестов DIY. Они собирают воедино случайную смесь головоломок, которые не связаны между собой и слишком сложны. Это приводит к утечке мозгов . Утечка мозгов приводит к зомбированию. А зомби — просто скучные гости вечеринки!
Но не волнуйтесь, этой ошибки легко избежать, включив равный баланс Головоломок, Задач, и Игры.
(Вы также можете попробовать разработать игру вместе с другом, чтобы обмениваться хорошими идеями. Эти дети сделали именно это, и их игра потрясающая!)
Вам понадобится примерно равное количество задач, игр и головоломок
Пазлы
Головоломки создают момент удара кулаком по воздуху момента, когда игроки кричат «А-ха» и чувствуют себя ниндзя из квест-комнаты.
Для их решения потребуется некоторое нестандартное мышление, и изрядное количество размышлений.
Когда головоломка сочетается с заданием, возникает то вдохновляющее чувство, которое любят все.
Задачи
Задачи заставляют игру двигаться , поскольку игроки сразу знают, как их решать. Как лабиринт или головоломка.
Кроме того, они избегают «чувства тупика», давая каждому шанс.
Лучший способ использовать их — предоставить игрокам то, что им нужно для решения Головоломка.
Игры
Игры превращают вашу квест-комнату в Escape Party и обеспечивают столь необходимое облегчение мыслей.
Например, стрельба по зомби из оружия Nerf или перемещение по минному полю с завязанными глазами.
В сочетании с задачами и головоломками они сделают вашу квест-комнату незабываемо увлекательной.
Лучшие квесты-пазлы «Сделай сам»:
Висячий замок, закрой ножницыПазл — замок — $10
Простой. Тем не менее восхитительно.
Тем не менее восхитительно.
Игроки знают, что делать, как только видят это. Ножницы нужны только для чего-то логического, например, для вырезания сложных фигур. Или добавьте немного фантазии с помощью этикетки, например:
Плазменные резаки. Подходит для цепи любого размера
Затем обмотайте веревкой дверь с надписью
Прочная цепочка, вам понадобится что-нибудь, чтобы перерезать меня.
Не волнуйтесь, ваша команда будет кататься с ним и получать удовольствие.
Цепочка из двух раздвижных дверейГоловоломка — замок — 15 долларов
Если вам больше по душе «подземелье», можно использовать цепь длиной 10 долларов из хозяйственного магазина и простой замок, чтобы соединить два объекта вместе (или держать французские дверцы холодильника закрытыми).
Вы спросите, почему вы хотите связать два объекта вместе? Возможно, ваши игроки застряли в биолаборатории и им нужно что-то взвесить; оберните его цепью, чтобы он был слишком тяжелым, пока они не найдут способ его разблокировать.
Время начать собирать коллекцию навесных замков
После того, как вы устроите свое первое приключение с побегом своими руками, вы, вероятно, обнаружите, что хотите сделать квест-вечеринки обычным делом … и вскоре вы будете копить необычные навесные замки, как какой-нибудь дракон из комнаты для побега!
Вот несколько для начала.
Я купил его несколько лет назад на Amazon, и он отлично работает во всем старомодном мире.
Этот кодовый замок несомненно подойдет для любого фэнтезийного приключения.
К этому замку прилагается классный (и забавный) ключ!
Устроить игру на тему принцессы для своей дочери и ее друзей? Такие замки, как этот , могут быть просто билетом.
Создание лабиринтного лабиринтаЗадача — Навигация — Стоимость бумаги
Дайте игрокам пройти лабиринт, но добавьте любопытный поворот. Например, этот лабиринт из нашего набора для квестов Envy () включает в себя случайные буквы на дорожках или перекрестках. Только нахождение правильного пути через лабиринт покажет комбинацию букв, которая составляет подсказку.
Только нахождение правильного пути через лабиринт покажет комбинацию букв, которая составляет подсказку.
ПРОВЕРЬТЕ ИГРОВОЙ НАБОР
Сообщение, спрятанное в воздушных шарах. Поп!Игра — Высокая энергия — $3
Это отличный удар для вас доллар.
(Ладно, хватит жутких шуток…)
Просто спрячьте подсказку, ключ или приз внутри всего в одном шарике .
Затем надуйте еще кучу и разложите их по всей комнате в качестве «декоративного» , чтобы игроки думали, что они просто часть темы.
Когда все настроено, направьте своих игроков в правильном направлении на оставляет подсказку такая маленькая записка, спрятанная внутри еще одной головоломки квеста. Лично мне нравятся простые загадки вроде:
- Я спрятался внутри чего-то желтого
- Что больше арбуза, но легче пера?
Затем откиньтесь на спинку кресла и наблюдайте за кровавой бойней, когда комната, полная детей, превратилась в разбушевавшуюся толпу зомби, жаждущих отведать сладкой сущности воздушного шара. .. (ладно, давайте посмотрим правде в глаза, вашим взрослым друзьям это тоже понравится).
.. (ладно, давайте посмотрим правде в глаза, вашим взрослым друзьям это тоже понравится).
Головоломка — Скрытое сообщение — Бесплатно
Помните те скрытые сообщения, которые вы видели зашифрованными на зеркалах в ванных комнатах в шпионских фильмах? Что ж, сегодня ваш день, чтобы войти в мир шпионажа.
Все, что вам нужно, это зеркало в ванной и немного мыла или медицинского спирта. Когда комната наполнится паром, появится сообщение в истинном стиле агента 007. Вот видео о том, как это сделать.
Наполнен паром? Легко — просто оставьте подсказку где-нибудь, например:
- Внимательно смотрите на себя в зеркало, пока ваш призрак не заговорит с вами.
- Мойте волшебный камень под горячей водой, пока он не раскроет свою древнюю мудрость.
Вы можете комбинировать это с любым закодированным сообщением, таким как
палочка-головоломка от эскимо. Разобрать сообщение
Разобрать сообщение Задача — Скрытое сообщение — Бесплатно
Разбейте секретный код на кусочки и разбросайте их по пазлу или пазлу-оригами, который нужно сложить определенным образом.
Когда все это сойдется вместе, ваши игроки точно почувствуют себя учтивым супершпионом или предприимчивым охотником за сокровищами! (Эта конкретная головоломка из нашего набора для побега Frost , и это одновременно головоломка и головоломка оригами!)
Превратите летнее фруктовое мороженое в шифрыГоловоломка — Закодированное сообщение — $1
Это отличная головоломка для летнего квеста, потому что вы можете дать всем эскимо в начале, и они поймут, что являются частью игры, только когда прогрызут себе путь!
Это также отличный способ превратить короткое слово в более длинное сообщение.
Начните с написания сообщения на выровненных палочках от эскимо, а также ключевого слова вверху. Сообщение доступно для чтения только в том случае, если они выровнены таким образом. Мы используем JOHNSON, и даже с одной неуместной палочкой сообщение совершенно нечитаемо). Если вы хотите усложнить задачу, добавьте несколько других символов и букв, но не переусердствуйте, так как это может быть утомительно. Наконец, сделайте фруктовое мороженое из палочек для дополнительного вкуса.
Мы используем JOHNSON, и даже с одной неуместной палочкой сообщение совершенно нечитаемо). Если вы хотите усложнить задачу, добавьте несколько других символов и букв, но не переусердствуйте, так как это может быть утомительно. Наконец, сделайте фруктовое мороженое из палочек для дополнительного вкуса.
Игроки должны будут угадать ключевое слово, чтобы разгадать шифр. Вот несколько вариантов:
- Мы положили палочки от эскимо в чашку со словом JOHNSON.
- Спрячьте большое слово где-нибудь в комнате, например, используйте невидимую надпись в Зеркальная головоломка.
- Пометьте каждую палочку от эскимо своим цветом, а затем расположите эти цвета по порядку на какой-нибудь подсказке (например, цвета радуги или набор цветных карандашей).
- Напишите первую букву ключевого слова довольно большой. Затем уменьшайте размер для каждой последующей буквы. Игрокам нужно будет установить соединение, что размер является порядком сортировки.

ПОМНИТЕ: Оберегайте территорию!
Не устраивайте минное поле рядом со стойками для мечей, бездонными ямами или лужами магической слизи! (Нам все еще жаль гоблина Грега…)
Осторожно, эти мины! Игра — Коммуникабельность — Бесплатно
Эта игра — верный способ добавить немного веселья на уровне супершпиона в вашу самодельную квест-комнату.
Все довольно просто: каждый игрок по очереди пересекает «минное поле» с завязанными глазами, при этом другие ваши игроки должны указывать им дорогу из другого коридора.
Препятствия могут быть любыми — в данном случае это электронные мины безопасности, через которые игроки должны пройти после отключения электричества в W.A.R. Объект, в который они только что проникли. Это часть нашей печатной версии Спасательный набор Rebel Revolt. Вы можете посмотреть, как настроить эту игру здесь (спойлеры!).
ПОПРОБУЙТЕ ИГРОВОЙ НАБОР
Сюжет может быть каким угодно, как и препятствия. Например,
Например,
- Положите на пол коврик Twister и предложите своим игрокам пересечь его, следуя вашим собственным творческим правилам.
- Когда соревнуются более крупные группы, вы можете заставить каждую команду тайком разработать полосу препятствий своего противника.
Вы делаете хорошее начало. Теперь просто вставьте эти головоломки в этот БЕСПЛАТНЫЙ шаблон, и все готово!
Просто введите свой адрес электронной почты ниже, чтобы загрузить этот бесплатный Builder’s Kit и начать свое приключение в квесте.
Или возьмите этот полный пакет шаблонов, чтобы получить полный опыт проектирования квестов:
Мы создали мастер-класс по квесту, который поможет вам пройти каждый шаг… и , чтобы превратить игровой дизайн в увлекательное семейное занятие !
Мастер-класс — это полностью загруженный набор головоломок, шаблонов и реквизитов для печати, которые вы сможете нужно разработать эпический квест.
То, что нужно для семейного отдыха или самого увлекательного урока в классе!
ПОПРОБУЙТЕ МАСТЕР-КЛАСС ПОБЕГ КОМНАТЫ
Используйте телефон как замокГоловоломка — Запертая коробка — Бесплатно
Превратите свой телефон в волшебный кодовый сейф за считанные минуты. Как работает большинство телефонов, ваша головоломка может быть традиционной числовой последовательностью или одним из этих скользящих шаблонов.
Что игроки получают, решая это? Попробуйте это:
- Секретный адрес электронной почты, который отображается на экране при разблокировке телефона. Просто сделайте скриншот письма, которое вы отправили себе, и отобразите его как картинку.
- Фотография комнаты «до» того, как вор ворвался в комнату, показывает вазу, которая находилась в другом месте. Затем спрячьте предмет внутри этой вазы. Обычно это было бы слишком хорошо спрятано, чтобы создать собственную комнату для побега, но эта подсказка делает это разрешимым.
 Вот еще один пример фото до/после.
Вот еще один пример фото до/после.
Как мой телефон заменяет игровой элемент?
Помните, что здесь вы полагаетесь на 90 927 отличную сделку 90 928 на 90 731 воображении 90 732. Положите телефон рядом с дверью и скажите игрокам, что это ввод с клавиатуры. Или скажи им, что это сейф. Или просто скажите им, что телефон проверит, нашли ли они правильный четырехзначный код.
Цель для них состоит в том, чтобы найти правильную комбинацию, и гораздо приятнее набрать код и увидеть, как телефон разблокируется, чем услышать: «Да, это открыло дверь».
Как настроить
- Измените пароль блокировки экрана на телефоне.
- Сфотографируйте все, что вы хотите, чтобы ваши игроки нашли «за дверью» или «в сейфе». Это может быть подсказка, головоломка или целая куча воображаемых денег.
- Откройте фотографию, чтобы она отображалась первой при разблокировке телефона.
- Заблокируйте экран и соберите головоломку, которая предоставит вашим игрокам код.

Головоломка — закодированное сообщение или замок — $1
Это похоже на головоломку с эскимо (см. выше), но дает вам дополнительное преимущество, заключающееся в том, что вы даете кому-то ключ или небольшой предмет при решении. (у-у-у-у! Искатели приключений любят добычу !)
Просто найдите набор стопочных стаканов и напишите сообщение на одной стороне, поместив по одной букве на каждый стакан. Это «разблокированное» состояние. Добавьте к чашкам кучу других символов и букв, чтобы скрыть решение. Поместите маленький ключ/подсказку в верхнюю чашку вместе со свернутой запиской, в которой говорится: «Недоступно, пока шифр чашки не будет выровнен. Вы узнаете, когда».
Кроме того, вы можете доставить сообщение, как в головоломке с эскимо. В этом примере мы использовали JOHNSON в качестве слова-решателя, а начало сообщения — «Красный свет»
. Выберите одно из решений головоломки с эскимо или используйте этот забавный трюк:
- Проделайте 1 отверстие в дне первой чашки
- Проделайте 2 отверстия в нижней части второй чашки.

- Продолжайте, пока все не закончите. Порядок сортировки — количество отверстий!
Если вы не хотите делать один из этих
, вы можете получить его здесь.(но они восхитительны для самостоятельной сборки).
Избавьтесь от хлопот — купите спасательный набор!Пазлы — игровой набор — 29 долларов США за полную игру «Побег»
Сделать приличную игру в квесте сложно ! Серьезно, наши гоблины-беглецы тратят 90 927 сотен часов 90 928, доводя головоломки до совершенства.
Так почему бы не сэкономить время и нервы и просто не выбрать отполированную, проверенную и готовую к игре квест-комнату?
Зависть — это верный способ сделать ваше мероприятие еще более классным и вызвать улыбки на лицах! Он полностью масштабируется до размера вашей группы, имеет захватывающую тематику и полностью настраивается. Вы даже можете использовать набор в качестве основы для своей собственной игры в побег из комнаты (точно так же, как этот учитель сделал с Потерянной Мумией).
ПРОВЕРЬТЕ ИГРОВОЙ НАБОР
Просто заприте дверь в домеГоловоломка — Замок — Бесплатно
Ничто не говорит о «квесте из комнаты» лучше, чем старая добрая стальная дверь с клавиатурой.
Что?? У вас нет одного из тех, кто охраняет вашу стиральную машину?
Ладно, ладно. Мы не можем все быть Брюсом Уэйном.
Скорее всего у вас есть обычные двери. Проявив немного воображения, любая дверь может легко стать порталом в другое измерение, люком в подземную шахту или воротами в сказочную страну!
Что ты говоришь? На вашей двери нет замка? Без проблем. Попробуйте повесить висячий замок или изображение висячего замка на дверную ручку и положиться на повествование и тематический декор до 9.0731 воплотите свой вызов в жизнь.
Использование велосипедной цепи для имитации замкаГоловоломка — замок — 5 долларов США
Это самый простой комбинированный сейф на планете. И, поверьте опытному волшебнику, скромная велосипедная цепь обладает большей силой, чем большинство заколдованных амулетов!
И, поверьте опытному волшебнику, скромная велосипедная цепь обладает большей силой, чем большинство заколдованных амулетов!
Конечно, это не самое настоящее, но помните, что это вечеринка для друзей, а не бизнес. Добавьте аутентичности с помощью письменной этикетки или укажите, как это вписывается в тему вашей квест-комнаты во вступлении.
Просто наденьте велосипедную цепь на ручку двери или ящик для хранения. Или пропустите его через опору, которая нужна вашим игрокам, чтобы решить другую головоломку, и закрепите ее на чем-то твердом.
Используйте скромный картотечный шкафPuzzle — Lock — Free
Превратите свою скучную офисную мебель в запирающуюся тайну. Идеально подходит для предстоящего дня тимбилдинга в квест-комнате .
Просто спрячьте что-нибудь сверхсекретное внутри, а затем спрячьте куда-нибудь ключ.
Хитрое место — просто положить ключ в маленькое пространство под шкафом с документами. Затем оставьте где-нибудь в комнате записку с сообщением:
Люди кладут на меня вещи. Люди помещают вещи в меня. Но вам понадобится то, что…
Люди помещают вещи в меня. Но вам понадобится то, что…
Задача — Поиск — $0-$20
Дома полны хлама. Твое барахло! Не пытайтесь отрицать это…
Вот как вы можете убедиться, что ваши игроки знают разницу между скрытой подсказкой и забытой заметкой:
- Положитесь исключительно на игровые карты для получения всех подсказок и предметов в игре. В этом сценарии никакие случайные объекты не будут ошибочно приняты за игровые фигуры, потому что все подсказки напечатаны на бумаге. Например, все подсказки в нашей распечатываемой игре-квесте « Escape Quest » печатаются на фотографиях, так что это МЕГА-ОЧЕВИДНО!
ПРОВЕРЬТЕ НАБОР ИГРЫ
- Возьмите набор из маленьких наклеек с красными точками (или проявите творческий подход и начните с 9 наклеек).0823 что-то, что соответствует теме вашей квест-комнаты ) и поместите один на все, что связано с игрой.
 Игроки по-прежнему могут наслаждаться охотой, но они точно узнают, когда им удастся найти что-то важное.
Игроки по-прежнему могут наслаждаться охотой, но они точно узнают, когда им удастся найти что-то важное. - Используйте только те реквизиты, которые четко связаны с вашей темой. Допустим, вы устраиваете пиратское приключение. Используйте длинную цепочку и старомодный замок . Если игроки найдут ключи от вашего дома, они поймут, что им нужно продолжать охоту за чем-то, что выпрыгивает и кричит «Аааааааааааа»!
- Назначить определенную область для игры и удалить из нее все случайные предметы. Скажите игрокам, что все, что внутри этих границ, может быть ключом к разгадке (и все, что снаружи, определенно является , а не ).
- Убедитесь, что вы определили правила перед началом игры. Если за произведениями искусства на ваших стенах может что-то скрываться, сообщите игрокам , что все в комнате является честной игрой, кроме, скажем, светильников. Указав, что такое , а не включены, вы намекаете им, что включено.

Ищете классные укрытия? Попробуйте эти:
- Под столом. Используйте скотч, чтобы прикрепить что-либо к нижней части стола или другого предмета мебели.
- За картиной. Приклейте что-нибудь маленькое к обратной стороне рамы для картины или к стене позади нее.
- Внутри пианино. Только не кладите на струны ничего тяжелого. Вы же не хотите, чтобы ваш сосед по комнате приходил домой и спрашивал, почему пианино звучит как кучка разъяренных котов!
- Вырежьте скрытое отделение на страницах старой книги (или используйте настоящий книжный сейф ).
- Соберите сцену LEGO , например, дом, и поместите что-нибудь внутрь него.
- Прорежьте отверстие во внутренней подкладке старого рюкзака или портфеля. Это идеально подходит для сокрытия документов и очень похоже на 007.
- Используй фальшивый камень и… спрячь в нем ключ!
- Поместите небольшой предмет в пульт дистанционного управления телевизором , вынув из него батарейки.

- Спрячьте маленькие записки внутри фундука (реально!).
- Составьте серию подсказок или элементов головоломки на очень маленьких записях.
- Сверните их и туго завяжите ниткой.
- Открой и съешь немного фундука (ням).
- Поместите банкноты в орехи и с помощью клея соедините их вместе.
- Они будут намного легче обычных лесных орехов, что поможет игрокам их найти.
Подлые записки видны при взломе
Распечатайте замок из набора Escape Room KitГоловоломка — замок — 29 долларов за полную игру с побегом
Если вы торопитесь, сэкономьте время, воспользовавшись готовым набором для квестов. Они загружаются на ваш компьютер, а затем вы просто распечатываете их и готовы к игре.
Вы даже можете дополнить их собственными идеями дьявольских головоломок и творческим чутьем, используя игровой редактор, который поставляется вместе с загрузкой.
ПОСМОТРЕТЬ НАБОРЫ ДЛЯ ИГРЫ ЗДЕСЬ
Возьмите деревенский портфель Mr. SpyPuzzle — Lock — $5+
Скорее всего, у вас есть багаж в шкафу со встроенным кодовым замком.
Эта игра-головоломка просто кричит.
Если нет, то вы можете довольно дешево забрать портфель или багаж из секонд-хенда. Просто убедитесь, что ключ или комбинация работают, прежде чем покупать их! И не волнуйтесь, если он не такой прочный. Просто скажите своим приятелям, чтобы они усердно ели закуски и поменьше занимались мебелью.
Слишком много головоломок? Download a complete escape room:
Adults
Kids
Spy mission
Teen Halloween parties 14+
Great for school camps
4+ Players
Show me
FAVORITE
Murder Mystery
Хэллоуин для взрослых
Корпоративный тимбилдинг
4+ игрока
Покажи мне
Зомби!
Adult Halloween parties
Corporate team building
4+ Players
Show me
Mad Max Wasteland
Adult Halloween parties
Competitive team challenges
12+ Players
Show я
Волшебное приключение
Смогут ли ваши дети вовремя помочь волшебному лесу Виспу?
8-12 лет
Покажи мне
ЛЮБИМОЕ
Тайна исследователя
Раскройте древние тайны Египта в Потерянной мумии.
Возраст 10+
Покажите мне
Шпионская миссия
Шпионская миссия по захвату правительственного учреждения.
Возраст от 14 лет
Покажи мне
Путешествие во времени
Почини машину времени, используя реликвии разных эпох.
Возраст 6-9 лет
Покажи мне
Головоломка — замок — 25 долларов
Они немного дороже, чем портфели, но сейфы также могут быть полезны для защиты ваших вещей, когда вы не устраиваете эпические побеги в своем доме!
Независимо от того, требуется ли комбинация или ключ, сейф — идеальное место, чтобы спрятать игровые элементы, кроме того, вы можете наполнить свою игру эпическим тематическим моджо , используя краску, мел, наклейки или другие декоративные элементы, чтобы добавить персонажа. Вы можете возьмите тот, что на картинке на Amazon.
Вы можете возьмите тот, что на картинке на Amazon.
Головоломка — Запертая дверь — Бесплатно
Не позволяйте отсутствию модного оборудования ограничивать ваше творчество.
Вы всегда можете дать своим игрокам листок бумаги, который сообщает им, что они столкнулись с запертой дверью (или сейфом, портфелем и т. д.), и дает некоторую подсказку относительно того, что им нужно сделать, чтобы открыть ее (найти ключ, найти четырехзначный код и др.).
Это фото — один из распечатываемых замков в наборе для вечеринки Escape Room Z.
ПОПРОБУЙТЕ ИГРОВОЙ НАБОР
Головоломка — Запертая коробка — $20
Эти сейфы предназначены для хранения ключа от входной двери и часто используются агентами по недвижимости и хозяевами Airbnb.
Но их также можно использовать для хранения других предметов размером с ключ, таких как золотые монеты, батарейки или подпружиненные пауки. ..
..
Мне нравятся эти головоломки для побега, сделанные своими руками, потому что они кажутся безопасной комбинацией.
Спрячьте снаряжение в шкафчиках на рабочем местеPuzzle — Locked Box — Free
Что может хранить объекты, иметь номера для их идентификации, существовать в фиксированном макете и доступно на вашем рабочем месте?
Шкафчики!
Выбросьте 2-летние закуски и используйте эти коробки с мгновенными головоломками в своей квест-комнате на работе. Просто дайте им подсказку, какая из них содержит то, что нужно, и правило, согласно которому, если они откроют не ту, им всем придется сделать 10 берпи или потерять несколько очков из своего счета.
Загадка может быть простой или сложной на ваше усмотрение. Например, Начать с возраста самого младшего члена команды. Затем сдвиньте влево количество игроков в вашей команде. Затем на одну шестую от самого старшего возраста игроков.
Создайте фото до и послеГоловоломка — наблюдение — бесплатно
Предоставьте фотографию своей квест-комнаты, но включите или удалите один объект. Пока это достаточно очевидно, игроки могут заметить, что это отличается, что привлекает внимание к чему-то.
Пока это достаточно очевидно, игроки могут заметить, что это отличается, что привлекает внимание к чему-то.
Этот пример из нашей распечатанной игры Escape Room Z требует, чтобы игроки заметили пропавшего зомби на Полароиде, вырезали его и наложили на него, чтобы прочитать сообщение.
ПРОВЕРЬТЕ ИГРОВОЙ НАБОР
Головоломка — Запертая коробка — $15
Это ящики со скрытыми ящиками и отсеком. Обычно им требуется некоторое количество критического мышления, чтобы понять, как открыть, что делает их идеальными для вашей квест-комнаты «сделай сам».
Вы можете купить их онлайн , в магазинах головоломок или у таинственных стариков в плащах. Часто они предназначены для хранения денег, но в них так же легко можно спрятать ключ или записку.
Некоторые из них чрезвычайно сложно открыть, и вы не хотите, чтобы ваши игроки слишком долго пытались получить доступ к одному предмету. Поэтому убедитесь, что вы готовы дать подсказки, если ваши игроки застрянут.
Поэтому убедитесь, что вы готовы дать подсказки, если ваши игроки застрянут.
Головоломка — Наблюдение за словами — Бесплатно
Это один из лучших моментов «ага», которые вы можете создать (без использования запрещенной магии). Что-то скрыто на виду, и никто этого не увидит… пока не увидит. Тогда они не могут не увидеть это!
Просто разместите объекты в виде шаблона, как в примере с кухонным столом. Чем нормальнее, тем лучше, главное, чтобы это заметили.
Вы можете увидеть решение здесь…
Ты не пройдешь! … до матаЗадание — Шахматы — Бесплатно
Установите шахматную доску так, чтобы казалось, что она находится в середине игры, и оставьте записку, призывающую игроков поставить мат одним ходом.
В профессиональных квестах это обычно прикреплялось к магниту или к какому-то другому трюку, который что-то менял. Тем не менее, это забавная игра-побег, поэтому просто смоделируйте всю эту магию, написав внизу заметки, что происходит, когда они решают ее.
Например: «Вы не должны проходить через дверь спальни, если не можете поставить мне мат в один ход».
P.S. Не стесняйтесь маркировать пешки и фигуры именами игроков… хахахаха!
Изменить уникальное изображениеЗадача — Сортировка — $10
Разделите готовую подсказку на несколько разных изображений и повесьте их или расположите в неправильном порядке. Как только игроки воссоздадут картинку, они увидят завершенную головоломку, как на картинке.
Вы, , могли бы просто раздать своим игрокам фигуры… или использовать это как дьявольскую возможность отправить их на грандиозный квест масштабов Зельды!
Эта головоломка с квестом очень веселая, когда изображение логически связано с чем-то еще в комнате. Например, этот 4-значный код может быть:
- PIN-код для разблокировки мобильного телефона
- Код для открытия замка на двери телефонной будки
- Игроки набирают номер телефона на стационарном телефоне, чтобы получить звуковую подсказку
Задача — Сортировка — $5
Это умное маленькое число — один из лучших способов помочь игрокам сразу же начать игру с побегом. В конце концов, как только они видят головоломку, они точно знают, как ее решить, что даст им первую подсказку и повысит уверенность в решении более сложных задач.
В конце концов, как только они видят головоломку, они точно знают, как ее решить, что даст им первую подсказку и повысит уверенность в решении более сложных задач.
Начните с написания сообщения, кода или подсказки на обратной стороне пазла. Лучше всего использовать детскую головоломку, состоящую из 30-60 элементов, чтобы игроки не бросили игру в ярости.
Альтернативное решение головоломки — написать заметку или карту на листе бумаги, а затем разорвать его на части.
Затем либо спрячьте детали в запертой коробке , либо спрячьте их в своей самодельной квест-комнате.
Скрыть сообщение лимонным соком.Головоломка — Скрытое сообщение — $19
Это старый школьный фокус из детства. Когда вы держите лист бумаги над свечой, появляется сообщение, как будто его пишет призрак.
Магия квеста своими руками во всей красе.
Просто возьмите немного лимонного сока и кисть или ватные наушники. Окуните его в лимонный сок и напишите все, что хотите. Вам понадобится где-нибудь поблизости свеча или зажигалка, а также причина, по которой игроки присоединятся к делу. Хороший намек — написать «Я освещаю путь к Х» сбоку от свечи (или что-то подобное, что больше подходит к ним, чем к пиратам 😉 )
Вам понадобится где-нибудь поблизости свеча или зажигалка, а также причина, по которой игроки присоединятся к делу. Хороший намек — написать «Я освещаю путь к Х» сбоку от свечи (или что-то подобное, что больше подходит к ним, чем к пиратам 😉 )
Наконец, сделайте ваше сообщение наградой, так как игрокам придется решить головоломку, чтобы прочитать его. Помните, вы хотите, чтобы все находились на стадии потока, когда все сложно, но не слишком сложно.
Вставьте неправильное количество батареекГоловоломка — логическое соединение — бесплатно
Этот простой лайфхак превращает скучный просмотр телевизора в захватывающий момент «ага». Он основан на том факте, что когда вы проектируете квест-комнату дома, везде будет мусор. В конце концов — это в вашей гостиной.
Это означает, что игроки, как правило, будут игнорировать такие вещи, как выключенный телевизор, даже если его включение покажет подсказку на экране.
Чтобы настроить это, нужно запереть набор батареек в маленькой коробке , что поначалу озадачит игроков, потому что не во что их положить. разблокируйте другую коробку, в которой скрытно находится пульт. В тот момент, когда оба игрока будут замечены, игроки установят связь и лихорадочно поспешат включить телевизор, который покажет подсказку или решение.
разблокируйте другую коробку, в которой скрытно находится пульт. В тот момент, когда оба игрока будут замечены, игроки установят связь и лихорадочно поспешат включить телевизор, который покажет подсказку или решение.
Несколько хороших идей для демонстрации:
- Видео на YouTube, где вы/друг что-то объясняете. Это можно записать и загрузить с телефона. Затем просто откройте приватное видео на своем Smart TV/ноутбуке и нажмите на паузу, чтобы оно не воспроизводилось. Затем выключите телевизор, чтобы игроки могли его «найти».
- Шоу Netflix, название которого является ключевым словом, необходимым для сортировки объектов, как в головоломке Popsicle Puzzle.
Еще один забавный трюк — взять фонарик с черным светом и использовать его вместо пульта от телевизора. Всегда весело 😉
Переставить известную последовательностьГоловоломка — Наблюдение — Бесплатно
Престо чанго! Эта задача может полностью вывести из строя людей, когда они понимают, что происходит. Все, что вам нужно сделать, это взять очень известную последовательность и изменить ее.
Все, что вам нужно сделать, это взять очень известную последовательность и изменить ее.
Например:
- Поменяйте местами клавиши клавиатуры, чтобы они находились в разных положениях. Затем напишите заметку, используя код, который можно взломать, сравнив с обычным макетом. Это не сработает на ноутбуке Mac, но на клавиатуре старой школы вы можете оторвать клавиши и вернуть их в неправильном порядке.
- Перемешать общий заголовок, например NEW YORK TIMES > NWE ORYK IMSET . Это идеально подходит для того, чтобы дать игрокам подсказку для более сложной головоломки, поскольку ее можно решить, не нуждаясь в собственной подсказке.
- Нарисуйте радугу, расставив цвета в неправильном порядке, и вставьте букву/слово каждого цвета. При правильной сортировке он показывает ответ.
Просто убедитесь, что вы используете что-то мега-известное, поддерживающее разные культуры, возрасты и интересы.
Чашка игральных костей может рассказать историюГоловоломка — Сортировка — $3
Но нет, на этот раз мы говорим не о ролевых играх.
В этой простой головоломке с побегом вы найдете слово из 3-6 букв, которое очень легко решить. Просто напишите по одной букве на каждой стороне игральной кости:
- Вам понадобится 6 кубиков, чтобы составить слово из 6 букв. Мы собираемся использовать JOHNSON.
- Расставь их по порядку и напиши буквы над цифрами 1-6.
- Когда игроки расставят кубики в правильном порядке, они увидят ваше сообщение.
Эта головоломка удивительна тем, что дает ключевое слово шифра
или комбинацию букв из 4-5 цифр для велосипедного замка
. Собери пазл в удобоваримых пропорцияхПазл — Сортировка — $3
Поскольку все любят еду и игры с побегами, мы собираемся объединить их. Приз? Вкусные глотки добра.
Просто возьмите любой простой рецепт, например пирожных, и каким-нибудь образом закодируйте рецепт. Не все, так как расшифровка может занять целую вечность, но достаточно, чтобы игрокам пришлось работать вместе.
Вы даже можете использовать эту головоломку в качестве финальной головоломки при разработке собственного квеста — каждая вторая головоломка дает игрокам подсказку для расшифровки рецепта, который они затем могут приготовить вместе.
Ням!
Слишком много головоломок? Скачать полный квест:
Взрослые
Дети
Шпионская миссия
Подростковые вечеринки на Хэллоуин 14+
Отлично подходит для школьных лагерей
4+ Игроки
9
ЛЮБИМОЕ
Тайное убийство
Хэллоуин для взрослых
Корпоративный тимбилдинг
4+ игрока
Взрослые вечеринки на Хэллоуин
Корпоративная команда здание
4+ игроки
Show Me
Mad Max Wasteland
Halloween Halloween
Соревновательная команда
Взрослые партии
. 0149
0149
12+ игроков
Покажите мне
Волшебное приключение
Смогут ли ваши дети вовремя помочь волшебному лесу Виспу?
Возраст 8-12 лет
Покажи мне
ЛЮБИМОЕ
Тайна исследователя
Раскопай древние тайны Египта в Потерянной мумии.
Возраст 10+
Покажите мне
Шпионская миссия
Шпионская миссия по захвату правительственного учреждения.
Возраст от 14 лет
Покажи мне
Путешествие во времени
Почини машину времени, используя реликвии разных эпох.
Для детей от 6 до 9 лет
Покажи мне
Головоломка — поиск — $5
Blacklights — самая часто используемая головоломка во всем мире квестов.
Если вы находитесь в профессиональной квест-комнате, то черный свет — это такая же новинка, как утренний завтрак.
Однако загадочные чудеса в квест-комнате «Сделай сам» — это чистая радость, пропитанная волшебством.
Напишите секретное сообщение невидимыми чернилами ( вот рецепт ), которые можно увидеть только в темноте. Вы также можете Превратить фонарик вашего телефона в черный фонарь с помощью скотча и фломастеров! Это может быть отличной наградой за разблокировку очень маленькой коробки, поскольку это просто кусок прозрачной ленты.
Используйте силу магнитов!Игра — Испытание на ловкость — 5 долларов + строка
Бросьте что-нибудь магнитное (может быть, ключ?) туда, где его нельзя будет достать (буквально или потому, что вы сказали об этом своим игрокам). Подготовьте магнит и отрезок веревки или проволоки. Требуйте от своих игроков комбинировать предметы и высвободить своего внутреннего МакГайвера, чтобы решить эту задачу!
Ваша миссия. .. починить блок предохранителей
.. починить блок предохранителей Головоломка — Логическая связь — Бесплатно
Хотите почувствовать себя участником невыполнимой миссии? Угу, да!!!
Все эти выключатели в вашем блоке предохранителей управляют разными комнатами в вашем доме. Это позволяет вам предоставить электрическое устройство, которое не работает, как часть многоступенчатой головоломки .
Соберите головоломку, требующую от игроков использования электрического устройства, например ноутбука. Например, создайте папку с четким названием, относящимся к игре («БИО ТОКСИНЫ» или «РАСПОЛОЖЕНИЕ ВОЙСК»), и включите в нее подсказку. Затем дайте аккумулятору ноутбука полностью разрядиться.
Затем подключите ноутбук к розетке, но отключите питание в этой комнате или розетке с помощью блока предохранителей. Когда игроки отправляются искать подсказку, а ноутбук не включается, им нужно выяснить, почему.
Убедитесь, что игрокам ясно, что блок предохранителей является частью игры (приведите их к нему кровавым следом или отметьте все предметы, связанные с игрой, наклейкой с красной точкой)
Отправьтесь в онлайн-охоту за мусоромЗадача — Поиск — Бесплатно
Представьте себе: вы ловко спрятали URL-адрес среди газетных вырезок на столе вашего пропавшего детектива.
Ваши игроки находят URL-адрес, загружают древний рабочий стол и переходят на веб-сайт, который вы специально для них подготовили, указывая им на следующую подсказку…
Звучит слишком громко? Не волнуйся; с современными онлайн-инструментами это намного проще, чем кажется!
Я не умею делать сайт. Разве это не супер сложно?
Вы можете создать бесплатный веб-сайт за 10 минут, используя службу Google под названием Blogger . Его так же легко настроить, как учетную запись электронной почты. Просто войдите, создайте новую страницу и добавьте туда свою подсказку.
Показанный выше пример свидания был создан в Blogger.
Как мне использовать Minecraft в игре с побегом?
В игре Minecraft можно сделать, ну, что угодно…
Включая головоломки квестов:
- Просто: создайте последовательность цветов или сообщение на стене или сделайте узор из стопок блоков разного размера.
- Дополнительно: создайте хранилище с вводом пароля, например в этом видео .

Insane: создайте целую комнату-головоломку, которая дополнит вашу реальную комнату квеста!
Вот несколько идей для создания веб-контента для вашей игры:- Создайте веб-страницу и добавьте на нее головоломку или скройте подсказки в сообщении. Вот пример того, что начинается с приключения побега на свидание .
- Если в вашем наборе инструментов есть волшебство по созданию видео, сделайте видео на YouTube. Вы можете использовать его для создания сцены или продемонстрировать задачу, которую должны выполнить игроки, например, смешать две жидкости в «научном эксперименте».
- Создайте пост или твит в Facebook, содержащий подсказку или закодированное сообщение.
- Предоставьте закодированное сообщение (возможно, шрифтом Брайля или кодом Морзе ) и оставьте ссылку на веб-сайт, который можно использовать для его расшифровки.
- Электронная почта Ножницы для бумаги с вашей подсказкой, и я создам подстраницу на веб-сайте для вас!
- Собери пазл Minecraft
Задача — логическое соединение — бесплатно
Расслабляться. Вы знаете, что такое QR-код, даже если не знали, как они называются.
Вы знаете, что такое QR-код, даже если не знали, как они называются.
QR-коды — это странные блочные квадратные изображения, которые вы видите на оборотной стороне бутылок с соусом, на которые никто никогда не смотрит… но они делают суперэпическую высокотехнологичную функцию побега . И вашим игрокам намного проще использовать их, чем длинный URL-адрес веб-сайта, который им нужно ввести. Интернет. Например, приведенный выше QR-код взят из комплекта Escape Room Z 9.0824 . Это приводит игроков к онлайн-сейфу, который они должны взломать.
Разрежьте свой QR-код на кусочки головоломки (протестируйте его и убедитесь, что он все еще работает после того, как вы это сделаете!), спрячьте его под предметом или в секретном отделении или оставьте на виду и ждите, пока ваши игроки спросят себя «Что это делает?»
Этот QR-код идеально подходит для моего научно-фантастического путешествия во времени! Как мне сделать один?
Это очень легко. Просто перейдите к этому генератору QR-кода и следуйте инструкциям!
Запишите сверхсекретные файлы на USB-накопительЗадача — логическое соединение — $15
Вам не нужен интернет, чтобы предоставлять подсказки в цифровом формате. Поместив подсказку или головоломку на USB-накопитель и спрятав его где-нибудь в своей квест-комнате, вы получите немыслимое количество забавных вариантов.
Поместив подсказку или головоломку на USB-накопитель и спрятав его где-нибудь в своей квест-комнате, вы получите немыслимое количество забавных вариантов.
- Аудиофайл разговора может дать подсказку или головоломку (вы можете легко создать ее с помощью диктофона на телефоне).
- Сделайте короткое видео , показывающее угол комнаты, в которой находятся игроки, но добавьте один дополнительный объект с номером сбоку (опять же, вы можете снять видео с помощью телефона).
- Если вы делаете суперсложную игру с побегом, создайте документ Word и сохраните важную подсказку или решение в свойствах автора. Это не будет интуитивно понятным, поэтому дайте своим игрокам подсказку, чтобы указать им правильное направление.
Головоломка — Скрытое сообщение — Стоимость бумаги
Эти головоломки включают в себя лист бумаги с сообщением, скрытым «визуальным шумом». Когда игроки кладут либо вторую страницу со стратегически расположенными отверстиями, либо кусок цветного ацетата поверх страницы, «шум» скрывается, оставляя сообщение четким.
Когда игроки кладут либо вторую страницу со стратегически расположенными отверстиями, либо кусок цветного ацетата поверх страницы, «шум» скрывается, оставляя сообщение четким.
Без «ключа» ваше сообщение может быть скрыто под эльфийским плащом-невидимкой!
Как сделать код визуального наложения?
Вот несколько онлайн-руководств по созданию различных типов скрытых сообщений, для решения которых требуется наложение:
Наложение сетки для печати дома
«Секретный декодер открыток»
Простое закодированное сообщение красного цвета
Инструкции красного цвета со ссылкой на загрузку файла примера Photoshop
Головоломки — Головоломки — $15
Не забудьте придумать эпическую историю, объясняющую, почему вашим игрокам нужно решать эти потенциально приводящие в бешенство головоломки.
Например, «разделите эти объекты, чтобы открыть портал».
Простая записка вместе с дополнительной опорой — это все, что требуется, и это дает вам очень простую головоломку «Сделай сам».
- Прикрепите ключ к одной из частей и привяжите их к чему-нибудь неподвижному. Когда игроки разделяют части, они могут использовать ключ в запертой двери. Если ваша головоломка не подходит к ключу, просто привяжите ее к одной из частей с помощью веревки и записки с надписью «Невозможно использовать, пока не будет разделена». В конце концов, ты делаешь это для друзей, а не ради побега.
- Используйте вес одной из частей в качестве пароля или комбинации. Просто оставьте комбинированную головоломку на цифровых кухонных весах рядом с замком. Игроки поймут идею.
Итак, у вас есть головоломки, что дальше? Используйте этот шаблон, чтобы объединить их в эпическое приключение в квесте «Сделай сам»!
Это просто . Набор для сборки представляет собой простой в использовании шаблон со всеми основными инструкциями, необходимыми для быстрой разработки игры . Просто введите свой адрес электронной почты ниже, и мы вышлем вам комплект БЕСПЛАТНО. Сладкая сделка, правда?!
Просто введите свой адрес электронной почты ниже, и мы вышлем вам комплект БЕСПЛАТНО. Сладкая сделка, правда?!
Задача — Поиск — $10
Поскольку это не профессиональный квест, вы можете заклеить области и объяснить, почему игроки не могут получить к ним доступ. Это дает вам множество вариантов, требующих творческого решения проблем для извлечения предметов из ваших закрытых областей.
Например:
- Ключ, «застрявший» за дверью душа, с запиской « Магически запечатан Высшими Волшебниками» . Игроки сразу видят, что им нужно найти способ получить ключи, не открывая дверь. Если на крючке для ключей рядом с входной дверью зловеще висит магнит, совершенно ясно, что должно произойти.
- Заблокируйте области полицейской лентой или даже липкой лентой и прикрепите записку с описанием того, как игроки могут с ней взаимодействовать. Например, Яма зыбучих песков. Без доски для серфинга не пересечь.

Головоломка — Математическая задача — Бесплатно
Если вы разрабатываете игру для детей, вы всегда можете использовать соответствующие возрасту математические уравнения для представления числового кода. Просто не забудьте сделать это актуальным и интересным, только тролли любят математику ради математики!
В нашей распечатанной игре-квесте The Lost Mummy игрокам предлагается решить несколько уравнений, после чего следует загадка, которая показывает правильную последовательность ответов.
ПОПРОБУЙТЕ ИГРОВОЙ НАБОР
Игра — испытание на точность — бесплатно, если у вас есть пистолет NERF
Просто возьмите пистолет NERF, несколько мишеней и достаточно боеприпасов, чтобы пробиться сквозь полчища орков у вашего порога.
Вы можете придумывать любые правила. Например, по одному выстрелу или точкам для разных объектов.
Убедитесь, что ваши игроки знают о наказании за огонь по своим. .. если только ваш квест не заканчивается смертельным матчем…
.. если только ваш квест не заканчивается смертельным матчем…
Цели в этом видео взяты из нашего набора для печати Квест Z.
ПРОВЕРЬТЕ НАБОР ИГРЫ
Игра — испытание на ловкость — 5 долларов за веревку
Сделайте веревочную полосу препятствий, как системы обнаружения лазеров в фильмах. Тогда не так-то просто ниндзя-пролистывать свой путь через это!
Чтобы усложнить задачу, повесьте на веревочки маленькие колокольчики и заставьте игроков вернуться и повторить попытку, если один из них зазвенит.
Детям нравится полоса препятствий, и вы можете сделать ее сами!
Полоса препятствийИгра — испытание на силу/ловкость — бесплатно
Немного воображения может превратить дешевую и простую полосу препятствий в волшебный квест невероятных масштабов!
Вот простой учебник по полосе препятствий для маленьких детей.
Игра — физическое испытание — бесплатно
На улице жарко? Вашей команде нужен , чтобы охладиться? Возможно, последним испытанием в вашей игре будет уничтожение врагов (из водяных пистолетов)! Или пройти через двор, не попадая под брызги кислоты (прерывистое орошение газона). Или пробежать полосу препятствий, неся драгоценные инопланетные яйца (воздушные шарики с водой).
Оружие из изоленты??? МакГайвер одобряет!
Зефир пусковая установкаИгра — Испытание на точность — $15
Действительно! Кому не понравится пусковая установка для зефира?!
Вот видео , в котором показано, как сделать пусковую установку для зефира из лапши для бассейна, воздушного шара и скотча.
Построить фортИгра — Строительство — $5–$30
Если игроки не могут победить врага, возможно, им нужно защитить себя от него. Дайте игрокам коллекцию объектов и ограниченное количество времени на строительство укреплений. Объектами могут быть одиночные чашки, зефир и кусочки спагетти (сырые) или игральные карты.
Объектами могут быть одиночные чашки, зефир и кусочки спагетти (сырые) или игральные карты.
Последний форт претендует на победу!
Теперь иди и закончи свою игру!
Итак, вдохновил ли этот список гениальных идей?
Готовы ли вы закончить свою игру и предложить своим друзьям, коллегам, студентам, молодежной группе, семье и команде восхитительный, сложный, незабываемый опыт?
Вы завершили самую сложную часть, так что дайте себе заслуженную похвалу. Затем вернитесь к пошаговому руководству 9 .0824 и закончи игру!
Чего ты ждешь?
Тогда вперед!
Нужна фора? Загрузите бесплатный Builder’s Kit, чтобы получить полезные инструкции и шаблоны для быстрого старта:
Не суетитесь. «Сделай это», распечатав готовую к игре побег:
В спешке, спешу? Возьмите один из этих наборов для квестов, которые можно распечатать.
Они мгновенно загружаются и готовы к печати и вечеринкам.
Вы даже можете редактировать игру, используя PowerPoint, чтобы добавить свой собственный стиль и головоломки.
Взрослые
Дети
Spy Mission
Teen Halloween Parties 14+
Отличный для школьных лагерей
45.
Show Me
Show Me
3
Show Me
.
Корпоративный тимбилдинг
4+ игрока
Покажи мне
Зомби!
Хэллоуин для взрослых
Corporate team building
4+ Players
Show me
Mad Max Wasteland
Adult Halloween parties
Competitive team challenges
12+ Players
Show me
Magical adventure
Смогут ли ваши дети вовремя помочь волшебному лесу Виспу?
Возраст 8-12 лет
Покажи мне
ИЗБРАННОЕ
Тайна исследователя
Раскройте древние тайны Египта в Потерянной Мумии.
Возраст 10+
Покажите мне
Шпионская миссия
Шпионская миссия по захвату правительственного учреждения.
Возраст от 14 лет
Покажи мне
Путешествие во времени
Почини машину времени, используя реликвии разных эпох.
Возраст 6-9 лет
Покажи мне
Ого.
Сэкономьте огромные $$, захватив целую коробку спасательных наборов:
KIDS BOX $49
4x Escape Room Kits
Lost Mummy
Rebel Revolt
Escape Quest
Bonus: Treasure Map Pack
Show Me
HALLOWEEN BOX $49
4 набора квестов
Escape Room Z
Потерянная мумия
Rebel Revolt
Бонус: хэллоуинские постеры
Bonus Xtraus 9000149
Бонус: Пакет карты сокровищ
Show Me
VIP-бокс $ 99
Все наши комплекты Escape Room (6x)
5x Kids Edu-Venture Games
VIP VIP VIP VIP.

Envy, Lost Mummy,
Escape Room Z, Rebel Revolt, Escape Quest и FrostНабор карт сокровищ
Карточная игра Skulls
Наборы для Хэллоуина, Дня Благодарения и Рождества
Пожизненные БЕСПЛАТНЫЕ копии всех будущих игр. Бум!
Show Me
KIDS BOX $49
4x Escape Room Kits for
Lost Mummy
Rebel Revolt
Escape Quest
Bonus: Treasure Map Pack
Show Me
HALLOWEEN BOX $49
4 набора квестов
Escape Room Z
Потерянная мумия
Rebel Revolt
Бонус: плакаты Хэллоуина
Бонус: игры XTRA + головоломки
Бонус: карта сокровищ
Покажите мне
VIP -бокс $ 99
Все наши Escape Kits (7x)
$ 9
.

 Повышаем
познавательный интерес и уверенность в себе.
Повышаем
познавательный интерес и уверенность в себе.
 Для той, что посередине, вероятность получит тайл в четыре раза больше, чем для любой внешней подходящей позиции, потому что у нее четыре общих края с ранее размещенными тайлами, а не только одна.
Для той, что посередине, вероятность получит тайл в четыре раза больше, чем для любой внешней подходящей позиции, потому что у нее четыре общих края с ранее размещенными тайлами, а не только одна. Сможете ли вы найти симметричный узор, обладающую этим свойством?
Сможете ли вы найти симметричный узор, обладающую этим свойством?
 Это будет работать для одностороннего сообщения. Если вы хотите сделать двухстороннее сообщение (например, то, что было выше), вам нужно помнить, что вы собираетесь повернуть головоломку на 180 градусов (сообщение будет выглядеть вверх ногами по сравнению с первой частью) и что ваша вторая часть появится в строках, которые вы не использовали для первой части.
Это будет работать для одностороннего сообщения. Если вы хотите сделать двухстороннее сообщение (например, то, что было выше), вам нужно помнить, что вы собираетесь повернуть головоломку на 180 градусов (сообщение будет выглядеть вверх ногами по сравнению с первой частью) и что ваша вторая часть появится в строках, которые вы не использовали для первой части.  Для моего 3-летнего ребенка у меня есть пазлы, состоящие всего из 3-4 частей. Малыши тоже любят собирать пазлы.
Для моего 3-летнего ребенка у меня есть пазлы, состоящие всего из 3-4 частей. Малыши тоже любят собирать пазлы. Каждая коробка будет составлять две головоломки, так что сохраните другую сторону.
Каждая коробка будет составлять две головоломки, так что сохраните другую сторону. Карандаш тоже подойдет.
Карандаш тоже подойдет.
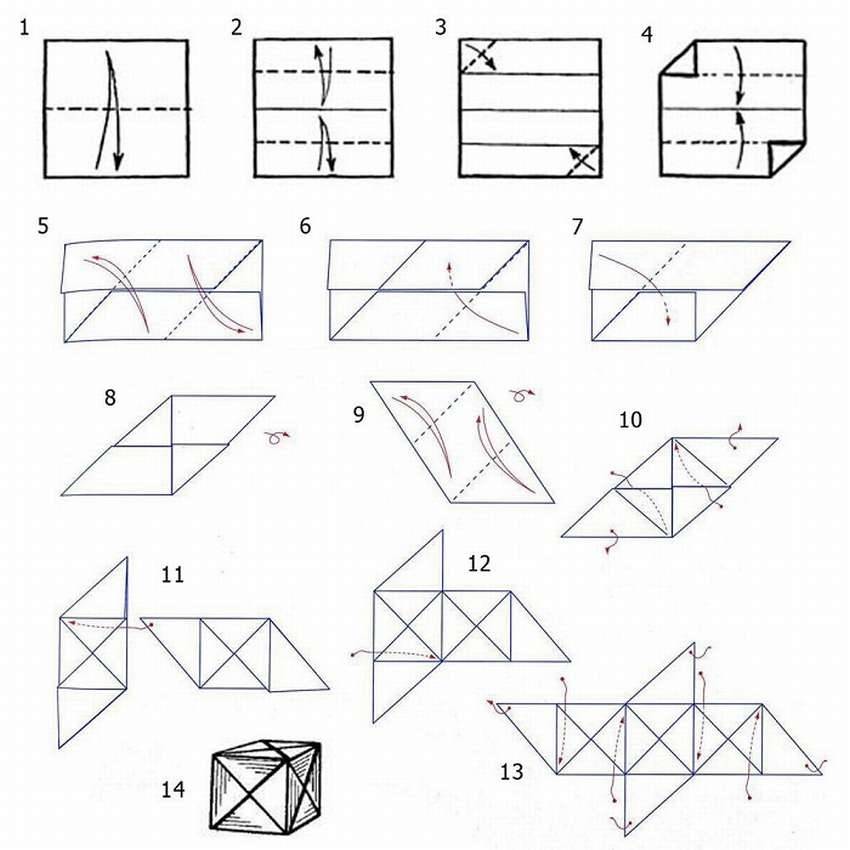 Подождите 5 секунд, затем плавным, равномерным движением снимите бумажную подложку с трансфера. Вот как можно сделать свою собственную головоломку с помощью термопресса!
Подождите 5 секунд, затем плавным, равномерным движением снимите бумажную подложку с трансфера. Вот как можно сделать свою собственную головоломку с помощью термопресса! Теперь у вас есть собственная головоломка!
Теперь у вас есть собственная головоломка!

 Подождите 3 секунды и снимите бумажную подложку с трансфера плавным, равномерным движением, пока трансфер еще горячий.
Подождите 3 секунды и снимите бумажную подложку с трансфера плавным, равномерным движением, пока трансфер еще горячий.
 Вот еще один пример фото до/после.
Вот еще один пример фото до/после. 

 Игроки по-прежнему могут наслаждаться охотой, но они точно узнают, когда им удастся найти что-то важное.
Игроки по-прежнему могут наслаждаться охотой, но они точно узнают, когда им удастся найти что-то важное.



