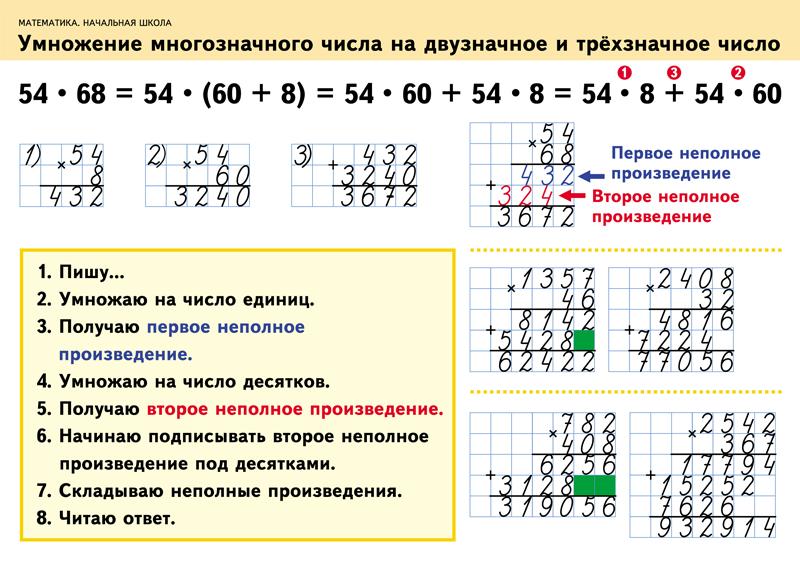
Алгоритм умножения столбиком

Основная дидактическая цель урока: познакомить с алгоритмом умножения столбиком, актуализировать знания о действии умножения, полученные ранее, создать условия для усвоения алгоритма умножения многозначного числа на однозначное и многозначное число; отрабатывать навыки устных вычислений; учить детей формулировать проблему, выдвигать гипотезы и находить правильное решение; развивать мышление, грамотную математическую речь.

УУД:

• Личностные: формирование представлений о математике как о части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества; развитие логического и критического мышления, умения работать в парах, группе, команде, уважение мнения товарищей; развитие интереса к математическому творчеству, исследованию и поисковой деятельности.
• Регулятивные: принимать и сохранять учебную задачу; учитывать выделенные учителем ориентиры действия в новом учебном материале, в сотрудничестве с учителем; планировать свои действия в соответствии с поставленной задачей и условиями её реализации, в том числе во внутреннем плане; оценивать правильность выполнения действия на уровне адекватной оценки соответствия результатов, требованиям данной задачи и задачной области; различать способ и результат действия;
• Познавательные: использовать знаково-символические средства и схемы для решения задач; анализировать и осмысливать текст задачи; строить сообщения в устной и письменной форме, логические цепочки; доказывать и опровергать утверждения, классифицировать по разным основаниям, выбирать существенное, устанавливать аналогии; уметь сравнивать, выделять общее, делать вывод; контролировать и оценивать результат деятельности; ставить, формулировать и решать проблемы.
• Коммуникативные: адекватно использовать коммуникативные, прежде всего речевые, средства для решения различных коммуникативных задач, строить монологическое высказывание, учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве; формулировать собственное мнение и позицию; договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов; строить понятные для партнёра высказывания, учитывающие, что партнёр знает и видит, а что нет; задавать вопросы; контролировать действия партнёра; использовать речь для регуляции своего действия;

Сценарий урока

I. Организационный момент

II. Определение темы и цели урока

На доске (слайд):

56*24	13*24	74*49
56*49	13*11	7*11

— Рассмотрите выражения.

— Чем они похожи?

— Чем мы будем заниматься на уроке?

— Придумайте задания с этими выражениями. (Прочитать выражения разными способами. Придумать задачи к данным выражениям. Не вычисляя расположить в порядке возрастания.)

— Значение какого выражения найти легко?

III. Устный счет

Ни костяшек, ни ручек, ни мела —
Устный счет. Мы творим это дело
Только силой ума и души!
Числа сходятся где-то во тьме,
И глаза начинают светиться!
И кругом только умные лица.
Устный счет! Мы считаем в уме.

1. Сегодня я научу вас умножать двузначное число на 11.

— Кто может объяснить по схеме, как умножить двузначное число на 11? (При умножении двузначного числа на 11 получается трехзначное число. Между цифрами, образующими двузначное число, помещаем цифру, которая обозначает сумму двух крайних цифр. )

Случай с переходом через разряд.

Вычислите.

45*11=	26*11=	34*11=
23*11=	72*11=	81*11=

IV. Работа по теме урока

1. Работа по учебнику.

• №53,стр. 22 (Коллективное выполнение с комментированием.)
• 2052*3
• №54, стр.23 (По заданию учебника)
• 2052*23

Предлагается повторить способ умножения столбиком многозначного числа на однозначное и двузначное. При этом речь идет не только о повторении этого способа умножения в практическом плане для конкретного случая умножения, но и о повторении соответствующих теоретических позициях, описывающие все возможные ситуации.

• №55,стр. 24 (По заданию учебника. Знакомство с алгоритмом умножения столбиком по словарику учебника (с.116))
• 2052*123

Учащимся предлагается сформулировать алгоритм умножения столбиком, отметив на соответствующие вопросы и опираясь на данный пример.

V. Физкультминутка

Раз, два, три, четыре, пять (шаги на месте)!
Все мы умеем считать (хлопки в ладоши),
Отдыхать умеем тоже (прыжки на месте).
Руки за спину положим (руки за спину),

Голову поднимаем выше (поднять голову выше)
И легко — легко подышим (глубокий вдох).
Подтянитесь на носочках столько раз,
Ровно столько, сколько пальцев (показали, сколько пальцев на руках)
На руке у вас (поднимаемся на носочках 10 раз).

VI. Закрепление изученного материала

1. Работа по учебнику

• №56,стр.24(В парах)
• № 57,стр.24(Самостоятельная работа, с проверкой у доски)

2. Работа в группах.

Для этого необходимо вычислить выражения. У каждого на парте лежит выражение, вычислите его. Результат вычисления совпадет с цветом вашей команды.

Деление на группы

• 608*47=28576-красный
• 537*98=52626-оранжевый
• 784*79=-61936-зеленый
• 235*56=13160-синий

Делятся на группы в зависимости от цвета команды.

• 1 группа (красные) — соберет урожай овощей.
• 2 группа (оранжевые) — построит лесенку.
• 3 группа (зеленые) — построят замок.
• 4 группа (синие) — найдут лишнее.

Задача (1 группа).

С первого участка собрали 42 огурца, со второго участка — в 11 раз больше, чем с первого участка, а с третьего — в 65 раз больше, чем со второго. Сколько всего огурцов собрали с трех участков?

Решение:

1) 42*11=462(ог.) — на втором участке;

2) 462*65=30030(ог.) — на третьем участке;

3) 42+462+30030=30534(ог.) — всего.

Ответ:30534огурца всего собрали.

Построй лесенку (2 группа).

Вычисли выражения. Распредели выражения в виде лесенки в порядке убывания в зависимости от результатов вычисления.

1) 483*56=27048

2) 1746*8=13968

3) 879*658=578382

4) 578382 27048 13968

Построй замок (3 группа).

Собери замок из 3 комнат. Найди площадь всего замка.

• 1 комната — длина 76 м, ширина — 42 м;
• 2 комната — длина 84 м, ширина — 13м;
• 3 комната — длина 69 м, ширина — 34 м.

Решение:

1) 76*42=3192 кв. м — S 1 комнаты;

2) 84*13=1092 кв. м — S 2 комнаты;

3) 69*34=2346 кв. м -S 3 комнаты;

4) 3192+1092+2346=6630 кв. м — S всего замка.

Ответ: 6630 кв. м площадь всего замка.

Создай пару (4 группа).

240см*58=13920 см	139 м 20 см
563 см*74=41662 см	416620 мм
709 м*67=47503 м	4750300 см

Проверка каждого задания. Задания высвечиваются на слайдах.

VII. Итог урока

Ребята могут самостоятельно оценит себя и своих товарищей, выделить тех, то принес больше баллов своей команде.

• Как связана тема урока с той работой, которую вы выполняли?
• Помогли ли вам в работе умения вычислять в столбик?
• Достигли ли мы на уроке нашей цели?
• Все ли работы были выполнены с использованием способа умножения в столбик?

IX. Рефлексия

На доске слайд:

— У каждого из вас на столе карточка (зеленая, желтая, красная). Уходя из класса, прикрепите на доску одну из них.

Карточка зеленого цвета обозначает: “Я удовлетворен уроком, урок был полезен для меня, я много, с пользой и хорошо работал на уроке и получил заслуженную оценку, я понимал все, о чем говорилось и делалось на уроке”.

Карточка желтого цвета обозначает: “Урок был интересен, я принимал в нем активное участие, урок был в определенной степени полезен для меня, я отвечал с места, я сумел выполнить ряд заданий, мне было на уроке достаточно комфортно”.

Карточка красного цвета обозначает: “Пользы от урока я получил мало, я не очень понимал, о чем идет речь, мне это не очень нужно, к ответам на уроке я был не готов”.

X. Домашнее задание

Тетрадь для самостоятельной работы: №22-24, стр.17.

ГДЗ по математике 3 класс учебник Моро, Волкова 1 часть

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бантова М. А.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

❤️️Ответ к странице 38. Математика 3 класс учебник 1 часть. Автор: М.И. Моро.

Решебник — страница 38Готовое домашнее задание

Номер 1.

1) Нарисуй 12 кружков, а треугольников в 3 раза меньше, чем кружков.
2) Нарисуй 12 красных кружков, а синих на 3 меньше, чем красных.

Ответ:

1) 12 : 3 = 4     Ответ: 4 треугольника.

2) 12 − 3 = 9     Ответ: 9 кружков.

Номер 2.

Проверь, верны ли равенства и неравенства.

Ответ:

4 ∙ 7 + 4 = 4 ∙ 8 – верно, так как слева 4 повторяется 8 раз (сначала 7 раз, потом добавляем еще одну 4), также как и справа.
3 ∙ 8 + 3 < 3 ∙ 9 – неверно, так как слева 3 повторяется 9 раз (сначала 8 раз, потом добавляем еще одну 3), также как и справа, значит выражения равны.
35 − (5 + 7) < 30 – верно, так как слева результат выражения равен 23. 48 + (14 − 12) > 50 – неверно, так как результат выражения слева равен 50.
36 : 4 < 36 – верно, так как слева результат выражения равен 9. 27 : 3 < 10 – верно, так как слева результат выражения равен 9.

Номер 3.

(Устно.) Назови в каждом уравнении значение х. Чем отличается одно уравнение от других?

Ответ:

х ∙ 7 = 14    х : 3 = 6    1 ∙ х = х х = 14 : 7    х = 6 ∙ 3    1 ∙ 3 = 3 х = 2           х = 18
Первое уравнение отличается от других, потому что оно решается умножением, а два других делением. Третье уравнение отличается от других, потому что значение Х может быть любым, так как при умножении любого числа на 1 получается тоже самое число.

Номер 4.

Ответ:

7 ∙ 4 = 28    24 : 6 = 4 3 ∙ 9 = 27    21 : 7 = 3 2 ∙ 3 = 6      27 : 9 = 3

Номер 5.

В школьный буфет привезли в ящиках 36 кг яблок, по 9 кг в каждом ящике. Сколько ящиков яблок привезли в буфет? Составь и реши две задачи, обратные данной.

Ответ:

36 : 9 = 4 (ящ.) Ответ: 4 ящика привезли в буфет.
Обратная задача 1: В школьный буфет привезли 4 ящика яблок, по 9 кг в каждом ящике. Сколько кг яблок привезли в буфет? 9 ∙ 4 = 36 (кг) Ответ: 36 кг яблок привезли в буфет.
Обратная задача 2: В школьный буфет привезли 36 кг яблок в 4 ящиках. Сколько кг яблок было в каждом ящике? 36 : 4 = 9 (кг) Ответ: 9 кг яблок в каждом ящике.

Номер 6.

Проверь, знаешь ли ты таблицу умножения на 3; на 4 (называй результат и проверяй по таблице на обороте обложки).

Ответ:

1 ∙ 3 = 3 2 ∙ 3 = 6 3 ∙ 3 = 9 4 ∙ 3 = 12 5 ∙ 3 = 15 6 ∙ 3 = 18
7 ∙ 3 = 21 8 ∙ 3 = 24 9 ∙ 3 = 27 10 ∙ 3 = 30
1 ∙ 4 = 4 2 ∙ 4 = 8 3 ∙ 4 = 12 4 ∙ 4 = 16 5 ∙ 4 = 20 6 ∙ 4 = 24
7 ∙ 4 = 28 8 ∙ 4 = 32 9 ∙ 4 = 36 10 ∙ 4 = 40

Задание внизу страницы

У хозяйки 15 цыплят, а утят в 3 раза меньше. Сколько утят у хозяйки?

Ответ:

15 : 3 = 5 (ут.) Ответ: у хозяйки 5 утят.

Задание на полях страницы

Какое число лишнее?

Ответ:

Лишнее число 30, потому что оно не делится на 4 без остатка. Лишнее число 8, потому что оно однозначное, а остальные числа двузначные.

Рейтинг

Выберите другую страницу

1 часть

2 часть

Ваше сообщение отправлено!

+

Строки.

Итак, о работе со строками мы немного поговорили, теперь поговорим о функциях и методах строк.

Я постарался собрать здесь все строковые методы и функции, но если я что-то забыл — поправляйте.

Базовые операции

• Конкатенация (сложение)

  >>> S1 = 'spam'
  >>> S2 = 'eggs'
  >>> print(S1 + S2)
  'spameggs'

• Дублирование строки

  >>> print('spam' * 3)
  spamspamspam

• Длина строки (функция len)

  >>> len('spam')
  4

• Доступ по индексу

  >>> S = 'spam'
  >>> S[0]
  's'
  >>> S[2]
  'a'
  >>> S[-2]
  'a'

  Как видно из примера, в Python возможен и доступ по отрицательному индексу, при этом отсчет идет от конца строки.

• Извлечение среза

  Оператор извлечения среза: [X:Y]. X – начало среза, а Y – окончание;

  символ с номером Y в срез не входит. По умолчанию первый индекс равен 0, а второй — длине строки.

  >>> s = 'spameggs'
  >>> s[3:5]
  'me'
  >>> s[2:-2]
  'ameg'
  >>> s[:6]
  'spameg'
  >>> s[1:]
  'pameggs'
  >>> s[:]
  'spameggs'

  Кроме того, можно задать шаг, с которым нужно извлекать срез.

  >>> s[::-1]
  'sggemaps'
  >>> s[3:5:-1]
  ''
  >>> s[2::2]
  'aeg'

Другие функции и методы строк

При вызове методов необходимо помнить, что строки в Python относятся к категории неизменяемых последовательностей, то есть все функции и методы могут лишь создавать новую строку.

>>> s = 'spam'
>>> s[1] = 'b'
Traceback (most recent call last):
  File "", line 1, in
    s[1] = 'b'
TypeError: 'str' object does not support item assignment
>>> s = s[0] + 'b' + s[2:]
>>> s
'sbam'

Поэтому все строковые методы возвращают новую строку, которую потом следует присвоить переменной.

Таблица «Функции и методы строк»

Функция или метод	Назначение
S = ‘str’; S = «str»; S = »’str»’; S = «»»str»»»	Литералы строк
S = «s\np\ta\nbbb»	Экранированные последовательности
S = r»C:\temp\new»	Неформатированные строки (подавляют экранирование)
S = b»byte»	Строка байтов
S1 + S2	Конкатенация (сложение строк)
S1 * 3	Повторение строки
S[i]	Обращение по индексу
S[i:j:step]	Извлечение среза
len(S)	Длина строки
S. find(str, [start],[end])	Поиск подстроки в строке. Возвращает номер первого вхождения или -1
S.rfind(str, [start],[end])	Поиск подстроки в строке. Возвращает номер последнего вхождения или -1
S.index(str, [start],[end])	Поиск подстроки в строке. Возвращает номер первого вхождения или вызывает ValueError
S.rindex(str, [start],[end])	Поиск подстроки в строке. Возвращает номер последнего вхождения или вызывает ValueError
S.replace(шаблон, замена[, maxcount])	Замена шаблона на замену. maxcount ограничивает количество замен
S.split(символ)	Разбиение строки по разделителю
S.isdigit()	Состоит ли строка из цифр
S.isalpha()	Состоит ли строка из букв
S.isalnum()	Состоит ли строка из цифр или букв
S.islower()	Состоит ли строка из символов в нижнем регистре
S. isupper()	Состоит ли строка из символов в верхнем регистре
S.isspace()	Состоит ли строка из неотображаемых символов (пробел, символ перевода страницы (‘\f’), «новая строка» (‘\n’), «перевод каретки» (‘\r’), «горизонтальная табуляция» (‘\t’) и «вертикальная табуляция» (‘\v’))
S.istitle()	Начинаются ли слова в строке с заглавной буквы
S.upper()	Преобразование строки к верхнему регистру
S.lower()	Преобразование строки к нижнему регистру
S.startswith(str)	Начинается ли строка S с шаблона str
S.endswith(str)	Заканчивается ли строка S шаблоном str
S.join(список)	Сборка строки из списка с разделителем S
ord(символ)	Символ в его код ASCII
chr(число)	Код ASCII в символ
S.capitalize()	Переводит первый символ строки в верхний регистр, а все остальные в нижний
S. center(width, [fill])	Возвращает отцентрованную строку, по краям которой стоит символ fill (пробел по умолчанию)
S.count(str, [start],[end])	Возвращает количество непересекающихся вхождений подстроки в диапазоне [начало, конец] (0 и длина строки по умолчанию)
S.expandtabs([tabsize])	Возвращает копию строки, в которой все символы табуляции заменяются одним или несколькими пробелами, в зависимости от текущего столбца. Если TabSize не указан, размер табуляции полагается равным 8 пробелам
S.lstrip([chars])	Удаление пробельных символов в начале строки
S.rstrip([chars])	Удаление пробельных символов в конце строки
S.strip([chars])	Удаление пробельных символов в начале и в конце строки
S.partition(шаблон)	Возвращает кортеж, содержащий часть перед первым шаблоном, сам шаблон, и часть после шаблона. Если шаблон не найден, возвращается кортеж, содержащий саму строку, а затем две пустых строки
S.rpartition(sep)	Возвращает кортеж, содержащий часть перед последним шаблоном, сам шаблон, и часть после шаблона. Если шаблон не найден, возвращается кортеж, содержащий две пустых строки, а затем саму строку
S.swapcase()	Переводит символы нижнего регистра в верхний, а верхнего – в нижний
S.title()	Первую букву каждого слова переводит в верхний регистр, а все остальные в нижний
S.zfill(width)	Делает длину строки не меньшей width, по необходимости заполняя первые символы нулями
S.ljust(width, fillchar=» «)	Делает длину строки не меньшей width, по необходимости заполняя последние символы символом fillchar
S.rjust(width, fillchar=» «)	Делает длину строки не меньшей width, по необходимости заполняя первые символы символом fillchar
S. format(*args, **kwargs)	Форматирование строки

Для вставки кода на Python в комментарий заключайте его в теги <pre><code>Ваш код</code></pre>

Свежее

• Модуль csv — чтение и запись CSV файлов
• Создаём сайт на Django, используя хорошие практики. Часть 1: создаём проект
• Онлайн-обучение Python: сравнение популярных программ

Категории

• Книги о Python
• GUI (графический интерфейс пользователя)
• Курсы Python
• Модули
• Новости мира Python
• NumPy
• Обработка данных
• Основы программирования
• Примеры программ
• Типы данных в Python
• Видео
• Python для Web
• Работа для Python-программистов

Полезные материалы

• Сделай свой вклад в развитие сайта!
• Самоучитель Python
• Карта сайта
• Отзывы на книги по Python
• Реклама на сайте

Мы в соцсетях

Mathematics for Life Notes, раздел 9-1

Примечания к уроку 9. 1
Операции с матрицами

Еще раз подтверждаем, что матрица представляет собой систему строк и столбцов чисел.

Определения:

Матрица	Система строк и столбцов чисел или элементов. Матрица может упростить и прояснить решение проблемы. Матрица особенно полезно при решении системы уравнений.
Элементы	Отдельные значения в матрице.
Равные матрицы	Две матрицы одинакового размера и соответствующие им элементы равны.
Размеры	Количество строк и столбцов в матрице. Мы всегда указываем номер или ряды первые. Матрица 4×7 — это матрица с 4 строками и 7 столбцами
Матрица строк	Матрица только с 1 строкой.
Колонна Матрица	Матрица только с 1 столбцом.
Квадрат Матрица	Матрица с тем же номером или строками, что и столбцы.
Идентификация Матрица	Квадратная матрица, в которой диагональ от верхнего левого угла к нижнему правому — все 1 и все остальные записи равны 0. Пример:
Скаляр	В контексте матричной задачи, скаляр — это нематричное, «нормальное» число.

Матрица может быть полезна при анализе проблемы и дает некоторые подсказки к решению проблемы. Теперь мы увидим, что матрица является математическим объектом которым можно манипулировать и оперировать.

Матрицы иногда идентифицируются по их размерам. Матрица 3×5 имеет 3 строки и 5 столбцов. Строка матрица — это матрица с одной строкой. Матрица-столбец — это матрица, содержащая только один столбец. Квадратная матрица представляет собой матрица с тем же количеством строк, что и столбцов.

Пример проблемы №1

	Данная проблема
	Потому что две матрицы могут быть равными только в том случае, если каждая из них соответствующий элемент равен, то это должно быть правдой.
	Решите первое уравнение относительно x.
	Подставьте это в другое уравнение и найдите y.
	Подставьте это значение y в другое уравнение и найдите x.
	Проверить значения x и y в уравнении 1.
	Проверить значения x и y в уравнении 2.
	Раствор.

Пример скалярного расчета:

Добавление матрицы @ Фиолетовая математика

Умножение матриц

 

Скаляр Умножение и матрица Дополнения были в основном интуитивными. Если бы я попросил вас предсказать, как эти было бы сделано две операции, вы бы наверное правильно догадались как они будут сделаны. Умножение матриц не так интуитивна и должна быть тщательно рассмотрена.

Определение:

 

Требование:

Чтобы иметь возможность умножать две матрицы, число столбцов в первой матрице должно быть равно количеству строк во второй матрице.

 

Наблюдение:

Матрица ответа на умножение матриц всегда будет иметь количество строк первой матрицы и количество столбцов в вторая матрица. ИЛИ Если матрица mxn умножается на матрица nxr, матрица ответов будет матрицей mxr.

 

Пример задачи №1.

	Данная проблема.
	Соответствующие элементы в этой строке первой матрицы умножаются на соответствующий элемент этого столбца второй матрицы, а потом добавил.
	Упрощенный.

 

Пример задачи №2.

	Данная проблема.
	Соответствующие элементы в этой строке первой матрицы умножаются на соответствующий элемент этого столбца второй матрицы, а потом добавил.
	Упрощенный.

Умножение матриц @ Фиолетовая математика

Я давно с моим учителем: (НЕТ, НЕ ДЕЙСТВИТЕЛЬНО)

Некоторые заметки из класса

 

Как умножать ячейки и числа в Excel тремя способами

• Вы можете умножать в Excel, используя несколько различных методов.
• В Excel легко умножить два числа, но вы также можете перемножить множество разных ячеек и чисел или умножить столбец значений на константу.
• Посетите домашнюю страницу Business Insider, чтобы узнать больше.

Умножение значений — одна из наиболее часто выполняемых функций в Excel, поэтому неудивительно, что это можно сделать несколькими способами.

Вы можете использовать любой метод, который лучше всего подходит для того, что вы пытаетесь выполнить в своей электронной таблице на Mac или ПК.

Вот несколько самых простых вариантов выполнения умножения.

Microsoft Office 365 Home (от $99,99 в Best Buy)

MacBook Pro (от $1299,99 в Best Buy)

Lenovo IdeaPad 130 (от $299,992 в Best Buy5)

Самый простой способ сделать это — умножить числа в одной ячейке с помощью простой формулы.

Например, если вы введете «=2*6» в ячейку и нажмете Enter на клавиатуре, вы должны увидеть в ячейке «12».

Вы также можете перемножить две разные ячейки.

1. В ячейке введите «=» 

2. Щелкните ячейку, содержащую первое число, которое нужно умножить.

3. Тип «*».

4. Щелкните вторую ячейку, которую нужно умножить.

5. Нажмите Enter.

Вы не ограничены перемножением только двух ячеек — вы можете умножать до 255 значений одновременно, используя формулу ПРОИЗВЕД.

Используя эту формулу, вы можете умножать отдельные ячейки и числа, разделяя их запятыми, и умножать ряды ячеек с помощью двоеточия.

Например, в формуле «=ПРОИЗВ(A1,A3:A5,B1,10)» — Excel умножит (A1 x A3 x A4 x A5 x B1 x 10), поскольку A3:A5 указывает, что следует умножить A3 , А4 и А5.

Помните, что порядок этих ячеек и чисел не имеет значения при умножении.

Предположим, у вас есть ряд чисел и вы хотите умножить каждое из них на одно и то же значение. Вы можете сделать это, используя абсолютную ссылку на ячейку, содержащую константу.

1. Настройте столбец чисел, которые вы хотите умножить, а затем поместите константу в другую ячейку.

2. В новой ячейке введите «=» и щелкните первую ячейку, которую нужно умножить.

3 . Введите имя ячейки, содержащей константу, добавив «$» перед буквой и цифрой. Знак доллара превращает его в абсолютную ссылку, поэтому он не изменится, если вы скопируете и вставите его в электронную таблицу.

4. Нажмите Enter.

5. Теперь вы можете скопировать и вставить это в дополнительные ячейки, чтобы выполнить умножение на другие числа. Самый простой способ сделать это — перетащить ячейку за правый нижний угол, чтобы скопировать ее.

• Четыре способа объединения и разделения ячеек в Microsoft Excel для очистки данных и форматирования

• Как заблокировать ячейки в Microsoft Excel, чтобы люди, которым вы отправляете электронные таблицы, не могли изменять определенные ячейки или данные

• Как расположить данные в электронной таблице Excel в алфавитном порядке по столбцам или строкам, а также с помощью сочетаний клавиш

• Как встроить видео YouTube в презентацию PowerPoint, в зависимости от версии PowerPoint

Дэйв Джонсон

Внештатный писатель

Дэйв Джонсон — журналист, пишущий о потребительских технологиях и о том, как индустрия трансформирует спекулятивный мир научной фантастики в современную реальную жизнь. Дэйв вырос в Нью-Джерси, прежде чем поступить в ВВС, чтобы управлять спутниками, преподавать космические операции и планировать космические запуски. Затем он провел восемь лет в качестве руководителя отдела контента в группе Windows в Microsoft. Как фотограф Дэйв фотографировал волков в их естественной среде обитания; он также инструктор по подводному плаванию и соведущий нескольких подкастов. Дэйв является автором более двух десятков книг и участвовал во многих сайтах и ​​публикациях, включая CNET, Forbes, PC World, How To Geek и Insider.

ПодробнееПодробнее

Insider Inc. получает комиссию, когда вы покупаете по нашим ссылкам.

Умножение матриц в R — GeeksforGeeks

Умножение матриц — самая полезная операция над матрицами. В настоящее время он широко используется в таких областях, как теория сетей, преобразование координат и во многих других областях. Матрица в R может быть создана с помощью функции matrix() , и эта функция принимает входной вектор, nrow, ncol, byrow, dimnames в качестве аргументов.
Создание матрицы  
Матрицу можно создать с помощью функции matrix().
 

Python3

Вывод:  
 

 [1] [2] [3] [4]
[1,] 1 3 5 7
[2,] 2 4 6 8 

Умножение матриц

Оператор умножения * используется для умножения матрицы на скалярное или поэлементное умножение двух матриц.
Умножение на скаляр
Если вы умножаете матрицу на скалярное значение, то каждый элемент матрицы будет умножен на этот скаляр.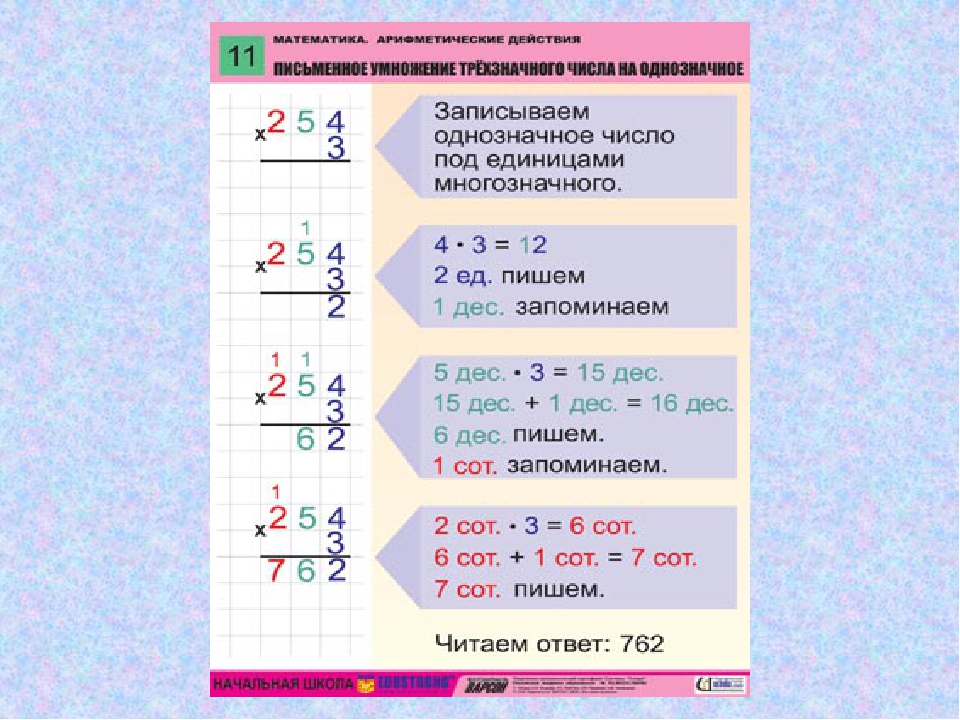
Пример:  
 

Python3

Вывод:  
 

 [1] [2] [3] [4]
[1,] 2 6 10 14
[2,] 4 8 12 16 

В приведенном выше коде скаляр умножается на каждый элемент исходной матрицы. Вот как происходит процесс умножения: 
 

 2*1=2 2*3=6 2*5=10 2*7=14
2*2=4 2*4=8 2*6=12 2*8=16 

Умножение между матрицами  
Когда матрица умножается на другую матрицу, происходит поэлементное умножение двух матриц. Все соответствующие элементы обеих матриц будут перемножены при условии, что обе матрицы будут одной размерности.
Пример:  
 

Python3

Output:  
 

 [1] [2] [3] [4]
[1,] 8 30 60 98
[2,] 18 44 78 120 

Вот как происходит процесс умножения:

 1*8=8 3*10=30 5*12=60 7*14=98
2*9=18 4*11=44 6*13=78 8*15=120 

Умножение на вектор
Если матрица умножается на вектор, то вектор будет преобразован в матрицу строк или столбцов, чтобы получить два аргументы созвучны.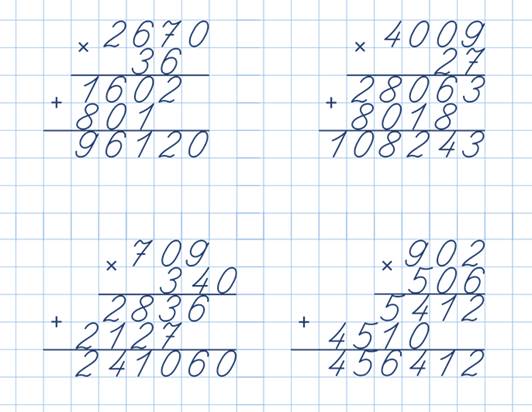
Пример:  
 

Python3

 [1] [2] [3] [4]
[1,] 1 3 5 7
[2,] 4 8 12 16 

1*1=1 1*3=3 1*5=5 1*7=7
2*2=4 2*4=8 2*6=12 2*8=16