Страница 34 — ГДЗ по Математике 3 класс Моро, Волкова 2 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бантова М. А.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

❤️️Ответ к странице 34. Математика 3 класс учебник 2 часть. Автор: М.И. Моро.

Решебник — страница 34Готовое домашнее задание

Номер 9.

С трех серых овец настригли в год 18 кг шерсти, со всех поровну. Сколько шерсти можно настричь с пяти черных овец, если с каждой овцы получили на 1 кг меньше?

Ответ:

Номер 10.

Выполни деление с остатком.

Ответ:

8 : 7 = 1 (ост. 1)    50 : 9 = 5 (ост. 5) 8 : 6 = 1 (ост. 2)    40 : 9 = 4 (ост. 4) 5 : 8 = 0 (ост. 5)    30 : 9 = 3 (ост. 3)
61 : 7 = 8 (ост. 5)    48 : 20 = 2 (ост. 8) 84 : 9 = 9 (ост. 3)    56 : 10 = 5 (ост. 6) 70 : 8 = 8 (ост. 6)    32 : 20 = 1 (ост. 12)

14 : 30 = 0 (ост. 14) 8 : 10 = 0 (ост. 8) 9 : 12 = 0 (ост. 9)

Номер 11.

1) Назови по 3 числа, при делении которых на 10 в остатке может получиться 2; 4; 0.
2) Может ли при делении на 6 получиться в остатке 9? при делении на 12 получиться в остатке 11? 13? 10?
3) Какие остатки могут получиться при делении на 5? на 8? на 3? на 12?

Ответ:

1) 12, 22, 32; 14, 24, 34; 10, 20, 30. 2) При делении на 6 не может быть остаток 9, так как остаток всегда меньше делителя.     При делении на 12 может быть остаток 11 и 9, 10, но не 13. 3) При делении на 5 остатки: 1, 2, 3, 4; на 8 – 1, 2, 3, 4, 5, 6, 7; на 3 – 1, 2;     на 12 – 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.

Номер 12.

1) Узнай, во сколько раз разность чисел 56 и 42 меньше их суммы.

2) Узнай, на сколько разность чисел 56 и 42 меньше их суммы.

Ответ:

Номер 13.

Для закладки сада заготовили ☐ яблонь. Сколько яблонь осталось посадить, если уже посажено 5 рядов, по 16 яблонь в каждом ряду? Дополни условие и реши задачу.

Ответ:

Номер 14.

Ответ:

Задание на полях страницы

Продолжи ряд чисел:

Ответ:

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

Ваше сообщение отправлено!

+

Длинное деление с остатками — Уроки Византа

Мы уже практиковали
деление в длину, но до сих пор все наши ответы были четными (другими словами,
наша последняя задача на вычитание закончилась ответом 0). Однако иногда наши задачи на деление
будут выходить неравномерно, и у нас будет другое число (не 0), когда
мы решим последнюю задачу на вычитание. Это оставшееся число называется остатком ,
и записывается как часть частного. Следуйте вместе с этим примером:

Номер в красном кружке внизу нашего остатка. Вам не нужно обводить остаток
; мы просто обвели наш, чтобы вы знали, какой это номер. После того, как у вас будет

остатка, вы записываете его поверх разделительной полосы с буквой r перед ним,
, вот так: 25 r 3.

Когда ваше деление заканчивается остатком, вы должны убедиться, что ваш остаток
меньше вашего делителя. Если ваш остаток больше вашего делителя, вам нужно
вернуться и проверить свой дивизион, потому что он неверный. Мы все еще можем использовать наш метод умножения
, чтобы проверить наше деление; вы умножите частное (25)
на делитель (5), а затем прибавите наш остаток к ответу на задачу умножения
, вот так:

Давайте попробуем это еще раз. Вот новый пример:

Наш ответ на эту задачу: 23 r 1; обратите внимание, что мы всегда пишем остаток после

частное над разделительной чертой. Также обратите внимание, что наш остаток (1) на
меньше нашего делителя (6).

Теперь давайте проверим нашу работу, вот так:

Есть также несколько различных способов записи остатков. Стандартный способ показан выше
с буквой r перед номером. Однако вы также можете записать остатки
как дроби
и как десятичные числа.

Длинное деление с остатками в виде дробей

Теперь, когда вы понимаете основы деления в большую сторону, вас могут попросить записать остаток
в виде дроби. Не волнуйся! Это совсем не сложно. Таким же образом вы будете выполнять длинное деление на
— делить, умножать, вычитать, сокращать, а затем выполнять
, чтобы получить остаток.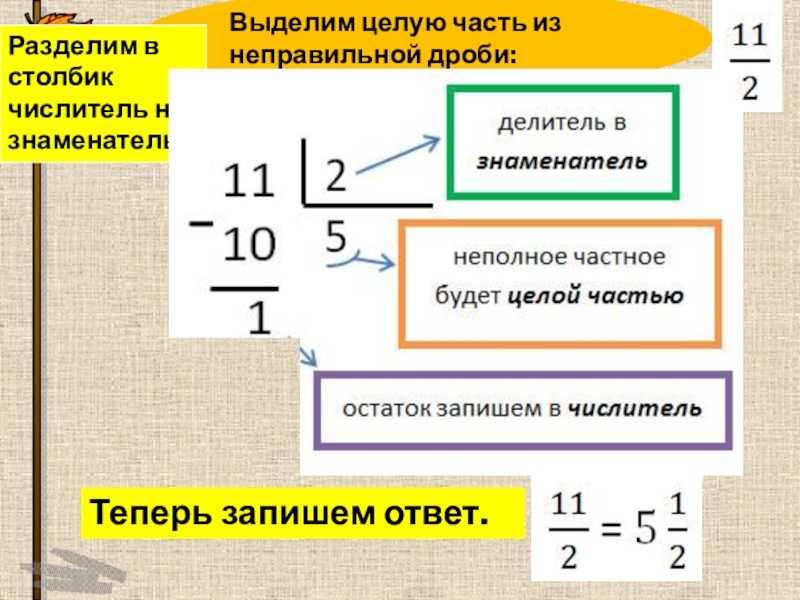 Вместо того, чтобы писать r, а затем число, вы возьмете

остатка и сделаете его числителем дроби. Знаменатель получается из
делителя — вы используете то же число, на которое делите, в знаменателе.

Давайте посмотрим на следующий пример:

Обратите внимание, что вы вообще не используете r перед остатком, когда превращаете
в дробь. Однако вы по-прежнему записываете дробь как часть частного
(ответ на вашу задачу о делении).

Кроме того, вы должны проверить эту задачу на деление так же, как и обычную задачу на деление;
умножьте частное (23) на делитель (6) и прибавьте остаток (1). Сделай
ничего не делать с дробью, чтобы проверить эту проблему.

Длинное деление с остатками в виде десятичных дробей

Вас также могут попросить выразить остаток в виде десятичной дроби.
Когда вас попросят выразить остаток в виде десятичной дроби, вы сначала закончите деление
как обычно, пока не дойдете до точки, в которой вы обычно заканчиваете
, когда вам больше нечего заносить. Однако вместо того, чтобы останавливаться на достигнутом, вы продолжите движение
с делением. Вы добавите десятичную точку (.) после последнего числа, данного в делимом
, и вы также поместите десятичную точку в частное после числа
, которое у вас есть до сих пор. После запятой в делимом вы добавите ноль (0) и
продолжите деление. Вы будете продолжать добавлять нули до тех пор, пока ваш шаг вычитания не приведет к результату
, равному 0. Следуйте вместе с этим примером:

Обратите внимание, что мы добавили десятичную дробь после 6 в делимом, а также десятичную 9.0003 после 5 в нашем частном. Затем мы начали добавлять нули к делимому. В этот
-й раз нам потребовался всего один добавленный ноль, прежде чем наш остаток стал равным нулю.

Теперь давайте рассмотрим задачу, в которой вам нужно добавить более одного нуля к делимому:

Когда у вас есть частное с десятичной дробью, вы проверяете ответ не так, как
, если он имеет остаток в виде дроби или просто остаток, записанный с помощью r.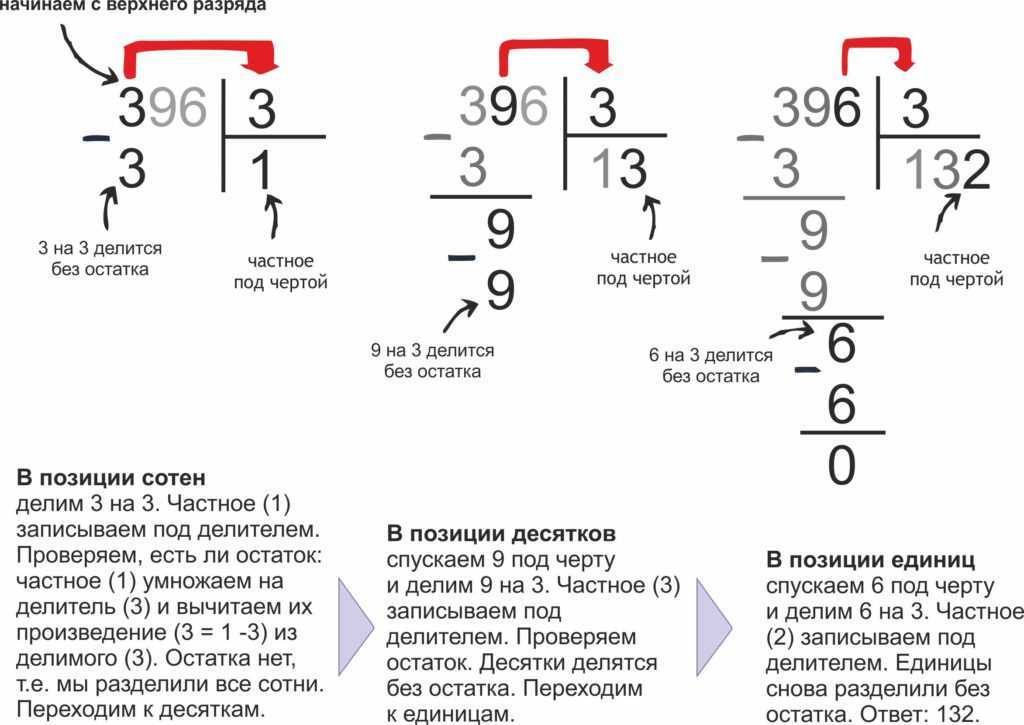 Вместо
сложения остатка отдельно, вы просто умножаете частное (включая десятичное)
на делитель, вот так:

Как делать длинное деление

Что такое метод длинного деления

Длинное деление — это метод, используемый для деления на большее число. Длинное деление отличается от короткого деления тем, что на каждом этапе показано больше работы для расчета остатков.

Метод длинного деления используется при делении на число, состоящее из двух и более цифр.

Причина, по которой мы используем длинное деление, состоит в том, чтобы предоставить структуру для деления на большие числа. Длинное деление включает в себя запись вычислений, связанных с нахождением остатка. Показывая такой уровень отработки, меньше шансов совершить ошибку.

Как сделать длинное деление

Чтобы выполнить деление в большую сторону, выполните следующие действия:

1. Составьте список кратных числа, на которое делится.
2. Используйте этот список, чтобы разделить первую цифру на это число.
3. Найдите наибольшее число раз, которое число делится на цифру, и запишите это выше.
4. Вычтите наибольшее кратное числа из цифры, которую делят, чтобы найти остаток.
5. Рядом с этим остатком запишите следующую цифру делимого числа.
6. Повторяйте шаги с 3 по 5, пока не закончатся остатки.

Вот пример пошагового деления числа с использованием длинного деления.

В этом вопросе имеем 8190 ÷ 15.

Чтобы задать деление в длинное, напишите число, на которое оно делится, слева от числа, на которое оно делится. Нарисуйте линию, чтобы разделить числа, которые проходят над делимым числом.

Первый шаг — составить список первых нескольких кратных числа, на которое оно делится.

Первые несколько кратных 15: 15, 30, 45, 60, 75, 90.

Следующим шагом будет деление первой цифры. 15 больше 8, поэтому мы просто пишем ноль над 8, потому что 15 делится на 8 нулей.

Теперь мы переносим 8 в качестве остатка, чтобы получить 81. Мы используем список кратных, чтобы решить, сколько раз 15 делится на 81.

5 × 15 = 75 и 6 × 15 = 90. Следовательно, 15 делится на 81 пять раз. Пишем 5 над чертой.

Наибольшее кратное 15, меньшее 81, равно 75. Следующий шаг — найти остаток, вычитая 75 из 81.

81 – 75 = 6, значит, остаток равен 6.

Следующим шагом является сокращение следующей цифры числа вместе с этим остатком. Следующая цифра 8190 для рассмотрения — это 9. Мы пишем 9 рядом с остатком 6, чтобы получить 69.

Теперь делим 69 на 15.

4 × 15 = 60 и 5 × 15 = 75. Следовательно, 15 делится на 69 четыре раза. Мы пишем 4 над чертой.

Следующим шагом является вычитание наибольшего числа, кратного 15, которое меньше 69. Мы вычитаем 60 из 69, чтобы найти остаток.

69 – 60 = 9, значит, в остатке 9.

Следующим шагом является ввод следующей цифры 819.0 вниз рядом с остатком.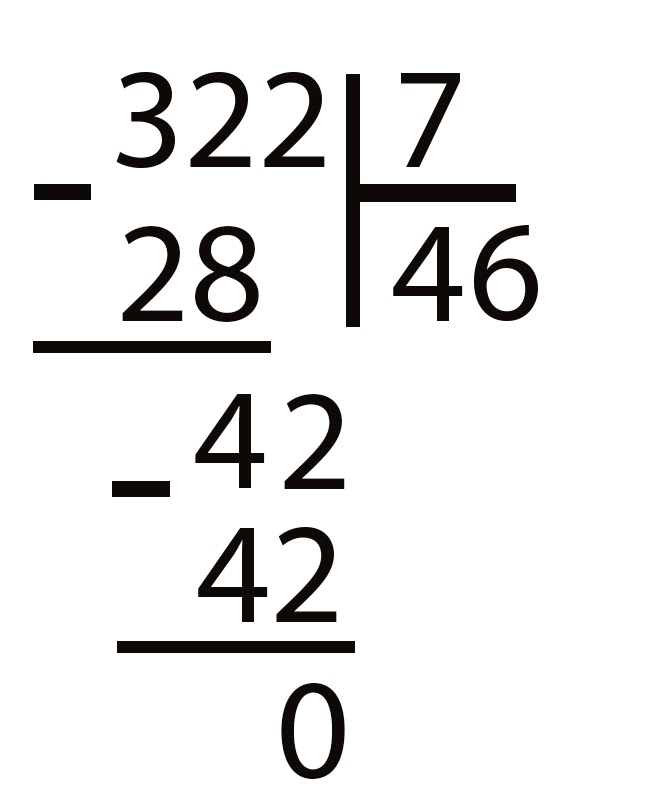 Следующей цифрой, которую нужно рассмотреть, является 0, поэтому мы опускаем этот 0 рядом с 9, чтобы получить 90.

Следующий шаг — разделить 90 на 15.

6 × 15 = 90 и, следовательно, 90 разделить на 15 равно 6. Мы пишем 6 над чертой.

Мы знаем, что метод длинного деления завершается, когда больше нет остатков и цифр делимого числа.

Ответом на вопрос о длинном делении является комбинация цифр, написанная над чертой.

8190 ÷ 15 = 546

Вот полный процесс длинного деления, показанный в виде анимации.

Длинное деление на одну цифру

Вот несколько примеров использования метода длинного деления для деления на однозначное число.

Метод длинного деления лучше всего представить на примере деления на однозначное число. Это потому, что легче сосредоточиться на следовании методу, а не на более сложных суммах умножения.

Вот пример использования метода длинного деления для деления на однозначное число. У нас есть 376 ÷ 4.

Пишем число, на которое делим, слева от числа, на которое делим. Мы разделяем числа чертой, которая также проходит над делимым числом.

Число 4 больше, чем первая цифра числа 3. Следовательно, оно не делится на 3. Мы пишем 0 над чертой, чтобы показать, что число делится ноль раз.

Теперь посмотрим на первые две цифры, которые равны 37.

Делим 37 на 4.

9 × 4 = 36 и 10 × 4 = 40. Следовательно, 4 делится на 37 девять раз. Пишем цифру 9 над чертой.

Наибольшее кратное 4, которое меньше 37, равно 36. Мы вычитаем 36 из 37, чтобы найти остаток.

37 – 36 = 1. Остаток от 1 записываем ниже.

Затем мы записываем следующую цифру рядом с этим остатком. Следующей цифрой в числе 376, которую следует рассмотреть, является 6.

Мы пишем 6 рядом с 1, чтобы получилось 16.

Наконец, мы делим 16 на 4, чтобы получить 4. Мы пишем 4 над чертой.

376 ÷ 4 = 94

Вот полный метод длинного деления, показанный в виде анимации.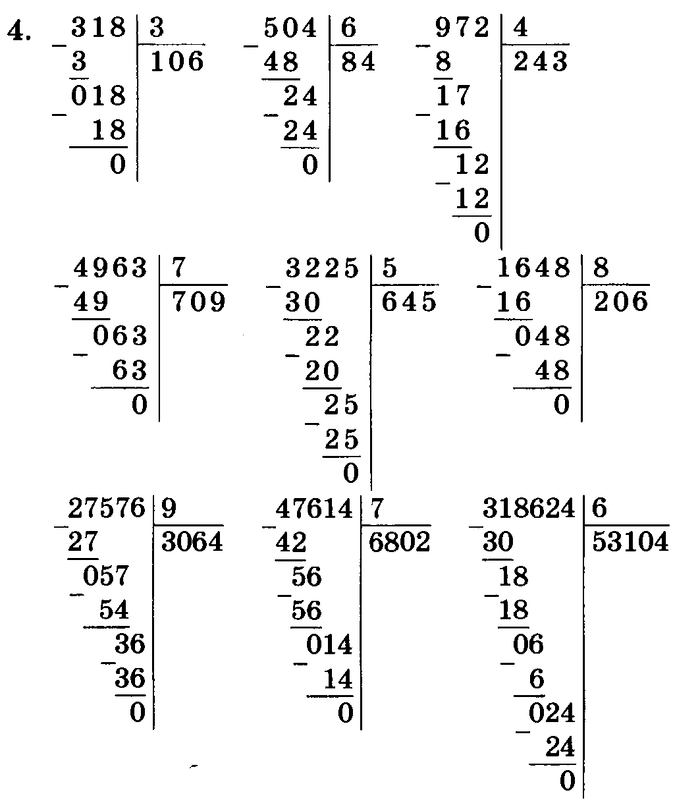

Вот еще один пример длинного деления на однозначное число.

У нас 380 ÷ 5.

5 делится на 3 нулевых раза с остатком 3.

Остаток 3 объединяется со следующей цифрой 8, чтобы получить 38.

38 ÷ 5 = 7, остаток 3, потому что 7 лотов по 5 составляют 35. Мы пишем 7 над чертой.

Мы вычитаем 35 из 38, чтобы найти остаток от 3.

Рядом с этим остатком пишем следующую цифру 380. Мы пишем 0 рядом с 3, чтобы получилось 30.

30 ÷ 5 = 6. Остатка нет, так как это точное деление. Мы пишем 6 над чертой.

380 ÷ 5 = 76

Вот еще один пример длинного деления на однозначное число. У нас есть 582 ÷ 6.

6 не делится на 5. Мы объединяем остаток от 5 рядом со следующей цифрой, чтобы получить 58.

58 ÷ 6 = 9, остаток 4, потому что 9 лотов из 6 равно 54. Мы пишем 9 над чертой.

Мы видим, что остаток равен 4, потому что 58 – 54 = 4.

Рядом с этим остатком пишем следующую цифру 582.