Как правильно умножать обыкновенные дроби
В статье мы рассмотрим правила умножения обыкновенных дробей, умножения их на натуральные числа и перемножения между собой трех и более обыкновенных дробей.
Как умножать обыкновенные дроби между собой
Правило
Для начала ознакомимся с основным правилом: при умножении двух обыкновенных дробей числители каждой из них перемножаются друг на друга, то же самое производится со знаменателями. Это можно представить в следующем виде: \[\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}\].
Применим вышеуказанную формулу для вычисления площади. Предложим, что имеется некий квадрат со стороной равной единице, его площадь соответственно тоже равна 1 кв. единице. Разделим квадрат на равные прямоугольники со стороной \[\frac{1}{8}\] и \[ \frac{1}{6}\] от единицы. Всего у нас получится \[8 \cdot 6=48\] прямоугольников. Легко подсчитать, что площадь каждого будет равняться \[\frac{1}{48}\] кв. единицы. Затем выделяем некую часть внутри фигуры.
Мы получили заштрихованный фрагмент со сторонами, равными \[\frac{4}{6}\] и \[ \frac{5}{8}\] от числовой единицы. Результат произведения двух этих дробей будет являться площадью заштрихованного участка. Однако мы можем просто сосчитать количество таких клеток, их 20, следовательно площадь фигуры составит \[\frac{20}{48}\] кв. единиц.
Так как \[5 \cdot 4=20 \text { и } 8 \cdot 6=48\], мы позволим себе записать следующее равенство: \[\frac{4}{6} \cdot \frac{5}{8}=\frac{20}{48}\].
Решение подтверждает ранее сформулированное правило умножения, которое выглядит как \[\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}\]. Оно применимо для правильных и неправильных дробей, с его помощью перемножаются дроби с разными и одинаковыми знаменателями.
Пройденную тему стоит закрепить, поэтому далее разберем решение нескольких примеров.
Пример 1
Умножьте \[\frac{6}{7} \text{ на } \frac{8}{9}\].
Решение
Умножаем числители дробей, помножив 6 на 8.
У нас получилось \[6 \cdot 8=48\]. Произведение знаменателей вычислим схожим образом \[7 \cdot 9=63\]. Запишем ответ из двух получившихся чисел \[\frac{48}{63}\].
Полное решение можно записать следующим образом:
\[\frac{6}{7} \cdot \frac{8}{9}=\frac{6.8}{7.9}=\frac{48}{63}\]
Ответ: \[\frac{6}{7} \cdot \frac{8}{9}=\frac{48}{63}\].
Если ответ подлежит сокращению, то нужно выполнить это действие, если полученная дробь — неправильная, то стоит выделить из нее целую часть.
Пример 2
Подсчитайте произведение \[\frac{6}{10} \text { и } \frac{45}{8}\].
Решение
Выше мы ознакомились с первым правилом перемножения дробей, применим этот способ и запишем решение в таком виде:
\[ \frac{6}{10} \cdot \frac{45}{8}=\frac{6.45}{10.8}=\frac{270}{80} \]
Полученная дробь является сократимой и имеет признаки делимости на 10.
Сократим полученную дробь: \[\frac{270}{80}\] НОД (270,80) = 10, \[\frac{270}{80}=\frac{270: 10}{80: 10}=\frac{27}{8}\].
Ответ: \[\frac{6}{10} \cdot \frac{45}{8}=3 \frac{3}{8}\].
Для удобства подсчета исходные значения можно привести к виду \[\frac{a \cdot c}{b \cdot d}\]. После чего переменные нужно разложить на простые множители, затем сократить одинаковые числа. Для этого запишем следующий пример.
Пример 3
Подсчитайте произведение \[\frac{6}{10} \cdot \frac{45}{8}\].
Решение
Запишем решение в соответствии с правилами умножения:
\[ \frac{6}{10} \cdot \frac{45}{8}=\frac{6.45}{10.8} \]
Представим числители и знаменатели как: \[6=3 \cdot 2,45=5 \cdot 9, 10=5 \cdot 2,8=4 \cdot 2\] следовательно \[\frac{6.45}{10.8}=\frac{3.2 .5 .9}{5.2 .4 .2}\].
Сокращаем некоторые множители:
\[ \frac{3 \cdot 2 \cdot 5 \cdot 9}{5 \cdot 2 \cdot 4 \cdot 2}=\frac{3 \cdot 9}{2 \cdot 4} \]
Осталось лишь перемножить числа и выделить целое число из неправильной дроби:
\[ \frac{3 \cdot 9}{2 \cdot 4}=\frac{27}{8}=3 \frac{3}{8} \]
Существует определенное правило, как умножать обыкновенные дроби, используя переместительное свойство.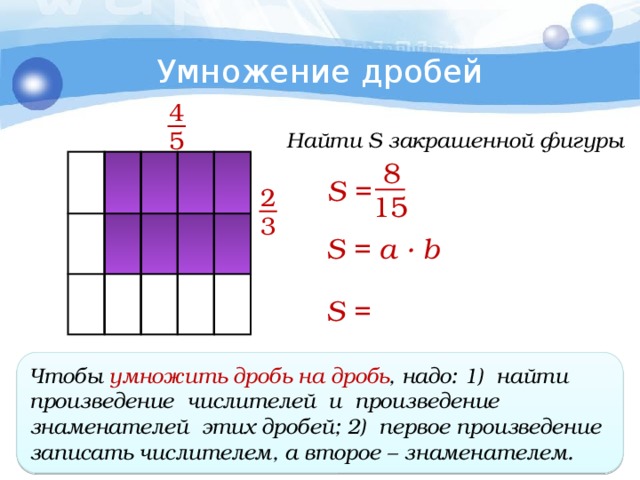
При необходимости порядок расстановки множителей можно изменить:
\[ \frac{a}{b} \cdot \frac{c}{d}=\frac{c}{d} \cdot \frac{a}{b}=\frac{a \cdot c}{b \cdot d} \]
Умножение обыкновенных дробей на натуральное число
Правило
Для умножения обыкновенной дроби на натуральное число достаточно умножить числитель на данное число, оставив знаменатель без изменения.
Произведение дроби \[\frac{a}{c}\] и натурального числа n можно записать как формулу \[\frac{a}{c} \cdot n=\frac{a \cdot n}{c}\].
Любое натуральное число можно представить в виде обыкновенной дроби, в математике умножение обыкновенных дробей на натуральное число можно представить следующим образом:
\[\frac{a}{c} \cdot n=\frac{a}{c} \cdot \frac{n}{1}=\frac{a \cdot n}{c \cdot 1}=\frac{a \cdot n}{b}\]
Поясним как умножить обыкновенную дробь на натуральное число на конкретных примерах.
Пример 4
Произведите умножение \[\frac{3}{20}\] на 5.
Решение
Выполним такое действие как умножение числителя обыкновенной дроби на целое натуральное число и получим 15.
Учитывая вышеназванное правило, получим \[\frac{15}{20}\]. Запишем полное решение:
\[ \frac{3}{20} \cdot 5=\frac{3 \cdot 5}{20}=\frac{15}{20}=\frac{3}{4} \]
Ответ: \[\frac{3}{20} \cdot 5=\frac{3}{4}\].
Такое действие как умножение обыкновенных дробей на натуральные числа, часто приводит к сокращению решения или представлению его в виде смешанного числа.
Пример 5
Найдите решение произведения 7 на \[\frac{12}{10}\].
Решение
Учитывая прошлый пример, перемножаем натуральное число на числитель — \[\frac{12}{10} \cdot 7=\frac{12 \cdot 7}{10}=\frac{84}{10}\]. Найденные два числа являются четными, поэтому нужно провести сокращение.
НОК (84,10) = 2, следовательно, \[\frac{84}{10}=\frac{84: 2}{10: 2}=\frac{42}{5}\].
Остается выделить целую часть и получить ответ: \[\frac{42}{5}=8 \frac{2}{5}\].
Итоговое решение можно представить в следующем виде: \[\frac{12}{10} \cdot 7=\frac{12 \cdot 7}{10}=\frac{84}{10}=\frac{42}{5}=8 \frac{2}{5}\].
Подобное решение можно было бы найти при помощи разложения числителя и знаменателя на простые множители, ответ остался бы без изменений.
Ответ: \[\frac{12}{10} \cdot 7=8 \frac{2}{5}\].
Подобные выражения так же обладают свойством перемещения, поэтому порядок размещения множителей не влияет на результат:
\[\frac{a}{c} \cdot n=n \cdot \frac{a}{c}=\frac{a \cdot n}{c}\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Произведение трех и более обыкновенных дробей в одном выражении
Переместительное и сочетательное свойства позволяют перемножать между собой неограниченное количество дробей. Мы можем умножать обыкновенные дроби как обычные натуральные числа. Приведем еще два примера. Не стоит использовать калькулятор для данного урока, поскольку такие примеры легко исчисляются в тетради.
Пример 6
Найдите произведение четырех дробей \[\frac{1}{8}, \frac{3}{10}, \frac{12}{7} H \frac{4}{9}\].
Решение
Сделаем необходимую запись произведения \[\frac{1}{8} \cdot \frac{3}{10} \cdot \frac{12}{7} \cdot \frac{4}{9}=\frac{1 \cdot 3 \cdot 12 \cdot 4}{8 \cdot 10 \cdot 7 \cdot 9}\].
Разложим некоторые множители, это позволит упростить задачу, нежели затем сокращать готовую дробь.
\[ \frac{1 \cdot 3 \cdot 12 \cdot 4}{8 \cdot 10 \cdot 7 \cdot 9}=\frac{1 \cdot 3 \cdot(4 \cdot 3) \cdot(2 \cdot 2)}{(4 \cdot 2) \cdot(5 \cdot 2) \cdot 7 \cdot(3 \cdot 3)}=\frac{1 \cdot 2}{2 \cdot 5 \cdot 7}=\frac{2}{70} \]
Ответ: \[\frac{1 \cdot 3 \cdot 12 \cdot 4}{8 \cdot 10 \cdot 7 \cdot 9}=\frac{2}{70}\].
Пример 7
Произведите действия умножения со следующими числами \[\frac{5}{6} \cdot 8 \cdot 6 \cdot \frac{3}{40} \cdot 10\].
Решение
Для удобства сгруппируем числа \[\frac{5}{6} \text { и } 6, 8 \text{ и } \frac{3}{40}\], поскольку их можно легко сократить. В итоге получим: \[\frac{5}{6} \cdot 8 \cdot 6 \cdot \frac{3}{40} \cdot 10=\left(\frac{5}{6} \cdot 6\right) \cdot\left(\frac{3}{40} \cdot 8\right) \cdot 10=\frac{5 \cdot 6}{6} \cdot \frac{3 \cdot 8}{40} \cdot 10=\frac{5}{1} \cdot \frac{3 \cdot(4 \cdot 2)}{(4 \cdot 2) \cdot 5} \cdot 10=5 \cdot \frac{3}{5} \cdot 10=\frac{150}{5}=30\].
Ответ: \[\frac{5}{6} \cdot 8 \cdot 6 \cdot \frac{3}{40} \cdot 10=30\].
Перевод смешанных дробей в неправильные
Когда числитель больше либо равен знаменателю, такие дроби принято называть неправильными. Существует правило, согласно которому из неправильной дроби нужно выделить целую часть и только тогда записывать ответ на задание. Достаточно разделить числитель на знаменатель, записав полученное целочисленное значение перед дробью, остаток поместить в числитель, а знаменатель оставить без изменений.
Обратное же действие требует умножить целочисленную часть на знаменатель, прибавить к полученному значению числитель. Итоговое число станет новым числителем, знаменатель останется без изменения. Рассмотрим на конкретном примере. Подобные темы проходятся обычно в младших классах.
Пример 8
Переведите смешанную дробь <span tabindex=»0″ data-mathml=»335″ role=»presentation» style=»font-size: 113%; text-align: center; position: relative;»>3353353 \frac{3}{5} в неправильную.
Решение
Согласно вышеназванному правилу, умножим знаменатель 5 на целое число 3, прибавив текущий числитель 3, получим следующее выражение:
\[ 3 \frac{3}{5}=\frac{3 \cdot 5+3}{5}=\frac{15+3}{5}=\frac{18}{5} \]
Ответ: \[3 \frac{3}{5}=\frac{18}{5}\].
Калькулятор вычисления НОД и НОК двух чисел
Умножение дробей | Учебно-методический материал по алгебре (6 класс) на тему:
Опубликовано 25.06.2015 — 23:40 — Могилева Анна Михайловна
Умножение дробей.
Скачать:
Предварительный просмотр:
Умножение дробей
1. Умножение дроби на дробь
Чтобы умножить дробь на дробь, надо:
1. умножить их числители ;
2. умножить их знаменатели;
3.первое произведение записать числителем, второе- знаменателем.
Важно запомнить! 1) Чтобы вычисления были проще, числители и знаменатели дробей нужно перемножать не сразу, а лишь после сокращения на общие множители( если это возможно).
2)Нельзя сокращать дроби не под общей дробной чертой ( нарушаем основное свойств
Пример.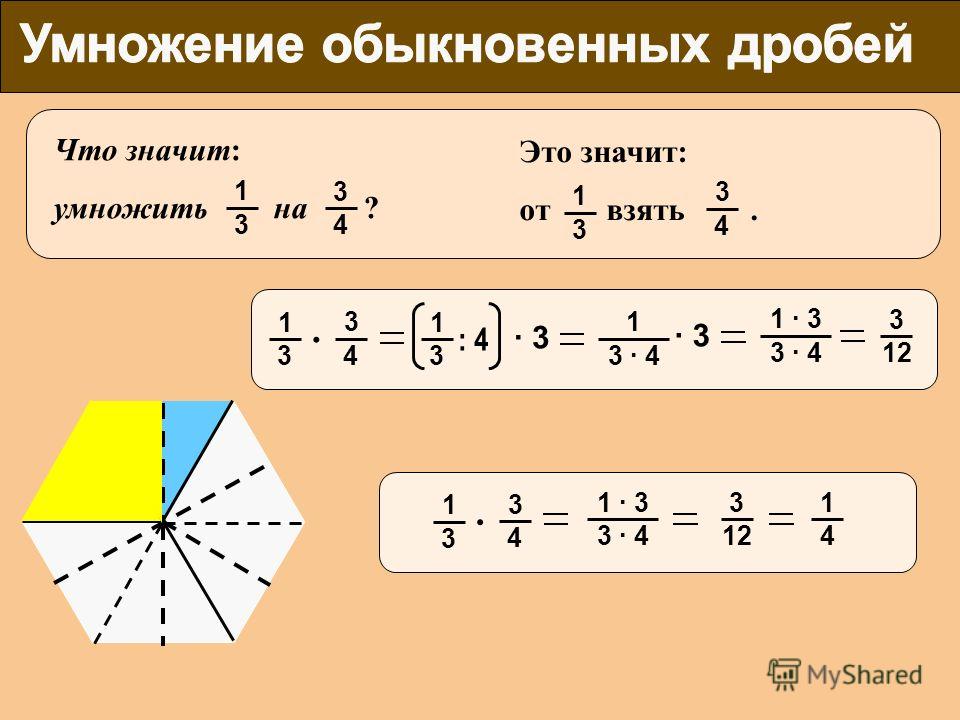
2.Умножение дроби на натуральное число
Первый способ.
- Чтобы умножить дробь на натуральное число, надо использовать правило ( пунк 1). Для этого нужно натуральное число записать в виде дроби со знаменателем 1.
Пример. .
Второй способ.
- Чтобы умножить дробь на натуральное число, нужно умножить числитель дроби на это число, а знаменатель оставить прежним.
Пример..
3.Умножение дроби на смешанную дробь
- Чтобы умножить дробь на смешанную дробь надо смешанную дробь перевести в неправильную дробь и использовать правило умножения дробей(пункт 1).
Пример.
4.Умножение смешанных дробей
- При умножении смешанных дробей нужно:
1) обратить смешанные дроби в неправильные
2) перемножить дроби по правилу умножения дробей.
По теме: методические разработки, презентации и конспекты
Умножения дробей и умножение дроби на натуральное число
Цель урока: Закрепить правило умножения дробей и умножения дроби на натуральное число, изучить правило умножения смешанных чисел, научить применять его при решении задач.
Ход урока. Расшифруй…
Умножение дробей.Нахождение дроби от числа.
Урок закрепления.Десятибалльная шкала оценивания….
Обобщающий урок экскурсия по теме «Умножение дробей. Нахождение дроби от числа»
Урок- презентация по математике в 6 классе.Последний урок перед контрольной работой по теме «Умножение дробей. Нахождение дроби от числа» Составлен в форме путешествиия в зоопарк. На этом уроке учащие…
Открытый урок по теме: «Умножение дробей. Нахождение дроби от числа. Леонард Эйлер.»
Урок и презентация по теме: » Умножение дробей. Нахождение дроби от числа» по математике в 6 классе. Урок обобщения …
Разработка урока по математике в 6 классе по теме «Умножение дробей» и «Нахождение дроби от числа».
Материал подобран для подготовки к контрольной работе как обобщение пройденного….
Урок в 5 классе по теме «Умножение дробей. Умножение смешанных чисел»
Урок в 5 классе по теме «Умножение дробей. Умножение смешанных чисел» по учебнику Дорофеева Г.
В. и Петерсон Л.Г….
Методическая разработка по темам: «Умножение дробей», «Нахождение дроби от числа «.
Материал подобран как обобщение пройденного. Задачи, представленные в презентации разного уровня сложности из учебников «Математика 6 класс» автор Виленкин Н.Я., «Математи…
Поделиться:
Как умножать дроби — PSAT Math
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Learn by Concept
PSAT Math Help » Арифметика » Фракции » Операции с дробями » Как умножать дроби
Если xy = 1 и 0 < x < 1, то какое из следующих утверждений должно быть верным?
Возможные ответы:
y = x
y < x
Y > 1
Y = 1
Y <1
Y = 1
y <1
= 1
.
:
г > 1
Объяснение:
Если x находится между 0 и 1, это должна быть правильная дробь (например, ½ или ¼). Решение первого уравнения для y , у = 1/ х . Когда вы делите 1 на правильную дробь от 0 до 1, результатом является величина, обратная этой дроби, которая всегда будет больше 1.
Чтобы проверить это, выберите любую дробь. Скажем, х = ½. Получается, что y = 2.
Сообщить об ошибке
Перед тем, как пойти в школу, Джоуи пробежал 1/3 своего ежедневного общего пробега. На уроке физкультуры Джоуи сделал 2/3 остатка. Какая часть его дневного пробега оставалась на после школы?
Возможные ответы:
1/3
4/9
2/3
7/9
2/9
Правильный ответ:
2/9
Пояснение:
До школы Джоуи пробежал 1/3 от общего числа миль.
В школе Джоуи бегал 2/3 оставшихся 2/3 или 4/9 бега. При добавлении к его пробегу в школе его пробег до школы 3/9 доводит его пройденные мили до 7/9 его общего количества за день. Таким образом, после школы остается только 2/9 от общего числа миль.
Сообщить об ошибке
Салли купила пять компьютеров для своего офиса по цене 300, 405, 485, 520 и 555 долларов соответственно. Она внесла первоначальный взнос в размере 2/5 от общей стоимости, а оставшуюся часть внесла девятью равными платежами в течение следующих девяти месяцев. Предполагая отсутствие налогов и процентов, какова стоимость каждого из девяти платежей?
Возможные ответы:
351
906
251
1359
151
9005 Правильный ответ:0016
151
Объяснение:
Общая стоимость 5 компьютеров составляет 2265.
2/5 от 2265 = 906, это то, что Салли платит вперед.
2265 – 906 = 1359, то есть сумма, которую Салли все еще должна.
1359/9 = 151, что является стоимостью каждого из 9 равных платежей.
Сообщить об ошибке
Цена компьютера снижена на 1/8. Затем новая цена уменьшается на 1/6. Какую часть первоначальной цены составляет текущая цена?
Возможные ответы:
13/48
35/48
1/24
23/24
1/48
Правильный ответ:
35/48 9005
Объяснение:
Пусть исходная цена = p .
После первого снижения цена составит (7/8) р
После второго снижения цена составит (5/6)(7/8)р = (35/48)р
Отчет Ошибка
Если автомобиль движется со скоростью 30 миль в час, сколько футов он проходит в секунду?
Possible Answers:
44 ft/s
4,400 ft/s
2,640 ft/s
264 ft/s
440 ft/s
Correct answer:
44 ft/s
Объяснение:
30 миль/1 час * 5280 футов/1 миля * 3600 секунд/1 час = 44 фута/сек
Сообщить об ошибке
В группе из 20 детей 25% составляют девочки.
Сколько мальчиков?
Возможные ответы:
5
15
10
16
4
Правильный ответ:
15
Объяснение:
Поскольку среди детей девочки, в группе всего девочки.
мальчики.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Пояснение:
Помните, что когда вы умножаете дроби, вы можете напрямую перемножать их знаменатели и числители; следовательно, вы можете начать эту задачу, превратив ее в одну большую дробь:
Теперь вы можете умножить все это, а затем разделить. Тем не менее, вы можете отменить все сразу. Входит в и в . Таким образом, у вас есть:
Сообщить об ошибке
Упростить:
Возможные ответы:
Правильный ответ:
0 Объяснение:
Во-первых, вспомните, что то же самое, что :
Теперь вспомните, что дроби умножаются путем умножения числителей и знаменателей друг на друга.
Это очень просто. Это даст вам:
Теперь вы можете отменить и:
Затем вы можете уменьшить и:
Вы также можете уменьшить результат и отчет:
4 Ошибка
Уведомление об авторских правах
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Учитесь по концепции
Как умножать дроби. Полное руководство от Prep Expert
Независимо от того, сдаете ли вы SAT или ACT, вам нужно научиться умножать дроби.
Вы увидите много вопросов, которые потребуют от вас не только понимания того, как работают дроби, но и умения умножать эти дроби за ограниченное время.
В разделах SAT Math у вас будет 75 секунд на вопрос в разделе Math (без калькулятора) и 87 секунд на вопрос в разделе Math (Calculator). В разделе ACT Math вы получаете 1 минуту на каждый вопрос.
Это означает, что вам нужно будет уметь быстро умножать дроби во время теста.
Хотя умножение дробей может показаться сложным, эту концепцию освоить намного проще, чем может показаться. Фактически, вы можете умножать дроби всего за четыре простых шага.
Это руководство поможет вам понять дроби и проведет вас через четыре шага, которые вам необходимо знать, чтобы умножить дроби.
Что такое дроби?
Проще говоря, дроби являются частью целого. Например, если вы съели половину пиццы, вы съели часть всей пиццы.
Когда вы видите определенные дроби, такие как ¾, ⅚ или ⅞, эти дроби означают, какая часть целого не была «потреблена». В приведенном выше примере, если вы съели половину пиццы, вы съели ½ пиццы, потому что есть две половинки, и вы съели одну из них. Это означает, что осталось ½ пиццы.
Дроби делятся на числители и знаменатели.
Числители — это числа в верхней половине дроби, которые представляют количество целого, которое не было использовано.
Например, в приведенной ниже дроби числитель равен 7.
Знаменатель числа представляет целое или сумму. В приведенном выше примере знаменатель равен 8.
Глядя на это через призму потребления пиццы, дробь ⅞ будет означать, что осталось семь кусков пиццы из пиццы, которая изначально состояла из восьми кусков.
Как только вы поймете, что обозначают числители и знаменатели, вам будет легче понимать дроби.
Если вы съедите 3 куска пирога, разрезанного на четыре части, у вас останется ¼ этого пирога. Если у вас есть целое число, например 1, и вы вычтете из него ⅓, то у вас останется ⅔ (⅔ + ⅓ = 1).
Благодаря этим знаниям у вас будет все необходимое, чтобы уметь умножать дроби, когда вы сталкиваетесь с такими задачами в разделах SAT или ACT по математике.
Умножение дробей
Умножение дробей требует четырех шагов:
1. Умножение числителей
Первое, что вам нужно сделать при умножении двух дробей, это умножить два числителя.
Например, если вы умножаете ⅔ и ⅞ , вам сначала нужно умножить 2 и 7, что даст вам 14 для вашего нового числителя.
2. Умножьте знаменатели
Затем вам нужно будет умножить два знаменателя. В этом случае вы должны умножить 3 на 8, что даст вам 24 в качестве нового знаменателя.
3. Создайте новую дробь
Теперь, когда у вас есть новый числитель и новый знаменатель, вам нужно создать новую дробь. Поместите новый числитель и знаменатель в формат дроби, как я сделал ниже.
| 2 | * | 7 | = | 14 |
| 3 | 8 | 24 |
4. Reduce your fraction
If possible, reduce your fraction to наименьшая возможная дробь, которая по-прежнему представляет то же количество целого.
Найдите наибольший общий делитель числителя и знаменателя новой дроби. В этом случае вам нужен наибольший общий делитель 14 и 24, который равен 2,9.0005
Получив этот множитель, разделите числитель и знаменатель на этот множитель. В случае приведенного выше примера у вас есть 14, деленное на 2, что равно 7 для вашего конечного числителя, и 24, деленное на 2, что составляет 12 для вашего конечного знаменателя.
| 14 | → | 7 |
| 24 | 12 |
.
Выполнив четыре описанных выше шага, вы сможете легко умножать дроби.
Попробуйте выполнить эти шаги на нескольких примерах (мы дадим вам ответы, чтобы вы могли проверить свою работу).
Когда вы закончите, проверьте свою работу ниже. У вас должны быть следующие ответы:
- Ответ= ⅕ . После выполнения шагов 1-3 у вас должно было получиться 4/20, которое можно уменьшить до ⅕, используя наибольший общий делитель 4.
- Ответ = ⅝ . После выполнения шагов 1-3 у вас должно было получиться 15/24, что можно уменьшить до ⅝, используя наибольший общий делитель 3.
- Ответ = 3/10. После выполнения шагов 1-3 у вас должно получиться 3/10, которое нельзя уменьшить.
Умножение смешанных дробей
Иногда на SAT или ACT можно увидеть смешанные дроби.
Смешанные дроби имеют целое число с дробью.
Например, 7 ⅔ — это смешанная дробь.
При умножении смешанных дробей сначала нужно преобразовать смешанную дробь в обыкновенную.
Для этого необходимо выполнить несколько шагов:
1. Умножить целое число на знаменатель
В приведенном выше примере 7 ⅔ нужно умножить 7 и 3, что равно 21.
2 , Добавьте свой ответ из шага 1 в числитель
В приведенном выше примере вы должны добавить 21 к 2, чтобы получить новый числитель 23. В результате ваша новая дробь будет выглядеть так:
3. Используйте эту новую дробь для умножения
Если вас попросили умножить 7 ⅔ и ¼, вы должны сначала преобразовать 7 ⅔ в 23/3, а затем вы можете использовать шаги, упомянутые ранее, чтобы умножить эту дробь на ¼. (Кстати, вы должны получить 23/12 или 1 11/12).
Изучение SAT и ACT Советы по математике
Если вы хотите узнать о сложении, вычитании или делении дробей, а также о других математических понятиях, которые вы увидите в математических разделах SAT или ACT, я настоятельно рекомендую записаться на ACT или Курс подготовки к SAT или работа с частным репетитором.