как объяснить ребенку деление в столбик
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.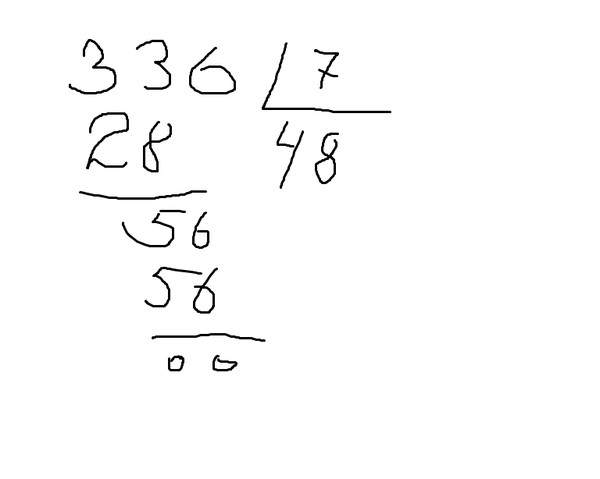
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.

Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Конечно же, дети постигают азы математики на уроках в школе. Но не всегда малышу бывают понятны объяснения учителя. А может ребенок заболел и пропустил тему. В таких случаях родителям стоит вспомнить свои школьные годы, для того чтобы помочь ребенку не упустить важную информацию, без которой дальнейшее обучение будет нереально.
Учить ребенка столбиком начинают в третьем классе. К этому времени таблицей умножения школьник должен уже пользоваться с легкостью. Но если существуют с этим проблемы, стоит немедленно ведь перед тем, как научить ребенка делить столбиком, не должно возникать никаких сложностей с умножением.
Как научить делить столбиком?
Возьмем для примера трехзначное число 372 и поделим его на 6. Выбирайте любую комбинацию, но так, чтобы деление прошло без остатка. На первых порах это может запутать юного математика.
Записываем числа, разделяя их уголком, и поясняем ребенку, что данное большое число мы будем постепенно делить на шесть равных частей. Попробуем сначала разделить первую цифру 3 на 6.
Попробуем сначала разделить первую цифру 3 на 6.
Она не делится, а значит, добавляем вторую, то есть попробуем, получится ли поделить 37.
Необходимо спросить у ребенка сколько раз шестерка поместится в цифре 37. Тот, кто без проблем знает математику, сразу догадается, что методом подбора можно подобрать нужный множитель. Итак, давайте подбирать, возьмем, к примеру, 5 и умножим на 6 – получается 30, вроде бы результат недалеко от 37, но стоит попробовать еще раз. Для этого 6 множим на 6 – равно 36. Вот это нам подходит, и первая цифра частного уже найдена – записываем ее под делителем, за линией.
Число 36 записываем под 37 и при вычитании получаем единицу. Она опять не делится на 6, а значит, к ней сносим оставшуюся наверху двойку. Теперь число 12 очень легко разделить на 6. В результате получаем второе число частного – двойка. Наш результат деления будет 62.
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Yandex.RTB R-A-339285-1
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55 , запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:
3 · 0 = 0 7
Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом.
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4 · 0 = 0 14 .
Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .
На место частного записываем множитель 3 .
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
Важно!
Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.
4 · 0 = 0 2
Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8 .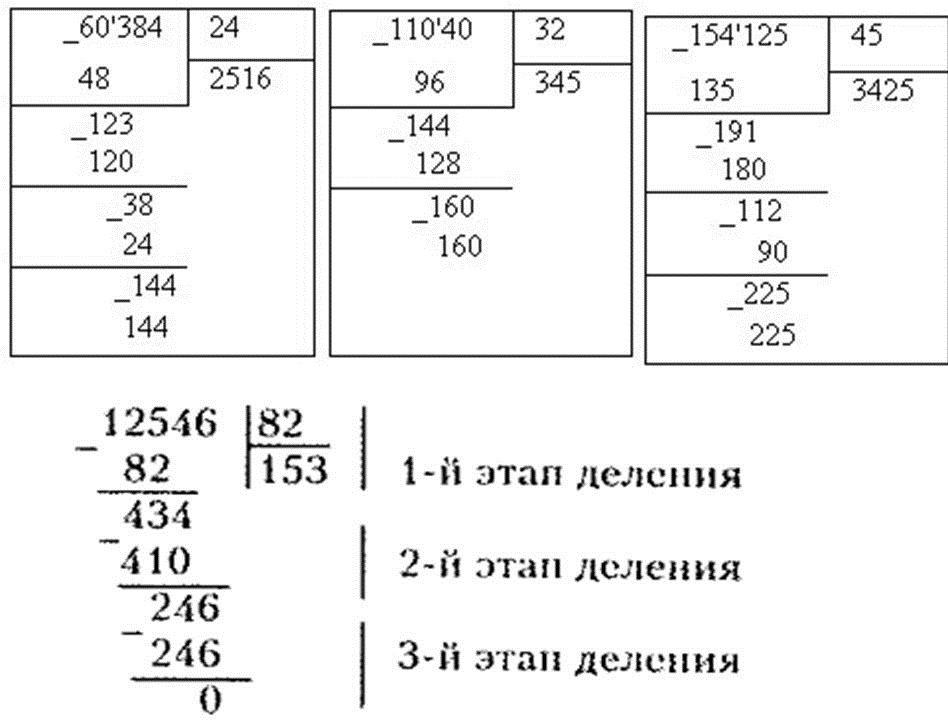 В последний раз повторяем пункты алгоритма 2 — 4 и получаем:
В последний раз повторяем пункты алгоритма 2 — 4 и получаем:
В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
Разделим натуральное число 7136 на натуральное число 9 .
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Деление натуральных чисел в столбик
Разделим число 7042035 на 7 .
Ответ: 1006005
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206 .
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.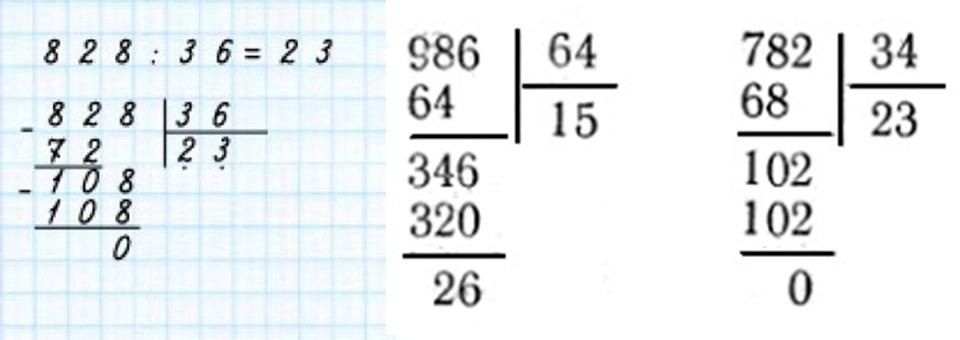
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:
206 · 0 = 0 556
618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442 .
Повторяем с ним пункты 2 — 4 . Получаем:
206 · 5 = 1030
Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Разделим натуральное число 238079 на 34 .
Ответ: 7002
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Первые годы школьной жизни в младших классах ребенку даются нелегко. Часто после урока математики они не совсем хорошо понимают пройденную тему. Чтобы помочь ребенку в усвоении пройденного материала, потребуется самому объяснить школьнику то, что ему не понятно. На помощь приходят родители, у которых моментально возникает вопрос: «Как объяснить ребенку деление?». Сделать это можно несколькими способами, но изначально стоит убедиться, что ребенок хорошо усвоил такие математические действия, как сложение, вычитание и умножение .(Прочитать про способы обучения детей сложению и умножению можете и ).
Обучение ребенка основам деления
Важно, чтобы ребенок понимал суть такого математического действия, как деление. Для этого необходимо ему объяснить, что деление представляет собой разделение чего-либо на равные доли. Рекомендуется превратить процесс обучения в интересную игру, чтобы ребенок был сконцентрирован.
СОВЕТ: Таблицу деления так же важно выучить, как и таблицу умножения. Лучше это делать на каникулах!
Помогите ребенку понять, что деление — это обратное действие умножению.
Самым простым способом объяснить деление является проведение наглядной демонстрации разделения предметов на равные доли . В качестве делимых предметов можно использовать все, что угодно, но желательно что-то интересное для ребенка. В качестве примера можно воспользоваться конфетами и игрушками.
Как объяснить ребенку деление при помощи игрушек?
Изначально нужно взять 2 конфеты и попросить ребенка разделить их между 2 плюшевыми игрушками. Благодаря такому простому примеру ребенок поймет суть математического деления. После этого можно переходить к более сложным примерам деления.
Как происходит деление, подробно и в игровой форме показывается в следующем видео:
Также вы можете взять коробку цветных карандашей, которая будет выступать одним целым, и предложить малышу разделить их между собой и вами поровну. После, попросите ребенка посчитать, сколько карандашей было вначале в коробке и сколько он смог раздать.
После, попросите ребенка посчитать, сколько карандашей было вначале в коробке и сколько он смог раздать.
По мере понимания ребенка, родитель может увеличивать число предметов и количество участников задачи. Затем нужно рассказать, что не всегда получается разделить что-либо поровну и некоторые предметы иногда остаются «ничейными». К примеру, можно предложить разделить 9 яблок между бабушкой, дедушкой, папой и мамой. Ребенок должен понять, что все получат лишь по 2 яблока, а одно окажется в остатке.
Деление в игровой формеТаким образом, вы объясните азы деления и подготовите ребенка к более сложным школьным задачам.
СОВЕТ: Старайтесь заниматься со своим ребенком в игровой форме. Тогда ему будет интересно заниматься, а значит, занятия пройдут весело и без особых усилий.
Также вам будет интересно и полезно распечатать таблицу деления в виде картинки.
Делить однозначные числа на однозначные проще всего с использованием . Для этого достаточно объяснить ребенку, что деление является действием обратным к умножению. Сделать это можно на любом правильном примере деления натуральных чисел.
Для этого достаточно объяснить ребенку, что деление является действием обратным к умножению. Сделать это можно на любом правильном примере деления натуральных чисел.
Например: 2 умножить на 3 будет 6. Основываясь на данном примере продемонстрировать ребенку процесс деления. Следует действовать следующим образом: разделить 6 на любой множитель, например, на число 2. В ответе получится 3, то есть множитель неиспользованный при делении.
Таким способом можно делить многозначные (двухзначные) числа на однозначные.
Алгоритм деления в столбикПрежде, чем начать объяснение деления в столбик, нужно рассказать ребенку о значении делимого, делителя и частного. В примере 20:4=5, 20 является делимым, 4 делителем, а 5 частным. У каждой отдельной цифры в примере одно наименование.
Многозначные числа (трехзначные и двухзначные) проще всего делить в столбик. Для этого нужно записать многозначные числа уголком.
Например, нужно разделить трехзначное число 369 на однозначное число 3.
В качестве делителя записано трехзначное число 369 , а в качестве делителя однозначное число 3. Первым делом важно объяснить ребенку, что деление в столбик происходит в несколько этапов:
- Определение части делимого подходящего для первичного деления. В данном случае цифра 3. 3:3=1. Цифру 1 нужно записать в графу частное.
- «Спустить» следующее делимое число. В данном случае это цифра 6. 6:3=2 . Полученное число 2 нужно записать в частное.
- Далее необходимо «спустить» следующее делимое число 9. 9 делится без остатка на 3, полученный результат необходимо записать в частное. Результатом деления трехзначного числа 369 на 3 получается 123.
Деление десятичного числа на двухзначное проходит примерно так же. В случае с десятичным числом необходимо объяснить ребенку, что запятую в делителе переносят на столько знаков, на сколько перенесли в делимом. Далее следует обычное деление в столбик.
Необходимо предупредить ребенка о встречающихся случаях деления с остатком. В качестве примера можно поделить двухзначное число 26 на 5 столбиком. В результате остается остаток 1.
В качестве примера можно поделить двухзначное число 26 на 5 столбиком. В результате остается остаток 1.
Важно после объяснения позволить ребенку самостоятельно решить несколько примеров, чтобы весь изученный материал надолго остался в памяти ребенка.
А еще Вы можете посмотреть видео, где все объясняют понятным языком.
И напоследок, не приучайте себя и ребенка пользоваться онлайн калькулятором, чтоб узнать, как разделить 145 на 9, 34 на 40, 100 на 4, 30 на 80, 416 на 52 и другие примеры. Это не принесет пользы не вам, ни ему.
В 1-ый класс идет не только ребенок – родители вместе с ним начинают и вместе с ним заканчивают образовательное учреждение. Учитель в школе не всегда успевает объяснить каждому отдельному ученику ту или иную дисциплину. Поэтому у — свои плюсы. Вы можете сами объяснить ребенку, индивидуально и не спеша то, что он не понял. В этот непростой период, главное — это набраться терпения и не ругать школьника из-за неправильных решений.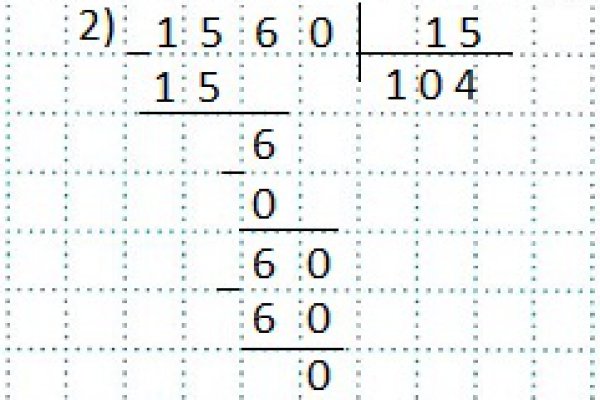 Тогда все у вас получится.
Тогда все у вас получится.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.

- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6.
 К цифре 6 тоже нужно дописать ноль. Получится 60.
К цифре 6 тоже нужно дописать ноль. Получится 60. - В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
Деление с остатком на 10, 100, 1000
Деление с остатком на 10, 100, 1000
Автор: edu1
Методическая копилка — Начальная школа
Тема: Деление с остатком на 10, 100, 1000.
Цели: ознакомление с делением на 10, 100 и 1000 с остатком.
Развивать творческое мышление, познавательную активность учащихся, стремление к достижению успеха в учебной деятельности ,совершенствовать вычислительные навыки, умение решать задачи;
Задачи:
Воспитывающая: воспитывать любовь к уроку математики, доброту.
Образовательная: учить выполнять деление с остатком на 10, 100, 1000;, умение решать задачи.
Развивающая: совершенствовать вычислительные навыки, развивать творческое мышление.
Планируемые результаты:
Личностные УУД: способствовать развитию интереса к математике, вычислительных навыков, формирование уважительного отношения к иному мнению, иной точки зрения.
Метапредметные результаты обучения:
Познавательные УУД: формирование умения самостоятельно формулировать проблему, ставить познавательные цели, самостоятельно создавать алгоритм для решения проблем творческого и поискового характера.
Регулятивные: формировать у обучающихся способность организовать свою учебную деятельность: целеполагание, планирование, контроль, коррекция и оценка своей деятельности, саморегуляция как способность к мобилизации сил и энергии, к волевому усилию и преодолению препятствий.
Коммуникативные: работать в парах, выполнять задания творческого и поискового характера, вступать в диалог с учителем, уметь высказываться.
Предметные результаты обучения:
Познавательные: научатся выполнять деление с остатком на 10, 100, 1000 и делать проверку; решать задачи изученных видов; выполнять преобразование единиц измерения, используя соотношения между ними; ориентироваться в материале учебника и находить по заданию учителя нужную информацию.
Оборудование: учебник 4 класс часть 2 М. И. Моро, мультимедийный проектор, презентация к уроку, карточки с заданиями, подарки-солнышки, рисунок яблони со съёмными яблоками, цветами и листьями, мяч.
Ход урока
I.Мотивация к уроку.
— Доброе утро, ребята! Меня зовут Людмила Михайловна. Сегодня я буду вести у вас урок.
Ребята моего класса из Пузачинской школы передали вам в подарок вот такое солнышко добра, чтобы вам на уроке было тепло и уютно. Положите его на ладошку. Оно согревает вас: ваши руки, тело и душу. Придаёт бодрость, заряжает энергией, будит воображение.
Положите его на ладошку. Оно согревает вас: ваши руки, тело и душу. Придаёт бодрость, заряжает энергией, будит воображение.
— Какое у вас настроение? Покажите жестами!!!
Вот с таким настроением мы и начнём урок.
II. Актуализация знаний
Устный счёт
1)Работаем в парах: в учебнике на с. 27 решим примеры, которые записаны на полях:
630: 70 *30- 89 + 29 : 3 + 30 = 100
2) №91
-Сколько раз по 100м содержится в 2 км? (20)
-Сколько раз по 15 с содержится в 1 мин? (4)
3) В бидоне было 36 л молока. Доярка наполнила 10 трёхлитровых банок. Сколько л молока осталось в бидоне? (36-3*10=6 (л))
4) В спортивную школу привезли 126 мячей. Их запаковали в 12 коробок по 10 мячей в каждой. Сколько мячей осталось? (126-10*12=6(м.))
5)Презентация:
-Решите примеры:
800 : 2= 400
4 • 20=80
6 • 7=42
60 : 3= 20
30 • 2=60
-Вставьте числа в окошки: 3*8=(?)+27=(?)-39=(?):2=(?)*8=(?)-40=(?)*8
-Вычисли:
50:10 500:10 5000:10
600:100 6000:100 60000:100
7000:1000 70000:1000 700000:1000
III. Создание проблемной ситуации. Постановка проблемы.
Создание проблемной ситуации. Постановка проблемы.
-Посмотрите на примеры, записанные на доске:
68:10 400:100 3456:1000
340:10 827:100 7000:1000
На какие две группы их можно разделить? (Примеры на деление без остатка и примеры на деление с остатком)
-Запишите примеры в два столбика:
400:100 68:10
340:10 827:100
7000:1000 3456:1000
Примеры какого столбика мы умеем решать?
Найдите значения выражения первого столбика: (4, 34, 7)
Посмотрите на второй столбик.
Как вы думаете, какую проблему нам нужно решить на уроке, чему научиться? (Деление с остатком на 10,100,1000).
— Прочитайте тему урока в учебнике на стр. 27)
-Поставьте задачи, чему мы будем учиться с вами на уроке?
V. Построение проекта выхода из затруднения. Реализация построенного проекта.
1) Вспомните, как мы делим на 10, 100 и 1000.
(Чтобы число разделить на 10, достаточно убрать один нуль. Чтобы число разделить на 100, надо убрать два нуля и на 1000 надо убрать три нуля).
— Откройте тетради, запишите сегодняшнее число.
— Найдем значение выражений второго столбика. Никто не спешит, следите за мной.
— А сейчас рассмотрим второй столбик.
-Кто может предложить способ деления 68:10?
-Можем ли 68:10 без остатка?
— Какое число можем разделить на 10 без остатка? (60:10=6)
Правильно, возьмем наибольшее число до 68, которое делится на 10, — это 60. Разделим 60 на 10, что получим? (получим 6). .
— Сколько останется в остатке?(68 – 60 = 8). Записываем это так 6 (ост. 8).
— Составим алгоритм деления с остатком на 10,100,1000:
1.Найдём наибольшее число, которое делится на 10,100,1000.
2.Разделим это число.
3. Найдём остаток (от делимого отнимем наибольшее число).
Мы вывели алгоритм деления с остатком на 10,100,1000. Давайте сверимся с научным источником – учебником с. 27
27
VI.Первичное закрепление с проговариванием.
-Решите второй пример с объяснением.(827:100=8) остаток 27.
— Выйдите к доске и решите 3 пример с объяснением. (3456 : 1000 = 3) ост 456
— Далее мы выполним задание 96. Начинаем с первой парты 1 ряда, по очереди выходим к доске, решаем пример и объясняем его решение. (Далее учащиеся решают с объяснением примеры, данные в задании 96)
69 : 10 = 6 (ост 9) 238 : 10 = 23 (ост 8) 691 : 100 = 6 (ост 91)
78 : 10 = 7 (ост 8) 238 : 100 = 2 (ост 38) 691 : 10 = 69 (ост 1)
7825 : 100 = 78 (ост 25) 7825 : 1000 = 7 (ост 825)
— Какой вывод по этому заданию вы можете сделать? ( При делении на 10, в остатке будет одна цифра, а в частном будет число, записанное остальными цифрами делимого; при делении на 100 в остатке будет число, записанное двумя последними цифрами делимого, а в частном число, записанное остальными цифрами делимого. )
)
Для того чтобы этот вывод был усвоен сознательно, важно объяснить, почему это так: на 10 можно разделить все содержащиеся в числе десятки, а единицы остаются; аналогично для 100 и 1000.
— Есть еще 1 способ деления: нужно закрыть в числе столько цифр, сколько нулей в делителе. Получим целое число, а то, что закрыли – остаток
VII. Физкультминутка (под музыку повторяем движения животных)
VIII. Самостоятельная работа в группах с самопроверкой по эталону.
-Работа по карточкам:
327:10 1684:100
358:10 1605:1000
615:100 1730:100
IX. Повторение материала.
Решение задачи изученного вида:
№89 стр.27
-Прочитайте задачу.
-Можем ли мы сразу ответить на вопрос задачи? (Нет, нам неизвестна скорость машины.)
-Как можно найти скорость? (Расстояние разделим на время. )
)
-Что вы заметили? (6 нельзя разделить на 5.)
— А кто догадался, что нужно сделать? (6км перевести в метры: 6км=6000м.)
-Как изменятся теперь единицы скорости? (Скорость будет измеряться в метрах в минуту.)
-Как мы узнаем расстояние, пройденное за 40 мин?
-Что нужно сделать, прежде чем узнать, сколько пройдёт машина с такой же скоростью за 1 ч? (Надо 1ч перевести в минуты.)
-Запишите решение задачи выражениями.
6000:5=1200(м/мин)
1200*40=48000(м)
1200*60=72000(м)
Ответ: 48000м,72000м
№92 стр.27
-Прочитайте задание.
-Составьте первое уравнение.(х-20=40*6)
-Как его можно упростить? (Можно найти произведение чисел: 40*6=240)
-Что неизвестно в уравнении? (Уменьшаемое)
-Вспомните, как найти уменьшаемое. (К разности прибавить вычитаемое.)
-Запишите решение.
х-20=240
х=240+20
х=260
260-20=240
-Второе уравнение решается самостоятельно в парах.
15+х=800:20
15+х=40
х=40-15
х=25
15+25=40
XII. Рефлексия
Игра в мяч:
Бросаю мяч и называю выражение, дети ловят и называют ответ:
152:10, 375:100, 54:10,786:100, 2546:1000, 3452:100, 79:10, 897:100, 2457:1000,385:10, 893:10, 715:100, 2413:1000, 81:10, 95:10
— Урок у нас заканчивается. За это время выросло удивительное дерево, благодаря которому каждый из вас оценить себя.
-Если урок для вас прошел плодотворно, и вы справлялись с заданиями без ошибок — сорвите с дерева плоды – яблоки.
-Если вы допускаете ещё незначительные ошибки – сорвите цветы.
-Если на уроке вы не усвоили новый материал, вам ещё многое непонятно – зеленые листочки.
XIII. Подведение итогов урока
-Как разделить число на 10, 100, 1000?
-Как выполнить деление с остатком?
-Как можно проверить вычисления?
-Что является продуктом нашей работы?
— Повторение алгоритма деления с остатком на 10, 100, 1000.
Домашнее задание: переверните другой стороной ваши яблоки, листочки, цветы. Для вас индивидуальные домашние задания:
На яблоках-№94 с.27;
На цветах – 15928:100 15862:10 34518:100 135628:10 36704:10 52080:100;
На листочках — №93 с.27
-Объяснение заданий.
-Оценки за урок.
Технологическая карта
|
Этапы урока |
Обучающие и развивающие компоненты задания |
Деятельность учителя |
Деятельность учащихся |
Формы организации взаимодействия на уроке |
Формируемые умения (универсальные учебные действия) |
|
Мотивация к уроку. Актуализация знаний. Создание проблемной ситуации. Постановка проблемы. Построение проекта выхода из затруднения. Реализация построенного проекта. Первичное закрепление с проговариванием. Физкультминутка Самостоятельная работа в группах с самопроверкой по эталону. Повторение материала. Рефлексия Подведение итогов урока Домашнее задание |
Эмоциональная, психологическая и мотивационная подготовка учащихся к усвоению изучаемого материала. Устный счёт 1)Работаем в парах: в учебнике на с. 27 решим примеры на полях: 630: 70 *30- 89 + 29 : 3 + 30 = 100 2) №91 -Сколько раз по 100м содержится в 2 км? (20) -Сколько раз по 15 с содержится в 1 мин? (4) 3) В бидоне было 36 л молока. Доярка наполнила 10 трёхлитровых банок. Сколько л молока осталось в бидоне? (36-3*10=6 (л)) 4) В спортивную школу привезли 126 мячей. 5)Презентация: -Решите примеры: 800 : 2= 400 4 • 20=80 6 • 7=42 60 : 3= 20 30 • 2=60 -Вставьте числа в окошки: 3*8=(?)+27=(?)-39=(?):2=(?)*8=(?)-40=(?)*8 -Вычисли: 50:10 500:10 5000:10 600:100 6000:100 60000:100 7000:1000 70000:1000 700000:1000 68:10 400:100 3456:1000 340:10 827:100 7000:1000 Вспомните, как мы делим на 10, 100 и 1000. (Чтобы число разделить на 10, достаточно убрать один нуль. Чтобы число разделить на 100, надо убрать два нуля и на 1000 надо убрать три нуля). — Откройте тетради, запишите сегодняшнее число. — Найдем значение выражений второго столбика. Никто не спешит, следите за мной. — А сейчас рассмотрим второй столбик. -Кто может предложить способ деления 68:10? -Можем ли 68:10 без остатка? — Какое число можем разделить на 10 без остатка? (60:10=6) Правильно, возьмем наибольшее число до 68, которое делится на 10, — это 60. Разделим 60 на 10, что получим? (получим 6). . — Сколько останется в остатке?(68 – 60 = 8). Записываем это так 6 (ост. 8). — Составим алгоритм деления с остатком на 10,100,1000: 1.Найдём наибольшее число, которое делится на 10,100,1000. 2.Разделим это число. 3. Найдём остаток (от делимого отнимем наибольшее число). Мы вывели алгоритм деления с остатком на 10,100,1000. Давайте сверимся с научным источником – учебником с.27 Решите второй пример с объяснением.(827:100=8) остаток 27. — Выйдите к доске и решите 3 пример с объяснением. (3456 : 1000 = 3) ост 456 — Далее мы выполним задание 96. 69 : 10 = 6 (ост 9) 238 : 10 = 23 (ост 8) 691 : 100 = 6 (ост 91) 78 : 10 = 7 (ост 8) 238 : 100 = 2 (ост 38) 691 : 10 = 69 (ост 1) 7825 : 100 = 78 (ост 25) 7825 : 1000 = 7 (ост 825) под музыку повторяем движения животных Работа по карточкам: 327:10 1684:100 358:10 1605:1000 615:100 1730:100 Решение задачи изученного вида: №89 стр.27 №92 стр.27-составление и решение уравнения. Игра в мяч. Яблоня успеха. Как разделить число на 10, 100, 1000? -Как выполнить деление с остатком? -Как можно проверить вычисления? Индивидуальное домашнее задание для каждого ученика на сорванных яблоках: -№94 с. На цветах – 15928:100 15862:10 34518:100 135628:10 36704:10 52080:100; На листочках — №93 с.27 |
— Доброе утро, ребята! — Какое у вас настроение? Покажите жестами!!! Ребята моего класса из Пузачинской школы передали вам в подарок вот такое солнышко добра, чтобы вам на уроке было тепло и уютно. Положите его на ладошку. Оно согревает вас: ваши руки, тело и душу. Придаёт бодрость, заряжает энергией, будит воображение. Вот с таким настроением мы и начнём урок Совершенствует вычислительные навыки обучающихся, умение решать задачи Демонстрирует разные виды заданий. На какие две группы их можно разделить? (Примеры на деление без остатка и примеры на деление с остатком) -Запишите примеры в два столбика: 400:100 68:10 340:10 827:100 7000:1000 3456:1000 Примеры какого столбика мы умеем решать? Найдите значения выражения первого столбика: (4, 34, 7) Как вы думаете, какую проблему нам нужно решить на уроке, чему научиться? (Деление с остатком на 10,100,1000). — Прочитайте тему урока в учебнике на стр. 27) Повторяют правило деления на 10, 100, 1000. Решают с проговариванием Выполняют упражнения Работают в парах Читают задачу, анализируют под руководством учителя, решают, самостоятельно записывают решение. Анализируют содержание и составляют задачу. Бросает мяч и называет выражение, которое надо решить. Проверяет уровень усвоения материала. Оценивает уровень обученности Подводит итог урока. Объясняет выполнение домашнего задания |
Слушают учителя, повторяют за ним движения. Демонстрируют готовность к уроку. Работают в парах Повторяют единицы длины, времени. Решают устно задачи. Повторяют умножение и деление на 10,100,1000 Замечают проблему. Такие выражения ещё решать не умеют. Определяют тему и цели урока. Контролирует правильность ответов. Направляет на исследование выражения. Контролирует правильность решения и объяснения. Вместе с детьми выполняет упражнения. Контролирует деятельность обучающихся в парах. Проверка по эталону в призентации. Задаёт вопросы для анализа: Можем ли мы сразу ответить на вопрос задачи? (Нет, нам неизвестна скорость машины.) -Как можно найти скорость? (Расстояние разделим на время.) -Что вы заметили? (6 нельзя разделить на 5.) — А кто догадался, что нужно сделать? (6км перевести в метры: 6км=6000м.) -Как изменятся теперь единицы скорости? (Скорость будет измеряться в метрах в минуту.) -Как мы узнаем расстояние, пройденное за 40 мин? -Что нужно сделать, прежде чем узнать, сколько пройдёт машина с такой же скоростью за 1 ч? (Надо 1ч перевести в минуты.) -Запишите решение задачи выражениями. 6000:5=1200(м/мин) 1200*40=48000(м) 1200*60=72000(м) Ответ: 48000м,72000м Прочитайте задание. -Составьте первое уравнение. (х-20=40*6) -Как его можно упростить? (Можно найти произведение чисел: 40*6=240) -Что неизвестно в уравнении? (Уменьшаемое) -Вспомните, как найти уменьшаемое. (К разности прибавить вычитаемое.) -Запишите решение. х-20=240 х=240+20 х=260 260-20=240 -Второе уравнение решается самостоятельно в парах. 15+х=800:20 15+х=40 х=40-15 х=25 15+25=40 Ловят мяч и называют ответ выражения Выбирают яблоко, если усвоили новый материал на отлично, не возникало затруднений на уроке; Цветы, если возникают затруднения при решении; листья, если материал плохо усвоен. Обобщают новые знания. Слушают пояснения и задают вопросы. |
Фронтальная, индивидуальная. Фронтальная, индивидуальная Фронтальная, индивидуаль-ная Фронтальная, индивидуаль-ная. Фронтальная. Фронтальная, индивидуаль-ная . Фронтальная. Фронтальная, индивидуаль-ная Фронтальная, индивидуаль-ная Фронтальная, индивидуаль-ная Фронтальная, индивидуаль-ная Фронтальная, индивидуаль-ная Фронтальная, индивидуаль-ная |
К.-планирует учебное сотрудничество с учителем и сверстниками. Л.— имеют желание учиться, проявляют интерес к изучаемому предмету, понимают его важность. П. – осмысленно читают тексты математического содержания в соответствии с поставленными целями и задачами; проводят несложные обобщения и используют математические знания в расширенной области применения; используют математические термины, символы и знаки. Р.— понимают, принимают и сохраняют различные учебные задачи; осуществляют поиск средств для достижения учебной задачи. К. – умеют слушать друг друга, строить понятные для партнёра по коммуникации речевые высказывания; могут работать в коллективе, уважают мнения других участников образовательного процесса. Л. – способны адекватно рассуждать о причинах своего успеха или неуспеха, связывая успехи с усилиями, трудолюбием; проявляют познавательный интерес к изучению предмета. Р. – принимают и сохраняют учебную задачу. К. – проявляют готовность слушать. П. — учатся выполнять деление с остатком на 10, 100, 1000 ; Р. — контроль, коррекция и оценка своей деятельности. Л. — способствовать развитию интереса к математике. Л. – имеют установку на здоровый образ жизни. К. – умение работать в парах, сотрудничать, выслушивать мнение собеседника, уметь высказываться. П. – проводят анализ, синтез, сравнение, обобщение, аналогию;осознанно и произвольно строят речевые высказывания; осуществляют построение логической цепи рассуждений, доказательство. Р. – осуществляют волевую саморегуляцию в ситуации затруднения. К. – понимают различные позиции в подходе к решению задачи, задают вопросы для уточнения. Чётко и аргументированно высказывают свои оценки и предложения. Л. – осуществление смыслообразова-ния; проявляют познавательный интерес к предмету. Р.- контроль и оценка собственной деятельности. П. – ориентируются в своей системе знаний – отличают новое от уже известного. Л. – проявляют интерес к предмету. П. –ориентируются в своей системе знаний – отличают новое от уже известного. Р. – оценивают собственную деятельность на уроке. Л. – проявляют интерес к предмету. Р.- принимают и сохраняют учебную задачу, осуществляют поиск средств для её выполнения. |
Конспект урока математики на тему «Деление многозначных чисел в столбик».
Разработка урока математики в 4 классе
Тема урока: Деление многозначных чисел в столбик.
Тип урока: урок обобщения и систематизации знаний.
Цель: Систематизировать навык деления многозначного числа на двузначное число.
Задачи:
— обучающие:
закрепить алгоритм деления на многозначное число и применять его на практике;
совершенствовать навыки по решению задач;
познакомить учащихся с уравнениями нового вида, имеющими более одного корня;
продолжать учить анализировать задачи.
— развивающие:
развивать умение осознавать и принимать учебную цель
развивать умение рассуждать и обобщать;
способствовать развитию внимания, памяти, логического мышления,а также математической речи.
— воспитывающие:
воспитывать усидчивость, аккуратность при работе в тетрадях;
воспитывать взаимопомощь к товарищам;
воспитывать осознанное отношение к своему здоровью.
Оборудование:
Учебник И. И. Аргинская, Е. И. Ивановская « Математика» 4 класс, тетради, карточки-сигналы, карточки с индивидуальными заданиями, компьютер и мультимедийная установка.
Структура урока
1. Организационный этап – 1 мин.
2. Постановка учебной проблемы — 4 мин.
3. Актуализация знаний — 12 мин.
4. Физкультминутка – 3 мин.
5.Систематизация знаний – 20 мин.
6. Рефлексивно-оценочный этап – 4 мин.
Ход урока.
1.Организационный этап.Эмоциональный настрой.
2. Постановка учебной проблемы.
— Доброе утро, ребята!
— А теперь проверь, дружок, ты готов начать урок?
Всё ль на месте, всё в порядке, книжка, ручка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получить
Только лишь оценку «5».
— Чтобы нам сегодня всё удалось, какими мы должны быть?
— Пусть нашим девизом и станут эти слова: Будь внимателен и трудолюбив!
— Ребята, сегодня на урок к нам пришли 3 смайлика: весёлый, задумчивый и грустный. (приложение 1). Они будут следить за вашими ответами в процессе всего урока. В конце урока, вы попробуете оценить себя и свои знания в математике, выберите себе тот смайлик, который посчитаете нужным.
— Посмотрите на запись, которая имеется на доске: (1слайд).
312:3= 2584:76=
1296:12=
-Решите, пожалуйста, выражения.
— Что нового в этих выражениях вы заметили?
— Какие из них вы можете решить, а какие нет и почему?
— Ребята, кто догадался и может уже назвать тему нашего сегодняшнего урока?
Деление многозначного числа на двузначное.
— Сегодня мы продолжим работу над этой темой.
— А как вы думаете, чему мы должны сегодня научиться?
Мы познакомимся с новым способом деления в столбик.
— Цель нашего урока — вспомнить алгоритм деления и научиться делить многозначные числа на двузначные в столбик.
Мотивационный компонент урока.
Эмоционально-положительный настрой на урок, создание ситуации успеха.
Постановка проблемной задачи.
Наблюдение над примерами.
Решение примеров в тетради.
Формулировка темы урока.
Рассуждения детей.
3.Актуализация знаний.
— Посмотрите на те выражения, которые вы не смогли решить. (слайд 2).
2584:76=
— Скажите, что нужно знать, для того, чтобы решить эти выражения?
Алгоритм деления.
— Давайте его составим.
1. Находим первое неполное делимое.
2. Определяем число цифр в частном.
3. Округляем делитель с наименьшей погрешностью.
4. Делим первое неполное делимое. Получаем первую цифру в результате частного. Узнаём, сколько единиц разделили. Остаток сравниваем с делителем.
5. Сносим следующую цифру. Продолжаем деление в том же порядке. (слайд 3).
(Памятку с алгоритмом деления на многозначное число раздаю ученикам). (приложение 2).
— А теперь ребята, давайте потренируемся в решении примеров на деление в столбик.
— Не забывайте, пожалуйста, что если новым неполным делимым является 0, то его переписываем в частное.
— Ребята, сейчас мы с вами вместе решим один пример на деление в столбик, а два других вы решите самостоятельно.
1376 43
-А теперь давайте проверим ваши результаты. (слайд 4).
-Решите два других выражения по вариантам:
I-вариант II-вариант
828 36 2584 76
-А теперь поменяйтесь тетрадочками и проверьте полученные результаты. (слайд 5).
Ответ при решении первого примера:23, второго -34.
— Ребята, эти выражения можно было выполнить и по-другому, сделав подробную запись.
-Кто из вас догадался как?
Разложив делитель в виде произведения двух чисел.
-Решите последний пример.
2.584:76=(2.280+304)=2.280:76+304:76=30+4=34
— Сверьте вашу запись с той, которая дана в учебнике на с.96 в №232(3). (приложение 3).
Рассуждение детей.
Повторение случаев табличного умножения и деления. Развитие логического мышления. Закрепление умения правильно вычислять.
Запись в тетрадь.
Работа в парах, запись в тетрадь
Работа в парах.
Запись в тетрадь.
Проверка знаний, умений и навыков.
4. Физкультминутка.
Используется физкультминутка «Бабочка».
Утром бабочка проснулась,
Потянулась, улыбнулась.
Раз – росой она умылась, Два – изящно покружилась.
Три – нагнулась и присела.
На четыре – улетела.
(по ходу физкультминутки ученики имитируют все движения бабочки).
Эмоциональное восприятие материала.
Переключение внимания.
Снятие напряжения.
Охрана здоровья.
5.Систематиза-ция знаний.
1. Реши задачу №233(1) с.97 (приложение 3), составив краткую запись.
1). 7+5=12(д)- яблонь и груш в одной части.
2). 4248:12=354(ч)- по 12 деревьев.
-Ребята, скажите, что нужно сделать для того, чтобы найти сколько яблонь посадили в саду?
—Нужно количество яблонь умножить на часть.
3). 7х354=2.478(д)- яблонь.
4). 5х354=1770(д)- груш.
Ответ: 2.478 яблонь, 1770 груш.
Развитие мыслительной деятельности. Оценка деятельности учащихся.
Создание проблемной ситуации.
2. Выполняем №234(первые уравнения 1-го и 2-го столбика с.97).
-Кто сможет решить первое уравнение?
-Решите его.
х+38=113
х=113-38
х=75
75+38=113
113=113
— Давайте проверим ваш ответ. (слайд 6).
-А кто может решить второе уравнение?
-Давайте решим его вместе.
-Скажите, как найти произведение множителей, если оно равно нулю?
а в=0, когда а=0 или в=0
(у-3)х(4-у)=о
у-3=0 или 4-у=0
у=3 у=4
Если у=3, тогда
(3-3)х(4-3)=0
0х1=0
0=0
Если у=4, тогда
(4-3)х (4-4)=0
1х0=0
0=0
— Молодцы ребята, хорошо вы сегодня потрудились. А теперь давайте подведём итог урока.
Закрепление пройденного материала. Решение уравнений.
Постановка проблемной задачи.
7. Рефлексивно-оценочный этап.
Итог урока.
Оценивание учащихся.
Домашнее задание.
— Ребята скажите, а какое открытие вы сегодня сделали на уроке?
-А над чем мы продолжим работу?
— Чем необходимо руководствоваться, для того, чтобы выполнить деление многозначных чисел в столбик?
— Итак, каждый из вас записал себе в тетрадь памятку с алгоритмом деления, давайте проведём проверку:
— Научились ли вы находить первое неполное делимое?
— Научились определять количество цифр в частном?
— Сумели ли вы определить цифру в частном?
— По результатам ответов выберите
тот смайлик, который считаете, что вам подходит и над чем предстоит вам ещё поработать.
— Если всё удалось на уроке, тогда весёлый смайлик. Если остались неразрешённые вопросы –задумчивый, если вам ещё понадобиться помощь, тогда – грустный.
Выставляются оценки ученикам, которые активно работали на уроке.
— Чтобы закрепить полученные на уроке знания и подготовиться к работе на следующем уроке, дома выполните:
№232 (7) 3,4,5 пример, №234 (2,7 уравнение) с.97; №61 с.29 рабочая тетрадь (ребус по желанию). (приложение 4).
Регулирующий момент.
Совершенствовать умения анализировать, обобщать, делать выводы.
Оценивание своих способностей.
Вызвать у учащихся чувство удовлетворённости от урока.
Дифференциация по содержанию.
Как решать примеры в столбик на деление. Деление многочлена на многочлен (двучлен) столбиком (уголком)
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик . Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
Итак, поделим 354 на 2 . Для начала разместим эти числа как показано на рисунке:
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое , для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
3 больше 2 , значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
2 × 1 = 2 (2
2 × 2 = 4 (4 > 3)
2 меньше 3 , а 4 больше, значит, берем первый пример и множитель 1 .
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
Полученное значение сравниваем с делителем. 15 больше 2 , значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15 :
2 × 7 = 14 (14
2 × 8 = 16 (16 > 15)
Искомый множитель 7 , записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Продолжаем деление, для чего находим третье неполное делимое . Спускаем следующий разряд делимого:
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
Разность мы получили равную нулю, значит деление произведено правильно .
Усложним задачу и приведем другой пример:
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Разряд тысяч делимого составляет 1 , сравниваем с делителем:
1
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
Делим 10 на 5 , получаем 2 , записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
10 – 10 = 0
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
2
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0 :
20 ÷ 5 = 4
Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0 , значит пример решён правильно .
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.
- Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
- Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
- Определяем первый неполный делитель:
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в) , если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4 ;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б) .
- Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов. Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
- Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
- Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
- Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
- Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10 .
- Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).
10. Если мы выполняли деление без остатка и последняя найденная разность равна 0 , то мы правильно выполнили деление .
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения .
a = b ⋅ c + d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.
Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое . Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 76
8:24. Первое неполное делимое 76
265
:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном . Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного . Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428: 42 30296: 56 254415: 35 16514: 718
конспект урока математики » Алгоритм деления столбиком. Закрепление» | План-конспект урока по математике (4 класс) на тему:
Краснодарский край Туапсинский район
Муниципальное автономное общеобразовательное учреждение
средняя общеобразовательная школа № 11 г. Туапсе
МО Туапсинский район
Открытый урок по математике
в 4 «В» классе.
Тема: «Алгоритм деления столбиком. Закрепление»
Учитель : Куадже Зурет Муратовна
г. Туапсе
2018 г.
Урок математики в 4 «В» классе
Тема урока: «Алгоритм деления столбиком»
Цель: создание условий для усвоения учащимися математического понятия алгоритм деления столбиком и применения его для решения;
Задачи:
- учить анализировать запись деления многозначного числа на двузначное столбиком;
- формировать умение формулировать алгоритм деления столбиком, отвечая на вопросы;
- развивать математическую речь учащихся;
- формировать соответствующие УУД
Личностные УУД:- способствовать самооценке на основе критерия успешности учебной деятельности.
Регулятивные УУД:- умение определить и формулировать цель на уроке с помощью учителя; планировать свое действие в соответствии с поставленной задачей; высказывать свое предположение; выбирать для выполнения посильные задания.
Коммуникативные УУД:- умение оформлять свои мысли в устной и письменной речи, слушать, понимать речь других; договариваться о правилах поведения и общения при работе в парах, в группе и следовать им.
Познавательные УУД:-выполнять действия по заданному алгоритму; строить логическую цепь рассуждений; отличать новое от уже известного с помощью учителя.
Прогнозируемые результаты:
Предметные:
- знание алгоритма письменного деления:
- умение делить многозначные числа на двузначные письменным способом.
Метапредметные:
- умение ставить учебные задачи и самостоятельно формулировать выводы.
- умение слушать собеседника, излагать своё мнение и аргументировать свою точку зрения.
Личностные:
- умение сотрудничать с учителем и сверстниками,
- умение определять успешность учебной деятельности.
Усваиваемые математические термины: «алгоритм деления столбиком», «запись делимого», «первое промежуточное делимое», «остаток первого промежуточного деления», «число цифр в записи неполного частного».
Оборудование: проектор, презентация, учебник, тетради на печатной основе, таблицы для рефлексии, пошаговый алгоритм в конверте, маршрутный лист, карточки, смайлики, жетоны.
Тип урока: урок закрепления изученного материала.
Методы обучения: словесный, наглядный, практический, аналитико-синтетический.
Формы работы учащихся: индивидуальная, фронтальная, парная, групповая.
Приёмы: устный счёт, работа у доски, решение задач, уравнений.
Технология: личностно-ориентированная.
Оборудование: учебник «Математика», 4 класс, авторы: А.Л.Чекин, презентация, письменные принадлежности, тетради.
Структура и основные этапы урока. (45 мин.)
1. Организационный момент, характеризующийся внешней и внутренней (психологической) готовностью учащихся к уроку.1 мин.
2. Целеполагание и мотивация. Введение в тему урока. Подготовка к формулированию задачи на урок. Формулировка задачи детьми. 6 мин.
3. Актуализация знаний (устный счет). 8 мин.
4. Закрепление изученного материала 25 мин.
5. Релаксация (Физкультминутка). 2 мин.
6. Итог урока. 2 мин.
7. Рефлексия. 1 мин.
Ход урока
Слайд I. Организационный момент
Приветствие детей и гостей.
Учитель: — Здравствуйте ребята. Сегодня на уроке у нас гости.
Поприветствуйте гостей.
— В природе есть солнце. Оно светит и всех нас любит и греет. Так пусть же каждый его лучик заглянет к нам в класс и не только обогреет вас своим теплом, но и придаст сил и уверенности в знаниях. А для этого нужно сесть красиво и приступить к работе
Давайте, ребята, учиться считать,
Делить, умножать, прибавлять, вычитать,
Запомните все, что без точного счета
Не сдвинется с места любая работа.
Учитель: Урок у нас необычный. Чему он посвящён вы определите после выполнения задания.
— Найдите значения выражений, буквы вставьте в порядке возрастания чисел. Считаем вместе, последовательно открывая ответы СЛАЙД
1. — Посмотрите внимательно и выполните действия.
200 : 5 =… К 40
480 : 8 =…О 60
200 х 2 =…Г 400
60 х 9 =…И 540
840 : 4 =…О 210
230 х 3 =… Я 690
400 : 4 =…Л 100
120 : 6 =… Э 20
Поставьте полученные результаты в порядке возрастания.
— Какое слово получилось? (Экология)
20 | 40 | 60 | 100 | 210 | 400 | 540 | 690 |
э | к | о | л | о | г | и | я |
Учащиеся: ЭКОЛОГИЯ СЛАЙД
Учитель: Правильно наш урок посвящён проблемам экологии. Вспомним, как мы определяли это слово на уроке окружающий мир?
Учитель Что такое экология?
Учащиеся:
«Логос» — наука
«Эко» — дом (на латинском языке)
Это наука о связях между живыми существами и окружающей их средой.
Учитель: — Экология – это наука о доме. Дом для человечества это наша огромная планета Земля.
Учитель: — Кто такие экологи?
– Эти люди стремятся, чтобы на нашей планете был чистый воздух, чистые воды, жизни животных и растений ничего не угрожало.
— О природе мы должны думать всегда и даже на нашем уроке мы с вами будем решать задачи, которые будут очень поучительными.
Все задания нашего урока будут связаны с экологией.
II.Введение в тему урока. Подготовка к формулированию задачи на урок.
Учитель:– Сегодня на уроке мы отправимся в экологическую экспедицию по нашей планете, нам предстоит выяснить какие экологические проблемы
существуют, постараемся эти проблемы решить, а помогут в этом наши знания полученные ранее на уроках математики. Откройте учебники на с.15 и прочитайте тему прошлого урока.
-Что такое алгоритм?
— С какими алгоритмами мы уже знакомы? Письменного сложения, вычитания, умножения и деления)
-Какие задачи поставим перед собой? Используйте для этого слова: повторение, решение, применение, закрепление.
Учитель: Правильно! Тема нашего урока «Алгоритм деление многозначного числа на двузначное»
СЛАЙД
Цели: Нам предстоит закрепить деление многозначного числа на двузначное, закрепить умения решать задачи, повторить решение уравнений, СЛАЙД
Учитель: Откроем тетради. Запишем число, классная работа
III. Актуализация знаний
Учитель: Вот и первые экологические задания, для решения которых нужны ваши математические знания. Записываем только ответы
1.Одно предприятие выбрасывает в атмосферу в год 200 тонн сажи . После установки очистных сооружений стало выбрасывать в 20 раз меньше. Сколько тонн сажи стало выбрасываться в атмосферу? (10)
2. Для естественного восстановления слоя почвы толщиной в 1 см требуется примерно 100 лет. Сколько лет потребуется для восстановления слоя почвы в 10см? (1000)
3.Липа живет 500 лет, а дуб 2000 лет. Во сколько раз меньше живет липа, чем дуб? (4)
4.В час из крана вытекает 5 г воды. Сколько воды вытечет из крана за сутки?(120)
5.Почтовый голубь должен доставить донесение на экологическую станцию, на расстояние 150 км. Скорость голубя 50 км/ч. За какое время голубь сможет доставить донесение? (3)
Учитель:-Как вы справились с заданием? Отвечает Пономарёва
СЛАЙД с ответами
ПРОВЕРЬ: Ответы: 10,1000,4,120,600,3,22
Молодцы! С заданиями справились. Наша экспедиция может отправляться в путь по следующему маршруту:
У каждого из вас есть маршрутный лист. Я вас прошу оценивать свои успехи по ходу преодоления каждого задания.
Учитель: Во время экспедиции мы посетим следующие острова СЛАЙД
Учитель: Отправляемся на остров «Арифметических действий» СЛАЙД
-Какие здесь ждут нас задания?
IV. Закрепление письменных приемов деления на двузначное число.
Учитель:- На доске и на экране примеры. Прежде чем вы начнёте их решать , повторим компоненты действия деления, алгоритм действия деления.
СЛАЙД
1.Два ученика решают у доски (примеры напечатаны прикреплены магнитом)
2 924 : 68 (Ответ 43)
29 736 : 56 (Ответ 531)
Консультанты проверяют ( Кравченко Н., Пономаренко Н., Черновол М.)
Раздаются карточки
2. Одна группа решает по карточкам. Выполняют взаимопроверку. Обмениваются тетрадями.
3912:12=326 11206:13=862 479120 : 53 10635:15=709
6748:14=482 14562:18=809 273150 : 45 15640:17=920
3.Класс решает по учебнику с.17 №42. Взаимопроверка
-Какие ошибки возможны при делении многозначных чисел? СЛАЙД
- Пропущен или добавлен нуль в частном при переходе к более мелким счетным единицам.
- Не снесены или снесены лишние нули при делении круглых чисел.
- Неверно подобрана цифра частного т.е. остаток больше делителя.
- Вычислительная ошибка.
- Не выполнена прикидка результата.
Учитель: Ребята! Поступил сигнал SOS! Природный дом оказался в опасности.
-Какие вы знаете раны, которые люди приносят природе?
Учащиеся: Исчезновение редких животных и растений, загрязнение рек, воздуха, загрязнение окружающей среды, вырубка леса СЛАЙД
Учитель: Нам предстоит помочь нашей планете избежать экологических катастроф. Для этого мы отправляемся на остров «Задач» СЛАЙД
1 человек у доски. У. с.17 №43 Решает Лахов Богдан
Задачи для индивидуальной работы: одной группе
Реши задачу и сделай свое заключение: надо ли охранять почву и почему?
Для образования слоя почвы толщиной в 5 см в природе требуется. по расчетам
специалистов, 2 000 лет. Сколько лет потребуется для образования слоя в 12 см?
2 000:5=400 лет – 1 см почвы
400х12=4 800 лет
После решения объясняет как решал.
Задачи для индивидуальной работы: второй группе
1.В среднем на 1 жителя в год приходится 200 кг бытовых отходов. В селе Зелёное проживает 651 человек. Сколько тонн поступит на свалку в год бытовых отходов
1 ч.- 200кг
651ч.-? кг
651х200=130200кг=130т.200кг
Ответь на вопрос. Как решить проблему свалки?
Ответ: Построить мусороперерабатывающие предприятия.
Задачи для индивидуальной работы: третьей группе
4. Из 250000 видов растений Земли 1/10 часть находится на грани исчезновения. Сколько видов растений на Земле на грани исчезновения? (25 000 видов)
-Ответь на вопрос. Какие ты знаешь растения, занесённые в Красную книгу?
По карточкам каждый объясняет своё решение
Класс работает по учебнику. Самостоятельная работа.
Учитель: Каждый успешно решил свою экологическую задачу. Молодцы! Пора нам и отдохнуть! Отправляемся на следующий остров «Отдыхай-ка»
СЛАЙД V. Физкультминутка
Учитель: Молодцы! Отдохнули, пора нам дальше в путь приводить нашу планету в порядок, держим курс к острову «Уравнений»
СЛАЙД РАБОТА НАД УРАВНЕНИЯМИ.
Учитель: Ребята, около острова плавала бутылка с запиской (у учителя бутылка, в которой записка с надписью SOS и листочки для учащихся с записанными уравнениями). Что в ней записано, узнаем, когда решим уравнения
Два человека работают у доски, остальные по вариантам
X · 3 = 375 – 120
540 : х=380 : 19
Класс решает по вариантам П.т. с.10 № 19
1вариант- 2столбик
2 вариант- 3 столбик
На местах проводят взаимопроверку. Кто справился с уравнениями?
У кого возникли трудности? Проверим ответы . СЛАЙД
Учитель: -Молодцы!
СЛАЙД МЕДУЗА
— Итак, давайте прочитаем записку. (SOS) От кого же она Отгадайте загадку
Что такое там плывёт?
Не желе это, не лёд,
И не мякоть от арбуза,
В море плавает… правильно медуза
Учитель: — О чем нас просят?
— Послушайте какая беда происходит в морях..
«Когда-то в море нас, медуз, было очень много, но сейчас в морях плавает много нефтяных танкеров, море становится грязным, и медуз становится меньше».Она просит нас помочь очистить море от нефтяных плёнок и отправляет нас к острову «Смекалка»
СЛАЙД
РАБОТА НАД РАЗВИТИЕМ ЛОГИЧЕСКОГО МЫШЛЕНИЯ.
Чтобы очистить море от нефтяных плёнок нам нужно очистить примеры, так как эти плёнки и на примеры попали СЛАЙД
Ваша задача: восстановить цифры .
Решают самостоятельно с проверкой на экране.
- 6 9 * 4
+ 7 * 8 *
* 4 2 6 3
- * 5 *
+ 8 * 4
* 7 5 6
- 3 4 * 3 2 8
_ — * 9 * 3 *
* 2 5 8 * 9 СЛАЙД
— МОЛОДЦЫ!
— Наш урок-экспедиция подходит к концу.
Я думаю вы стали и умнее и мудрее.
Давайте еще раз посмотрим на мир глазами математика.
Какую цель мы поставили в начале нашего урока?
— Достигли мы цели урока? (повторяли и закрепляли алгоритм деления, учились его применять при решении примеров)
-Как надо относится к окружающей нас природе, чтобы не происходило экологических катастроф? (беречь и реки и леса, и почву и все что нас окружает)
— А теперь каждый оценит себя – достиг ли он цели урока — насколько хорошо вы усвоили алгоритм деления столбиком. Оценивайте свои умения по островам на маршрутном листе.
СЛАЙД VI. Рефлексия.
— Встаньте, пожалуйста, те, кто устал от сегодняшнего урока; кому было трудно; кто был уверен в себе; у кого осталось отличное настроение.
Молодцы! Вы сегодня хорошо поработали на уроке.
— Кроме знаний по математике мы говорили с вами о нашем общем доме – планете Земля. Человек неотделим от природы. Он учится у природы. Уважайте законы природы.
-Поэтому и урок хочется закончить стихотворением, напоминающим о бережном отношении к природе. СЛАЙД
Стихотворение читает ученик.
Любите родную природу –
Озера, леса и поля!
Ведь это же наша с тобою
Навеки родная земля.
На ней мы с тобою родились,
Живем мы с тобою на ней.
Так будем же, люди, все вместе
Мы к ней относиться добрей!
СЛАЙД VII . Домашнее задание карточки по уровням
Выставление отметок. По ходу урока жетон разного цвета
Красный 5
Зелёный 4
Синий 3
СЛАЙД Спасибо за урок
Разделение в столбик. Деление многочлена на многочлен (двучлен) столбиком (уголком)
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105
, а делителем – 5
5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808
на 51 234
(614 808
– шестизначное число, 51 234
– пятизначное число, разница в количестве знаков в записях равна 6−5=1
) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058
и 4
(здесь разница в количестве знаков равна 4−1=3
). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пример.
Пусть нам нужно разделить столбиком 8 на 2 .
Решение.
Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4 .
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8
и делитель 2
так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0 , 1 , 2 , 3 , … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0
; 2·1=2
; 2·2=4
; 2·3=6
; 2·4=8
. Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4
. При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8 на 2 . Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).
Ответ:
8:2=4 .
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Пример.
Разделим столбиком 7 на 3 .
Решение.
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=07
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7
и 3
будет завершено.
Таким образом, неполное частное равно 2 , и остаток равен 1 .
Ответ:
7:3=2 (ост. 1) .
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288
является цифра 1
. Число 1
меньше, чем делитель 4
, поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14
, с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x ). Для этого последовательно умножаем делитель на 0 , 1 , 2 , 3 , … до того момента, пока не получим число x или число больше, чем x . Когда получается число x , то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4 пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4
на числа 0
, 1
, 2
, …, пока не получим число, которое равно 14
или больше 14
. Имеем 4·0=014
. Так как на последнем шаге мы получили число 16
, которое больше, чем 14
, то под выделенным числом записываем число 12
, которое получилось на предпоследнем шаге, а на место частного записываем число 3
, так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14
число 12
(для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2
. Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2
меньше делителя 4
, то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2
записываем цифру 0
, так как именно цифра 0
находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой образуется число 20
.
Это число 20
мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2
, так как именно она находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2
.
Число 2
принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4
пунктов алгоритма.
Умножаем делитель на 0
, 1
, 2
и так далее, и сравниваем получающиеся числа с отмеченным числом 2
. Имеем 4·0=02
. Следовательно, под отмеченным числом записываем число 0
(оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0
(на 0
мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2
Под горизонтально чертой справа от числа 2 дописываем цифру 8
(так как она находится в этом столбце в записи делимого 140 288
). Таким образом, под горизонтальной линией оказывается число 28
.
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4
пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2
, 3
, 4
(предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288
и 4
в столбик:
Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Пример.
Выполните деление в столбик, если делимое равно 7 136 , а делителем является однозначное натуральное число 9 .
Решение.
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136
и 9
Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .
Ответ:
7 136:9=792 (ост. 8) .
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Пример.
Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .
Решение.
Удобнее всего выполнить деление столбиком.
Ответ:
7 042 035:7=1 006 005 .
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел . Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Пример.
Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .
Решение.
Так как в записи делителя 206
участвуют 3
знака, то смотрим на первые 3
цифры слева в записи делимого 5 562
. Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206
на числа 0
, 1
, 2
, 3
, … до того момента, пока не получим число, которое либо равно 556
, либо больше, чем 556
. Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556
. Так как мы получили число, которое больше числа 556
, то под выделенным числом записываем число 412
(оно было получено на предпоследнем шаге), а на место частного записываем число 2
(так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144
, это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2
, так как она находится в записи делимого 5 562
в этом столбце:
Теперь мы работаем с числом 1 442
, выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
- Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
- Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Калькулятор онлайн примеры в столбик по действиям. Как научиться делить столбиком: примеры и решения
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.
Особенности
Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
- Цифры.
- Знаки арифметических действий.
- Удаление раннее введенных символов.
Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.
Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:
- умножение;
- деление;
- сложение;
- вычитание.
Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Достоинства и недостатки
- Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
- Очень простой, интуитивно понятный интерфейс для каждого пользователя.
- Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
- Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.
Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.
Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.
Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
полиномов — длинное деление
Полином выглядит так:
| пример полинома у этого 3 члена |
Разделение
Многочлены иногда можно разделить с помощью простых методов, показанных в разделе «Деление многочленов».
Но иногда лучше использовать «Длинное деление» (метод, аналогичный Длинному делению для чисел)
Числитель и знаменатель
Мы можем дать каждому многочлену имя:
- верхний полином является числителем
- нижний полином знаменатель
Если у вас проблемы с запоминанием, подумайте, что знаменатель равен вниз — знаменатель.
Метод
Запишите аккуратно:
- знаменатель идет первым,
- , затем «)»,
- , затем числитель с чертой над
Оба полинома должны сначала содержать члены «более высокого порядка» (те, которые имеют наибольшие показатели, например, «2» в x 2 ).
Тогда:
| |
| Повторите , используя новый многочлен |
Проще показать на примере!
Пример:
Запишите аккуратно, как показано ниже, а затем решите пошагово (нажмите кнопку воспроизведения):
Проверьте ответ:
Умножьте ответ на нижний многочлен, мы должны получить верхний многочлен:
Остаток
Предыдущий пример работал отлично, но это не всегда так! Попробуйте это:
После деления у нас осталось «2», это «остаток».
Остаток — это то, что осталось после разделения.
Но у нас все еще есть ответ: поместите остаток , разделенный на нижний многочлен , как часть ответа, например:
«Отсутствующие» термины
Могут быть «пропущенные термины» (пример: может быть x 3 , но нет x 2 ). В этом случае либо оставьте пробелы, либо включите пропущенные члены с нулевым коэффициентом.
Пример:
Запишите его с коэффициентами «0» для отсутствующих членов, затем решите его обычным образом (нажмите кнопку воспроизведения):
Видите, как нам понадобилось место для «3x 3 «?
Более одной переменной
До сих пор мы делили многочлены только с одной переменной ( x ), но мы можем обрабатывать многочлены с двумя или более переменными (например, x и y ), используя тот же метод.
Пример:
Делительные многочлены — объяснения и примеры
Деление многочленов может показаться самой сложной и пугающей из операций, которые нужно освоить. Тем не менее, если вы помните основные правила деления целых чисел в столбик, это на удивление простой процесс.
Эта статья покажет вам , как выполнить деление между двумя одночленами, одночленом и многочленом, и, наконец, между двумя многочленами.
Прежде чем перейти к теме деления многочленов, давайте кратко обсудим здесь несколько важных терминов.
Полином
Полином — это алгебраическое выражение, состоящее из двух или более членов, которые вычитаются, складываются или умножаются . Многочлен может содержать коэффициенты, переменные, показатели, константы и операторы, такие как сложение и вычитание.
Также важно отметить, что у многочлена не может быть дробных или отрицательных показателей.Примеры полиномов: 3y 2 + 2x + 5, x 3 + 2 x 2 — 9 x — 4, 10 x 3 + 5 x + y, 4x 2 — 5x + 7) и т. Д.
Существует три типа полиномов: мономиальные, биномиальные и трехчленные.
Моном — это алгебраическое выражение, состоящее только из одного члена. Примеры одночленов: 5, 2x, 3a 2 , 4xy и т. Д.
Биномом называется выражение, содержащее два члена, разделенных знаком сложения (+) или вычитания (-).Примеры биномиальных выражений: 2 x + 3, 3 x — 1, 2x + 5y, 6x − 3y и т. Д.
Трехчлен — это выражение, содержащее ровно три члена. Примеры трехчленов:
4x 2 + 9x + 7, 12pq + 4x 2 — 10, 3x + 5x 2 — 6x 3 и т. Д.
Как разделить многочлены?
Деление — это арифметическая операция разделения количества на равные количества. Процесс деления иногда называют повторным вычитанием или обратным умножением.
В математике есть два метода деления многочленов.
Это метод длинного деления и синтетический метод. Как следует из названия, метод длинного деления является наиболее громоздким и устрашающим процессом для освоения. С другой стороны, синтетический метод представляет собой способ деления многочленов « fun ».
Как разделить одночлен на другой одночлен?
При делении одночлена на другой одночлен, мы делим коэффициенты и применяем к переменным закон частного x m ÷ x n = x m — n .
ПРИМЕЧАНИЕ: Любое число или переменная, возведенная в степень нуля, равна 1. Например, x 0 = 1.
Давайте попробуем здесь несколько примеров.
Пример 1
Разделите 40x 2 на 10x
Решение
Сначала разделите коэффициенты
40/10 = 4
Теперь разделите переменные, используя правило частного
2/ x = x 2 -1
= x
Умножьте частное коэффициентов на частное переменных;
⟹ 4 * x = 4x
Альтернативно;
40x 2 / 10x = (2 * 2 * 5 * 2 * x * x) / (2 * 5 * x)
Поскольку x, 2 и 5 являются общими множителями как знаменателя, так и числителя, мы отмените их, чтобы получить;
⟹ 40x 2 / 10x = 4x
Пример 2
Divide -15x 3 yz 3 by -5xyz 2
Solution
Разделить и использовать обычно коэффициенты закон частного x m ÷ x n = x m — n для разделения переменных.
-15x 3 yz 3 / -5xyz 2 ⟹ (-15 / -5 ) x 3-1 y 1-1 z 3-2
= 3 x 2 y 0 z 1
= 3x 2 z.
Пример 3
Разделить 35x 3 yz 2 на -7xyz
Решение
Использование закона Quotient
35x 3 yz 2 / -9007xyz 35 ⟹ / -7 ) x 3-1 y 1-1 z 2-1
= -5 x 2 y 0 z 1
= -5x 2 z.
Пример 4
Разделить 8x 2 y 3 на -2xy
Решение
8x 2 y 3 / -2xy ⟹ ( 8 / -2 ) x 2 — 1 y 3 — 1
= -4xy 2 .
Как разделить многочлены на одночлены?
Чтобы разделить многочлен на одночлен, разделите каждый член многочлена на одночлен и сложите частное каждой операции, чтобы получить ответ.
Давайте попробуем здесь несколько примеров.
Пример 5
Разделить 24x 3 — 12xy + 9x на 3x.
Решение
(24x 3 –12xy + 9x) / 3x ⟹ (24x 3 / 3x) — (12xy / 3x) + (9x / 3x)
= 8x 2 — 4y + 3
Пример 6
Разделить 20x 3 y + 12x 2 y 2 — 10xy на 2xy
Решение
(20x 3 y + 12x 2 y 2 — 10xy) / (2xy) ⟹ 20x 3 y / 2xy + 12x 2 y 2 / 2xy — 10xy / 2xy
= 10x 2 + 6xy — 5.
Пример 7
Разделить x 6 + 7x 5 — 5x 4 на x 2
Решение
= (x 6 + 7x 5 — 5x 4 ) / (x 2 ) ⟹ x 6 / x 2 + 7x 5 / x 2 — 5x 4 / x 2
Для разделения переменные
= x 4 + 7x 3 — 5x 2
Пример 8
Разделить 6x 5 + 18x 4 — 3x 2 на 3x 2
Решение
= (6x 5 + 18x 4 — 3x 2 ) / 3x 2 ⟹ 6x 5 / 3x 2 + 18x 4 / 3x 2 — 3x 2 / 3x 2
= 2x 3 + 6x 2 — 1.
Пример 9
Разделение 4 м 4 n 4 — 8 м 3 n 4 + 6 мес 3 на -2 мин
Решение
= (4m 4 n 4 — 8 млн. 3 n 4 + 6 млн. 3 ) / (- 2 млн.) ⟹ 4 млн. 4 n 4 / — 2 млн. — 8 млн. 3 n 4 / -2 млн. + 6 млн. 3 / -2mn
= 2m 3 n 3 + 4m 2 n 3 — 3n 2
Пример 9
Решить (a 3 — a 2 b — a 2 b 2 ) ÷ a 2
Решение
= (a 3 — a 2 b — a 2 b 2 ) ÷ a 2 ⟹ a 3 / a 2 — a 2 b / a 2 — a 2 b 2 / a 2
= a — b — b 2
Как сделать полиномиальное деление в столбик?
Деление в столбик является наиболее подходящим и надежным методом деления многочленов, хотя процедура немного утомительна, эта техника применима для всех задач.
Процесс деления многочленов аналогичен делению целых чисел или чисел с использованием метода деления в столбик.
Чтобы разделить два многочлена, выполните следующие действия:
- Расположите делитель и делимое в порядке убывания их степеней.
- Разделите 1 -й член дивиденда на 1 -й член делителя, чтобы получить 1 -й член частного.
- Найдите произведение всех членов делителя и частного 1 st и вычтите ответ дивиденда.
- Если в приведенном выше есть остаток, продолжайте повторять процедуру 3 до тех пор, пока вы не получите ноль в качестве остатка или не получите выражение, имеющее меньшую степень, чем у делителя.
Пример 10
Разделите следующие многочлены методом деления в столбик:
3x 3 — 8x + 5 на x — 1
Решение
Пример 11 Разделите 12 — 14a² — 13a на 3 + 2a. Решение Пример 12 Разделите полиномы ниже: 10x⁴ + 17x³ — 62x² + 30x — 3 на (2x² + 7x — 1). Решение Практические вопросы Разделите следующие многочлены: Если вы делите многочлен на что-то более сложное, чем просто одночлен (то есть на что-то более сложное, чем одночленный многочлен), то вам нужно использовать другой метод для упрощения.Этот метод называется «долгим полиномиальным делением», и он работает так же, как долгое (числовое) деление, которое вы делали в начальной школе, за исключением того, что теперь вы делите с помощью переменных. Вспомните, когда вы делали длинное деление с простыми старыми числами.Вам будет дано одно число (называемое делителем), которое вы должны разделить на другое число (называемое делимым). Вы установили символ длинного деления, вставили два числа, которым они принадлежали, а затем начали гадать, что должно быть поверх символа. И вы не сразу угадали весь ответ; вместо этого вы начали работать с «лицевой» частью (то есть с большей размеченной частью) числа, которое вы делили.Например, если вы делили 1137 на 82, вы бы посмотрели на «8» и «10» и предположили бы, что, вероятно, «1» должна быть сверху, над «11», потому что 8 входит один раз в 11. Деление в столбик многочленов работает примерно так же: Сначала я настрою деление, поместив делимое (то, на что делится) внутри, а делитель (то, что делит) снаружи и влево: На данный момент я проигнорирую все, кроме ведущих терминов.Как и в случае с числовым делением в столбик, я буду рассматривать только ведущие x делителя и ведущие x 2 делимого. Если я разделю ведущие x 2 внутри на ведущие x спереди, что я получу? Я бы взял x . Поэтому я поставлю x поверх символа деления, прямо над x 2 внутри: Теперь возьму x сверху и умножу на делитель x + 1.Сначала я умножу x (вверху) на x (на «стороне») и перенесу получившееся x 2 внизу, поместив его прямо под x 2 от дивиденда: Затем я умножу x (вверху) на 1 (на «стороне») и перенесу 1 x внизу, поместив его прямо под –9 x в делимом: Затем я нарисую горизонтальную полосу «равно» под тем, что я только что поместил под делимым, чтобы я мог произвести вычитание. Чтобы вычесть многочлены, я сначала меняю все знаки во второй строке … … а потом складываю. Первый член ( x 2 ) будет сокращен (по дизайну), а –9 x — 1 x станет –10 x : Мне нужно не забыть перенести последний член (то есть член «вычесть десять») из дивиденда: На этом этапе я начинаю игнорировать дивиденды и вместо этого работаю над нижней строкой моего длинного деления. Я смотрю на x от делителя и новый ведущий член, –10 x , в нижней строке деления. Если я разделю –10 x на x , я получу –10, поэтому я поставлю это сверху, прямо над –9 x : Теперь я умножу –10 (сверху) на ведущие x (на «стороне») и перенесу –10 x вниз, прямо под –10 x в предыдущей строке: …и я умножу –10 (сверху) на 1 (на «стороне») и перенесу –10 вниз, прямо под –10: Я нарисую еще одну горизонтальную полосу «равно» и поменяю знаки на всех терминах в нижнем ряду: Затем складываю: По дизайну, 10 x отменены.Случайно и десятки тоже отменили. Тогда мой ответ сверху символа деления: Так как остаток от деления выше был равен нулю (то есть, поскольку ничего не осталось), деление «получилось четным». Когда вы делаете обычное деление с числами, и деление «получается четным», это означает, что число, на которое вы делите, является множителем числа, которое вы делите. Например, если вы разделите 50 на 10, ответом будет аккуратная цифра «5» с нулевым остатком, потому что 10 — это коэффициент 50. В случае вышеупомянутого полиномиального деления нулевой остаток говорит нам, что x + 1 является множителем x 2 -9 x -10, что вы можете подтвердить факторизацией исходного квадратичного делимого, x 2 — 9 x — 10. Каждый раз, когда вы получаете нулевой остаток, делитель является множителем делимого. Между прочим, обратите внимание на то, как я выяснил, что поставить поверх символа длинного деления в приведенном выше упражнении: я разделил главный член того, на что я делил, на главный член того, на что я делил.Независимо от того, будет ли у конкретного деления ненулевой остаток, этот метод всегда будет давать правильное значение для того, что вам нужно наверху. Таким образом, полиномиальное деление в столбик проще, чем числовое деление в столбик, когда вам приходилось угадывать и проверять, чтобы выяснить, что было наверху. Давайте сделаем еще один пример с делением, которое выходит «четным», чтобы мы могли проверить наш результат, выполнив факторизацию и отмену. Это дробное сокращение может быть выполнено одним из двух способов: я могу разложить квадратичный множитель на множители, а затем отменить общий множитель, например: Но что, если я не знаю, как разложить на множители (или если мне нужно «показать свою работу» для длинного полиномиального деления на тесте)? Как и раньше, я начну длинное деление с работы с ведущими членами делителя и дивиденда. Старший член дивиденда — x 2 , а старший член делителя — x . Разделив x 2 на x , я получу x , так что это то, что я поставил поверх x 2 в дивиденде: Затем я умножаю x сверху на делитель x + 7 и помещаю полученное x 2 + 7 под делимое: Затем я рисую горизонтальную полосу «равно», меняю знаки, складываю вниз и перемещаю +14 вниз, получая 2 x + 14 под полосой «равно»: Деление первых 2 x на ведущие x делителя дает мне 2, так что это то, что я поместил поверх символа деления, прямо над 9 x в делимом: Затем я умножаю это 2 сверху на x + 7 и помещаю результат 2 x + 14 под: Затем я меняю знаки и складываю, получая нулевой остаток: Ответом на деление является частное, являющееся полиномом в верхней части символа деления в столбик: URL: https: // www.purplemath.com/modules/polydiv2.htm Быстро! Мне нужна помощь с:
Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation и Y-intation , Поиск шансов, Математика, Практика многочленов, Математика, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание чисел Квадратные многочлены, Деление многочленов, Факторизация разности квадратов Многочлены, Факторинг триномов Полиномы, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок Длинное деление часто считается одной из самых сложных тем для преподавания.К счастью, есть стратегии, которым мы можем научить, чтобы упростить понимание и выполнение многозначного деления. Метод Grid — одна из таких стратегий. Метод сетки предназначен для тех, кто планирует обучать традиционному делению в столбик. Он следует тем же шагам, что и традиционное деление в столбик, но использует другой метод организации. Это упрощает традиционное деление в столбик для некоторых студентов. Метод сетки — это не математический подход.Если вы ищете математический подход к делению в столбик, обязательно ознакомьтесь с моими сообщениями о методе прямоугольников / площадей и частичных частных. Давайте узнаем, как использовать сеточный метод для деления в столбик! Ниже я включил видеоурок и пошаговые инструкции. ВИДЕОУЧИТЕЛЬ: ПОШАГОВАЯ ИНСТРУКЦИЯ Предположим, что мы хотим решить уравнение 324 ÷ 2. ШАГ 1: ШАГ 2: ШАГ 3: Теперь мы спрашиваем себя: «Сколько раз 2 переходит в 12?» Ответ — 6, поэтому мы пишем 6 в верхней части сетки. Теперь умножаем 6 × 2, чтобы получилось 12, и убираем 12 из 12. Остается 0. ШАГ 4: Теперь мы спрашиваем себя: «Сколько раз 2 переходит в 4?» Это повторяется 2 раза, поэтому мы пишем 2 поверх нашей сетки. Теперь мы умножаем 2 × 2, чтобы получить 4, и убираем это 4 из 4. У нас остается 0, что означает, что у нас нет остатка. Чтобы найти окончательное частное, мы просто перечисляем цифры сверху сетки: 1, 6, 2. Итак, 324 ÷ 2 = 162 . ПОПРОБУЕМ ДРУГОЙ ПРИМЕР На этот раз мы попробуем пример с остатком.В нем также больше цифр, чем в нашем последнем примере. Обратите внимание: когда в дивиденде больше цифр, мы просто расширяем нашу сетку. Решим 6542 ÷ 5. Вот шаги, которые мы выполнили, чтобы решить это уравнение: СЛЕДУЮЩИЕ ШАГИ: Я хотел бы помочь вам научить вас методу сетки и другим концепциям деления в вашем классе.Вам могут быть полезны следующие ресурсы: БЕСПЛАТНЫЙ МИНИ-КУРС Зарегистрируйтесь здесь, чтобы получить бесплатный мини-курс многозначного умножения и деления. Это займет у вас всего около часа, и вы уйдете с множеством новых идей, стратегическим планом действий, бесплатными ресурсами, сертификатом PD и многим другим! КАРТОЧКИ ЗАДАЧ СЕТЧАТОГО МЕТОДА Эти карточки с заданиями дают студентам возможность попрактиковаться в сеточном методе деления в столбик различными способами.Студенты будут вычислять частные, решать задачи деления, вычислять недостающие дивиденды и делители, думать о том, как эффективно решить уравнение с использованием метода сетки, и многое другое. См. Карточки задач метода сетки ЗДЕСЬ или большой набор карточек задач с длинными делениями ЗДЕСЬ. СТАНЦИЯ ДЛИННОГО РАЗДЕЛЕНИЯ Станция «Длинное деление» — это математическая станция для самостоятельного обучения, ориентированная на учащихся и предназначенная для деления в столбик. 2q) / (4q)` Ответ В этом примере мы разделим его на 2 дроби, обе со знаминателем 4 q , чтобы было легче понять, что делать.2) / 2` После того, как вы попрактикуетесь с ними, вы сможете делать это, не разделяя их сначала на 2 части. Помните следующее при делении
алгебраические выражения. , обратное числа x , равно `1 / x`. Например, величина, обратная 5 — это «1/5», а обратная величина для «1 2/3» — «3/5». Чтобы разделить на дробь, умножьте на — величина, обратная дроби. Например, `3/4 -: 7 / x = 3 / 4xxx / 7 = (3x) / 28` Упростить `(3 + 1 / x) / (5 / x + 4)` Ответ Я покажу вам, как это сделать двумя разными способами. Стоит увидеть оба, потому что они оба полезны. Вы сами решаете, что проще 😉 Я беру верхнее выражение (числитель) и превращаю его в единую дробь со знаминателем x . `3 + 1 / x = (3x + 1) / x` Аналогично поступаем с нижним выражением (знаменателем): `5 / x + 4 = (5 + 4x) / x` Итак вопрос стал: `(3 + 1 / x) / (5 / x + 4) = ((3x + 1) / x) / ((5 + 4x) / x)` Мы думаем о правой стороне как о делении верхней части на нижнюю: `(3x + 1) / x — 🙁 5 + 4x) / x` Чтобы разделить на дробь, умножьте на обратную: `(3x + 1) / (x) xxx / (5 + 4x) = (3x + 1) / (5 + 4x)` x исключены, и у нас есть окончательный ответ, который больше не может быть упрощен. Я понимаю, что у меня есть «/ x » как в числителе, так и в знаменателе. Итак, если я просто умножу верхнюю и нижнюю части на x , это упростит все, удалив дробные части сверху и снизу. `(3 + 1 / x) / (5 / x + 4) xxx / x` Я просто умножаю на «1» и не меняю исходное значение дроби — просто меняю ее форму. Итак, я умножаю каждый элемент верха на x и каждый элемент низа на x , и я получаю: `(3 + 1 / x) / (5 / x + 4) xxx / x = (3x + 1) / (5 + 4x)` Я не могу дальше упрощать. Прежде чем мы рассмотрим пример с использованием алгебры, давайте сначала вспомним, как выполнить деление в столбик с числами . Давайте сделаем 23 576 разделенных на 13. Мы можем записать это в виде дроби: `23576/13` Теперь, чтобы разделить это (при условии, что у нас нет калькулятора), мы могли бы поступить следующим образом. 23 делится на 13 = 1 с остатком 10. Опускаем 5 (следующее число после 3) вниз.2-11x-4) — 🙁 x-4) ` Ответ Мы делим многочлен степени 2 на многочлен степени 1. Это алгебраическое деление в столбик. Шаг 1: Мы смотрим на первый член (3 x 2 — 11 x — 4) и первый член ( x — 4). Разделить следующим образом: 3 x 2 ÷ x = 3 x Мы пишем 3 x в верхней части нашего деления в столбик и умножаем (3 x ) ( x — 4) = 3 x 2 -12 x , чтобы получить вторую строку нашего решения. Шаг 2: Вычитание второй строки из первой дает: Будьте осторожны с -11 x — (-12 x ) = -11 x + 12 x = x Шаг 3: Убавьте -4 из первого ряда: Шаг 4: Разделите x (в 3-м ряду) на x из ( x — 4) в вопросе.Наш ответ — 1, и мы пишем «+1» в верхней части нашего длинного деления. Затем умножьте (1) на ( x — 4), чтобы получить 4-ю строку. Шаг 5: Вычтем 4-ю строку из 3-ей: Итак (3 x 2 -11 x -4) ÷ ( x -4) = 3 x + 1 Вы можете проверить свой ответ, умножив (3 x + 1) на ( x — 4), и вы получите (3 x 2 — 11 x — 4).2 + 6 + 7x) / (2x + 1) `как (6 x 2 + 7 x + 6) ÷ (2 x + 1) Мы снова делим многочлен степени 2 на многочлен более низкой степени (1). Это алгебраическое деление в столбик. Шаг 1: 6 x 2 ÷ 2 x = 3 x Итак, мы запишем следующее, используя (3 x ) (2 x + 1) = 6 x 2 + 3 x для второй строки: Шаг 2: Из первой строки вычитаем 6 x 2 + 3 x : Шаг 3: Опустите 6: Шаг 4: Разделите 4 x на 2 x .2 + 6 + 7x) / (2x + 1) = 3x + 2 + 4 / (2x + 1) ` ПРИМЕЧАНИЕ: Некоторые люди предпочитают записывать проблему со всеми x 2 , x и единицами в строке следующим образом: Вы можете увидеть, как алгебраическое деление в столбик используется в следующем разделе, теоремы об остатке и множитель. Когда вы начинаете деление, вам может быть предложено Вы могли бы подумать, какое число, умноженное на 9, дает мне 27? И ваш ответ Например, у вас может быть проблема, которая выглядит так: Вы бы переписали задачу так, чтобы она выглядела так: В этом случае 5 — это делитель (число, на которое мы делим), и он идет на Теперь мы можем начать наше деление в столбик. Есть четыре шага деления в столбик; они Наш первый шаг в длинном делении — разделить. На этом шаге Наш следующий шаг в длинном делении — умножение.На этом шаге Наш следующий шаг в длинном делении — вычитание. На этом шаге Теперь перейдем к нашему последнему шагу — сбить. Как только вы наберете следующее число, вы начнете весь процесс с деления! Это был полный этап (деление, умножение, вычитание Обратите внимание, что когда вы пошли сбивать, других цифр после 5, Некоторым людям нравится запоминать шаги к делению в столбик, поэтому они придумали Прежде чем двигаться дальше, давайте рассмотрим еще один такой пример. Наш новый пример: Давайте перепишем задачу, используя полосу длинного деления, а затем проделаем шаги И снова наш ответ (частное) написано над полосой деления.У нас написано Когда у нас есть ответ на нашу проблему деления, легко вернуться и проверить его Вот работа для проверки последней задачи деления: Мы видим, что наш продукт, 100, совпадает с дивидендом, поэтому мы знаем, что правильно выполнили А теперь вот один, который вы должны попробовать, чтобы убедиться, что вы его повесили! Вот в чем проблема: Что нам делать в первую очередь? Мы всегда начинаем с деления, смотрим, сколько раз мы можем поставить делитель Наше подразделение выглядит так: Что мы делаем дальше? Мы всегда следуем делению за умножением, умножая делитель на число Теперь наша задача выглядит так: Что мы делаем дальше? Мы всегда следуем умножению с вычитанием, поэтому вычитаем 11-7. Теперь наша проблема выглядит так: Что мы делаем дальше?
Предыдущий урок | Главная страница | Следующий урок Длинное полиномиальное деление | Purplemath
Purplemath
Разделить
x 2 — 9 x — 10 на x + 1 MathHelp.com
Упростить
Разделите два числа — WebMath
Метод сетки для длинных делений
Сначала рисуем сетку. Количество разделов в сетке зависит от количества цифр в нашем дивиденде. Для этого уравнения наша сетка будет состоять из 3 частей. Мы записываем цифры из 324 внутри сетки, а наш делитель (2) пишем слева.
Теперь мы спрашиваем себя: «Сколько раз 2 может перейти в 3?» Ответ — 1, поэтому мы пишем 1 в верхней части сетки. Теперь умножаем 1 × 2, чтобы получилось 2, и убираем 2 из 3.Остается 1.
Теперь мы переносим эту единицу на место десятков следующего участка сетки. Это дает нам 12 в следующем разделе.
Мы переносим этот 0 на десятки следующего участка сетки.Это не повлияет на это число, поэтому в следующем разделе у нас останется 4. Деление на дробь
Пример 4
Решение 1. Умножение на обратное
Решение 2. Умножение верха и низа
Длинное деление в алгебре
Пример 5
Long Division — Wyzant Lessons
простых задач деления, которые вы можете решить в уме, используя математику в уме.
Эти проблемы будут выглядеть так:
будет 3. Однако в конечном итоге вы столкнетесь с более серьезными проблемами деления, которые вы не можете решить с помощью
, используя математические вычисления. В этих случаях вам придется использовать длинное деление.
за пределами полосы деления, как показано.125 — это делимое (число, которое мы делим)
, и он находится внутри полосы деления. Когда мы закончим, частное (ответ) в конечном итоге окажется наверху шкалы деления. Прямо сейчас верхняя часть полосы деления
должна быть пустой, потому что мы еще не начали.
: делить, умножать, вычитать и уменьшать. Каждый шаг будет объяснен, и
будет показан другим цветом на пошаговом изображении.
мы должны спросить себя, сколько раз делитель входит в первое число
делимого; или, в этом случае, мы спрашиваем себя, сколько раз мы можем поместить 5 в
1. Вы заметите, что мы не можем поместить 5 в 1, потому что 5 больше единицы; таким образом,
наше первое деление дает 0. Мы пишем это число над полосой деления,
над числом, которое мы использовали (в данном случае 1). Ваша проблема пока выглядит так:
мы умножаем делитель (5) на ответ, который мы получили в нашем делении (в этом случае
, 0). Мы умножаем два числа вместе следующим образом: 5 x 0 = 0. Мы записываем это число
под делимым, выравнивая его с числом, которое мы разделили.
мы вычитаем результат умножения (ответ) из исходного числа
в делимом. В этом случае наша проблема будет 1-0 = 1.Мы бы записали ответ
в созданную колонку (см. Диаграмму ниже).
Чтобы уменьшить, мы должны посмотреть на следующее число в дивиденде, с которым
мы еще не работали; в данном случае это 2. Чтобы сбить, мы рисуем
стрелку от числа в делимом вниз до того места, где мы только что закончили вычитание,
, и записываем это число (2) рядом с ответом от нашего вычитания ( 1) сформировать
новый номер (12).Это показано на схеме ниже.
На изображении ниже вы увидите следующий набор выполненных шагов, начиная с этого вопроса о делении
: сколько раз мы можем сложить 5 на 12? Следуйте схемам:
и понижение)
, который мы только что прошли! Продолжаем повторять процесс, пока не останется больше
номеров, которые нужно сбивать.В этой задаче у нас есть еще один полный шаг, который нужно пройти через
, прежде чем мы получим ответ. Вот как пройти последний шаг:
не было, поэтому вам нечего было сбивать. Это означает, что все готово! Ваш ответ — это число
, которое вы написали над полосой деления. Для этой задачи наш ответ —
25, и он написан красным цветом над полосой деления.
поговорку, которая поможет вам запомнить порядок. Порядок следующий:
D ivide, M ultiply,
S ubtract, B кольцо вниз. Поговорка
гласит: продает ли McDonald’s гамбургеры? Первые буквы этой поговорки совпадают с номером
и первыми буквами в порядке длинного деления: D – M – S – B.
Если это вам поможет, не стесняйтесь использовать его для запоминания; если это вас смущает, не используйте
— просто запомните шаги для деления в столбик. Примеры длинного деления
до длинного деления (разделить – умножить – вычесть – уменьшить). Если проблема не исчезнет, еще раз прочтите
, шаги по устранению первой проблемы. Вот проблема, которую решила
:
красным. Обе эти задачи имели частное 25, но это не всегда будет так! Вы можете использовать любое число в качестве частного для задачи деления.
. Чтобы проверить проблему деления, вы умножаете частное (ответ) на
делитель, и ваш продукт (ответ на задачу умножения) должен быть
таким же, как делимое.
по нашему делению. Длинные ступени дивизиона
на первую цифру (или первые две цифры, если она не войдет в первую цифру)
деления.
, которое мы помещаем в начало нашей задачи деления.В этом случае это будет 7 x 1, что
равно 7, поэтому мы должны написать 7 под цифрой 11.

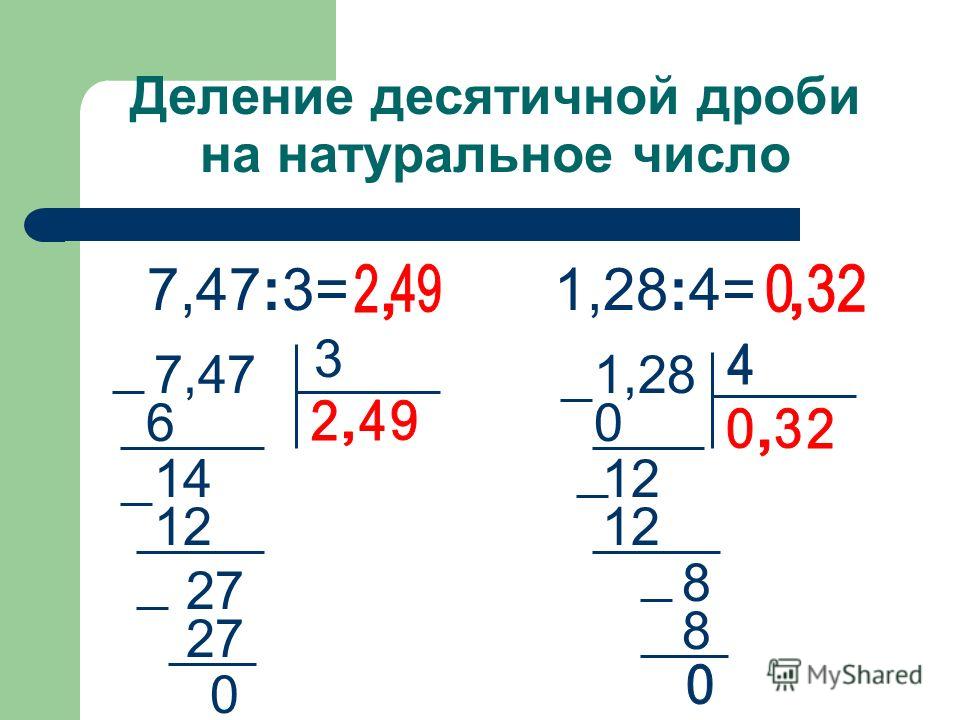
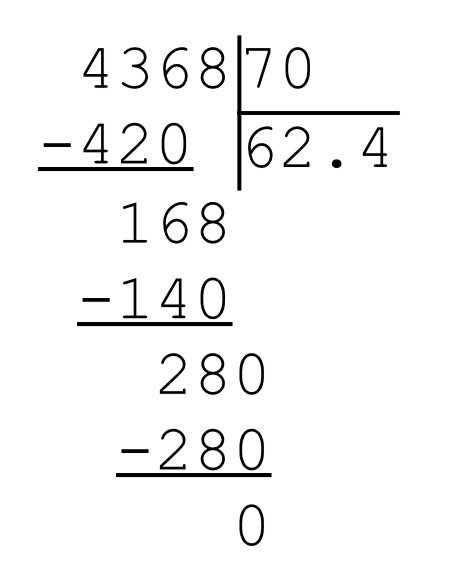 К цифре 6 тоже нужно дописать ноль. Получится 60.
К цифре 6 тоже нужно дописать ноль. Получится 60.
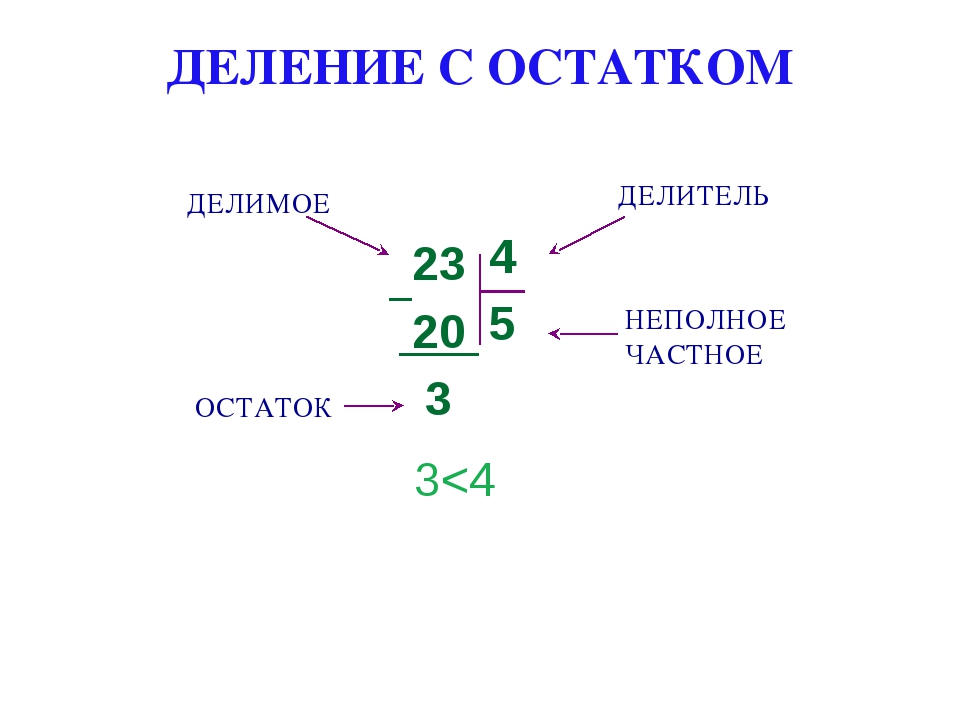 Их запаковали в 12 коробок по 10 мячей в каждой. Сколько мячей осталось? (126-10*12=6(м.))
Их запаковали в 12 коробок по 10 мячей в каждой. Сколько мячей осталось? (126-10*12=6(м.))
 Начинаем с первой парты 1 ряда, по очереди выходим к доске, решаем пример и объясняем его решение. (Далее учащиеся решают с объяснением примеры, данные в задании 96)
Начинаем с первой парты 1 ряда, по очереди выходим к доске, решаем пример и объясняем его решение. (Далее учащиеся решают с объяснением примеры, данные в задании 96) 27;
27;



