Десятичные дроби — как решать примеры 5, 6 класс

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной.

Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

• 0,600 = 0,6
• 21,10200000 = 21,102

Основные свойства
Дробь не имеет значения, при условии, если делитель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.

Как решаем:

1. Знаменатель равен 10 — это один ноль.
2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Ответ: 16/10 = 1,6.

Пример 2. Перевести 37/1000 в десятичную дробь.

Как решаем:

1. Знаменатель равен 1000 — это три нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Так как в числителе только две цифры, то на пустующие места пишем нули.
4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ: 37/1000 = 0,037.

Приходите решать увлекательные задачки с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный вводный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.

Как читать десятичную дробь

Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:

Сколько цифр после запятой?	Читается, как
одна цифра — десятых;	1,3 — одна целая, три десятых;
две цифры — сотых	2,22 — две целых, двадцать две сотых;
три цифры — тысячных;	23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных;
четыре цифры — десятитысячных;	0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных;
и т. д.

Сохраняй наглядную картинку, чтобы быстрее запомнить.

 

Преобразование десятичных дробей

Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!

Как перевести десятичную дробь в проценты

Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.

1% = 1/100 = 0,01

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.

А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:

0,15 = 0,15 · 100% = 15%.

Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.

2/5 = 0,4
0,4 · 100% = 40%

8/25 = 0,32
0,32 · 100% = 32%

Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого.

Наглядная табличка — наш друг-помощник:

Преобразование десятичных дробей

Быстрая напоминалка:

Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.

Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).

Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!

Пример 1. Перевести 5,4 в смешанное число.

Как решаем:

1. Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
2. А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.

Ответ: 5,4 = 5 2/5.

Пример 2. Перевести 4,005 в смешанное число.

Как решаем:

1. Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.

Ответ: 4,005 = 4 1/200.

Пример 3. Перевести 5,60 в смешанное число.

Как решаем:

1. Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
2. Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.

Ответ: 5,60 = 5 6/10.

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:

 

1. Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
   • 0,35 = 0,35/1
   • 2,34 = 2,34/1
2. Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
   • 0,35 = 0,35/1 = 3,5/10 = 35/100
   • 2,34 = 2,34/1 = 23,4/10 = 234/100
3. А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
   • 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
   • 2,34 = 234/100 = 117/50 = 2 17/50.

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!

Действия с десятичными дробями

С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.

Как разделить десятичную дробь на натуральное число

1. Разделить целую часть десятичной дроби на это число.
2. Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Пример 1. Разделить 4,8 на 2.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
3. Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
4. Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:

Ответ: 4,8 : 2 = 2,4.

Пример 2. Разделить 183,06 на 45.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
3. Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
4. Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную

Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.

Пример 1. Разделить 0,25 на 3/4.

Как решаем:

1. Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
2. Разделить дробь по правилам:

Ответ: 0,25 : 3/4 = 1/3.

Пример 2. Разделить 2,55 на 1 1/3.

Как решаем:

1. Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
2. Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
3. Разделить дробь по правилам:

Ответ: 2,55 : 1 1/3 = 1 73/80.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.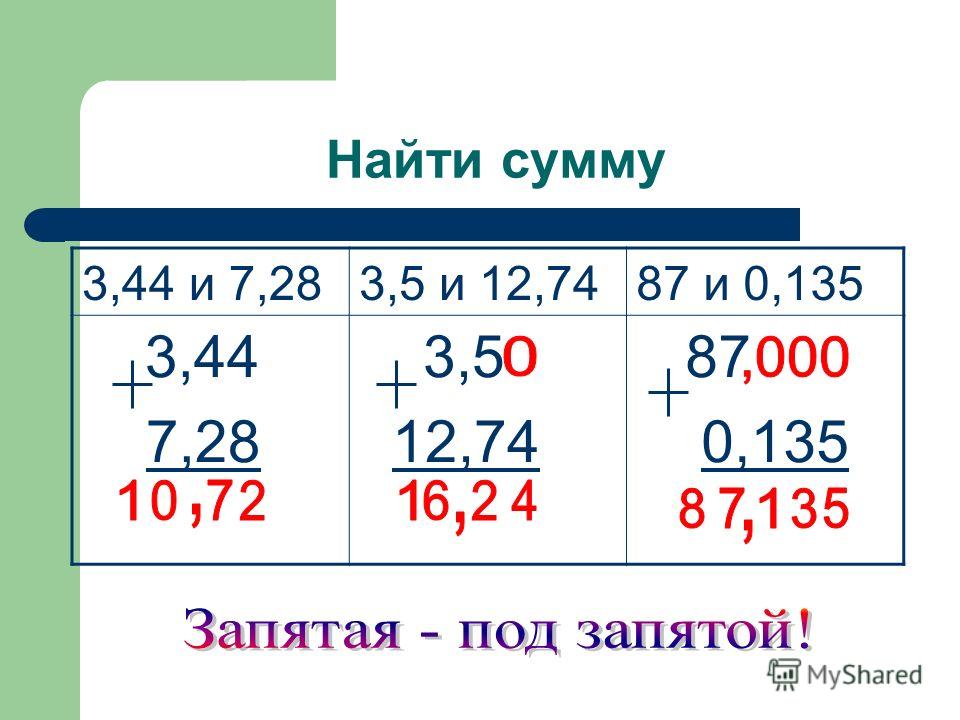

Пример 1. Умножить 2/5 на 0,8.

Как решаем:

1. Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
2. Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.

Ответ: 2/5 ∗ 0,8 = 0,32.

Пример 2. Умножить 0,28 на 6 1/4.

Как решаем:

1. Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
2. Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.

Ответ: 0,28 ∗ 6 1/4 = 0,8.

А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

---

---

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

определения, запись, примеры, действия с десятичными дробями, бесконечные периодические десятичные дроби

Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.

Что такое десятичная запись дробных чисел

Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.

Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.

Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34,21, 0,35035044, 0,0001, 11 231 552,9 и др.

В некоторых учебниках можно встретить использование точки вместо запятой (5.67, 6789.1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.

Определение десятичных дробей

Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:

Определение 1

Десятичные дроби представляют собой дробные числа в десятичной записи.

Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000, 100, 10 и др. или смешанное число. Например, вместо 610 мы можем указать 0,6, вместо 2510000 – 0, 0023, вместо 5123100 –  512,03.

О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.

Как правильно читать десятичные дроби

Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0,14, которой соответствует 14100, читается как «ноль целых четырнадцать сотых».

Если же десятичной дроби можно поставить в соответствие смешанное число, то она читается тем же образом, как и это число. Так, если у нас есть дробь 56,002, которой соответствует 5621000, мы читаем такую запись как «пятьдесят шесть целых две тысячных».

Что такое разряды в десятичных дробях

Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0,7 семерка – это десятые доли, в 0,0007 – десятитысячные, а в дроби 70 000,345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа.

Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:

Разберем пример.

Пример 1

У нас есть десятичная дробь 43,098. У нее в разряде десятков находится четверка, в разряде единиц тройка, в разряде десятых – ноль, сотых – 9, тысячных – 8.

Принято различать разряды десятичных дробей по старшинству. Если мы движемся по цифрам слева направо, то мы будем идти от старших разрядов к младшим. Получается, что сотни старше десятков, а миллионные доли младше, чем сотые. Если взять ту конечную десятичную дробь, которую мы приводили в качестве примера выше, то в ней старшим, или высшим будет разряд сотен, а младшим, или низшим – разряд 10-тысячных.

Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.

Пример 2

Попробуем разложить дробь 56,0455 по разрядам.

У нас получится:

56,0455 =50+6+0,4+0,005+0,0005

Если мы вспомним свойства сложения, то сможем представить эту дробь и в других видах, например, как сумму 56+0,0455, или 56,0055+0,4 и др.

Что такое конечные десятичные дроби

Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:

Определение 1

Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.

Примерами таких дробей могут быть 0,367, 3,7, 55,102567958, 231 032,49 и др.

Любую из этих дробей можно перевести либо в смешанное число (если значение их дробной части отличается от нуля), либо в обыкновенную дробь (при нулевой целой части). Тому, как это делается, мы посвятили отдельный материал. Здесь просто укажем пару примеров: так, конечную десятичную дробь 5,63 мы можем привести к виду 563100, а 0,2 соответствует 210 (или любая другая равная ей дробь, например, 420 или 15.)

Но обратный процесс, т.е. запись обыкновенной дроби в десятичном виде, может быть выполнен не всегда. Так, 513 нельзя заменить на равную дробь с знаменателем 100, 10 и др., значит, конечная десятичная дробь из нее не получится.

Основные виды бесконечных десятичных дробей: периодические и непериодические дроби

Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.

Определение 2

Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.

Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0,143346732…, 3,1415989032…, 153,0245005…, 2,66666666666…, 69,748768152…. и т.д.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.

Определение 3

Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.

К примеру, для дроби 3,444444…. периодом будет цифра 4, а для 76, 134134134134… – группа 134.

Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3,444444…. правильно будет записать как 3,(4), а 76, 134134134134…– как 76,(134).

В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0,677777 – это то же самое, что 0,6(7) и 0,6(77) и т.д. Также допустимы записи вида 0,67777(7), 0,67(7777) и др.

Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.

То есть для указанной выше дроби основной будем считать запись 0,6(7), а, например, в случае с дробью 8,9134343434 будем писать 8,91(34).

Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2, то при переводе в десятичную запись из них получатся бесконечные дроби.

В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45,32. В периодическом виде она будет выглядеть как 45,32(0). Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.

Отдельно следует остановиться на периодических дробях с периодом 9, например, 4,89 (9), 31,6(9). Они являются альтернативной записью схожих дробей с периодом 0, поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают (0). Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.

К примеру, дробь 8,31(9) можно заменить на соответствующую ей дробь 8,32(0). Или 4,(9)=5,(0)=5.

Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.

Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.

Определение 4

К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.

Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9,03003000300003… на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.

Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.

Основные действия с десятичными дробями

С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.

Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.

Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.

Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.

Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.

Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.

Положение десятичных дробей на оси координат

Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.

Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 1410 – это то же самое, что и 1,4, поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:

Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15,4008, то мы предварительно представим это число в виде суммы 15+0,4+,0008. Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15,4008.

Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2=1,41421…, и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.

Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.

Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.

Выше мы приводили рисунок с точкой M. Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1,4.

Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.

Сложение и вычитание десятичных дробей. Тест. — Kid-mama

Десятичные дроби складывают столбиком так же, как обыкновенные числа, при этом их записывают так, чтобы запятая находилась строго под запятой. Далее следуют алгоритму:

• Количество знаков после запятой уравнивают, приписывая нули на конце дроби.
• Выполняют сложение или вычитание как обычно, не обращая внимания на запятую.
• Ставят запятую под запятой в данных дробях.

---

Если вы складываете целое число и десятичную дробь, то просто прибавляете это число к целой части, которая находится перед запятой. Например:

5 + 2,43 = 7,43

74 + 0,004 = 74,004

---

Если нужно из целого числа вычесть десятичную дробь, то уравниваете количество знаков после запятой и вычитаете столбиком, как описано в начале этой статьи. Например, как выполнить вычитание   52 — 3,614 = ?

Вы можете потренироваться решать примеры на сложение и вычитание десятичных дробей на нашем тренажёре.

Сложение и вычитание десятичных дробей

Лимит времени: 0

0 из 20 заданий окончено

Вопросы:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7
8. 8
9. 9
10. 10
11. 11
12. 12
13. 13
14. 14
15. 15
16. 16
17. 17
18. 18
19. 19
20. 20

Информация

Выполните сложение или вычитание и введите ответ. В ответе вставляйте запятую, а не точку, иначе будет засчитан неправильный ответ.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7
8. 8
9. 9
10. 10
11. 11
12. 12
13. 13
14. 14
15. 15
16. 16
17. 17
18. 18
19. 19
20. 20

1. С ответом
2. С отметкой о просмотре

Этот тест можно проходить много раз.5\cdot 5\), то есть \(\dfrac3{160}=0,01875\).   Для того, чтобы перевести рациональную (обыкновенную) дробь в десятичную, нужно разделить в столбик ее числитель на знаменатель. Если предварительно не убедиться, что данную дробь действительно можно перевести в конечную десятичную, то делить в столбик можно до бесконечности 🙂   \(\bullet\) Любую конечную десятичную дробь можно легко привести в рациональный вид. Например, \(0,63\) равно \(\dfrac{63}{100}\); \(1,102\) равно \(\dfrac{1102}{1000}\); \(0,0003\) равно \(\dfrac3{10000}\).   Таким образом, действует следующее правило: в числителе дроби мы записываем то число, которое у нас получается при отбрасывании запятой и “лишних” нулей, находящихся слева; в знаменателе мы записываем \(10\), если в дроби был 1 знак после запятой, \(100\), если в дроби было 2 знака после запятой, \(1000\), если в дроби было 3 знака после запятой и т.д.  

Факт 2.
\(\bullet\) Сложение или вычитание десятичных дробей удобно осуществлять столбиком. Для этого необходимо записать одну дробь под другой так, чтобы запятая находилась под запятой (то есть цифры, находящиеся в одних и тех же разрядах, должны находиться друг под другом). Затем, не обращая внимания на запятую, сложить два числа привычным для нас алгоритмом сложения в столбик. После этого нужно перенести запятую в результат, руководствуясь тем же правилом “запятая под запятой”.
Пример: сумма дробей \(1,42\) и \(7,103\) равна \(8,523\)
\(\bullet\) Для того, чтобы умножить две десятичные дроби, нужно отбросить их запятые, полученные целые числа умножить привычным способом и в найденном результате запятой отделить столько знаков, сколько их суммарно было в обеих дробях.
Пример: чтобы умножить \(1,2\) на \(0,03\), умножим \(12\) на \(3\) (получим \(36\)), а затем в числе \(36\) отделим запятой 3 знака (так как в первой дроби один знак после запятой, во второй – два). Получим \(0,036\).   \(\bullet\) Чтобы разделить одну десятичную дробь на другую, нужно в обеих дробях перенести запятую вправо на одно и то же количество знаков так, чтобы получить два целых числа. Затем выполнить деление одного числа на другое привычным способом.
Пример: чтобы разделить \(30,5\) на \(1,02\), нужно разделить \(3050\) на \(102\) (запятая была перенесена вправо на 2 знака).   \(\bullet\) Чтобы умножить десятичную дробь на 10, нужно передвинуть запятую на 1 знак вправо; при умножении на 100 нужно передвинуть запятую на 2 знака вправо; при умножении на 1000 – на 3 знака и т.д.

 

Если в задаче нужно сложить, умножить или разделить дроби разного вида: десятичные и рациональные, то часто бывает удобно привести все дроби к одному и тому же виду, то есть работать либо только с рациональными дробями, либо только с десятичными.
Пример: найти значение выражения \[\dfrac{0,4\cdot (1-0,91)}{2-\frac14\cdot 0,8}\] Вспомним, что в первую очередь мы выполняем действие в скобках, затем умножение/деление, затем сложение/вычитание.
Вычислим числитель. Так как в первую очередь выполняется действие в скобках, то вычислим \(1-0,91=1,00-0,91=0,09\). Второе действие – это умножение \(0,4\cdot 0,09\). Для этого умножим \(4\) на \(9\), получим \(36\), и запятой в числе \(36\) отделим 3 знака: получим \(0,036=\frac{36}{1000}\).
Вычислим знаменатель. Так как в первую очередь выполняется умножение, то найдем \(\frac14\cdot 0,8\). Для этого переведем \(0,8\) в рациональную дробь: \(0,8=\frac8{10}\) и сократим: \(\frac8{10}=\frac45\). Следовательно, \(\frac14\cdot \frac45=\frac{1\cdot 4}{4\cdot 5}=\frac15\). Второе действие – вычитание \(2-\frac15\). Для этого запишем \(2\) как \(\frac21=\frac{10}5\). Следовательно, \(\frac{10}5-\frac15=\frac{10-1}5=\frac95\).
Найдем значение дроби. Для этого нужно разделить числитель на знаменатель, то есть найти \(\frac{36}{1000}:\frac95\). Получим: \[\dfrac{36}{1000}:\dfrac95=\dfrac{36}{1000}\cdot \dfrac59= \dfrac{36\cdot 5}{1000\cdot 9}=\dfrac{4\cdot 9\cdot 5}{1000\cdot 9}=\dfrac{4\cdot 1}{200}=\dfrac1{50}=0,02\] Таким образом, ответ: \(0,02\).  

Факт 3.
Округление десятичных дробей.
При округлении десятичных дробей до какого-то разряда важно помнить:

 

\(\blacktriangleright\) если цифра, стоящая справа от нужного нам разряда, \(\leqslant 4\), то округляем в меньшую сторону (то есть отбрасываем хвост после нужного нам разряда, а цифру, стоящую на нужном нам разряде, оставляем неизменной).

 

Пример: число \(0,8\underline94\) при округлении до сотых дает \(0,8\underline{9}\).

 

\(\blacktriangleright\) если цифра, стоящая справа от нужного нам разряда, \(\geqslant 5\), то округляем в большую сторону (то есть отбрасываем хвост после нужного нам разряда, а цифру, стоящую на нужном нам разряде, увеличиваем на \(1\)).

 

Пример: число \(1,45\underline{7}9\) при округлении до тысячных дает \(1,45\underline{8}\).

Как сравнивать десятичные дроби: способы, примеры

В данной публикации мы рассмотрим способы, пользуясь которыми можно сравнить десятичные дроби или десятичную и обыкновенную дроби. Также разберем примеры для закрепления изложенного материала.

Сравнение десятичных дробей

Способ 1

Для того, чтобы сравнить десятичные дроби выполняем следующие шаги:

1. Уравниваем длину обеих дробей – к той, у которой меньше знаков после запятой, дописываем нули в конце (их количество зависит от того, сколько цифр в дробной части у более “длинной” дроби). Это действие не изменит величину “короткой” дроби согласно Основному свойству десятичной дроби.
2. По очереди сравниваем составные части дробей: целые с целыми, десятые с десятыми, сотые с сотыми и т.д.
3. Как только одна из частей одной дроби окажется больше аналогичной части второй дроби, это означает, что она больше другой.

Примечание: десятичная дробь всегда больше целого натурального числа, если ее целая часть равна данному числу. То есть:

• 4,3 > 4
• 5,46 > 5
• 7,017 > 7
• и т.д.

Способ 2

Чтобы сравнить две десятичные дроби, можно из одной вычесть другую. Если результат окажется положительным (т.е. больше нуля), то уменьшаемое больше вычитаемого и наоборот (см. Пример 2 ниже).

Сравнение десятичной и обыкновенной дробей

Чтобы сравнить десятичную дробь с обыкновенной, последнюю представляем в виде десятичной, затем выполняем сравнение, пользуясь способами выше.

Или можно сделать наоборот – преобразовать десятичную дробь в простую и далее уже сравнивать две обыкновенные дроби.

Примеры

Пример 1

Сравним десятичные дроби 6,4 и 6,45.

Решение

Воспользуемся первым способом. Т.к. в дроби 6,45 две цифры после запятой, следовательно, нам не хватает в числе 6,4 одного знака в дробной части, и мы дописываем на конце ноль, получив в итоге – 6,40.

Теперь приступим к сравнению:

• Целые части рассматриваемых дробей равны: 6 = 6.
  Значит переходим к сравнению дробных частей.
• Десятые равны: 4 = 4.
  Движемся дальше .
• Сотые: 4 < 5.

Сотые второй дроби больше, следовательно, и она сама больше.

Ответ: 6,40 < 6,45 или 6,4 < 6,45.

Пример 2

Определим, какая из дробей больше: 5,146 или 5,14.

Решение

Применим второй способ:

Разность больше нуля (0,006 > 0), следовательно, 5,146 > 5,14.

Пример 3

Сравним дроби 

7/25

 и 0,25.

 
Решение

Мы можем поступить по-разному: превратить дробь 

7/25

 в десятичную или, наоборот, преобразовать дробь 0,25 в простую.

 
Например, выберем первый вариант:

7/25

=

7 ⋅ 4/25 ⋅ 4

=

28/100

= 0,28.

 
Теперь остается только сравнить две десятичные дроби: 0,28 и 0,25.

• Целые части равны: 0 = 0.
• Десятые: 2 = 2.
• Сотые: 8 > 5.

Ответ: 0,28 > 0,25 или  

7/25

 > 0,25.

Электронный справочник по математике для школьников арифметика конечные и бесконечные десятичные дроби умножение и деление десятичных дробей на степени 10 обращение конечной десятичной дроби в простую дробь

Обыкновенные и десятичные дроби

Содержание

Десятичные дроби делятся на три следующих класса: конечные десятичные дроби, бесконечные периодические десятичные дроби и бесконечные непериодические десятичные дроби.

Конечные десятичные дроби

ОПРЕДЕЛЕНИЕ. Конечной десятичной дробью (десятичной дробью) называют дробь или смешанное число, имеющее знаменатель   10, 100, 1000, 10000   и т.д.

Например,

К десятичным дробям относят также и такие дроби, которые можно привести к дробям, имеющим знаменатель   10, 100, 1000, 10000   и т.д., с помощью основного свойства дробей.

Например,

УТВЕРЖДЕНИЕ. Несократимая простая дробь или несократимое смешанное нецелое число являются конечной десятичной дробью тогда и только тогда, когда разложение их знаменателей на простые множители содержит в качестве множителей лишь числа   2   и   5 ,   причем в произвольных степенях.

Для десятичных дробей существует специальный способ записи, использующий запятую. Слева от запятой записывается целая часть дроби, а справа – числитель дробной части, перед которым дописывается такое количество нулей, чтобы число цифр после запятой было равно числу нулей в знаменателе десятичной дроби.

Например,

Заметим, что десятичная дробь не изменится, если приписать несколько нулей справа или слева от неё.

Например,

3,14 = 3,140 =
= 3,1400 = 003,14 .

Цифры, стоящие перед запятой (слева от запятой) в десятичной записи конечной десятичной дроби, образуют число, которое называют целой частью десятичной дроби. 

Цифры, стоящие после запятой (справа от запятой) в десятичной записи конечной десятичной дроби, называют десятичными знаками.

В конечной десятичной дроби конечное число десятичных знаков. Десятичные знаки формируют дробную часть десятичной дроби.

Умножение и деление десятичных дробей на   10, 100, 1000   и т.д.

Для того, чтобы  умножить десятичную дробь на   10, 100, 1000, 10000   и т.д., достаточно перенести запятую вправо на   1, 2, 3, 4   и т.д. десятичных знаков соответственно.

Для того, чтобы разделить десятичную дробь на   10, 100, 1000, 10000   и т.д., достаточно перенести запятую влево на   1, 2, 3, 4   и т.д. десятичных знаков соответственно.

Например,

Обращение конечной десятичной дроби в простую дробь

Обращение конечной десятичной дроби в простую дробь осуществляется очень просто, например,

1.2.2. Десятичные дроби

Глава 1. Арифметика

1.2.

1.2.2.

Дробь, знаменатель которой равен 10, 100, 1000 и вообще , может быть записана в виде десятичной дроби.

Например, Аналогично можно записывать неправильную дробь и смешанное число, например По сути, десятичное число – просто удобная форма записи дроби с указанными знаменателями.

Рассмотрим десятичную дробь 3,1415. Имеем:

Таким образом, в десятичной дроби 3,1415 содержится 3 единицы, 1 десятая, 4 сотых, 1 тысячная, 5 десятитысячных. Вообще, в десятичной дроби может быть сколько угодно разрядов: десятые, сотые, тысячные, десятитысячные, стотысячные и т. д.

Рассмотренную дробь можно записать так:

Но  а Таким образом, десятичная дробь не изменится, если к ней справа приписать любое количество нулей.

Ясно, что верно и обратное: десятичная дробь не изменится, если отбросить нули, стоящие справа в конце неё. Например, (нули, не стоящие в конце числа, отбрасывать нельзя).

Перечислим, как с десятичными числами можно проводить известные нам арифметические операции.

Модель 1.9. Сложение и вычитание десятичных дробей

Сложение и вычитание. Сложение и вычитание десятичных чисел производится точно так же, как сложение и вычитание целых чисел, нужно только записывать одноимённые разряды один под одним. Например,

1

Умножение. Умножение десятичных дробей проводится следующим образом. Перемножаем данные числа, как целые, не обращая внимания на запятые. Затем ставим в произведении запятую по следующему правилу: число знаков после запятой в произведении равно сумме чисел знаков после запятой во всех сомножителях. Заметим, что до постановки запятой отбрасывать знаки нельзя.

Модель 1.10. Умножение и деление десятичных дробей

Пример 1

Вычислить 0,225 ∙ 0,04.

225 ∙ 4 = 900. Число знаков после запятой должно быть 3 + 2 = 5. Приписывая к 900 нули слева (00900), отделяем справа пять знаков. Получаем 0,009. Итак, 0,225 ∙ 0,04 = 0,009.

В частности, из этого правила следует, что десятичная дробь увеличится в 10, 100, 1000 и т. д. раз, если запятую перенести через один, два, три и т. д. разряда вправо.

Пример 2

Число 34,0945876 увеличится в 1000 раз, если мы напишем 34094,5876.

Десятичная дробь уменьшится в 10, 100, 1000 и т. д. раз, если запятую перенести через один, два, три и т. д. разряда влево.

Пример 3

Число 3409458,76 уменьшится в 100 раз, если мы напишем 34094,5876.

Деление. Деление десятичной дроби на натуральное число производится так же, как и натурального числа на натуральное. Запятую в частном ставят после того, как закончено деление целой части.

Пример 4

Разделить 18,75 : 15.

2 Итак, 18,75 : 15 = 1,25.

Если целая часть делимого меньше делителя, то в ответе получается нуль целых.

Пример 5

Разделить 0,806 : 31.

3 Итак, 0,806 : 31 = 0,026.

Для того чтобы разделить десятичную дробь (или целое число) на десятичное дробь, нужно отбросить запятую в делителе; в делимом же переносим запятую вправо на столько знаков, сколько их было в дробной части делителя (в случае необходимости в конце делимого приписывают нули). После чего делим полученное число на натуральное.

Пример 6

Разделить 9,43 : 0,23.

4 Итак, 9,43 : 0,23 = 41.

 

Пусть дана некоторая десятичная дробь, например 34,2741. Если приписать справа (после запятой) к ней любое число нулей, то, как известно, значение этой дроби не изменится:

5

Допустима также запись этой дроби с бесконечным количеством нулей: 34,274100…

Если у десятичной дроби после запятой содержится бесконечно много знаков, то такая дробь называется бесконечной десятичной дробью. Справедлива важная теорема:

Любую обыкновенную дробь можно представить в виде бесконечной десятичной дроби.

Рассмотрим, например, дробь и будем делить числитель на знаменатель, постепенно получая десятичные знаки. При этом для нас будет важным то, что число 2 можно представить в виде 2,000…

Получаем:

6

Значит,

Если записать последовательно все получающиеся при этом делении остатки, то получится:

13, 11, 8, 12, 10, 15, 14, 4, 6, 9, 5, 16, 7, 2, 3, 13, …

Понятно, что все эти остатки меньше делителя, то есть 17; это означает, что на некотором шаге должен появиться остаток, который уже встречался раньше. После этого остатки, а значит и цифры в десятичной записи частного, будут повторяться. В нашем примере это происходит на 16 шаге и, начиная с 17-й, все цифры повторяются. Такая повторяющаяся группа цифр называется периодом. Для краткости период часто пишут в круглых скобках:
Если период начинается сразу после запятой, как в нашем примере, то дробь называется чисто периодической. Если же период не начинается сразу после запятой, а ему предшествуют несколько цифр, то такая десятичная дробь называется смешанной периодической. Например, 0,234(2837468).

Модель 1.11. Обыкновенные и десятичные дроби

Оказывается, что можно провести и обратную операцию, а именно, по любой десятичной дроби найти обыкновенную дробь, ей равную. Как это делается, покажем на примере.

Пример 7

Обратить в обыкновенную дробь число 0,(15).

Обозначим искомую дробь через x: x = 0,(15). Умножим x на такое число, кратное 10, чтобы запятая переместилась ровно на период. В нашем случае нужно x умножить на 100. Имеем Значит, 100x = 15 + x, то есть 99x = 15. Следовательно, Это и есть представление заданного числа в виде обыкновенной дроби. Выполняя сокращение: получаем: Ответ.

Пример 8

Обратить в обыкновенную дробь число 2,14(21).

Обозначим искомую дробь через x: x = 2,14(21). Ясно, что число x можно представить в виде x = 2,14 + 0,01 · 0,(21). По определению десятичной дроби имеем: Перевод числа y = 0,(21) в обыкновенную дробь выполним как в предыдущем примере: Окончательно получаем: Ответ:

 

Все дроби вида m/n, где m – целое число, а n – натуральное, могут быть представлены в виде конечных или периодических десятичных дробей.

Выясним, как можно сравнивать десятичные дроби. Из всего вышесказанного следует, что сумма, разность, произведение и частное двух десятичных дробей снова будут десятичной дробью.

Говорят, что десятичная дробь a больше другой десятичной дроби b, и обозначают этот факт так: a > b, если разность a – b – положительное число. Говорят, что десятичная дробь a меньше другой десятичной дроби b, и обозначают этот факт так: a < b, если разность (a – b) – отрицательное число. На десятичные дроби совершенно аналогично переносятся понятия отношений ≤ и ≥. Также сохраняется геометрическая интерпретация чисел. Так дроби соответствует точка на числовой оси, которую можно получить следующим образом: нужно отложить вправо от начала координат единичный отрезок два раза, затем отложить ещё длины этого отрезка. Если рассмотреть точку, симметричную данной относительно начала координат, то получим точку, которая соответствует числу

7

Аналогично можно поступить с десятичными дробями. Так, десятичному числу 3,14 отвечает точка на координатной прямой, которая получается следующим образом. Нужно от начала координат отложить три раза единичный отрезок, после отложить один раз отрезок длины от единичного; затем отложить отрезок длины единичного. Полученная точка и соответствует числу 3,14.

8



Деление десятичных знаков — объяснения и примеры

Как разделить десятичные знаки?

Работа с десятичными числами кажется немного утомительной, когда ученики сталкиваются с задачей деления десятичных чисел. Студенты проводят большую часть своего времени, выясняя, как решать задачи, связанные с делением десятичных знаков.

Десятичные числа обеспечивают большую точность при работе с числовыми значениями величин. В связи с этим достоинством возникает проблема работы с десятичными числами, которые более сложны по сравнению с целыми числами.

Цель этой статьи — дать представление о том, как применить пошаговый подход к решению поставленной задачи и максимально упростить деление десятичных чисел. По этой причине решение проблем, связанных с делением десятичных чисел, можно упростить, если предположить, что делитель является целым числом.

Как разделить десятичные дроби на целое число?

Деление десятичного числа на целое — одна из самых простых операций с десятичными знаками. Прежде чем узнать, как выполнять операцию деления, давайте рассмотрим некоторые термины, используемые в этом случае:

• Дивиденд — это число, которое нужно разделить.Например, при делении десятичного числа: 0,208 ÷ 65 = 0,0032 дивиденд будет 0,208.
• Делитель — это число, разделенное на делимое. В этом примере делителем является число 65.
• Это результат после деления.
• Остаток — это число, оставшееся после деления. В этом примере нет частного.

Следующие шаги выполняются при выполнении этой операции:

• Когда делимое — десятичное число, а делитель — целое число, десятичная точка в делимом игнорируется и обрабатывается как целое число.
• , рассматривая дивиденд как целое число, разделите его на делитель, используя обычный метод деления в столбик.
• Вставьте в частное такое же количество десятичных знаков, как и в дивиденде

Давайте разберемся с этими шагами, решив несколько примеров:

Пример 1

Рассмотрим: 8,4 ÷ 6

Предположим, нам нужно найти его частное; процесс выполняется, как описано ниже:

• Первый шаг — игнорировать десятичную точку в делимом и переписать уравнение как: 84 ÷ 6
• Выполните операцию деления, используя обычный метод деления в столбик.

	14
6	84
	6
	24-24 = 0

В этом случае частное равно 14.

• Следовательно, такое же количество десятичных знаков помещается в частное, как и в дивиденде.
• Окончательный ответ: 1,4

Пример 2

Разделите 0,625 на 25.

Решение

• Игнорируйте десятичную точку и обрабатывайте десятичную дробь как целое число: 625 ÷ 25
• Теперь выполните операция деления с использованием обычного метода длинного деления.
• 625 ÷ 25 = 25
• Поскольку делимое имеет 3 десятичных разряда, частное также будет содержать 3 десятичных знака.
• Вставьте 3 десятичных разряда в частное, начните отсчет справа налево от частного h.
• Окончательный ответ: 0,025.

Как разделить десятичные дроби на десятичное число?

В этом случае делимое и делитель являются десятичными числами. Деление десятичного числа на другое десятичное число можно выполнить следующим способом:

• Подсчитывается количество десятичных разрядов в делителе.
• Число десятичных знаков в делителе вставляется в делимое, начиная с десятичной точки вправо.
• В этом случае делитель записывается без десятичной точки, в то время как делимое получает новые десятичные разряды.
• Деление осуществляется обычным способом с использованием метода длинного деления.
• Поместите в частное такое же количество десятичных знаков, как и в новом дивиденде.

Пример 3

Деление 8,005 ÷ 0,05

Решение

• Делитель 0,05 имеет два десятичных знака, поэтому вставьте такое же количество точек в делимое, начиная с десятичной точки и идя до право.
• Наши новые дивиденды и делитель теперь равны 800.5 и 5 соответственно: 5 ÷ 5
• Выполните деление как обычно. 5 ÷ 5
• Рассматривайте новый дивиденд как целое число. 8005 ÷ 5 = 1601
• Поместите то же количество десятичных знаков, что и в новом дивиденде
• Окончательный ответ: 160,1

Практические вопросы

1. Мед хочет купить дыню весом 4,6 кг. Если общая стоимость дыни составляет 16,1 доллара, какова стоимость одного килограмма дыни?
2. Мухаммед пробегает трусцой в общей сложности 128.7 километров в апреле месяце. Какое среднее расстояние он пробегает трусцой в день?
3. Человек весит 133,3 фунта и хочет знать его вес в килограммах. Помоги ему. 1 кг = 2,2 фунта.

Ответы

1. $ 3,5
2. 29 км
3. 59 кг

Предыдущий урок | Главная страница | Следующий урок

Десятичные дроби

Уловка состоит в том, чтобы избавиться от десятичной точки в числе, на которое мы делим.

Как? Мы можем «сдвинуть десятичную точку» в сторону, умножив на 10 столько раз, сколько нам нужно.

Но мы должны сделать то же самое, что и , с обоими числами в делении.

Пример: 15 разделить на 0,2

Давайте умножим 0,2 на 10, что сдвинет десятичную точку в сторону:

0,2 × 10 = 2

Но мы должны также сделать это с 15:

15 × 10 = 150

Так 15 ÷ 0.2 стало 150 ÷ ​​2 (они оба в 10 раз больше):

150 ÷ ​​2 = 75

Итак, ответ:

15 ÷ 0,2 = 75

Число, на которое мы делим, называется делителем.

Для деления десятичных чисел:

Умножьте делитель на необходимое количество десятков, пока не получите целое число.
Не забудьте умножить делимое на такое же количество десятков.

Для умножения на 10 проще просто «сдвинуть десятичную дробь»:

Пример: разделить 6.4 по 0,4

Давайте просто сдвинем десятичную точку на один пробел для обеих :

переезд 1
6,4		64
0,4		4
переезд 1

6.4 / 0.4 в точности совпадает с 64/4 ,
, поскольку мы переместили десятичную точку на оба числа .

Теперь мы можем рассчитать:

64/4 = 16

Итак, ответ:

6,4 / 0,4 = 16

Действительно ли в 6,4 имеется 16 лотов из 0,4 ? Посмотрим:

Для более сложных вопросов может потребоваться длинное деление:

Пример: разделить 0,539 на 0,11

Переместите десятичную запятую так, чтобы делитель (0,11) был целым числом:

переместить 2 ячейки
0.539		5,39		53,9
0,11		1,1		11
переместить 2 ячейки

А как насчет 53,9? В нем все еще есть десятичная точка.

Ну, мы можем игнорировать десятичную точку в делимом, если мы помним, чтобы вернули ее позже .Сначала делаем расчет без десятичной точки:

049 11) 539 0 53 44 99 99 0

Теперь поместите десятичную точку в ответе непосредственно над десятичной точкой в ​​делимом:

Ответ: 4,9

Другой пример:

Пример: разделить 9.1 по 7

Нам вообще не нужно сдвигать десятичную точку, так как делитель (7) уже является целым числом.

Игнорируйте десятичную точку в делимом и используйте длинное деление:

13 7) 91 7 21 21 0

Поместите десятичную точку в ответе непосредственно над десятичной точкой в ​​делимом:

Ответ — 1.3

Анимации

Для получения дополнительной помощи ознакомьтесь с этими анимациями с десятичным делением.

Наконец …

В качестве последней проверки мы можем надеть шляпу «здравого смысла» и подумать: «Подходит ли это размер?», Потому что мы не хотим ни за что платить в десять раз больше, и мы не хотим получать только один — десятая часть того, что нам нужно!

Узнайте, как решить деление с помощью десятичных чисел

В этом посте мы узнаем, как решить деление с помощью десятичных чисел. Мы увидим различные примеры.

Наконец, мы увидим, как решать задачи деления, пока остаток не станет равен нулю.

Деление десятичного числа на целое

Вы делите как целые числа. Просто поместите десятичную запятую в частное прямо над его позицией в дивиденде.

Мы собираемся увидеть пример, разделив 77,5 на 25.

77 разделить на 25 равно 3, а остаток — 2.

Теперь выпадает следующая цифра. Поскольку 5 является первым десятичным числом, мы запишем десятичную точку в частном и разделим 25 на 25, что равно 1.

1 x 25 = 25, таким образом, 25 идет один раз без остатка.

Результатом десятичного деления на целое число является 3,1, а остаток равен нулю.

Деление целого числа на десятичное

Например, мы собираемся разделить 278 на 3.6.

В делителе не может быть десятичных знаков; поэтому удалите десятичную точку с делителя и добавьте к делимому столько нулей, сколько цифр после десятичной точки.

В этом случае нам нужно добавить только один ноль. Итак, теперь нам нужно разделить 2780 на 36.

36 переходит в 278 семь раз с остатком 26.

Теперь опустите 0, чтобы мы могли разделить 260 на 36, что равно 7 с остатком 8.

Решение деления — 77 с остатком 8.

Разделение десятичного числа d на десятичное

Удалите десятичную точку из делителя и переместите десятичную точку делимого вправо на столько цифр, сколько у делителя после десятичной точки. При необходимости добавьте к дивидендам нули.

Теперь мы разделим 278,1 на 2,52.

Сначала удалите десятичную точку с делителя, и, поскольку делитель имеет два десятичных знака, вы должны переместить десятичную точку делимого на две позиции.Если в дивиденде всего одна десятичная дробь, добавьте столько нулей, сколько осталось позиций. В этом случае мы добавляем один ноль и делим 27810 на 252

.

252 переходит в 278 один раз с остатком 26.

Мы выпадаем следующее число, которое является 1, поэтому теперь нам нужно разделить 261 на 252, что входит один раз, с остатком 9.

Мы выпадаем следующее число, которое является 0, поэтому теперь нам нужно разделить 90 на 252. Поскольку 90 меньше 252, мы должны записать 0 в частном и опустить следующую цифру.

Мы уже закончили решение деления, потому что цифр больше нет. Решением будет 110 с остатком 90.

Теперь мы увидим , как извлечь десятичные дроби . Если в конце деления у нас остается остаток, мы записываем десятичную точку в частном и добавляем ноль к делимому. Если мы хотим и дальше убирать десятичные дроби, нам придется добавлять нули к дивидендам.

Мы собираемся увидеть пример удаления десятичных знаков, деление 33 на 6.

6 переходит в 33, 5 раз с остатком 3.

Итак, если мы хотим добавить десятичные дроби, мы должны поставить десятичную точку в частном после 5.

Затем мы можем добавить к остатку ноль.

Теперь нам нужно разделить 30 на 6, что равно 5.

И решение 33, разделенное на 6, равно 5,5.

Кроме того, теперь вы можете узнать больше о десятичном разделении!

Подпишитесь на бесплатную пробную версию на Smartick сегодня!

Подробнее:

Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.

10 примеров десятичного деления, которые учителя должны использовать

В этом посте мы поговорим о десятичном делении, показывая различные примеры для облегчения понимания. Давайте сначала узнаем немного о теме.

Как следует из названия, в этом разделе рассматривается операция деления чисел на десятичные дроби.Когда используются десятичные дроби, детей немного запутывают. Не волнуйтесь, из этого поста вы узнаете несколько хороших методов работы с десятичными знаками.

Мы также говорили о простом подходе к решению таких операций с соответствующими примерами. Не только школьные экзамены, если хорошо практиковаться в повседневной жизни, они будут полезны на конкурсных экзаменах, где время решает все.

Дивиденд — целое число, делитель — десятичный.

Пример № 1

375 деление на 1.5

Типичный способ выполнения таких примеров — умножение делимого и делителя на степень 10 в качестве десятичных знаков. Если после десятичной точки стоит одно число, мы умножим делитель на 10. Таким образом, мы получим целое число в качестве делителя для деления делимого.

После этого получаем,

375 x 10 = 3750, 1,5 x 10 = 15

Далее мы разделим его обычным способом.

Пример № 2

484 делить на 0,22

Здесь после десятичной точки в делителе стоят два числа, поэтому мы возьмем двойную степень 10 i.е. 100. Таким образом, мы умножим делитель и делимое на 100. Получаем:

484 x 100 = 48400, 0,22 x 100 = 22

Далее мы разделим обычным способом.

Дивиденд выражен в десятичном формате, делитель — целое число

Пример № 3

В примерах, где делимое выражено в десятичном формате, а делитель — нет, мы будем использовать наиболее распространенный метод деления в столбик. Подход здесь состоит в том, чтобы решить операцию, игнорируя десятичную дробь и просто помещая десятичную точку в ответ непосредственно над десятичной точкой в ​​делимом.

Давайте возьмем пример: 134,4, деленное на 4

Игнорируя десятичную дробь, сначала мы разделим 1344 на 4

Затем мы поместим десятичную точку в частное непосредственно над делимым 134,4. Ответ: 33,6

Пример № 4

Давайте воспользуемся примером деления 564,775 на 5

Опять же, мы проигнорируем десятичную точку и решим методом деления в столбик

После получения частного мы поместим десятичная точка, как было сказано ранее.

И делимое, и делитель в десятичном формате.

Пример № 5

Когда и дивиденд, и делитель находятся в десятичном формате, мы сосредоточимся на десятичном значении делителя. Сделаем делитель на целое число.

Либо мы могли бы умножить и делитель, и делимое на мощность кратных, аналогичную числу после десятичных знаков делителя, либо удалить десятичную дробь из делителя и переместить десятичную точку делимого вправо на столько цифр, сколько имеет делитель. после десятичной точки.

После этого шага мы будем использовать тот же метод, который мы использовали для примера 3 и примера 4.

Давайте решим 37,5, разделенное на 2,5

Сначала удалим десятичную точку делителя и переместим десятичную дробь в делимую единицу. шаг вправо.

Получаем 375 деление на 25.

Далее решаем методом деления в столбик.

Пример № 6

Давайте решим 449,5, деленное на 1,45

Сначала удалим десятичную точку делителя и переместим десятичную дробь делимого на два шага вправо.Поскольку после десятичного числа идет только одно число, в конце мы поставим 0.

Получаем 44950 делим на 145

Далее решаем методом деления в столбик.

Пример № 7

Давайте разделим 56,55 на 2,5 ,

Сначала мы удалим десятичные дроби делителя и переместим десятичные дроби делимого аналогично рассмотренному выше.

Здесь мы все еще остались с десятичной дробью. Используйте длинное деление, как мы использовали в примерах 3 и 4.

Десятичное деление на дробное

При работе с десятичными числами всегда рекомендуется делать вопрос как можно более простым.Упростите его так, как вам удобно. В следующем разделе мы обсудили возможные способы сделать это.

Обратите внимание, что не существует фиксированного метода для этого. Он разный для разных типов задач десятичных операций. Основная идея — следовать подходу, который вам удобен. Давайте посмотрим на некоторые из них.

Example # 8

Это, вероятно, наиболее распространенный подход, используемый для ускорения десятичного деления. Мы записываем операцию деления в форме дроби и отменяем десятичную дробь в соответствии с ее положением.Продолжайте упрощать форму, разделив числитель и знаменатель на общее кратное.

Решите 94,5, разделив на 1,5

Запишите операцию в дробной форме. Это будет выглядеть как 94,5 / 1,5.

Затем мы отменяем десятичную дробь -> 945/15

Далее мы упростим, как показано на диаграмме.

Example # 9

Иногда мы умножаем числитель и знаменатель, отличные от 10, чтобы упростить задачу. Подход здесь состоит в том, чтобы преобразовать его в удобную для нас форму, поскольку мы уже делали это довольно много раз.

Возьмем этот пример: 6,3 разделить на 1,4

Игнорируя десятичную дробь для этого шага, мы получаем 63/14

Одно общее между числителем и знаменателем состоит в том, что оба они кратны 7.

Далее мы будем разделите 14 на 2, чтобы получилось 7. Точно так же мы разделим 63 на 2, чтобы сбалансировать. Все это можно записать в дробной форме, как показано на рисунке. Далее упрощаем операцию и получаем ответ.

Example # 10

Давайте воспользуемся тем же подходом, описанным выше, чтобы решить случай «Дивиденд — это целое число, а делитель — в десятичном формате».

Решить 387 разделить на 4,5

Вместо того, чтобы отменять десятичную дробь здесь, умножая ее на 10, лучше сделать делитель целого числа, умножив его на 2, что дает 9. Чтобы сбалансировать его, мы умножаем делимое на 2 также.

Причина, по которой мы выбираем умножение на 2, потому что делитель становится 9, а поскольку мы знаем, что 387 делится на 9, вычисления стали намного проще. Если мы выберем умножение на 10 маршрутов, дробь станет 3870/45, что требует небольшого вычисления.

---

Поделитесь словом

Если вы найдете этот пост полезным, пожалуйста, помогите нам распространить информацию. Поделитесь публикацией с друзьями, семьей и коллегами. Не забывайте подписываться на наши обновления. Любые предложения и рекомендации настоятельно рекомендуются. Вы можете связаться с нами через контактную форму, и мы свяжемся с вами в ближайшее время.

Что такое десятичная дробь? — Определение, факты и пример

Игры с десятичными числами

Добавить десятичные дроби

Работайте с визуальными моделями, чтобы получить представление о сложении десятичных чисел.Расширьте знания о сложении многозначных чисел, добавляя десятичные дроби (до сотых разрядов)

Охватывает общую базовую учебную программу 5.NBT.7Играть сейчас Умножить десятичные дроби на 10

Определить образец размещения десятичной точки, когда десятичная дробь умножается на степень 10. Иногда вам может потребоваться добавить нули в продукт.

охватывает общий основной учебный план 5.NBT.7Играть сейчасПосмотреть все игры с десятичными знаками >>

Учитесь с полной программой обучения математике K-5

Что такое десятичная дробь? В алгебре десятичное число может быть определено как число, целая и дробная части которого разделены десятичной точкой.Точка в десятичном числе называется десятичной точкой. Цифры, следующие за десятичной точкой, показывают значение меньше единицы.

Вот пример десятичного числа 17,48, в котором 17 — целое число, а 48 — десятичная часть.

десятичных знаков основаны на предшествующих степенях 10. Таким образом, при перемещении слева направо разрядное значение цифр делится на 10, что означает, что десятичное значение определяет десятые, сотые и тысячные доли.Десятая часть означает одну десятую или 1/10. В десятичной форме это 0,1. Сотня означает 1/100. В десятичной форме это 0,01.

Вот пример того, как дробная часть может быть преобразована в десятичные числа.

Десятичные знаки можно записывать как в развернутом виде, так и прописью.

Десятые, сотые и тысячные доли могут быть представлены на числовой строке. Чтобы представить десятые доли, расстояние между каждым целым числом на числовой прямой делится на 10 равных частей, где каждая часть представляет собой десятую часть.

Интересные факты Десятичные дроби были впервые разработаны и использованы китайцами в конце 4 века до нашей эры, а затем распространились на Ближний Восток, а оттуда в Европу.

Давай сделаем это!

Вместо того, чтобы учить десятичные дроби и затем раздавать детям рабочие листы, дайте им примеры из реальной жизни, в которых они могут использовать десятичные дроби или преобразовывать числа в десятичные.Например, делая покупки, попросите ребенка вычислить цену товара в десятичных дробях (полдюжины яблок).

Связанный математический словарь

Решение большего количества задач с десятичными словами

Пример 1. Школьные обеды стоят 14,50 долларов в неделю. Примерно сколько будет стоить 15,5 недель обедов?

Анализ: Нам нужно оценить произведение 14,50 долларов и 15,5 долларов. Для этого мы округлим на один множитель в большую и на меньшую сторону.

Оценка недвижимости:

Ответ: Стоимость 15.5 недель школьных обедов обойдутся примерно в 200 долларов.

---

Пример 2: Студент зарабатывает 11,75 долларов в час за садоводство. Если в этом месяце она проработала 21 час, то сколько она заработала?

Анализ

: Чтобы решить эту проблему, умножим 11,75 доллара на 21.

Умножить:

Ответ: В этом месяце учащийся заработает на садоводстве 246,75 долларов.

---

Пример 3: автомобиль Рика проезжает по шоссе 29,7 миль на галлон. Если его топливный бак вмещает 10,45 галлона, то как далеко он сможет проехать на одном полном баке бензина?

Анализ: Чтобы решить эту задачу, умножим 29.7 по 10,45

Умножить:

Ответ: Рик может проехать 310,365 миль с одним полным баком бензина.

---

Пример 4: Член школьной команды по легкой атлетике пробежал в общей сложности 179,3 мили на тренировке за 61,5 дня. Примерно сколько миль он в среднем пробегал в день?

Анализ: Нам нужно оценить частное 179,3 и 61,5.

Оценка недвижимости:

Ответ: В среднем он проезжал около 3 миль в день.

---

Пример 5: У владельца магазина 7.11 фунтов. конфет. Если она разложит конфеты по 9 банкам, сколько конфет будет в каждой банке?

Анализ: Мы разделим 7,11 фунта. на 9, чтобы решить эту проблему.

Разделить:

Ответ: Каждая банка будет содержать 0,79 фунта. конфет.

---

Пример 6: Пол будет платить за свою новую машину 36 ежемесячных платежей. Если его автокредит составляет 19 061 доллар, то сколько Пол будет платить каждый месяц? Округлите ответ до ближайшего цента.

Анализ: Чтобы решить эту проблему, мы разделим 19 061 доллар.00 на 36, затем округлите частное до ближайшего цента (сотых).

Разделить:

Ответ: Пол будет делать 36 ежемесячных выплат по 529,47 долларов каждый.

---

Пример 7: Какова средняя скорость в милях в час автомобиля, который преодолевает 956,4 мили за 15,9 часа? Округлите ответ до ближайшей десятой.

Анализ: мы разделим 956,4 на 15,9, а затем округлим частное до ближайшей десятой.

Шаг 1:

Шаг 2:

Ответ: Округляя до десятых, средняя скорость автомобиля составляет 60.2 мили в час.

---

Резюме: В этом уроке мы узнали, как решать задачи со словами, используя десятичные дроби. Для решения этих задач мы использовали следующие навыки:

1. Расчет десятичных произведений
2. Умножение десятичных знаков на целые числа
3. Умножение десятичных знаков на десятичные
4. Оценка десятичных частных
5. Разделение десятичных знаков на целые числа
6. Округление десятичных частных
7. Деление десятичных знаков на десятичные

---

Упражнения

Указания: прочтите каждый вопрос ниже.Вы можете использовать бумагу и карандаш, чтобы решить эти проблемы. Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.

1.	Оцените сумму денег, которую вам нужно заплатить за бак бензина, если один галлон стоит 3,04 доллара, а в баке — 11,9 галлона.

2.	На наклейке на новой машине Дина указано, что скорость автомобиля в среднем составляет 32,6 мили на галлон. Если топливный бак вмещает 12,3 галлона, то как далеко Дин сможет проехать на одном полном баке бензина?

3.	Ларри проработал 15 дней, в общей сложности 116,25 часа. Сколько часов он в среднем проводил в день?

4.	Шесть коробок с бумагами стоили 159 долларов.98. Сколько стоит одно дело? Округлите ответ до ближайшего цента.

5.	В одном дюйме 2,54 сантиметра. Сколько дюймов в 51,78 сантиметре? Округлите ответ до ближайшей тысячной.

Десятичные дроби

Делить на десятичные дроби немного сложно. В наши дни большинство учителей не возражают, если вы воспользуетесь калькулятором. Но хорошо знать, как это сделать самому, и вам всегда нужно уметь оценивать ответ, чтобы вы могли убедиться, что ответ калькулятора разумный.

Напомним, что в задаче Икс ÷ y знак равно z , также написано

y z Икс

Икс называется дивиденд , y это делитель , а также z это частное .

Шаг 1: Оцените ответ округление . Вы будете использовать эту оценку, чтобы проверить свой ответ позже.

Шаг 2: Если делитель не целое число, переместите десятичный разряд п места справа, чтобы превратить его в целое число. Затем переместите десятичный знак в делимом на такое же количество разрядов вправо (при необходимости добавив несколько дополнительных нулей).

Шаг 3: Делить как обычно. Если делитель не входит равномерно, добавьте нули справа от дивиденда и продолжайте делить, пока не получите 0 остаток или пока не появится повторяющийся узор.

Шаг 4: Поместите десятичную запятую в частное прямо над тем местом, где теперь десятичная запятая в делимом.

Шаг 5: Сравните свой ответ со своей оценкой, чтобы увидеть, является ли он разумным.

Пример:

Делить.

0,45 ÷ 3,6

Шаг 1: Поскольку делитель больше делимого, мы получим ответ меньше, чем 1 .С 0,45 примерно в десять раз меньше 3,6 , мы ожидаем ответа, близкого к 0,1 .

Шаг 2: Делитель не является целым числом, поэтому переместите десятичную запятую на одну позицию вправо, чтобы сделать ее целым числом. Также переместите десятичную запятую в делимом на одну позицию вправо.

36 4.5

Шаг 3: Делите нормально, добавляя дополнительные нули справа от 4.5 когда вы закончите.

36 125 4.500 3 6 _ 90 72 _ 180 180 _ 0

Шаг 4: Поместите десятичную точку в частном непосредственно над десятичной точкой в ​​делимом.

36 0,125 4.500 3 6 _ 90 72 _ 180 180 _ 0

Мы получили 0.125 .

Шаг 5: Сравните с вашей первоначальной оценкой. 0,125 близко к 0,1 , так что у нас все хорошо!

Иногда проще решить задачу десятичного деления с помощью мысленной математики. Это хорошая стратегия, когда вы видите, что, перемещая десятичные точки, вы можете превратить проблему в ту, на которую вы запомнили ответ.

Пример:

Делить.

0,42 ÷ 70

Мы знаем это 42 ÷ 7 знак равно 6 .

Если дивиденд является уменьшился с коэффициентом 10 , то коэффициент также уменьшится в 10 .

42 ÷ 7 знак равно 6 4.2 ÷ 7 знак равно 0.