§ Деление в столбик. Как делить столбиком без остатка
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность.
 Площадь круга
Площадь круга - Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Там где кончается терпение, начинается выносливость.
на главную
Введите тему
Русский язык Поддержать сайт
Сложение в столбик Вычитание в столбик Умножение в столбик Деление в столбик
Для деления чисел из двух и более цифр (знаков) применяют деление в столбик.
По традиции, разбираться как делить столбиком будем на примере.
Вычислить:
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра «8».
Начинаем делить «512» на «8» следующим образом:
- Определяем неполное частное. Для этого слева направо сравниваем
цифры делимого и делитель. Берём «5».
Цифра «5» меньше «8», значит нужно взять еще одну цифру из делимого.

- «51» больше «8». Значит это неполное частное. Ставим точку в частном (под уголком делителя).
Запомните!
Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.
Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас после «51» стоит только одно цифра «2». Значит и добавляем в результат ещё одну точку.
- Приступаем к делению. Вспоминая таблицу умножения на
«8», находим ближайшее к
«51» произведение.
«6 · 8 = 48»
Записываем цифру «6» в частное.Записываем «48» под «51».
При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.
Между «51» и «48» слева поставим «−» (минус).
 Вычтем по правилам
вычитания в столбик «48» и под чертой запишем результат.
Вычтем по правилам
вычитания в столбик «48» и под чертой запишем результат. - В остатке получилось «3».
Сравним остаток с делителем. «3» меньше «8».
Запомните!
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
Спишем из делимого «512» цифру «2» к «3».
Число «32» больше «8». И опять по таблице умножения на «8», найдем ближайшее произведение.
8 · 4 = 32
В остатке получился ноль. Значит числа разделились нацело (без остатка).
Сложение в столбик Вычитание в столбик Умножение в столбик Деление в столбик
Как делить в столбик | BeginPC.ru
В настоящее время современные технологии развиваются стремительными темпами, и все больше работы за нас выполняют компьютеры и различные другие электронные устройства. Тем не менее, умение выполнять арифметические операции без помощи калькулятора остаются все еще востребованными.
Тем не менее, умение выполнять арифметические операции без помощи калькулятора остаются все еще востребованными.
Ранее мы уже рассматривали, как складывать, вычитать и умножать в столбик на листе бумаги. Поэтому сегодня давайте освежим в памяти, а возможно кто-то узнает впервые алгоритм деления столбиком без калькулятора. В этом нет ничего сложного, главное внимательность и аккуратность.
Для начала запомним, что число которое делится называется делимое. Число на которое делят называют делителем, а результат деления частным. Чтобы было проще, давайте рассмотрим деление в столбик на конкретном примере и разделим 834 на 6. Первое что нам необходимо сделать, это записать их соответствующим образом.
Пишем делимое, затем правее него делитель и отделяем их друг от друга так называемым уголком. Все подготовительные операции выполнены и переходим непосредственно к делению в столбик.
Для этого необходимо в делимом двигаясь слева на право найти наименьшее число большее или равное делителю.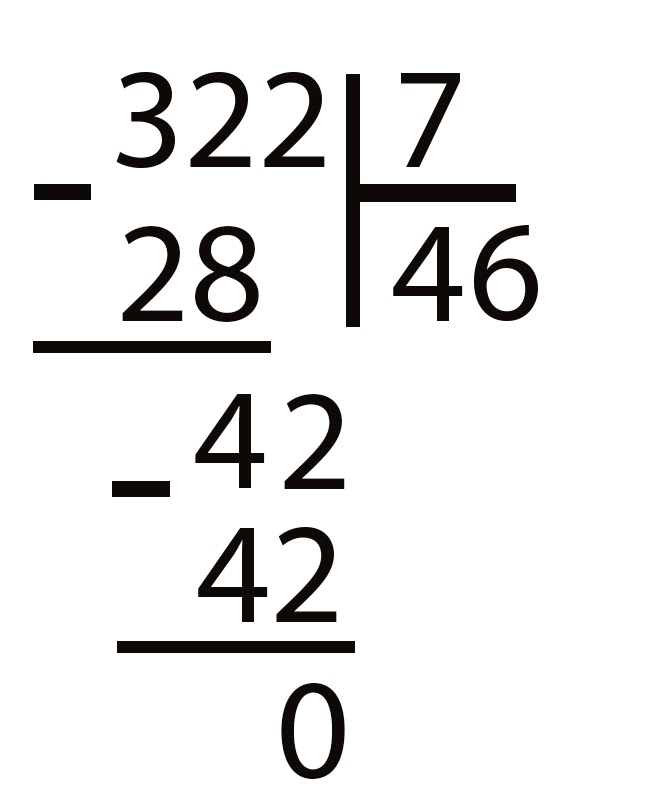 Делитель у нас равен 6, а первая цифра в делителе равна 8 и она больше 6. Теперь необходимо найти сколько целых раз делитель помещается в неполном делимом, в данном случае всего один раз. Поэтому под делителем пишем 1, а под 8 записываем 6 проводим горизонтальную черту и находим их разность по правилам вычитания столбиком, то есть 2. Поскольку 2 меньше нашего делителя (6), то все сделано правильно, в противном случае, где то допущена ошибка.
Делитель у нас равен 6, а первая цифра в делителе равна 8 и она больше 6. Теперь необходимо найти сколько целых раз делитель помещается в неполном делимом, в данном случае всего один раз. Поэтому под делителем пишем 1, а под 8 записываем 6 проводим горизонтальную черту и находим их разность по правилам вычитания столбиком, то есть 2. Поскольку 2 меньше нашего делителя (6), то все сделано правильно, в противном случае, где то допущена ошибка.
Теперь сносим вниз следующую цифру исходного делимого (3) и проверяем чтобы получившееся число (23) было больше делителя (6). В данном случае это так. Снова находим сколько раз делитель помещается в неполном делимом, получается 3 раза. Поэтому под делителем записываем 3, а под делимым находим разность 23 и 18 (6*3), которая равна 5.
Дальше делаем все точно также, сносим вниз следующее число из делимого (4), получается число 54 и находим сколько раз в нем умещается делитель (6). Он умещается 9 раз, значит под делителем записываем 9, а под неполным делимым 54 (6*9). Поскольку 54 отнять 54 равно нулю и в делимом не осталось больше чисел, то деление закончено и частное равно 139. Можете проверить на калькуляторе или выполнив умножение в столбик 6 на 139.
Поскольку 54 отнять 54 равно нулю и в делимом не осталось больше чисел, то деление закончено и частное равно 139. Можете проверить на калькуляторе или выполнив умножение в столбик 6 на 139.
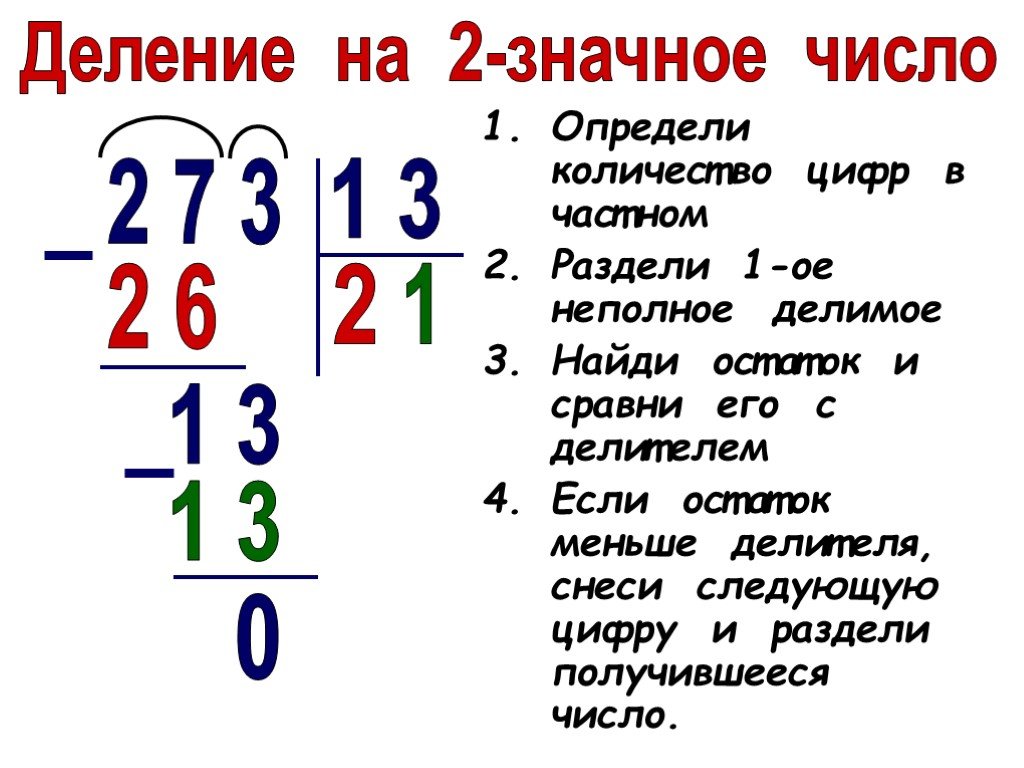
Чтобы закрепить навык деления столбиком давайте рассмотрим еще один пример и разделим 1587 на 23. Согласно уже известному нам алгоритму находим в делимом наименьшее число большее или равное делителю, таким числом является 158. Делитель 23 умещается в неполном делимом 6 раз. Соответственно под делителем пишем 6, а под делимым 138 (23*6) и находим разность 158 и 138.
Поскольку 20 меньше делителя все сделано правильно, теперь сносим вниз следующее число (7) и находим сколько раз умещается делитель в получившемся числе 207. Он умещается 9 раз, а поскольку 207-207=0 и в делимом больше нет чисел, то деление в столбик законченно и ответ равен 69.
Как видите, ничего особо сложного нет, главное внимательность. Хотя внимательный читатель наверняка уже обратил внимание, что в обоих приведенных примерах делитель помещается в делимом целое число раз. Однако так бывает далеко не всегда, поэтому рассмотрим пример деления столбиком с остатком, для этого разделим 46 на 8.
Однако так бывает далеко не всегда, поэтому рассмотрим пример деления столбиком с остатком, для этого разделим 46 на 8.
Поскольку 4 меньше 8, то наименьшим неполным делимым является 46. В числе 46 делитель содержится 5 раз, следовательно под делителем пишем 5, а под делимым 40 (5*8).
Разность 46 и 40 равна 6. Число 6 меньше делителя, значит мы все сделали верно, но в делимом больше не осталось чисел, а разность не равна 0. Это значит, что разделить эти два числа без остатка нельзя. Чтобы найти остаток поступаем следующим образом. В разности ставим запятую, а к остатку приписываем 0. В остатке имеем число 60. Делитель умещается в нем 7 раз, значит пишем в разность 7 и вычитаем из 60 число 56 (8*7).
В остатке имеем 4, снова приписываем 0. Получается 40 и делитель умещается в нем 5 раз. В частное записываем 5 и вычитаем из остатка 40, получается 0.
Таким образом, мы разделили 46 на 8 столбиком и получили ответ 5,75. Теперь вы знаете, как делить в столбик без калькулятора. Кстати в Windows есть встроенный калькулятор «Пуск» ⇒ «Стандартные» ⇒ «Калькулятор», в котором всегда можно быстро выполнить необходимые вычисления.
Кстати в Windows есть встроенный калькулятор «Пуск» ⇒ «Стандартные» ⇒ «Калькулятор», в котором всегда можно быстро выполнить необходимые вычисления.
Что такое длинное деление? [Определение, факты и примеры]
Определение длинного деления
В математике длинное деление — это математический метод деления больших чисел на более мелкие группы или части. Это помогает разбить проблему на простые и легкие шаги. Длинные деления имеют делимые, делители, частные и остатки. В задаче на длинное деление делимое — это большое число, которое делится на другое число, называемое делителем . частное есть результат деления, а избыточное количество, которое нельзя разделить, называется остатком .
Пример длинного деления
Вот пример, который поможет нам понять эту концепцию:
Поскольку 75 не кратно 4, оно не делится на 4 и оставит остаток в конце.
Символ деления
Чтобы показать, что два числа делятся, мы можем добавить между ними знак деления «÷». Так, например, если нам нужно показать 36, разделенное на 6, мы можем записать это как 36 ÷ 6.
Так, например, если нам нужно показать 36, разделенное на 6, мы можем записать это как 36 ÷ 6.
Мы также можем представить это в форме дроби как 366.
Шаги для выполнения длинного деления
Есть пять шагов, чтобы легко решить любую задачу на длинное деление.
Давайте посмотрим на приведенные ниже примеры, чтобы лучше понять концепцию.
Деление десятичных чисел с помощью длинного деления
Длинное деление также можно использовать для деления десятичных чисел на равные группы. Он следует тем же шагам, что и при делении в длину, а именно — разделить, умножить, вычесть, свести и повторить или найти остаток.
Вот пример длинного деления с десятичными дробями.
Интересные факты о длинном делении
- Если делимое равно 0, частное всегда будет равно нулю.
- Остаток всегда меньше делимого.
- Умножение частного на делитель и добавление остатка даст делимое.
(делитель x частное) + остаток = делимое
- Когда остаток равен 0, делимое является произведением делителя и частного.

Делитель x Частное = Делимое, когда остаток = 0
Заключение
Длинное деление — это инструмент, позволяющий разделить большие числа на несколько меньших групп или частей. Когда мы делим делимое на делитель, полученное частное представляет собой количество групп, которые можно составить, а остаток определяет, сколько элементов или чисел останется несгруппированным. Чтобы еще лучше понять эту концепцию, ознакомьтесь с широким спектром интересных упражнений, доступных на SplashLearn, и станьте мастером деления на деления!
Решенные примеры
Вопрос 1: Разделите 726 на 4
Ответ:
Следовательно, частное задачи равно 181, а остаток равен 9, когда 2:
Остаток равен 2.3 делим 248 на 8?
Ответ:
Значит, частное задачи равно 31, а остаток равен 0.
Вопрос 3: Мама Лейлы собрала все семейные фотографии и хотела поместить их все в альбом. Если каждая страница альбома может содержать 9фотографий, сколько страниц альбома ей понадобится, если фотографий 285?
Если каждая страница альбома может содержать 9фотографий, сколько страниц альбома ей понадобится, если фотографий 285?
Ответ:
Частное задачи равно 31, а остаток равен 6. Значит, ей нужно 31 + 1 (для оставшихся шести картинок) или 32 страницы.
Практические задачи
2
4
6
Правильный ответ: 2
на разделение 426 на 4, мы получим коэффициент 106, а оставшаяся в 2
562
560
576
562
560
576
0013
572
Правильный ответ: 572
Dividend = (Divisor x Cotent) + оставшаяся часть = (8 x 71) + 4 = 572
3
4
5
6
Правильный ответ: 6
01 A × 5 = 30. Таким образом, A должно быть 30 ÷ 5 или 6.
Часто задаваемые вопросы
Может ли делитель быть 0?
Нет, деление на 0 в математике вообще не определено.
Что такое метод длинного деления?
В математике длинное деление — это математический метод деления больших чисел на несколько меньших групп или частей. Число, которое мы делим на маленькие группы, называется делимым, число, на которое мы делим, называется делителем. Это помогает разбить проблему на простые и легкие шаги.
Число, которое мы делим на маленькие группы, называется делимым, число, на которое мы делим, называется делителем. Это помогает разбить проблему на простые и легкие шаги.
Как мы можем проверить частное и остаток от задачи деления?
Мы можем проверить частное и остаток от деления, используя формулу деления: (Делитель x Частное) + Остаток = Делимое
В чем разница между прямым делением и коротким делением?
Короткое деление удобно для деления больших чисел на однозначные числа, тогда как длинное деление удобно для деления больших чисел на числа с двумя и более цифрами.
Калькулятор длинного деления с остатком
Базовый калькулятор
Поделись этим калькулятором и страницей
Калькулятор Использование
Разделите два числа, делимое и делитель, и найдите ответ как частное с остатком. Узнайте, как решить деление в длинное с остатками, или попрактикуйтесь в решении собственных задач на деление в длинное и используйте этот калькулятор, чтобы проверить свои ответы.
Узнайте, как решить деление в длинное с остатками, или попрактикуйтесь в решении собственных задач на деление в длинное и используйте этот калькулятор, чтобы проверить свои ответы.
Деление в длинное с остатком — это один из двух методов деления в длинное вручную. Это несколько проще, чем решение задачи на деление путем нахождения частного ответа с десятичной дробью. Если вам нужно сделать длинное деление с десятичными знаками, используйте наш Длинное деление с калькулятором десятичных дробей.
Каковы части деления
Для предложения деления 487 ÷ 32 = 15 R 7
- 487 является дивидендом
- 32 это делитель
- 15 является частной частью ответа
- 7 — оставшаяся часть ответа
Как сделать длинное деление с остатками
Из приведенного выше примера давайте разделим 487 на 32, показывая работу.
Задайте задачу деления с помощью длинного символа деления или длинной скобки деления.
Поместите 487, делимое, внутрь кронштейна. Делимое — это число, которое вы делите.
Разделите первое число делимого, 4, на делитель, 32.
4 разделить на 32 равно 0 с остатком 4. Вы можете пока игнорировать остаток.
Поставьте 0 над скобкой деления.
Это начало частного ответа.
Далее умножьте 0 на делитель 32 и подставьте результат 0 под первой цифрой делимого внутри скобки.
0 * 32 = 0
Нарисуйте линию под 0 и вычтите 0 из 4.
4 — 0 = 4
Запишите следующее число делимого и вставьте его после 4, чтобы получилось 48.
Разделите 48 на делитель 32. Ответ: 1. Вы можете пока игнорировать остаток.
48 ÷ 32 = 1
Обратите внимание, что вы можете пропустить все предыдущие шаги с нулями и сразу перейти к этому шагу. Вам просто нужно понять, сколько цифр в делимом вам нужно пропустить, чтобы получить первое ненулевое значение в частном ответе. В этом случае вы можете сразу разделить 32 на 48.
Поместите 1 над разделительной чертой, справа от 0. Затем умножьте 1 на 32 и запишите ответ под 48.
1 * 32 = 32
Нарисуйте линию и вычтите 32 из 48.
48 — 32 = 16
Сократите следующее число из делимого и вставьте его после 16, чтобы получилось 167.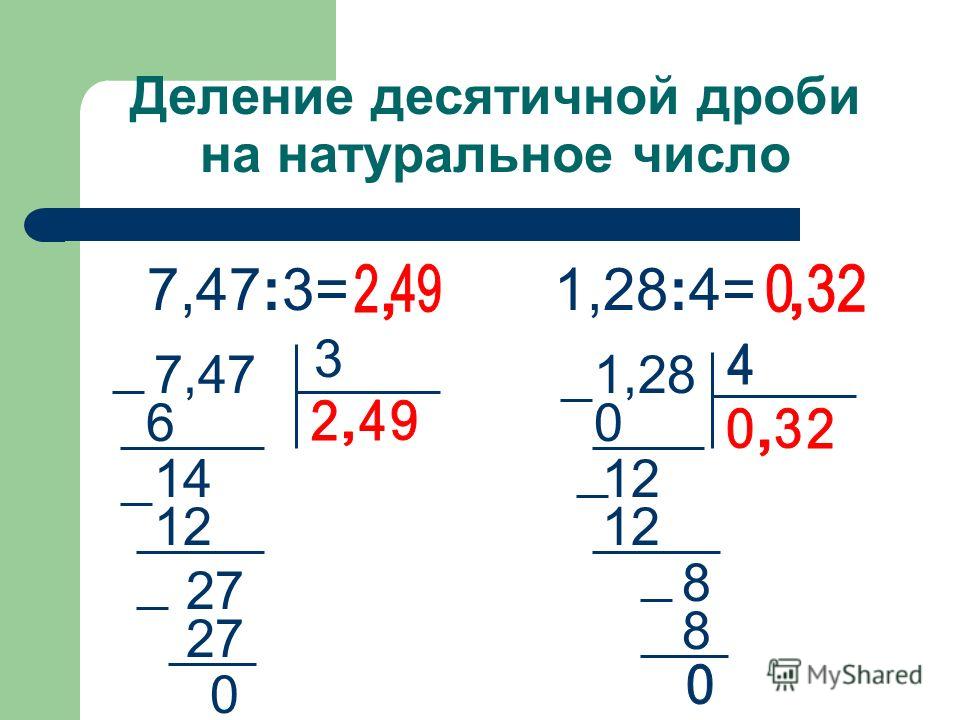
 Площадь круга
Площадь круга
 Вычтем по правилам
вычитания в столбик «48» и под чертой запишем результат.
Вычтем по правилам
вычитания в столбик «48» и под чертой запишем результат.