Как преподавать успешные стратегии деления на длинное деление

Деление на длинное деление долгое время было одним из самых сложных понятий для учащихся 4-х и 5-х классов. Есть несколько причин, по которым учащиеся борются с делением в длинное деление, поэтому мы попытались разобрать некоторые из способов, которыми мы настраиваем наших учеников на успех.

Начните с умножения

Ученикам, которые знают факты умножения наизусть, легче научиться выполнять деление в большую сторону. Это в основном потому, что они могут оценивать более эффективно. Практика нашей таблицы умножения является важной частью повышения эффективности при делении в большую сторону, но это всего лишь один шаг.

Мы практикуем умножение и деление с помощью наших наборов упражнений и графиков. Мы не измеряем время студентов, но поощряем улучшение с течением времени. Каждый день учащиеся выполняют одно упражнение. Мы оцениваем их вместе, как класс, а ученики оценивают свои собственные. Затем они фиксируют свой прогресс на графике.

В нашем магазине вы можете найти нашу серию Multiplication Drill and Graph. 3 класс включает вопросы на умножение и деление до 5 x 5. В наборе для 4 класса вопросы на умножение и деление составляют до 7 x 7. Версия для 5 класса содержит вопросы до 9x 9. Набор для 6 класса включает вопросы на умножение и деление до 12 x 12. Вы также можете получить все четыре набора в одном комплекте, чтобы вы могли легко различать их для всех ваших учеников.

Сначала начните с простого деления

Забавно, как студенты, у которых проблемы с элементарным вопросом на деление из двух цифр, могут легко разделить пакет конфет вплоть до дроби. Таким образом, вместо того, чтобы говорить ученикам, что они будут заниматься делением, мы начинаем с того, что делимся угощениями.

Простые конфеты, такие как мармеладки или кегли, прекрасно работают. Положите несколько в чашку. Обычно мы стремимся к 20-30, но все ученики должны начинать с одинакового количества конфет. Если конфеты не вариант, подойдут любые маленькие кусочки. Мы использовали счетчики бинго, числа с основанием 10 и даже карандаши. Попросите учащихся убедиться, что их парты чистые, и напомните им не есть свои угощения, пока урок не закончится.

Попросите учеников представить, что они должны поделиться своим угощением с одним другом. Сколько получит каждый? Иногда наши ученики даже указывают, что одну конфету нужно разделить пополам, чтобы она была равной.

Явное обучение шагам деления в длинное число

Начнем со стандартного алгоритма. В первый раз, когда мы показываем это студентам, мы получаем много пустых взглядов и замешательства. Это нормально. Ступеней много, поэтому не стоит ожидать, что ученики все усвоят сразу.

Начните с объяснения, что деление — это просто повторяющееся вычитание (а умножение — многократное сложение). Одной из причин того, что деление в длинную очередь представляет собой такую ​​сложную задачу, является то, что для ее эффективного выполнения требуется овладение другими операциями. Если ваши ученики не могут точно умножать или вычитать, возможно, они не готовы к делению в длинные числа.

Мы используем наши интерактивные математические тетради для обучения делению. Секция деления — это только часть модуля «Операции с числами». В группе операций с числами 3 класса преподается простое деление (до 5×5). В классе 4/5 единица операций с числами длинное деление включает одиночные делители, до трех цифр в делимых и включает вопросы с остатком и без остатка. Длинное деление модуля операций с числами 5/6 классов включает одиночные делители, до трех цифр в дивидендах и включает вопросы с остатками и без них, но позволяет учителям различать добавление двузначных делителей или четырехзначных дивидендов с остатками и без них. Он не распространяется на преобразование остатков в десятичные дроби или дроби.

Индивидуальные стратегии

Мы учим наших студентов четырем различным способам деления в столбик, но они должны освоить только один. Учащиеся могут выбрать стратегию, которая сначала кажется им наиболее понятной, а затем мы медленно продвигаемся к стандартному алгоритму (но некоторым учащимся требуется больше времени, чтобы добраться до него).

Единственная проблема, с которой мы обычно сталкиваемся, позволяя учащимся выбирать личную стратегию, заключается в том, что родители этого не понимают. Конечно, нет. Родителям не дали возможности изучить другие методы. Они либо поняли правильно, либо не поняли вообще (и тогда начались их нездоровые отношения с математикой). Мы просим родителей дать нам свободу экспериментировать и показать им, что понимание, которое они получают, используя личную стратегию, обычно в любом случае приводит к стандартному алгоритму, потому что учащиеся обнаруживают, насколько он быстрее.

Стандартный алгоритм

Нам нравится это видео Math Antics на YouTube. Мы не можем сделать видео лучше этого, поэтому мы рекомендуем его.

Частичные произведения

Другой способ деления в большую сторону — использование частичных произведений или частичных частных.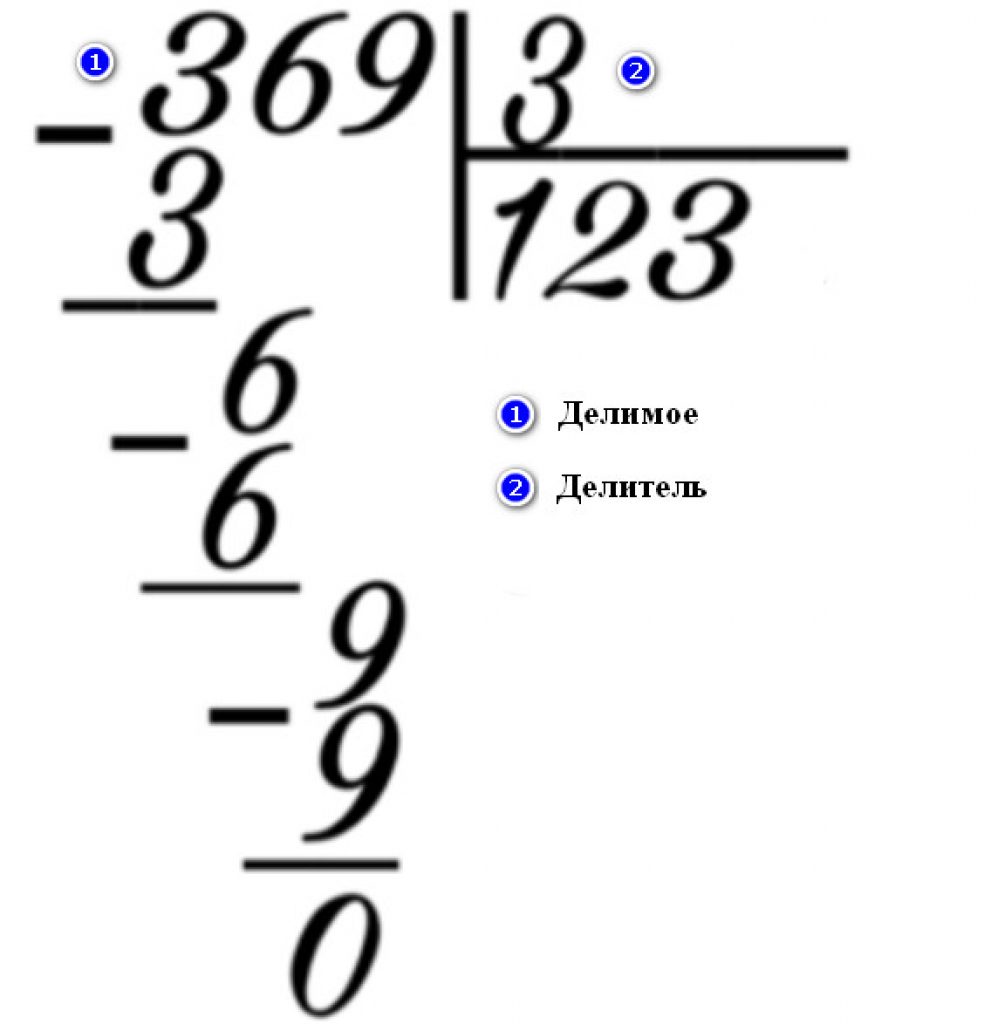 В этом видео показан метод от Khan Academy.

Блочный метод

Математика с мистером Дж. на YouTube показывает примеры использования блочного метода для деления в большую сторону в этом видео.

Частичные произведения с использованием модели площадей

Эллисон Уолберг прекрасно объясняет, как использовать модель площадей с частичными частными.

Способы попрактиковаться в длинном делении

Пусть учащиеся попрактикуются в своей стратегии, они могут обнаружить, что их стратегия работает для определенных типов чисел, но не для других, или что традиционный алгоритм становится наиболее эффективным способом (но не всегда, если они не т знаю свои математические факты).

Использование манипуляций

Тот факт, что ваши ученики учатся в старших классах, не означает, что им не нужны конкретные модели, помогающие освоить обучение. На самом деле, я впервые использовал алгебраические плитки на уроке математики в университете, когда понял, что наконец понял алгебру. Нормализуйте манипуляторы, чтобы помочь учащимся продумать свой процесс, побуждая всех учащихся показать вам, что они могут продемонстрировать разделение с помощью манипуляторов.

Не забудьте про опоры для умножения. Если вашим ученикам нужна помощь в умножении, позвольте им использовать калькулятор или таблицу умножения, пока они учатся осваивать этапы деления. Это особенно важно, поскольку они пытаются изучить алгоритм. Да, в конечном итоге им нужно будет знать, как делать это без этих поддержек, но пока они изучают алгоритм, избавьтесь от проблем с умножением с помощью поддержек.

Использование опорных диаграмм и справочных страниц

Вместе с нашими учениками мы создаем опорную диаграмму для каждого из методов и развешиваем ее по всему классу. Таким образом, у студентов есть ориентир для шагов, независимо от того, какой метод они используют. Если у вас мало места, сфотографируйте якорные диаграммы и распечатайте их на бумаге формата Letter. Держите наборы диаграмм доступными для учащихся. Мы кладем несколько в пластиковую папку и вешаем их на угол доски, чтобы ученики могли встать и взять то, что им нужно. По окончании дня они возвращают их в классную комнату.

У каждого ученика есть примеры того, как делить в своих математических журналах из урока, который мы делаем в начале деления. Математические журналы перечислены под заголовком о явном обучении студентов делению в длину.

И мы связываем каждое видео YouTube в нашем Google Classroom, чтобы учащиеся могли просматривать их снова и снова, если это необходимо. Мы даже призываем наших студентов найти другие видео. Они присылают нам ссылки, и после того, как мы их просматриваем, мы публикуем ссылки для всех в нашем Google Classroom.

Рабочие листы могут помочь с делением в длину

К сожалению, единственный способ стать лучше в делении на деления — делать это много. В этом могут помочь рабочие листы. Если вы ищете новые способы использования математических рабочих листов, ознакомьтесь с нашей публикацией Математические рабочие листы, которые понравятся вашим ученикам.

У нас есть несколько комплектов рабочих листов в нашем магазине учителей для учителей.

Операции с числами, 3 класс (включает все простые операции)
Умножение и деление, 4 класс (включает длинное умножение и деление без остатка)
Умножение и деление 5 класс (включает умножение и деление в длинное число с остатком)

Использование карточек с заданиями для деления в длинное число

Нам нравится использовать карточки с заданиями в нашем классе. На самом деле, у нас есть целый ящик, посвященный им. Нашим ученикам они тоже нравятся. Чтобы узнать, как использовать карточки с заданиями в классе, прочитайте нашу статью «Проблемы с карточками с заданиями и способы их решения». Наши карточки задач всегда поставляются с бумажной версией (в цвете и с экономией чернил), версией Google Slides и версией Google Forms с самопроверкой. Каждый набор состоит из трех наборов по 24 карты, поэтому их легко отличить друг от друга.

Карточки с заданиями на деление (Простое деление) 3 класс
Карточки с заданиями на длинное деление на 4/5 класс
Карточки с заданиями на операции с целыми числами 4/5 класс (включает все операции)

И если вы любите карточки с заданиями так же сильно, как мы , попробуйте эту бесплатную игру, чтобы играть с бумажной версией. Ваму! был изобретен классом один год, и год за годом он становится фаворитом.

Попробуйте карты Boom для длинной дивизии

Вы слышали о картах Boom? Думайте о них как о цифровых карточках с заданиями, где учащиеся могут вводить ответы (например, заполнять пустые поля) или выбирать из списка с несколькими вариантами ответов, но карточки самопроверяются! Начать пользоваться картами Boom можно бесплатно. Чтобы узнать больше, прочитайте «Взрывайте свое обучение с помощью карт Boom».

Длинное деление 2 цифры на 1 цифру (класс 4): на TpT или на штанге
Длинное деление с остатками (класс 5): на TpT или на штанге

Вы преподаете математику в Канаде?

Другие сообщения в блоге могут оказаться полезными, особенно если вы преподаете математику в Канаде. Все наши ресурсы создаются с использованием нотации SI, где запятые не ставятся между разрядными значениями целых чисел. Мы также используем метрические измерения и ориентируем наши ресурсы сначала на Альберту, а затем на другие канадские провинции и территории.

Покорите математику с помощью этих проверенных стратегий умножения

Вся правда о новой математике

Как изменить математику с помощью интерактивных тетрадей

Как использовать интерактивные тетради для обучения чувству чисел

Способы обучения понятиям формы и пространства

Как учить Студенты должны анализировать ошибки в математике

Как помочь вашим ученикам освоить десятичные операции

Дифференцировать ваши уроки математики

Какими другими способами вы обучаете делению в столбиках? Оставьте нам комментарий, чтобы рассказать нам все об этом.

Длинное деление: стратегии и расширения для старших классов математики

Я так рад поговорить со всеми о преподавании длинного деления! А, дивизия. У вас волосы на руках встают дыбом от одного упоминания об этом? И сроки! Почему нам всегда кажется, что мы учим делению на длинные числа во время курортного сезона, когда энергии много, а внимания мало? Вне зависимости от времени года наличие четкой, хорошо продуманной последовательности уроков деления может устранить большую часть обычного беспокойства, связанного с преподаванием длинного деления в 4-м классе… и за его пределами!

Этот стандарт 4-го класса призывает учащихся использовать стратегии разрядных значений для нахождения целых чисел и остатков с делимыми до четырех цифр и одноразрядными делителями, используя стратегии, основанные на разрядном значении, свойствах операций и/или связь между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей. Это мелочь, но давайте разбираться!

Когда мы думаем о дивизии и планируем нашу дивизию, первое, о чем я думаю, — это конкретная стратегия развития, которую я собираюсь использовать для обучения этой концепции. Студенты просто должны иметь концептуальное представление о том, КАК работают процедуры деления. Несмотря на то, что это не является стандартом для 4-го класса, в конечном счете, наша цель — овладеть 9-м уровнем.0133 стандартный алгоритм для деления в длинное число , чтобы, когда они начнут выполнять множество шагов процедуры, они могли осмыслить каждый шаг и понять, что они делают, а не просто запомнить. У меня нет абсолютно ничего против аббревиатуры, и я определенно использовал ее на якорной диаграмме, но понимание фактического процесса поможет им значительно больше, чем заучивание шагов, которые легко перепутать и перепутать. Вы можете увидеть мои 9Якорные диаграммы деления 0133 и другие стратегии длинного деления на этом посту .

Повторение умножения и деления

Первое, что мне нужно сделать на этом этапе, это убедиться, что я уже подробно повторил умножение и деление со своими учениками. Мы говорим о том, что это обратные операции, мы говорим о том, что такое деление, моделируем базовое деление и убеждаемся, что учащиеся знают, как использовать умножение для проверки своих ответов на деление (и наоборот). Почти ВСЕ стратегии деления, о которых мы собираемся поговорить, основаны на аналогичных стратегиях умножения, которые всегда кажутся менее сложными для учащихся, поэтому я призываю вас сначала заняться этими стратегиями умножения. Нужно освежить в памяти стратегию умножения? Прочтите в этом блоге все о стратегиях умножения .

Стратегии длинного деления

Давайте поговорим о стратегиях деления! Когда я говорю о стратегиях, я всегда представляю несколько, прежде чем перейти к стандартному алгоритму. Это очень важно для учащихся, чтобы понять, ПОЧЕМУ работает стандартный алгоритм. ПОЧЕМУ я представляю все эти стратегии студентам? Потому что у большинства детей ОДИН из них вызовет момент озарения, когда они скажут: «А! Я понимаю, ПОЧЕМУ я делаю то, что я делаю с этой конкретной процедурой прямо сейчас, и я знаю, ПОЧЕМУ я делаю этот шаг следующим». ЭТО моя конечная цель при обучении этим стратегиям.

Вот краткий обзор стратегий, которым я обучаю своих четвероклассников:

• Стратегии разрядности: использование чисел, кратных 10 (это должно было быть уже введено с умножением, так что это первое, с чего я начинаю работу со студентами)
  • 6400 / 8 на самом деле 64 / 8 x 100
  • Расширенная форма или свойство распределения (246 / 2) = (200 +400+6) / 2
• Модель площади
• Частичные частные
• Стандартный алгоритм — Не бросать помидоры, но я всегда ввожу стандартный алгоритм, даже в 4-м классе, потому что я обнаружил, что, как только у них есть эти стратегии, они довольно быстро приходят к некоторым ученикам и становятся еще одной стратегией, которую они могут использовать. Наша конечная цель — полное и полное концептуальное понимание.

Я создал эти бесплатных постера с длинными делениями , чтобы помочь вам и вашим ученикам освоить эти стратегии!

Beyond Long Division Strategies

Вы еще не закончили, когда ваши ученики развили понимание стандартного алгоритма или другой стратегии! Есть так много других частей и частей деления, которым важно учить. Давайте углубимся в две области, которые имеют решающее значение для глубокого понимания деления и о которых часто забывают. Включение анализа ошибок и интерпретации остатков в вашу инструкцию деления имеет решающее значение. Независимо от того, обучали ли вы только стратегиям или стандартному алгоритму, я умоляю вас включить эти два компонента в ваш модуль дивизии.

Анализ ошибок длинного деления

Я большой поклонник анализа ошибок, который помогает развить критическое мышление и понимание. Вы можете прочитать все об анализе ошибок здесь . Марцано особо отмечает, что анализ ошибок имеет решающее значение для формирования у учащихся критического мышления и концептуального понимания. Способность судить, защищать, интерпретировать и исправлять ошибки требует гораздо больше размышлений и понимания, чем простое решение проблемы.

Использование анализа ошибок с делением в длину

• После того, как учащиеся продемонстрируют владение стандартным алгоритмом (или стратегиями), сделайте еще один шаг и попросите их погрузиться в анализ ошибок, где они смогут продемонстрировать «обратное» понимание, оценивая сделанные ошибки. и исправить их. Способность выявить ошибку в чужой работе требует мышления более высокого порядка, которого нет в большинстве других проектов или видов деятельности и, конечно же, в базовом завершении математических фактов.
  • Сначала научите учащихся различать вычислительная ошибка и концептуальная ошибка.
    • Вычислительный — это когда ошибаются в основных математических фактах. Это может выглядеть так просто, как 64/8 не равно 7. Упс!
    • Концептуальная или процедурная ошибка — это когда они допускают ошибку в процедуре или концепции. Обычно это происходит, когда учащиеся не понимают, почему стратегии или алгоритмы работают, и просто запоминают шаги.
    • Я не могу сказать вам, сколько раз учащиеся показывают, что не владеют темой, когда ошибки, которые они делают, являются ВЫЧИСЛИТЕЛЬНЫМИ, а не концептуальными или процедурными. Им не нужно больше повторять, как использовать стратегию… им нужно замедлиться и уделить больше внимания своим математическим фактам.
  • После того, как мы представили типы ошибок (концептуальные и вычислительные), на которые должны обращать внимание учащиеся, мы переходим к фактическому анализу этих ошибок в чьей-либо работе и исправление ошибки.
  • Я создал задачи по анализу ошибок для вас, чтобы вы могли использовать их со своими учениками, чтобы они могли определить ошибки, типы ошибок, переработать проблему, создать свою собственную версию проблемы и решить ее. Я добился больших успехов, включив эти задачи во ВСЕ мои математические разделы. У меня даже есть дети, которые умоляют взять свои задания по анализу ошибок на перерыв, чтобы закончить!

• Последним шагом в использовании анализа ошибок является то, что учащиеся исправляют СОБСТВЕННЫЕ ошибки. После того, как я проинструктировал о типах ошибок, я начну с того, что просто скажу им: «Ой! Вы сделали здесь вычислительную ошибку!» Таким образом, они не будут яростно искать ошибку в процедуре, вместо этого они будут искать, где они вычислили неправильно. И наоборот, я скажу им, если они допустили процедурную ошибку, и это может помочь им понять, что им нужно искать.
  • Наблюдение за различными типами ошибок, которые допускают учащиеся, также важно для управления моим обучением, поэтому, несмотря на то, что оценка таких вещей занимает немного больше времени, это очень помогает мне, когда я вношу коррективы в свое обучение.

Проблемы со словами на деление

Еще один небольшой совет, который поможет еще большему критическому пониманию деления… Пусть ваши ученики придумают свои собственные задачи! Как только они смогут решить и проверить свою работу, им пора создавать свои собственные сценарии деления/словные задачи!

• Это не столько алгоритм, сколько критическое понимание цели разделения и возможность генерировать реальные сценарии, применимые к делению.
• Учащимся будет очень сложно, если мы попросим их просто решить задачу на деление, поэтому дайте им некоторые указания. Дайте им числа и темы, которыми они будут руководствоваться при создании проблем, чтобы они не застряли на двух довольно незначительных частях этого процесса. Например, я создал эти Напишите и решите карточки задач длинного деления . Он дает им числа и сценарий, и учащиеся должны сгенерировать и решить задачу на деление.

Устный перевод

• Остатки — серьезная проблема для учащихся, особенно в 4-м классе. Помочь им интерпретировать свои остатки и оценить их на предмет разумности — это ключ к их успеху в делении. У меня есть несколько оставшихся напоминаний, которые я ВСЕГДА настаиваю на своих учениках. Этот плакат также включен в бесплатную загрузку выше!

• Подсказка Напоминания об остатках для студентов:
  • Не бойтесь Словарь предметной области ! Обратите внимание, что слово «остаться» находится в слове «остаток». Это значение, которое остается и не может быть равномерно разделено на ваш делитель.
  • Остаток не может быть больше делителя. Я сторонник математической лексики, поэтому для меня очень важно, чтобы учащиеся могли использовать этот конкретный язык (делитель, частное, делимое).
  • Остаток МОЖЕТ иметь значение больше вашего частного. Такое бывает, и случается часто, поэтому обязательно приведите много примеров этому.
  • Когда одно число делится на другое число без остатка, технически остаток равен НОЛЬ.
  • Четное число, деленное на 2, никогда не должно иметь остатка.
  • Ваш остаток всегда служит цели. Это не всегда просто «остатки». Мы поговорим об этом подробнее в ближайшее время.
• Визуализация остатков:
  • Используйте массивы, чтобы визуализировать остатки как остатки.
  • Используйте манипуляторы для визуализации.
  • Используйте самый простой способ манипулирования: человеческие тела! Разыграйте множество сценариев, используя учащихся вашего класса, в том числе задачи с остатками… сейчас самое время решить транспортную задачу. Например: Класс мисс Смит собирался на экскурсию. В классе было 24 ребенка, и в каждом микроавтобусе по 7 учеников. Сколько фургонов им понадобится?
  • Используйте числовые линии для представления остатков 
• Интерпретация остатков: Когда я начал добавлять урок или два по интерпретации остатков , понимание моими учениками не только остатка, но и понимания текстовых задач резко возросло. Акту интерпретации остатков следует обучать после того, как учащиеся хорошо разберутся в выполнении деления с использованием стратегий или алгоритма. Мы сосредоточимся на трех различных способах использования остатков:
  • Использование остатка — Это происходит, когда остаток на самом деле является ответом.
  • Округление в большую сторону — Когда вы используете остаток для округления ответа. Частное — это не ваш ответ, но оно на единицу больше, потому что у вас есть остаток. (Например: когда вы распределяете детей по машинам, чтобы поехать в летний лагерь.