«Число и цифра 6. Написание числа 6. «
Цель: познакомить учащихся с новым числом 6 и соответствующей ему цифрой; формировать умения писать цифру 6; упражнять в сравнении чисел, составлении выражений на сложение в пределах 6 по предметным рисункам; закреплять знание состава числа 5. Развивать наблюдательность, зрительную и слуховую память, математическую речь, мыслительные операции у учащихся. Воспитывать культуру поведения, умение следить за ответом товарищей. Формировать здоровьесберегающую компетентность путём чередования различных видов деятельности и активного отдыха, создания комфортной и доверительной атмосферы в классе.
Тип урока: урок усвоения новых знаний.
- ноутбук, электронная презентация, геометрические фигуры, индивидуальный набор цифр, образцы написания цифры 6, тетради с печ. основой, учебник, простой карандаш.
Слайд № 1
- Организационный момент.

Теперь глазки все на меня.
Встало солнышко давно, Заглянуло к нам в окно. На урок торопит нас, Математика сейчас.
2.Тренинг-настрой на урок.
— У вас хорошее настроение? — Радость, улыбка помогают нам жить, учиться и справляться с трудностями, быть здоровым. Ребята! Вы готовы помочь друг другу в преодолении трудностей? Тогда улыбнитесь друг другу. Поделитесь своим хорошим настроением. Я желаю вам успеха на уроке.
А теперь проверь, дружок: Ты готов начать урок? Все ль на месте, Все ль в порядке: Ручка, книжка и тетрадка? Все ли правильно сидят? Все ль внимательно глядят?
- (обращение к Цветку порядка) Распускается1 лепесток
II. Актуализация знаний (развитие внимания, зрительной памяти)
— Посмотрите на доску. Как всё это можно назвать? Фигуры)
— Каким по счёту слева является ромб? (шестым)
— А справа, какая фигура является шестой? (треугольник)
— Какая фигура находится между кривой и квадратом? (круг)
— Какая фигура следует за треугольником? (ломаная)
— Какая фигура стоит перед кругом? (кривая)
— Сейчас я проверю, какие вы внимательные. Мы проведём игру на внимание «День-ночь». Запомните расположение фигур. Сфотографируйте глазками. Ночь (переставляю). День.
Мы проведём игру на внимание «День-ночь». Запомните расположение фигур. Сфотографируйте глазками. Ночь (переставляю). День.
— Что изменилось?
Ночь (переставляю). День. — Что изменилось?
Ночь (переставляю). День. — Что изменилось? (появилась новая фигура)
— Как называется эта фигура? (шестиугольник)
— Почему вы так её назвали? (шесть углов)
— А ещё чего шесть в этой фигуре? (шесть сторон)
— Ребята, а для чего мы с вами выполняли это задание? — Продолжаем дальше учиться? Отвечайте хором. (Да).
III. «Открытие» нового знания, формулирование темы урока.
1.Разминка. (используем знак «ХОР»)
— Сколько углов у шестиугольника? (Шесть)
— Сколько звуков в слове задача? (Шесть)
-В корзине сидят котята. Но котят не видно, а видно 6 хвостиков. Сколько котят в корзине? (Шесть)
— Сколько глаз у 3 щенят? (Шесть)
— Что интересного вы заметили?
( В условии и ответе встречается слово шесть).
— Подумайте, что может это означать?
2. Определение темы урока.
Какова же сегодня тема урока? Выслушиваются ответы детей и выводится тема урока «Число и цифра 6». Слайд №2
(На слайде высвечивается тема урока).
4. Актуализация опорных знаний и постановка проблемы
— У вас имеется на парте набор цифр. Будете работать в парах. Работать надо дружно, сообща, не ссорясь. Слайд
1) Сосчитайте, сколько столов на рисунке и обозначьте их количество нужным числом. Положите карточку на середину парты. (1)
2) Сколько ящиков у тумбы? Найдите карточку с нужным числом. (4)
3) Сколько деток на поляне? Обозначьте нужным числом. (2)
4) Сколько зверят на лугу? Обозначьте их количество числом. (3)
5) Сколько шариков в небе? Положите карточку. (5)
- — Молодцы. Вы были внимательные, не ошиблись.
— Посмотрите на числа. Что можете сказать? (стоят не по порядку)
Что можете сказать? (стоят не по порядку)
— Измените последовательность так, чтобы они стояли по порядку. (1 2 3 4 5)
— Умницы. Можно ли продолжить этот ряд чисел? Какое число будет следующее? (6) - Слайд (познакомить с числом 6, развитие умения доказывать свою точку зрения).
— Посмотрите на доску. Здесь много разных знаков. Каким знаком можно обозначить число 6?
8 + 9 – < 6 VI ( на доске)
(1 ученик выбирает знак).
— А я бы выбрала вот этот знак 9. Посмотрите, он так похож, есть закругление и кружок.
— Как мне, ребята, запомнить знак цифры 6? (ответы детей)
— Найдите у себя на парте карточку с цифрой 6. Поверните её правильно.
— Посмотрите на свой числовой ряд. Куда мы поставим число 6?
— А никто не знает, есть ли ещё знак цифры 6?
— VI – вот этот знак – римская цифра 6.
— Ребята, а где мы уже сталкивались сегодня с числом 6? К чему новому привёл нас шестиугольник? Видите, какая замечательная фигура пришла к нам сегодня на урок!
Посмотрите на наш кабинет и назовите 6 предметов, находящихся в нём - Назовите 6 имен своих друзей
Где в жизни встречается число шесть?
V. Физкультминутка (рисуем цифры).
Физкультминутка (рисуем цифры).
Работа по учебнику. (с. 26, № 2) Сравнения чисел.
Составление выражений на сложение в пределах 6 (Слайд)
— Посмотрите на эти картинки. Попробуйте догадаться, как они связаны с числом 6?
— Есть печатная цифра 6 и письменная. На иллюстрациях какая? Почему?
— А вот это письменная (показать). Чем отличается письменная цифра от печатной?
— Может догадался кто-то о нашей следующей работе? (Будем учиться писать цифру 6)
— А для чего нам надо уметь её писать? (ответы детей)
Работа в тетрадях (знакомство с цифрой 6, формировать умение правильно писать цифру 6).
Я тетрадочку открою
И наклонно положу.
Я, друзья, от вас не скрою,
Ручку я вот так держу.
Сяду прямо, не согнусь,
За работу я возьмусь.
— Сколько элементов у цифры 6? (2)
— Послушайте внимательно моё объяснение. (у детей локоть на парте)
— Сначала пишется большой левый полуовал, а затем малый правый. Начинаю писать большой полуовал немного ниже верхнего правого угла клетки, закругляю, касаясь верхней стороны клетки и веду вниз, закругляя, касаясь нижней стороны клетки и веду вверх, затем закругляю влево, немного выше середины клетки.
— Правильно возьмите ручки, спинки прямые. Напишите цифру 6 в воздухе. . Кто запомнил, как пишется цифра 6? (пишут самостоятельно. Кто не запомнил, пишу ещё раз). -Какая цифра самая красивая? Подчеркните её простым карандашом.
— Для чего научились писать цифру 6? Кто знает числа, в записи которых есть цифра 6? (ответы детей).
— Кто может назвать это число? 16, 36, 66, 666. СЛАЙД
VII. Суперфизминутка (аудио- видео)
VIII. Закрепление изученного материала.
Закрепление изученного материала.
— Ребята, вы готовы работать дальше?
— Продолжение работы в тетради. № 3,4.
IX. Итог урока (формирование самооценки, самоконтроля).
Рефлексия
— Как вы себя чувствуете? — О чём бы вы хотели рассказать родителям? — Какие задания вам понравились больше всего? — Какое задание для вас было трудным?
-Поднимите руку у кого веселое настроение. — Объясните, почему у вас весёлое настроение? У меня всё получилось. Я хорошо отвечал. Я правильно выполнил все задания.
— А у кого грустное настроение? Почему? У меня не все получилось. Я не смог выполнить все задания правильно.
— Не нужно грустить, если что-то не получилось. На следующем уроке вы будете успешнее. Я в это верю. Ваше хорошее настроение- залог успеха в любом деле. Я желаю вам хорошего настроения на следующем уроке. — Урок окончен. Вы славно потрудились!
Прозвенел опять звонок
и закончился урок!
Вы, ребятки, отдохните,
силы новой наберите.
Просмотр содержимого документа
«»Число и цифра 6. Написание числа 6. » »
Артемовская общеобразовательная школа І-ІІІ ступеней №18
Артемовского горсовета
Донецкой области
Рожанская Ирина Николаевна,
учитель начальных классов Артемовской общеобразовательной
школы І-ІІІ ступеней№18 Артемовского горсовета
Донецькой области
Квалификационнаа категория: специалист высшей категории
Год присвоения: 2003
2014 г.
Урок математики в 1-ом классе
Цель: познакомить учащихся с новым числом 6 и соответствующей ему цифрой; формировать умения писать цифру 6; упражнять в сравнении чисел, составлении выражений на сложение в пределах 6 по предметным рисункам; закреплять знание состава числа 5.
Тип урока: урок усвоения новых знаний.
Оборудование: ноутбук, электронная презентация, геометрические фигуры, индивидуальный набор цифр, образцы написания цифры 6, тетради с печ. основой, учебник, простой карандаш.
Слайд № 1
Организационный момент. 1. — Ребята, сегодня на нашем уроке присутствуют гости. Посмотрите, пожалуйста, на них. Поздоровайтесь.
Теперь глазки все на меня.
Встало солнышко давно, Заглянуло к нам в окно. На урок торопит нас, Математика сейчас.
2.Тренинг-настрой на урок.
— У вас хорошее настроение? — Радость, улыбка помогают нам жить, учиться и справляться с трудностями, быть здоровым.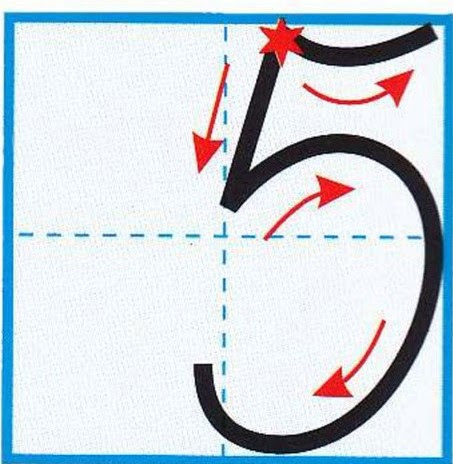 Ребята! Вы готовы помочь друг другу в преодолении трудностей? Тогда улыбнитесь друг другу. Поделитесь своим хорошим настроением. Я желаю вам успеха на уроке.
Ребята! Вы готовы помочь друг другу в преодолении трудностей? Тогда улыбнитесь друг другу. Поделитесь своим хорошим настроением. Я желаю вам успеха на уроке.
А теперь проверь, дружок: Ты готов начать урок? Все ль на месте, Все ль в порядке: Ручка, книжка и тетрадка? Все ли правильно сидят? Все ль внимательно глядят?
(обращение к Цветку порядка) Распускается1 лепесток
II. Актуализация знаний (развитие внимания, зрительной памяти)
— Посмотрите на доску. Как всё это можно назвать? Фигуры)
— Каким по счёту слева является ромб? (шестым)
— А справа, какая фигура является шестой? (треугольник)
— Какая фигура находится между кривой и квадратом? (круг)
— Какая фигура следует за треугольником? (ломаная)
— Какая фигура стоит перед кругом? (кривая)
— Сейчас я проверю, какие вы внимательные. Мы проведём игру на внимание «День-ночь». Запомните расположение фигур. Сфотографируйте глазками. Ночь (переставляю). День.
День.
— Что изменилось?
Ночь (переставляю). День. — Что изменилось?
Ночь (переставляю). День. — Что изменилось? (появилась новая фигура)
— Как называется эта фигура? (шестиугольник)
— Почему вы так её назвали? (шесть углов)
— А ещё чего шесть в этой фигуре? (шесть сторон)
— Ребята, а для чего мы с вами выполняли это задание? — Продолжаем дальше учиться? Отвечайте хором. (Да).
III. «Открытие» нового знания, формулирование темы урока.
1.Разминка. (используем знак «ХОР»)
— Сколько углов у шестиугольника? (Шесть)
— Сколько звуков в слове задача? (Шесть)
-В корзине сидят котята. Но котят не видно, а видно 6 хвостиков. Сколько котят в корзине? (Шесть)
— Сколько глаз у 3 щенят? (Шесть)
— Что интересного вы заметили?
( В условии и ответе встречается слово шесть).
— Подумайте, что может это означать?
2. Определение темы урока.
Какова же сегодня тема урока? Выслушиваются ответы детей и выводится тема урока «Число и цифра 6». Слайд №2
Слайд №2
(На слайде высвечивается тема урока).
4. Актуализация опорных знаний и постановка проблемы
— У вас имеется на парте набор цифр. Будете работать в парах. Работать надо дружно, сообща, не ссорясь. Слайд
1) Сосчитайте, сколько столов на рисунке и обозначьте их количество нужным числом. Положите карточку на середину парты. (1)
2) Сколько ящиков у тумбы? Найдите карточку с нужным числом. (4)
3) Сколько деток на поляне? Обозначьте нужным числом. (2)
4) Сколько зверят на лугу? Обозначьте их количество числом. (3)
5) Сколько шариков в небе? Положите карточку. (5)
— Молодцы. Вы были внимательные, не ошиблись.
— Посмотрите на числа. Что можете сказать? (стоят не по порядку)
— Измените последовательность так, чтобы они стояли по порядку. (1 2 3 4 5)
— Умницы. Можно ли продолжить этот ряд чисел? Какое число будет следующее? (6)Слайд (познакомить с числом 6, развитие умения доказывать свою точку зрения).

— Посмотрите на доску. Здесь много разных знаков. Каким знаком можно обозначить число 6?
8 + 9 – ( на доске)
(1 ученик выбирает знак).
— А я бы выбрала вот этот знак 9. Посмотрите, он так похож, есть закругление и кружок.
— Как мне, ребята, запомнить знак цифры 6? (ответы детей)
— Найдите у себя на парте карточку с цифрой 6. Поверните её правильно.
— Посмотрите на свой числовой ряд. Куда мы поставим число 6?
— А никто не знает, есть ли ещё знак цифры 6?
— VI – вот этот знак – римская цифра 6.
— Ребята, а где мы уже сталкивались сегодня с числом 6? К чему новому привёл нас шестиугольник? Видите, какая замечательная фигура пришла к нам сегодня на урок!
Посмотрите на наш кабинет и назовите 6 предметов, находящихся в нёмНазовите 6 имен своих друзей
Где в жизни встречается число шесть?
V. Физкультминутка (рисуем цифры).
Работа по учебнику. (с. 26, № 2) Сравнения чисел.
Составление выражений на сложение в пределах 6 (Слайд)
— Посмотрите на эти картинки. Попробуйте догадаться, как они связаны с числом 6?
— Есть печатная цифра 6 и письменная. На иллюстрациях какая? Почему?
— А вот это письменная (показать). Чем отличается письменная цифра от печатной?
— Может догадался кто-то о нашей следующей работе? (Будем учиться писать цифру 6)
— А для чего нам надо уметь её писать? (ответы детей)
Работа в тетрадях (знакомство с цифрой 6, формировать умение правильно писать цифру 6).
— Откройте рабочие тетради на стр. 21
Я тетрадочку открою
И наклонно положу.
Я, друзья, от вас не скрою,
Ручку я вот так держу.
Сяду прямо, не согнусь,
За работу я возьмусь.
— Сколько элементов у цифры 6? (2)
— Послушайте внимательно моё объяснение. (у детей локоть на парте)
— Сначала пишется большой левый полуовал, а затем малый правый. Начинаю писать большой полуовал немного ниже верхнего правого угла клетки, закругляю, касаясь верхней стороны клетки и веду вниз, закругляя, касаясь нижней стороны клетки и веду вверх, затем закругляю влево, немного выше середины клетки.
Начинаю писать большой полуовал немного ниже верхнего правого угла клетки, закругляю, касаясь верхней стороны клетки и веду вниз, закругляя, касаясь нижней стороны клетки и веду вверх, затем закругляю влево, немного выше середины клетки.
— Правильно возьмите ручки, спинки прямые. Напишите цифру 6 в воздухе. . Кто запомнил, как пишется цифра 6? (пишут самостоятельно. Кто не запомнил, пишу ещё раз). -Какая цифра самая красивая? Подчеркните её простым карандашом.
— Для чего научились писать цифру 6? Кто знает числа, в записи которых есть цифра 6? (ответы детей).
— Кто может назвать это число? 16, 36, 66, 666. СЛАЙД
VII. Суперфизминутка (аудио- видео)
VIII. Закрепление изученного материала.
— Ребята, вы готовы работать дальше?
— Продолжение работы в тетради. № 3,4.
IX. Итог урока (формирование самооценки, самоконтроля).
Рефлексия
— Как вы себя чувствуете? — О чём бы вы хотели рассказать родителям? — Какие задания вам понравились больше всего? — Какое задание для вас было трудным?
-Поднимите руку у кого веселое настроение. — Объясните, почему у вас весёлое настроение? У меня всё получилось. Я хорошо отвечал. Я правильно выполнил все задания.
— Объясните, почему у вас весёлое настроение? У меня всё получилось. Я хорошо отвечал. Я правильно выполнил все задания.
— А у кого грустное настроение? Почему? У меня не все получилось. Я не смог выполнить все задания правильно.
— Не нужно грустить, если что-то не получилось. На следующем уроке вы будете успешнее. Я в это верю. Ваше хорошее настроение- залог успеха в любом деле. Я желаю вам хорошего настроения на следующем уроке. — Урок окончен. Вы славно потрудились!
Прозвенел опять звонок
и закончился урок!
Вы, ребятки, отдохните,
силы новой наберите.
Урок математики «Число 6. Цифра 6». 1-й класс
Цель: познакомить с составом числа шесть, написание цифры 6.
Задачи.
- Систематизировать знания о цифре 6 и её составе.
- Закреплять умения складывать и вычитать при помощи числового отрезка.
- Развитие познавательных способностей: память,
мышление, внимание.

- Воспитывать умение работать в парах.
Планируемые результаты:
Личностные УУД: способность к самооценке
на основе критерия успешности учебной
деятельности.
Регулятивные УУД: уметь определять и
формулировать цель на уроке с помощью учителя,
проговаривать последовательность действий на
уроке; уметь высказывать свое предположение на
основе работы с материалом учебника; планировать
свое действие в соответствии с поставленной
задачей.
Коммуникативные УУД: уметь оформлять свои
мысли в устной форме; слушать и понимать речь
других; учиться работать в паре, формулировать
собственное мнение и позицию.
Познавательные УУД: уметь ориентироваться в
своей системе знаний: отличать новое от уже
известного с помощью учителя; добывать новые
знания: находить ответы на вопросы, используя
учебник, свой жизненный опыт и информацию,
полученную на уроке.
Предметные УУД: обозначать изученные
числа цифрами; рассмотреть связанные с составом
натурального числа случаи сложения и вычитания.
Этапы урока |
Деятельность учителя |
Деятельность учащихся |
Примечание |
| 1. Мотивация Оргмомент. | – Чем вы хотите удивить народ на уроке
математике? – Для чего вы учите математику? – Очень ли важен урок математики? Успехов Вам! |
||
| 2. Актуализация знаний и пробное учебное действие | – Вспомните наше путешествие по
числовому отрезку. – На какой станции мы остановились? – Стоит ли нам продолжить наше путешествие по числовому отрезку? – Для чего? – Но для того, чтобы узнать новое необходимо повторить то, что мы уже знаем. – Приготовьте карточки. – Я задумала число, если к этому числу прибавить 1, то получится 4. Какое число задумала? – Уменьшите это число на 2 – покажите следующее число за числом 3. – Как получить следующее число? (+ 1) – Назовите соседей числа 4. – Составьте числовое выражение. – Что вас удивило? – Как быть? |
На станции 5 Стоит 5 + 1 = ? |
У детей карточки. на доске запись: |
3. Постановка проблемы Постановка проблемы |
– Почему здесь возникло затруднение? – А можем объяснить правильность решения по числовому отрезку? – А ещё? |
Таких соседей нет ни в одном домике. На нашем числовом отрезке нет числа шесть, значит надо найти место числу шесть на числовом отрезке. Не умеем записывать цифру 6. Такого домика нет. Надо познакомиться с составом числа шесть. |
|
| Физминутка | |||
| 4. Построение проекта выхода из затруднения | Составим план на данный урок. – Не умеем записывать цифру 6. Надо научиться писать цифру 6) – Почему не можем объяснить правильность решения по числовому отрезку? (надо найти место числу шесть на числовом отрезке ) – Почему не смогли воспользоваться домиком? (Такого “домика” нет, надо познакомиться с составом числа 6.  – Что в нашей жизни связано с числом шесть? – Что в жизни бывает только 6? Презентация. Слайд |
6 материков, 6 ног у насекомых |
|
| 5. Реализация построенного проекта
Открытие нового знания и формулирование темы урока. |
– Давайте посмотрим на поставленные
цели? Что предстоит выполнить вначале? Знакомство
с цифрой 6 – Какая это цифра?
– На что похожа цифра? Цифра 6 состоит из большого левого и
малого правого полуовалов.
– Попробуйте в воздухе обвести несколько раз
цифру . – Первый пункт мы выполнили? Научились писать
цифру 6? Для чего научились? Работа в парах. |
Научиться писать Полуовала
Самооценка.
Теперь сможем не только считать до 6, но
записывать числа до 6. Состав числа.
|
Показ цифры 6. Листочки с точками |
| 6. Первичное закрепление с проговариванием во внешней речи | – Какую работу мы выполнили? – Для чего необходимо знать состав числа? – Значит, состав числа нужно быстрее выучить наизусть. Для этого мы ещё раз с помощью выражений вслух проговорим состав числа и заселим жильцов в “домик” № 6. – Все ли поставленные цели мы выполнили? Обращаясь к целям урока: – Писать цифру научились? – На числовом отрезке нашли место числу 6? – С составом числа 6 поработали? – Чем необходимо заняться теперь? – Верно. Чтобы быстрей и лучше запомнить состав числа 6, давайте решим следующее задание Посмотрим, какое задание нам предлагает учебник. Составить
равенства к 1 рисунку. |
Познакомились с составом числа. Чтобы быстро решать примеры. Открыли число 6?
|
|
| 7. Рефлексия учебной деятельности на уроке | – Вспомните, какой была тема нашего
урока? – Чему мы хотели научиться? – Нам это удалось? (Да.) – Какое задание было трудное? – О чём хотели бы вы рассказать родителям? |
Да |
Число и цифра 6.
 Написание цифры 6. Сравнение чисел. Составление выражений на сложение в пределах 6.
Написание цифры 6. Сравнение чисел. Составление выражений на сложение в пределах 6.Драчук Лариса Сергеевна
Розробка відкритого уроку в 1 класі
Вилковская ООШ I-III ст. № 1
Тема: Число и цифра 6. Написание цифры 6. Сравнение чисел. Составление выражений на сложение в пределах 6.
Цель: познакомить учащихся с новым числом 6 и соответствующей ему цифрой; формировать умения писать цифру 6; упражнять в сравнении чисел, составлении выражений на сложение в пределах 6 по предметным рисункам; закреплять знание состава числа 5. Развивать наблюдательность, зрительную и слуховую память, математическую речь, мыслительные операции у учащихся. Воспитывать культуру поведения, умение следить за ответом товарищей. Формировать здоровье сберегающую компетентность путём чередования различных видов деятельности и активного отдыха, создания комфортной и доверительной атмосферы в классе.
Тип урока: урок усвоения новых знаний.
Оборудование: ноутбук, электронная презентация, геометрические фигуры, индивидуальный набор цифр, образцы написания цифры 6, тетради с печатной основой, учебник, простой карандаш.
учителя начальных классов
Драчук Л.С.
2016-2017 год
ХОД УРОКА
Слайд № 1
- Организационный момент. 1. — Ребята, сегодня на нашем уроке присутствуют гости. Посмотрите, пожалуйста, на них. Поздоровайтесь.
Теперь глазки все на меня.
Встало солнышко давно, Заглянуло к нам в окно. На урок торопит нас, Математика сейчас.
2.Тренинг-настрой на урок.
— У вас хорошее настроение? — Радость, улыбка помогают нам жить, учиться и справляться с трудностями, быть здоровым. Ребята! Вы готовы помочь друг другу в преодолении трудностей? Тогда улыбнитесь друг другу. Поделитесь своим хорошим настроением. Я желаю вам успеха на уроке.
Поделитесь своим хорошим настроением. Я желаю вам успеха на уроке.
А теперь проверь, дружок: Ты готов начать урок? Все ль на месте, Все ль в порядке: Ручка, книжка и тетрадка? Все ли правильно сидят? Все ль внимательно глядят?
- (обращение к Цветку порядка) Распускается1 лепесток
II. Актуализация знаний (развитие внимания, зрительной памяти)
— Посмотрите на доску. Как всё это можно назвать? Фигуры)
— Каким по счёту слева является ромб? (шестым)
— А справа, какая фигура является шестой? (треугольник)
— Какая фигура находится между кривой и квадратом? (круг)
— Какая фигура следует за треугольником? (ломаная)
— Какая фигура стоит перед кругом? (кривая)
— Сейчас я проверю, какие вы внимательные. Мы проведём игру на внимание «День-ночь». Запомните расположение фигур. Сфотографируйте глазками. Ночь (переставляю). День.
— Что изменилось?
Ночь (переставляю). День. — Что изменилось?
День. — Что изменилось?
Ночь (переставляю). День. — Что изменилось? (появилась новая фигура)
— Как называется эта фигура? (шестиугольник)
— Почему вы так её назвали? (шесть углов)
— А ещё чего шесть в этой фигуре? (шесть сторон)
— Ребята, а для чего мы с вами выполняли это задание? — Продолжаем дальше учиться? Отвечайте хором. (Да).
III. «Открытие» нового знания, формулирование темы урока.
1.Разминка. (используем знак «ХОР»)
— Сколько углов у шестиугольника? (Шесть)
— Сколько звуков в слове задача? (Шесть)
-В корзине сидят котята. Но котят не видно, а видно 6 хвостиков. Сколько котят в корзине? (Шесть)
— Сколько глаз у 3 щенят? (Шесть)
— Что интересного вы заметили?
( В условии и ответе встречается слово шесть).
— Подумайте, что может это означать?
2. Определение темы урока.
Какова же сегодня тема урока? Выслушиваются ответы детей и выводится тема урока «Число и цифра 6». Слайд №2
(На слайде высвечивается тема урока).
4. Актуализация опорных знаний и постановка проблемы
— У вас имеется на парте набор цифр. Будете работать в парах. Работать надо дружно, сообща, не ссорясь. Слайд
1) Сосчитайте, сколько столов на рисунке и обозначьте их количество нужным числом. Положите карточку на середину парты. (1)
2) Сколько ящиков у тумбы? Найдите карточку с нужным числом. (4)
3) Сколько деток на поляне? Обозначьте нужным числом. (2)
4) Сколько зверят на лугу? Обозначьте их количество числом. (3)
5) Сколько шариков в небе? Положите карточку. (5)
- — Молодцы. Вы были внимательные, не ошиблись.
— Посмотрите на числа. Что можете сказать? (стоят не по порядку)
— Измените последовательность так, чтобы они стояли по порядку. (1 2 3 4 5)
— Умницы. Можно ли продолжить этот ряд чисел? Какое число будет следующее? (6) - Слайд (познакомить с числом 6, развитие умения доказывать свою точку зрения).

— Посмотрите на доску. Здесь много разных знаков. Каким знаком можно обозначить число 6?
8 + 9 – < 6 VI ( на доске)
(1 ученик выбирает знак).
— А я бы выбрала вот этот знак 9. Посмотрите, он так похож, есть закругление и кружок.
— Как мне, ребята, запомнить знак цифры 6? (ответы детей)
— Найдите у себя на парте карточку с цифрой 6. Поверните её правильно.
— Посмотрите на свой числовой ряд. Куда мы поставим число 6?
— А никто не знает, есть ли ещё знак цифры 6?
— VI – вот этот знак – римская цифра 6.
— Ребята, а где мы уже сталкивались сегодня с числом 6? К чему новому привёл нас шестиугольник? Видите, какая замечательная фигура пришла к нам сегодня на урок!
Посмотрите на наш кабинет и назовите 6 предметов, находящихся в нём
- Назовите 6 имен своих друзей
Где в жизни встречается число шесть?
V. Физкультминутка (рисуем цифры).
Физкультминутка (рисуем цифры).
Работа по учебнику. (с. 26, № 2) Сравнения чисел.
Составление выражений на сложение в пределах 6 (Слайд)
— Посмотрите на эти картинки. Попробуйте догадаться, как они связаны с числом 6?
— Есть печатная цифра 6 и письменная. На иллюстрациях какая? Почему?
— А вот это письменная (показать). Чем отличается письменная цифра от печатной?
— Может догадался кто-то о нашей следующей работе? (Будем учиться писать цифру 6)
— А для чего нам надо уметь её писать? (ответы детей)
Работа в тетрадях (знакомство с цифрой 6, формировать умение правильно писать цифру 6).
— Откройте рабочие тетради на стр. 21
Я тетрадочку открою
И наклонно положу.
Я, друзья, от вас не скрою,
Ручку я вот так держу.
Сяду прямо, не согнусь,
За работу я возьмусь.
— Сколько элементов у цифры 6? (2)
— Послушайте внимательно моё объяснение. (у детей локоть на парте)
— Сначала пишется большой левый полуовал, а затем малый правый. Начинаю писать большой полуовал немного ниже верхнего правого угла клетки, закругляю, касаясь верхней стороны клетки и веду вниз, закругляя, касаясь нижней стороны клетки и веду вверх, затем закругляю влево, немного выше середины клетки.
— Правильно возьмите ручки, спинки прямые. Напишите цифру 6 в воздухе. . Кто запомнил, как пишется цифра 6? (пишут самостоятельно. Кто не запомнил, пишу ещё раз). -Какая цифра самая красивая? Подчеркните её простым карандашом.
— Для чего научились писать цифру 6? Кто знает числа, в записи которых есть цифра 6? (ответы детей).
— Кто может назвать это число? 16, 36, 66, 666. СЛАЙД
VII. Суперфизминутка (аудио- видео)
VIII. Закрепление изученного материала.
— Ребята, вы готовы работать дальше?
— Продолжение работы в тетради. № 3,4.
IX. Итог урока (формирование самооценки, самоконтроля).
Рефлексия
— Как вы себя чувствуете? — О чём бы вы хотели рассказать родителям? — Какие задания вам понравились больше всего? — Какое задание для вас было трудным?
-Поднимите руку у кого веселое настроение. — Объясните, почему у вас весёлое настроение? У меня всё получилось. Я хорошо отвечал. Я правильно выполнил все задания.
— А у кого грустное настроение? Почему? У меня не все получилось. Я не смог выполнить все задания правильно.
— Не нужно грустить, если что-то не получилось. На следующем уроке вы будете успешнее. Я в это верю. Ваше хорошее настроение- залог успеха в любом деле. Я желаю вам хорошего настроения на следующем уроке. — Урок окончен. Вы славно потрудились!
Прозвенел опять звонок
и закончился урок!
Вы, ребятки, отдохните,
силы новой наберите.
Письмо цифр по точкам для 6 лет. Учим ребёнка писать цифры правильно
С 3-4 летними детьми стараемся запомнить графический образ числа- цифру, чтобы обозначать количество посчитанных предметов. Как и с буквами, подключаем к решению проблемы все органы чувств: цифры лепим из пластилина, выгибаем из проволочек, проходим ножками, дорисовываем, сочиняем сказки и т.д. Обыгрываем и запоминаем форму цифр . Мне очень нравится, как хорошо работают сказки про форму цифр . В этом возрасте пальчики ещё только развиваются, поэтому учимся писать упрощённые цифры. Полезно использовать доску с мелом, рисование в манке или стирающийся маркер, чтобы можно было удалить ошибку. Удобно пособие «Нарисую и сотру» , листы которого лучше сразу заламинировать. Мы любим, когда у нас всё получается. Вместо ламинирования можно просто класть сверху листы плёнки для кодоскопа, старинные канцелярские пластиковые папки и мн. др. прозрачное. Замечательно, если найдётся копировальная бумага- это вообще чистое волшебство для детей:)
Надо заметить, что эта упрощённая форма букв остаётся у иностранцев навсегда, например в латышском дошкольном учреждении
мы учили писать двойку с прямым хвостиком и шестёрку с девяткой без
хвостиков на американский манер.
Учим стихи о цифрах, запоминаем на что похожа цифра, рассматриваем цифры «с глазками»
Делаем шнуровки с цифрами
Учимся обводить и закрашивать, изучаем состав числа
.
На 15-минутных занятиях с детьми 5-7летнего возраста начинаем писать цифры с наклоном. Дети этого возраста видят цифры в целом, не разделяя их на
элементы. Поэтому, и случаются нередкие искажения и цифровых элементов
при письме. Чтобы избежать этого, при обучении письма цифр, важно
уделять внимание анализу каждой цифры, сравнению и сопоставлению
одинаковых элементов разных цифр. Ребенку
необходимо помочь научиться определять «опорные» точки, с которых
начинается письмо каждого составляющего элемента цифры,
последовательность элементов и их расположение в клетке.
Следует обратить внимание на то, что
некоторые элементы в разных (например: «большая палочка» в цифрах 1 и 7,
«волнистая линия» в цифрах 2, 5 и 7 и т.д.), а некоторые из них
начинаются в одной и той же точке клетке (например: в цифрах 2 и 3, 9 и 0
и т. д.). Так и говорим: «начинаем писать тройку так же, как цифру два…»
д.). Так и говорим: «начинаем писать тройку так же, как цифру два…»
Большое значение при обучении письму цифр имеет определение
правильного наклона. При письме в клетке наклон определяется отрезком,
соединяющим правый верхний угол клетки с серединой её нижней стороны.
Прежде чем приступить к объяснению написания цифры, необходимо показать
ребёнку её образец и проанализировать, из каких элементов состоит цифра
(палочка, волнистая линия, овал, полуовал). Показ написания цифры должен
сопровождаться краткими пояснениями о том, где начинается линия, в
каком направлении ведётся, где заканчивается, в каком месте ручка должна
быть оторвана от бумаги и какой будет следующая линия. Первые цифры,
написанные ребёнком самостоятельно, должны быть просмотрены взрослым,
который делает необходимые замечания.
Цифры наклоняются не вдруг, а после знакомства с клетками, графических
диктантов-«путешествий по клеточкам». В начале каждого занятия мы,
например, летели на самолётиках целую строчку по указаниям
меня-диспетчера: три клеточки вправо, две вниз и т.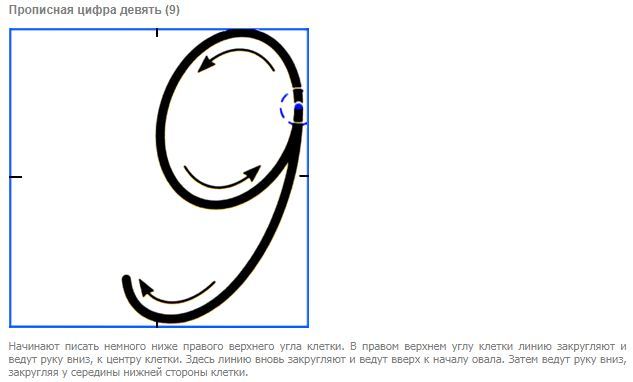 д. Сначала по указанию, но заканчивали строчку уже самостоятельно, угадав узор. Устраивали физкультминутку «Самолётики»(и другие по теме графического диктанта):
д. Сначала по указанию, но заканчивали строчку уже самостоятельно, угадав узор. Устраивали физкультминутку «Самолётики»(и другие по теме графического диктанта):
Руки в стороны — в полёт
Отправляем самолёт .
Правое крыло вперёд.
Левое крыло вперёд.
Раз, два, три, четыре-
Полетел наш самолёт.
В большой клетке
на доске начинали писать цифру. После графических диктантов и заданий в
тетради мы уже хорошо представляем верхнюю, нижнюю часть, правую и левую
сторону клетки. Отмечаем углы клетки точками и чёрточками серединки
всех сторон. Отмечаем красными точками углы, в которые цифры не попадают никогда. Договариваемся, что все цифры начинаем писать в правом верхнем углу и отмечаем его, на первых порах, зелёным цветом. А в нижний правый угол попадает своим хвостиком одна только двойка- хулиганка.
Презентация «Алгоритм написания цифр»
Начинают писать маленькую палочку немного выше и правее центра
клетки, ведут линию вверх к правому верхнему углу клетки. Затем пишут
большую палочку от верхнего правого угла почти до середины нижней
стороны клетки.
Затем пишут
большую палочку от верхнего правого угла почти до середины нижней
стороны клетки.
Живой учитель скажет всё это так:
Сейчас мы научимся писать единицу по школьным правилам. А правила такие:
1) головка у всех цифр должна быть в правом углу клетки;
2) ножка цифры должна встать на середину нижней стороны клетки;
3) цифру начинаем писать с головы, ручку не отрываем до конца.
Посмотрите на мою большую клетку на доске. Обведите в своих тетрадях клетку и поставьте точки, в тех уголках, где нельзя писать цифру(в левом верхнем, в левом нижнем, в правом нижнем) Покажите, куда должна стать ножка у цифры(отмечаем чёрточкой серединку нижней стороны клетки)
Ведём остренькую головку цифры 1 в правый верхний угол, а потом ставим ножку на середину нижней стороны клетки. Ножка будет под наклоном. Сейчас я в ваших тетрадях красной ручкой напишу цифру 1. Вы её обведите и напишите ряд цифр. Между ними пропускайте по одной клетке, а чтобы не забыть ставьте в пропускаемых клетках точки.
Но сначала скажите волшебные слова для ручки:
Ручка, ручка, мы с тобой друзья!
Плохо нам писать нельзя!
Тому, кто дошёл до конца строчки на полях улыбнётся солнышко:)
Начинают писать немного ниже середины верхней стороны клетки. Ведут
линию вверх, закругляя в правом верхнем углу клетки. Затем ведут линию
вниз к середине нижней стороны клетки. Вдоль нижней стороны клетки.
Вдоль нижней стороны клетки пишут волнистую линию, ведя руку к правому
нижнему углу клетки.
Живой учитель:
1)Рисуем в правом верхнем углу клетки круглую головку;
2) Потом, не отрывая руки, ставим ножку на середину нижней стороны клетки;
3) Теперь пишем хвостик, приговаривая:
вверх, вниз, вверх(~). На что похож хвостик? На гусеницу. Она не скачет, а еле ползёт. Гусеничка должна быть маленькой. Двойка- «хулиганка»: она единственная из цифр залезла в правый нижний угол клетки
Здесь и далее быть живым учителем для ребёнка можно научиться у Р.М Хамидулиной «Подготовка к школе.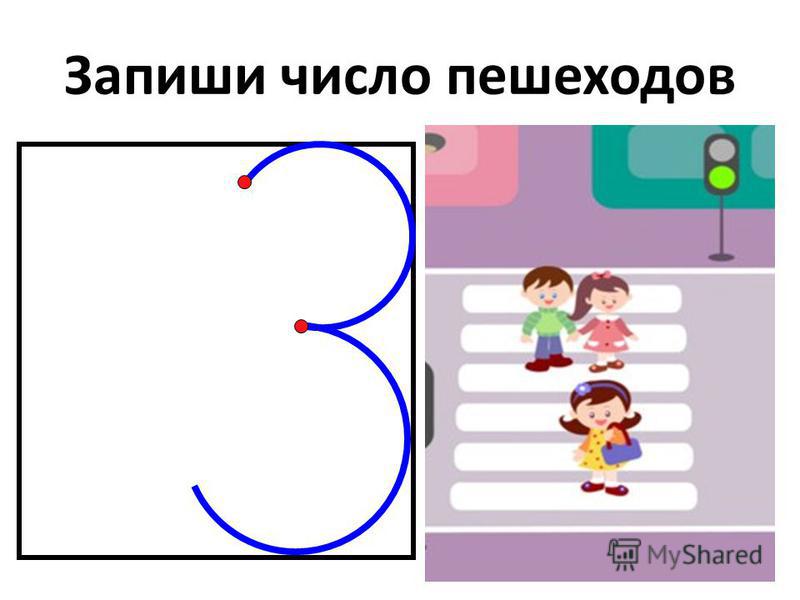 Сценарии занятий»
Сценарии занятий»
Начинают писать немного ниже середины верхней стороны клетки. Ведут линию вверх, закругляя в правом верхнем углу клетки. Затем ведут линию вниз, немного не доводят до середины клетки и пишут нижний полуовал.
Начинают писать немного правее середины верхней стороны клетки. Ведут прямую линию почти к центру клетки, затем ведут палочку вправо и немного не доводят до правой стороны клетки. Пишут длинную палочку, начиная выше середины правой стороны клетки и доводя её до нижней стороны клетки.
Начинают писать наклонную палочку немного правее середины верхней стороны клетки и ведут её почти до центра клетки. Затем пишут полуовал. Сверху от палочки пишут вправо волнистую линию.
Начинают писать полуовал немного ниже верхнего правого угла клетки, закругляют, касаясь верхней стороны клетки, и ведут руку вниз. Закругляют линию, касаясь нижней стороны клетки и ведут руку вверх. Затем закругляют линию влево немного выше центра клетки.
Начинают писать волнистую линию немного ниже середины верхней стороны
клетки и доводят её до правого верхнего угла клетки.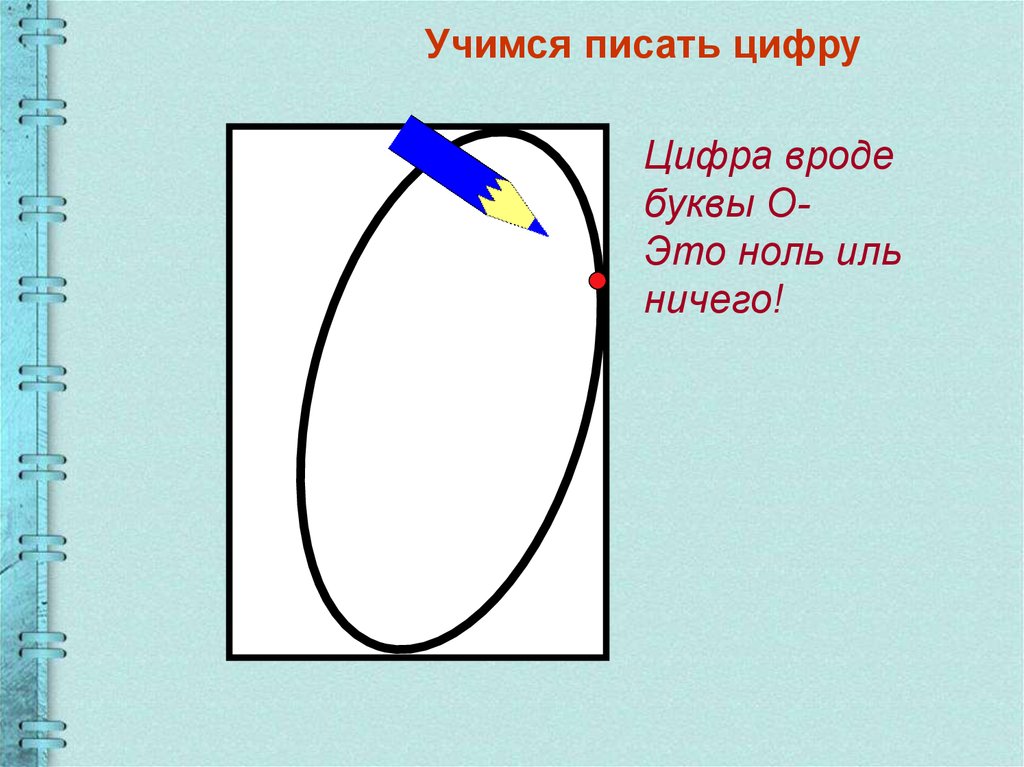 Потом пишут
большую палочку, доводя её почти до середины нижней стороны клетки, а
затем перечёркивают её маленькой палочкой посередине.
Потом пишут
большую палочку, доводя её почти до середины нижней стороны клетки, а
затем перечёркивают её маленькой палочкой посередине.
Начинают писать немного ниже и правее середины верхней стороны клетки. Ведут линию вверх и вправо, закругляют, касаясь верхней и правой сторон клетки. Затем ведут руку вниз, закругляют линию, касаясь нижней стороны клетки. Далее, закругляясь, линия идёт вверх к начальной точке.
Начинают писать немного ниже правого верхнего угла клетки. В правом
верхнем углу клетки линию закругляют и ведут руку вниз, к центру клетки.
Здесь линию вновь закругляют и ведут вверх к началу овала. Затем ведут
руку вниз, закругляя у середины нижней стороны клетки.
Овал начинают писать немного левее правого верхнего угла клетки.
Ведут линию вниз, закругляя на середине нижней стороны клетки. Затем
ведут руку вверх к началу овала.
Дидактические игры, прописи и всевозможные задания по возрастным группам(3-4 года, 5-6 лет, 6-7 лет),которые мы выполняли в детском развивающем центре собраны
Прописи — специальные альбомы и пособия для тренировки правильного написания букв и подготовки руки дошкольника к письму. Если раньше мы, родители, знали прописи только в школе (это были тетрадки, в которых первоклассники учились аккуратно писать буквы), то сейчас можно найти специальные прописи для малышей и дошкольников. Прописи для детей: фигуры, цифры, буквы учат малышей красиво писать и тренируют руку.
Если раньше мы, родители, знали прописи только в школе (это были тетрадки, в которых первоклассники учились аккуратно писать буквы), то сейчас можно найти специальные прописи для малышей и дошкольников. Прописи для детей: фигуры, цифры, буквы учат малышей красиво писать и тренируют руку.
Есть прописи которые предназначены для определенного возраста ребенка. На прилавках магазинов вы можете найти прописи для детей 3-4 или 5-6 лет.
В этой статье я подготовила для вас комплекты прописей которые можно бесплатно скачать и самостоятельно распечатать. Вы можете сохранить нужные картинки и давать ребенку каждый день новый листок с прописями.
Прописи для малышей
Вы думаете, что прописи только для подготовки к школе? Это не совсем так. Маленькие дети могут обводить по контуру или пунктиру простые картинки или большие буквы. Это прописи для малышей. В таких прописях почти нет текста, ведь ребенок еще не может читать. Зато они очень крупные, а картинки забавные. Почему бы не предложить малышу обвести веселого петушка по точкам или раскрасить утенка.
Деткам 4-5 лет можно предложить поиграть с — это тоже своеобразные прописи. В таких прописях вы не найдете цифр или букв, они для малыша еще сложны. Но задания на логику или точность движений будут обязательно. Выполняя обводку фигур, проводя кривые и ровные линии ребенок осваивает ручку или карандаш, учится нажиму и рисованию без отрыва от бумаги.
Среди прописей для малышей можно выделить особую группу прописей — это штриховки . Они представляют собой рисунки, которые нужно заполнять ровными или пунктирными линиями, в зависимости от задания.
Прописи для детей 5-6 лет
Для детей 5-6 лет прописи будут с более сложными заданиями. В них включены печатные и письменные буквы, а также палочки, крючки и другие части из которых строятся письменные буквы. Но пунктирные линии в этих прописях сохраняются. По ним ребенок обводит буквы, учится вести линию ровно и без отрыва. Лучше обводить буквы в прописях хорошей ручкой, потому что работая карандашом, ребенок может слишком сильно нажимать на карандаш, а от этого будет уставать рука.
Используя такие прописи ребенок не только познакомится с буквами русского алфавита, но и станет лучше их запоминать, а также выучит как они пишутся письменно. Также в прописях для дошкольников часто встречаются цифры. Дошкольник знакомится с цифрами и счетом.
Прописи для детей 5-6 лет можно условно разделить на:
- прописи АЛФАВИТ,
- прописи ЦИФРЫ.
Прописи для школьников
Чтобы ребенок научился красиво писать, а почерк у него сохранялся и не портился, нужно много заниматься. В школе учителя не придают большого значения правильной постановке руки во время письма и почерку. Но родители могут сами попробовать позаниматься с ребенком с помощью специальных прописей для школьников.
Каллиграфическое письмо — хороший навык, который может быть выработан у каждого ребенка. Скачайте и распечатайте прописи и потренируйтесь со школьником в написании красивых букв. В
Заметьте, что в этих прописях нет картинок или штриховок. В основном эти прописи направлены на тренировку хорошего красивого почерка.
В основном эти прописи направлены на тренировку хорошего красивого почерка.
Во время занятий обращайте внимание на то, как ученик держит ручку, как проводит линии. Следите, чтобы ребенок прописывал буквы без отрыва от бумаги. Не ругайте ребенка, если сразу у него не получается писать красивые буквы. Следите, чтобы ребенок начинал писать букву с нужной точки, а не так, как ему нравится. Например, начинают писать заглавную букву Р снизу вверх. Следите за этим. Сейчас во многих прописях даже стоят стрелочки и точки — ориентиры для деток. Покажите им эти стрелочки, объясните для чего они.
Надеюсь, прописи помогут вашему ребенку научиться красиво и правильно писать!
Прописи — замечательная придумка взрослых, для развития навыков письма у детей. Использовать прописи можно с самого раннего возраста, начиная с 3 лет.
Сейчас можно найти огромное количество прописей. Главное, подобрать прописи для ребенка, соответствующие его возрасту. На этой странице вы сможете бесплатно скачать и распечатать прописи для детей 3-4 лет, 5-6 лет (дошкольников) и первокласcников.
Не стоит начинать занятия сразу с прописей цифр, букв и слов — это очень сложно. Малышам в 3-4 года будут интересны прописи с увлекательными заданиями на внимательность, точность и координацию движений.
Это прописи с достаточно простыми фигурами, линиями, различными завитками. Пусть малыш сначала потренирует руку, обводя фрагменты картинок, забавные крючочки и палочки.
Малыш должен научиться проводить различные фигурные и непрерывные линии ровно и красиво, стараться не отрывать карандаш от бумаги. Это не так просто.
Скачать прописи для малышей
Прописи И.Попова отлично подойдут малышам для самых первых занятий. Палочки и крючочки встроены в рисунки прописи. Сначала можно раскрасить рисунок, а потом перейти к «строчному письму».
Скачать прописи для мальчиков
Веселые прописи для детей 5-6 лет
Для детей 5-6 лет возьмите прописи с более трудными заданиями. Используя такие прописи, ваш ребенок научится аккуратно обводить пунктирные линии, освоит первые навыки письма и рисования, приобретет ловкость при работе с ручкой и карандашом.
Скачать прописи для детей 5-6 лет
Скачать весёлые прописи для дошкольников
Прописи для дошкольника подготовят ребенка к письму, познакомят его с конфигурацией букв русского алфавита, научат писать буквы прописью. Используйте данные прописи, и ваш ребенок быстрее запомнит название и написание букв.
Скачать прописи — алфавит для дошкольников
Прописи по математике с цифрами и задачками помогут ребенку заранее научиться правильно писать цифры и познакомиться со счетом. Нажав на ссылку, вы можете скачать несколько видов прописей по математике быстро и бесплатно
Скачать прописи с цифрами
Прописи для школьников
Чтобы выработать красивый почерк, ребенку потребуется не мало времени. Но сейчас в школе очень мало уделяют внимания на правильное и каллиграфическое написание букв и цифр. Поэтому вы можете распечатать прописи с алфавитом для школьников и дополнительно заниматься. Эти прописи — без картинок, направлены на более серьезную работу по обучению письму. Кроме самих букв в прописях есть и отдельные элементы букв.
Кроме самих букв в прописях есть и отдельные элементы букв.
Скачать прописи для школьников «Алфавит прописью»
Знакомя ребенка с математикой в дошкольном возрасте, родители стараются привить любовь к этой науке. Прописи цифры помогут малышу научиться писать числа красиво и правильно. Написать цифры прописью вовсе не так легко. На освоение этого навыка в школе у непоседливого первоклассника часто не хватает времени и сил, поэтому к пятому классу его тетради по математике выглядят весьма печально. Как научить ребенка писать цифры, занимаясь с ним дома, чтобы занятия были в радость и на пользу?
Из этой статьи вы узнаете
Когда начинать
В каком возрасте лучше учить ребенка писать цифры прописью зависит не только от желания родителей. Многие хотят пораньше обучить своего малыша, как правильно писать цифры. Но если у ребенка еще неразвита мелкая моторика рук, он не умеет считать, и заниматься ему не очень хочется, покупать прописи с цифрами еще рано. Опытные педагоги не советуют предлагать прописи цифры для детей в три–четыре года по нескольким причинам:
Опытные педагоги не советуют предлагать прописи цифры для детей в три–четыре года по нескольким причинам:
- формируются неправильные навыки письма, так как ребенок еще не способен оценить прием написания чисел;
- у ребенка пропадает интерес осваивать новый материал в школе, если учитель объясняет то, что ему давно знакомо и успело надоесть;
- ребенок должен получить начальную подготовительную базу, которая включает умение держать ручку, ровно сидеть за партой, быть аккуратным и внимательным;
Когда малыш сам выявит желание заниматься, заполняя пропись цифр, можно скачивать материал для обучения из интернета бесплатно. Скачать прописи для дошкольников и распечатать можно самые разные: с картинками раскрасками, с узорами из различных элементов, образец, который нужно обводить по точкам. Первые занятия должны проходить в игровой форме и не утомлять ребенка.
Упражнения для развития мелкой моторики
Распечатанный цифровой образец, который нужно обвести, является хорошим упражнением для развития мелкой моторики. Но в два или три года давать ребенку прописи еще рано. Начинать нужно с простых занятий аппликацией, лепкой из пластилина или соленого теста.
Но в два или три года давать ребенку прописи еще рано. Начинать нужно с простых занятий аппликацией, лепкой из пластилина или соленого теста.
Можно делать самостоятельно или покупать в игрушечных магазинах сенсорные коробки с сыпучими материалами, фигурками зверей из пластика или резины, камешками разной формы и размера. Построение из элементов игры различных сценок будет способствовать развитию мелкой моторики рук ребенка с одного года.
С малышом старшего возраста можно заниматься нанизыванием бус на ниточку. В качестве бус могут служить большие пуговицы, крышечки от пластиковых бутылок, деревянные катушки из-под ниток.
Нужно делать с малышом пальчиковую гимнастику, рассказывая забавные стишки про сороку-ворону, которая кашу варила и деток кормила, про зайчиков и белочек, про мальчиков и девочек.
Можно устраивать театр теней при помощи рук, складывать оригами, плести макраме, делать фигурки и браслеты из резинок, вырезать новогодние снежинки, плести фигурки из крупного бисера. Собирание мелкого конструктора тоже прекрасно развивает мелкую моторику пальчиков, но старайтесь не давать мелкие детали деткам до трех лет, чтобы они их случайно не проглотили.
Собирание мелкого конструктора тоже прекрасно развивает мелкую моторику пальчиков, но старайтесь не давать мелкие детали деткам до трех лет, чтобы они их случайно не проглотили.
Важно научить ребенка правильно держать карандаш и ручку. Чтобы карандаш лежал на среднем пальце руки, будучи зажат большим и указательным пальцами, потренироваться придется долго. Не ругайте малыша, если он держит карандаш неправильно, раскрашивая картинки. Объясните, что если он хочет научиться рисовать и писать, карандаш нужно держать, так как это делает мама или папа. Хвалите ребенка за старание и малейшие успехи, стараясь не замечать промахов и ошибок.
Как проводить занятия
Учимся писать цифры играя. Урок письма должен стать не сухим заучиванием правил написания по клеточкам, а творческим занятием, развивающим воображение. Желательно, чтобы ребенок понимал то, что он пишет. Учить значение чисел можно с двух лет.
В пять лет можно начинать учить, как пишутся числа в прописях. Сначала необходимо объяснить ребенку, из каких частей состоит клетка в тетради. Где у нее верхняя сторона, где нижняя, правая и левая. Малыш должен сам находить центр клетки. Правильное написание цифр – это мамина гордость. Но нельзя торопить малыша.
Где у нее верхняя сторона, где нижняя, правая и левая. Малыш должен сам находить центр клетки. Правильное написание цифр – это мамина гордость. Но нельзя торопить малыша.
Навык письма формируется по наблюдениям психологов в течение нескольких лет жизни. Привычка выполнять задание торопливо и небрежно, чтобы быстрее окончить урок и заняться более интересными делами – это нежелательное поведение, которое нужно сразу корректировать. Вносить в дошкольный период обучения элемент игры можно самыми разными способами.
Заполнение прописи
Заполняя с ребенком прописи пишем цифры правильно, чтобы в школе не пришлось переучиваться. Правила написания по клеточкам от 1 до 10 показывают малышу в виде небольших карточек со стрелками, так он лучше поймет движение ручки во время письма и запомнит.
Вариант для цифры 1
Письмо цифры 1 начинается почти от середины клетки. Рисуют короткую палочку до угла клеточки. Потом вниз из правого угла длинную палочку, которая опускается на сторону основание клеточки.
Вариант для цифры 2
Писать цифру 2 начинают выше центра клеточки. Рисуют плавный полукруг, который касается середины правой части верха клеточки и середины верхней части правой стороны клеточки. Плавно закругляясь в виде ровной палочки, полукруг числа два опускается на черту-основание клетки немного левее середины. Теперь рисуют хвостик, который красивой волной упирается в правую сторону клеточки недалеко от основания. На этом письмо цифры 2 окончено.
Вариант для цифры 3
Число три состоит из двух полуокружностей. Начинают писать из точки, которая находится немного ниже середины верхней грани клеточки. Закругляя, ведут полуовал, который соприкасается с верхней гранью и с правой, ближе к углу. Оканчивается верхний полуовал чуть выше и правее центра клетки. За ним рисуют второй полуовал, который опирается одним боком на правую сторону клеточки и, доходя до основания, оканчивается чуть левее его середины.
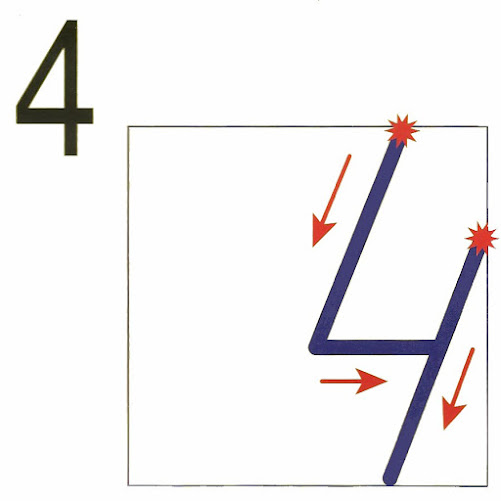
Вариант для цифры 4
Число четыре так же как один, не имеет симпатичных округлостей и плавных линий. Она состоит из прямых линий и углов. Письмо цифры 4 начинают из точки, лежащей на середине правой части верхней грани. Ведут линию до точки, которая находится немного ниже центра клеточки. Рисуют угол, со стороной параллельной основанию. Останавливаются, не доходя до правой стороны. Из точки, лежащей немного выше середины правой стороны, рисуют под наклоном линию до основания клеточки.
Она состоит из прямых линий и углов. Письмо цифры 4 начинают из точки, лежащей на середине правой части верхней грани. Ведут линию до точки, которая находится немного ниже центра клеточки. Рисуют угол, со стороной параллельной основанию. Останавливаются, не доходя до правой стороны. Из точки, лежащей немного выше середины правой стороны, рисуют под наклоном линию до основания клеточки.
Вариант для цифры 5
У числа пять рисуют ровную палочку вниз, по направлению к центру, из точки немного правее середины верхней грани клеточки. Красивый полукруг, отходящий от палочки, соприкасается с правой стороной клеточки посредине и опускается на сторону основание клетки. В конце из начальной точки рисуют хвостик в виде полукруга, который упирается в угол клеточки.
Вариант для цифры 6
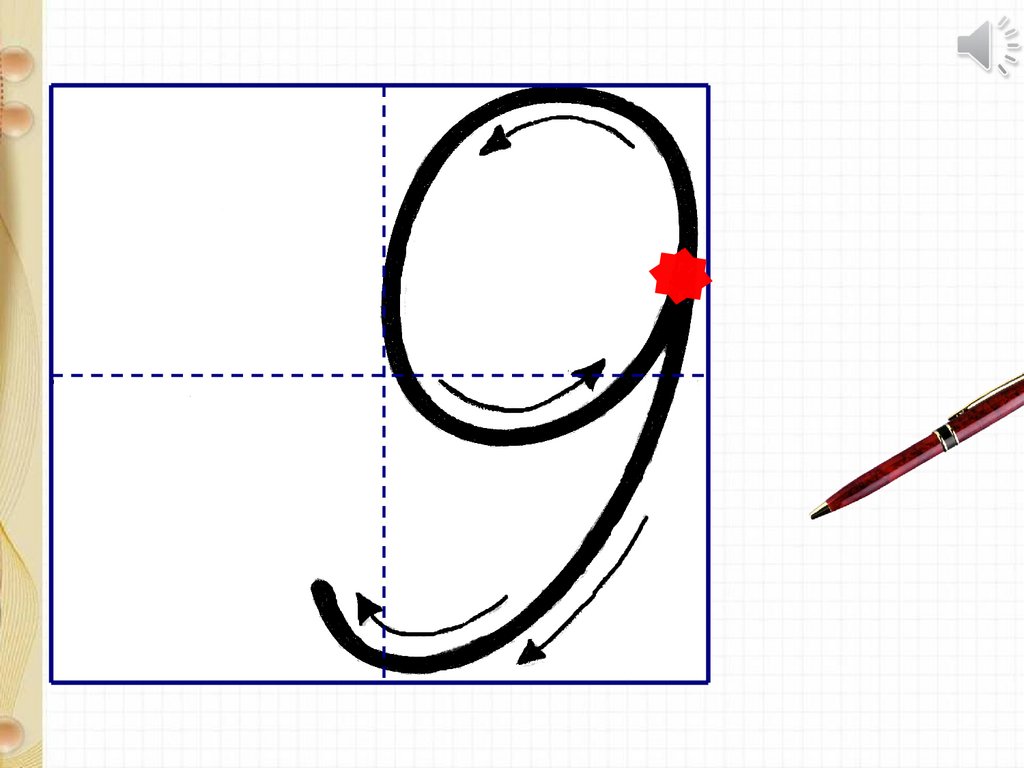
Число шесть похоже на девять, которое поставили на голову. Начинают писать шестерку из точки на правой стороне клеточки, недалеко от верхнего угла. Ведут полукруглый хвостик до нижней стороны клеточки. Против часовой стрелки рисуют овал, который занимает чуть больше одной четвертой части пространства.
Против часовой стрелки рисуют овал, который занимает чуть больше одной четвертой части пространства.
Вариант для цифры 7
Число семь пишут почти так же, как один. Только начинают вести не ровную линию, а плавную, как волну, из точки немного ниже середины верхней грани клеточки. Потом из правого угла клетки рисуют ровную ножку до основания, немного правее середины. Перечеркивают ножку цифры посередине короткой ровной чертой слева направо.
Вариант для цифры 8
Писать цифру 8 проще простого. Рисуют полукруг, как для числа два, начиная вести из точки немного выше центра клетки. На основании закругляют линию и рисуют второй полукруг больше, возвращая ручку в первоначальную точку написания числа восемь.
Вариант для цифры 9
Писать цифру 9 нужно из точки, которая находится в середине верхней части правой стороны клетки. Нарисовав небольшой овал, который почти помещается в одной четвертой части клетки, возвращаются в первоначальную точку и рисуют полукруглую ножку у овала. Ножка овала, доходя до середины основания клетки, закругляется немного вверх.
Ножка овала, доходя до середины основания клетки, закругляется немного вверх.
Вариант для цифры 0
Ноль, похожий на круглый бублик, начинают рисовать из точки, которая лежит на верхней грани клетки, недалеко от правого угла. Движение идет против часовой стрелки, через центр клетки, опускается на ее основание посередине и возвращается в исходную точку, соприкасаясь с правой стороной клетки вверху.
Освоив, как красиво писать первый десяток чисел, не забывайте повторять с ребенком простые правила сложения и вычитания. Тогда красиво написанные числа в тетради по математике для 1 класса будут стоять в правильно решенных задачках.
Большое значение при обучении письму цифр имеет определение правильного наклона. При письме в клетке наклон определяется отрезком, соединяющим правый верхний угол клетки с серединой её нижней стороны. Прежде чем приступить к объяснинию написания цифры, необходимо показать ребёнку её образец и проанализировать, из каких элементов состоит цифра (палочка, волнистая линия, овал, полуовал). Показ написания цифры должен сопровождаться краткими пояснениями о том, где начинается линия, в каком направлении ведётся, где заканчивается, в каком месте ручка должна быть оторвана от бумаги и какой будет следующая линия. Первые цифры, написанные ребёнком самостоятельно, должны быть просмотрены взрослым, который делает необходимые замечания.
Показ написания цифры должен сопровождаться краткими пояснениями о том, где начинается линия, в каком направлении ведётся, где заканчивается, в каком месте ручка должна быть оторвана от бумаги и какой будет следующая линия. Первые цифры, написанные ребёнком самостоятельно, должны быть просмотрены взрослым, который делает необходимые замечания.
Особенности написания цифр и образцы цифры
Начинают писать маленькую палочку немного выше и правее центра клетки, ведут линию вверх к правому верхнему углу клетки. Затем пишут большую палочку от верхнего правого угла почти до середины нижней стороны клетки.
Начинают писать немного ниже середины верхней стороны клетки. Ведут линию вверх, закругляя в правом верхнем углу клетки. Затем ведут линию вниз к середине нижней стороны клетки. Вдоль нижней стороны клетки. Вдоль нижней стороны клетки пишут волнистую линию, ведя руку к правому нижнему углу клетки.
Начинают писать немного ниже середины верхней стороны клетки. Ведут линию вверх, закругляя в правом верхнем углу клетки. Затем ведут линию вниз, немного не доводят до середины клетки и пишут нижний полуовал.
Ведут линию вверх, закругляя в правом верхнем углу клетки. Затем ведут линию вниз, немного не доводят до середины клетки и пишут нижний полуовал.
Начинают писать немного правее середины верхней стороны клетки. Ведут прямую линию почти к центру клетки, затем ведут палочку вправо и немного не доводят до правой стороны клетки. Пишут длинную палочку, начиная выше середины правой стороны клетки и доводя её до нижней стороны клетки.
Начинают писать наклонную палочку немного правее середины верхней стороны клетки и ведут её почти до центра клетки. Затем пишут полуовал. Сверху от палочки пишут вправо волнистую линию.
Начинают писать полуовал немного ниже верхнего правого угла клетки, закругляют, касаясь верхней стороны клетки, и ведут руку вниз. Закругляют линию, касаясь нижней стороны клетки и ведут руку вверх. Затем закругляют линию влево немного выше центра клетки.
Начинают писать волнистую линию немного ниже середины верхней стороны клетки и доводят её до правого верхнего угла клетки. Потом пишут большую палочку, доводя её почти до середины нижней стороны клетки, а затем перечёркивают её маленькой палочкой посередине.
Потом пишут большую палочку, доводя её почти до середины нижней стороны клетки, а затем перечёркивают её маленькой палочкой посередине.
Начинают писать немного ниже и правее середины верхней стороны клетки. Ведут линию вверх и вправо, закругляют, касаясь верхней и правой сторон клетки. Затем ведут руку вниз, закругляют линию, касаясь нижней стороны клетки. Далее, закругляясь, линия идёт вверх к начальной точке.
Начинают писать немного ниже правого верхнего угла клетки. В правом верхнем углу клетки линию закругляют и ведут руку вниз, к центру клетки. Здесь линию вновь закругляют и ведут вверх к началу овала. Затем ведут руку вниз, закругляя у середины нижней стороны клетки.
Овал начинают писать немного левее правого верхнего угла клетки. Ведут линию вниз, закругляя на середине нижней стороны клетки. Затем ведут руку вверх к началу овала.
Прописи цифр
Натуральные числа: определение, примеры, свойства
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
| Особенности натуральных чисел |
|---|
|
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
0 и 15;
20 и 50;
100 и 130?
Как помочь ребенку запомнить графическое изображение цифр
Как помочь ребёнку запомнить
графическое изображение цифр?
Очень часто бывает так, что ребёнок прекрасно считает от 1 до 10, но самостоятельно найти цифру, изображённую на картинке, никак не может. Графический образ цифры для него – это сложное абстрактное понятие. Развитие абстрактного мышления не простой процесс, как считают детские психологи. И без помощи взрослых здесь не обойтись.
Графический образ цифры для него – это сложное абстрактное понятие. Развитие абстрактного мышления не простой процесс, как считают детские психологи. И без помощи взрослых здесь не обойтись.
Часто дети путают цифры, немного похожие друг на друга, например 6 и 9, 3 и 8, 4 и 7. И эту проблему ни в коем случае нельзя упускать. Детям нужно помочь разобраться в таких сложных для его восприятия графических образах. Ребёнку будет гораздо легче запомнить цифру, если он сможет найти её сходство с каким-нибудь предметом или животным: 2 – лебедь, 8 – очки.
Если педагог в детском саду или мама смогут подобрать интересные стихотворения о цифрах, то процесс запоминания будет ещё более лёгким. Главное, не стоит сердиться на детей, если они не схватывает всё «на лету». Это для вас, взрослых, всё легко и просто, а для детей, только приступивших к овладению цифрами и счётом, всё очень сложно. Любой педагог подтвердит, что самым действенным способом запоминания нового материала для детей послужат игровые занятия по математике.
Рекомендую почитать своему ребёнку эти забавные стихотворения и, возможно, обучение пойдет быстрее и легче.
Цифры живут на различных предметах:
В календарях и трамвайных билетах,
На циферблатах часов, на домах,
Прячутся цифры в книжных томах,
И в магазине, и в телефоне,
И на машине, и на вагоне…
Цифры повсюду, цифры кругом.
Мы их поищем и сразу найдём.
Стихи про цифру 0
Эту цифру знать изволь:
На баранку похож ноль.
Ноль похож на колобок.
Он пузат и круглобок.
На него похожа кошка,
Если сложится в клубок.
Цифра 0 похожа на кольцо или баранку. Внутри кольца ничего нет — пусто. Цифра ноль обозначает число ноль, т.е. когда ничего нет — пусто.
Стихи про цифру 1
Вот один, иль единица,
Очень тонкая, как спица. С. Маршак
Похожа единица на крючок,
А может, на обломанный сучок.
Г. Виеру
Стихи про цифру 2
Два похожа на гусенка
С длинной шеей,
Шеей тонкой. Г. Виеру
Г. Виеру
А вот это цифра два.
Полюбуйся, какова:
Выгибает двоййка шею,
Волочится хвост за нею.
С. Маршак
Стихи про цифру 3
А вот это – посмотри,
Выступает цифра три.
Тройка – третий из значков —
Состоит из двух крючков.
С. Маршак
Стихи про цифру 4
Цифру 4 можно написать с помощью нескольких прямых линий. Сначала сверху вниз проведем карандашом самую левую наклонную линию, затем перекладинку, а потом правую вертикальную линию.
Смотри – 4 это стул,
Который я перевернул. Цифра новая – четыре.
Г. Виеру
Стихи про цифру 5
На что похожа цифра 5?
На серп, конечно,
Как не знать. Г. Виеру
А потом пошла плясать
по бумаге цифра пять.
Руку вправо протянула,
Ножку круто изогнула. С. Маршак
Стихи про цифру 6
Цифра шесть – дверной замочек:
Сверху – крюк, внизу кружочек. С. Маршак
С. Маршак
Стихи про цифру 7
Цифра 7 или, как ее еще называют, семерка, похожа на косу, которой косят траву. Цифра 7 состоит из двух палочек. Одна палочка лежит горизонтально сверху, а вторая палочка, как ножка, держит верхнюю. Иногда у цифры 7 посредине рисуют перекладинку.
Семь — точно острая коса.
Коси, коса, пока остра. Г. Виеру
Вот семерка-кочерга.
У нее одна нога. С. Маршак
Стихи про цифру 8
Цифру восемь, цифру восемь
На носу всегда мы носим,
Цифра восемь плюс крючки –
Получаются очки…
То ли нуль с другим нулем
Рядышком уснули,
То ли дедушка очки
Позабыл на стуле. Ф. Дагларджа
К этой цифре ты привык.
Это цифра-снеговик.
Лишь зима сменяет осень,
Дети лепят цифру восемь!
Только к цифре ты, дружок,
Третий не лепи кружок. В. Бакалдин
Цифра восемь или, как ее еще называют, восьмерка, похожа на снеговика или на куклу Неваляшку.
Стихи про цифру 9
Цифра 9 – девятка похожа на толстого кота, который отвернулся от нас и хочет вздремнуть. Цифра 9 – это колечко с хвостиком, она похожа на перевернутую цифру 6.
Девять, как и шесть, вглядись.
Только хвост не вверх, а вниз. Г. Виеру
Цифра девять, иль девятка,
Цирковая акробатка:
Если на голову встанет,
Цифрой шесть девятка станет. С. Маршак
Стихи про число 10
Цифра вроде буквы О —
Это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не значит ничегошеньки!
Если ж слева рядом с ним
Единицу примостим,
Он побольше станет весить,
Потому что это — десять. С. Маршак
Ноль встает за единицей —
Цифра 10 на странице. Г. Виеру
Математическая игра «Найди цифру»
Для этой игры потребуется:
нарисованные (напечатанные) на бумаге цифры от 1 до 9
рисунки, похожих на цифры, предметов.

Малыш смотрит на рисунок и затем угадывает, какая же цифра в нем спряталась. Затем мама показывает цифру 2 и просит малыша найти рисунок, похожий на эту цифру.
Математическая игра «Картонные цифры»
Для этой игры надо будет заранее вырезать цифры из картона. Малыш закрывает глазки, берет одну картонную цифру и на ощупь угадывает, что же это за цифра.
Математическая игра «Потерянные цифры»
На картоне печатаются цифры от 1 до 9. Затем каждая из них разрезается на две части. Малыш должен их восстановить. Если для него это задание слишком легкое, его можно усложнить, разрезав цифры на 3, 4 или 6 частей.
Игра «Что там на спинке»
Малыш ложится на живот, а мама рисует у него на спинке пальчиком цифру. Кроха должен угадать, что же это за цифра.
Консультацию составила:
учитель-дефектолог
Болдовская К. В.
В.
десятичных знаков
Десятичное число ( на основе числа 10 ) содержит десятичную точку .
Сначала приведем пример:
Вот число «сорок пять и шесть десятых» , записанное в виде десятичного числа:
Десятичная точка ставится между единицами и десятыми.
45,6 имеет 4 десятка, 5 единиц и 6 десятых, например:
Теперь давайте узнаем, как все это работает…
Место Значение
Все дело в Place Value!
Когда мы пишем числа, важна позиция (или « место ») каждой цифры
.
В номере 327:
- «7» находится в позиции единиц , что означает 7 единиц (то есть 7),
- «2» стоит в позиции десятков , что означает 2 десятка (то есть двадцать),
- и «3» в Сотни позиций, что означает 3 сотни.
| «Триста двадцать семь» |
| При движении влево каждая позиция увеличивается в 10 раз! | |
| Десятки в 10 раз больше, чем Единицы Сотни в 10 раз больше, чем Десятки |
. .. и …
.. и …
| При движении вправо каждая позиция становится в 10 раз меньше . | |
| От Сотни до Десятки до Единицы |
Но что, если мы продолжим прошлое? Что в 10 раз меньше , чем Единицы? 1 10 тыс. (Десятых) есть! |
| Но сначала мы должны поставить десятичную точку , , чтобы мы точно знали, где находится единица: | ||
«триста двадцать семь и четыре десятых » , но мы обычно просто говорим «триста двадцать семь целых четыре » | ||
И , что — это десятичное число!
Мы можем продолжать с меньшими и меньшими значениями, от десятых до сотых и так далее, как в этом примере:
Поиграйте сами с десятичными числами:
Большой и маленький
Итак, наша десятичная система позволяет нам записывать числа как большие, так и меньшие, чем
мы хотим, используя десятичную точку. Цифры можно располагать слева
или справа от десятичной точки, чтобы показать значения больше единицы
или меньше одного.
Цифры можно располагать слева
или справа от десятичной точки, чтобы показать значения больше единицы
или меньше одного.
Десятичная точка — самая важная часть десятичного числа. Без этого мы потеряны и не знаем, что означает каждая позиция.
| 17 | 591 | |||
| Слева от десятичной точки
целое число (например, 17) | ||||
| По мере продвижения влево каждое место получает 10 раз больше . | ||||
| Первая цифра справа означает десятых (1/10).  | ||||
| По мере продвижения вправо, каждое место получает в 10 раз меньше (на одну десятую больше). | ||||
Увеличить до десятичных дробей …
См. десятичные дроби в масштабируемой числовой строке
Определение десятичной дроби
Слово «десятичный» на самом деле означает «на основе 10» (от латинского десятичная : десятая часть ).
Мы иногда говорить «десятичный», когда мы имеем в виду что-либо, связанное с нашей нумерацией системы, но «десятичное число» обычно означает, что десятичная точка.
Способы думать о десятичных числах …
… как целое число плюс десятые, сотые и т. д.
Мы можем думать о десятичном числе как о целом числе плюс десятые, сотые и т. д.:
Пример 1: Что такое 2.3?
- Слева «2», то есть целое число часть.
- 3 находится в позиции «десятых», что означает «3 десятых», или 3/10
- Итак, 2.
 3 это «2 и 3 десятых»
3 это «2 и 3 десятых»
Пример 2: Что такое 13,76?
- Слева «13», то есть целое число часть.
- С правой стороны две цифры, 7 в «десятых» позиция, а 6 — позиция «сотых»
- Итак, 13,76 это «13 и 7 десятых и 6 сотых»
… как десятичная дробь
Или мы можем думать о десятичном числе как о десятичной дроби.
Десятичная дробь — это дробь, в которой знаменатель (нижнее число) представляет собой число, например 10, 100, 1000 и т. д. (другими словами, степень десяти)
| Итак, «2.3» выглядит так: | 23 10 |
| И «13,76» выглядит так: | 1376 100 |
… в виде целого числа и десятичной дроби
Или мы можем думать о десятичном числе как о целом числе плюс десятичная дробь.
Итак, «2. 3″ выглядит так: 3″ выглядит так: | 2 и 3 10 |
| И «13,76» выглядит так: | 13 и 76 100 |
Все это хорошие способы думать о десятичных числах.
Что такое порядковые номера? Определение, список, примеры, факты
Что такое порядковые числительные?
Числа, которые используются для обозначения ранга или положения объекта или человека, известны как порядковые числительные. Их также называют номерами позиционирования или ранжирования. Последовательность порядковых номеров зависит от параметров, основанных на определенных позициях, таких как вес, рост, отметки, размер и т. д. Такие числа также известны как порядковые номера.
Как писать порядковые номера?
Порядковые числительные или порядковые номера записываются с использованием числительных в качестве префиксов и прилагательных в качестве суффиксов.
Например, 1-й, 2-й, 3-й, 4-й, 5-й, 6-й, 7-й, 8-й и так далее. Мы можем легко определить порядковый номер: он говорит о позиционировании.
Итак, если бы мы сказали: «Принеси мне бутылку варенья, которая лежит на 4-й полке», то можно было бы знать, что порядковый номер здесь равен 4, что информирует нас о положении бутылки с вареньем.
На картинке выше показаны разные этажи здания. Здесь мы можем использовать порядковые номера для определения положения этажей.
Цифры 1-й (первый), 2-й (второй), 3-й (третий), 4-й (четвертый), 5-й (пятый), 6-й (шестой), 7-й (седьмой), 8-й (восьмой), 9-й (девятый) и 10-й (десятый) расскажите о расположении различных этажей в здании. Следовательно, все они являются порядковыми числами.
Применение порядковых числительных
Порядковые числительные — отличный способ рассказать о порядке чего-либо. Например, порядок дат. Эти номера используются только тогда, когда данные предоставлены и данные должны быть расположены по порядку.
Например: Тот, кто хорошо выступал в течение года, может получить шанс быть прощальным. Они будут первыми в очереди. Но тот, кто показал хорошие результаты, но не смог набрать столько же баллов, сколько предыдущий, на различных тестах и экзаменах, может быть 90 132 вторым 90 133 в очереди на прощальное выступление. У человека, который вообще не показал себя хорошо, меньше всего шансов.
На приведенном ниже рисунке показаны спортсмены, соревнующиеся в беге на 500 м. Мы также можем использовать порядковые номера для определения их позиций, чтобы увидеть, кто является победителем и кто занял второе место в гонке.
Другие примеры порядковых номеров:
- Дженнифер всегда занимает второе место в классе.
Здесь 2 — это порядковый номер, который говорит вам о должности, которую получила Дженнифер.
- Джейн стоит на пятом месте в очереди.
Под этим порядковый номер 5-й, мы понимаем позицию Джейн в очереди.
- Дженни заняла третье место в гонке.
Здесь 3rd — это порядковый номер, который говорит вам о месте, которое Дженни заняла в гонке.
- 10-й стол зарезервирован.
Здесь порядковый номер 10 означает количество забронированных столиков.
Порядковые числительные 1
– 50 списокПорядковые числительные 51
– 100 списокПорядковые числительные против количественных числительных . Этот тип чисел используется для представления количества элементов в наборе.
Кардинальность означает знание количества элементов в наборе.
Числа могут быть натуральными числами, которые мы используем при счете, например, один, два, три, четыре, пять и так далее.
С другой стороны, порядковые номера используются для определения ранга или положения любого объекта или лица. Мы пишем порядковые числа, используя числа в качестве префиксов и прилагательные в качестве суффиксов.
Давайте поймем разницу на примере.
Некоторых учеников попросили собрать шарики.
Том собрал 1, Джейн собрала 2, а Гвоздика собрала 3 шарика.
Здесь числа 1, 2, 3 являются количественными числами, так как они обозначают количество шариков.
Теперь побеждает тот, кто наберет максимальное количество очков. Итак, Гвоздика занимает 1-е место, Джейн — 2-е, а Том — 3-е.
Здесь числа 1-й, 2-й и 3-й являются порядковыми номерами, так как они обозначают положение студентов.
Порядковые номера v. Номинальные номера
Набор номеров, которые используются для маркировки определенных предметов или мест, чтобы их можно было легко идентифицировать, известен как номинальные номера. Всякий раз, когда нам нужно однозначно идентифицировать объект, мы используем номинальные номера. Эти числа не очень полезны, потому что они просто дадут информацию о местоположении, а не о его количестве, качестве и т. д. Номинальные числа могут использоваться в качестве кодов городов, на номерных знаках транспортных средств и т. д. Такие операции, как сложение, вычитание , умножение и деление бессмысленны на номинальных числах.
д. Такие операции, как сложение, вычитание , умножение и деление бессмысленны на номинальных числах.
Например: в телефонном номере 202 588-6500 это номинальный номер. Даже если мы применим операцию, она не даст нам ничего осмысленного.
На стрелке порядка порядковые номера говорят нам о ранге или положении любого предмета или человека.
Например: София живет в 34-м доме на Сан-Пабло-авеню, Калифорния.
Интересный факт!
11, 12 и 13 — единственные числа, в которых используется суффикс «–th», но все остальные числа, оканчивающиеся на 1, используют «–st», числа, оканчивающиеся на 2, используют «–nd», а заканчивающиеся на 3 используют «–rd». ‘.
Решенные примеры
Пример 1: Какой английский алфавит является 12-м с начала?
Решение : Алфавит, стоящий 12-й с начала, — L.
Пример 2. Ким, Кети, Киа и Каина сидят в очереди в алфавитном порядке. Каково положение Киа с самого начала?
Решение : Согласно алфавитному порядку, они будут сидеть в следующем порядке: Каина, Кети, Киа, Ким. Итак, Киа находится на 3-й позиции.
Итак, Киа находится на 3-й позиции.
3. Рождество приходится на _____ декабря. Решение . Рождество приходится на 25 декабря.
Практические задачи
Номер автомобиля Сары — KL23AB89.
На дереве 9 яблок.
Кэтлин заняла 4-е место в конкурсе рисунков.
Ничего из этого
Правильный ответ: Кэтлин заняла 4-е место в конкурсе рисунков.
В варианте С число 4 говорит о позиции Кэтлин в конкурсе рисунков.
51
51-й
51-й
51-й
Правильный ответ: 51-й
Порядковый номер 51 для 51-го.
M и O
M и N
P и I
E и O
Правильный ответ: P и I
Четвертая буква P, десятая буква I. Является ли 0 порядковым числом?
Нет, мы не можем писать 0 как порядковый номер.
Что такое исключительные порядковые номера?
Исключительные порядковые номера — это порядковые номера, которые не заканчиваются на -th. Например: 1st (первый), 2nd (второй), 3rd (третий) и т. д.
Например: 1st (первый), 2nd (второй), 3rd (третий) и т. д.
Кто изобрел порядковые числительные?
Порядковые числа были изобретены Георгом Кантором в 1883 году.
Что такое рациональное число? Определение и примеры
Вы слышали термин «рациональные числа»? Вы задаетесь вопросом: «Что такое рациональное число?» Если это так, вы находитесь в правильном месте!
В этой статье мы обсудим определение рационального числа, приведем примеры рациональных чисел и предложим несколько советов и приемов, чтобы понять, является ли число рациональным или иррациональным.
Что такое рациональное число?
Для того чтобы понять, что такое рациональные числа, нам сначала нужно рассмотреть некоторые основные математические определения:
- Целые числа — это целые числа (такие как 1, 2, 3 и 4) и их отрицательные аналоги (например — 1, -2, -3 и -4).

- Дроби — это числа, выражаемые в виде отношений. Дробь является частью целого.
- Дроби имеют числители, которые являются числами в верхней части дроби, которые показывают части, взятые из целого.
- Дроби также имеют знаменатели, которые представляют собой числа в нижней части дроби, которые показывают, сколько частей в целом.
Хорошо! Теперь, когда мы знаем эти термины, давайте обратимся к нашему первоначальному вопросу.
Что такое рациональное число?
Рациональное число — это число, которое можно представить в виде дроби , где и числитель, и знаменатель дроби являются целыми числами. Знаменатель рационального числа не может быть равен нулю.
Рациональное число, выраженное уравнением, — это число
a/b, b≠0
, где a и b — целые числа.
Это уравнение показывает, что все целые числа, конечные десятичные дроби и повторяющиеся десятичные дроби являются рациональными числами. Другими словами, большинство чисел являются рациональными числами.
Другими словами, большинство чисел являются рациональными числами.
Вот подсказка: если вы работаете с числом с длинным рядом различных десятичных знаков, то ваше число иррационально! Если вы работаете с целым числом или числом с терминальными или повторяющимися десятичными знаками (например, 1,333333), то ваше число рационально! Примеры рационального числа
Начнем с числа 6.
Число 6 является целым числом. Это тоже рациональное число. Почему?
Потому что 6 также может быть выражено как 6/1.
При выражении в виде 6 и числитель, и знаменатель являются целыми числами. Знаменатель не равен 0.
А число -6?
-6 можно записать как -6/1. Или 6/-1.
В любом случае -6 является рациональным числом, потому что его можно представить в виде дроби, где числитель и знаменатель являются целыми числами, а знаменатель не равен 0,
Что такое иррациональное число?
Противоположностью рациональных чисел являются иррациональные числа.
Проще говоря, иррациональные числа — это действительные числа, которые нельзя записать в виде простой дроби, например 6/1.
Возьми π.
π — действительное число. Но это также иррациональное число, , потому что вы не можете записать π в виде простой дроби:
π = 3,14155897932384626433832795 (и считать)
Невозможно записать π в виде простой дроби, поэтому это иррационально.
То же самое касается √2.
√2 равно 1,4142135623730950…(и т.д.).
Вы не можете превратить √2 в простую дробь, так что это иррациональное число.
Известные иррациональные числа
Известных рациональных чисел не существует, потому что подавляющее большинство чисел рациональны. Есть несколько известных иррациональных чисел. Вот некоторые из них, которые вы могли видеть:
- e: Число e (число Эйлера) — еще одно известное иррациональное число. Люди также рассчитали e до большого количества знаков после запятой без какой-либо закономерности.
 Первые несколько цифр выглядят так: 2,71828182845
Первые несколько цифр выглядят так: 2,71828182845353602874713527.
- π: Люди вычислили Пи с точностью до квадриллиона знаков после запятой, но закономерности нет. Первые несколько цифр выглядят так: 3.1415 5897932384626433832795
- √: Многие квадратные корни, кубические корни и т. д. также являются иррациональными числами. Примеры:
- √3 = 1,7320508075688772935274463415059 (и т. д.)
- √99 = 9,9498743710661995473447982100121 (и т. д.)
Однако не все квадратные корни являются иррациональными числами! Если ваш квадратный корень дает целое число (например, √4 или √9), то на самом деле вы работаете с рациональным числом!
Это не единственное, с чем вам нужно быть осторожным! Иногда при умножении двух иррациональных чисел получается рациональное число. Например,
√2 * √2 = 2
2 — рациональное число.
Основные выводы
Рациональные числа — это числа, которые можно представить в виде простых дробей.
Иррациональные числа — это числа, которые нельзя представить в виде простых дробей.
Что дальше?
Хотите узнать самые быстрые и простые способы конвертации между градусами Фаренгейта и Цельсия? Мы вас прикроем! Ознакомьтесь с нашим руководством по лучшим способам преобразования градусов Цельсия в градусы Фаренгейта (или наоборот).
Вы изучаете логарифмы и натуральные логарифмы на уроках математики? У нас есть руководство по всем правилам естественного журнала , которые вам необходимо знать.
Знаете ли вы, что вода имеет особую плотность? Ознакомьтесь с нашим руководством, чтобы узнать, что такое плотность воды и как плотность может меняться.
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
У вас есть друзья, которым также нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Хейли Миллиман
Об авторе
Хейли Миллиман — бывшая учительница, ставшая писателем и ведущая блоги об образовании, истории и технологиях. Когда она была учителем, ученики Хейли регулярно набирали 99-й процентиль благодаря ее страсти к тому, чтобы делать темы удобоваримыми и доступными. В дополнение к своей работе для PrepScholar, Хейли является автором Путеводителя Museum Hack по самым свирепым женщинам в истории.
Обучение абсолютному значению числа в математике
- Твитнуть Твитнуть
Поделиться
Делиться- Штырь Сохранять
- Соединять Соединять
Если вы преподаете математику учащимся, которые готовы узнать об абсолютном значении, как правило, в 6 классе, вот обзор темы, а также два урока, чтобы познакомить учащихся с этой концепцией и развить ее.
Что означает абсолютное значение?
Абсолютное значение описывает расстояние от нуля что число находится на числовой прямой, без учета направления. Абсолютное значение числа никогда не бывает отрицательным. Взгляните на некоторые примеры.
- Абсолютное значение 5 равно 5.
 Расстояние от 5 до 0 равно 5 единицам.
Расстояние от 5 до 0 равно 5 единицам.
- Абсолютное значение –5 равно 5. Расстояние от –5 до 0 равно 5 единицам.
- Абсолютное значение 2 + (-7) равно 5. При представлении суммы на числовой прямой полученная точка находится на расстоянии 5 единиц от нуля.
- Абсолютное значение 0 равно 0. (Вот почему мы не говорим, что абсолютное значение числа положительное. Ноль не является ни отрицательным, ни положительным.)
Примеры абсолютных значений и уравнения
Самый распространенный способ представить абсолютное значение числа или выражения — окружить его символом абсолютного значения: двумя вертикальными прямыми линиями.
- |6| = 6 означает « абсолютное значение 6 равно 6».
- |–6| = 6 означает “ абсолютное значение –6 равно 6. ”
- |–2 – x| означает » абсолютное значение выражения -2 минус x. ”
- –| х | означает » отрицательное значение абсолютного значения x.
 ”
”
Числовая линия — это не просто способ показать расстояние от нуля; это также полезный способ графического отображения равенств и неравенств, содержащих выражения с абсолютным значением.
Рассмотрим уравнение | х | = 2. Чтобы показать x на числовой строке, вам нужно показать каждое число, абсолютное значение которого равно 2. Есть ровно два места, где это происходит: в 2 и в -2:
Теперь рассмотрим | х | > 2. Чтобы отобразить x на числовой строке, вам нужно показать каждое число, абсолютное значение которого больше 2. Когда вы рисуете это на числовой строке, используйте открытые точки на -2 и 2, чтобы указать, что эти числа не часть графика:
В общем, вы получаете два набора значений для любого неравенства | х | > к или | х | ≥ k , где k — любое число .
Теперь рассмотрим | х | ≤ 2. Вы ищете числа, абсолютные значения которых меньше или равны 2. Это верно для любого числа от 0 до 2, включая как 0, так и 2. Это также верно для всех противоположных чисел между –2 и 0. Когда вы рисуете это на числовой прямой, закрытые точки у –2 и 2 указывают на то, что эти числа включены. Это связано с неравенством с использованием ≤ (менее или равно ) вместо < (меньше).
Вы ищете числа, абсолютные значения которых меньше или равны 2. Это верно для любого числа от 0 до 2, включая как 0, так и 2. Это также верно для всех противоположных чисел между –2 и 0. Когда вы рисуете это на числовой прямой, закрытые точки у –2 и 2 указывают на то, что эти числа включены. Это связано с неравенством с использованием ≤ (менее или равно ) вместо < (меньше).
В общем, вы получаете только один набор значений для любого неравенства | х | < к или | х | ≤ k , где k — любое число .
Один из способов представить это так: вы по-прежнему получаете два набора значений («отрицательный» набор и «положительный» набор), но поскольку они встречаются в нуле, они сходятся в один набор. Эти неравенства можно переписать без знаков абсолютного значения, записав выражение внутри абсолютного значения как попадающее между двумя числами:
- Можно переписать | х | < 2 вот так: –2 < x < 2
- Вы можете переписать | х | ≤ 4 следующим образом: –4 ≤ x ≤ 4
- Вы можете переписать | х + 6| < 25 вот так: –25 < x + 6 < 25
 Знакомство с концепцией
Знакомство с концепцией Материалы: Числовая линия и цветные точки, которые может видеть весь класс
2 90 Подготовка Если у вас нет серийно выпускаемой числовой линии, нарисуйте ее либо на доске, либо на длинном (желательно тонком) листе бумаги. При дистанционном обучении поделитесь числовой строкой с абсолютным значением, которую может видеть весь класс. Включите как минимум от –20 до 20.
Стандарты:
- Интерпретируйте утверждения о неравенстве как относительное положение чисел на числовой прямой. (6.NS.C.7.A)
- Создание и интерпретация операторов порядка для рациональных чисел в контексте реального мира. (6.NS.C.7.B)
Предварительные навыки и понятия: Учащиеся должны быть знакомы с символами неравенства и способами построения и использования числовой прямой. Кроме того, они должны уметь работать с отрицательными числами.
- Встаньте так, чтобы дверь была справа от вас.

- Спросите: О том, как далеко я от двери? Учащиеся должны указать примерное количество футов.
- Спросите: Если бы мне завязали глаза, как бы вы сказали мне, где дверь? Учащиеся должны указать примерное количество футов и направление. Если учащиеся предлагают разные единицы измерения, даже нестандартные, такие как «шаги» или «длина рук», обращайте внимание на различия и поощряйте их.
- Теперь встаньте так, чтобы дверь была слева от вас.
- Спросите: О том, как далеко я сейчас от двери? Учащиеся должны указать примерное количество футов.
- Спросите: Если бы мне завязали глаза, как бы вы сказали мне, где дверь? Учащиеся должны указать предполагаемую длину и направление.
- Скажи: Когда я спросил, как далеко я от двери, ты назвал мне количество футов, и не имело значения, в какую сторону я смотрел.
 Но когда я спросил, где находится дверь по отношению к моему положению, вы дали мне направление, а также число, и тогда имело значение, в какую сторону я смотрю. Сегодня мы обсудим абсолютное значение. Абсолютное значение говорит вам, насколько далеко число от нуля. Но он не говорит вам, куда идти! Это не говорит вам, что направление номер от нуля.
Но когда я спросил, где находится дверь по отношению к моему положению, вы дали мне направление, а также число, и тогда имело значение, в какую сторону я смотрю. Сегодня мы обсудим абсолютное значение. Абсолютное значение говорит вам, насколько далеко число от нуля. Но он не говорит вам, куда идти! Это не говорит вам, что направление номер от нуля. - Укажите на 6 на числовой прямой.
- Спросите: Какой это номер? Насколько это далеко от нуля? Продолжайте этот вопрос с -6, 0, 14 и -14 и так далее, пока не убедитесь, что учащиеся могут отличить направленное расстояние от абсолютного расстояния. Подкрепите ответ на каждый вопрос о расстоянии, сказав: » Абсолютное значение [пробел] равно [пробел]» и написав |___| знак равно
- Разделите класс на две команды. Команда 1 — это команда Signed Numbers, а команда 2 — это команда Absolute Value.
- Спросите: Может ли кто-нибудь из команды 1 задать вопрос, на который в качестве ответа требуется номер со знаком или направление?
Вас интересуют такие вопросы, как: Какая была температура в градусах по Фаренгейту? Как мне отсюда добраться до озера Эри? Если это подходит вам и вашим учащимся, сравните, как различные числа со знаком и направление появляются в ответах учащихся.
 Например, значение температуры имеет только «направление», потому что градусы по Фаренгейту включают отрицательные и положительные значения, поэтому для ясности необходим знак. Направления к озеру Эри потребуют множества чисел со знаком: куда ехать на восток (положительный) против запада (отрицательный) и куда ехать на север (положительный) по сравнению с югом (отрицательный).
Например, значение температуры имеет только «направление», потому что градусы по Фаренгейту включают отрицательные и положительные значения, поэтому для ясности необходим знак. Направления к озеру Эри потребуют множества чисел со знаком: куда ехать на восток (положительный) против запада (отрицательный) и куда ехать на север (положительный) по сравнению с югом (отрицательный). - Спросите: Может ли кто-нибудь из команды 2 задать тот же вопрос, чтобы , а не требовали в качестве ответа номер со знаком или направление?
Вам интересны такие вопросы, как: Насколько выше нуля градусов по Фаренгейту была температура? Как далеко на север отсюда находится озеро Эри?
Попросите команды поочередно начать сначала, придумывая вопросы, для ответа на которые требуется число со знаком или абсолютное число, а затем попросите другую команду пересмотреть вопрос. Поощряйте учащихся творчески подходить к вопросам.
- Снова соберите весь класс вместе.
 Поместите цветные точки на -6 и +3 на числовой строке.
Поместите цветные точки на -6 и +3 на числовой строке. - Спросите: Как бы вы сравнили эти два числа? Выясните ответы учащихся и сопоставьте различия в точности, порядке и словарном запасе. Попросите учащихся произнести и написать сравнение: –6 < +3 или –6 < 3.
- Спросите: Как бы вы сравнили абсолютные значения этих двух чисел? Попросите учащихся произнести и написать сравнение. |–6| > |+3| или |–6| > |3|.
Обсудите, почему изменилось направление символа сравнения, используя большую числовую линию, чтобы проиллюстрировать то, что говорите вы и учащиеся. Сделайте еще несколько примеров, пока не убедитесь, что учащиеся могут сравнивать как числа со знаком, так и абсолютные значения.
Урок 2: Разработка концепции
Материалы: Каталожные карточки или цифровые «карточки», которые можно распределить между классами
Стандарты:
- Понимать под рациональным числом его абсолютное значение расстояния от 0 на числовой прямой.
 (6.NS.C.7.C)
(6.NS.C.7.C)
Подготовка: Сделать карточки для задания У меня есть… У кого есть?
Игра для подведения итогов и оценки
- Попросите учащихся написать и поделиться своими определениями и примерами из реальной жизни ситуаций с абсолютными значениями.
- Играть У меня есть… у кого есть? Составьте набор из 15 карточек с уравнениями абсолютного значения и 15 карточек со значениями переменной. Если каталожные карточки недоступны или вы адаптируете это для дистанционного обучения, создайте способ, чтобы приведенные ниже 30 уравнений были максимально равномерно распределены между вашими учащимися.
| Карты абсолютной стоимости | Карты переменной стоимости |
| | х + 5| = 20 | x = 15 |
| |5 – x | = 30 | x = –25 |
| | х + 6| = 41 | x = 35 |
| |–27 – x | = 20 | х = –47 |
| –7 + | х | = 0 | x = –7 |
| |25 – x | = 18 | x = 7 |
| | х + –5| = 38 | x = 43 |
| |37 – x | = 70 | x = –33 |
| 114 – | х | = 7 | x = 107 |
| |– x + 100| = 21 | х = 121 |
| –|1 + x | = -80 | x = 79 |
| | х | = 81 | x = –81 |
| | х + 3| = 84 | x = 81 |
| |25 + x | = 62 | x = –87 |
| | х – 26| = 11 | x = 37 |
Каждая указанная карта абсолютного значения имеет два значения для х . Эти значения перекрываются, так что каждая карта значений переменных удовлетворяет двум заданным уравнениям абсолютного значения (первое и второе значения удовлетворяют первому уравнению, второе и третье значения удовлетворяют второму уравнению и так далее, пока последнее и первое значения не удовлетворяют заданному уравнению). последнее уравнение).
Эти значения перекрываются, так что каждая карта значений переменных удовлетворяет двум заданным уравнениям абсолютного значения (первое и второе значения удовлетворяют первому уравнению, второе и третье значения удовлетворяют второму уравнению и так далее, пока последнее и первое значения не удовлетворяют заданному уравнению). последнее уравнение).
Раздайте карточки или уравнения поровну. Убедитесь, что все они были распределены. Выберите учащегося, который скажет «У меня есть», а затем прочитайте значение или уравнение на его карточке. Затем попросите студента сказать: «У кого есть совпадение с моей карточкой?» Любой ученик, у которого есть совпадение, должен сказать «У меня есть… У кого есть…», и игра продолжается до тех пор, пока не будут прочитаны все карточки. Вы можете предложить учащимся встать, когда игра начнется, и сидеть, когда они предлагают ответ. Чтобы все были вовлечены, предложите вознаграждение за успешное завершение игры, поощряя вызовы на подозрительные ответы.
***
Ищете учебную программу по математике, которая повысит уверенность учащихся в математике и предоставит вам насыщенные уроки и задания для учащихся средних классов? Изучите HMH Into Math , наше основное математическое решение для классов K–8.
Математика Мероприятия и уроки 6-8 классы
Будьте первым, кто прочитает последнюю из Фасонный .
Похожие сообщения
Что такое четные числа? Определение
Четные числа — это числа, которые можно разделить на две равные группы или пары и которые точно делятся на 2. Например, 2, 4, 6, 8, 10 и так далее. Эти числа можно сгруппировать в равные пары. Однако эту группировку нельзя выполнить для таких чисел, как 5, 7, 9 или 11. Таким образом, 5, 7, 9 или 11 не являются четными числами. Давайте узнаем больше о четных числах и их свойствах на этой странице.
Давайте узнаем больше о четных числах и их свойствах на этой странице.
| 1. | Что такое четные числа? |
| 2. | Нечетные и четные числа |
| 3. | Свойства четных чисел |
| 4. | Часто задаваемые вопросы о четных числах |
Что такое четные числа?
Четное число — это число, кратное 2. Можно сказать, что любое число, которое полностью делится на 2, является четным числом. Это можно понять с помощью примера. Предположим, у Джона 6 мячей. Если он попытается сгруппировать их, он может соединить все 6 шаров и сформировать 3 пары. Нет шаров, которые остались непарными. Следовательно, он может сделать вывод, что 6 — четное число. Теперь разделим 6 на 2. Получим частное 3, равное количеству образовавшихся пар. Получаем остаток как 0, что равно количеству шаров, которые нельзя спарить. Всякий раз, когда Джон пытается соединить четное количество мячей, он останется без мяча. Другими словами, всякий раз, когда четное число делится на 2, мы всегда получаем в остатке 0,9.0009
Всякий раз, когда Джон пытается соединить четное количество мячей, он останется без мяча. Другими словами, всякий раз, когда четное число делится на 2, мы всегда получаем в остатке 0,9.0009
Нечетные и четные числа
Целые числа можно разделить на четные и нечетные. Нечетные числа — это те числа, которые не делятся полностью на 2. Тогда как четные числа полностью делятся на 2. Давайте пройдемся по списку всех четных чисел от одной до двухсот. Обратите внимание на числа, указанные ниже. Сможете ли вы найти закономерность или связь между всеми четными числами от одного до двухсот?
| Список четных чисел (1-200) | ||||
|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 |
| 12 | 14 | 16 | 18 | 20 |
| 22 | 24 | 26 | 28 | 30 |
| 32 | 34 | 36 | 38 | 40 |
| 42 | 44 | 46 | 48 | 50 |
| 52 | 54 | 56 | 58 | 60 |
| 62 | 64 | 66 | 68 | 70 |
| 72 | 74 | 76 | 78 | 80 |
| 82 | 84 | 86 | 88 | 90 |
| 92 | 94 | 96 | 98 | 100 |
| 102 | 104 | 106 | 108 | 110 |
| 112 | 114 | 116 | 118 | 120 |
| 122 | 124 | 126 | 128 | 130 |
| 132 | 134 | 136 | 138 | 140 |
| 142 | 144 | 146 | 148 | 150 |
| 152 | 154 | 156 | 158 | 160 |
| 162 | 164 | 166 | 168 | 170 |
| 172 | 174 | 176 | 178 | 180 |
| 182 | 184 | 186 | 188 | 190 |
| 192 | 194 | 196 | 198 | 200 |
Давайте выполним сложение различных комбинаций нечетных и четных чисел и посмотрим на результаты. Мы увидим, как числа изменяются от нечетных к четным, когда нечетные и четные числа складываются друг с другом. Записывайте полученные результаты.
Мы увидим, как числа изменяются от нечетных к четным, когда нечетные и четные числа складываются друг с другом. Записывайте полученные результаты.
| Номер 1 | Номер 2 | Число 1 + Число 2 = Сумма |
|---|---|---|
| 4 [четный] | 8 [четный] | 4 + 8 = 12 [четное] |
| 7 [Нечетный] | 3 [Нечетный] | 7 + 3 = 10 [четное] |
| 1 [Нечетный] | 6 [четный] | 1 + 6 = 7 [Нечетное] |
| 2 [Четный] | 9 [Нечетный] | 2 + 9 = 11 [Нечетное] |
Подведем итоги.
Последовательные четные числа
Последовательные числа могут быть перечислены как 2, 4, 6, 8, 10, 12, 14 и т. д. Последовательные числа — это те числа, которые непрерывно следуют друг за другом в порядке от наименьшего числа к наибольшему. Например, 1, 2, 3, 4 и т. д. — последовательные натуральные числа. Итак, когда нам нужно перечислить последовательные четные числа, мы можем перечислить все четные числа в порядке от наименьшего числа до наибольшего числа. Например, 2, 4, 6, 8, 10, 12, 14 и так далее — последовательные четные числа.
Например, 1, 2, 3, 4 и т. д. — последовательные натуральные числа. Итак, когда нам нужно перечислить последовательные четные числа, мы можем перечислить все четные числа в порядке от наименьшего числа до наибольшего числа. Например, 2, 4, 6, 8, 10, 12, 14 и так далее — последовательные четные числа.
Четные натуральные числа
Четные натуральные числа могут быть указаны как 66, 24, 8, 100 и т. д. Четные числа — это те числа, которые делятся на 2, а натуральные числа — это счетные числа, начинающиеся с 1, 2, 3, 4, 5 и так далее. Итак, если мы выберем все четные числа из списка натуральных чисел, они будут называться четными натуральными числами.
Свойства четных чисел
Давайте посмотрим на различные свойства чисел, такие как сложение, умножение и вычитание, и на то, как ведет себя четное число в таких случаях:
Свойство сложения четных чисел
- Сумма двух четных чисел является четным числом. Например, 14 + 8 = 22 .
- Сумма четного числа и нечетного числа является нечетным числом. Например, 8 + 9 = 17 900 51.
- Сумма двух нечетных чисел является четным числом. Например, 13 + 7 = 20 .
Свойство вычитания четных чисел
- Разница между двумя четными числами является четным числом. Например, 42 — 8 = 34
- Разница между четным числом и нечетным числом является нечетным числом. Например, 22 — 7 = 15 900 51.
- Разница между двумя нечетными числами является четным числом. Например, 35 — 15 = 20 .
Свойство умножения четных чисел
- Произведение двух четных чисел является четным числом. Например, 12 × 4 = 48 .
- Произведение четного числа на нечетное число является четным числом. Например, 8 × 5 = 40 .
Четные простые числа
Существует только одно четное простое число, равное 2. Все остальные четные числа имеют делители, отличные от 1 и самого числа. Например, делители 4 равны 1, 2 и 4. Следовательно, существует только одно четное простое число, равное 2.
☛Статьи по теме
- Составные номера
- Нечетные числа
- Реальные числа
- Натуральные числа
- Целые числа
- Иррациональные числа
- Подсчет чисел
- Кардинальные числа
- Четные и нечетные числа
- Сумма четных чисел
- Четные числа от 1 до 100
- Четные числа от 1 до 1000
- Рабочие листы с четными и нечетными числами
- Рациональные числа
Часто задаваемые вопросы о четных числах
Что такое четные числа в математике?
Числа, которые полностью делятся на 2, называются четными числами . Эти числа при делении на 2 оставляют 0 в остатке. Например, 2, 4, 6, 8 и так далее — четные числа.
Какие четные числа от 1 до 100?
Список четных чисел от 1 до 100 выглядит следующим образом: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36 , 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70,72, 74, 76, 78, 80, 82, 84, 86 , 88, 90, 92, 94, 96, 98, 100.
Какое самое маленькое четное число?
2 — наименьшее четное число. Это также единственное четное простое число.
Все ли четные числа натуральные?
Да, все четные числа, которые полностью делятся на 2, тоже натуральные числа. Например, 14, 18, 22, 24 и т. д.
Что такое формула четных чисел?
Так как каждое четное число кратно 2, его формула задается как n = 2k, где ‘k’ — целое число. Если мы заменим «k» на любое число, мы получим четное число. Например, если «k» заменить на 3 в 2k, (2 × 3) = 6. Мы получим 6, которое является четным числом.
Является ли 0 четным или нечетным числом?
Любое число, которое можно разделить на два, чтобы получить еще одно целое число, считается четным. Ноль также является одним из них, потому что когда 0 делится на 2, он дает остаток 0, что означает, что 0 делится на 2. Следовательно, 0 — четное число.
Почему 4 четное число?
Поскольку 4 кратно 2 и может быть разделено на две равные группы, это четное число. Другими словами, это четное число, потому что оно полностью делится на 2.
Другими словами, это четное число, потому что оно полностью делится на 2.
В чем разница между нечетными и четными числами?
Четное число — это число, кратное 2. Например, тогда как нечетное число не кратно 2.
Что такое HCF двух последовательных четных чисел?
HCF двух последовательных четных чисел равен 2. Наибольший общий делитель (HCF) любых двух чисел является их наибольшим общим делителем. Например, 16 и 18 — два последовательных четных числа, и их HCF равен 2.
Как найти четное число?
Чтобы найти четное число, мы должны разделить данное число на 2. Если оно полностью делится на 2 без остатка, то это четное число. Если данное число не делится полностью на 2, то это нечетное число.
Какие четные числа меньше 10?
Четные числа меньше 10 могут быть записаны как 2, 4, 6 и 8. Эти числа полностью делятся на 2 без остатка.
Что такое четные составные числа?
Четные числа — это те числа, которые полностью делятся на 2. Например, 2, 4, 6, 8, 10 и т. д. — четные числа. Составные числа — это те числа, у которых делители больше 1 и само число. Например, 4, 6, 9, 15 и так далее. Мы знаем, что все четные числа, кроме 2, имеют делители больше 1 и самого числа. Интересно, что 2 — единственное четное число, которое считается простым числом. Следовательно, кроме 2, все четные числа являются составными числами. Например, 4, 6, 8, 10, 12, 14 и так далее — четные составные числа. Это также показывает, что наименьшее четное составное число равно 4.
Например, 2, 4, 6, 8, 10 и т. д. — четные числа. Составные числа — это те числа, у которых делители больше 1 и само число. Например, 4, 6, 9, 15 и так далее. Мы знаем, что все четные числа, кроме 2, имеют делители больше 1 и самого числа. Интересно, что 2 — единственное четное число, которое считается простым числом. Следовательно, кроме 2, все четные числа являются составными числами. Например, 4, 6, 8, 10, 12, 14 и так далее — четные составные числа. Это также показывает, что наименьшее четное составное число равно 4.
Какое самое большое четырехзначное четное число?
Самое большое 4-значное четное число — 9998. Мы знаем, что самое большое 4-значное число — 9999, значит, первое четное число после этого — 9998.
Какова сумма двух последовательных четных чисел?
Сумма двух последовательных четных чисел всегда является четным числом. Например, 4 + 16 = 20 или 66 + 12 = 78 и так далее.
Номера стилей AP — объяснение написания
Как правило, числа от первого до девятого следует писать по буквам в стиле AP. Рассмотрим следующие примеры номеров AP Style:
Рассмотрим следующие примеры номеров AP Style:
- Чикаго Уайт Сокс заняли второе место.
- Ей оставалось шесть месяцев беременности.
Вы должны использовать числа от 10 и выше и всякий раз, когда они предшествуют единице измерения или относятся к возрасту людей, животных, событий или вещей. Также используйте цифры во всех табличных материалах, а также в статистических и последовательных формах.
Использование рисунков для Номера академических курсов :- Расчет 2
- Английский 101
- 1600 Pennsylvania Avenue
Укажите пронумерованные улицы девять и меньше. Например,
- Адрес: Шестая улица, 5, .
- Сходить в ресторан по адресу 1500 32-я улица
См. также Адреса стилей AP.
Возраст:- 6-летний мальчик
- 8-летний автомобиль
- 4-летний дом
Используйте дефисы для возрастов, выраженных в виде прилагательных перед существительным или вместо существительного. Например,
Например,
- Мальчик 5 лет
-а-
- Мальчику 5 лет
Также
- У мальчика 5 лет есть сестра 10 лет.
- Гонка предназначена для детей от 3 лет.
- Женщине около 30 лет.
- Ей около 30 лет.
-но-
- Тридцать с чем-то, чтобы начать предложение.
См. также AP Style Ages .
Обозначения самолетов, кораблей и космических аппаратов:- Бомбардировщик B-2
- Королева Елизавета 2
- QE2
- Аполлон 9
- Викинг 2
(Не используйте дефисы.)
Исключением для написания номеров самолетов, кораблей и т. д. является «Air Force One», самолет президента.
Используйте римские цифры, если они являются частью официального обозначения. Например,
- Титан I
- Титан II
См. также Названия самолетов в стиле AP, обозначения лодок, кораблей в стиле AP и обозначения космических аппаратов в стиле AP.
Используйте цифры для чисел от 10 и выше.
- 21 век
Расшифруйте цифры девять и ниже.
- пятый век
Обратите внимание, «столетие» пишется строчными буквами. Для имен собственных используйте код организации:
- 20th Century Fox
- Фонд двадцатого века
- Верховный суд постановил 5-4.
- Решение 5-4.
Слова «кому» не нужны, кроме как в кавычках. Например,
- «Суд вынес решение с 5 по 4».
- 8 февраля 2005 г.
- Класс 99
- 1940-е
Для террористических атак 11 сентября 2001 года 11 сентября приемлемо во всех ссылках.
Десятичные числа, проценты и дроби с числами больше 1:- Землетрясение магнитудой 7,2
- 3 ½ круга
- 3,7% годовых
- 4 процентных пункта
В большинстве текстовых материалов десятичная дробь не должна превышать двух знаков. Исключением является содержание алкоголя в крови, которое выражается тремя десятичными знаками. Например,
Исключением является содержание алкоголя в крови, которое выражается тремя десятичными знаками. Например,
- .056
Для сумм меньше 1 перед десятичной дробью ставится ноль. Например,
- Стоимость жизни выросла на 0,05 процента.
Если десятичное число равно 1 или меньше, тип измерения должен быть единственным. Например,
- 0,35 метра
- 0,55 куб. фута
- 0,75 км
Расшифруйте дроби меньше 1, используя дефисы между словами. Например,
- две трети
- три пятых
В цитатах используйте цифры для дробей. Например,
- «Он отставал на 3,5 секунды за 2 круга до финиша».
См. также Десятичные единицы стиля AP, Дроби стиля AP и Проценты стиля AP.
Размеры:- Его рост 5 футов 6 дюймов.
- Мужчина ростом 5 футов 6 дюймов здесь (подразумевается дюйм)
- 5-футовый мужчина
- Баскетбольная команда подписала 7-футовый.

- Автомобиль имеет длину 17 футов, ширину 6 футов и высоту 5 футов.
- Размер ковра 9 на 12 футов.
- Ковер размером 9 на 12.
- 9-дюймовый снегопад.
Исключение: два на четыре. Назовите существительное, которое относится к любой длине строительного пиломатериала толщиной 1,5 дюйма и шириной 3,5 дюйма.
См. также Размеры модели AP .
Расстояния:- Она прошла 5 миль.
- Он промазал в прыжке с 10 футов.
- 3 дерева
- 7-железный
- 3-гибридный (обратите внимание на дефис)
- Автомагистраль между штатами 5
- Шоссе США 1
- штат Маршрут 1A
- Маршрут 66 (Не сокращайте «Маршрут» и не используйте дефис.)
См. также Обозначения шоссе в стиле AP
Математическое использование:- Умножить на 4
- Разделить на 6
- Он добавил 2 и 2, но получил 5.

Используются как звания с именами, военными терминами и оружием.
- Старшина 2-го класса Алан Маркоу
- 1-й сержант. Дэвид Триплетт
- Винтовка М16
- 9-мм пистолет (обратите внимание на пробел)
- 6-й флот
В воинских званиях расшифровывайте цифру, когда она используется после имени или без имени. Например,
- Смит был младшим лейтенантом.
- Цель — стать первым сержантом.
См. также Боевые единицы стиля AP.
Миллионы, миллиарды, триллионы долларов:Используйте комбинацию цифр и слов.
- 1 миллион человек, а не один миллион
- 2 миллиарда долларов, а не два миллиарда
Также обратите внимание на отсутствие дефиса между цифрами и словами миллион, миллиард или триллион.
См. также AP Style Миллионы, миллиарды, триллионы долларов.
Денежные единицы:- 5 центов
- 5-долларовая банкнота
- 8 евро
- 4 фунта
См. также Центы стиля AP
также Центы стиля AP
- 9-1 лонгшот
- 3 части цемента на 1 часть воды
- шанс 1-4, но один шанс из трех
См. также раздел «Коэффициенты ставок в стиле AP», «Пропорции стиля AP» и «Коэффициенты стиля AP».
Ранг:- Он был моим выбором №1.
Обратите внимание на аббревиатуру «Номер». Не используйте эту аббревиатуру в названиях школ или адресах. Например,
- Государственная школа 19
Есть одно исключение: «Нет. Даунинг-стрит, 10», резиденция премьер-министра Великобритании.
Классы школы:Используйте цифры для 10 классов и старше.
- 10 класс
- 12 класс
Расшифровка для классов с первого по девятый.
- четвертый класс
- пятиклассник (обратите внимание на дефис)
- стр.
 1, стр. 20A
1, стр. 20A - Размеры 4 и 5 закончились.
- Землетрясение магнитудой 6
- Комнаты 3 и 4
- Глава 2
- Строка 1, но первая строка
- Акт 3, сцена 4, но третий акт, четвертая сцена
- Игра 1, но лучшая из семи
См. также номера актов стиля AP, главы стиля AP, землетрясения в стиле AP, номера строк стиля AP, номера страниц стиля AP, номера сцен стиля и AP.
Политические округа:- Район 9
- 9-й участок
- 3-й избирательный округ
- Пятый окружной апелляционный суд США
См. также Округа по выборам в Конгресс AP и Политические подразделения AP Style.
Рецепты:- 2 столовые ложки на 1 стакан молока
См. также Рецепты стилей AP
Скорости:- 7 миль в час
- скорость ветра от 5 до 10 миль в час
- скорость ветра от 7 до 9 узлов
- «Гиганты» победили «Львов» со счетом 14–7 (между командой и счетом нет запятой).

В игре «Гольф»
- 3 вверх, но преимущество в 3 очка, 3-2
- рекорд 6-1-2 (шесть побед, одно поражение, две ничьи)
- п. 3
- 5 гандикап
- 5 ниже номинала 67
- он был на 5 меньше номинала (или «на 5 меньше» с пониманием «номинальной»)
В описательной части укажите девять и меньше, за исключением ярдовых линий в футболе и статистических показателей индивидуальных и командных результатов.
- Мяч находился на 5-ярдовой линии.
- Седьмая лунка
- Трехочковый бросок, но трехочковый
В статистических характеристиках дефис в качестве модификатора.
- Он выполнил 8 из 12 передач.
- Сделал 5 из 6 (выстрелы понятны).
- Он прошел 5 из 12.
- У него был день 3 из 5.
- Он был 3 из 5.
- Он пошел 3 из 5 (отбивание мяча, бросок, пас и т. д. понятно).
Используйте цифры, кроме нуля.
- Было 8 градусов ниже нуля или минус 8.
- Температура упала с 38 до 8 за два часа.
См. также Температуры типа AP.
Время:Используйте цифры для времени суток, за исключением полудня и полуночи.
- 13:00
- 10:30
- 5 часов
- 8 часов
- 30 минут
- 20 секунд
- выигрышное время 2:17,3 (два часа, 17 минут, 3 секунды)
Укажите по буквам числа меньше 10, стоящие отдельно и в модификаторах.
- Буду через пять минут.
- Он забил за две секунды до конца.
- Восьмичасовой рабочий день.
- Двухминутное предупреждение.
См. также Время стиля AP, Последовательности времени стиля AP, и Полдень: утро или вечер?
Голосов:- Законопроект был отклонен 6 голосами против 4.
-а-
- Законопроект был отклонен с перевесом в два голоса.

В начале предложения:
- Пятьдесят лет — это долгий срок ожидания.
- В аварии участвовало от 20 до 30 автомобилей.
Единственным исключением являются годы.
- 1995 год был очень хорошим.
См. также Годы стиля AP.
При неопределенном и случайном использовании:
- Огромное спасибо!
- Он прошел четверть мили.
- По одному
- Тысяча клоунов
- Однажды мы узнаем
- Решение одиннадцатого часа
- Магазин долларов
В причудливых именах или именах собственных:
- Chicago Seven
- Великолепная четверка
- Большая тройка автопроизводителей
- Финал четырех
- Четыре вершины
На формальном языке, риторических цитатах и фигурах речи:
- «Fourscore и семь лет назад…»
- Двенадцать апостолов
- Десять заповедей
- Дай пять
- День первый
В дробях менее единицы, не используемых в качестве модификаторов:
- уменьшено на одну треть
- он сделал три четверти своих выстрелов.

Римские цифры могут использоваться для войн и для установления личной последовательности людей и животных.
- Первая мировая война
- Местная танцовщица II
- Король Георг V
- Папа Иоанн Павел II
Также для некоторых законодательных актов (Раздел IX). В противном случае используйте экономно. За исключением формальной ссылки, Суперкубки профессионального футбола должны обозначаться годом, а не римскими цифрами.
- Суперкубок 1969 года, а не Суперкубок III
Числа, используемые для обозначения порядка (первый, второй, 10-й, 25-й и т. д.), называются порядковыми номерами. Расшифруй с первого по девятый.
- четвертый класс
- первая база
- Первая поправка
- он был вторым в очереди
Используйте цифры, начинающиеся с 10-го числа.
Кардинальные числа: Числа, используемые для подсчета или показа количества (2, 40, 627 и т. д.), называются количественными числами. Следующие отдельные записи являются дополнительным руководством для количественных чисел.
д.), называются количественными числами. Следующие отдельные записи являются дополнительным руководством для количественных чисел.
- Поправки к Конституции в стиле AP
- Канал стиля точки доступа
- Названия судов в стиле AP
- Десятилетия стиля AP
- Результаты выборов в стиле AP
- Автопарк в стиле AP
- Формула стиля AP
- Широта и долгота стиля точки доступа
- Миля стиля AP
- AP Parallels
- Пропорции стиля AP
- Серийные номера моделей AP
- Телефонные номера в стиле точки доступа
- Грузы типа AP
Некоторые другие примеры пунктуации и использования для номеров стилей AP,
- 3 унции
- 4 фута в длину
- 4-футовое ограждение
- «Речь сенатора длилась 18 1/2 минут», — сказала она.
- DC-10, но 747B
- 1980-е, но 80-е
- Палата представителей проголосовала 230-205 (менее 1000 голосов).

- Джимми Картер опередил Джеральда Форда с 40 827 292 до 39 146 157 (более 1000 голосов).
- Картер опередил Форда на 10 голосов против 2 голосов в Little Junction (во избежание путаницы с соотношением)
- Выбор № 3, но государственная школа 3
- повышение заработной платы на 12-15 процентов
-или-
- повышение заработной платы от 12 до 15 процентов
-но-
- от 12 миллионов долларов до 14 миллионов долларов
- соотношение 2 к 1, соотношение 2 к 1
- 1 из 4 избирателей
- семь домов на расстоянии 7 миль друг от друга
- Он прошел 4 мили.
- минус 10, ноль, 60 градусов
Для использования, не охваченного этими списками, укажите целые числа ниже 10 и используйте цифры от 10 и выше.
- У них было три сына и две дочери.
- У них был парк из 10 универсалов и двух автобусов.
Применяйте стандартные рекомендации:
- У них было 11 собак, пять кошек и 90 песчанок.

- У них было пять четырехкомнатных домов, 10 трехкомнатных и 12 десятикомнатных.
Содержание
- 1 Использовать рисунки для
- 2 Номера академических курсов:
- 3 Адреса:
- 4 Эпохи:
- 5 Обозначения самолетов, кораблей и космических аппаратов:
- 6 Столетий:
- 7 Судебные решения:
- 8 Даты, Годы, Десятилетия:
- , Дроби
- , Дроби Числа больше, чем 1:
- 10 измерений:
- 11 Расстояния:
- 12 Гольф -клубы:
- 13 Наслаждающихся направлений:
- 14 Математические использование:
- 15 военные ряды:
- 16 миллионов, билл.0051
- 17 Монетарные единицы:
- 18 шансов, пропорции и коэффициенты:
- 19 Ранг:
- 20 Школьные классы:
- 21 Последовательные обозначения:
- 22 Политические районы:
- 23 Рецепты:
- 22.
- 25 Спортивных баллов, турнирных баллов и стандартов:
- 26 Температура:
- 27 раз:
- 28 голосов:
- 29 ЗАКЛЮЧЕНИЯ:
- 30 Римские цифры:
- 31 Орден:
- 32.


 Что можете сказать? (стоят не по порядку)
Что можете сказать? (стоят не по порядку)

 Начинают писать цифру
немного ниже верхнего правого угла клетки. В
правом верхнем углу клетки делают закругление,
пишут большой левый полуовал, касаются середины
нижней стороны клетки, ведут линию вверх,
закругляя ее влево немного выше середины клетки.
Начинают писать цифру
немного ниже верхнего правого угла клетки. В
правом верхнем углу клетки делают закругление,
пишут большой левый полуовал, касаются середины
нижней стороны клетки, ведут линию вверх,
закругляя ее влево немного выше середины клетки.

 1 ученик у доски.
1 ученик у доски.

 3 это «2 и 3 десятых»
3 это «2 и 3 десятых»
 Первые несколько цифр выглядят так: 2,71828182845
Первые несколько цифр выглядят так: 2,71828182845 Расстояние от 5 до 0 равно 5 единицам.
Расстояние от 5 до 0 равно 5 единицам. ”
” 
 Но когда я спросил, где находится дверь по отношению к моему положению, вы дали мне направление, а также число, и тогда имело значение, в какую сторону я смотрю. Сегодня мы обсудим абсолютное значение. Абсолютное значение говорит вам, насколько далеко число от нуля. Но он не говорит вам, куда идти! Это не говорит вам, что направление номер от нуля.
Но когда я спросил, где находится дверь по отношению к моему положению, вы дали мне направление, а также число, и тогда имело значение, в какую сторону я смотрю. Сегодня мы обсудим абсолютное значение. Абсолютное значение говорит вам, насколько далеко число от нуля. Но он не говорит вам, куда идти! Это не говорит вам, что направление номер от нуля.  Например, значение температуры имеет только «направление», потому что градусы по Фаренгейту включают отрицательные и положительные значения, поэтому для ясности необходим знак. Направления к озеру Эри потребуют множества чисел со знаком: куда ехать на восток (положительный) против запада (отрицательный) и куда ехать на север (положительный) по сравнению с югом (отрицательный).
Например, значение температуры имеет только «направление», потому что градусы по Фаренгейту включают отрицательные и положительные значения, поэтому для ясности необходим знак. Направления к озеру Эри потребуют множества чисел со знаком: куда ехать на восток (положительный) против запада (отрицательный) и куда ехать на север (положительный) по сравнению с югом (отрицательный). Поместите цветные точки на -6 и +3 на числовой строке.
Поместите цветные точки на -6 и +3 на числовой строке. (6.NS.C.7.C)
(6.NS.C.7.C)

 1, стр. 20A
1, стр. 20A