другую дробь, целое натуральное число

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Вычитание десятичных дробей: правила, примеры

В данной публикации мы рассмотрим, каким образом из десятичной дроби можно вычесть другую дробь (десятичную и обыкновенную) или целое натуральное число (и наоборот). Также разберем примеры для лучшего понимания представленного материала.

• Правило вычитания десятичных дробей
• Примеры

Правило вычитания десятичных дробей

Разность десятичных дробей находится путем их вычитания столбиком. Алгоритм приведен ниже:

1. Располагаем дроби так, чтобы их запятые были строго друг под другом. Таким образом, друг под другом окажутся и одноименные разряды: десятые под десятыми, сотые под сотыми, тысячные под тысячными и т. д.

Примечание: Если число знаков после запятой у дробей разное, в конце дроби с меньшим количеством цифр в дробной части добавляем нули, чтобы уравнять ее по длине с другой. Согласно основному свойству десятичной дроби, это никак не повлияет на ее величину.

Примеры неправильной записи разности:

Примеры правильной записи разности:

2. Не обращая внимания на запятые вычитаем из одной дроби другую (т.е. условно принимаем их за целые числа).

3. В полученном результате добавляем запятую в том же месте, где расположены запятые дробей выше.

Разность десятичной дроби и целого натурального числа

Если требуется найти разность десятичной дроби и целого натурального числа, в конце последнего ставим запятую, после которой дописываем столько нулей, сколько знаков содержится после запятой в десятичной дроби. Далее выполняем требуемое действие, т.е. вычитание.

Разность десятичной и обыкновенной дробей

Чтобы найти разность десятичной и простой дробей, последнюю переводим в десятичную.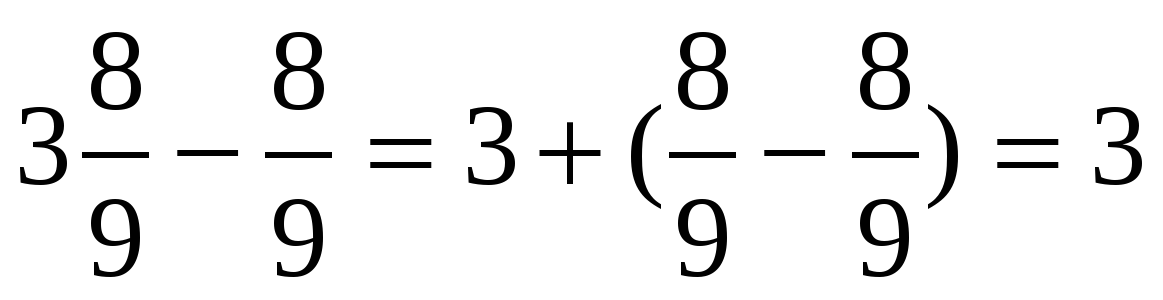 Далее выполняем вычитание.

Альтернативный вариант – наоборот, десятичную дробь преобразовать в обыкновенную. Здесь мы уже будем вычитать простые дроби.

Примеры

Вычислим разности десятичных дробей, которые рассмотрели выше:

А теперь давайте посмотрим примеры вычитания из десятичной дроби целого натурального числа и наоборот.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Сложение и вычитание смешанных чисел 6 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

Тема урока: «Сложение и вычитание смешанных чисел».

 

Но дело в том, что это не новые числа. Смешанное число  – это два и еще . Просто сумма двух чисел.

Мы умеем уже складывать целые числа, дробные числа. А сложение смешанных чисел – это то же самое, это сложение целых чисел и сложение обыкновенных дробей. Надо использовать те знания, которые у нас уже есть.

Остается рассмотреть, почему они так пишутся и так называются, и убедиться на примерах, что никаких новых знаний нам не нужно, никаких новых правил учить не понадобится.

 

Пример 1

 

 

Сложить два смешанных числа: , .

 

Напишем у каждого знак «+».

Теперь мы лучше видим все 4 слагаемых. Сложим теперь так, как нам удобнее.

Целые числа 7 и 2 сложить легко.

Обыкновенные дроби мы тоже умеем складывать. Приведем их к общему знаменателю.

Ответ: .

 

Пример 2

 

 

 

Поставим знаки «+»:

Сложим отдельно целые числа и отдельно обыкновенные дроби.

Дробь  уже можно записать как смешанную, убрав знак плюс, но обыкновенную дробь можно записать и проще. Выделим целую часть.

К целой части добавляется еще единица.

Ответ: 
.

 

Пример 3

 

 

 

Поставим знаки «+»:

Можно сложить отдельно целые числа и дроби, но у дроби  можно выделить целую часть, станет проще.

Ответ: .

 

Пример 4

 

 

 

 

Вычитание смешанных дробей

 

 

А как вычитать? Все опять просто.

 

Как можно иначе записать смешанную дробь с минусом впереди?

Минус относится ко всей дроби. Можно поставить скобки и минус перед ними или раскрыть скобки. Минус будет у каждого слагаемого.

 

Пример 5

 

 

 

Здесь полезный навык – это уметь отнять от единицы или другого целого числа правильную дробь.

 

Вычитание правильной дроби из целого числа

 

 

1) 

 

2) 

3) 

Сложение двух отрицательных смешанных дробей не представляет проблемы.

Пример 6

Ответ: .

Необязательно расписывать все подробно.

Если вы чувствуете себя уверенно, то многое можно делать в уме.

 

Задание

 

 

Самостоятельно выполните несколько заданий, а потом проверьте.

 

Проверяем.

 

---

Смешанные числа

Дроби нужны для записи нецелых количеств: треть пути, четверть часа, половина яблока. Это все примеры, когда количество меньше одного. Но нецелое количество может быть и больше одного: полтора литра молока; два с половиной часа; три с половиной километра. Как удобнее всего записывать эти количества?

Если мы делим 7 яблок на троих, то это можно сделать двумя способами:

1) Каждое яблоко делим на три части и раздаем эти части всем участникам. Каждый такой кусочек – это  яблока.

В итоге каждый получит 7 таких кусочков: .

2) Проще каждому раздать по два яблока.

А оставшиеся разделить на три части и раздать. Все-таки легче резать одно яблоко, чем семь.

В итоге каждый получит по два целых и еще по одной трети: .

Это разные записи одного и того же количества.

Такие количества, целое плюс дробное, встречаются часто.

Чтобы упростить запись, договорились, что можно не писать знак «+»:

.

В последней записи смешались целое и дробное число. Поэтому такую запись назвали смешанным числом или смешанной дробью.

И неправильная дробь, и смешанная обозначают одно и то же количество.

Какая удобнее? Это зависит от ситуации.

По смешанной легче представить количество.

По левой записи мы понимаем только, что это число больше единицы. А вот по правой – что число почти равно трем, чуть-чуть больше трех, на .

Складывать и вычитать дроби удобнее в виде смешанного числа, а умножать и делить – в виде обыкновенной дроби.

Десятичные дроби очень близки к смешанным числам – это почти одно и то же. Просто разная запись, но смысл один. Сначала записывается целая часть, потом дробная.

Если у десятичной дроби целая часть равна нулю, то она легко записывается обыкновенной правильной дробью, просто ноль целых в смешанной дроби не пишем.

Итак, между целой и дробной частями смешанной дроби пропущен знак «+». Если это помнить, то не нужно никаких дополнительных правил.

Чтобы превратить смешанную дробь в обыкновенную, нужно сложить целое число и дробь.

Чтобы сложить целое число с дробью, представим 4 как дробь со знаменателем единица, приведем ее к знаменателю 7, домножив числитель и знаменатель на 7.

Или, в другую сторону, вынесем целую часть из неправильной дроби.

Нам давно знаком этот способ. Деление столбиком с остатком – это и есть вынесение целой части.

Вернемся к 7 яблокам, которые мы делим на троих.

Разделим столбиком 7 на 3 с остатком.

Ответ: 2 и 1 в остатке. То есть по два целых яблока уже досталось всем, и одно осталось. Его нужно делить на три части.

Конечно, в таком простом случаем мы обойдемся без деления столбиком.

Число 7 больше трех и не делится на три. Его можно разбить на две части – часть, которая делится на 3 – 6, и остаток, который меньше трех, – 1. 6 яблок делится на 3, это два, и еще одно делим на три. Это .

В более сложных случаях все-таки нужно воспользоваться делением в столбик.

Чтобы вынести целую часть, разделим числитель на знаменатель в столбик.

Получили 27 и 5 в остатке. То есть, мы разбили число 221 на две части: первая, которая делится на 8 и дает в результате 27 (саму эту часть мы не видели, но нетрудно догадаться по остатку, что она равна 216) и остаток, меньший 8, – это 5:

 

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. – М.: Мнемозина, 2012.

2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия, 2006.

3. Депман И. Я., Виленкин Н.Я. За страницами учебника математики. – Просвещение, 1989. 

4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – ЗШ МИФИ, 2011. 

5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – ЗШ МИФИ, 2011.

6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. – Просвещение, 1989.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт «Школьный помощник» (Источник)

2. Интернет-сайт «Гипермаркет знаний» (Источник)

3. Интернет-сайт фестиваля педагогических идей «Открытый урок» (Источник)

 

Домашнее задание

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. – М.: Мнемозина, 2012. № 376.

2. 

3. 

 

Как вычитать смешанные числа

Независимо от того, имеют ли смешанные числа одинаковые знаменатели или разные знаменатели, их вычитание очень похоже на вычитание целых чисел: вы складываете их одно над другим, рисуете линию и вычитаете. По этой причине некоторые учащиеся чувствуют себя более комфортно при вычитании смешанных чисел, чем при вычитании дробей.

1. Найдите разность дробных частей.

2. Найдите разность двух целых частей числа.

Однако по пути вы можете столкнуться с еще парочкой поворотов. Следующие инструкции помогут вам в решении любой задачи на вычитание смешанных чисел.

Вычитание смешанных чисел с одинаковыми знаменателями

Вычитание намного проще, когда знаменатели совпадают. Например, предположим, что вы хотите вычесть 7 3/5 – 3 1/5. Вот как проблема выглядит в виде столбца:

В этой задаче вы вычитаете 3/5 – 1/5 = 2/5. Затем вы вычитаете 7 – 3 = 4. Не так уж и страшно, согласитесь?

Одна сложность возникает, когда вы пытаетесь вычесть большую дробную часть из меньшей. Предположим, вы хотите найти 11 1/6 – 2 5/6. На этот раз, если вы попытаетесь вычесть дроби, вы получите

.

Очевидно, вы не хотите, чтобы в вашем ответе оказалось отрицательное число. Вы можете решить эту проблему, позаимствовав из столбца слева. Эта идея очень похожа на заимствование, которое вы используете при обычном вычитании, с одним ключевым отличием.

При заимствовании при вычитании смешанных чисел,

1. Заимствуйте 1 из целочисленной части и прибавьте ее к дробной части, превратив дробь в смешанное число.

   Чтобы найти 11 1/6 – 2 5/6, одолжите 1 из 11 и прибавьте к 1/6, получив смешанное число 1 1/6:

2. Замените это новое смешанное число неправильной дробью.

   Вот что получится, если заменить 1 1/6 на неправильную дробь:

   Результат равен 10 7/6. Этот ответ представляет собой странную смесь смешанного числа и неправильной дроби, но это то, что вам нужно для выполнения задания.

3. Используйте результат при вычитании.

   В этом случае нужно уменьшить дробную часть ответа:

Вычитание смешанных чисел с разными знаменателями

Вычитание смешанных чисел при разных знаменателях — едва ли не самое сложное, что вам когда-либо приходилось делать в предварительной алгебре.

Предположим, вы хотите вычесть 15 4/11 — 12 3/7. Поскольку знаменатели разные, вычитание дробей усложняется. Но у вас есть еще один вопрос для размышления: в этой задаче вам нужно брать взаймы? Если 4/11 больше, чем 3/7, вам не нужно брать взаймы. Но если 4/11 меньше 3/7, то да.

Поскольку 28 меньше 33, 4/11 меньше 3/7, так что вам придется брать взаймы. Сначала избавьтесь от займа:

Теперь проблема выглядит так:

Первый шаг, вычитание дробей, будет самым трудоемким, так что вы можете позаботиться об этом на стороне:

Хорошая новость заключается в том, что эту дробь нельзя уменьшить. (Они не могут быть уменьшены, потому что 72 и 77 не имеют общих делителей: 72 = 2 2 2 3 3, а 77 = 7 11.) Таким образом, трудная часть задачи решена, а остальное следует за ней легко:

Эта задача не уступает по сложности задаче на вычитание смешанных чисел. Посмотрите на это шаг за шагом. Или, что еще лучше, скопируйте задачу, а затем попытайтесь выполнить шаги самостоятельно. Если вы застряли, это нормально. Лучше сейчас, чем на экзамене!

Об этой статье

Эту статью можно найти в категории:

• Предварительная алгебра,

Калькулятор смешанных чисел

Этот калькулятор выполняет основные и расширенные операции со смешанными числами, дробями, целыми и десятичными дробями. Смешанные числа также называют смешанными дробями. Смешанное число — это целое число и правильная дробь, то есть одна и три четверти. Калькулятор оценивает выражение или решает уравнение с пошаговой информацией о ходе вычислений. Решите задачи с двумя и более дробями смешанных чисел в одном выражении.

Что такое смешанное число?

Смешанное число — это целое число и дробь acb, значение которого равно сумме этого целого числа и дроби. Например, мы пишем две и четыре пятых как 254​. Его значение равно 254=2+54=510+54=514. Смешанное число является исключением: отсутствующий операнд между целым числом и дробью является не умножением, а сложением: 254​​=2⋅ 54​. Отрицательное смешанное число — знак минус также применяется к дробному числу −254​=−(254​)=−(2+54​)=−514​. Смешанное число иногда называют смешанной дробью. Обычно смешанное число содержит натуральное число и правильную дробь, а его значением является неправильная дробь, то есть такая, у которой числитель больше знаменателя.

Как представить смешанное число?

Мы можем представить смешанные числа на примере тортов. У нас есть три лепешки, и мы разделили каждую на пять частей. Таким образом, мы получили 3 * 5 = 15 кусочков торта. Один кусок, когда мы ели, осталось 14 кусков, а это 254 торта. Когда мы съедаем два куска, остается 253 торта.

Примеры:

• сумма двух смешанных чисел: 1 3/4 + 2 3/8
• сложение трех смешанных чисел: 1 3/8 + 6 11/13 + 5 7/8
• сложение двух смешанных чисел числа: 2 1/2 + 4 2/3
• вычитание двух смешанных чисел: 7 1/2 — 5 3/4
• умножение смешанных чисел: 3 3/4 * 2 2/5
• сравнение смешанных чисел: 3 1/4 2 1/3
• замена неправильного дробь в смешанном числе: 9/4
• Что такое 3/4 как смешанное число: 3/4
• вычитание смешанного числа и дроби: 1 3/5 — 5/6
• суммирование смешанного числа и неправильной дроби: 1 3/5 + 11/5

Смешанное число в текстовых задачах:

• Какое 5
  Какое смешанное число эквивалентно 2,68? A:2 и 6 восьмых B:2 и 68 десятых C:2 и 6 больше 68
• Смешанные с неправильными
  Замените данные смешанные числа на неправильную дробь: пять и четыре на девять (5 4/9)
• Вычисление Петра
  Петр написал следующее: 7 1/4 — 3 3/4 = 4 2/4 = 4 1/2.