урок с примерами, карточками и видео

Простые арифметические действия — это основа дальнейшего обучения детей точным наукам. Математика сопровождает людей повсюду на протяжении всей жизни, а потому важно понимать её с самых азов. Вычитание десятичных дробей в столбик вызывает у многих школьников трудности, тогда как с действиями с простыми числами они отлично справляются. На самом деле в этом нет ничего сложного — главное уяснить алгоритм решения.

Как вычитать десятичные дроби в столбик

При записи десятичных дробей нижние и верхние разряды чисел должны соотвествовать друг другу: целые под целыми, десятые под десятыми, сотые под сотыми, тысячные под тысячными

Действия с десятичными дробями производятся так же, как и с натуральными. Основные правила, которые важно знать при решении примеров на вычитание в столбик:

1. Сначала следует уравнять количество знаков после запятой. Это делается путём добавления нулей. Например, необходимо вычесть из дроби 5,5 число 2,03. Как видно из примера, количество знаков после запятой разное. Чтобы сделать их одинаковым, в дробь 5,5 (пять целых пять десятых) в конце добавляем ноль и получаем 5,50 (пять целых пятьдесят сотых). Это правило следует из правил вычитания простых дробей. Как известно, дроби с разными знаменателями нельзя складывать или вычитать. Прежде их необходимо привести в общему знаменателю. В приведённом примере десятичные дроби можно записать в виде 5 5/10 и 2 3/100. Из целых чисел нужно вычитать целые, из дробных — дробные. В примере знаменатели у дробей разные, наименьший общий знаменатель равен 100. Следовательно, числитель и знаменатель дроби 5/10 следует умножить на 10, в итоге получим 50/100, что в переводе в десятичную дробь будет выглядеть как 5,50.
2. Числа записать таким образом, чтобы запятая нижнего находилась в том же месте, что и у верхнего. Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними.
3. Выполнить действие, не обращая внимания на запятую. Вычитают десятичные дроби справа налево, то есть начиная с самой правой цифры после запятой.
4. Поставить в ответе запятую под запятой. Так мы сможем правильно отразить результат вычисления.

Вычитать нужно по цифрам разрядов: целые из целых, сотые из сотых и так далее

Вычитание всегда можно проверить сложением.

Карточки для уроков

Чтобы было проще изучить алгоритм действий, можно распечатать для детей специальные карточки-памятки, которые помогут быстрее освоить новый материал.

Фотогалерея: варианты карточек для занятий

Видео: как вычитать десятичные дроби столбиком

Освоив это простое действие, дети смогут в дальнейшем лучше учиться, ведь примеры с десятичными дробями решают не только на математике, но и на физике, химии, астрономии. Главное — понять алгоритм.

• Автор: Alla82
• Распечатать

Оцените статью:

(2 голоса, среднее: 5 из 5)

Поделитесь с друзьями!

Большой сборник презентаций в помощь школьнику.

Вычитание дробей с разными знаменателями. Сложение и вычитание обыкновенных дробей

Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить абстрактное мышление и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.

Как вычесть дроби, знаменатели которых одинаковые

Дроби – это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:

• Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m – b/m = (k-b)/m.

Примеры вычитания дробей, знаменатели которых одинаковы

Рассмотрим, как это выглядит на примере:

7/19 — 3/19 = (7 — 3)/19 = 4/19.

От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби – «19».

На картинке ниже приведено еще несколько подобных примеров.

Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:

29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.

От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей – «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».

Сложение дробей, имеющих одинаковый знаменатель

Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.

• Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.

Рассмотрим, как это выглядит на примере:

1/4 + 2/4 = 3/4.

К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».

Дроби с различными знаменателями и их вычитание

Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.

• Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.

О том, как это сделать, мы поговорим подробнее.

Свойство дроби

Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.

Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:

2/3 = 4/6 = 6/9 = 8/12…

Как привести несколько дробей к одному и тому же знаменателю

Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.

Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.

Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.

Аналогично производим действия с оставшимися дробями.

• 2/3 – в знаменателе не хватает одной тройки и одной двойки:
  2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18.
• 7/9 или 7/(3 х 3) – в знаменателе не хватает двойки:
  7/9 = (7 х 2)/(9 х 2) = 14/18.
• 5/6 или 5/(2 х 3) – в знаменателе не хватает тройки:
  5/6 = (5 х 3)/(6 х 3) = 15/18.

Все вместе это выглядит так:

Как вычесть и сложить дроби, имеющие различные знаменатели

Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.

Рассмотрим это на примере: 4/18 – 3/15.

Находим кратное чисел 18 и 15:

• Число 18 состоит из 3 х 2 х 3.
• Число 15 состоит из 5 х 3.
• Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.

После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.

• 90 поделить на 15. Полученное число «6» будет множителем для 3/15.
• 90 поделить на 18. Полученное число «5» будет множителем для 4/18.

Следующий этап нашего решения – приведение каждой дроби к знаменателю «90».

Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:

(4 х 5)/(18 х 5) – (3 х 6)/(15 х 6) = 20/90 – 18/90 = 2/90 = 1/45.

Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.

Аналогично производится и сложение дробей, имеющих различные знаменатели.

Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:

• Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, – числитель неправильной дроби. Знаменатель же остается неизменным.
• Если дроби имеют различные знаменатели, следует привести их к одинаковому.
• Произвести сложение или вычитание с одинаковыми знаменателями.
• При получении неправильной дроби выделить целую часть.

Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.

Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.

Вычитание дробей из целого числа

Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от натурального числа.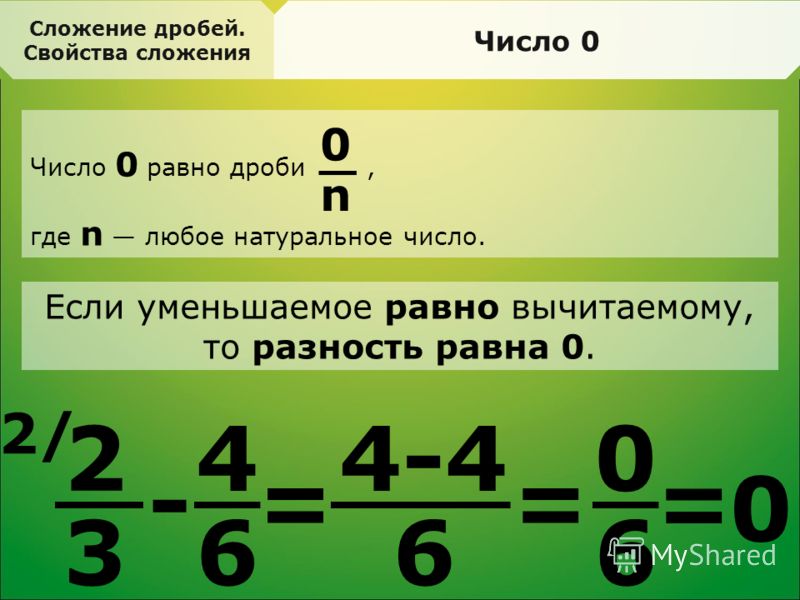 На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:

7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.

Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.

SuperKids Math Review — Вычитание дробей

математические задания > > дроби > > вычитание дробей

Как вычитать дроби

• Вычитание дробей с ОБЩИМИ знаменателями
• Создание общих знаменателей
• Вычитание дробей с РАЗНЫМИ знаменателями

Помните . . . Вот трюк с памятью: Знаменатель — это низ, или Down число в дроби — и D знаменатель, и D собственные начинаются с буквы D .

Вычитание дробей с ОБЩИМИ знаменателями
Вычитание дробей с ОБЩИМ знаменателем очень просто. Просто вычтите верхние числа (числители) и поместите полученный ответ в начало дроби, используя существующий знаменатель для нижнего числа. Затем сократите дробь, если это возможно

Пример 1: Вычитание простой дроби

Сокращение невозможно, поэтому мы нашли ответ!

---

Пример 2: Уменьшение дроби ответ

Затем уменьшить:

=

---

Пример 3: Вычитание со смешанным числом

—

=

?

Сначала преобразуйте смешанное число в неправильную дробь:

=

Затем вычтите:

Затем сократите дробь:

=

---

Создание общих знаменателей Как мы это делаем? Простой! Помните, что если вы умножаете верх и низ дроби на одно и то же число, это не влияет на значение дроби. Пример 1: Если у нас есть дробь 2/3, мы можем умножить верх и низ на 2, не меняя их значения: (2/2) x (2/3) = 4/6. Тогда, если мы уменьшим 4/6, мы все равно получим исходное число, 2/3. Пример 2: Если у нас есть дробь 2/3, мы могли бы умножить верх и низ на 5, не изменяя их значения: (5/5) х (2/3) = 10/15. Тогда, если мы уменьшим 10/15, мы все равно получим исходное число, 2/3. Почему это работает? Потому что любое число, деленное само на себя, равно единице. 2/2 = 1, 5/5 = 1 и т. д. И любое число, умноженное на 1, равно самому себе! Дело в том, что вы не измените значение дроби, если умножите ее верхнее и нижнее число на одно и то же число!

Вычитание дробей с РАЗНЫМИ знаменателями

Вычитать можно только дроби с одинаковым знаменателем, поэтому сначала нужно изменить одну или обе дроби, чтобы получить две дроби с общим знаменателем. Самый простой способ сделать это — просто выбрать знаменатель противоположной дроби, чтобы использовать его в качестве верхнего и нижнего множителя.

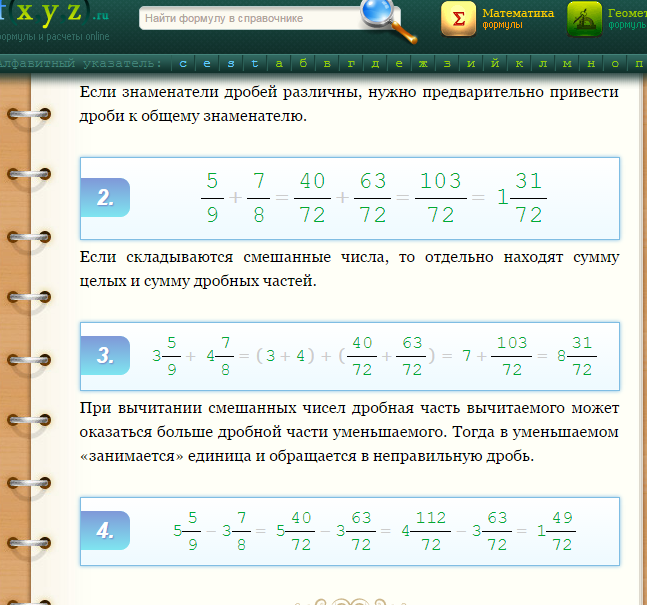
Пример 1: Допустим, у вас есть дроби 2/3 и 1/4.
Выберите знаменатель второй дроби (4) и умножьте верхнюю и нижнюю часть первой дроби (2/3) на это число:

Выберите знаменатель первой дроби (3) и умножьте верх и низ второй дроби (1/4) на это число:

Эти две дроби (8/12 и 3/12) имеют общие знаменатели — число 12 в нижней части дроби.

Вычтите, используя эти две новые дроби:

---

Пример 2: Допустим, у вас есть дроби 3/5 и 2/7.
Выберите знаменатель второй дроби (7) и умножьте верхнюю и нижнюю части первой дроби (3/5) на это число

Выберите знаменатель первой дроби (5) и умножьте верх и низ второй дроби (2/7) на это число.

Эти две дроби (21/35 и 10/35) имеют общие знаменатели — число 35 в нижней части дроби.

Теперь мы можем вычитать, потому что две новые дроби имеют общий знаменатель:

---

---

Понятно? Большой! Тогда перейдите к Создателю математических рабочих листов SuperKids для основных дробей и попробуйте!

[Вопросы?]

Сделайте это домашней страницей вашего браузера!

---

Вопросы или комментарии относительно этого сайта? webmaster@superkids. com
Copyright © 1998-2022 ООО «Обмен знаниями». Все права защищены. Политика конфиденциальности

Дроби Часть 6: Сложение и вычитание дробей

C. Elkins, OK Math and Reading Lady

Начиная с 3-го класса учащиеся начинают понимать, как складывать и вычитать дроби, составляя и разлагая простые дроби с использованием конкретных и визуальных моделей . Составление: 1/4 и 3/4 объединяются, чтобы получить 4/4 (целое). Разложение: 8/8 состоит из 2/8 и 6/8. В четвертом классе учащиеся начинают складывать и вычитать дроби с одинаковыми знаменателями, но все же должны использовать модели, рисунки и числовые линии для иллюстрации и упрощения. В пятом классе учащиеся должны складывать и вычитать дроби всех типов (правильные, неправильные, с разными знаменателями и т. д.).

Имея прочную основу для составления и разложения, разбиения, сравнения, называния эквивалентных дробей и понимания отношений между определенными дробями (такими как половинки / четверти / восьмые / шестнадцатые; и трети / девятые / шестые / двенадцатые; или пятые / десятые ), то учащиеся более подготовлены к выполнению действий с дробями.

Вот отличный ресурс Донны Баучер из Math Coach’s Corner: задание «Составление и разложение дробей» на TPT (6 долларов США)

Оценка: Это важная часть операций с дробями. Ожидаете ли вы, что ваш ответ будет меньше 1/2, больше 1/2, больше 1? Откуда вы знаете? Если бы я добавлял 8/9 + 11/12, мой ответ должен был быть примерно _____? Оно должно быть немного меньше 2, потому что обе эти дроби почти равны 1.

Если я складываю 4/6 и 6/8, мой ответ должен быть больше 1, потому что каждая из этих дробей больше 1/2.

Различные стратегии:  Существует множество «хитростей» или способов быстрого сложения, вычитания или умножения дробей. Я считаю, что эти ярлыки полезны только после ученик хорошо понимает, почему и как найти общий знаменатель и эквивалентную дробь. Эти ярлыки не помогают построить концептуальное понимание дробей. Я сосредоточусь на способах понять

почему с помощью визуальных и графических моделей. Получите БЕСПЛАТНУЮ копию следующих руководств, нажав ЗДЕСЬ.

Сложение или вычитание дробей с одинаковыми знаменателями: Чтобы объяснить учащимся, что 1/4 + 1/4 НЕ равно 2/8, покажите с помощью предметов и рисунков. Разделите целое, чтобы смоделировать это. Помните о лучшей последовательности обучения: конкретное и наглядное, а затем абстрактное.

Сложение дробей с разными знаменателями:  Посмотрите мой предыдущий пост «Дроби, часть 2» о рисовании дробных частей, особенно с использованием полос или прямоугольников. Это базовый навык для составления эквивалентных дробей (который необходим для сложения дробей с разными знаменателями). Хотя может быть утомительно рисовать картинки для каждой задачи на сложение или вычитание, я рекомендую это как способ представить концепцию, чтобы учащиеся снова увидели, что умножение дроби на представитель 1 (2/2, 3/3 и т. название эквивалентной дроби (чтобы было легче складывать или вычитать) не меняет заштрихованную часть, а просто делит заштрихованную часть на более мелкие части.

Помните, что деление целого числа на 1 не меняет ответ — то же самое относится и к дробям.

Упрощение дробей: Я упоминал об этом в части 5, но здесь это снова. Чем больше учащиеся практиковали деление фигур, тем больше они должны начать усваивать взаимосвязь между некоторыми обычными дробями (чтобы нарисовать восьмые, вы можете начать с половин или четвертых; чтобы нарисовать шестые или двенадцатые, вы можете начать с третей и т. д.). Используйте обратный процесс удаления линий из секционированных фигур для упрощения.

Использование Prime Factorization для поиска LCD/LCM и GCF: На Learn Zillion есть действительно хорошее видео, иллюстрирующее эти шаги ниже. Нажмите здесь: Узнайте Zillion видео  

 

Подробнее о сложении и вычитании смешанных дробей в следующем посте.