Сложение и вычитание смешанных чисел (Слупко М.В.) 5 класс онлайн-подготовка на Ростелеком Лицей
Введение
Сумму целого числа и обыкновенной правильной дроби для краткости часто записывают без знака плюс и называют смешанным числом, имея в виду, что в этой записи есть и целая и дробная части: .
Если дробь неправильная (числитель больше и равен знаменателю), то сначала выделяют целую часть, а потом записывают в виде смешанного числа: .
Сложение и вычитание смешанных чисел
Тогда вопрос сложения или вычитания смешанных чисел сводится к сложению или вычитанию целых чисел и обыкновенных дробей:
Но все это мы уже умеем делать. Поэтому никаких новых правил нам изучать не нужно.
Примеры со сложением
1) Сумма целого числа и дроби: .
Здесь мы просто пользуемся определением смешанного числа. Сумму записываем кратко, без знака плюс: .
2) Сумма целого и смешанного чисел: .
Распишем подробнее смешанное число. Сложим целые слагаемые, снова запишем сумму кратко в виде смешанного числа: .
Для краткости записи можно не расписывать смешанное число как сумму, а сразу складывать целые числа: .
3) Сумма смешанного числа и дроби: .
Распишем смешанное число как сумму. Сложим дроби, запишем сумму кратко как смешанное число: .
Необязательно расписывать смешанное число. Сразу сложим дроби: .
4) Сумма двух смешанных чисел.
Распишем каждое смешанное число. Сложим отдельно целые числа и отдельно дроби. Запишем сумму в виде смешанной дроби: .
В этой сумме распишем каждое смешанное число. Сложим целые числа и дроби. Полученная дробь оказалась неправильной. Вынесем целую часть. Сложим целое и смешанное числа:
Запись будет короче, если не расписывать смешанные числа: .
Итак, чтобы складывать целые, дробные и смешанные числа, удобнее всего складывать целые с целыми, а дробные с дробными числами.
Примеры с вычитанием
1) Разность целого и дробного чисел.
Представим единицу в виде дроби . Вычтем из одной дроби другую: .
- ·
Мы уже умеем вычитать из единицы правильную дробь. Распишем 5 как и . Вычитаем из единицы дробь, записываем ответ в виде смешанного числа: .
Постараемся выполнить вычитание, не расписывая целое число: .
2) Разность целого и смешанного чисел.
Распишем смешанное число. Так как минус перед ним относится ко всем числу (и к целой и дробной части), то .
Попробуем выполнить действия, не расписывая смешанное число. Вычтем сначала целую часть. Осталось вычесть дробь: .
3) Разность смешанных чисел.
Вычтем отдельно целые части, отдельно дробные: .
- ·
Сначала вычтем целые части. Мы не можем вычесть сразу из первой дробной части вторую, так как вторая больше первой.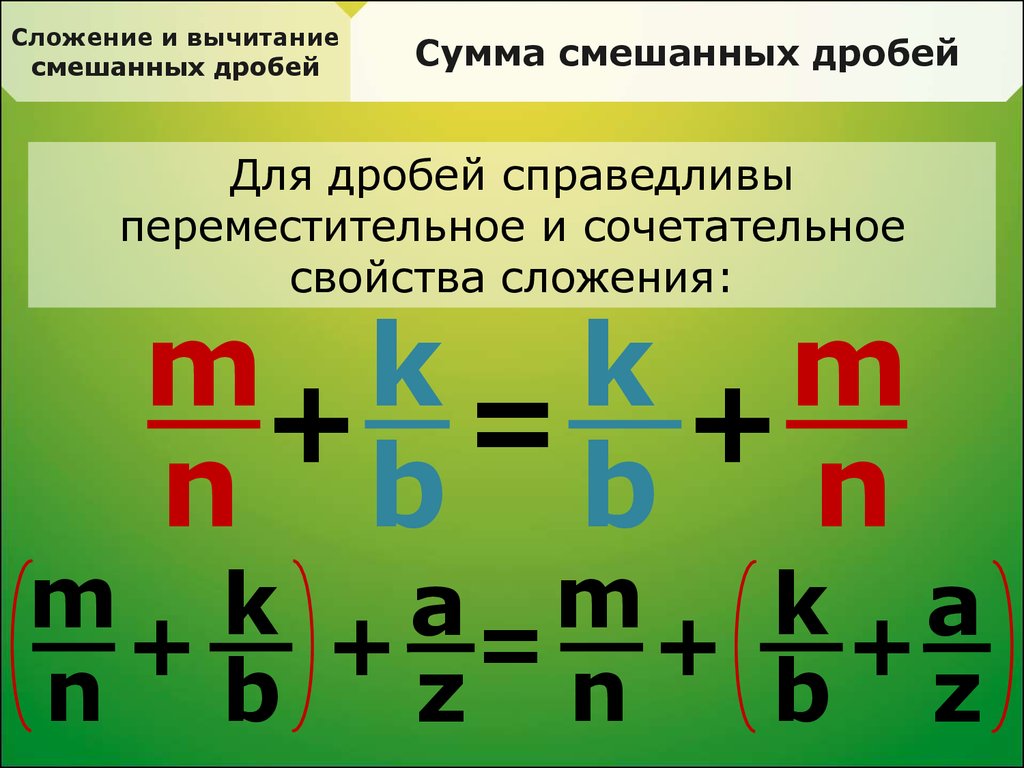 Вычтем тогда, то, что можем, . Осталось вычесть из целого числа дробное. Мы это уже делали:
Вычтем тогда, то, что можем, . Осталось вычесть из целого числа дробное. Мы это уже делали:
Случаи при вычитании смешанных чисел
Итак, при вычитании из одного смешанного числа другого смешанного числа могут встретиться два случая.
- Первая дробная часть больше или равна второй. Тогда из целой части вычитаем целую, из дробной – дробную: .
Первая дробная часть меньше второй. Тогда из целой части вычитаем целую. Из дробной части вычитаем столько, сколько сможем (то есть первую дробную часть). И в конце вычитаем из целого числа остаток дробной части: .
Алгоритм
Если нужно сложить или вычесть целые числа, дроби и смешанные числа, то удобнее всего поступить так.
- Выполнить действие с целыми числами.
- Выполнить действия с дробными частями.
Если сразу не удается вычесть из первой дробной части вторую, то делаем это в два этапа.
Примеры.
 Обобщение
Обобщение
Заключение
Чтобы закрепить навыки, обязательно выполните примеры в тренажерах к этому уроку. Чтобы научиться ездить на велосипеде, не так важно смотреть, как ездят другие, а необходимо пробовать это делать самостоятельно.
Список рекомендованной литературы
- Математика 5 класс. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И., 31-е изд., стер. М: Мнемозина, 2013.
- Математика 5 класс. Ерина Т.М.. Рабочая тетрадь к учебнику Виленкина Н.Я., М.: Экзамен, 2013.
- Математика 5 класс. Мерзляк А.Г., Полонский В.Б., Якир М.С. М.: Вентана – Граф, 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Yaklass.ru (Источник).
- School-assistant.
 ru (Источник).
ru (Источник). - Libraryedu.ru (Источник).
Домашнее задание
- Вычислите: ; ; .
- Вычислите: ; ; .
- Вычислите: .
правила, примеры, решения, вычитание из целого числа смешанной дроби
В данной статье рассмотрим правила, согласно которым выполняется действие вычитания смешанных чисел. Разберем конкретные примеры и некоторые нюансы при их решении. Изучим вычитание обыкновенной дроби и натурального числа из смешанного числа, а также — вычитание смешанного числа из дроби и натурального числа. Рассматривать вычитание мы будем при условии вычитания из большего числа меньшее.
Вычитание смешанных чисел
Пусть в качестве исходных данных даны два смешанных числа: abc и def , необходимо выполнить вычитание данных смешанных чисел.
Нам известно, что любое смешанное число возможно представить, как сумму его целой и дробной части, тогда получим:
abc-def=a+bc-d+ef
Свойства действий сложения и вычитания дают возможность выполнить вычисление полученного выражения различными способами. Опираясь на значения дробных частей смешанных чисел
Опираясь на значения дробных частей смешанных чисел
abc и def , необходимо придерживаться следующих схем вычисления:
- если дробная часть уменьшаемого больше, чем дробная часть вычитаемого:
bc>ef, то вычитание оптимально будет произвести так:
abc-def=(a-d)+bc-ef
Пример 1Произвести вычитание смешанных чисел: 356-249 .
Решение
Сравним дробные части смешанных чисел, т.е. 56 и 49 . Чтобы определить, какая из дробей больше, приведем их к общему наименьшем знаменателю или наименьшему общему кратному: НОК (6, 9) = 18. При этом дополнительным множителем для дроби 56 станет 18 : 6 = 3; а для дроби 49 – 18 : 9 = 2, поэтому : 56=5·36·3=1518 и 49=4·29·2=818 .
Оценим полученный результат: 1518>818, что означает 56>49. Т.е. дробная часть уменьшаемого больше дробной части вычитаемого, и тогда действие вычитания производится путем раздельного вычитания целых и дробных частей заданных смешанных чисел:
3-2=156-49=1518-818=15-818=718
Т. е.: (3-2)+56-49=1+718=1718
е.: (3-2)+56-49=1+718=1718
Ответ: 356-249=1718
- если дробные части заданных смешанных чисел равны: bc=ef , а, соответственно разность их равна нулю, то результатом вычитания таких смешанных чисел будет разность их целых частей:
abc-def=(a-d)+bc-ef=a-d+0=a-d
Пример 2Произвести вычитание смешанных чисел 15710 и 2710 .
Решение
Мы видим, что дробные части заданных чисел равны, т.е. их разность есть нуль. Таким образом, действие вычитания заданных чисел сводится к нахождению разности их целых частей: 15710-2710=15+710-2+710=15-2+710-710=15-2+0=13
Ответ: 15710-2710=13
- если дробная часть уменьшаемого меньше дробной части вычитаемого: bc<ef , то действие вычитания оптимально произвести так:
abc-def=a-d-ef+bc
Пример 3Произвести вычитание смешанных чисел: 2625-81415 .
Решение
Проведем сравнение дробных частей заданных чисел, определив для начала наименьший общий знаменатель: НОК (5, 15) = 15, тогда 25=2·35·3=615 .
Следовательно: 615<1415, т.е. дробная часть уменьшаемого меньше дробной части вычитаемого. Таким образом, находить разность заданных смешанных чисел будем так: 2625-81415=26615-81415=26+615-8+1415==26-8-1415+615=18-1415+615
Для начала вычтем дробь из натурального числа (в скобках): 18-1415=(17+1)-1415=17+1+1415=17+11+1415==17+1515-1415=17+115
Тогда 18-1415+615=17+115+615=17+115+615==17+715=17715
Ответ: 2625-81415=17715 .
Вычитание обыкновенной дроби из смешанного числа
Схема вычитания правильной дроби из смешанного числа такая же, как при действии вычитания смешанных чисел.
Пример 4Найти разницу: 356-415
Решение:
Приведем дробные части заданных чисел к единому наименьшему общему кратному: НОК (6, 15) = 30, тогда 65=5·56·5=2530 и 415=4·215·2=830 .
Таким образом, 56>415 .
В итоге вычитание возможно произвести так: 356-415=3+56-415=3+56-415=3+2530-830=3+1730=31730
Ответ: 356-415=31730
Пример 5Произвести действие вычитания: 127-37
Решение
Дробные части исходных чисел имеют одинаковый знаменатель, что дает возможность их легко сравнить.
Тогда находить разницу будем так:
127-37=1+27-37=1-37+27=11-37+27==77-37+27=47+27=67
Ответ: 127-37=67.
Добавим еще одну, в общем очевидную деталь вычислений: если дробная часть смешанного числа равна вычитаемой дроби, то итогом вычисления будет число, равное целой части уменьшаемого смешанного числа. К примеру:
16311-311=16+311-311=16+311-311=16+0=16
Чтобы вычесть неправильную дробь из смешанного числа, необходимо выделить целую часть из неправильной дроби, а затем производить вычисление.
Пример 6Вычислить значение разности: 7512-199 .
Решение: вычитаемая дробь является неправильной, выделим из нее целую часть и получим: 199=219
Приведем к общему знаменателю дробные части заданных чисел и согласно указанным выше схемам произведем вычитание смешанных чисел:
7512-219=7+512-2+19=7-2+512-19==5+1536-436=5+1136=51136
Ответ: 7512-199=51136 .
Вычитание натурального числа из смешанного
Определение 1 Для совершения действия вычитания натурального числа из смешанного, необходимо вычесть заданное натуральное число из целой части смешанного числа, а дробную часть оставить без изменений: abc-n=a-n+bc Пример 7Необходимо вычесть из смешанного числа 1511528 натуральное число 44.
Решение: 1511528-44=151+1528-44=151-44+1528=107+1528=1071528
Ответ: 1511528-44=1071528
Вычитание смешанного числа из обыкновенной дроби
Очевидно, что любое заданное смешанное число будет больше единицы. Уменьшаемая дробь должна быть больше вычитаемого, тогда эта дробь – неправильная. Необходимо выделить целую часть из неправильной дроби, и далее выполнение действия вычитания смешанного числа из обыкновенной дроби сведется к вычитанию смешанных чисел.
Пример 8Необходимо выполнить вычитание: 749-612
Решение
В первую очередь выделим целую часть неправильной уменьшаемой дроби: 749=829 , тогда заданный пример примет вид: 749-612=829-612
Найдем наименьший общий знаменатель: НОК (9, 2) = 18.
Получим: 29=2·29·2=418 и 12=1·92·9=918.
Тогда:
829-612=8418-6918=8+418-6+918=8-6-918+418==2-918+418=1+1-918+418=1+1-918+418==1+1-918+418=1+918+418=1+918+418==1+9+418=1+1318=11318
Ответ: 749-612=11318
Вычитание смешанного числа из натурального
Чтобы произвести действие вычитания смешанного числа из натурального, сначала от натурального числа отнимаем целую часть смешанного, после чего из полученного результата вычитаем дробную часть:
n-abc=n-a+bc=n-a-bc
Пример 9Необходимо вычесть из натурального числа 18 смешанное число.
Решение
18-535=18-5+35=18-5-35=13-35=12+1-35==12+1-35=12+11-35=12+55-35=12+5-35==12+25=1225
Ответ: 18-535=1225
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Вычитание смешанных дробей – методы, этапы, примеры
Смешанные дроби – это еще одна форма представления неправильной дроби, состоящей из целого числа и правильной дроби. Вычитание смешанных дробей — это операция вычитания, выполняемая между любыми двумя смешанными дробями. В этой статье мы изучим различные методы и правила, чтобы понять вычитание смешанных дробей.
1. | Вычитание смешанных дробей с одинаковыми знаменателями |
| 2. | Вычитание смешанных дробей с разными знаменателями |
| 3. | Вычитание смешанных дробей с перегруппировкой |
| 4. | Часто задаваемые вопросы о вычитании смешанных дробей |
Вычитание смешанных дробей с одинаковыми знаменателями
Две или более дроби, имеющие общий знаменатель, называются подобными дробями. Следовательно, смешанные дроби с одинаковыми знаменателями будут иметь одинаковые знаменатели, такие как \(3\dfrac{2}{7}\) и \(2\dfrac{1}{7}\). Обратите внимание на следующие моменты, которые следует учитывать при вычитании смешанных дробей.
- Смешанная дробь \(a\dfrac{b}{c}\) также может быть записана как + (b/c).
- Чтобы преобразовать смешанное число в неправильную дробь, нужно умножить целое число на знаменатель и прибавить результат к числителю правильной дроби, сохранив знаменатель.
 Например, чтобы преобразовать \(1\dfrac{6}{11}\) в неправильную дробь, мы умножаем 1 и 11, т. е. 1 × 11 = 11, и результат прибавляем к 6, т. е. 11 + 6 = 17. Таким образом, неправильная дробь равна 17/11.
Например, чтобы преобразовать \(1\dfrac{6}{11}\) в неправильную дробь, мы умножаем 1 и 11, т. е. 1 × 11 = 11, и результат прибавляем к 6, т. е. 11 + 6 = 17. Таким образом, неправильная дробь равна 17/11. - Чтобы преобразовать неправильную дробь в смешанное число, разделим числитель неправильной дроби на ее знаменатель. Частное становится целой частью числа, остаток становится числителем правильной дроби, а знаменатель остается прежним. Например, чтобы преобразовать 22/3 в смешанное число, мы сначала разделим 22 на 3 и получим частное как 7, а остаток как 1. Таким образом, смешанное число равно \(7\dfrac{1}{3}\) .
Теперь давайте разберемся с этапами вычитания смешанных дробей с одинаковыми знаменателями.
Пример: Вычтите смешанную дробь \(2\dfrac{1}{3}\) из \(4\dfrac{2}{3}\).
Мы должны выполнить \(4\dfrac{2}{3}\) — \(2\dfrac{1}{3}\). Давайте посмотрим на шаги.
- Шаг 1: Вычтем целые числа обеих дробей.
 т. е. 4 — 2 = 2,
т. е. 4 — 2 = 2, - Шаг 2: Теперь вычтем дробные части. т. е. (2/3) — (1/3) = 1/3.
- Шаг 3: Мы объединим результат двух последних шагов, чтобы получить результат. т. е. 2 + (1/3) = \(2\dfrac{1}{3}\).
Следовательно, значение \(4\dfrac{2}{3}\) — \(2\dfrac{1}{3}\) равно \(2\dfrac{1}{3}\).
Вычитание смешанных дробей с разными знаменателями
Дроби с неравными знаменателями называются неодинаковыми. Таким образом, некоторыми примерами смешанных дробей с разными знаменателями являются \(5\dfrac{2}{3}\) и \(1\dfrac{2}{5}\). Давайте возьмем пример, чтобы понять шаги вычитания смешанных дробей с разными знаменателями.
Пример: Вычесть \(3\dfrac{1}{6}\) из \(5\dfrac{2}{3}\).
Мы должны выполнить \(5\dfrac{2}{3}\) — \(3\dfrac{1}{6}\). У нас есть два способа выполнить вычитание.
Метод I: Вычитая целые числа отдельно и дроби отдельно, делая их знаменатели равными.
- Шаг 1: Вычтите целые числа обеих дробей. т. е. 5 — 3 = 2,
- Шаг 2: Теперь вычтем дробные части. Для этого мы должны сделать знаменатели 2/3 и 1/6 равными, найдя их НОК.
- Шаг 3: Поскольку НОК 3 и 6 равен 6, мы запишем 2/3 как (2 × 2) / (3 × 2) = 4/6.
- Шаг 4: Теперь вычтем дроби. т. е. (4/6) — (1/6) = 3/6.
- Шаг 5: Результат, полученный на предыдущем шаге, будет упрощен. т. е. 3/6 = 1/2.
- Шаг 6: Результат шагов 1 и 5 будет объединен для получения окончательного результата. т. е. 2 + (1/2) = \(2\dfrac{1}{2}\).
Метод II: Путем преобразования их в неправильные дроби с последующим вычитанием их, делая их знаменатели равными.
- Шаг 1: Преобразуйте данные смешанные дроби в неправильные дроби. т. е. \(5\dfrac{2}{3}\) = 17/3 и \(3\dfrac{1}{6}\) = 19/6.

- Шаг 2: Для дробей, полученных на последнем шаге, мы приравняем знаменатели, взяв их НОК.
- Шаг 3: НОК знаменателей 3 и 6 равно 6. Таким образом, 17/3 можно записать как (17 × 2) / (3 × 2) = 34/6.
- Шаг 4: Теперь вычтем дроби. т. е. (34/6) — (19/6) = 15/6.
- Шаг 5: Результат предыдущего шага будет упрощен. т. е. 15/6 = 5/2.
- Шаг 6: Наконец, мы преобразуем результат, полученный на последнем шаге, в смешанную дробь. т. е. 5/2 = \(2\dfrac{1}{2}\).
Отсюда значение \(5\dfrac{2}{3}\) — \(3\dfrac{1}{6}\) равно \(2\dfrac{1}{2}\ ).
Вычитание смешанных дробей с перегруппировкой
При вычитании смешанных дробей может возникнуть ситуация, когда вычитаемая дробь больше дроби, из которой она вычитается. В таких случаях мы будем использовать понятие перегруппировки. Давайте теперь разберемся с вычитанием смешанных дробей с перегруппировкой на примере.
Пример: Вычесть \(7\dfrac{2}{3}\) из \(10\dfrac{4}{9}\).
Мы должны выполнить \(10\dfrac{4}{9}\) — \(7\dfrac{2}{3}\).
- Шаг 1: Рассмотрим дробные части обеих смешанных дробей и сравним их, сделав их знаменатели равными. т. е. мы будем сравнивать 4/9 и 2/3.
- Шаг 2: НОК знаменателей 9 и 3 равен 9. Таким образом, 2/3 можно записать как (2 × 3) / (3 × 3) = 6/9. Отсюда мы видим, что 6/9 > 4/9 или, можно сказать, 2/3 > 4/9.
- Шаг 3: Как видно из предыдущего шага 4/9 < 6/9, мы не можем вычесть 6/9с 4/9. Следовательно, теперь 4/9 будет занимать 1 из целой части смешанной дроби \(10\dfrac{4}{9}\).
- Шаг 4: Целое число 10 отдает 1 в качестве заимствования для 4/9. Мы знаем, что 1 также можно записать как 9/9. Следовательно, когда заимствование 9/9 добавляется к 4/9, мы получаем 4/9 + 9/9 = 13/9.
- Шаг 5: Теперь мы перепишем дробь после перегруппировки.
 Целое число 10 становится 9 после заимствования 4/9, а 4/9 становится 13/9. Следовательно, \(10\dfrac{4}{9}\) = \(9\dfrac{13}{9}\).
Целое число 10 становится 9 после заимствования 4/9, а 4/9 становится 13/9. Следовательно, \(10\dfrac{4}{9}\) = \(9\dfrac{13}{9}\). - Шаг 6: Теперь мы легко вычтем смешанные дроби, так как у них одинаковые знаменатели. т. е. \(9\dfrac{13}{9}\) — \(7\dfrac{6}{9}\) = \(2\dfrac{7}{9}\).
Связанные статьи о вычитании смешанных дробей
Проверьте эти статьи, связанные с концепцией вычитания смешанных дробей.
- Смешанные фракции
- Неправильные дроби
- Правильная дробь
- Дроби
Вычитание смешанных дробей Примеры
Пример 1. Вычтите смешанную дробь \(15\dfrac{1}{3}\) из \(20\dfrac{2}{3}\) .
Решение: Для решения этого вопроса мы будем использовать концепцию вычитания смешанных дробей. Даны смешанные дроби \(15\dfrac{1}{3}\) и \(20\dfrac{2}{3}\) с одинаковым знаменателем. Мы должны выполнить \(20\dfrac{2}{3}\) — \(15\dfrac{1}{3}\).
 Мы будем вычитать целые числа и дробные части отдельно и объединять их, как показано ниже.
Мы будем вычитать целые числа и дробные части отдельно и объединять их, как показано ниже.= (20 — 15) + [(2/3) — (1/3)]
= 5 + (1/3)
= \(5\dfrac{1}{3}\)
Таким образом, значение \(20\dfrac{2}{3}\) — \(15\dfrac{1}{3}\) равно \(5\dfrac{1}{3}\).
Пример 2. Вычтите смешанную дробь \(16\dfrac{1}{4}\) из \(27\dfrac{1}{12}\) , используя концепцию перегруппировки.
Решение: Для решения этого вопроса воспользуемся этапами вычитания смешанных дробей с перегруппировкой. Мы должны выполнить \(27\dfrac{1}{12}\) — \(16\dfrac{1}{4}\). Здесь необходима перегруппировка, потому что, сравнивая дроби 1/12 и 1/4, мы видим, что 1/12 < 1/4. Это потому, что дроби различны, и при преобразовании их в одинаковые дроби мы получаем 1/4 = 3/12. Таким образом, 1/12 < 3/12. Мы не можем вычесть большую дробь из меньшей, поэтому мы используем концепцию перегруппировки. В дроби \(27\dfrac{1}{12}\) 1/12 нужно заимствовать 1 из 27.
 Поэтому мы изменим эту дробь. 27 дает заем 1 целого к 1/12 и сам становится 26. Этот заем 1 целого добавляется к 1/12. Мы знаем, что 1 также можно представить как 12/12. Таким образом, 1/12 + 12/12 = 13/12. Следовательно, модифицированная дробь равна \(27\dfrac{1}{12}\) = \(26\dfrac{13}{12}\).
Поэтому мы изменим эту дробь. 27 дает заем 1 целого к 1/12 и сам становится 26. Этот заем 1 целого добавляется к 1/12. Мы знаем, что 1 также можно представить как 12/12. Таким образом, 1/12 + 12/12 = 13/12. Следовательно, модифицированная дробь равна \(27\dfrac{1}{12}\) = \(26\dfrac{13}{12}\).Теперь выполним \(26\dfrac{13}{12}\) — \(16\dfrac{3}{12}\).
= (26 — 16) + (13/12) — (3/12)
= 10 + (10/12)
= \(10\dfrac{10}{12}\)
Об упрощении получаем
= \(10\dfrac{5}{6}\)
Следовательно, значение \(27\dfrac{1}{12}\) — \(16\dfrac{1} {4}\) равно \(10\dfrac{5}{6}\).
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по вычитанию смешанных дробей
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о вычитании смешанных дробей
Как решить вычитание смешанных дробей?
Вычитание смешанных дробей можно выполнить двумя способами. Для одинаковых знаменателей можно просто вычесть целые числа, также можно вычесть дробную часть смешанных дробей и объединить два результата для получения результата. Другой способ сделать это — преобразовать смешанные дроби в неправильные дроби и вычесть их. Для разных знаменателей их можно сначала преобразовать в одинаковые знаменатели, найдя НОК, и можно выполнить те же шаги, что и вычитание смешанных дробей с одинаковыми знаменателями.
Для одинаковых знаменателей можно просто вычесть целые числа, также можно вычесть дробную часть смешанных дробей и объединить два результата для получения результата. Другой способ сделать это — преобразовать смешанные дроби в неправильные дроби и вычесть их. Для разных знаменателей их можно сначала преобразовать в одинаковые знаменатели, найдя НОК, и можно выполнить те же шаги, что и вычитание смешанных дробей с одинаковыми знаменателями.
Как брать взаймы при вычитании смешанных дробей?
При вычитании смешанных дробей, если правильная дробная часть смешанной дроби, из которой вычитается другая смешанная дробь, меньше, то целое число дает заем правильной дроби, чтобы сделать ее больше. Например, для выполнения \(3\dfrac{1}{3}\) — \(1\dfrac{2}{3}\) мы видим, что 2/3 > 1/3. Таким образом, 1/3 заимствует 1 целое из 3. 1 целое можно записать как 3/3. Целое число 3 после предоставления займа 1 становится 3 — 1 = 2, а дробь 1/3 становится (1/3) + (3/3) = 4/3. Таким образом, новая модифицированная смешанная дробь после заимствования равна \(2\dfrac{4}{3}\). Теперь вычитание будет \(2\dfrac{4}{3}\) — \(1\dfrac{2}{3}\) = \(1\dfrac{2}{3}\).
Теперь вычитание будет \(2\dfrac{4}{3}\) — \(1\dfrac{2}{3}\) = \(1\dfrac{2}{3}\).
Как перегруппировать при вычитании смешанных дробей?
Перегруппировка выполняется, когда большая дробь вычитается из меньшей дроби. Например, давайте выполним \(8\dfrac{4}{9}\) — \(5\dfrac{2}{3}\) . Мы приравняем знаменатели 4/9 и 2/3, чтобы сравнить их. Дробь 2/3 также может быть записана как 6/9. Но 6/9 > 4/9. Мы не можем вычесть большую дробь из меньшей дроби. Таким образом, 4/9 нужно сделать больше. Для этого 4/9 заимствует 1 из 8. Целое 1 также можно записать как 9./9. Теперь целое число 8 становится 8 — 1 = 7, а дробь 4/9 становится (4/9) + (9/9) = 13/9. Таким образом, новая дробь будет \(7\dfrac{13}{9}\). Таким образом, теперь вычитание выглядит следующим образом: \(7\dfrac{13}{9}\) — \(5\dfrac{6}{9}\) = \(2\dfrac{7}{9}\) .
Как вычитать смешанные дроби с одинаковыми знаменателями?
Вычитание смешанных дробей с одинаковыми знаменателями осуществляется путем вычитания целой и дробной частей смешанных дробей по отдельности с последующим их объединением для получения результата.
Например, выполним \(23\dfrac{3}{4}\) — \(21\dfrac{1}{4}\)
= (23 — 21) + (3/4) — (1/4)
= 2 + (2/4)
= \(2\dfrac{2}{4}\)
При упрощении получаем
= \(2\dfrac{1}{2}\)
Как вычитать смешанные дроби с разными знаменателями?
Вычитание смешанных дробей с разными знаменателями может быть выполнено путем преобразования их в неправильную дробь с последующим преобразованием их в одинаковые знаменатели путем взятия их НОК и, наконец, вычитания их числителей. Затем окончательный результат преобразуется обратно в смешанную фракцию.
Например, выполним \(6\dfrac{2}{3}\) — \(2\dfrac{1}{4}\)
= (20/3) — (9/4)
= [(20 × 4) / (3 × 4)] — [(9 × 3) / (4 × 3)]
= (80/12) — (27/12)
= 53/12
= \(4\dfrac{5}{12}\)
Как вычитать смешанные дроби из целых чисел?
Целые числа можно изменить и записать в виде смешанной дроби. После того, как целое число записано в виде смешанной дроби, можно выполнить общие шаги вычитания смешанных дробей.
Например, выполним 5 — \(2\dfrac{2}{3}\)
Обратите внимание, что 5 также можно записать как 4 + 1 = 4 + (3/3) = \(4\dfrac{3}{3}\)
Таким образом, мы выполним \(4\dfrac{3}{3}\) — \(2\dfrac{2}{3}\)
= (4 — 2) + (3/3) — (2/3)
= 2 + (1/3)
= \(2\dfrac{1}{3}\)
Как складывать и вычитать смешанные дроби?
Смешанные дроби вычитаются из смешанных дробей путем их преобразования в неправильные дроби и вычитания их числителей, если они имеют одинаковый знаменатель. Если у них разные знаменатели, то сначала они преобразуются в одинаковые знаменатели путем взятия их НОК с последующим вычитанием их числителей. Окончательный результат будет преобразован обратно в смешанную дробь. Шаги для добавления смешанных фракций также остаются прежними. Единственная разница в том, что мы складываем числители, а не вычитаем.
Например, выполним \(4\dfrac{2}{7}\) — \(3\dfrac{1}{6}\)
= (30/7) — (19/6)
= [(30 × 6) / (7 × 6)] — [(19 × 7) / (6 × 7)]
= (180/42) — (133/42)
= 47/42
= \(1\dfrac{5}{42}\)
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по вычитанию смешанных дробей
Калькулятор смешанных чисел
Использование калькулятора
Выполнять математические вычисления со смешанными числами (смешанными дробями), выполняя операции над дроби, целые числа, целые числа, смешанные числа, смешанные дроби и неправильные дроби. Калькулятор смешанных чисел может складывать, вычитать, умножать и делить смешанные числа и дроби.
Калькулятор смешанных чисел может складывать, вычитать, умножать и делить смешанные числа и дроби.
Калькулятор смешанных чисел (также известный как смешанные дроби):
Этот онлайн-калькулятор выполняет простые операции с целыми числами, целыми числами, смешанными числами, дробями и неправильными дробями путем сложения, вычитания, деления или умножения. Ответ дается в сокращенной дроби и смешанном числе, если оно существует.
Введите смешанные числа, целые числа или дроби в следующих форматах:
- Смешанные числа: введите 1 1/2, что составляет полторы секунды, или 25 3/32, что составляет двадцать пять и три тридцать секунд. Оставьте ровно один пробел между целым числом и дробью и используйте косую черту для ввода дробей. Вы можете ввести до 3 цифр для каждого целого числа, числителя или знаменателя (123 456/789).
- Целые числа: до 3 цифр в длину.
- Дроби: введите 3/4, что составляет три четвертых, или 3/100, что составляет три сотых.
 Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).
Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).
Сложение смешанных чисел с использованием формулы сложения дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу сложения дробей:
a/b + c/d = (ad + bc) / bd - Сократите дроби и упростите, если возможно
Формула сложения дробей
\( \dfrac{a}{b} + \dfrac{c}{d} = \dfrac{(a \times d) + (b \times c)}{b \times d} \)
Пример
Добавить 1 2/6 и 2 1/4
\( 1 \dfrac{2}{6} + 2 \dfrac{1}{4} = \dfrac{8}{6} + \dfrac{9}{4} \)
\( = \dfrac{(8 \times 4) + (9 \times 6)}{6 \times 4} \)
\( = \dfrac{32 + 54}{24} = \dfrac{86}{24} = \dfrac{43}{12} \)
\( = 3 \dfrac{7}{12} \)
1 2/6 + 2 1/4 = 8/6 + 9/4 = (8*4 + 9*6) / 6*4 = 86 / 24
Получаем 86/24 и упрощаем до 3 7/12
Вычитание смешанных чисел по формуле вычитания дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу для вычитания дробей: a/b — c/d = (ad — bc) / bd
- Сократите дроби и упростите, если возможно
Формула вычитания дробей
\( \dfrac{a}{b} — \dfrac{c}{d} = \dfrac{(a \times d) — (b \times c)}{b \times d} \)
Пример
Вычесть 2 1/4 из 1 2/6
1 2/6 — 2 1/4 = 8/6 — 9/4 = (8*4 — 9*6) / 6*4 = -22 / 24
Уменьшите дробь, чтобы получить -11/12
Умножение смешанных чисел с помощью формулы умножения дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу умножения дробей: a/b * c/d = ac / bd
- Сократите дроби и упростите, если возможно
Формула умножения дробей
\( \dfrac{a}{b} \times \dfrac{c}{d} = \dfrac{a \times c}{b \times d} \)
Пример
умножить 1 2/6 на 2 1/4
1 2/6 * 2 1/4 = 8/6 * 9/4 = 8*9 / 6*4 = 72 / 24
Сократите дробь, чтобы получить 3/1 и упростите до 3
Деление смешанных чисел с помощью формулы деления дробей
- Преобразование смешанных чисел в неправильные дроби
- Используйте алгебраическую формулу деления дробей: a/b ÷ c/d = ad / bc
- Сократите дроби и упростите, если возможно
Формула деления дробей
\( \dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a \times d}{b \times c} \)
Пример
разделить 1 2/6 на 2 1/4
1 2/6 ÷ 2 1/4 = 8/6 ÷ 9/4 = 8*4 / 9*6 = 32 / 54
Уменьшите дробь, чтобы получить 16/27
Связанные калькуляторы
Для выполнения математических операций над простыми правильными или неправильными дробями используйте наш
Калькулятор дробей.
 ru (Источник).
ru (Источник).  Например, чтобы преобразовать \(1\dfrac{6}{11}\) в неправильную дробь, мы умножаем 1 и 11, т. е. 1 × 11 = 11, и результат прибавляем к 6, т. е. 11 + 6 = 17. Таким образом, неправильная дробь равна 17/11.
Например, чтобы преобразовать \(1\dfrac{6}{11}\) в неправильную дробь, мы умножаем 1 и 11, т. е. 1 × 11 = 11, и результат прибавляем к 6, т. е. 11 + 6 = 17. Таким образом, неправильная дробь равна 17/11. т. е. 4 — 2 = 2,
т. е. 4 — 2 = 2,
 Целое число 10 становится 9 после заимствования 4/9, а 4/9 становится 13/9. Следовательно, \(10\dfrac{4}{9}\) = \(9\dfrac{13}{9}\).
Целое число 10 становится 9 после заимствования 4/9, а 4/9 становится 13/9. Следовательно, \(10\dfrac{4}{9}\) = \(9\dfrac{13}{9}\). Мы будем вычитать целые числа и дробные части отдельно и объединять их, как показано ниже.
Мы будем вычитать целые числа и дробные части отдельно и объединять их, как показано ниже.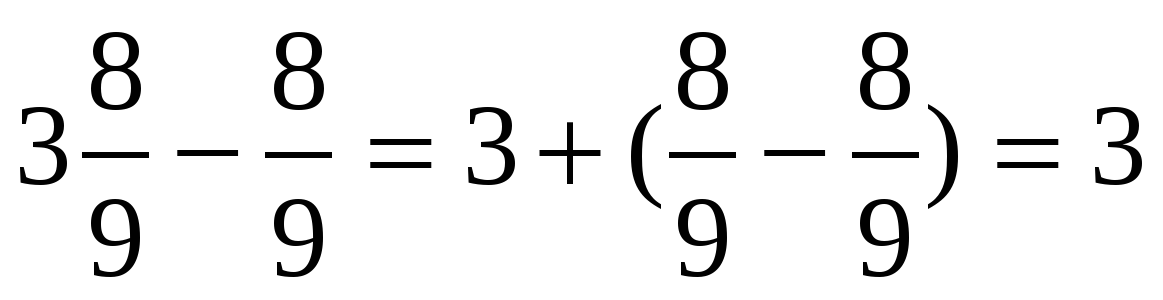 Поэтому мы изменим эту дробь. 27 дает заем 1 целого к 1/12 и сам становится 26. Этот заем 1 целого добавляется к 1/12. Мы знаем, что 1 также можно представить как 12/12. Таким образом, 1/12 + 12/12 = 13/12. Следовательно, модифицированная дробь равна \(27\dfrac{1}{12}\) = \(26\dfrac{13}{12}\).
Поэтому мы изменим эту дробь. 27 дает заем 1 целого к 1/12 и сам становится 26. Этот заем 1 целого добавляется к 1/12. Мы знаем, что 1 также можно представить как 12/12. Таким образом, 1/12 + 12/12 = 13/12. Следовательно, модифицированная дробь равна \(27\dfrac{1}{12}\) = \(26\dfrac{13}{12}\). Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).
Вы можете ввести до 3 цифр для каждого числителя и знаменателя (например, 456/789).