Как научиться быстро считать в уме? — Meduza

1

Зачем в уме, когда можно на калькуляторе или в столбик?

Минимальные навыки счета, чувство числа — такой же элемент общечеловеческой культуры, как грамотное письмо и речь, владение иностранным языком, базовое представление об искусстве и окружающем мире.

Кроме того, когда вы легко считаете без подручных средств, вы чувствуете совершенно другой уровень управления реальностью — вы заранее знаете, сколько сдачи вам дадут в магазине или стоит ли набиваться всемером в лифт грузоподъемностью 400 килограммов.

Подумайте и о том, что калькулятор и действия в столбик — это же такая разновидность магии. Скорее всего, вы не понимаете, как это работает, и вынуждены просто доверять им. А когда вы хорошо понимаете, как устроены математические операции и можете их воспроизвести «руками», ваше чувство контроля (и уверенности в себе) получает серьезный бонус.

И наконец, устный счет развивает ваши ментальные способности: внимание, память, концентрацию, переключение между несколькими потоками мышления, а также может послужить средством для медитации или отвлечения от грустных мыслей.

2

Но где брать задания для тренировки? Самому себе примеры придумывать?

Конечно, нет. В сети полно мобильных приложений, которые предложат вам тренировку математических навыков на любой вкус.

При выборе учтите, что хорошее приложение, как минимум, должно обладать достаточно гибкими настройками сложности и вести статистику решенных вами заданий.

Попробуйте эти приложения под iOS и Android или поищите альтернативные варианты в App Store и Google Play.

3

А как именно нужно тренироваться?

Основных математических действий всего четыре — сложение, вычитание, умножение и деление. У каждого действия есть свои особенности, но они не сложные. Надо один раз разобраться, а потом тренироваться минут по 5−10 в день, и очень скоро вы почувствуете, что считаете лучше. Скорее всего, за два-три месяца вы выйдете на достаточно приличный уровень, который можно будет поддерживать эпизодическими тренировками.

4

И с чего же начать?

Начните с самого простого уровня — сложения однозначных чисел, и доведите его до совершенства: 99% правильных ответов, на каждый ответ 1−2 секунды. Для решения примеров «с переходом через 10» попробуйте использовать следующую технику — «Опора на десяток».

Допустим, вам нужно сложить 8 и 7.

1) Спросите себя, сколько числу 8 не хватает до 10 (это 2).

2) Представьте 7 как сумму 2 и какого-то второго кусочка (это 5).

3) Прибавляйте к 8 сначала ту часть числа 7, которой недоставало до 10, а потом тот второй кусочек — получится 10 и 5, и это, конечно, 15.

5

Как складывать многозначные числа?

Здесь самый важный принцип — это сложение одинаковых разрядов друг с другом. Разбив оба числа на «разрядные части», начните складывать со старших разрядов — тысячи с тысячами, сотни с сотнями, десятки с десятками, единицы с единицами. То, что получится, при необходимости укрупняйте и снова считайте все вместе.

Например, как сложить 456 и 789?

1) 456 состоит из трех разрядных частей — 400, 50 и 6.

789 тоже разбивается на три разрядные части — это 700, 80 и 9.

2) Складываем сотни с сотнями: 400+700 = 1100, десятки с десятками: 50+80 = 130, единицы с единицами: 6+9 = 15.

3) Укрупняем, разбивая на удобные части, снова группируем и складываем одинаковые разряды: 1100+130+15 — это 1100+100+30+10+5, то есть, 1200+40+5 = 1245.

Поправка. При сложении разрядов мы перепутали единицы и к 6 прибавили 8 вместо 9. В итоге сумма тоже оказалась неправильной — 1244 вместо 1245. Приносим извинения за ошибку, и не повторяйте ее — внимательно следите за числами, особенно в устном счете!

6

Что насчет вычитания?

И здесь надо начинать с базового уровня — вычитания однозначного числа из чисел первого и второго десятка — и довести этот навык до совершенства. Как и в случае сложения, проблемы обычно возникают с вычитанием «с переходом через 10». И здесь поможет аналогичный способ «опоры на десяток».

Допустим, нам нужно из 12 вычесть 8.

1) Спросим себя, сколько нужно отнять от 12, чтобы получилось 10 (это 2).

2) Будем из 12 вычитать 8 по частям — сначала вычтем эту 2, а потом все остальное. А остальное — это сколько? (это 6).

3) После вычитания 2 из 12 мы получили 10, и нужно вычесть еще 6, получится 4. Готово!

7

А что с многозначными числами? С ними все сложно?

Не особенно. Важно только не путать технику вычитания с техникой сложения. При сложении нам было удобно разбивать каждое из чисел на разрядные части, а здесь мы разбиваем только то число, которое вычитаем.

Итак, допустим, нам нужно вычесть 512−259.

1) Число 259, которое мы вычитаем, состоит из трех разрядных частей — 200, 50 и 9. Их-то по очереди мы и вычтем.

2) 512−200 — вычитание сотен никак не затрагивает десятков и единиц числа 512, влияет только на сотни, так что результат будет такой — 312.

3) Из того, что получилось после вычитания сотен, теперь вычтем десятки, 312−50.

Это похоже на вычитание через десяток. Вычтем из 312 сначала 10 до целых сотен (единицы не будут затронуты), получим 302. А потом вычтем все остальное (всего нужно было вычесть 50, 10 уже вычли, осталось вычесть 40), получается 262.

4) Осталось вычесть единицы: 262−9.

Чистый переход через десяток — вычитаем сначала 2, получим 260, а потом вычитаем остальную часть, 7, получаем 260−7 = 253. Вот и ответ.

8

Как устроено умножение?

Начнем с умножения однозначных чисел. Для начала нужно вспомнить, что умножение — это когда несколько раз складывают одно и то же. Например, умножить 4 на 7 означает сложить четыре семерки. Пользуясь техникой сложения, мы можем легко посчитать — две семерки, 7 и 7, будет 14, если еще добавить третью 7, получится 21, и, добавляя последнюю, четвертую семерку, в результате получим 28.

Постепенно в результате тренировок вы запомните удобные вам опорные значения умножения и с их помощью сможете быстрее вычислять соседние. Например, если нужно умножить 6 на 7 (то есть, сложить шесть семерок), а вы помните, что 5 умножить на 7 (то есть, сложить пять семерок) будет 35, то чтобы получить итоговый результат, нужно просто добавить шестую семерку — получится 42.

Самым сложным примером в таблице умножения считается 7∙8. Для его запоминания есть неплохое мнемотехническое правило «пять шесть семь восемь», которое означает 56 = 7∙8.

9

Как умножать многозначное число на однозначное?

Разберем на примере. Допустим, нам нужно умножить 468 на 6.

1) 468 состоит из 400, 60 и 8, и все это нужно умножить на 6. Что ж, по отдельности эти задачи не сложнее умножения однозначных чисел.

2) Идем от старшего разряда к младшему: 400∙6 = 2400 (поскольку 400 в 100 раз больше, чем 4, то и результат 400∙6 будет в 100 раз больше, чем результат 4∙6).

Соответственно, 60∙6 = 360, а 8∙6 = 48.

3) А теперь, как при сложении, складываем все это вместе, группируя одинаковые разряды:

(2000+400)+(300+60)+(40+8) = [перегруппируем] =

= 2000+(400+300)+(60+40)+8 = [сложим одинаковые разряды] =

= 2000+700+100+8 = [сгруппируем и сложим одинаковые разряды] =

= 2000+800+8 = [дальше укрупнять нечего, получаем ответ] = 2808.

10

Как перемножать двузначные числа?

Для обычного человека это уже высший пилотаж! Если вы освоили умножение двузначных, считайте, что вы приняты в мир элиты устного счета. Но на самом деле, и тут ничего принципиально сложного нет, просто выше нагрузка на краткосрочную память (заодно и потренируем ее).

Итак, например, умножим 78 на 56. Это означает, что нам нужно число 78 сложить («взять») 56 раз.

1) Эти 56 раз можно разбить на этапы — сначала 78 сложим 50 раз, потом 6 раз, а потом объединим результаты.

2) Число 78 сложить 50 раз несложно — это в 10 раз больше, чем сложить его 5 раз. 78∙5 = 70∙5+8∙5 = 350+40 = 390. А значит, 78∙50 = 3900, запомним это число.

3) Теперь посчитаем 78∙6 = 70∙6+8∙6 = 420+48 = 468.

4) Ну а теперь сложим вместе оба результата: 3900+468 = 3000+900+400+60+8 = 3000+1300+60+8 = 4368. Вуаля!

Поправка. На заключительном этапе при сложении 3900 и 468 мы неправильно разбили второе число на разряды — забыли про 60. В итоге в сумме получилось 4308. Приносим извинения за ошибку, и не повторяйте ее — нельзя терять в устном счете слагаемые.

11

Ничего себе, осталось последнее только действие, деление?

Да, мы на финишной прямой. И снова начнем с самого простого уровня: деления на однозначное число тех чисел, которые знакомы нам по умножению однозначных.

Итак, что же такое деление? По сути, это «обратная» операция к умножению.

Например, разделить 56 на 7 — значит подобрать такое число, что если его умножить на 7, то получится 56. Поскольку вы к этому моменту уже хорошо ориентируетесь в таблице умножения, то наверняка вспомните, что именно 8, умноженное на 7, дает 56. Значит, искомое число — это 8, 56:7 = 8.

И так всегда — вспоминайте, какое число при умножении дает нужный результат — это и есть то число, которое вам нужно.

12

Как делить многозначные числа на однозначное?

Давайте разделим 6144 на 8. Наш способ — «отрезать» от исходного числа максимальные «круглые» части, каждая из которых будет гарантированно делиться на 8 по таблице умножения.

1) Выделим из 6144 как можно большую часть, которая делится на 8 по таблице умножения. Это будет 5600, ведь 56 делится на 8, а следующее число, которое делится на 8 — это уже 64, что нам не подходит, так как 6400 больше, чем 6144. Прекрасно, 6144 — это 5600 и 544 (тут нам пригодился навык вычитания).

По ходу дела будем делить:

6144:8 = [выделяем максимальную удобную круглую часть] =

= (5600+544):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =

= 700+544:8. 

700 запомним как частичный результат, а сами займемся делением 544:8.

2) Аналогично, из числа 544 самая большая часть, которую можно удобно разделить на 8 по таблице умножения, это 480 (ведь 48 делится на 8, а следующее число — 56 — нам не подходит, т. к. 560 > 544). Итак, 544 = 480+64.

Продолжаем деление:

544:8 = [выделяем максимальную удобную круглую часть] =

= (480+64):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =

= 60+64:8.

60 добавим к 700, 700+60 = 760 — запомним это как вторую часть результата и перейдем к последнему делению, 64:8.

3) Оставшийся кусочек, 64, тоже делится на 8 по таблице умножения, 64:8 = 8.

Соответственно, полный результат деления — это 760+8=768. Все!

13

Как делить на двузначное число?

Техника деления на двузначное число — самая разнообразная, непохожая ни на что, изысканная. Познакомимся с ней на примере 5148:66.

1) Подгадаем, в каком десятке лежит наш результат. Напомним, что 5148:66 означает: мы ищем число, которое при умножении на 66 даст 5148. Будем использовать технику «пристрелки». 

Просто наугад попробуем число 20 как возможного кандидата. 20∙66 = 1320, это раза в 4 меньше, чем 5148, которое нам нужно. 

В 4 раза больше, чем 20 — это 80, попробуем его. 80∙66 = 5280, получилось больше, чем нужное 5148, но немного, скорее всего, это «верхний» десяток. 

Проверим для надежности 70, предыдущий перед 80 десяток. 70∙66 = 4620, это как раз меньше 5148, отлично! Значит, число, которое мы ищем, лежит между 70 и 80.

2) Воспользуемся математическим законом о последней цифре результата умножения двух чисел.

Оказывается, она всегда совпадает с последней цифрой результата умножения последних цифр этих чисел (попробуйте подумать, почему это так). Например, на какую цифру закончится 1234∙5678? На ту же, что и 4∙8, то есть на 2 (4∙8 = 32). 

Поэтому, если мы ищем число, которое при умножении на 66 даст 5148, то чтобы гарантировать эту 8 на последнем месте, искомое число может заканчиваться только либо на 3, либо на 8 (3∙6 = 18, 8∙6 = 48).

3) С такими окончаниями между 70 и 80 у нас два всего кандидата — 73 и 78. 

5148 явно ближе к 5280, поэтому сперва проверим 78.

78∙66 = 78∙60+78∙6 = 4680+468 = 5000+148 = 5148, ура! 

(Ну а если бы результат не сошелся, то мы бы проверили второе число, и оно бы уже точно подошло).

14

Какие рекомендации напоследок?

Вот, в общем-то, и все способы, которые достаточно знать для тренировки уверенного счета в пределах 10000 (а умение работать в уме с большими числами, пожалуй, уже выходит за рамки необходимого общего развития).

Наверняка вы также столкнетесь с другими приемами, т. н. «хитростями» быстрого счета, но не торопитесь увлекаться ими. Кроме того, помните, что регулярность важнее интенсивности — старайтесь заниматься на тренажере каждый день по 5−10 минут, больше не нужно, иначе велик риск «перегореть» и забросить. 

В процессе занятия никуда не торопитесь — ловите свой ритм, делайте упор на правильность ответов, а не на скорость, скорость придет потом.

Обязательно пробуйте проговаривать свои действия вслух, особенно на первых порах — у вас будет шанс почувствовать, как все это похоже на стихи, да и решать так будет проще.

И не расстраивайтесь, если что-то не выходит — дорогу осилит идущий, и рано или поздно у вас точно все получится.

Как научиться быстро считать в уме любые числа: техники устного счета

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а  минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

 

Карл Фридрих Гаусс

 

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить.  Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6.  Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

 

Таблица умножения

 

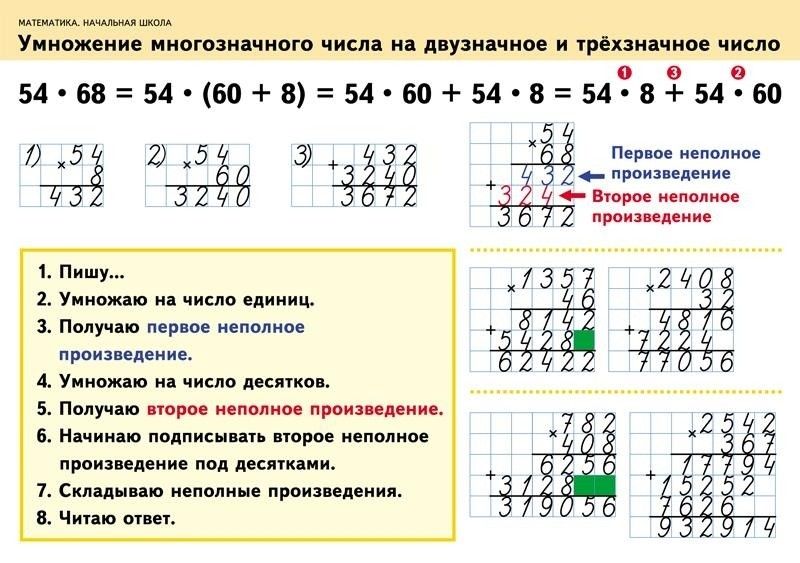
Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57

раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим

54 на 11.

• 5+4=9
• 54*11=594

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5

.

Проверим! Возведем в квадрат число 75.

• 7*8=56
• 5*5=25
• 75*75=5625

 

Раньше все считали без калькуляторов

 

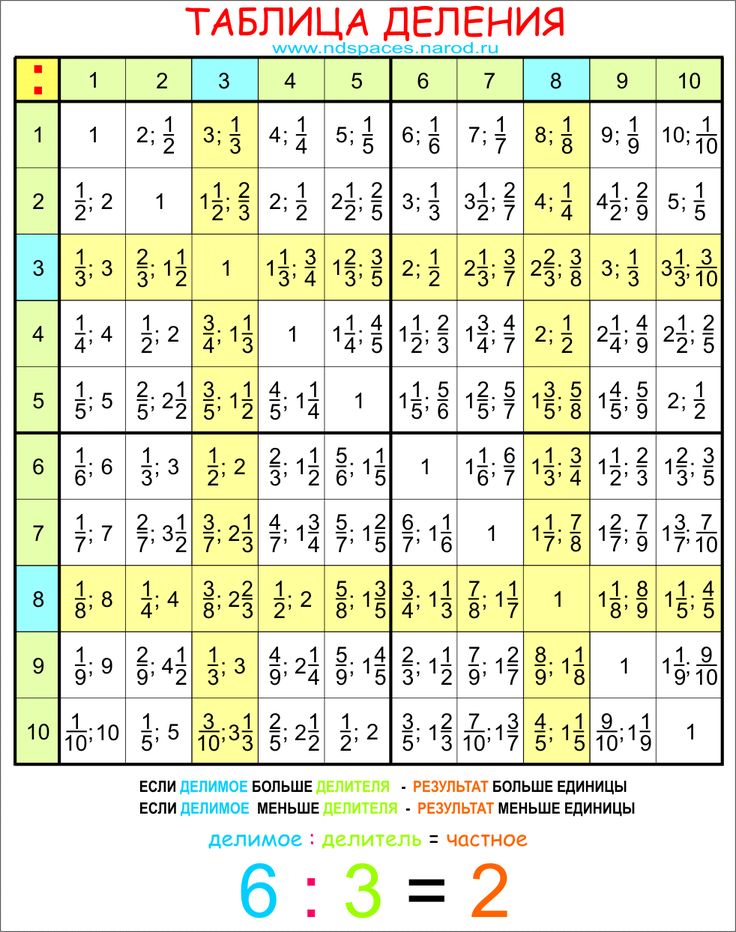
Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

64:8=8

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления  может быть либо число

74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

 

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

 

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

• Не забывайте тренироваться каждый день;
• не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
• скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
• почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима.

Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

Факты об умножении: как учить таблицу умножения — Кейт Сноу

Изучите простой и эффективный метод обучения вашего ребенка таблице умножения. Кроме того, это ошибка № 1, которую допускают родители, обучая своих детей правилам умножения.

Как НЕЛЬЗЯ учить таблицу умножения

В этой статье вы узнаете пошаговый план обучения ваших детей правилам умножения.

Но сначала давайте разберемся, чего НЕЛЬЗЯ делать.

Для многих людей  запоминание фактов умножения равно  механическому обучению . Итак, эти замечательные, благонамеренные родители считают, что есть только один способ помочь своим детям освоить факты умножения: сделать большую стопку карточек и начать сверлить.

Эти родители хотят для своих детей самого лучшего, но пропускают несколько шагов… и делают весь процесс намного более болезненным и утомительным, чем он должен быть. Практика и упражнение действительно помогают детям запомнить факты умножения. Но они приходят в конец процесса, а не начало .

Пссс… хотите универсальный, открытый и доступный ресурс для обучения фактам умножения? Я собрал все эти шаги в одну книгу, чтобы помочь вашим детям освоить факты умножения.

Какие факты умножения (или таблицы умножения)? Почему они так важны?

Факты умножения (также известные как таблицы умножения) — это все задачи на умножение от 1 × 1 = 1 до 10 × 10 = 100.

• Связанный: Бесплатная печатная таблица умножения (пустая и заполненная)

Можете ли вы представить себе попытку найти общие знаменатели или эквивалентные дроби, не зная 5 × 6? Или пытаетесь выполнить деление в длинное, когда не совсем уверены, что такое 7 × 7? И даже не заставляйте меня разлагать полиномы на множители…

Помните это из Алгебры 1?

Без полного овладения фактами умножения дети с трудом начинают решать деление, дроби и задачи с большими числами. Они используют так много своей рабочей памяти для простых вычислений, что у них остается мало места в мозгу для понимания новых концепций.

В каком классе мои дети должны изучать факты умножения?

Третий класс . Таким образом, они хорошо подготовлены к решению математических тем третьего и четвертого классов, таких как многозначное умножение, эквивалентные дроби и деление. Но независимо от того, сколько лет вашему ребенку, изучение фактов умножения сделает его более уверенным и успешным в математике. Если ваш старший ребенок не усвоил факты умножения, еще не поздно.

Что мои дети должны знать, прежде чем запоминать факты умножения?

Прежде чем запоминать факты умножения, ваш ребенок должен сначала выучить факты сложения и факты вычитания. Каждый набор фактов логически строится на предыдущем наборе, поэтому важно, чтобы ваш ребенок изучал их именно в этом порядке.

Прежде чем ваш ребенок начнет запоминать факты умножения, вы должны сначала убедиться, что он понимает, что означает умножение. (Например, 3 × 8 означает «3 группы по 8».) Также помогает, если она умеет мысленно складывать однозначные числа с двузначными. (Вы узнаете больше о том, почему в шаге 3 ниже.)

Как быстро мои дети должны знать факты умножения?

Не более 3 секунды на каждый факт и быстрее, если возможно. Но многое зависит от вашего ребенка. Дети, которые очень быстро обрабатывают информацию, вполне способны усвоить каждый факт менее чем за 1 секунду, но детям с более медленным процессором всегда может понадобиться несколько секунд. Вы родитель и знаете своего ребенка лучше всех, поэтому подстраивайте свои ожидания под каждого конкретного ребенка.

Независимо от того, сколько лет вашему ребенку, старайтесь, чтобы время занятий было расслабленным и позитивным. Тесты на умножение и упражнения на время не нужны, если только ваш ребенок не чувствует цейтнота и не находит удовлетворение в том, чтобы бить часы.

Как научить ребенка фактам умножения

Обучение предшествует практике

Чтобы освоить факты умножения, нужно выполнить 5 шагов:

• Шаг 1. Разбейте факты на удобные фрагменты.
• Шаг 2. Конкретизируйте факты с помощью простого наглядного изображения.
• Шаг 3. Научите ребенка использовать простые факты в качестве трамплина к более сложным фактам.
• Шаг 4: Практикуйте каждую таблицу умножения отдельно, пока не освоите ее.
• Шаг 5. Попрактикуйтесь в сочетании фактов умножения.

Обратите внимание, что практика не приходит до шага 4? Практика важна, но это не то, с чего вы начинаете! Обучение предшествует практике .

Шаг 1: Разбейте его.

Это короткий и простой шаг, но важный. Не перегружайте ребенка всеми 100 фактами умножения сразу. Вместо этого сосредоточьтесь только на одной таблице умножения за раз. (Таблица умножения — это всего лишь один набор фактов умножения. Например, таблица × 6 — это 1 × 6, 2 × 6, 3 × 6 и так далее до 10 × 6.)

Разбивка фактов умножения делает освоение таблиц намного более выполнимым (для детей и родителей ). Кроме того, ваш ребенок может затем использовать более простые факты в качестве трамплина к более сложным фактам.

Шаг 2: Конкретизируйте факты с помощью массива умножения.

Для каждой таблицы умножения сначала убедитесь, что ваш ребенок точно понимает, что означают задачи на умножение. В противном случае числа — это просто последовательности абстрактных символов, и их намного сложнее запомнить.

В общем, я большой поклонник практических манипуляций, помогающих детям понять математику. Но с умножением манипуляции могут стать довольно громоздкими. У вас может уйти весь урок математики только на то, чтобы сосчитать 6 групп из 8 предметов, и ваш ребенок, вероятно, не будет намного ближе к тому, чтобы запомнить, что 6 × 8 равно 48.

Вместо этого я предпочитаю использовать простую сетку кругов, называемую точечный массив. С точечным массивом вы можете надеть L-образную крышку на верхнюю часть массива и показать любой факт умножения, который вы хотите, от 1 × 1 до 10 × 10. Вот как выглядит массив точек и L-покрытие.

 

Вот как их использовать. Например, допустим, мы хотели помочь вашему ребенку понять, как выглядит 6 × 8. 6 × 8 означает «6 групп по 8», поэтому сдвиньте L-образную крышку, чтобы массив точек выглядел так.

В каждом из 6 рядов по 8 точек, поэтому имеется 6 групп по 8 точек. Таким образом, общее количество точек в массиве является ответом на 6 × 8.

• Связано: Загрузите свой собственный печатный массив умножения и L-обложку.

Как визуализация фактов умножения помогает детям запомнить ответы? Вот где начинается Шаг 3.

Шаг 3: Научите ребенка использовать более простые факты в качестве трамплина к более сложным фактам.

Умножение немного похоже на восхождение на огромную кучу камней. Когда вы пытаетесь достичь вершины, гораздо проще взобраться на несколько небольших камней, чем пытаться взобраться на отвесную скалу.

Вам определенно не стоит пытаться разобраться в этом!

С фактами умножения гораздо проще использовать факты, которые вы уже выучили, в качестве «трамплина» к более сложным фактам, чем запоминать их наизусть.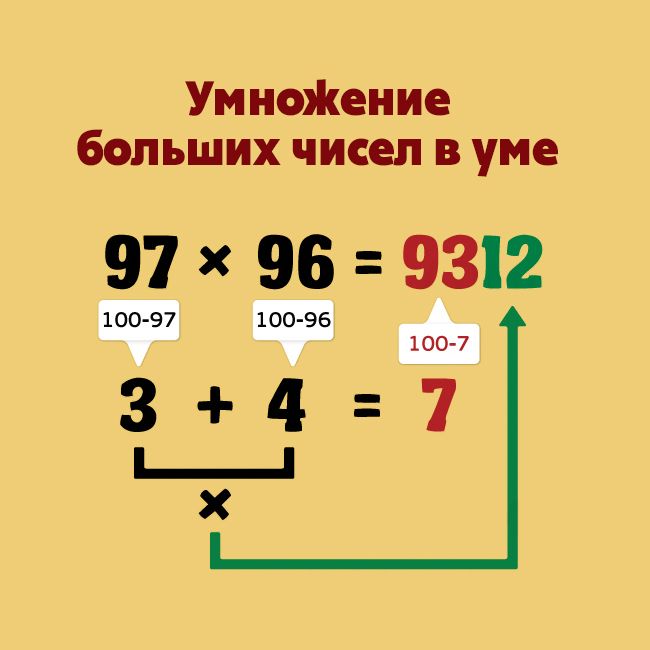 Массив точек поможет вашему ребенку сделать это!

Например, давайте вернемся к 6 × 8. Это один из самых сложных фактов для запоминания детьми, но большинству детей это довольно легко, когда они используют 5 × 8 в качестве трамплина.

Вот как вы научите своего ребенка использовать более простые факты в качестве трамплина к 6 × 8:

1. 5 × 8 равно 40. арифметика обычно упрощает изучение фактов ×5.)
2.  6 × 8 — это всего лишь еще одна группа из 8, чем 5 × 8.
3. Итак, вы можете просто сложить 40 + 8, чтобы найти ответ: 6 × 8 = 48.

Эта стратегия работает для всех фактов ×6. И хорошая новость заключается в том, что для всех фактов умножения есть похожие стратегии!

• Связанный: Стратегии умножения, которые помогут вашему ребенку освоить таблицу умножения

Чтобы использовать ступени, полезно, если ваш ребенок умеет мысленно прибавлять однозначное число к двузначному. Если вашему ребенку не помешало бы еще немного попрактиковаться в умственном сложении, я подготовил небольшой урок и игру, которые помогут ему освежить этот навык.

• Связанный: Умственная игра на сложение, которая на самом деле является игрой на умножение

С помощью этой комбинации массива точек и ступенчатых фактов у вашего ребенка есть план игры, чтобы навсегда освоить все факты умножения. (Без необходимости запоминать каждый факт по отдельности.) Теперь все, что вам нужно, это несколько эффективных практических приемов, которые помогут вашему ребенку полностью автоматизировать все факты умножения.

Шаг 4: Практикуйте каждую таблицу умножения отдельно, пока не освоите ее.

Как только ваш ребенок научится использовать начальные факты для таблицы умножения, сосредоточьтесь на этой конкретной таблице умножения в течение нескольких дней. Используйте сочетание практических методов, чтобы дать вашему ребенку разнообразие и сделать обучение умножению увлекательным. Мне нравится сочетать декламацию, игры и рабочие листы, чтобы дети говорили, видели и записывали факты.

Чтение

Я знаю, чтение таблицы умножения может показаться старомодным.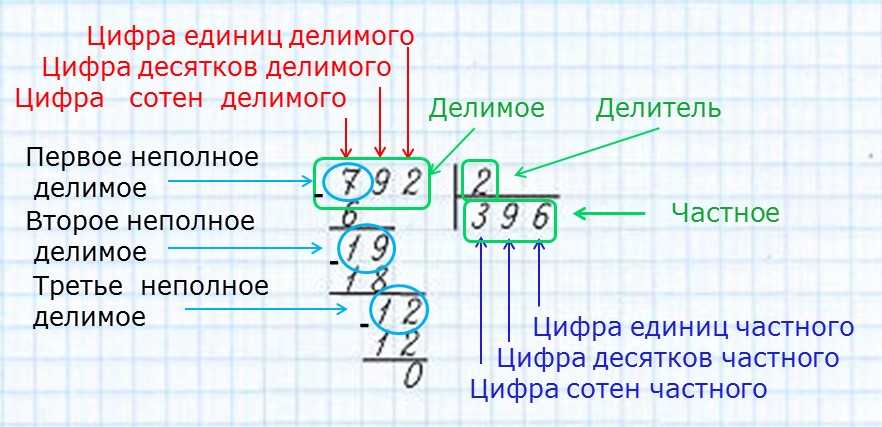 Но произнесение информации вслух помогает закрепить ее в памяти вашего ребенка. Кроме того, чтение каждой таблицы по порядку помогает вашему ребенку понять, как связаны факты в таблице. Например, повторение «1 × 7 равно 7. 2 × 7 равно 14. 3 × 7 равно 21…» напомнит вашему ребенку, что каждый новый факт в таблице × 7 на 7 больше, чем предыдущий факт. Таким образом, он может добавить 7 к каждому предыдущему факту, чтобы помочь ему запомнить следующий, потому что факты в таблице каждый раз добавляют новую группу из 7.

Игры

Люблю математические игры! Они делают математику веселой и общительной, но они также имеют огромное обучающее преимущество: когда вы играете с ребенком в игру на умножение, вы можете следить за тем, насколько хорошо ваш ребенок использует стратегии, и исправлять любые ошибки до того, как они укоренятся.

Рабочие листы

Рабочие листы не самые интересные, но они являются важным компонентом практики, так как ваш ребенок будет часто использовать умножение в своих письменных работах. Рабочие листы должны быть короткими и понятными, чтобы ваш ребенок оставался бдительным и сосредоточенным.

Шаг 5: Смешайте эти факты умножения с другими таблицами умножения.

После того, как ваш ребенок освоил новую таблицу умножения, пришло время смешать эти факты умножения с фактами, которые он уже освоил. Смешивание их вместе обеспечивает кумулятивный обзор, так что факты закрепляются в ее долговременной памяти. Продолжайте использовать декламацию, игры и рабочие листы (и даже карточки, если хотите), пока ваш ребенок не выучит наизусть все 100 фактов.

• Связанный: 3 Веселые (и бесплатные!) Игры с фактами на умножение для печати  для отработки фактов смешанного умножения

Обучение фактам умножения, которые НАПИСЫВАЮТСЯ

Итак, это все 5 шагов! Теперь у вас есть все необходимое для того, чтобы научить вашего ребенка фактам умножения (а не просто разучивать стопки карточек). . (И эй, если вам нравится делать такие вещи, дерзайте!) Но если у вас есть другие дела, я уже сделал всю работу за вас.

Умножение фактов, которые запоминаются Он дает вам подробные планы уроков, веселые игры и простые рабочие листы для каждого шага процесса, так что вы можете научить своего ребенка фактам умножения, которые действительно склеивают .

 

Советы по обучению умножению и делению

В третьем классе одной из самых важных задач по математике является обучение умножению и делению.

Не совершайте ошибку, сразу приступая к решению уравнений, не выработав предварительного четкого понимания концепций умножения и деления. . Это поможет им позже решить более сложные проблемы.

Третьеклассники, у которых проблемы с умножением и делением, часто прибегают к счету на пальцах.

Хотя это может помочь им получить правильный ответ в краткосрочной перспективе, это чрезвычайно усложняет задачу, когда они переходят в 4-й класс, когда от них ожидают, что они будут умножать дроби на целые числа или решать двузначные двузначные задачи и не имеют базовых понятийных навыков. понимание.

Хотите знать, как предотвратить это?

Во-первых, давайте рассмотрим некоторые распространенные заблуждения учащихся об умножении и делении. Затем вы узнаете, что делать, чтобы предотвратить и исправить их.

Умножение Понимание заблуждений

При умножении один коэффициент представляет количество групп, а другое число представляет количество элементов в группе.

Хотя это кажется достаточно простым, чрезвычайно важно, как мы сообщаем об этом нашим ученикам. Если мы слишком расплывчаты в нашем языке, нашим ученикам трудно понять, о чем мы спрашиваем. И проблема просто становится фактом умножения без контекста.

Давайте рассмотрим пример:

Как вы думаете, какое утверждение способствует лучшему пониманию?

• «5 групп по 2 равно 10»
• «5 умножить на 2 равно 10»

Первый!

Важно, чтобы мы использовали точный язык, потому что это помогает развивать понимание и делает изучение новых понятий более понятным для детей.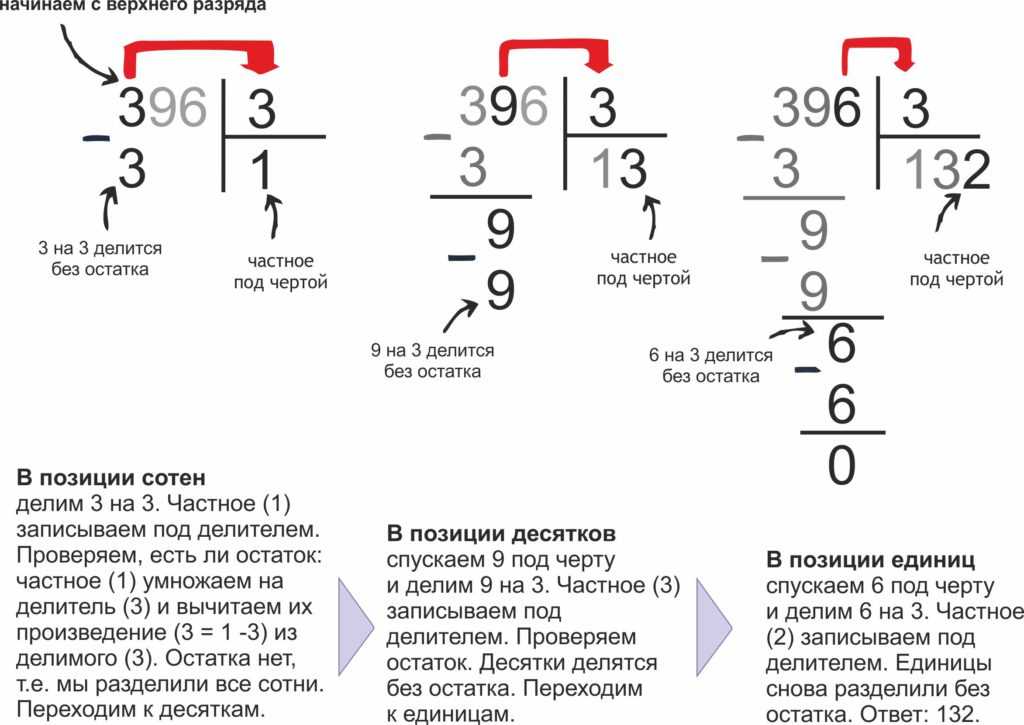

Теперь поговорим о делении.

Отдел понимания заблуждений

Существуют две разные модели деления: раздельное деление и измерительное деление.

В подразделении модель мы пытаемся выяснить сколько элементов находится в группе .

В модели единиц измерения мы пытаемся выяснить сколько существует групп .

Это может сбивать с толку детей, которым сложно определить информацию в задаче (т. е. какое число представляет количество групп, какое число представляет количество элементов в группе).

Давайте рассмотрим пример:

Тина делает подвески для ожерелья. На каждый шарм нужно 3 бусины. Если у Тины всего 21 бусина, сколько амулетов она может сделать, используя все бусины?

Часто, как только дети видят 3 и 21, они автоматически начинают умножать или делить числа, не понимая, что происходит в задаче.

Они могут не знать, если ответ:

• 7 ожерелий
• 7 бусин
• 7 подвесок

Чтобы избежать недоразумений, мы можем показать нашим детям язык и цифры в задаче. Этот простой процесс — быстрый способ улучшить понимание учащимися.

Во-первых, переформулируйте известную им информацию .

В этой задаче…

• Тина делает амулеты
• На каждый шарм нужно 3 бусины
• Всего у Тины 21 бусина

Далее объясните, что обозначают числа и что их нужно найти.

• 21 представляет собой общее количество предметов (бусинок), которые есть у Тины
.
• 3 представляет количество объектов (бусинок) в каждой группе (шарм)
• нужно найти количество групп (брелоков), которые Тина может составить из 21 предмета (бусинок)

Поскольку мы ищем количество групп, это проблема деления измерения.

Наконец, решите проблему.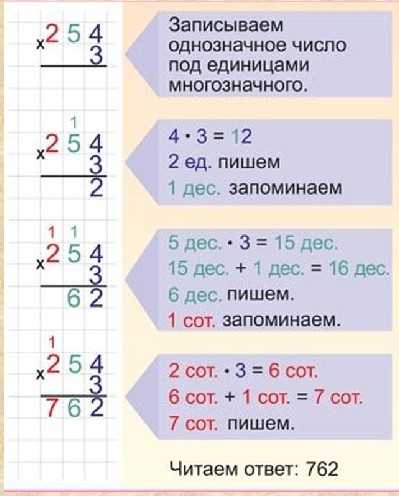

Эту задачу можно решить, нарисовав модель деления измерений или используя уравнение 21 ÷ 3 = ? Рисование модели помогает при ознакомлении с этой концепцией и помогает обучать студентов, которым требуется дополнительная поддержка.

Решение 7. Итак, Тина может составить 7 групп (брелоков).

Наиболее важной частью этого процесса является НЕ ответ . Наоборот, именно так дети получают ответ.

Мы можем настроить наших учеников на успех, научив их определять, что задача требует от них решения! Как только они овладеют этим, они смогут самостоятельно решать широкий спектр проблем.

СОВЕТ ПРОФЕССИОНАЛЬНОМУ УЧИТЕЛЮ: Включайте реальные задачи на деление и умножение в свои уроки и работайте со своими учениками, чтобы разобрать язык в задаче.

Итак, что еще вы можете сделать, чтобы ваши ученики лучше понимали умножение и деление?

Как научить понимать умножение и деление

• Используйте точный язык при обсуждении ситуаций с умножением и делением, чтобы добавить контекст для понимания. Например, , 5 групп по 3 яблока равны 15 яблокам

• Используйте различные модели, представления и стратегии умножения и деления, чтобы учащиеся могли легко определять группы и количество элементов в группе

• Разработайте разнообразные задачи на деление, чтобы учащиеся получили опыт решения задач на деление (сколько элементов в группе?) и задач на измерение (сколько групп?)

• Соедините конкретные модели и графические изображения с символическими изображениями, чтобы устранить неправильные представления

• Попросите учащихся показать свою работу и объяснить свое мнение

Лучшие советы для преподавателей

• Использование модели равных групп , массивы , и модели областей чтобы помочь учащимся визуализировать проблемные ситуации на умножение и деление

• Используйте манипуляторы, такие как счетные фишки и квадратные плитки при вводе тем и продолжайте использовать для учащихся, которым все еще нужны конкретные примеры

• Предложите задачу со словами s, чтобы учащиеся видели умножение и деление в контексте

Сделайте обучение умножению и делению легким с помощью этих уроков «Сделано для вас»

Если вы хотите научить умножению и делению так, чтобы ваши ученики действительно усвоили их, вам понадобится учебник для 3-го класса «Упрощенная математика по умножению и делению» Учебный раздел .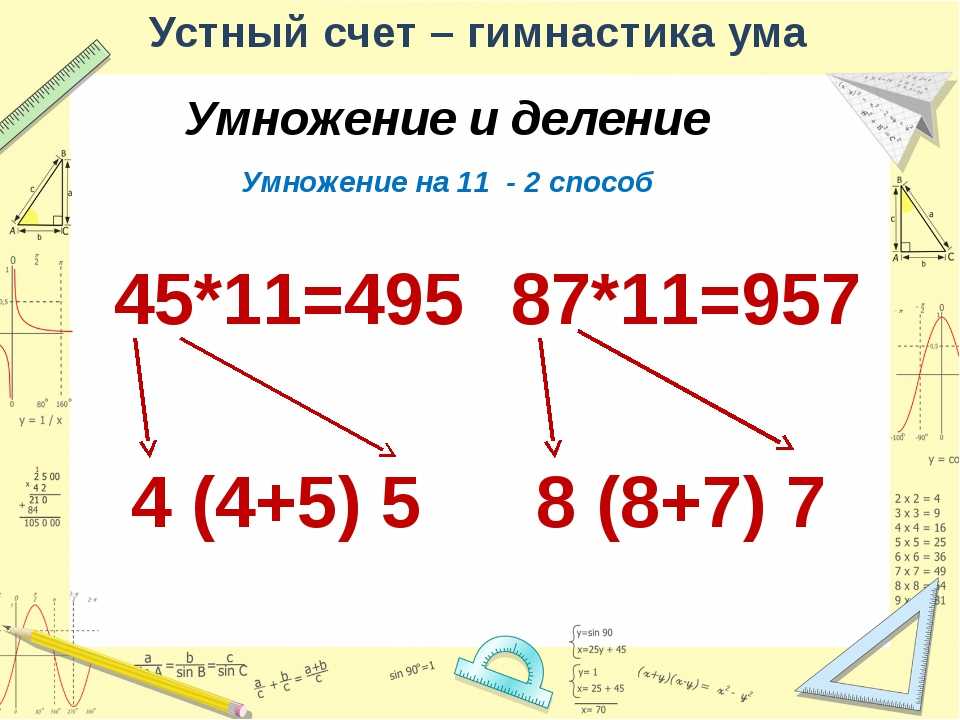

У вас будет все необходимое для преподавания, включая контрольные работы до и после уроков, учебные журналы по математике и многое другое!

Узнайте больше, нажав ниже.

Купить упрощенную программу обучения математике

Умножение и деление

Легко обучайте умножению и делению с помощью этого готового для вас математического модуля , включающего: обучающие слайды, контрольные работы, разминки, дневник учащихся и многое другое.

Кроме того, ознакомьтесь со всеми другими разделами по математике, включенными в упрощённую программу по математике.

Купить сейчас

Свободное владение фактами умножения

Трудно ли вашим учащимся усвоить основные факты умножения? Возьмите этот математический модуль «Сделано для вас» с реальными стратегиями, чтобы ваши дети понимали факты . Он включает в себя: учебные слайды, оценки, разминки, студенческий журнал и многое другое.