Как научить ребёнка самостоятельно решать задачи по математике
Как научить ребёнка решать задачи по математике? Таким вопросом задаются родители, чьи дети начинают ходить в школу. Многим ребятам бывает сложно не то чтобы решить саму задачу, но даже правильно понять ее условие. В этой статье рассказываем, как научить ребенка понимать и решать задачи по математике просто и с удовольствием, а родителям сберечь нервы. Ведь после рабочего дня больше всего хочется отдохнуть, а не сидеть до ночи с ребенком над уроками.
Задачи бывают разные
Прежде чем перейти к практическим советам, как научить ребенка решать математику, рассмотрим, какие типы задач бывают:
Простые
Пожалуй, это самые любимые задачи детей и родителей. Решаются в одно действие (сложение, вычитание). Для их решения ребенку необходимо запомнить разницу между «+» и «-», понятиями «больше» и «меньше», «стало» и «осталось».
Например:
На тарелку, на которой лежало 5 яблок, положили еще 3 яблока. Сколько яблок стало на тарелке? (5+3 = 8)
Сколько яблок стало на тарелке? (5+3 = 8)
С косвенным вопросом
Их уже любят меньше. Решение по-прежнему остается простым, но чтобы не ошибиться, важно правильно понять условие.
Например:
На одной тарелке 7 яблок. Это на 2 яблока больше, чем на другой тарелке. Сколько яблок на другой тарелке? (7 – 2 = 5)
Совет: В таких задачах перечитывайте условия несколько раз, пока ребенок не поймет.
Составные
Для их решения понадобится выполнить несколько действий, поэтому пригодится мини-план.
Например: В одной корзине 10 яиц, а в другой – на 3 яйца меньше. Сколько яиц в обеих корзинах? (10 – 3 = 7, 10 + 7 = 17)
Ребенку можно предложить задать следующие вопросы:
- Что нам нужно узнать? (Сколько всего яиц в двух корзинах).
- Что для этого нужно сделать? (Узнать, сколько яиц во второй корзине).
- Что нужно сделать после того, как мы это узнаем? (Посчитать яйца в обеих корзинах).

Простые задачи на умножение и деление
Например: Катя читала 4 книги, по 5 страниц в каждой книге. Сколько всего страниц прочитала Катя? (5 * 4 = 20)
Здесь ребенок должен понимать, каким образом он может получить ответ: сложить 5 + 5 + 5 + 5 или воспользоваться умножением 5 * 4. Второй способ предполагает понимание множителей и произведений (первый множитель показывает, какое число повторяется, а второй множитель показывает, сколько раз оно повторяется). В случае с делением – делимое, делитель частное.
Составные задачи на разные арифметические действия
Например: После того, как на 3 тарелки положили по 8 апельсинов, осталось еще 13 апельсинов. Сколько всего было апельсинов?
Здесь ребенку стоит предложить написать для себя краткое понятное условие, где будет видно, что дано, что ищем и с помощью каких действий вычислить.
Краткое условие:
Положили 8 апельсинов на 3 тарелки;
Осталось 13 апельсинов;
Сколько было — ?
Решаем задачу в два действия:
- 8 * 3 = 24 (всего апельсинов положили)
- 24 + 13 = 37 (ответ: было 37 апельсинов)
Есть еще задачи на движение, цену, количество, стоимость. Далее разберемся, как научить ребенка решать задачи по математике любой сложности.
Далее разберемся, как научить ребенка решать задачи по математике любой сложности.
Теперь давайте обобщим то, о чем говорили выше. Придерживаясь определенного алгоритма, ребенок быстрее освоит навык решения задач и будет пользоваться им на протяжении всей учебы.
Читаем условия внимательно
Сначала пусть ребенок прочитает задачу вслух сам. Затем спросите, что он понял. Если что-то понял не так, пусть прочтет еще раз. Спросите снова и при необходимости перечитайте условие вместе, делая паузы на непонятных моментах. Главное не нервничайте и позвольте ребенку спокойно разобраться в задаче самостоятельно. Особое внимание уделяйте задачам с косвенным вопросом, в них дети путаются чаще всего.
Описываем задачу своими словами
Можно выписать краткое условие, как мы делали в примерах выше, или составить наглядную схему. Визуальные образы воспринимаются мозгом лучше всего. Визуализация задачи на бумаге поможет ребенку быстро разобраться в условии и увидеть возможные решения уже на этом этапе.
Визуализация задачи на бумаге поможет ребенку быстро разобраться в условии и увидеть возможные решения уже на этом этапе.
Выбираем способ решения
Предыдущий шаг может помочь ребенку увидеть решение, но если нет, следует воспользоваться вспомогательными вопросами, как в примере с составной задачей про яйца.
⠀
Если и это способ не сработает, то попробуйте, например, разыграть сценку из подручных предметов или игрушек. Только не повторяйте один вопрос по несколько раз, это точно не работает, а только повышает напряжение у родителя и ребенка.
⠀
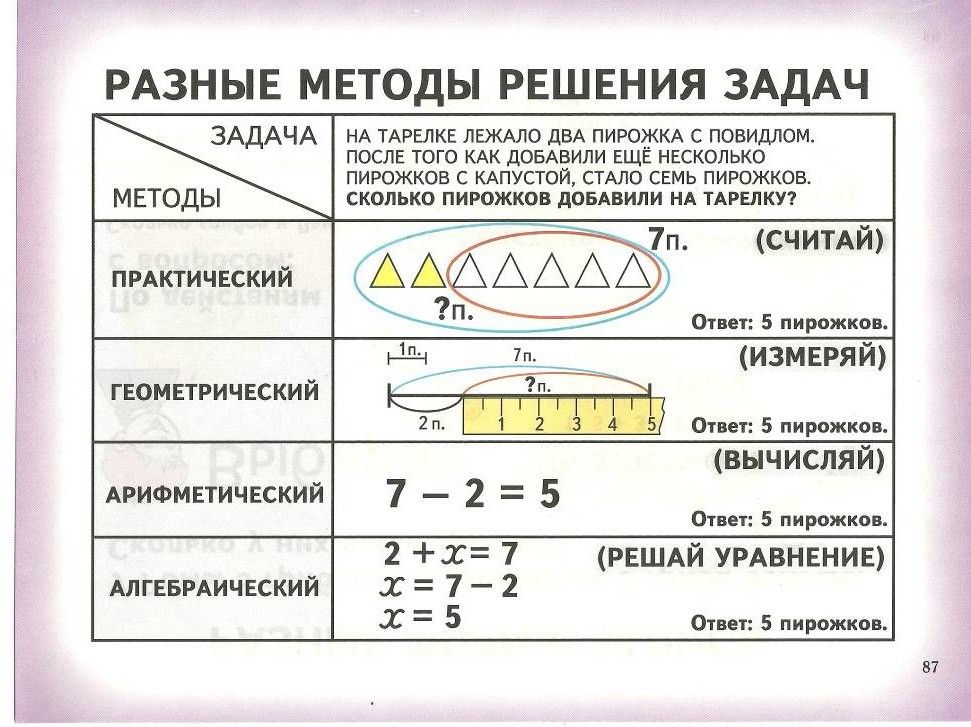
Каждая математическая задача строится по принципу «неизвестное получается из 2 известных». Но чтобы найти нужные числа, необходимо разложить условие на несколько простых действий и выбрать подходящий способ вычисления. Перед этим следует запомнить, какими способами можно находить неизвестное.
Решение тоже можно расписать подробно, чтобы лучше запомнить последовательность и затем использовать для других задач.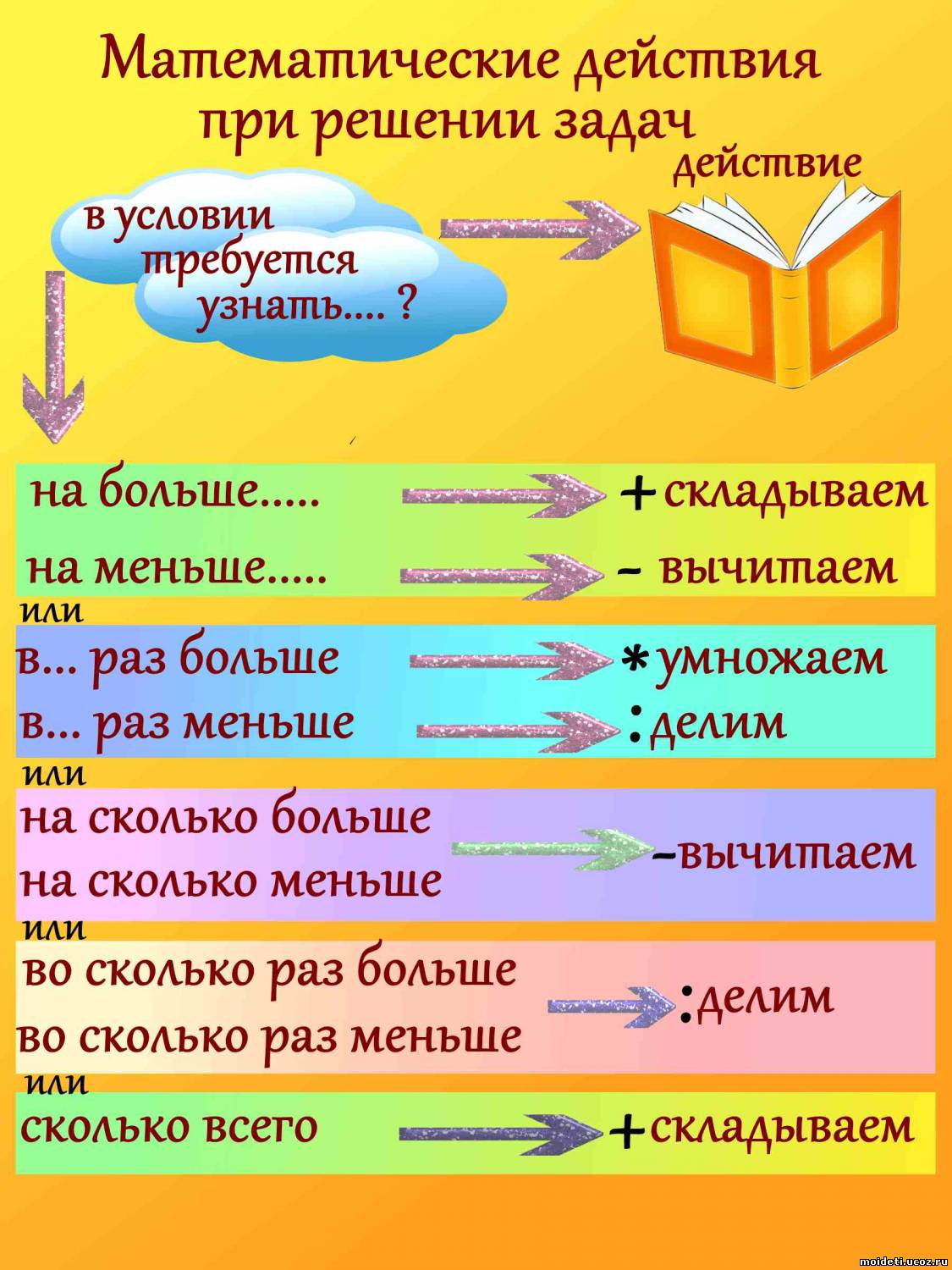
Формулируем ответ
Ребенок должен записать ответ четко и точно. Если это «2 яблока», значит, никакой другой информации в ответе быть не должно. Самая часто встречающаяся ошибка – переносить в ответ те данные, которые были в условии.
⠀
Привыкая к правильным формулировкам, ребенок учится нести ответственность за свои действия и серьезно относится к полученному результату.
Закрепляем навыки
Правильно решив задачу один раз, ребенок сразу не станет гением в точных науках. Полученный результат следует закреплять, как говорится, повторение – мать учения. Можно, например, «поиграть» с задачей и поменять условия, попросив ребенка решить ее еще раз. Главное, чтобы он запомнил, как нужно рассуждать и какие действия выполнять для получения ответа. Благодаря регулярному закреплению ребенок научится правильно рассуждать при решении задач любой сложности.
Читайте также:
Математические игры для дошкольников: считаем, измеряем быстро и легко
Что еще поможет ребенку решать задачи
Конечно, мы не откроем секрет, если скажем, чтобы научить ребенка решать математику, сначала нужно научить его хорошо считать. Ниже несколько рекомендации, которые помогут сделать процесс решения задач легче и увлекательнее:
Ниже несколько рекомендации, которые помогут сделать процесс решения задач легче и увлекательнее:
- Нужно научить ребенка решать простые примеры, выучить с ним таблицу умножения, освоить простые уравнения.
- Лучше подходить к обучению творчески. Детям младшего школьного возраста интереснее всего учиться в игровой форме. Например, можно менять условия задач, подставляя вместо обычных «Кать и Миш», любимых героев из книг и мультфильмов.
Математика в стихах: занимательные задачи для детей от 4 до 7 лет
- Стоит параллельно развивать логическое мышление. Детям с развитым мышлением учеба дается легче. Пробуйте решать с ребенком не только математические задачи, но и логические. Это поможет ему быстрее находить несколько вариантов решения и уходить от шаблонного мышления.
Погрузиться в тему развития логического мышления:
Математическое мышление у ребенка: в чем польза и как его развить?
Как развить креативное мышление у ребенка в домашних условиях? Методы ТРИЗ для детей от 5 лет
- Запишите ребенка на курс математики в онлайн-школу Kidskey.
 Все наши уроки проходят онлайн в игровой форме, после чего ребенку открывается домашнее задание, и он сразу закрепляет пройденный материал. А главное, что ему настолько нравится математика в Kidskey, что ваше присутствие во время урока абсолютно не обязательно. На занятии правильность ответов контролирует педагог, а домашнее задание – сама система.
Все наши уроки проходят онлайн в игровой форме, после чего ребенку открывается домашнее задание, и он сразу закрепляет пройденный материал. А главное, что ему настолько нравится математика в Kidskey, что ваше присутствие во время урока абсолютно не обязательно. На занятии правильность ответов контролирует педагог, а домашнее задание – сама система.
Не уверены, подойдет ли онлайн-формат вашему ребенку? Попробуйте урок бесплатно. Нажимайте на кнопку ниже, и мы подберем для вас удобное время.
Как научить ребенка решать задачи по математике
03.05.2021
Решение задач – одна из неотъемлемых составляющих школьного процесса обучения. В начальных классах дети решают простенькие арифметические задачи, потом наступает пора задач по алгебре и геометрии, физике, химии, биологии.
Содержание:
- Почему важно научить школьника решать задачи?
- Пошаговый алгоритм действий
- Шаг 1.
 Чтение условия
Чтение условия - Шаг 2. Составление краткого описания
- Шаг 3. Поиск алгоритма решения
- Шаг 4. Запись ответа
- Шаг 1.
- Какие навыки необходимы для решения задач
Почему важно научить школьника решать задачи?
Условия задач по разным предметам совершенно не похожи друг на друга, однако методы и приемы решения имеют много общего. И если ребенок не научится решать задачи по арифметике в младшей школе, он будет испытывать нарастающие сложности по мере перехода из класса в класс.
Проблемы с математическими задачами в младших классах – прямой путь к тому, что ребенок сопротивляется изучению точных наук в средней и старшей школе. Преподаватели и родители «записывают» таких учеников в гуманитарии и считают, что им «не дано» научиться решать задачи. А в учебниках написаны сухие формальные правила, которые никак не помогают и не мотивируют учащихся.
На самом деле, умение логически мыслить и решать задачи необходимо все ученикам, даже абсолютным гуманитариям. Без этого во взрослом возрасте невозможно решать даже простейшие бытовые вопросы – к примеру, посчитать количество стройматериалов для ремонта или пропорции ингредиентов при приготовлении блюд. А для программиста, инженера или управленца логическое и аналитическое мышление – неотъемлемая составляющая профессии.
Пошаговый алгоритм действий
Родителям необходимо ребенка учить решать задачи уже с первого класса, причем делать это надо в доброжелательной форме. Нельзя кричать, сердиться или решать задания вместо школьника, как бы вам этого не хотелось. Не ругайте ребенка за ошибки, ведь в процессе обучения они неизбежны, без этого невозможно научиться делать что-либо в принципе.
Функция родителей – объяснить условие задачи и алгоритм рассуждений, который позволяет получить ответ. Стоит сразу запастись терпением, просто не будет. Это кропотливая и длительная работа, за один раз даже самого талантливого ребенка невозможно научить решать задачи.
Это кропотливая и длительная работа, за один раз даже самого талантливого ребенка невозможно научить решать задачи.
Шаг 1. Чтение условия
Умение читать условие и вникать в детали – обязательный навык для успешного решения задачи. Попросите ребенка прочитать условие вслух и задайте ему вопросы, чтобы убедиться в понимании текста. Если в задаче употребляются незнакомые понятия и формулировки, объясните их значения.
Особое внимание обратите на то, правильно ли ребенок понял вопрос. Зачастую сложности проистекают из того, что школьник путает математические понятия «больше в», «больше на» и прочие.
Шаг 2. Составление краткого описания
В школе детей учат составлять описание по определенным правилам, что вызывает у них сложности. Помимо того, что надо понять смысл задачи, школьник вынужден думать, как это записать в соответствии с требованиями учителя.
Значительно проще для ребенка нарисовать условие задачи. Графическая схема позволяет наглядно увидеть связи между элементами задачи и разобраться в условии.
Шаг 3. Поиск алгоритма решения
Наглядная графическая схема в большинстве случаев наталкивает школьника на правильный ход рассуждений. Но что делать, если этого не происходит? В этом случае попробуйте иллюстрировать задачу подручными предметами, разыграйте с ними сценку, задайте наводящие вопросы. Единого метода не существует, вам нужно будет найти подход к ребенку.
Схему решения нужно подробно записать и убедиться, что школьник понимает общий принцип. Тогда он сможет пользоваться в дальнейшем для аналогичных задач.
Шаг 4. Запись ответа
Ответ нужно формулировать полно и точно. Убедитесь, что ребенок отвечает именно на тот вопрос, который спрашивается в задаче. Если это не так, нужно вернуться на первый шаг и заново пройти всю цепочку.
Какие навыки необходимы для решения задач
Для нахождения ответа во многих задач нужно выполнить несколько действий. Убедитесь, что ребенок усвоил правила нахождения слагаемого, уменьшаемого, вычитаемого, множителя, делителя, делимого. Он должен уметь вычислять эти данные на «автомате».
Убедитесь, что ребенок усвоил правила нахождения слагаемого, уменьшаемого, вычитаемого, множителя, делителя, делимого. Он должен уметь вычислять эти данные на «автомате».
Чтобы сохранить мотивацию, проявите творческий подход. К примеру, замените груши и яблоки любимыми лакомствами ребенка, а поезда и катера – космическими кораблями.
Развитая логика и аналитическое мышление – помощники в решении задач. Обязательно решайте с ребенком логические задания, разгадывайте головоломки и ребусы, учите его анализировать окружающие предметы и явления.
Обучение решению проблем | Центр обучения
Версия для печати
- Советы и методы
- Эксперты против начинающих решателей проблем
Советы и методы
Связь- Предложите учащимся определить конкретные проблемы, трудности или недоразумения .
 Не тратьте время на решение проблем, которые учащиеся уже понимают.
Не тратьте время на решение проблем, которые учащиеся уже понимают. - Если учащиеся не могут сформулировать свои опасения, определите, где у них возникли проблемы, с помощью с просьбой определить конкретные концепции или принципы, связанные с проблемой.
- Предложите учащимся сформулировать свой процесс решения проблем
- На занятии один на один попросите ученика решить свою проблему вслух . Это замедляет мыслительный процесс, делая его более точным и позволяя вам получить доступ к пониманию.
- При работе с большими группами вы можете попросить учащихся предоставить письменное «решение в две колонки». Предложите учащимся записать свое решение задачи, поместив все свои расчеты в одну колонку, а все свои рассуждения (полными предложениями) в другую колонку. Это помогает им критически относиться к решению собственных проблем, а вам легче определить, где у них могут возникнуть проблемы.

Решение в две колонки (математика)
Решение в две колонки (физика)
- Моделирование решения проблемы , а не просто давать ученикам ответ. Работая над задачей, подумайте, как новичок может столкнуться с проблемами, и сделайте свое мышление ясным
- Предложите учащимся самостоятельно решить задачи. Задавайте направляющие вопросы или давайте полезные советы, но оказывайте лишь минимальную помощь и только тогда, когда это необходимо для преодоления препятствий.
- Не бойся групповая работа ! Учащиеся часто могут помогать друг другу, а разговор о проблеме помогает им более критически обдумать шаги, необходимые для ее решения. Кроме того, групповая работа помогает учащимся осознать, что проблемы часто имеют несколько стратегий решения, некоторые из которых могут быть более эффективными, чем другие
- Часто при решении рабочих задач студенты не уверены в себе.
 Эта неуверенность может помешать их обучению. Важно осознавать это, когда студенты обращаются к нам за помощью, и давать каждому студенту ощущение мастерства. Сделайте это, предоставив
Эта неуверенность может помешать их обучению. Важно осознавать это, когда студенты обращаются к нам за помощью, и давать каждому студенту ощущение мастерства. Сделайте это, предоставив
- Попытайтесь сообщить, что процесс важнее ответа , чтобы учащийся понял, что не иметь мгновенного решения – это нормально. Этому можно научиться благодаря тому, что вы принимаете его/ее темп действий, отказываетесь позволить тревоге заставлять вас давать правильный ответ, а также благодаря вашему примеру пошагового решения проблемы.
Эксперт против начинающих решателей проблем
Эксперты (преподаватели) в определенной области часто настолько свободно решают проблемы из этой области, что им трудно сформулировать принципы и стратегии решения проблем, которые они используют, новичкам (студентам) в своей области, потому что эти принципы и стратегии второстепенны.
Математик Джордж Полиа описал принципы и стратегии решения задач, которые он использовал в своей дисциплине, в книге «Как решить: новый аспект математического метода » (Princeton University Press, 1957). Книга включает в себя краткое изложение эвристики решения проблем Поли, а также советы по обучению решению проблем.
Новички в определенной области, как правило, еще не разработали эффективные принципы и стратегии решения проблем. Помощь учащимся в выявлении собственных ошибок при решении задач является частью помощи им в развитии навыков эффективного решения проблем. Список распространенных ошибок при решении проблем, составленный Беверли Блэк и Элизабет Аксельсон, адаптированный из книги Артура Уимби и Джека Лоххеда 
Это учебное пособие находится под лицензией Creative Commons Attribution-NonCommercial 4.0 International License.
Обучение решению проблем | Шеридан Центр
На днях подруга-физик работала в лаборатории со своими летними студентами-исследователями. Они говорили о работе, которую проделывали этим летом, и о том, что для всего этого не было никаких руководств или инструкций; ни учебника, ни лабораторной процедуры. Как будто они придумывали это на ходу. Смеясь над этим, один из студентов сказал: «Знаете, что нам нужно? Нам нужен целый курс, в котором нет ничего, кроме проблем. Просто давайте нам одну задачу за другой, и мы придумываем, как их решить. Потому что это и есть настоящее исследование». Остальные студенты рассмеялись. А потом все кивнули.
-Ханштедт, 2018, с. 41
Работодатели, ректоры колледжей, преподаватели и студенты демонстрируют удивительный консенсус в отношении того, что решение проблем является одним из наиболее важных результатов обучения в колледже (Bok, 2017; Hart Research Associates, 2015; Hora, Benbow, Oleson, 2016; Passow & Passow, 2017). ). На момент выпуска этого информационного бюллетеня в этом году было предложено 28 курсов, которые включали слова «проблема*» и «решение» в [email protected]. Описания курсов варьировались от сосредоточения внимания на том, как применять методы или навыки, до решения проблем, решения общих проблем, возникающих в этой области, и концепций, которые включали «проблемы» в свое название. Несомненно, существует больше курсов, которые явно и неявно фокусируются на решении проблем в кампусе. В свете этого акцента важно задаться вопросом: «Что такое проблема и что такое решение проблемы?» и «Как я могу развивать навыки решения проблем на своем курсе?» и, наконец, «Как я буду четко указывать решение проблем в моем курсе и описании курса?» Хотя решение проблем часто ассоциируется с курсами STEM, этот информационный бюллетень предлагает точки зрения и подходы к обучению из разных дисциплин.
). На момент выпуска этого информационного бюллетеня в этом году было предложено 28 курсов, которые включали слова «проблема*» и «решение» в [email protected]. Описания курсов варьировались от сосредоточения внимания на том, как применять методы или навыки, до решения проблем, решения общих проблем, возникающих в этой области, и концепций, которые включали «проблемы» в свое название. Несомненно, существует больше курсов, которые явно и неявно фокусируются на решении проблем в кампусе. В свете этого акцента важно задаться вопросом: «Что такое проблема и что такое решение проблемы?» и «Как я могу развивать навыки решения проблем на своем курсе?» и, наконец, «Как я буду четко указывать решение проблем в моем курсе и описании курса?» Хотя решение проблем часто ассоциируется с курсами STEM, этот информационный бюллетень предлагает точки зрения и подходы к обучению из разных дисциплин.
Что такое «проблема» и решение проблем?
Проблемы и решение проблем могут зависеть от контекста и дисциплины, но концепция и процесс имеют всеобъемлющие компоненты и сходства в разных контекстах. Йонассен (2000, стр. 65) определяет проблему как «неизвестную сущность в некоторой ситуации (разница между целевым состоянием и текущим состоянием)», так что «нахождение или решение неизвестного должно иметь некоторые социальные, культурные или интеллектуальные возможности». ценить.» В рамках курсов студенты могут столкнуться с широким разнообразием текущих (например, постановка задачи) и целевых (например, решение) состояний с разными мотивами их решения. Студенты будут сталкиваться с «хорошо структурированными» проблемами на одном конце спектра, которые имеют типичный путь решения и решение, и «плохо структурированными» проблемами, которые сильно зависят от контекста и не имеют единого пути решения (Jonassen, 2000). ).
Йонассен (2000, стр. 65) определяет проблему как «неизвестную сущность в некоторой ситуации (разница между целевым состоянием и текущим состоянием)», так что «нахождение или решение неизвестного должно иметь некоторые социальные, культурные или интеллектуальные возможности». ценить.» В рамках курсов студенты могут столкнуться с широким разнообразием текущих (например, постановка задачи) и целевых (например, решение) состояний с разными мотивами их решения. Студенты будут сталкиваться с «хорошо структурированными» проблемами на одном конце спектра, которые имеют типичный путь решения и решение, и «плохо структурированными» проблемами, которые сильно зависят от контекста и не имеют единого пути решения (Jonassen, 2000). ).
Мы предлагаем учащимся общие сценарии и пытаемся разработать рамки, необходимые им для решения проблемы, а не просто для поиска ответа. Чтобы помочь учащимся обдумать этот процесс, мы годами разрабатываем сценарии с помощью модулей для самостоятельного изучения, которые учащиеся могут выполнять самостоятельно.
Сценарии остаются прежними, но учащиеся могут вернуться к ним с новой информацией и концепциями, которые они изучили, более глубоким набором инструментов, которые можно использовать в различных клинических условиях. Это позволяет учащимся учиться на протяжении всей жизни и быть более гибкими и адаптируемыми в будущем. -Доктор Стивен Ругас, директор программы докторантуры, Медицинская школа Альперта
Решение проблем — это «целенаправленный» процесс, который включает в себя создание и манипулирование проблемами как ментальными моделями (Jonassen, 2000). Преподаватели Брауна из различных дисциплин были опрошены сотрудниками Sheridan и спросили: «Какие навыки нужны студентам для эффективного решения проблем?» Они ответили, что учащиеся должны уметь делать следующее:
- Рассуждайте, наблюдайте и распознавайте закономерности
- Используйте текущую информацию, чтобы понять прошлое
- Знать, как разбить сложные проблемы на более мелкие, более управляемые компоненты
- Установите связи между понятиями и дисциплинами
- Творчески продумайте несколько путей решения
Эти навыки, среди прочего, нацелены на следующие этапы решения проблем (Pretz, Naples, & Sternbergy, 2003):
- Распознать или определить проблему
- Определите и мысленно представьте проблему
- Разработайте стратегию решения
- Систематизируйте свои знания о проблеме
- Выделить умственные и физические ресурсы для решения проблемы
- Следите за своим продвижением к цели
- Оцените решение на точность
Решение проблем — это итеративный процесс, и поэтому эти шаги не обязательно проходят линейно.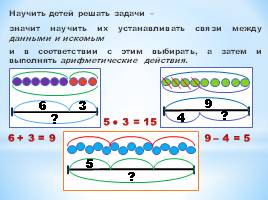 При создании домашних заданий, проектов, экзаменов и т. д. полезно определить конкретные навыки, которые вы хотите, чтобы учащиеся практиковали, стратегии, которые они должны использовать, и то, как вы будете оценивать решения, которые они предлагают.
При создании домашних заданий, проектов, экзаменов и т. д. полезно определить конкретные навыки, которые вы хотите, чтобы учащиеся практиковали, стратегии, которые они должны использовать, и то, как вы будете оценивать решения, которые они предлагают.
Как мне развивать навыки решения проблем в моем курсе?
Преподаватели могут указать, какие навыки решения задач учащиеся должны развить в своих курсах, адаптировав существующие наборы задач в соответствии с рекомендациями проекта «Прозрачность в обучении и преподавании» (TILT). Процесс повышения прозрачности заданий включает в себя доведение до учащихся цели, задачи и критериев задания (Winkelmes et al., 2016):
- Цель обычно связана с одной целью обучения для курса, навыками, которые учащиеся разовьют в результате выполнения задания, или реальным применением, которое учащиеся могут испытать за пределами вашего класса. Таким образом, проблема, которую вы поставили перед студентом, становится актуальной, потому что она имеет «некоторую социальную, культурную или интеллектуальную ценность» (Jonassen, 2000, стр.
 65).
65). - Затем в задании указывается стратегия или стратегии, которые учащиеся должны использовать для выполнения задания. Это включает в себя руководство студентов путем организации информации, доступной для разработки стратегии.
- Наконец, критерием может быть рубрика или аннотированные примеры, которые даются учащимся до выполнения задания, чтобы они знали о стандартах для задания.
В одном исследовании исследователи обнаружили, что на курсах, где по крайней мере два задания имели черты прозрачных заданий, учащиеся сами сообщали о повышении своей академической уверенности, чувстве принадлежности и овладении навыками, такими как решение проблем (Winkelmes et al., 2016). . Ниже приведены примеры различных навыков, необходимых для решения проблем, с предложениями о том, как вы можете развивать эти навыки с помощью адаптированных или новых заданий и упражнений в классе.
Общение
Ключевым навыком решения проблем является умение определить и представить проблему и ее решения. Это верно для всех студентов, независимо от дисциплины. Например, Беркенкоттер (1982, стр. 33) утверждает: «Писатель решает проблемы определенного рода. «Решения» писателей будут определяться тем, как они формулируют свои проблемы, целями, которые они перед собой ставят, и средствами или планами, которые они используют для достижения этих целей». Чтобы помочь студентам понять и подключиться к исследованиям в своей области, преподаватели могут назначать короткие статьи и направлять студентов через риторические практики, чтобы сделать экспертное мышление более явным. Предоставление учащимся множества возможностей для улучшения своего письма позволяет им научиться «формулировать свои проблемы».
Это верно для всех студентов, независимо от дисциплины. Например, Беркенкоттер (1982, стр. 33) утверждает: «Писатель решает проблемы определенного рода. «Решения» писателей будут определяться тем, как они формулируют свои проблемы, целями, которые они перед собой ставят, и средствами или планами, которые они используют для достижения этих целей». Чтобы помочь студентам понять и подключиться к исследованиям в своей области, преподаватели могут назначать короткие статьи и направлять студентов через риторические практики, чтобы сделать экспертное мышление более явным. Предоставление учащимся множества возможностей для улучшения своего письма позволяет им научиться «формулировать свои проблемы».
Далекое прошлое может показаться современным наблюдателям неприятно странным. Когда мы обсуждаем наши классные чтения, мне нравится делать со своими учениками то, что кажется им странным или даже оскорбительным в наших текстах и обществах, которые их создали. Размышление о разрыве между древними и современными взглядами, взглядами, верованиями и ценностями может быть невероятно продуктивным способом осмыслить культурные различия в пространстве и времени.
— Профессор Джонатан Конант, история и классика
Критическое мышление
Критическое мышление — это «способность оценивать свои предположения, убеждения и действия» (Merriam & Bierema, 2014, стр. 222) с намерением изменить свои действия в будущем и необходимо при решении проблем. Это навык, необходимый на всех этапах процесса решения проблем. Воспитание критического мышления у ваших учеников — это один из способов создать более инклюзивный класс, потому что вы по своей сути просите учеников бросить вызов своим предположениям и предубеждениям.
Преподаватели могут использовать следующие условия для развития критического мышления в вашем классе (Merriam & Bierema, 2014):
- Стимулируйте критическое размышление, исследуя предположения (см. Содействие метапознанию для конкретных стратегий размышлений), например, попросите учащихся прочитать научную статью и определить возможные предположения, сделанные в заданных вопросах, используемых методах или интерпретации результатов.
 Например, чтобы способствовать критическому осмыслению, вы можете попросить учащихся определить источники знаний, которые они ценят и используют при выполнении домашних заданий, и написать размышления о том, какие предположения они сделали об этих источниках. Каковы личности людей, создающих эти источники знаний? Какие системы или люди являются привратниками этих знаний?
Например, чтобы способствовать критическому осмыслению, вы можете попросить учащихся определить источники знаний, которые они ценят и используют при выполнении домашних заданий, и написать размышления о том, какие предположения они сделали об этих источниках. Каковы личности людей, создающих эти источники знаний? Какие системы или люди являются привратниками этих знаний? - Создайте учебное сообщество, в котором ожидается, что учащиеся смогут полностью присутствовать, быть честными, задавать вопросы и продуктивно терпеть неудачи (Kapur, 2016).
- Практикуйте диалогический разговор, обучая осознанию отношений власти в классе, таких как микроагрессии или микроаффирмации, и как использовать активное слушание (см. Микроагрессии и микроагрессии для примеров и конкретных практик).
- Предоставьте учащимся возможность установить связь между содержанием и их опытом, например, спрашивая учащихся в домашних заданиях, как они применяют концепции к недавнему опыту, или спрашивая учащихся, почему они выбрали ваш курс и как он связан с их карьерными целями.

Сотрудничество/работа в команде
Преподаватели могут развивать аспекты решения проблем, преднамеренно формируя команду, знакомя студентов с альтернативными точками зрения и четко объясняя ожидания от совместной работы в поле (например, в качестве исследователя, отраслевого партнера, консультанта и т. д.). .). Вы можете создавать домашние задания, используя структуру TILT, которая просит учащихся оценить как свое собственное взаимодействие, так и взаимодействие сверстников в командах. Существует несколько моделей или критериев для оценки командной работы, например, Рубрика ценности командной работы AAC&U, которая фокусируется на поведении учащихся, или Комплексная оценка эффективности членов команды (CATME), представляющая собой бесплатный упакованный инструмент, который собирает информацию от учащихся и объединяет их в команды.
Мы используем групповые учебные упражнения и совместное решение проблем. Студентам назначается предварительное чтение, чтобы расширить свои знания, чтобы они могли обдумать различные аспекты сценария, прежде чем они придут в класс.
В классе обсуждение фокусируется на том, что команда решает и согласовывает, какими будут следующие шаги в кейсе. Навыки решения проблем, на которых фокусируется это групповое обсуждение, — это межличностное общение, способность быть активным слушателем и сотрудничающий член команды. Ставки невелики, но вместе команда добьется успеха или потерпит неудачу.
— Сарита Уорриер, помощник декана по медицинскому образованию, Медицинская школа Альперт
Мозаика — это еще один совместный подход к обучению студентов тому, как разбить проблему на более мелкие компоненты. Например, на уроке романтизма и романтической философии трем группам студентов задаются следующие вопросы о пяти стихотворениях: «Как писатель смотрит на природу?» (1-я группа): «Как писатель смотрит на общество?» (Группа 2): «Как писатель видит цель поэзии?» (Группа 3). После обсуждения три новые группы с представителями каждого из этих трех кластеров могут обсудить более широкий вопрос, например: «Используя информацию, собранную в первых группах [. ..], каковы цели романтизма? Какова повестка дня поэтов-романтиков?» (Хандштедт, 2018, стр. 121-122).
..], каковы цели романтизма? Какова повестка дня поэтов-романтиков?» (Хандштедт, 2018, стр. 121-122).
Рефлексия или задания
Опытные исследователи, практики и преподаватели включают рефлексию и итерацию как часть своей практики. Ключевые этапы процесса решения проблем включают размышления о процессе и о том, что работает или не работает для достижения цели. В предыдущем информационном бюллетене, Продвижение метапознания , Центр Шеридана предоставил список нескольких видов деятельности и заданий, которые вы могли бы использовать, чтобы помочь учащимся задуматься над вашим курсом. Эти мероприятия варьируются от коротких минутных статей до ведения журналов для размышлений на семестр. Мысли вслух, или когда учащийся устно решает проблему с другим учащимся, также может помочь учащимся развить рефлексивные навыки решения проблем, потому что «обеспечивает учащимся структуру, позволяющую наблюдать как за своим, так и за чужим процессом обучения» (Баркли, 2010, с. стр. 259).
стр. 259).
Чтобы узнать больше о том, как привлечь учащихся к этим навыкам и темам, ознакомьтесь с информационным бюллетенем Sheridan Center «Инклюзивное обучение через активное обучение». Важно четко указать, как вы подходите к решению проблем, и передавать эту информацию как через описание вашего курса, учебные программы, так и через содержание.
Возможности в Sheridan для развития решения проблем
Решение проблем является необходимым навыком во всех дисциплинах, и центр Sheridan уделяет особое внимание этому в рамках программы Brown Learning Collaborative, которая предоставляет учащимся возможность достичь новых уровней мастерства в шести ключевые навыки, традиционно оттачиваемые в гуманитарном образовании – критическое чтение, письмо, исследование, анализ данных, устное общение и решение проблем. Чтобы помочь вам продумать, как интегрировать возможности студентов для эффективного решения проблем в ваш курс, Центр Шеридана предлагает возможности профессионального развития для решения проблем для преподавателей и студентов, стремясь привлечь преподаватели разных поколений, преподаватели-студенты.
Институт разработки курсов решения проблем
Повышение прозрачности заданий лежит в основе Института разработки курсов решения проблем (PSCDI). PSCDI — это двухдневный семинар для преподавателей, сотрудников, постдоков и аспирантов, посвященный (пере)разработке заданий, которые вовлекают студентов в процесс решения проблем. После успешного завершения участники факультета получат грант в размере 2000 долларов США для реализации своих идей. Для получения дополнительной информации о PSCDI и предыдущих рецептах см. этот веб-ресурс Sheridan.
Программа стипендиатов по решению проблем
Студентам бакалавриата, которые в настоящее время или планируют стать наставниками по принципу «равный-равному-равному-равному-равному-равному-равному-равному»-(например,-специалистам-консультантам-лаборантам, наставникам-врачам и т. д.), рекомендуется пройти курс UNIV 1110: The Theory and Teaching of Problem Solving . В рамках этого курса мы фокусируемся на разработке эффективных решений проблем с помощью практики обучения студентов. Мы обсуждаем рефлексивные практики, необходимые для обучения и решения проблем; теоретические рамки для эффективного обучения; как культура, контекст и идентичность влияют на решение проблем и обучение; и влияние цикла решения проблем. Для получения дополнительной информации посетите этот веб-ресурс Sheridan и свяжитесь с доктором Кристиной Смит, Sheridan Center (через [email protected]).
Мы обсуждаем рефлексивные практики, необходимые для обучения и решения проблем; теоретические рамки для эффективного обучения; как культура, контекст и идентичность влияют на решение проблем и обучение; и влияние цикла решения проблем. Для получения дополнительной информации посетите этот веб-ресурс Sheridan и свяжитесь с доктором Кристиной Смит, Sheridan Center (через [email protected]).
Ссылки
Беркенкоттер, К. (1982). Написание и решение задач. В T. Fulwiler & A. Young (Eds.), Языковые связи: письмо и чтение по учебной программе (стр. 33-44). Урбана, Иллинойс: Национальный совет учителей английского языка.
Баркли, Э. Ф. (2010). Методы вовлечения студентов: пособие для преподавателей колледжей . Сан-Франциско, Калифорния: Джосси-Басс.
Бок, Д. (2017). Борьба за реформирование наших колледжей. Принстон, Нью-Джерси: Издательство Принстонского университета.
Ханстедт, П. (2018). Создание злых учеников: разработка курсов для сложного мира . Стерлинг, Вирджиния: Стилус.
Создание злых учеников: разработка курсов для сложного мира . Стерлинг, Вирджиния: Стилус.
Харт Рисерч Ассошиэйтс. (2015). Недотягивает? Учеба в колледже и карьерный успех . Опрос, проведенный для AAC&U. Доступно: https://www.aacu.org/sites/default/files/files/LEAP/2015employerstudents…
Хора, М.Т., Бенбоу, Р.Дж., и Олесон, А.К.. (2016). Вне пробела в навыках: подготовка студентов к жизни и работе . Кембридж, Массачусетс: Издательство Гарвардского университета.
Йонассен, Д. Х. (2000). К дизайн-теории решения проблем. Исследования и разработки в области образовательных технологий , 48(4), 63-85.
Капур, М. (2016). Изучение продуктивных неудач, продуктивных успехов, непродуктивных неудач и непродуктивных успехов в обучении. Педагог-психолог , 51(2), 289-299.
Мерриам, С.Б., и Бирема, Л.Л. (2014). Обучение взрослых: связь теории и практики . Джон Уайли и сыновья.
Пассоу, Х.

 Все наши уроки проходят онлайн в игровой форме, после чего ребенку открывается домашнее задание, и он сразу закрепляет пройденный материал. А главное, что ему настолько нравится математика в Kidskey, что ваше присутствие во время урока абсолютно не обязательно. На занятии правильность ответов контролирует педагог, а домашнее задание – сама система.
Все наши уроки проходят онлайн в игровой форме, после чего ребенку открывается домашнее задание, и он сразу закрепляет пройденный материал. А главное, что ему настолько нравится математика в Kidskey, что ваше присутствие во время урока абсолютно не обязательно. На занятии правильность ответов контролирует педагог, а домашнее задание – сама система. Чтение условия
Чтение условия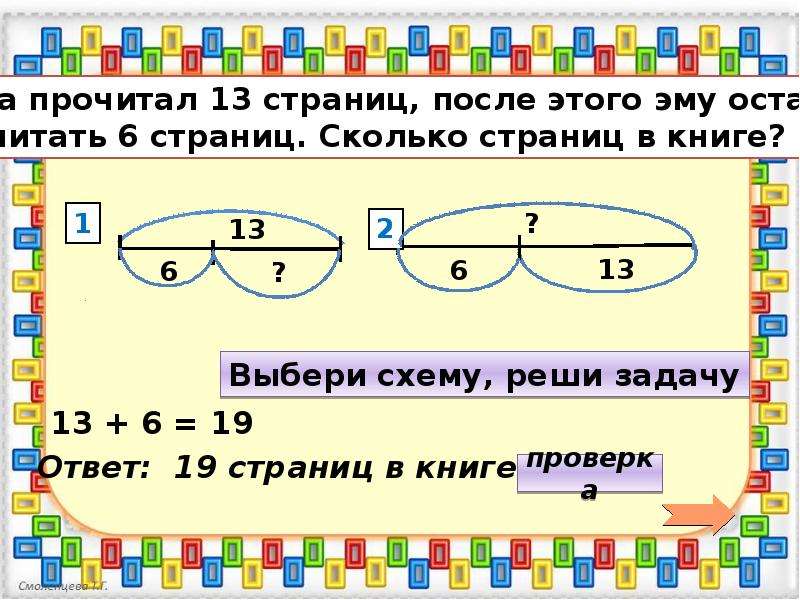 Не тратьте время на решение проблем, которые учащиеся уже понимают.
Не тратьте время на решение проблем, которые учащиеся уже понимают.
 Эта неуверенность может помешать их обучению. Важно осознавать это, когда студенты обращаются к нам за помощью, и давать каждому студенту ощущение мастерства. Сделайте это, предоставив
Эта неуверенность может помешать их обучению. Важно осознавать это, когда студенты обращаются к нам за помощью, и давать каждому студенту ощущение мастерства. Сделайте это, предоставив 
 65).
65).
 Например, чтобы способствовать критическому осмыслению, вы можете попросить учащихся определить источники знаний, которые они ценят и используют при выполнении домашних заданий, и написать размышления о том, какие предположения они сделали об этих источниках. Каковы личности людей, создающих эти источники знаний? Какие системы или люди являются привратниками этих знаний?
Например, чтобы способствовать критическому осмыслению, вы можете попросить учащихся определить источники знаний, которые они ценят и используют при выполнении домашних заданий, и написать размышления о том, какие предположения они сделали об этих источниках. Каковы личности людей, создающих эти источники знаний? Какие системы или люди являются привратниками этих знаний?
 В классе обсуждение фокусируется на том, что команда решает и согласовывает, какими будут следующие шаги в кейсе. Навыки решения проблем, на которых фокусируется это групповое обсуждение, — это межличностное общение, способность быть активным слушателем и сотрудничающий член команды. Ставки невелики, но вместе команда добьется успеха или потерпит неудачу.
В классе обсуждение фокусируется на том, что команда решает и согласовывает, какими будут следующие шаги в кейсе. Навыки решения проблем, на которых фокусируется это групповое обсуждение, — это межличностное общение, способность быть активным слушателем и сотрудничающий член команды. Ставки невелики, но вместе команда добьется успеха или потерпит неудачу.