Общий знаменатель дробей онлайн | umath.ru

Калькулятор приводит несколько дробей к общему знаменателю. Просто введите дроби и получите подробное решение и ответ. Можно вводить две, три дроби и более. Числители и знаменатели дробей должны быть натуральными числами.

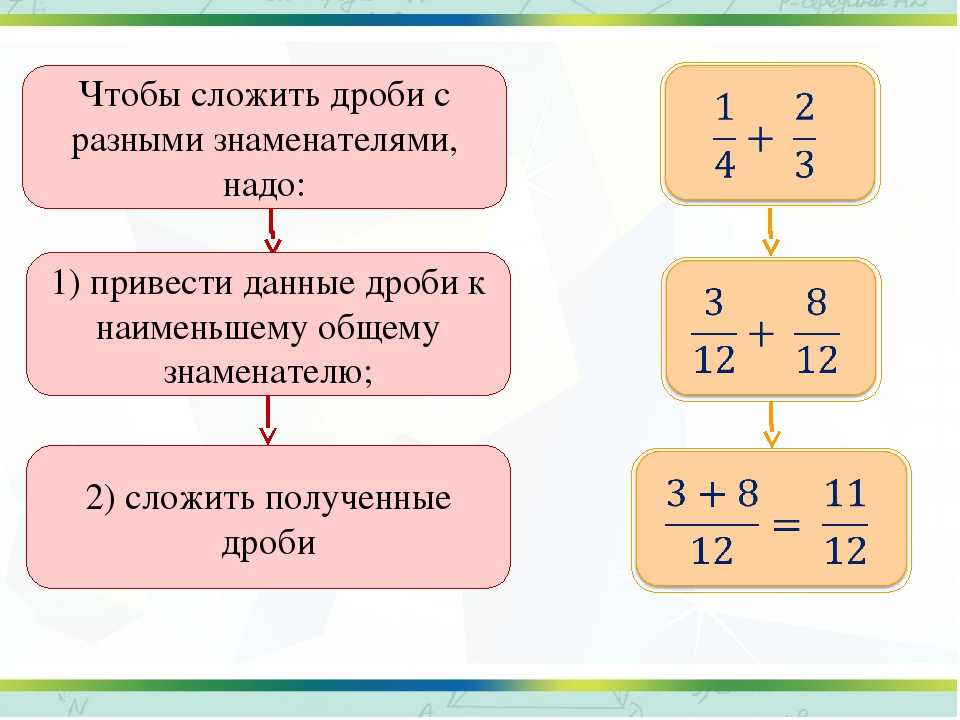
Как привести дроби к общему знаменателю?

Чтобы выполнить с дробями такие операции, как сравнение, сложение и вычитание, дроби нужно привести к общему знаменателю.

Рассмотрим алгоритм приведения дробей к общему знаменателю. Пусть даны две дроби и Чтобы привести их к общему знаменателю, надо:

1. Найти наименьшее общее кратное знаменателей дробей. Пусть оно равно .
2. Числитель и знаменатель первой дроби умножить на число
3. Числитель и знаменатель второй дроби умножить на число

В результате мы получим две дроби со знаменателем, равным

Пример.

Привести к общему знаменателю дроби и

Решение. Находим наименьшее общее кратное знаменателей дробей. НОК(12, 8) = 24. Это число и будет новым знаменателем.

Чтобы знаменатели обеих дробей стали равны 24, числитель и знаменатель первой дроби нужно домножить на 2 = 24:12, а числитель и знаменатель второй дроби — на 3 = 24:8.

Приводим к общему знаменателю первую дробь:

   

Приводим к общему знаменателю вторую дробь:

   

Общий знаменатель трёх дробей

Если к общему знаменателю требуется привести три дроби и более, то алгоритм действий в таком случае аналогичен алгоритму для двух дробей.

1. Находим наименьшее число , которое делится на знаменатели всех дробей (наименьшее общее кратное знаменателей всех дробей). Найденное число будет новым знаменателем.
2. Домножаем числитель и знаменатель каждой дроби на частное

В результате знаменатели всех дробей будут равны .

Чтобы разобраться лучше, рассмотрим пример.

Пример. Привести к общему знаменателю три дроби и

Решение. Сначала найдём наименьшее общее кратное знаменателей дробей. Число 12 делится на знаменатели всех дробей, и это наименьшее такое число. Поэтому НОК(3, 4, 6) = 12. Число 12 будет новым знаменателем.

Чтобы знаменатели дробей стали равны 12, числитель и знаменатель первой дроби нужно домножить на 4 = 12:3, числитель и знаменатель второй дроби — на 3 = 12:4, а числитель и знаменатель третьей дроби — на 2 = 12:6.

Приводим дроби к общему знаменателю и получаем:

   

   

   

Всё — дроби приведены! Пожалуй, самая большая сложность — правильно найти (или угадать) число, которое будет новым знаменателем.

Приведение дробей к общему знаменателю. Онлайн калькулятор

• Общий знаменатель обыкновенных дробей
• Приведение дробей к общему знаменателю
• Калькулятор приведения к общему знаменателю

Общий знаменатель обыкновенных дробей

Если обыкновенные дроби имеют одинаковые знаменатели, то про эти дроби говорят, что они имеют общий знаменатель. Например, дроби

  и  

имеют общий знаменатель  7.

Общий знаменатель — это число, которое является знаменателем для двух и более обыкновенных дробей.

Дроби, имеющие разные знаменатели, можно привести к общему знаменателю.

Приведение дробей к общему знаменателю

Приведение дробей к общему знаменателю — это замена данных дробей, имеющих разные знаменатели, на равные им дроби, у которых одинаковые знаменатели.

Дроби можно привести либо просто к общему знаменателю, либо к наименьшему общему знаменателю.

Наименьший общий знаменатель — это наименьшее общее кратное знаменателей данных дробей. Чтобы привести дроби к наименьшему общему знаменателю нужно:

1. Выполнить сокращение дробей, если это возможно.
2. Найти наименьшее общее кратное знаменателей данных дробей. Именно НОК и станет их наименьшим общим знаменателем.
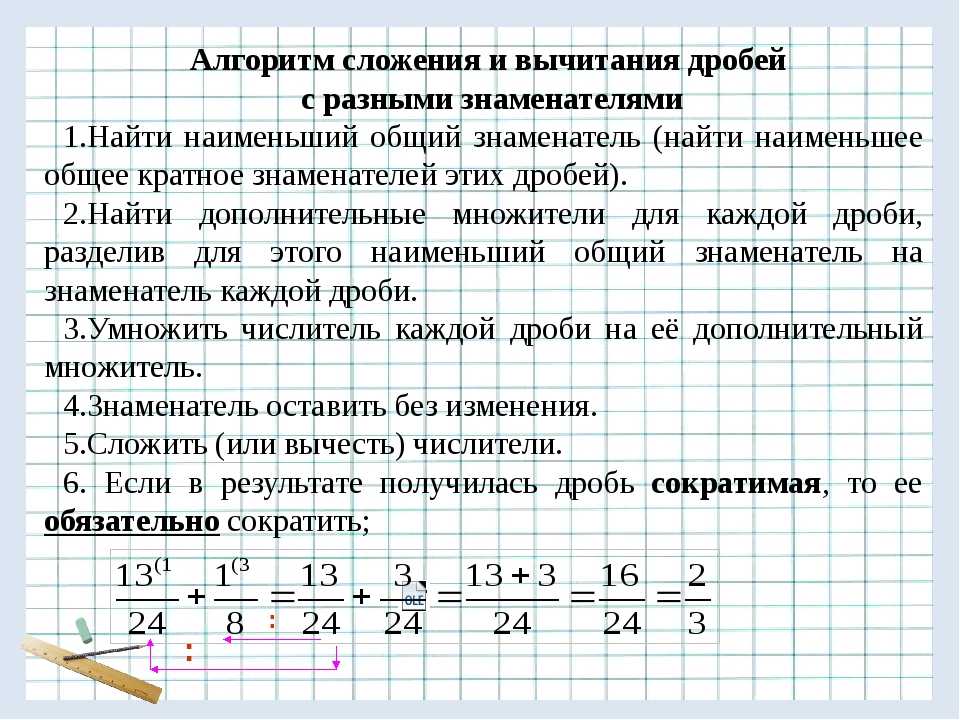
3. Разделить НОК на знаменатели данных дробей. Этим действием мы находим дополнительный множитель для каждой из данных дробей. Дополнительный множитель — это число, на которое надо умножить члены дроби, чтобы привести её к общему знаменателю.
4. Умножить числитель и знаменатель каждой дроби на дополнительный множитель.

Пример. Привести к общему знаменателю дроби    и  .

Решение:

1. Находим НОК знаменателей данных дробей:

   НОК (8, 12) = 24.

2. Находим дополнительные множители:

   24 : 8 = 3  (для  )

   и

   24 : 12 = 2  (для  ).

3. Умножаем члены каждой дроби на свой дополнительный множитель:

Приведение к общему знаменателю можно записывать в более краткой форме, указывая дополнительный множитель рядом с числителем каждой дроби (сверху справа или сверху слева) и не записывая промежуточные вычисления:

К общему знаменателю можно привести и более простым способом, умножив члены первой дроби на знаменатель второй дроби, а члены второй дроби — на знаменатель первой.

Пример. Привести к общему знаменателю дроби    и  :

В качестве общего знаменателя дробей можно взять произведение их знаменателей.

Приведение дробей к общему знаменателю используется при сложении, вычитании и сравнении дробей, у которых разные знаменатели.

Калькулятор приведения к общему знаменателю

Данный калькулятор поможет вам привести обыкновенные дроби к наименьшему общему знаменателю. Просто введите две дроби и нажмите кнопку Привести.

Вычитание дробей с общими знаменателями

Результаты обучения

• Используйте круги дробей, чтобы найти разницу между двумя дробями с одинаковыми знаменателями
• Вычитание дробей с одинаковыми знаменателями без дробных кругов

Модель Вычитание дробей

Вычитание двух дробей с общими знаменателями очень похоже на сложение дробей. Представьте себе пиццу, нарезанную на [латекс]12[/латекс] кусочков. Предположим, что за ужином съедено пять штук. Это означает, что после обеда в коробке осталось семь кусков (или [латекс]{\большой\фрак{7}{12}}[/латекс] пиццы). Если Леонардо съест [латекс]2[/латекс] из этих оставшихся кусков (или [латекс]{\большой\фрак{2}{12}}[/латекс] пиццы), сколько останется? Осталось [латекс]5[/латекс] кусочков (или [латекс]{\большой\фрак{5}{12}}[/латекс] пиццы).

[латекс] {\ Большой \ гидроразрыва {7} {12}} — {\ Большой \ гидроразрыва {2} {12}} = {\ Большой \ гидроразрыва {5} {12}} [/латекс]

Давайте используйте дробные круги для моделирования того же примера, [латекс] {\ большой \ гидроразрыв {7} {12}} — {\ большой \ гидроразрыва {2} {12}} [/латекс].

Начните с семи [латексных] {\ больших \ гидроразрывов {1} {12}} [/ латексных]. Уберите два куска [латекс]{\Large\frac{1}{12}}[/latex]. Сколько двенадцатых осталось?

Опять же, у нас есть пять двенадцатых, [латекс] {\ большой \ гидроразрыв {5} {12}} [/латекс].

Пример

Используйте дробные круги, чтобы найти разницу: [латекс] {\ большой \ гидроразрыв {4} {5}} — {\ большой \ гидроразрыва {1} {5}} [/латекс]

Решение:
Начните с четырех [латексных] {\ больших \ гидроразрывов {1} {5}} [/латексных] частей. Уберите один кусок [латекса]{\Large\frac{1}{5}}[/latex]. Посчитайте, сколько пятых осталось. Осталось три куска [латекс]{\большой\фрак{1}{5}}[/латекс].

Попробуйте

Вычитание дробей с общим знаменателем

Мы вычитаем дроби с общим знаменателем почти так же, как складываем дроби с общим знаменателем.

Вычитание дроби

Если [latex]a,b,\text{ и }c[/latex] — числа, где [latex]c\ne 0[/latex], то

[latex]{\Large\frac{a}{c }}-{\Large\frac{b}{c}}={\Large\frac{a-b}{c}}[/latex]

Чтобы вычесть дроби с общим знаменателем, мы вычитаем числители и помещаем разницу над общим знаменателем.

Пример

Найдите разницу: [латекс]{\Large\frac{23}{24}}-{\Large\frac{14}{24}}[/latex]

Показать решение

Попробуйте

Посмотрите следующее видео, чтобы увидеть больше примеров вычитания дробей с одинаковыми знаменателями.

Пример

Найдите разницу: [латекс]{\большой-\frac{10}{7}-\frac{4}{7}}[/latex]

Показать решение

Теперь давайте сделаем пример, включающий сложение и вычитание.

Пример

Упрощение: [латекс]{\Large\frac{3}{8}}+\left(-{\Large\frac{5}{8}}\right)-{\Large\frac{1 {8}}[/latex]

Показать решение

Попробуйте

Вычитание дробей Упражнения с общими и необычными знаменателями

В сегодняшнем посте, мы будем объяснять упражнения с вычитанием дробей. Мы также увидим некоторые упражнения Smartick по вычитанию дробей, которые дети выполняют во время своих занятий.

В предыдущем сообщении в блоге мы объяснили, как вычитать дроби. Вы можете посмотреть и просмотреть этот пост, прежде чем читать дальше.

Чтобы вычитать дроби, нам нужно знать, как вычислить наименьшее общее кратное между различными числами.

Если вы уже знаете, как найти наименьшее общее кратное чисел, давайте продолжим!

Вычитание дробей с общим знаменателем

Действия для вычитания дробей с общим знаменателем

Мы можем вычитать дроби без дополнительных действий когда они имеют общий знаменатель , вам просто нужно:

1. Записать общий знаменатель дробей в результате.
2. Вычтите числа в числителе и запишите результат в числителе результата.

Примеры

• \(\frac{7}{3}\) – \(\frac{2}{3}\) = \(\frac{5}{3}\)
• \(\frac{10}{5}\) – \(\frac{2}{5}\) = \(\frac{8}{5}\)

Решенные упражнения

Теперь мы увидим несколько заданий, которые дети решают во время занятий Smartick на вычитание дробей с общими знаменателями.

Как видите, торт — это визуальное представление, помогающее вычитать дроби. Он делится на 10 равных частей, что в итоге дает нам 4 куска торта .

\(\frac{7}{10}\) – \(\frac{3}{10}\) = \(\frac{4}{10}\) раз плюнуть.

Так как первая дробь, \(\frac{4}{10}\), имеет четные числитель и знаменатель, ее можно упростить, что даст вам \(\frac{2}{5}\) пирога даже если части были разрезаны и не могут быть собраны вместе.

 

В этом упражнении вы используете кружков , чтобы представить дроби. Сначала нам нужно разделить два круга на 5 равных частей и затем нам нужно раскрасить 3 части одного круга, а 2 части другого. Мы видим, что в результате получился круг, который имеет только одну оранжевую часть.

\(\frac{3}{5}\) – \(\frac{2}{5}\) = \(\frac{1}{5}\) цветных частей круга.

Вычитание дробей с необычными знаменателями

Их можно найти:

• Вычитание еще сложных дробей . Эти типы дробей имеют необычные знаменатели: не кратны друг другу . Например: \(\frac{5}{6}\) – \(\frac{7}{13}\)
• Вычитание более простых дробей. Эти типы дробей имеют необычные знаменатели, а знаменатели кратны друг другу . Например: \(\frac{5}{6}\) – \(\frac{7}{12}\) (12 кратно 6).

В обоих случаях мы должны создать дроби с общими знаменателями, чтобы мы могли завершить вычитание.

Действия по вычитанию сложных дробей с необычными знаменателями

Чтобы вычесть более сложные дроби , у нас должны быть дроби, имеющие общий знаменатель, и этот знаменатель должен быть кратен двум текущим знаменателям.

Это может быть любое общее кратное, но мы рекомендуем использовать наименьшее общее кратное:

1. Найдите наименьшее общее кратное знаменателей.
2. Запишите новые дроби, эквивалентные исходным дробям, используя наименьшее общее кратное в знаменателе.
3. Полученные дроби будут иметь общий знаменатель, поэтому мы можем действовать так же, как в предыдущем примере: вычесть числители и записать их результат как числитель получившейся дроби.

Пример 1

\(\frac{2}{3}\) – \(\frac{3}{5}\)

Первое, что мы собираемся сделать, это найти наименьшее общее кратное между знаменателями дробей:

л.с.м. (3, 5) = 15

Теперь запишем эквивалентные дроби предыдущих дробей со знаменателем 15:

\(\frac{2}{3}\) = \(\frac{?}{15}\)

Чтобы найти числитель, нам нужно умножить его (2) на то же число, которое мы использовали чтобы получить знаменатель.

Чтобы получить от 3 до 15, мы умножаем на 5. Вот почему мы также умножим числитель на 5.

\(\frac{2}{3}\) = \(\frac{10}{15} \)

Проделаем то же самое с другой дробью:

\(\frac{3}{5}\) = \(\frac{?}{15}\)

Знаменатель был умножен на 3, поэтому числитель тоже умножится на 3:

\(\frac{3}{5}\) = \(\frac{9}{15}\)

Теперь, когда дроби имеют одинаковый знаменатель , мы можем вычесть:

\(\frac{ 10}{15}\) – \(\frac{9}{15}\) = \(\frac{1}{15}\)

Пример 2

\(\frac{5}{6} \) – \(\frac{3}{10}\)

Наименьшее общее кратное между 6 и 10 равно 30.

Мы нашли эквивалентных дробей :

\(\frac{5}{6 }\) = \(\frac{?}{30}\)

Знаменатель был умножен на 5, поэтому числитель также должен быть умножен на 5:

\(\frac{5}{6}\) = \(\frac{25}{30}\)

Теперь делаем другую дробь:

\(\frac{3}{10}\) = \(\frac{?}{30}\)

Знаменатель был умножен на 3, поэтому числитель также нужно умножить на 3:

\(\frac{3}{10}\) = \( \frac{9}{30}\)

Наконец, мы вычитаем дроби:

\(\frac{25}{30}\) – \(\frac{9}{30}\) = \(\frac {16}{30}\)

Последнюю дробь также можно упростить:

\(\frac{16}{30}\) = \(\frac{8}{15}\)

Шаги для вычитания простых дробей с необычными знаменателями

Мы могли бы найти наименьшее общее кратное между знаменателями, но мы увидим другой способ вычитания более простых дробей , только для следующих типов дробей:

1. Найдите эквивалентная дробь дроби, знаменатель которой является делителем другой дроби так, что знаменатели двух дробей равны.
2. Полученные дроби уже имеют одинаковый знаменатель, поэтому мы вычтем числители и запишем получившуюся дробь.

Пример 1

\(\frac{5}{6}\) – \(\frac{7}{12}\)

Дробь, эквивалентная \(\frac{5}{6}\ ) равно \(\frac{10}{12}\), мы умножили числитель и знаменатель на 2.

Теперь у нас есть две дроби с одинаковым знаменателем, 12:

\(\frac{10}{12 }\) – \(\frac{7}{12}\)

Итак, результат вычитания:

\(\frac{10}{12}\) – \(\frac{7}{12 }\) = \(\frac{3}{12}\)

Пример 2

Мы также можем искать эту эквивалентную дробь визуально и интуитивно. Давайте рассмотрим несколько примеров деятельности Smartick.

Чтобы решить эту задачу, нам нужно сделать две вещи:

1. Найти л.с.м 12 и 6, что равно 12.
2. Создайте эквивалентные дроби, как мы видели в предыдущих примерах.

В этом упражнении вы можете использовать столбцов , чтобы помочь вам найти результат дроби, просто представив одинаковое количество частей на двух столбцах, в этом случае они будут разделены на 12 равных частей.

Как только мы получим одинаковый знаменатель для двух дробей, мы можем вычесть, и вы уже знаете, что для того, чтобы у дробей были общие знаменатели, нам нужно найти l.c.m или найти эквивалентные дроби. Я уже сделал это за вас :

\(\frac{8}{12}\) – \(\frac{2}{6}\) = \(\frac{4}{12}\), как видите, это уже представлено на полосе есть только четыре цветных квадрата  и полоса разделена на 12 частей .

Решенные упражнения

И, наконец, мы рассмотрим несколько примеров действий, которые дети могут выполнять в Smartick, чтобы потренироваться в вычитании дробей с необычными знаменателями .

Это действие такое же, как и предыдущее, только на этот раз мы используем окружает , чтобы представить дроби.

Вы можете использовать кругов , чтобы показать результат дроби, вам просто нужно поместить одинаковое количество частей в оба круга , что в данном случае равно 10.

Как видите, результат вычитания дроби равны \(\frac{11}{10}\). Вы можете проверить, правильно ли вы это сделали, посмотрев на результат кружков. Один полный круг и одна цветная часть.

 

Это задание очень простое, вот пиццы  может помочь нам понять результат вычитания дробей.

Вы уже знаете, что у вас есть два варианта решения упражнения:

1. Найдите мкм 6 и 1, что равно 6.
2. Создайте эквивалентные дроби, как мы видели в предыдущих примерах.

Вы научились вычитать дроби?

Теперь я дам вам следующие упражнения, чтобы попрактиковаться в том, что вы узнали.

1. \(\frac{8}{5}\) – \(\frac{3}{5}\) 
2. \(\frac{3}{2}\) – \(\frac{2}{3}\)
3. \(\frac{7}{4}\) – \(\frac{7}{8}\)
4. \(\frac{5}{6}\) – \(\frac{1}{15}\)

Решения:

1. \(\frac{5}{5}=1\) 
2. \(\frac{5}{6}\)
3. \(\frac{7}{8}\)
4. \(\frac{23}{30}\)

Видео для понимания эквивалентных дробей

Следующее видео поможет вам лучше понимать эквивалентные дроби, чтобы помочь вам вычитать дроби с необычными знаменателями .

Это видео одного из наших интерактивных учебных пособий, и, хотя оно больше не является интерактивным, вы можете просматривать его столько раз, сколько вам нужно, и можете поделиться им с друзьями. Если вы хотите получить доступ к нашим интерактивным руководствам, зарегистрируйтесь в Smartick! Онлайн-метод, который помогает детям в возрасте от 4 до 14 лет изучать и практиковать математику.

А если вы хотите продолжать изучать вычитание дробей и другие элементарные математические темы, адаптированные к вашему уровню, зарегистрируйтесь в Smartick и попробуйте бесплатно.

Подробнее:

• Автор
• Последние сообщения

Smartick

Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.