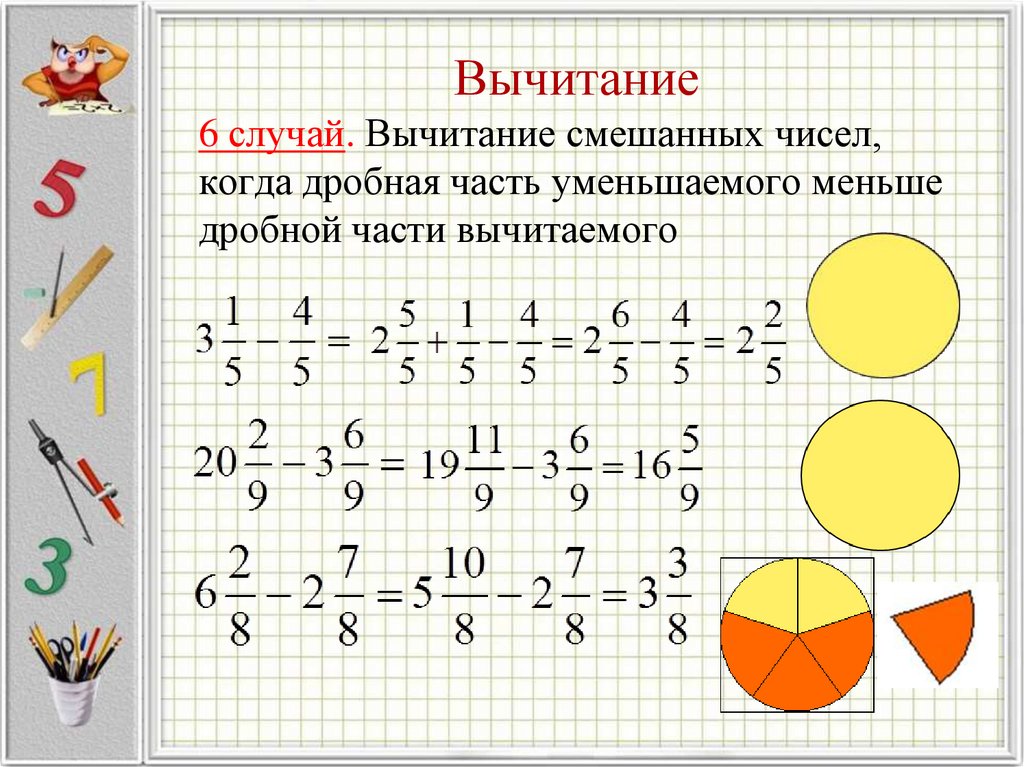
Как от меньшей дроби отнять большую дробь: Вычитание смешанных дробей
Содержание
правила, примеры, решения, как вычесть из десятичной дроби обыкновенную дробь
Изучаем другие действия, которые можно совершать с десятичными дробями. В этом материале мы узнаем, как правильно подсчитать разность десятичных дробей. Отдельно разберем правила для конечных и бесконечных дробей (как периодических, так и непериодических), а также посмотрим, как считать разность дробей столбиком. Во второй части мы объясним, как вычесть десятичную дробь из натурального числа, обыкновенной дроби, смешанного числа.
Отметим заранее, что в этой статье рассмотрены только случаи, когда меньшая дробь вычитается из большей, т.е. результат этого действия положителен; другие случаи относятся к нахождению разности рациональных и действительных чисел и должны быть объяснены отдельно.
Основные правила вычитания десятичных дробей
Процесс вычисления как конечных, так и бесконечных периодических десятичных дробей можно свести к нахождению разности дробей обыкновенных. Раньше мы говорили о том, что десятичные дроби можно записывать в виде обыкновенных дробей. Исходя из этого правила, разберем несколько примеров нахождения разности.
Раньше мы говорили о том, что десятичные дроби можно записывать в виде обыкновенных дробей. Исходя из этого правила, разберем несколько примеров нахождения разности.
Пример 1
Найдите разность 3,7-0,31.
Решение
Переписываем десятичные дроби в виде обыкновенных: 3,7=3710 и 0,31=31100.
Что делать потом, мы уже изучали. Мы получили ответ, который переводим обратно в десятичную дробь: 339100=3,39.
Подсчеты, связанные с десятичными дробями, удобно производить столбиком. Как же пользоваться этим методом? Покажем, решив задачу.
Пример 2
Вычислите разность между периодической дробью 0, (4) и периодической десятичной дробью 0,41(6).
Решение
Переведем записи периодических дробей в обыкновенные и подсчитаем.
0,4(4)=0,4+0,004+…=0,41-0,1=0,40,9=49.0,41(6)=0,41+(0,006+0,0006+…)=41100+0,0060,9==41100+6900=41100+1150=123300+2300=125300=512
Итого: 0,(4)-0,41(6)=49-512=1636-1536=136
Если нужно, ответ мы можем представить в виде десятичной дроби:
Ответ: 0,(4) −0,41(6) =0,02(7).
Разберем далее, как найти разность, если у нас в условиях стоят бесконечные непериодические дроби. Такой случай также можно свести к нахождению разности конечных десятичных дробей, для чего понадобится округлить бесконечные дроби до определенного разряда (обычно самого меньшего из возможных).
Пример 3
Найдите разность 2, 77369…-0,52.
Решение
Вторая дробь в условии – конечная, а первая – бесконечная непериодическая. Мы можем округлить ее до четырех знаков после запятой: 2,77369…≈2,7737. После этого можно выполнять вычитание: 2,77369…−0,52≈2,7737−0,52.
Ответ: 2,2537.
Как считать разность десятичных дробей столбиком
Вычитание столбиком – быстрый и наглядный способ узнать разность конечных десятичных дробей. Процесс подсчета очень схож с аналогичным для натуральных чисел.
Определение 1
Чтобы подсчитать разность десятичных дробей столбиком, необходимо:
- если в указанных десятичных дробях отличается количество знаков после запятой, уравняем его.
 Для этого допишем к нужной дроби нули;
Для этого допишем к нужной дроби нули; - запишем вычитаемую дробь под уменьшаемой, разместив значения разрядов строго друг под другом, а запятую под запятой;
- выполним подсчет столбиком так же, как мы это делаем для натуральных чисел, запятую при этом игнорируем;
- в ответе отделим нужное количество чисел запятой так, чтобы она располагалась на том же месте.
Разберем конкретный пример использования этого метода на практике.
Пример 4
Найдите разность 4 452,294-10,30501.
Решение
Для начала выполним первый шаг – уравняем количество десятичных знаков. Допишем два нуля в первую дробь и получим дробь вида 4 452,29400, значение которой идентично исходной.
Запишем получившиеся числа друг под другом в нужном порядке, чтобы получился столбик:
Считаем как обычно, игнорируя запятые:
В получившемся ответе поставим запятую в нужном месте:
Подсчеты окончены.
Наш результат : 4 452,294−10,30501=4 441,98899.
Как вычесть натуральное число из десятичной дроби и наоборот
Найти разность между конечной десятичной дробью и натуральным числом легче всего описанным выше способом – столбиком. Для этого число, из которого мы вычитаем, необходимо записать в виде десятичной дроби, в дробной части которой стоят нули.
Пример 5
Вычислите 15-7,32.
Запишем уменьшаемое число 15 в виде дроби 15,00, поскольку дробь, которую нам нужно вычесть, имеет два знака после запятой. Далее выполняем подсчет столбиком, как обычно:
Таким образом, 15−7,32=7,68.
Если из натурального числа нам нужно вычесть бесконечную периодическую дробь, то мы опять же сводим эту задачу к аналогичному вычислению. Заменяем периодическую десятичную дробь на обыкновенную.
Пример 6
Вычислите разность 1-0, (6).
Решение
Указанной в условии периодической десятичной дроби соответствует обычная 23.
Считаем: 1−0,(6)=1−23=13.
Полученный ответ можно перевести в периодическую дробь 0,(3).
Если данная в условии дробь непериодическая, поступаем так же, предварительно округлив ее до нужного разряда.
Пример 7
Отнимите 4,274… от 5.
Решение
Указанную бесконечную дробь мы округлим до сотых и получим 4,274…≈4,27.
После этого вычисляем 5−4,274…≈5−4,27.
Преобразуем 5 в 5,00 и запишем столбик:
В итоге 5−4,274…≈0,73.
Если перед нами стоит обратная задача – вычесть натуральное число из десятичной дроби, то мы выполняем вычитание из целой части дроби, а дробную часть не трогаем совсем. Мы поступаем так и с конечными, и с бесконечными дробями.
Пример 8
Найдите разность 37,505 – 17.
Решение
Отделяем от дроби целую часть 37 и вычитаем требуемое число из нее. Получаем 37,505−17=20,505.
Как вычесть десятичную дробь из смешанного числа или обыкновенной дроби и наоборот
Эту задачу также необходимо свести к вычитанию обыкновенных дробей – как в случае со смешанными числами, так и с десятичными дробями.
Пример 9
Вычислите разность 0,25-45.
Решение
Представим 0,25 в виде обыкновенной дроби – 0,25=25100=14.
Теперь нам нужно найти разность между 14и 45.
Считаем: 45−0,25=45−14=1620−520=1120.
Запишем ответ в виде десятичной записи: 0,55.
Если в условии стоит смешанное число, из которого надо вычесть конечную или периодическую десятичную дробь, то поступаем аналогично.
Пример 10
Условие: отнимите 0,(18) от 8411.
Решение
Перепишем периодическую дробь в виде обыкновенной. 0,(18)=0,18+0,0018+0,000018+…=0,181-0,01=0,180,99=1899=211
Получается, что 8411-0,(18)=8411-211=8211.
В виде десятичной дроби ответ можно записать как 8,(18).
Таким же образом мы действуем, когда вычитаем смешанное число или обыкновенную дробь из конечной или периодической дроби.
Пример 11
Подсчитайте 940-0,03.
Решение
Заменяем дробь 0,03 на обыкновенную 3100.
У нас получается, что: 940−0,03=940−3100=90400−12400=78400=39200
Ответ можно оставить так или преобразовать в десятичную дробь 0,195.
Если нам требуется выполнять вычитание с участием бесконечных непериодических дробей, то нам нужно будет свести их к конечным. Со смешанными числами поступаем аналогично. Для этого запишем обыкновенную дробь или смешанное число в виде десятичной дроби и округлим вычитаемую дробь до определенного разряда. Проиллюстрируем нашу мысль примером:
Пример 12Отнимите 4,38475603…. из 1027.
Решение
Преобразуем смешанное число в неправильную дробь.
1027=10·7+27=727
Далее эту дробь запишем в десятичном виде и получим 10, (285714).
В итоге 1027-4,38475603…=10,(285714)-4,38475603….
Теперь округлим вычитаемые числа до седьмого знака: 10, (285714) =10,285714285714…≈10,2857143 и 4,38475603…≈4,3847560
Тогда 10, (285714) −4,38475603…≈10,2857143−4,3847560.
Единственное, что осталось сделать – вычесть одну конечную десятичную дробь из другой. Выполним подсчет столбиком:
Ответ: 1027-4,38475603…≈5,9009583
Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.
Найдите p3+q3, если известно, что p+q=5 и p+q+p2q+pq2=31…. -reshimne.ru
Новые вопросы
Ответы
Похожие вопросы
(4x+x)*2=60 помогите срочно. ..
Длина прямоугольного участка 175см,что в 5 раз больше ширины. Найди периметр этого прямоугольника…
Найди периметр этого прямоугольника…
Пожалуйста, помогите! Спасибо!
Несколько фирм приняли участие в конкурсе дизайнерских работ. Каждая работа оценивалась баллами от 3 до 5. Фирма «АХ» получила на 10 баллов меньше суммы баллов остальных фирм. Фирма «УХ» получила на 8 баллов меньше суммы баллов остальных фирм, фирма «ОХ» — на 6 баллов меньше суммы баллов остальных фирм. Скольк…
Исеользуя рисунок,составь и реши задачи,соответствующие выражением:78-10*2; (78-10*2)плюс35…
Плыз зделайте ото я сем не могу…
КАК ОТ МЕНЬШЕЙ ДРОБИ ОТНЯТЬ БОЛЬШУЮ ДРОБЬ(нету смешанного числа и знаменатели одинаковые).
..
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Вычитание смешанных чисел — методы и примеры
Смешанное число — это число, состоящее из целого числа и дроби, например, 2 ½ — это смешанное число.
Как вычитать смешанные числа?
В этой статье мы узнаем способы вычитания смешанных дробей или вычитания смешанных чисел. Вычитание смешанной дроби включает два метода.
Метод 1
Первый метод включает в себя:
- Вычитание целых чисел.
- Вычитание дробей путем преобразования их сначала в подобные дроби.
- Сложение разностей целых чисел и подобных дробей.
Пример 1
6 1 /3 — 3 1 / 12
= (6 — 3) + (1/3-12).
= 3 + (1/3 – 1/12)
Найти L.C.M. из 12 и 3 как 12
= 3 + (1 × 4/3 × 4 – 1 × 1/12 × 1)
= 3 + 4/12 – 1/12
= 3 + (4 – 1)/12
= 3 + 3/12
= 3 + ¼
= 3 ¼
Метод 2
Второй метод вычитания смешанных дробей включает: первый шаг — преобразовать смешанные дроби в неправильные дроби

Пример 2
Вычитание: 6 1 / 3 — 3 1 / 12
= (6 × 3) + 1/3 + (3 × 1/12
= 19/3 – 37/12
L.C.M. из 3 и 12 равно 12
= 19 х 4/3 х 4 – 37 х 1/12 х 1 = 13/4
= 3 ¼
Как вычитать смешанные дроби с отличным знаменателем?
Пример 3
8 5 / 6 — 3 2 /
- . Первая процедура — «Непосредственная процедура». Первая процедура — на первую процедуру.
Умножьте целое число на знаменатель дроби, а затем добавьте числитель. Это число становится числителем неправильной дроби. Знаменатель неправильной дроби остается таким же, как знаменатель смешанной дроби.
{(6 x 8) + 5}/6 = 53/6
{(3 x 9) + 2}/9 = 29/9
- Измените дроби, чтобы они содержали общие знаменатели
L. C. M дробей 9 и 6 = 18
C. M дробей 9 и 6 = 18
53/6 = 159/18
29/9 = 58/18
- Умножив начальную дробь на 3/3, а вторую дробь на 2/2, получим 18 для обоих знаменателей. Вы можете заметить, что 3/3 и 2/2 равны 1, поэтому на самом деле мы умножаем обе дроби на 1, не изменяя значения дробей.
- В настоящее время выполняйте вычитание
159/18 — 58/18
- Вычтите числители при поддержании конфессий
= 59. 58). / 18
More Examples with Solution
- Subtract:7 5 / 12 – 2 7 / 12
Solution
7 5 / 12 – 2 7 / 12
Так как дробные части имеют общие знаменатели, чтобы вычесть большую дробную часть 7/12 из меньшей единицы 5/12, одолжить один.
7 5 / 12 = 6 + (1+ 5/12) = 6 17 / 12
Вычитание целых чисел и дробей по отдельности 12 – 7/12
Вычесть числители дробей, сохранив знаменатель
(17 – 7)/12 = 10/12
Упростите дробь до минимума
10/12 = 5/6
Прибавьте дробную часть к целому числу
(4 + 5/6) = 4 5 / 6 5 902 В конце баскетбольного матча главный тренер понял, что бутылка воды, которая изначально составляла девять и три восьмых литра воды, уменьшилась до трех и девяти шестнадцатых литров. Сколько литров воды выпили игроки?
Сколько литров воды выпили игроки?
Раствор
Начальный объем воды = девять и три восьмых = 9 3 / 8
Окончательный объем воды = три и девять-шестнадцатые. 3 / 8 — 3 / 16
Преобразование смешанных фракций в ненадлежащие фракции
9 3 / 8 = {9 x 8) + 3} / 8
= = {9 x 8). 75/8
3 9 / 16 = {(3 x 16) + 9}/16
= 57/16
Измените дроби, чтобы они содержали общий знаменатель.
НОК чисел 8 и 16 равно 16 , следовательно,
75/8 = 150/16
А 57/16 = 57/16
Вычесть дроби
150/16 – 57/15 9000 вычесть числители при сохранении знаменателей
(150 – 57)?16
=93/16
= 5 13 / 16
Таким образом, игроки израсходовали литров воды = 5 13 / 16
Итак, для вычитания смешанных чисел:
Если знаменатели не совпадают, найдите наименьшее общее кратное эквивалентных неправильных дробей. А если первая дробь меньше второй дроби, то следует брать одну единицу из ее целого числа. Теперь вычтите целые числа и дроби отдельно. Найдите сумму разности дробей и разности целых чисел. Упростите окончательный ответ до самых минимальных возможных условий.
А если первая дробь меньше второй дроби, то следует брать одну единицу из ее целого числа. Теперь вычтите целые числа и дроби отдельно. Найдите сумму разности дробей и разности целых чисел. Упростите окончательный ответ до самых минимальных возможных условий.
Предыдущий урок | Главная страница | Next Lesson
Subtracting Fractions
Share to PinterestPinterestShare to FacebookFacebookShare to PocketPocketShare to TwitterTwitterShare to EmailEmailShare to FlipboardFlipboard
Worksheets
Printables
Puzzles
T-Shirts
Math Worksheets
Go Ad Free!
Основные математические рабочие листы
Дробные рабочие листы
Словесные задачи
Алгебра
Прочие рабочие листы
Измерение и преобразования
Структуры и головоломки
Цвет по номеру
Праздничные и сезонные
Раннее обучение
ПЕЧАТНЫЕ
Калькуляторы
Математические линии.

для задач на вычитание дробей. Нажмите одну из кнопок ниже, чтобы увидеть все рабочие листы в каждом наборе. Вы также можете использовать меню «Рабочие листы» сбоку этой страницы, чтобы найти рабочие листы по другим математическим темам.
Общий знаменатель, без целых частей
16 Рабочие листы по вычитанию дробей
Вычитание дробей с общим знаменателем и без целых частей.
Общий знаменатель, без целых частей
Смешанные дроби с общим знаменателем
16 Рабочие листы для вычитания дробей
Вычитание смешанных дробей с общим знаменателем.
Смешанные дроби с общим знаменателем
Половины, четверти, восьмые
16 Вычитание дробей Рабочие листы
Вычитание обыкновенных дробей с половинками и четвертями.
Половины, четверти, восьмые
Различные знаменатели
24 Рабочие листы по вычитанию дробей
Эти рабочие листы содержат практические задания на вычитание дробей с разными знаменателями.
Различные знаменатели
Смешанные дроби с разными знаменателями
16 Рабочие листы для вычитания дробей
Вычитание смешанных дробей с разными знаменателями.
Смешанные дроби с разными знаменателями
Неправильные дроби с одинаковым знаменателем
16 Рабочие листы по вычитанию дробей
Сложение дробей с неправильными дробями.
Неправильные с одинаковым знаменателем
Неправильные с разными знаменателями
16 Вычитание дробей Рабочие листы
Сложение неправильных дробей с разными знаменателями
Неправильные дроби с разными знаменателями
Как вычитать дроби
Вычитание дробей аналогично сложению дробей. Большая часть работы связана со знаменателем. Если знаменатели двух дробей уже одинаковы, большая часть работы выполнена.
Большая часть работы связана со знаменателем. Если знаменатели двух дробей уже одинаковы, большая часть работы выполнена.
Десятичные дроби — примеры действий с решениями
Определение и понятие
История возникновения десятичных дробей тесно связана с учением о мерах. В Древнем Китае десятичную систему использовали для обозначения порядка. Полную теорию дробей в XV веке предложил узбекский астроном Джемшид Гиясэддин ал-Каши. Позже Стевин в своей книге «Десятая» начал записывать такие выражения в одну строку. Таким же образом их обозначал и Иоганн Кеплер. Используемая им запись осталась актуальной и сегодня.
Под дробью в математике понимают число, в состав которого входит одна или несколько равных долей единицы. Если стоит задача определить дробь конкретной величины, то её считают соответствующей единице. Например, пусть имеется круг, разделённый на шесть равных частей. Эти части называют долями. Всего их шесть, то есть каждая доля составляет шестую часть круга, исходную величину которого принимают как равную единице.
В математике это отношение обозначают в виде записи 1/6 и называют дробью. Читают его как «одна шестая». Любая дробь состоит из трёх элементов:
- Числителя — цифры или числа, стоящей в верхней части. Он показывает, сколько частей отобрано у целого, и является делимым.
- Знаменателя — числа, показывающего, на какое количество долей разделяют числитель.
- Дробной черты — разделяет числитель со знаменателем и фактически заменяет собой знак деления.
В школьных классах для того, чтобы ученики запомнили, где находится числитель, а где — знаменатель, предлагают ассоциации. Например, человек стоит на земле, она снизу, знаменатель — внизу. Таким образом, запись 3/6 будет обозначать, что круг разделили на шесть частей и три из них убрали.
Форма записи
При записи десятичной дроби используют следующую форму: сначала пишут целую часть, затем ставят разделитель целой и дробной доли (запятую), а после уже указывают дробную составляющую. Количество цифр, идущих после запятой, зависит от размерности. Различают десятые доли, их записывают одной цифрой, сотые — двумя, тысячные — тремя и так далее.
Количество цифр, идущих после запятой, зависит от размерности. Различают десятые доли, их записывают одной цифрой, сотые — двумя, тысячные — тремя и так далее.
Записанные десятичные отношения выглядят так: 6,7; 3,26; 0, 234. Их принято указывать без знаменателя. Например, 7/10 = 0,7; 32/100 = 0,32. Удобнее всего пояснить на реальном примере. Пусть есть дробь 69/10. В знаменателе стоит число десять, имеющее один ноль. Отсчитав справа налево в числителе количество знаков, соответствующих числу нулей, в этом случае один, ставят запятую. В рассматриваемом примере запись будет выглядеть как 6,9. Тут 6 — целая часть, а 9 — дробная.
С отношениями можно выполнять любые действия. Их можно складывать, вычитать, делить и умножать. Десятичные дроби — это один из видов отношений. Они соответствуют выражениям, где знаменатель определяется как 10 в степени n, а n — натуральное число, то есть возникающее при счёте естественным образом.
youtube.com/embed/ZqBov_auZIA»>Виды дробей
Дробные числа используют не только в математике, но и повседневной жизни. Наиболее типичное применение — это кулинария, где приготовление еды происходит с помощью смешивания определённых частей ингредиентов между собой. В качестве примера можно привести и спортивные состязания, пошив одежды, нумерацию.
Кроме десятичных отношений, существуют ещё и другие виды дроби:
- обыкновенная (простая) — записывают как отношение двух рациональных чисел;
- правильная — это выражение, у которого значение числителя меньше знаменателя;
- неправильная — в этом случае числитель больше или совпадает по величине со знаменателем;
- смешанная — образуется из неправильных как сумма натурального числа и правильной дроби.
Любую дробь можно преобразовать в другую. Самая простая операция, которую можно сделать — это перевод обыкновенного отношения в десятичное.
Для этого вначале конвертируют числитель, а затем знаменатель. Но не с каждой дробью это возможно сделать.
Есть правило, по которому легко определить, существует ли возможность преобразования. Согласно ему, обыкновенную дробь можно преобразовать в конечную десятичную лишь в том случае, если её знаменатель можно разложить на множители два и пять, которые имеют свойство повторяться. Например, 11/40, знаменатель можно представить в виде произведения 2*2*2*5, поэтому привести к десятичной её возможно. А вот 13/60 преобразовать нельзя, так как в знаменателе при разложении есть число три: 5 * 2 * 2 * 3 = 60.
Для переведения простого отношения в десятичное нужно верхнюю и нижнюю часть выражения умножить на одно и то же число, но таким образом, чтобы внизу записи появилось число, кратное десяти. Например, 7/20 = 7*5/20*5 = 35/100 = 0,35. Или такой пример: 13/40 = 13/2*2*2*5 = 13*25/40*25 = 325/1000 = 0,325.
Есть и более сложный способ приведения, но при этом используют его чаще. В основе метода лежит деление уголком. То есть выполняют просто деление числителя на знаменатель. Например, 69/200. На первом этапе следует убедиться, что дробь может быть конечной десятичной, для этого раскладывают знаменатель: 200 = 5*5*2*2*2. На втором шаге выполняют деление в столбик и получают ответ: 0,345.
Популярность второго способа связана с тем, что всё же некоторые отношения проще разделить, чем подбирать, как правильно преобразовать знаменатель. Наиболее часто встречаются следующие дроби, которые поддаются преобразованию: ½ = 0,5; ¼ = 0,25; ¾ = 0,75; 1/5 = 0,2; 1/8 = 0,125; 1/10 = 0,1. А вот такие выражения, как 1/3, 1/7, 5/6, преобразовать в десятичные числа невозможно.
Преобразование отношения
Любое число можно преобразовать в дробь. Десятичные числа как слышатся, так и пишутся. Ноль целых три сотых — дробь 3/100. Выражение одна целая десять сотых можно записать как 1 (10/100).
Преобразуя десятичное число в дроби, можно сокращать. Например, 1,06 = 1 (5/100) = 1 (1/20). Часто приходится выполнять и обратное преобразование: 4/100 = 0,04. Смешанное отношение вида 3 (4/5) может быть преобразовано в неправильное. Для этого нужно целую часть умножить на нижнюю часть дроби и сложить с верхней. Знаменатель оставляют без изменений. То есть (3*5+4)/5 = 19/5.
При превращении смешанной дроби в неправильную используют правило сложения дробей. Например, выражение 3 (2/13) можно записать как 3 + 2/13 = 3/1 + 2/13 = (3*13+2)/13 = (39+2)/13 = 41/13. Для того чтобы перевести смешанную дробь в десятичную, необходимо выделить целую долю.
Выделяя часть, нужно определить, сколько целых знаменателей вмещается в числитель. Пусть нужно преобразовать 27/6. Вначале следует определить, сколько шестёрок помещается в числе 27. Для этого нужно 27 разделить на шесть, число, стоящее перед запятой, будет искомым. Это четыре. Далее найти числитель по правилу 4*6 = 24 и вычесть полученное значение из знаменателя 27 − 24 = 3. Теперь находят лишнее, что осталось от числителя 27, если убрать максимально помещающее число шестёрок. В результате получится ответ: 27/6 = 4 (2/3).
Теперь находят лишнее, что осталось от числителя 27, если убрать максимально помещающее число шестёрок. В результате получится ответ: 27/6 = 4 (2/3).
По похожему алгоритму выполняется преобразование периодической дроби в обыкновенную. Для решения задания нужно из числа, занимающего позицию до второго периода, отнять число, стоящее до первого периода, а полученную разницу перенести в числитель. В знаменатель записать девятку столько раз, сколько цифр в периоде. После девяток пишут нули, количество которых определяется числом цифр стоящих между запятой и первым периодом. Например, 0,23 (7) = (237 — 23)/900 = 214/900 = 107/450.
Действия с десятичными числами
С дробями можно также выполнять и сравнения. Для этого используют алгебраические правила. Сложение дробей между собой осуществляют по правилу столбика. Это удобный метод, практически не позволяющий допускать ошибок. Согласно объяснению способа в математике, для сложения нужно записать два числа друг под другом так, чтобы их правые цифры были в одном столбике. Затем сложить цифры в нём, используя способ переноса десятков.
Согласно объяснению способа в математике, для сложения нужно записать два числа друг под другом так, чтобы их правые цифры были в одном столбике. Затем сложить цифры в нём, используя способ переноса десятков.
При сложении десятичных дробей происходит всё то же самое, но при этом нужно обязательно расположить выражения так, чтобы их запятые стояли чётко друг под другом. Сложение выполняют так, как и с натуральными числами, не учитывая запятые. После подсчёта запятую просто сносят вертикально вниз, отделяя целую часть от дольной.
При вычитании происходит всё аналогичным образом. При сложении и вычитании выполняют четыре пункта:
- Уравнивают количество знаков после запятой.
- Записывают дроби друг под другом так, чтобы запятые совпадали по вертикали.
- Складывают или вычитают по правилам арифметики.
- В полученном числе ставят запятую соответственно другим записям.
Для умножения дробей их записывают в столбик, а далее находят произведение, как и с обычными числами. Затем считают количество знаков после запятой первого умножаемого и умножителя и складывают их количество. Для получения ответа справа налево отсчитывают такое же количество знаков и после последнего ставят запятую. Умножаться могут любые дроби, исключений нет.
Затем считают количество знаков после запятой первого умножаемого и умножителя и складывают их количество. Для получения ответа справа налево отсчитывают такое же количество знаков и после последнего ставят запятую. Умножаться могут любые дроби, исключений нет.
Чтобы разделить десятичную дробь, следует знать правило: если целая часть делимого меньше делителя, то в частном целых не будет. Деление выполняют по правилу того же столбика. Две части записывают через уголок и определяют неполное частное, сравнивая делимое с делителем. Далее выполняют действие, записывая цифру в частное. При записи под неполным частным правая его величина должна располагаться над правой цифрой произведения. После того как закончится деление целой части делимого, ставят запятую.
Если число после запятой бесконечно повторяется, то оно будет называться периодом. В этом случае используют сокращение записи. Например, если в ответе получают 4, 67644444, то его можно заменить на запись 4,67 (4).
Такое выражение называют бесконечной десятичной дробью.
Сравнение выражений
Чтобы сравнить две дроби, нужно составить уравнение из их целых частей. Если их части равные, то сравниваются десятые доли. Стоит отметить, что в этом случае учитывают разряд числа. Меньшей будет та дробь, у которой значение числа в разряде меньше.
Для того чтобы провести сравнение дробей, применяют следующую последовательность действий:
- Пробуют сократить выражения.
- Приводят дроби к одинаковому числу знаков путём дописывания в случае необходимости нулей.
- Выполняют сравнение по старшинству разрядов, начиная с целой части, а в случае равенства — с десятой, сотой и так далее.
- Если при сравнении разрядов один из них будет больше или меньше, задача считается выполненной.
Например, нужно сравнить дроби 237,4 и 238,2 и результат выразить через процентное отношение. Так как 237 меньше 238, то дробные части сравнивать уже будет не нужно. Для того чтобы определить процентное отношение, большую часть принимают за 100%, а меньшую — за X. Составляют пропорцию и делают вычисление: 237,4 * 100 = 238,2 * Х.
Так как 237 меньше 238, то дробные части сравнивать уже будет не нужно. Для того чтобы определить процентное отношение, большую часть принимают за 100%, а меньшую — за X. Составляют пропорцию и делают вычисление: 237,4 * 100 = 238,2 * Х.
Это обыкновенное уравнение с одним неизвестным: Х = 237,4 * 100 / 238,2 = 99,66%. То есть первое выражение меньше второго на 100 — 99,66 = 0,34%. Десятичные выражения, как и натуральные, можно записывать в ряд, а значит, откладывать на координатной прямой. На ней правее будет стоять отношение, которое больше.
Небольшие задания решать несложно. Но существуют задачи, для решения которых нужно не только проявить максимальное внимание, но и затратить много времени. Например, как при вычислении совместных дробей. В таких случаях есть резон использовать калькулятор десятичных дробей с запятыми онлайн. Чтобы им воспользоваться, особых знаний не нужно. Загрузив сайт и введя в таблицу исходные данные, пользователю нужно всего лишь нажать кнопку «Рассчитать» и получить точный результат.
Сравнение дробей | Типы, сравнение, что такое дробь? Примеры
Введение
В повседневной жизни мы часто имеем дело с дробями. В большинстве случаев нас просят сравнить, какая часть меньше или больше, или если обе части разделены поровну. В этой статье мы вернемся к определению дробей и их типам, а затем рассмотрим методы их сравнения.
Что такое дробь?
Чтобы побудить нас узнать о дробях, мы придумаем популярную аналогию. Представьте, что у нас есть коробка с пиццей, нарезанная на равные части:
Каждый кусочек представляет собой часть всей пиццы. Если мы подсчитаем количество кусочков, из которых состоит пицца, мы можем выразить кусок, который мы возьмем, в виде математической величины. Это то, что мы представим как дробь .
Когда мы говорим о дробях, мы думаем о частях целого . С математической точки зрения это количество, которое выражается как частное или отношение между двумя числами. Возвращаясь к коробке пиццы, которую мы использовали в качестве аналогии, если мы возьмем количество съеденных ломтиков от общего количества ломтиков в коробке, мы можем выразить это соотношение следующим образом:
Возвращаясь к коробке пиццы, которую мы использовали в качестве аналогии, если мы возьмем количество съеденных ломтиков от общего количества ломтиков в коробке, мы можем выразить это соотношение следующим образом:
$\frac{номер\: из\: пиццы\: ломтики\: съедены}{количество\: из\: ломтики\: в\: в\: коробка}$
Предположим, друг съел три ломтика пицца. Тогда мы можем сказать, что у нашего друга было три восьмых пиццы:
$\frac{no.\: of\: pizza\: slices\: eaten}{no.\: of\: slices\: in\: the\: box}=\frac{3}{8}$
Теперь мы определяем части дроби. Число выше называется числителем , а число под ним называется знаменателем . Числитель и знаменатель разделены чертой, которую мы называем 9.0011 дробь бар .
$\frac{3}{8}$ ←числитель ← знаменатель
Типы дробей
Дроби можно разделить на три типа в зависимости от соотношения числителя и знаменателя:
Правильные дроби
Правильные дроби 9001 — это дроби, числитель которых меньше знаменателя:
числитель<знаменатель
Некоторые примеры, которые мы можем придумать, это $\frac{1}{3}$, $\frac{4}{7}$, и $\frac{5}{8}$:
Мы можем думать о правильных дробях как о «правильных», поскольку количество частей меньше целого. В математическом смысле отношение, образованное правильными дробями, меньше 1:
В математическом смысле отношение, образованное правильными дробями, меньше 1:
$\frac{числитель}{знаменатель}$<1
Это происходит потому, что при делении меньшего числа на большее число получается меньшее частное чем один.
Неправильные дроби
С другой стороны, Неправильные дроби — это дроби, у которых числитель больше знаменателя:
числитель>знаменатель
Вот некоторые примеры, которые мы можем привести: $\frac{3}{2}$, $\frac{5}{4}$ и $\frac{9}{8}$.
Мы можем думать о неправильных дробях как о «неправильных», поскольку число частей больше, чем целое. С математической точки зрения отношение, образованное неправильными дробями, больше 1:
$\frac{числитель}{знаменатель}$>1
В отличие от правильных дробей, деление большего числа на меньшее приводит к частному что больше единицы.
Смешанные числа
A Смешанное число можно рассматривать как комбинацию целого и дроби. Это еще один способ записать неправильную дробь, беря части, составляющие целое, а затем выражая оставшиеся части в виде правильной дроби.
Это еще один способ записать неправильную дробь, беря части, составляющие целое, а затем выражая оставшиеся части в виде правильной дроби.
Например, рассмотрим неправильную дробь $\frac{11}{8}$. Визуализируя, у нас есть 11 равных частей, которые будут сгруппированы в 8 частей в целом:
Если мы сложим 8 частей в одно целое, то останется правильная дробь $\frac{3}{8}$ . В связи с этим мы можем выразить неправильную дробь как количество целых и дробных частей:
$\frac{11}{8}=\frac{8}{8}+\frac{3}{8}=1\frac{3}{8}$
Этот метод удобно использовать для преобразовать неправильные дроби в смешанные числа.
Подобные дроби
Мы также можем связать две (или более) дроби на основе числа их знаменателей. Подобные дроби — это дроби, имеющие одинаковый знаменатель . Мы можем рассматривать одинаковые дроби как части одного и того же целого. Например, у нас есть $\frac{1}{5}$, $\frac{2}{5}$, $\frac{3}{5}$ и $\frac{4}{5}$ как подобны дробям, так как все их знаменатели равны 5,
В отличие от дробей
Что делать, если две дроби не похожи на дроби? В этом случае мы имеем разноименные дроби. В отличие от дробей это дроби, которые имеют различных знаменателей . Мы можем думать о разных дробях как о частях разных целых. Например, $\frac{1}{4}$ и $\frac{2}{8}$ не являются дробями, так как их знаменатели не равны.
В отличие от дробей это дроби, которые имеют различных знаменателей . Мы можем думать о разных дробях как о частях разных целых. Например, $\frac{1}{4}$ и $\frac{2}{8}$ не являются дробями, так как их знаменатели не равны.
Что такое эквивалентные дроби?
Прежде чем мы начнем сравнивать дроби, мы должны знать еще одну важную концепцию: как дроби могут быть эквивалентны. Равные дроби — это дроби, имеющие одинаковое значение, даже если они имеют разные числители и знаменатели. Чтобы помочь нам понять, как работают эквивалентные дроби, давайте рассмотрим две разные дроби $\frac{1}{4}$ и $\frac{2}{8}$:
Мы видим, что для одного и того же круга, разделенного на равные части , площадь, покрытая одной частью из четырех равных частей, равна площади, покрытой двумя частями из восьми равных частей. Отсюда можно сделать вывод, что и $\frac{1}{4}$, и $\frac{2}{8}$ являются эквивалентными дробями.
В предыдущем примере мы легко показали, что они эквивалентны, визуализируя дроби. Но как мы можем определить, эквивалентны ли две такие дроби для дробей, которые будут состоять из больших чисел?
Но как мы можем определить, эквивалентны ли две такие дроби для дробей, которые будут состоять из больших чисел?
Две дроби называются эквивалентными, если они имеют общий делитель , который можно разделить или умножить как на числитель, так и на знаменатель одной дроби, чтобы получить другую дробь.
Опять же, возьмем в качестве примера $\frac{1}{4}$ и $\frac{2}{8}$. Мы можем умножить на 2 как числитель, так и знаменатель $\frac{1}{4}$ и $\frac{2}{8}$:
$\frac{1×2}{4×2}=$\frac{2}{8}$
Точно так же мы можем разделить множитель 2 как на числитель, так и на знаменатель $\frac{2}{ 8}$ для получения $\frac{1}{4}$:
$\frac{2÷2}{8÷2}=$\frac{1}{4}$
Следовательно, кроме визуализации мы сделали ранее, мы также докажем, что обе дроби $\frac{1}{4}$ и $\frac{2}{8}$ являются эквивалентными дробями.
Сравнение дробей
Теперь, когда мы изучили основные понятия, касающиеся дробей, мы можем перейти к нашей основной теме, которая вращается вокруг сравнения двух дробей. Отметим, что методы, обсуждаемые ниже, обычно применимы к двум фракциям.
Отметим, что методы, обсуждаемые ниже, обычно применимы к двум фракциям.
Интуитивный подход
Подобно тому, что мы делали с аналогией с пиццей, мы используем Интуитивный подход , который позволяет нам думать о дробях визуально. Для этого метода мы можем использовать любую фигуру, какую пожелаем, но для удобства мы будем использовать прямоугольники для представления частей целого:
Предположим, мы хотим сравнить две дроби $\frac{6}{8}$ и $\фракция{2}{9}$. Представим первую дробь, разделив прямоугольник на 8 равных частей, затем заштриховав 6 его частей:
Мы также представляем вторую дробь, разделив прямоугольник на 9 равных частей, затем заштриховав 2 его части:
Если мы сравним обе фигуры друг с другом, мы увидим, что $\frac{6}{8}$ покрывает больше площадь, чем $\frac{2}{9}$.
Следовательно, мы заключаем, что первая дробь $\frac{6}{8}$ на больше, чем вторая дробь $\frac{2}{9}$:
$\frac{6}{8} $>$\frac{2}{9}$
Еще раз отметим, что этот подход может быть удобен для дробей, которые легко представить. Поскольку мы рассматриваем большие знаменатели, разделение может быть не таким эффективным, как для меньших знаменателей. Поэтому рассмотрим другие методы.
Поскольку мы рассматриваем большие знаменатели, разделение может быть не таким эффективным, как для меньших знаменателей. Поэтому рассмотрим другие методы.
Десятичный подход
Другой метод, который мы можем использовать для сравнения дробей, — это использование Десятичного подхода . В этом подходе мы находим точные значения каждой дроби, используя калькулятор или выполняя деление в длинное число, а затем сравниваем эти десятичные числа.
Например, мы хотим узнать, какая дробь больше: $\frac{15}{24}$ или $\frac{30}{40}$. Вычислив точные значения обеих дробей, мы получим следующие десятичные числа:
$\frac{15}{24}$=0,625
$\frac{30}{40}$=0,75
Заметим, что обе дроби являются правильными, у которых числители меньше знаменателей. Следовательно, мы ожидаем, что их точные значения будут меньше единицы.
Затем мы сравниваем десятичные значения обеих дробей. Глядя на десятые доли обоих десятичных знаков, мы замечаем, что 0,7 больше, чем 0,6, поэтому мы заключаем, что 0,75>0,625 и что $\frac{30}{40}$ больше, чем $\frac{15}{24}$ :
$\frac{30}{40}$>$\frac{15}{24}$
Перекрестное умножение
Если мы хотим работать с умножением чисел вместо получения их частного, мы можем использовать Перекрестное умножение для сравнения двух дробей. Чтобы выполнить перекрестное умножение, мы умножаем числитель одной дроби на знаменатель другой дроби, а затем сравниваем, какое перекрестное произведение больше, и впоследствии определяем, какая дробь больше.
Чтобы выполнить перекрестное умножение, мы умножаем числитель одной дроби на знаменатель другой дроби, а затем сравниваем, какое перекрестное произведение больше, и впоследствии определяем, какая дробь больше.
Мы можем использовать предыдущий пример $\frac{15}{24}$ и $\frac{30}{40}$ и проверить, какая дробь больше.
Сначала мы возьмем перекрестное произведение числителя 15 и знаменателя 40, затем запишем результат, представляющий первую дробь:
Затем мы также возьмем перекрестное произведение числителя 30 и знаменателя 30, затем запишем результат в представляют вторую дробь:
Наконец, мы сравниваем два произведения, полученные в результате перекрестного умножения:
600<720
Поскольку 720 больше 600, то мы заключаем, что $\frac{30}{40}$ больше, чем $\фрак{15}{24}$. Это согласуется с выводом, который мы сделали, используя десятичный подход.
Сравнение одинаковых дробей
Предположим, у нас есть две одинаковые дроби. Помимо общих методов, которые мы уже открыли, есть более быстрый способ сравнить эти дроби без особых проблем.
При сравнении двух дробей с одинаковым знаменателем сравнение дробей можно рассматривать как сравнение их числителей. Соотношение между числителями обеих дробей также относится к соотношению между двумя дробями.
Рассмотрим пример и сравним следующие дроби $\frac{2}{7}$ и $\frac{6}{7}$. Поскольку обе дроби подобны дробям с одинаковым знаменателем 7, сравниваем числители 2 и 6.
2<6
Поскольку числитель первой дроби меньше числителя второй дроби, заключаем, что первая дробь также меньше второй дроби:
$\frac{2}{7}$<$\frac{6}{7}$
Интуитивно мы можем согласиться с этим выводом, поскольку из пиццы из семи кусков, съедая два ломтика из целого меньше, чем съесть шесть ломтиков из той же коробки!
Сравнение непохожих дробей
Как насчет случая двух непохожих дробей? Мы можем использовать аналогичный подход для сравнения одинаковых дробей, но мы добавим дополнительные шаги для преобразования разных дробей в одинаковые дроби. Мы делаем это, находя общий знаменатель для обеих дробей или наименьший общий знаменатель.
Нахождение общего знаменателя
Общий знаменатель между двумя дробями можно получить, взяв произведение обоих знаменателей. Затем мы преобразуем обе дроби в одинаковые дроби, умножая числитель и знаменатель одной дроби на знаменатель другой дроби.
В качестве примера сравним дроби $\frac{22}{45}$ и $\frac{6}{9}$. Их общий знаменатель равен:
45×9=405
Затем мы перепишем первую дробь $\frac{22}{45}$, умножив числитель и знаменатель на знаменатель второй дроби 9:
$ \frac{22×9}{45×9}$=$\frac{198}{405}$
Затем мы перепишем вторую дробь $\frac{6}{9}$, умножив числитель и знаменатель на знаменатель второй дроби 45:
$\frac{6×45}{9×45}$=$\frac{270}{405}$
Теперь, когда у нас есть две одинаковые дроби, мы можем сравнить их числители, чтобы определить, какая дробь больше:
270>198 ∴ $\frac{270}{405}$>$\frac{198}{405}$
Так как $\frac{270}{405}$ больше, чем $\frac{198}{405 }$, то заключаем, что их эквивалентные дроби $\frac{6}{9}$ больше, чем $\frac{22}{45}$:
$\frac{6}{9}$>$\frac {22}{45}$
Нахождение наименьшего общего знаменателя
Альтернативно, Наименьший общий знаменатель (LCD) между двумя дробями можно получить, взяв наименьшее общее кратное обоих знаменателей. Затем мы перепишем эквивалентные дроби так, чтобы получилось две одинаковые дроби. Таким образом, мы можем сравнить их как дроби.
Затем мы перепишем эквивалентные дроби так, чтобы получилось две одинаковые дроби. Таким образом, мы можем сравнить их как дроби.
Рассмотрим две дроби из предыдущего примера $\frac{22}{45}$ и $\frac{6}{9}$, знаменатели которых равны 45 и 9 соответственно. Если мы возьмем наименьшее общее кратное обоих знаменателей, 45, то мы можем переписать обе дроби так, чтобы они имели одинаковый знаменатель.
Так как $\frac{22}{45}$ уже выражено через наименьший общий знаменатель, нам нужно только получить эквивалентную дробь второй дроби $\frac{6}{9}$:
$ \frac{6×5}{9×5}$=$\frac{30}{45}$
Таким образом, мы можем сравнить обе одинаковые дроби, используя их числители:
30>22 ∴ $\frac{30} {45}$>$\frac{22}{45}$
Поскольку $\frac{30}{45}$ больше, чем $\frac{22}{45}$, мы заключаем, что их эквивалентные дроби $ \ гидроразрыв {6} {9}$ больше, чем $\frac{22}{45}$:
$\frac{6}{9}$>$\frac{22}{45}$
Заметим, что мы пришли к одному и тому же вывод, когда мы использовали общий знаменатель ранее.
Примеры решения задач
Теперь мы можем приступить к решению примеров задач, чтобы применить то, что мы уже узнали. Каждая проблема связана с различными обсуждаемыми подходами и методами и ставит перед нами задачу, как работать с предоставленной нам информацией.
Сравнение дробей с использованием интуитивного подхода
Пример задачи 1:
Тимоти сделал плитку шоколада, чтобы поделиться с пятью своими друзьями. На перемене к ним присоединился еще один друг, и Тимоти решил разделить шоколад на всех семерых (включая себя).
Однако Тимоти не хочет получать меньше той доли, которую он должен был разделить с пятью друзьями. Он думает, что должен разделить шоколад на восемь частей, взять себе две части, а оставшиеся части разделить с друзьями. Получит ли он таким образом больше шоколада?
Решение:
Сначала рассмотрим плитку шоколада, разделенную на шесть частей, и возьмем одну часть для Тимати, как показано на рисунке ниже:
Затем мы рассмотрим плитку шоколада, разделенную на восемь частей, и возьмем две части. для Тимати, как показано на рисунке ниже:
для Тимати, как показано на рисунке ниже:
Сравнивая общий размер шоколада, который Тимоти получит в любом случае, мы заключаем, что он получит больше шоколада, разделив плитку на восемь частей и взяв две части себе.
Пример задачи 2:
В свой день рождения Мелисса получила три круглых торта одинакового размера: шоколадный торт от одиннадцати родственников утром, клубничный торт от восьми коллег по работе днем и черничный торт. торт от десяти ее кузенов вечером.
Если она решила поделиться каждым тортом с группой, которая дала его ей, какого торта у нее было больше всего?
Решение:
Сначала рассмотрим шоколадный торт, который она получила утром, где она получила кусочек из одиннадцати частей. Мы сравним это с клубничным тортом, который она съела днем, где ей достался кусочек из восьми частей.
Визуализируя кусочки торта, которые она ела, как части целого, мы можем заключить, что у нее было больше клубничного торта, чем шоколадного торта:
Затем мы сравним ее клубничный торт с черничным тортом, который она съела вечером , где она получила кусок из десяти частей.
Опять же, визуализируя кусочки торта, мы можем заключить, что у нее было больше клубничного торта, чем черничного:
Таким образом, мы заключаем, что из всех трех тортов, которые Мелисса съела на свой день рождения, у нее была наибольшая доля в клубничный пирог.
Сравнение дробей с использованием десятичной системы счисления
Пример задачи 3:
Предположим, у нас есть две неправильные дроби $\frac{52}{11}$ и $\frac{47}{8}$. Используя десятичный подход, определите, какая дробь больше.
Решение:
В этом примере мы используем деление в длину, чтобы показать процесс получения десятичных значений каждой дроби. Начнем с того, что возьмем частное между числителем и знаменателем первой дроби $\frac{52}{11}$:
Отсюда округляем десятичное число до тысячных долей:
$\frac{52}{11}$≈4,727
Аналогично возводим частное между числителем и знаменателем второй дроби $\frac {47}{8}$:
Следовательно, точное десятичное значение дроби определяется как:
$\frac{47}{8}$=5,875
Наконец, мы сравниваем два десятичных числа, представляющих их эквивалент дроби:
4. 727<5.875
727<5.875
Поскольку десятичное значение второй дроби больше десятичного значения первой дроби, то делаем вывод, что вторая дробь $\frac{47}{8}$ больше первой дробь $\frac{52}{11}$.
Сравнение дробей с помощью перекрестного умножения
Пример задачи 4:
Предположим, у нас есть две правильные дроби $\frac{7}{23}$ и $\frac{16}{35}$. Какая дробь меньше? Покажите свои вычисления с помощью перекрестного умножения.
Решение:
Сначала рассмотрим перекрестное произведение числителя первой дроби 7 и знаменателя второй дроби 35, а затем запишем его в виде числа, представляющего первую дробь:
Затем мы рассматриваем перекрестное произведение числителя второй дроби, 16, и знаменателя второй дроби, 23, затем записываем его как число, представляющее вторую дробь:
Сравнивая два перекрестных произведения, мы можем заключаем, что первое перекрестное произведение меньше другого:
245<368
Следовательно, мы заключаем, что первая дробь $\frac{7}{23}$ меньше второй дроби $\frac{16 {35}$.
Пример задачи 5:
Если даны две правильные дроби $\frac{8}{24}$ и $\frac{12}{36}$, какая дробь больше? Используя перекрестное умножение, покажите свои вычисления.
Решение:
Сначала рассмотрим перекрестное произведение числителя первой дроби, 8, и знаменателя второй дроби, 36, затем запишем его как число, представляющее первую дробь:
Затем мы возьмем перекрестное произведение числителя второй дроби, 16, и знаменателя второй дроби, 23, затем запишем его как число, представляющее вторую дробь:
Сравнивая два перекрестных произведения, мы видим, что оба перекрестных произведения равны:
288=288
Следовательно, мы заключаем, что ни одна дробь не меньше другой, поскольку обе дроби эквивалентны:
$\frac{8 }{24}$=$\frac{12}{36}$
Сравнение одинаковых дробей
Пример задачи 6:
Какая дробь больше, $\frac{3}{17}$ или $\frac {10}{17}$?
Решение:
Поскольку обе дроби подобны дробям с одним и тем же знаменателем 17, мы просто сравним числители обеих дробей:
3<10
Так как числитель второй дроби больше числителя первой дроби, то мы заключаем, что вторая дробь больше первой дроби:
$\frac{10}{17}$ >$\frac{3}{17}$
Сравнение различных дробей
Пример задачи 7:
Даны две дроби $\frac{3}{10}$ и $\frac{16}{30 }$. Затем нам задают следующие вопросы:
Затем нам задают следующие вопросы:
- Каков общий знаменатель двух дробей?
- Чему равны дроби каждой дроби по общему знаменателю?
- Какая дробь меньше, $\frac{3}{10}$ или $\frac{16}{30}$?
Решение:
- Чтобы получить общий знаменатель данных дробей, мы умножаем их знаменатели, чтобы получить произведение: .
- Из первой дроби $\frac{3}{10}$ умножаем ее знаменатель на 30, чтобы получить общий знаменатель 300. Чтобы получить ее эквивалентную дробь, мы также умножаем числитель на то же число:
$ \frac{3×30}{10×30}$=$\frac{90}{300}$
Следовательно, эквивалентная доля первой дроби равна $\frac{90}{300}$.
Затем из второй дроби $\frac{16}{30}$ умножаем ее знаменатель на 10, чтобы получить общий знаменатель 300. Чтобы получить ее эквивалентную дробь, мы также умножаем числитель на то же число:
$\frac{16×10}{30×10}$=$\frac{160}{300}$
Таким образом, эквивалентная доля второй дроби равна $\frac{160}{300} $.

- Сравнивая эквивалентные дроби $\frac{90}{300}$ и $\frac{160}{300}$, мы упрощаем сравнение между $\frac{3}{10}$ и $\frac {16}{30}$ как сравнение числителей 90 и 160:
90<160
Поскольку числитель второй эквивалентной дроби больше числителя первой эквивалентной дроби, мы заключаем, что $\frac {160}{300}$>$\фракция{90}{300}$. Кроме того, это означает, что вторая дробь $\frac{16}{30}$ больше, чем $\frac{3}{10}$:
$\frac{16}{30}$>$\frac{3 {10}$
Пример задачи 8:
Предположим, мы используем две заданные дроби из примера задачи 7. Опять же, нам задают следующие вопросы:
Решение:
- Что такое ЖК из двух фракций?
- Чему равны дроби каждой дроби по наименьшему общему знаменателю?
- Какая дробь меньше, $\frac{3}{10}$ или $\frac{16}{30}$?
Решение:
- Чтобы получить наименьший общий знаменатель данных дробей, находим наименьшее общее кратное обоих знаменателей.
 Поскольку оба знаменателя кратны 10, наименьший общий знаменатель обеих дробей равен 30 .
Поскольку оба знаменателя кратны 10, наименьший общий знаменатель обеих дробей равен 30 .
- Из первой дроби $\frac{3}{10}$ умножаем ее знаменатель на 3, чтобы получить наименьший общий знаменатель 30. Чтобы получить ее эквивалентную дробь, мы также умножаем числитель на то же число. :
$\frac{3×3}{10×3}$=$\frac{9}{30}$
Таким образом, эквивалентная доля первой дроби равна $\frac{9}{30 }$.
Затем заметим, что вторая дробь уже выражена через наименьший общий знаменатель. Следовательно, нам не нужно переписывать вторую дробь $\frac{16}{30}$.
- Сравнивая эквивалентные дроби $\frac{9}{30}$ и $\frac{16}{30}$, мы упрощаем сравнение между $\frac{3}{30}$ и $\frac {16}{30}$ в качестве сравнения между числителями 9и 16:
9<16
Поскольку числитель второй эквивалентной дроби больше числителя первой эквивалентной дроби, мы заключаем, что $\frac{16}{30}$>$\frac{9} {30}$. Кроме того, это означает, что вторая дробь $\frac{16}{30}$ больше, чем $\frac{3}{10}$:
$\frac{16}{30}$>$\frac{3 }{10}$
Заметим, что такой же вывод был получен из предыдущего примера задачи.

Сводка
- А Дробь можно представить как частей целого . С математической точки зрения, это отношение между числителем и знаменателем .
- Существует три типа дробей в зависимости от соотношения их числителей и знаменателей:
- Правильная дробь — это дробь, числитель которой на меньше знаменателя на . Отношение между числителем и знаменателем всегда меньше единицы.
- Неправильная дробь , с другой стороны, является дробью, числитель которой на больше, чем знаменатель на . Отношение между числителем и знаменателем всегда больше единицы.
- Мы также можем представить неправильную дробь как Смешанное число . Смешанное число можно представить как комбинацию целого числа и дроби .
- Две дроби можно связать по значению их знаменателей:
- Подобные дроби — это дроби, знаменатели которых равны.

- В отличие от дробей — это дроби, знаменатели которых не равны.
- Эквивалентные дроби отличаются от дробей, дающих одинаковое значение.
- Как правило, мы можем сравнивать дроби, используя три подхода:
- Интуитивный подход позволяет нам визуализировать каждую дробь и сравнивать площади, покрытые каждой дробью, чтобы определить, какая из них больше или меньше.
- Десятичный подход сообщает нам точные десятичные значения каждой дроби в качестве основы для их сравнения.
- Выполняя перекрестное умножение , мы берем перекрестное произведение обеих дробей, чтобы сравнить, какая дробь больше или меньше.
- В случае, когда мы сравниваем одинаковые дроби, мы можем рассматривать сравнение одинаковых дробей как сравнение их числителей.
- В случае, если мы сравниваем разные дроби, мы сначала переписываем их эквивалентные одинаковые дроби, затем сравниваем их числители, а затем исходные дроби.

- Мы можем найти общий знаменатель двух разных дробей и выразить обе дроби через их общий знаменатель. В качестве альтернативы, мы можем найти их наименьший общий знаменатель , взглянув на наименьшее общее кратное их знаменателей, а затем выразив оба дроби по наименьшему общему знаменателю.
Дроби (на тему Дня матери) Рабочие листы по математике
Правильные и неправильные дроби (на зимнюю тематику) Рабочие листы по математике
Умножение и деление дробей (на тему Дня ветеранов) Рабочие листы по математикеМы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Обзор дробей (видео и практические вопросы)
СтенограммаЧасто задаваемые вопросыИнформационный бюллетеньПрактические рабочие листы
Привет, ребята, добро пожаловать в это видео Mometrix о дробях.
 Фракции могут быть простыми и сложными. В этом видео мы расскажем о различных типах дробей и о том, как их сложите дроби с разными знаменателями.
Фракции могут быть простыми и сложными. В этом видео мы расскажем о различных типах дробей и о том, как их сложите дроби с разными знаменателями.Что такое дробь?
Итак, что такое дробь? Дробь — это часть целого, а это значит, что дробь никогда не может быть целым числом. Подумайте об этом так:
Наш круг разделен на восемь равных частей. Допустим, было заполнено три части.
Это означает, что \(\frac{3}{8}\) нашего круга заполнено. Верхнее число (3) называется числителем . Нижнее число дроби называется 9.0011 знаменатель (в данном случае 8). При произнесении дробей вслух знаменатель обычно произносится как порядковый номер числа. Вы бы сказали «восьмой» вместо «восемь» или «третий» вместо «три».
Давайте взглянем на список наших знаменателей и посмотрим, как бы мы их назвали.
2 = половина
3 = третья
4 = четвертая или четверть0011 7 = седьмой
8 = восьмой
9 = девятый
10 = десятыйКак видите, есть несколько исключений.
 Если наш знаменатель равен 2, вы можете сказать «половина» вместо «секунда», или если наш знаменатель равен 4, вы можете сказать «четверть» вместо «четверть»; любой из них приемлем. Надеюсь, это поможет вам понять, как определяются дроби, а также как произносить их вслух. Но есть разные типы фракций. Давайте посмотрим на них.
Если наш знаменатель равен 2, вы можете сказать «половина» вместо «секунда», или если наш знаменатель равен 4, вы можете сказать «четверть» вместо «четверть»; любой из них приемлем. Надеюсь, это поможет вам понять, как определяются дроби, а также как произносить их вслух. Но есть разные типы фракций. Давайте посмотрим на них.Правильные дроби
Во-первых, у нас есть правильная дробь. Правильная дробь всегда имеет числитель (на который мы смотрели), который меньше знаменателя. Наш пример, который мы использовали ранее, \(\frac{3}{8}\), поэтому наш числитель 3 меньше нашего знаменателя 8. Некоторые другие примеры правильных дробей включают \(\frac{4}{5 }\), \(\frac{5}{9}\) и \(\frac{23}{50}\). Неправильная дробь является противоположностью правильной дроби в том смысле, что числитель больше знаменателя. Таким образом, в то время как \(\frac{3}{8}\) — правильная дробь, \(\frac{8}{3}\) — неправильная дробь, потому что числитель больше нашего знаменателя.
 Неправильные дроби всегда равны или больше 1. Это означает, что \(\frac{9{9}\) — неправильная дробь, так как равна 1. Есть также смешанных дробей , которые содержат целое число и правильную дробь. Вот пример: 2\(\frac{3}{4}\). Обратите внимание, что за целым числом 2 следует правильная дробь \(\frac{3}{4}\).
Неправильные дроби всегда равны или больше 1. Это означает, что \(\frac{9{9}\) — неправильная дробь, так как равна 1. Есть также смешанных дробей , которые содержат целое число и правильную дробь. Вот пример: 2\(\frac{3}{4}\). Обратите внимание, что за целым числом 2 следует правильная дробь \(\frac{3}{4}\).Эквивалентные дроби
У нас также есть эквивалентные дроби. Равные дроби — это две разные дроби, которые называют одно и то же число. Например: \(\frac{6}{8}\) и \(\frac{3}{4}\) выглядят по-разному, но это одно и то же. \(\frac{3}{4}\) — это просто упрощенная или сокращенная версия \(\frac{6}{8}\). Чтобы упростить \(\frac{6}{8}\), вы просто делите числитель и знаменатель на 2, чтобы получить \(\frac{3}{4}\). Теперь, когда мы знаем различные типы дробей, мы можем изучить, как их складывать. Если у двух дробей один и тот же знаменатель, сложение не составит труда. Вы просто складываете числители вместе, и это дает вам ответ. Например: \(\frac{1}{4} + \frac{2}{4} = \frac{3}{4}\)
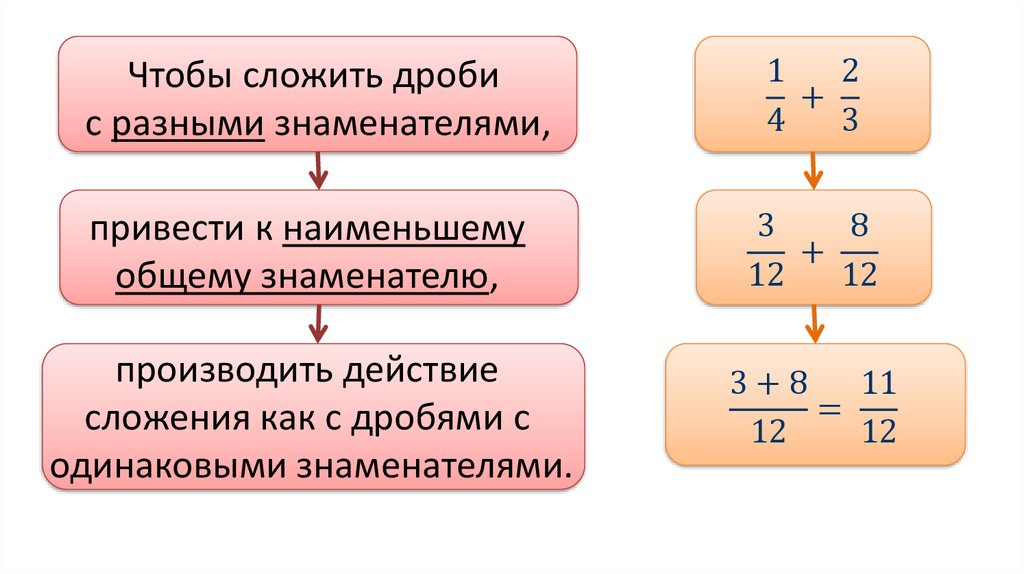
Сложение дробей с разными знаменателями
Итак, обратите внимание, что мы сделали, чтобы получить \(\frac{3}{4}\).
 Все, что нам нужно было сделать, это добавить из нашей первой дроби 1 из нашего числителя, а из нашей второй дроби 2 из нашего числителя. Сложите их вместе, чтобы получить 3, и просто вынесите наши 4 из знаменателя. Простой. Но что произойдет, если знаменатели будут другими? Ну, в этом случае вам нужно преобразовать знаменатели, чтобы они были одинаковыми. Итак, давайте рассмотрим пример: \(\frac{3}{8} + \frac{1}{2} = x\)
Все, что нам нужно было сделать, это добавить из нашей первой дроби 1 из нашего числителя, а из нашей второй дроби 2 из нашего числителя. Сложите их вместе, чтобы получить 3, и просто вынесите наши 4 из знаменателя. Простой. Но что произойдет, если знаменатели будут другими? Ну, в этом случае вам нужно преобразовать знаменатели, чтобы они были одинаковыми. Итак, давайте рассмотрим пример: \(\frac{3}{8} + \frac{1}{2} = x\)На самом деле вы не можете упростить \(\frac{3}{8}\) во что-то, что можно было бы легко добавить с помощью \(\frac{1}{2}\), но мы можем сделать что-то с \(\frac {1}{2}\), которые мы можем легко сложить с помощью \(\frac{3}{8}\), и это умножение 2 на 4, что даст нам 8. Но что бы мы ни делали с нашим знаменателем, мы также должны сделать с нашим знаменателем. Это будет выглядеть так: \(\frac{3}{8} + \frac{1\times 4}{2\times 4} = x\)
Таким образом, наше уравнение теперь принимает вид: \(\frac{3 {8} + \frac{4}{8} = \frac{7}{8}\)
Вычитание дробей с разными знаменателями
Вычитание работает таким же образом.
 Если вы вычитаете дроби с одинаковым знаменателем, вы можете просто вычесть верхние числа, как в этом примере: \(\frac{3}{4} – \frac{1}{4} = \frac{2}{ 4} = \frac{1}{2}\)
Если вы вычитаете дроби с одинаковым знаменателем, вы можете просто вычесть верхние числа, как в этом примере: \(\frac{3}{4} – \frac{1}{4} = \frac{2}{ 4} = \frac{1}{2}\)Итак, в этом примере все, что нам нужно было сделать, это вычесть наши верхние числители здесь, чтобы получить \(\frac{2}{4}\), что упрощает в \(\frac{1}{2}\). Упрощение чисел просто облегчает работу с ними. Но если вы вычитаете с другим знаменателем, вы должны сделать так, чтобы знаменатели совпадали. Например: \(\frac{3}{8} – \frac{1}{4} = x\)
Итак, в этом примере, \(\frac{3}{8} – \frac{1}{4} = x\), мы рассматриваем ту же проблему, что и здесь (\(\frac{ 3}{8} + \frac{1}{2} = x\)), нам нужно, чтобы наши знаменатели совпадали. Итак, нам нужно выяснить, что мы можем сделать, чтобы наши знаменатели совпадали? Что ж, в этом случае мы можем умножить \(4\x 2\), но помните, что мы должны сделать то же самое, что мы сделали со знаменателем, мы должны сделать с нашим числителем. Итак, мы умножаем его на 2, и вот что мы получаем: \(\frac{3}{8}-\frac{1\times 2}{4\times 2}=\frac{3}{8} – \frac {2}{8} = \фракция{1}{8}\)
Итак, умножив вторую дробь на 2, мы получим \(\frac{3}{8} – \frac{2}{8} = \frac{1}{8}\).
 Таким образом, эти задачи были довольно простыми, потому что они либо имели один и тот же знаменатель, либо их было легко преобразовать.
Таким образом, эти задачи были довольно простыми, потому что они либо имели один и тот же знаменатель, либо их было легко преобразовать.Нахождение наименьшего общего знаменателя
Но давайте рассмотрим еще одно уравнение, которое немного сложнее: \(\frac{3}{4} + \frac{6}{7}\)
Итак, на первый взгляд, это не похоже, что эти числа имеют много общего, так что мы могли бы умножить или разделить 4 на что-нибудь, чтобы получить 7, или 7 на что-нибудь, чтобы получить 4. Итак, во многих случаях, когда у вас возникают такие проблемы, что в конечном итоге вам нужно будет умножить эту дробь (\(\frac{3}{4}\)) на знаменатель другой дроби. И точно так же мы умножим эту дробь (\(\frac{6}{7}\)) на знаменатель этой дроби (\(\frac{3}{4}\)). Вот как это выглядит: \(\frac{3 \times 7}{4 \times 7} + \frac{6 \times 4}{7 \times 4}=\frac{21}{28} + \frac {24}{28}\)
Таким образом, после умножения мы получаем общий знаменатель, который равен 28. Итак, теперь все, что нам нужно сделать, это сложить наши числители вместе, что дает нам: \(\frac{21}{28} + \frac{ 24}{28} = \frac{45}{28}\)
Вот и наш ответ! С помощью этого расчета мы нашли наименьший общий знаменатель.
 Наименьший общий знаменатель — это наименьшее общее число между знаменателями. Каждый раз, когда вы выполняете вычисления с разными знаменателями, вы должны найти наименьший общий знаменатель, чтобы решить задачу. Итак, это наш взгляд на дроби.
Наименьший общий знаменатель — это наименьшее общее число между знаменателями. Каждый раз, когда вы выполняете вычисления с разными знаменателями, вы должны найти наименьший общий знаменатель, чтобы решить задачу. Итак, это наш взгляд на дроби.Надеюсь, это видео было для вас полезным! Увидимся, ребята, в следующий раз!
Часто задаваемые вопросы
Q
Какие существуют 3 типа дробей?
A
Дроби бывают трех типов: правильные дроби, неправильные дроби и смешанные числа.
Правильная дробь — это дробь, числитель которой меньше знаменателя, например \(\frac{2}{5}\).
Неправильная дробь — это дробь, числитель которой больше знаменателя, например \(\frac{5}{2}\).
Смешанное число — это дробь, состоящая из целой части числа и правильной дробной части, например \(3\frac{1}{5}\).
Q
Что такое дроби?
A
Дроби — это числа, представляющие часть целого.

Q
Что такое неправильная дробь?
A
Неправильная дробь — это дробь, числитель которой больше знаменателя. Представляет число больше 1.
Примеры:\(\frac{7}{2}\),\(\frac{14}{11}\),\(\frac{9{5}\),\(\frac{17}{6}\)
Q
Откуда вы знаете, что дроби подобны?
A
Вы можете узнать, подобны ли дроби, посмотрев на их знаменатели. Если у них одинаковые знаменатели, то они подобны. Если у них разные знаменатели, они не подобны.
Похожие дроби: \(\frac{1}{4}\) и \(\frac{3}{4}\)
Неподобные дроби: \(\frac{1}{3}\) и \( \frac{1}{5}\)
Q
Как описать дробь словами?
A
Чтобы написать дробь словами, напишите числитель, затем дефис, затем знаменатель в виде порядкового числа (как место в строке).
Пример. \(\frac{3}{4}=\) три четверти
\(\frac{7}{11}=\) семь одиннадцатыхQ
Как писать дроби?
A
Запишите дроби, поместив часть над целым, например: \(\frac{\text{часть}}{\text{целое}}\)
Пример.
 Я съел 2 печенья из 7. Что это представлено в виде дроби?
Я съел 2 печенья из 7. Что это представлено в виде дроби?
Часть съеденного мной равна 2. Всего печенек равно 7. Таким образом, дробь, представляющая количество съеденных печенек, равна \(\frac{2}{7}\).Информационный бюллетень
Загрузить информационный бюллетень
Практические вопросы
Вопрос №1:
Что из перечисленного является неправильной дробью?\(\frac{6}{9}\)
\(\frac{11}{17}\)
\(\frac{21}{8}\)
\(\frac{14}{30}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{21}{8}\). Неправильная дробь – это дробь, у которой числитель больше знаменателя.
Скрыть ответ
Вопрос № 2:
Какая из следующих дробей эквивалентна \(\frac{6}{8}\)?\(\frac{3}{4}\)
\(\frac{7}{9}\)
\(\frac{16}{18}\)
\(\frac{8}{10}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{3}{4}\).
 Равные дроби — это дроби, обозначающие одно и то же число. \(\frac{6}{8}\) совпадает с \(\frac{3}{4}\), потому что деление числителя и знаменателя на \(\frac{6}{8}\) на 2 приводит к \(\frac{3}{4}\).
Равные дроби — это дроби, обозначающие одно и то же число. \(\frac{6}{8}\) совпадает с \(\frac{3}{4}\), потому что деление числителя и знаменателя на \(\frac{6}{8}\) на 2 приводит к \(\frac{3}{4}\).Скрыть ответ
Вопрос №3:
\(\frac{2}{12}+\frac{7}{12}=\)\(\frac{5}{12}\ )
\(\frac{9}{12}\)
\(\frac{11}{12}\)
\(\frac{14}{12}\)
Показать ответ
Ответ :
Чтобы сложить дроби с одинаковым знаменателем, просто сложите числа в числителях и оставьте знаменатель одинаковым. \(2+7=9\), поэтому \(\frac{2}{12}+\frac{7}{12}=\frac{9}{12}\).
Скрыть ответ
Вопрос №4:
\(\frac{5}{6}-\frac{2}{3}=\)\(\frac{3}{3}\ )
\(\frac{3}{6}\)
\(\frac{1}{3}\)
\(\frac{1}{6}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{1 {6}\).
 Чтобы вычесть дроби, сначала преобразуйте их в дроби с одинаковым знаменателем. \(\frac{2}{3}\) можно преобразовать в \(\frac{4}{6}\) путем умножения числителя и знаменателя на 2.
Чтобы вычесть дроби, сначала преобразуйте их в дроби с одинаковым знаменателем. \(\frac{2}{3}\) можно преобразовать в \(\frac{4}{6}\) путем умножения числителя и знаменателя на 2.
\(\frac{5}{6}- \frac{4}{6}\)
Затем вычтите числители и оставьте знаменатель прежним. \(5-4=1\), поэтому \(\frac{5}{6}-\frac{4}{6}=\frac{1}{6}\).Скрыть ответ
Вопрос № 5:
\(\frac{3}{7}+\frac{2}{5}=\)\(\frac{29}{35}\ )
\(\frac{5}{7}\)
\(\frac{1}{5}\)
\(\frac{16}{35}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{29}{35}\). Чтобы сложить дроби, сначала преобразуйте их в дроби с одинаковым знаменателем. Это можно сделать, умножив \(\frac{3}{7}\) на \(\frac{5}{5}\) и \(\frac{2}{5}\) на \(\frac{ 7}{7}\).
\(\frac{3}{7}\times\frac{5}{5}+\frac{2}{5}\times\frac{7}{7}\)
\(\frac{15} {35}+\frac{14}{35}\)
Затем сложите числители и оставьте знаменатель прежним.
 Для этого допишем к нужной дроби нули;
Для этого допишем к нужной дроби нули; Для этого вначале конвертируют числитель, а затем знаменатель. Но не с каждой дробью это возможно сделать.
Для этого вначале конвертируют числитель, а затем знаменатель. Но не с каждой дробью это возможно сделать. Такое выражение называют бесконечной десятичной дробью.
Такое выражение называют бесконечной десятичной дробью.
 Поскольку оба знаменателя кратны 10, наименьший общий знаменатель обеих дробей равен 30 .
Поскольку оба знаменателя кратны 10, наименьший общий знаменатель обеих дробей равен 30 . 


 Фракции могут быть простыми и сложными. В этом видео мы расскажем о различных типах дробей и о том, как их сложите дроби с разными знаменателями.
Фракции могут быть простыми и сложными. В этом видео мы расскажем о различных типах дробей и о том, как их сложите дроби с разными знаменателями. Если наш знаменатель равен 2, вы можете сказать «половина» вместо «секунда», или если наш знаменатель равен 4, вы можете сказать «четверть» вместо «четверть»; любой из них приемлем. Надеюсь, это поможет вам понять, как определяются дроби, а также как произносить их вслух. Но есть разные типы фракций. Давайте посмотрим на них.
Если наш знаменатель равен 2, вы можете сказать «половина» вместо «секунда», или если наш знаменатель равен 4, вы можете сказать «четверть» вместо «четверть»; любой из них приемлем. Надеюсь, это поможет вам понять, как определяются дроби, а также как произносить их вслух. Но есть разные типы фракций. Давайте посмотрим на них. Неправильные дроби всегда равны или больше 1. Это означает, что \(\frac{9{9}\) — неправильная дробь, так как равна 1. Есть также смешанных дробей , которые содержат целое число и правильную дробь. Вот пример: 2\(\frac{3}{4}\). Обратите внимание, что за целым числом 2 следует правильная дробь \(\frac{3}{4}\).
Неправильные дроби всегда равны или больше 1. Это означает, что \(\frac{9{9}\) — неправильная дробь, так как равна 1. Есть также смешанных дробей , которые содержат целое число и правильную дробь. Вот пример: 2\(\frac{3}{4}\). Обратите внимание, что за целым числом 2 следует правильная дробь \(\frac{3}{4}\). Все, что нам нужно было сделать, это добавить из нашей первой дроби 1 из нашего числителя, а из нашей второй дроби 2 из нашего числителя. Сложите их вместе, чтобы получить 3, и просто вынесите наши 4 из знаменателя. Простой. Но что произойдет, если знаменатели будут другими? Ну, в этом случае вам нужно преобразовать знаменатели, чтобы они были одинаковыми. Итак, давайте рассмотрим пример: \(\frac{3}{8} + \frac{1}{2} = x\)
Все, что нам нужно было сделать, это добавить из нашей первой дроби 1 из нашего числителя, а из нашей второй дроби 2 из нашего числителя. Сложите их вместе, чтобы получить 3, и просто вынесите наши 4 из знаменателя. Простой. Но что произойдет, если знаменатели будут другими? Ну, в этом случае вам нужно преобразовать знаменатели, чтобы они были одинаковыми. Итак, давайте рассмотрим пример: \(\frac{3}{8} + \frac{1}{2} = x\) Если вы вычитаете дроби с одинаковым знаменателем, вы можете просто вычесть верхние числа, как в этом примере: \(\frac{3}{4} – \frac{1}{4} = \frac{2}{ 4} = \frac{1}{2}\)
Если вы вычитаете дроби с одинаковым знаменателем, вы можете просто вычесть верхние числа, как в этом примере: \(\frac{3}{4} – \frac{1}{4} = \frac{2}{ 4} = \frac{1}{2}\) Таким образом, эти задачи были довольно простыми, потому что они либо имели один и тот же знаменатель, либо их было легко преобразовать.
Таким образом, эти задачи были довольно простыми, потому что они либо имели один и тот же знаменатель, либо их было легко преобразовать. Наименьший общий знаменатель — это наименьшее общее число между знаменателями. Каждый раз, когда вы выполняете вычисления с разными знаменателями, вы должны найти наименьший общий знаменатель, чтобы решить задачу. Итак, это наш взгляд на дроби.
Наименьший общий знаменатель — это наименьшее общее число между знаменателями. Каждый раз, когда вы выполняете вычисления с разными знаменателями, вы должны найти наименьший общий знаменатель, чтобы решить задачу. Итак, это наш взгляд на дроби.
 Я съел 2 печенья из 7. Что это представлено в виде дроби?
Я съел 2 печенья из 7. Что это представлено в виде дроби?  Равные дроби — это дроби, обозначающие одно и то же число. \(\frac{6}{8}\) совпадает с \(\frac{3}{4}\), потому что деление числителя и знаменателя на \(\frac{6}{8}\) на 2 приводит к \(\frac{3}{4}\).
Равные дроби — это дроби, обозначающие одно и то же число. \(\frac{6}{8}\) совпадает с \(\frac{3}{4}\), потому что деление числителя и знаменателя на \(\frac{6}{8}\) на 2 приводит к \(\frac{3}{4}\). Чтобы вычесть дроби, сначала преобразуйте их в дроби с одинаковым знаменателем. \(\frac{2}{3}\) можно преобразовать в \(\frac{4}{6}\) путем умножения числителя и знаменателя на 2.
Чтобы вычесть дроби, сначала преобразуйте их в дроби с одинаковым знаменателем. \(\frac{2}{3}\) можно преобразовать в \(\frac{4}{6}\) путем умножения числителя и знаменателя на 2.