Сумма и разность дробей. Произведение и частное дробей. Возведение дроби в степень 8 класс онлайн-подготовка на

113. Сумма и разность дробей. Произведение и частное дробей. Возведение дроби в степень.

При сложении обыкновенных дробей с одинаковыми знаменателями складывают их числители, а знаменатель оставляют прежним. Например:

27+37=2+37=57.

Таким же образом складывают любые рациональные дроби с одинаковыми знаменателями:

ac+bc=a+bc,

где а, b и с — многочлены, причем с — ненулевой многочлен.

Это равенство выражает правило сложения рациональных дробей с одинаковыми знаменателями:

Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.

Вычитание рациональных дробей выполняется аналогично сложению:

ac-bc=a-bc.

Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

Пример 1. Сложим дроби:

3a-7b15ab+2a+2b15ab=3a-7b+2a+2b15ab=5a-5b15ab=5(a-b)15ab=a-b3ab.

Пример 2. Вычтем дроби:

a2+95a-15-6a5a-15=a2+9-6a5a-15=a-325a-3=a-35.

Сложение и вычитание дробей с разными знаменателями

Сложение и вычитание рациональных дробей с разными знаменателями сводится к сложению и вычитанию рациональных дробей с одинаковыми знаменателями. Для этого данные дроби приводят к общему знаменателю.

Пример 3. Сложим дроби x4a3b+56ab4.

Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателем является одночлен 12а³b⁴. Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей дробей, а каждая переменная взята с наибольшим показателем, с которым она входит в знаменатели дробей. Дополнительные множители к числителям и знаменателям этих дробей соответственно равны 3b

3и 2a².

Имеем

x4a3b+56ab4=x∙3b3+5∙2a212a3b4=3b3x+10a212a3b4.

Пример 4. Преобразуем разность a+3a2+ab-b-3ab+b2.

Чтобы найти общий знаменатель, разложим знаменатель каждой дроби на множители:

a+3a2+ab-b-3ab+b2=a+3a(a+b)-b-3b(a+b).

Простейшим общим знаменателем служит выражение ab(a+b). Дополнительные множители к числителям и знаменателям этих дробей соответственно равны b и а.

Имеем:

a+3a(a+b)-b-3ba+b=a+3b-b-3aaba+b=ab+3b-ab+3aaba+b=3a+baba+b=3ab.

Преобразование рационального выражения, которое является суммой или разностью целого выражения и дроби, сводится к преобразованию суммы или разности дробей.

Пример 5. Упростим выражение a-1-a2-3a+1

Представим выражение a-1 в виде дроби со знаменателем 1 и выполним вычитание дробей:

a-1-a2-3a+1=a-11-a2-3a+1=a-1a+1-a2-3a+1=a2-1-a2+3a+1=2a+1.

Умножение и деление дробей. Возведение дроби в степень.

При умножении обыкновенных дробей перемножают отдельно их числители и их знаменатели и первое произведение записывают в числителе, а второе — в знаменателе дроби. Например: 23∙45=2∙43∙5=815.

Таким же образом перемножают любые рациональные дроби:

ab∙cd=acbd,

где а, b, с и d — некоторые многочлены, причем b и d — ненулевые многочлены. Это равенство выражает правило умножения рациональных дробей:

чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе — знаменателем дроби.

Пример 6. Умножим дроби a34b2∙6ba2.

Воспользуемся правилом умножения дробей:

a34b2∙6ba2=a3∙6b4b2∙a2=6a3b4a2b2=3a2b.

Правило умножения дробей распространяется на произведение трех и более рациональных дробей. Например:

ab∙cd∙mn=acbd∙mn=acmbdn.

Выясним теперь, как выполняется возведение рациональной дроби в степень.

Рассмотрим выражение abn, являющейся n-й степенью рациональной дроби ab и докажем, что

abn=anbn.

По определению степени имеем

abn=ab·ab∙…∙ab (n раз).

Применяя правило умножения рациональных дробей и определение степени, получим

ab·ab∙…∙ab=a∙a∙…∙ab∙b∙…∙b=anbn.

Следовательно, abn=anbn.

Из доказанного тождества следует правило возведения рациональной дроби в степень:

чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй — в знаменателе дроби.

Пример 7. Возведем дробь 2a2b4 в третью степень.

Воспользуемся правилом возведения в степень:

2a2b43=(2a2)3(b4)3=8a6b12.

Деление дробей

При делении обыкновенных дробей первую дробь умножают на дробь, обратную второй. Например: 38:25=38∙52=1516.

Так же поступают при делении любых рациональных дробей:

ab:cd=ab∙dc=adbc,

где а, b, с и d — некоторые многочлены, причем b, c и d — ненулевые многочлены.

Это равенство выражает правило деления рациональных дробей:

чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.

Пример 8. Разделим дроби 7a2b3:14ab.

Воспользуемся правилом деления дробей:

7a2b3:14ab=7a2b3·b14a=7a2b14ab3=a2b2.

Тема сложение дробей. Сложение и вычитание дробей с разными знаменателями.

Сложение – это арифметическое действие, в результате которого получают новое число, содержащее столько единиц, сколько было во всех заданных числах вместе взятых.

Дробь обозначает тип деления, который рассматривается как часть целого и  указывает на разделение целого на равные доли или части, где знаменатель показывает, на сколько частей мы разделили, а числитель — сколько взяли частей от этого целого. 

 

Сложение или вычитание дробей могут быть двух видов:

• знаменатели одинаковые;
• знаменатели разные;

Правила сложения дробей:

1. Одинаковые знаменатели. Складываем числители этих дробей. 
2. Разные знаменатели. Находим общий знаменатель с помощью наименьшего общего кратного чисел, и складываем их числители.

Чтобы вычислить НОК, необходимо разбить числа на простые множители и найти разложение большего числа, добавив к нему простые недостающие множители другого разложения. Полученные числа перемножить. Алгоритм решения для двух, трех и более чисел одинаков, если числа простые, то надо перемножить их.

 

Примеры решения задач: сложение дробей с одинаковым знаменателем.

Задача 1. Сложить две дроби с одинаковыми знаменателями \(\frac{7}{8}\) и \(\frac{1}{8}\).

Решение:

\(\frac{7}{8}+\frac{1}{8}=\)\(\frac{(7+1)}{8}\)\(=\frac{8}{8}=\frac{1}{1}\)

 

 

Ответ:\(1\).

Задача 2. Сложить две дроби с одинаковыми знаменателями \(\frac{6}{5}\)и \(\frac{3}{5}\).

Решение:

\(\frac{6}{5} +\frac{3}{5}\)\(=\frac{(6+3)}{5}\)\(=\frac{9}{5}=1\frac{4}{5}\)

 

 

Ответ:\(1\frac{4}{5}\).

3адача 3. Сложить две  дроби \(\frac{11}{3}\) и \(\frac{5}{3}\).

Решение:

\(\frac{11}{3}\) + \(\frac{5}{3}\)\(=\)\(\frac{(11+5)}{3}=\frac{16}{3}=5\frac{1}{3}\)

 

16/3 

Ответ:\(5\frac{1}{3}\).

3адача 4. Сложить две  дроби  с разными знаменателями \(\frac{11}{3}\) и \(\frac{5}{8}\).

Решение:

НОК\((3;8)\) \(=24\)

\(\frac{11*8}{3*8}+\frac{5*3}{8*3}\)\(=\)\(\frac{88}{24}+\frac{15}{24}=\)\(\frac{88+15}{24}\)\(=\frac{103}{24}=4\frac{7}{24}\)

 

 

 

Ответ: \(4\frac{7}{24}\)

Задача 5. Сложить две дроби с разными знаменателями \(\frac{27}{3}\) и \(\frac{55}{13}\).

Решение.

\(НОК(3;13) =39\)

\(\frac{(27*13)}{3*13} +\frac{(55*3)}{13*3}=\)\(\frac{351}{39}+\frac{165}{39}\)\(=\frac{351+165}{39}=\)

 

\(=\frac{516}{39}-\) сокращаем обе части дроби на 3

\(\frac{175}{13}=13\frac{6}{13}\)

Ответ: \(13\frac{6}{13}\).

Выводы:

для того чтобы сложить или вычесть два и более дробных числа нам необходимо привести их к общему знаменателю;

основное свойство дробей: значение дробного числа не изменится, если числитель и знаменатель умножить или разделить на одно и то же число.

 

 

 

`

 

 

 

 

 

 

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Вычитание дробей

Главная » Дроби и все, что с ними связано » Вычитание дробей
Перевод смешанного числа в неправильную дробь, Как неправильные дроби перевести в смешанные числа, Перевод десятичной дроби в обыкновенную, Перевод обыкновенной дроби в десятичную, Сокращение дробей, Сложение дробей, Вычитание дробей, Умножение дробей, Деление дробей, Сравнение дробей

Вычитание дробей

Задача вычитания дробей подразделяется на две поздадачи:

1. Вычитание дробей с одинаковыми знаменателями;
2. Вычитание дробей с разными знаменателями.

Вычесть дроби с одинаковыми знаменателями – простейшая задача: нужно просто вычесть числители дробей, а знаменатель оставить прежним. Это достаточно легко понять, взглянув на рисунок 1:

Рис. 1. Вычитание дробей с одинаковыми знаменателями:

Вычитание дробей с разными знаменателями выполняется несколько иначе.

Для примера отнимем дроби

Рис. 2. Вычитание дробей с разными знаменателями:

Сначала нам потребуется разбить обе дроби на одинаковые части, которые можно вычесть по правилу вычитания с одинаковыми знаменателями. В данном случае это будут шестые части (см. рисунок). 6 – это наименьшее число, которое делится и на 2, и на 3.

Рис. 3. «Разбиваем» дроби на одинаковые части:

Затем следует ответить на вопрос, сколько шестых частей поместятся на

Для этого нужно общий знаменатель 6 разделить на знаменатель соответствующей дроби:

6 : 2 = 3, 6 : 3 = 2

Полученные числа 3 и 2 – дополнительные множители. Они записываются над числителями каждой из дробей.

Теперь нужно умножить дополнительные множители на числители дробей и вычесть:

Онлайн калькулятор
для вычитания дробей

Для того, чтобы вычесть две обыкновенные дроби, вы можете воспользоваться онлайн калькулятором вверху страницы. Просто введите дроби и нажмите на кнопку «=» — получите готовое решение.

Замечание. Данный калькулятор можно использовать для вычитания смешанных чисел. Просто сначала воспользуйтесь калькулятором для перевода смешанных чисел в неправильную дробь, а затем введите полученные дроби вверху страницы.
Аналогично можно вычитать обыкновенную и десятичную дроби. Переведите десятичную дробь в обыкновенную с помощью соответствующего онлайн калькулятора, а затем отнимите на этой странице две обыкновенные дроби.

Как вычесть дробь с разными знаменателями

Основной особенностью человеческого разума является способность к абстрактному мышлению. Одной из наивысших форм абстракции в человеческом мире является число. Выделяют несколько категорий чисел, различающихся свойствами. Наиболее привычными и часто используемыми в повседневной жизни являются целые и действительные числа. Как правило, числа записываются в десятичной системе счисления. Действительные числа обозначаются десятичными дробями. Одним из недостатков записи дробных чисел в виде десятичных дробей является их ограниченная точность. Когда точность особо важна, числа записывают в виде дробей (пары числитель-знаменатель). В ряде случаев дроби весьма удобны, но арифметические операции с ними более сложны, чем с десятичными числами. Например, чтобы вычесть дробь с разными знаменателями, нужно совершить несколько математических действий.Вам понадобится

Приведите дроби к одному знаменателю. Помножьте числитель и знаменатель первой дроби на знаменатель второй. Помножьте числитель и знаменатель второй дроби на знаменатель первой. Например, если исходные дроби равны 6/7 и 5/11, то дроби, приведенные к общему знаменателю, будут равны 66/77 и 35/77. В данном случае числитель и знаменатель первой дроби были помножены на число 11, а числитель и знаменатель второй дроби — на число 7.

Произведите вычитание дробей. Вычтите из числителя первой дроби числитель второй дроби. Запишите полученное значение в качестве числителя результирующей дроби. В качестве знаменателя результата подставьте общий знаменатель, полученный на предыдущем шаге. Так, при вычитании из дроби 66/77 значения дроби 35/77, получится результат 31/77 (из числителя 66 был вычтен числитель 35, а знаменатель оставлен прежним).

Произведите сокращение дроби-результата, если это необходимо. Подберите наибольший общий делитель, отличный от 1 для числителя и знаменателя результирующей дроби. Разделите на него числитель и знаменатель. Запишите новые значения в качестве числителя и знаменателя итоговой дроби. Наибольшего общего делителя, отличного от 1 может и не существовать. В этом случае оставьте в качестве результата исходную .

Сравнение, сложение и вычитание дробей с разными знаменателями

Ещё в 5 классе вы научились складывать, вычитать и сравнивать дроби с одинаковыми знаменателями.

Напомним,

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же.

Чтобы вычесть дроби с одинаковыми знаменателями, надо вычесть их числители, а знаменатель оставить тот же.

Чтобы сравнить две дроби с одинаковыми знаменателями, надо сравнить их числители. Больше та дробь, у которой числитель больше. Меньше та дробь, у которой числитель меньше.

Все эти правила простые и понятные.

Теперь попробуем сложить дроби .

Правило

Таким образом, чтобы сложить дроби с разными знаменателями, нужно их сначала привести к наименьшему общему знаменателю, а потом производить действие сложения как с дробями с одинаковыми знаменателями.

Теперь попробуем вычесть из дроби  дробь .

Как сравнить дроби  и ? Возможно, вы уже сами догадались.

Сформулируем правило сравнения дробей с разными знаменателями:

Чтобы сравнить дроби с разными знаменателями, надо привести дроби к общему знаменателю и сравнить полученные дроби, то есть сравнить их числители.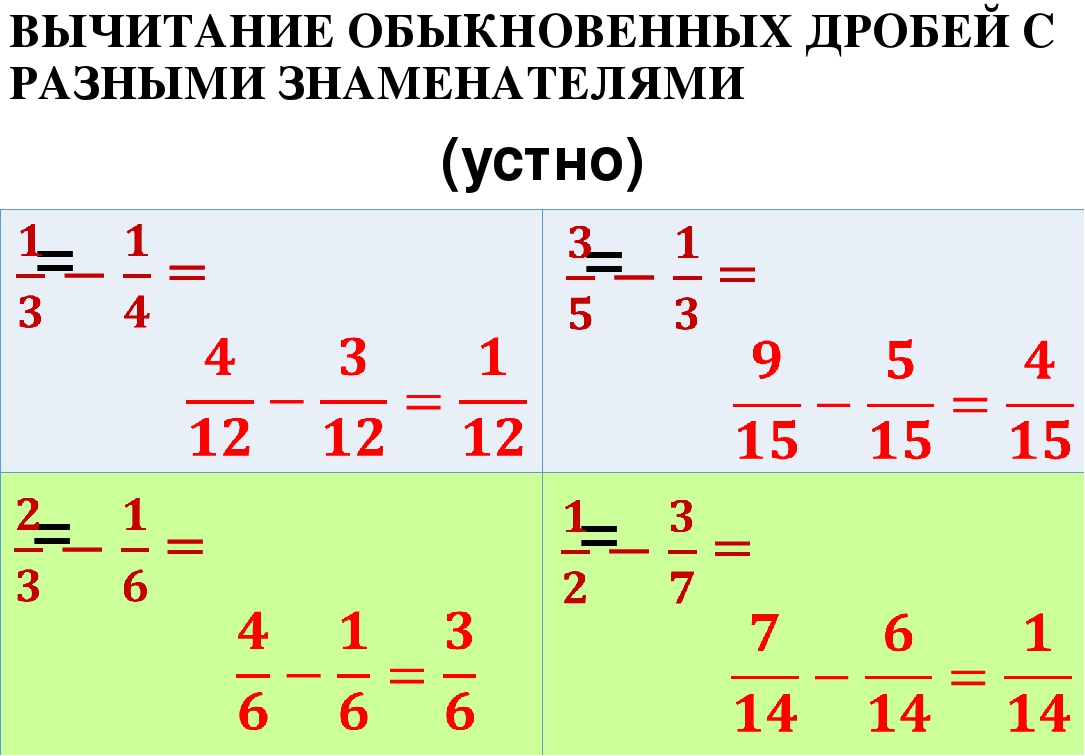 Больше та дробь, у которой числитель больше. Меньше та дробь, у которой числитель меньше.

Задача

Итоги

Складывать и вычитать дроби с разными знаменателями можно только тогда, когда в процессе вычисления дроби приведены к одному общему знаменателю.

То есть, чтобы сложить или вычесть дроби с разными знаменателями, нужно их сначала привести к наименьшему общему знаменателю, а потом производить действия сложения или вычитания как с дробями с одинаковыми знаменателями.

Не забывайте сокращать дроби в ответе, пока не получите несократимую дробь.

Чтобы сравнить дроби с разными знаменателями, надо привести дроби к общему знаменателю и сравнить полученные дроби, то есть сравниваем их числители. Больше та дробь, у которой числитель больше. Меньше та дробь, у которой числитель меньше.

Урок математики в 6 классе «Сложение и вычитание дробей с разными знаменателями»

Материал опубликовала

Захарова Татьяна Николаевна1548 Мой педагогический стаж — 25 лет, из них 14 лет — в должности заместителя директора по учебно-воспитательной работе; высшая квалификационная категория Россия, Нижегородская обл., Павлово

Автор – разработчик: Захарова Т.Н., учитель математики МБОУ СШ №16 г.Павлово Нижегородской области Презентация к уроку по учебному предмету «Математика» в 6-м классе на тему «Сложение и вычитание дробей с разными знаменателями» (учебник под редакцией А.Г.Мерзляка)

Тип урока — урок открытия новых знаний Формируемые результаты Предметные: формировать умение складывать и вычитать обыкновенные дроби с разными знаменателями. Личностные: формировать интерес к изучению темы и желание применять приобретенные знания и умения. Метапредметные: формировать умение определять способы действий в рамках предложенных условий

План урока 1. Повторяем изученное. 2. «Открываем» новый алгоритм. 3. Закрепляем алгоритм. 4. Проверяем и подводим итоги. 5. Домашнее задание.

Повторяем изученное 1. Сократите дроби:

Повторяем изученное 2. Выделите целую часть из неправильной дроби:

Повторяем изученное 3. Приведите дроби к наименьшему общему знаменателю:

Повторяем изученное 4. Вычислите:

Повторяем изученное Вспомните алгоритм сложения (вычитания) дробей с одинаковыми знаменателями 1. Сложить (или вычесть) числители и записать ответ в числитель суммы (или разности) 2. Знаменатель оставить без изменения, записав его в знаменатель 3. Если возможно, сократить полученную дробь или выделить из нее целую часть

«Открываем» новый алгоритм Вычислите:

Тема урока: «Сложение и вычитание дробей с разными знаменателями» Цель урока: Учиться складывать и вычитать дроби с разными знаменателями.

дополнить известный алгоритм, чтобы можно было по нему выполнить сложение и вычитание дробей с разными знаменателям, и показать на предложенных примерах, как он действует. дополнить известный алгоритм, чтобы можно было по нему выполнить сложение и вычитание дробей с разными знаменателям, и показать на предложенных примерах, как он действует. «Открываем» новый алгоритм Задание в группах:

«Открываем» новый алгоритм «Открываем» новый алгоритм Алгоритм сложения (вычитания) дробей с разными знаменателями 2. Сложить (или вычесть) числители и записать ответ в числитель суммы (или разности) 3. Знаменатель оставить без изменения, записав его в знаменатель 4. Если возможно, сократить полученную дробь или выделить из нее целую часть 1. Привести дроби к общему знаменателю

«Открываем» новый алгоритм Алгоритм можно сформулировать короче, объединив некоторые шаги 2. Сложить (или вычесть) дроби с одинаковыми знаменателями 3. Если возможно, сократить полученную дробь или выделить из нее целую часть 1. Привести дроби к общему знаменателю

«Открываем» новый алгоритм Образец записи

7/12 — 3/8 5/24 23/24 4/4 Закрепляем алгоритм

365 : (х – 13) = 73 4/15 + 7/12 5/24 29/30 11/27 51/60 Закрепляем алгоритм

4/5 – 2/3 + 4/15 5/24 51/60 26/15 6/15 2/5 6/18 Закрепляем алгоритм

Выполните задания из учебника, работая в парах № 268 (1 – 6) № 270 (1, 3, 5) Закрепляем алгоритм

1 вариант 1) 1) 2) 3) 3) 2 вариант Проверяем и подводим итоги Самостоятельная работа

1 вариант 2 вариант ОТВЕТЫ

Рефлексия – Какую цель мы ставили в начале урока? – Наша цель достигнута? – Что нам помогло справиться с затруднением? – Какие знания нам пригодились при выполнении заданий на уроке? – Как вы можете оценить свою работу на уроке? Проверяем и подводим итоги

Домашнее задание 1) составить и решить задачу на сложение и вычитание дробей с разными знаменателями; 2) составить задачу на сложение и вычитание дробей с разными знаменателями для своего друга из класса.

СПАСИБО ЗА УРОК

Сложение и вычитание дробей

То, каким образом мы будем складывать или вычитать дроби, напрямую зависит от знаменателей этих дробей. Самое простое: сложение и вычитание дробей с одинаковыми знаменателями. С него и начнем.

Cложение и вычитание дробей с одинаковыми знаменателями

Вспоминаем законы сложения дробей из четвертого класса.

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Чтобы вычесть друг из друга дроби с одинаковыми знаменателями, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.

Убедимся в справедливости этого высказывания на примере. Разделим круг на 5 равных частей. Возьмем из этих пяти 1-у часть и 2 части. Сложим. Вместе они составят 3 части. А поскольку изначально круг был разделен на 5 таких частей, то это 3/5 круга.

1/5 + 2/5 = 3/5

Уберем из целого круга 2 зеленые части (2/5). Останется 3 части (3/5).

5/5 — 2/5 = 3/5

Но если знаменатели разные, то ни сложить, ни вычесть такие дроби сразу нельзя.

Можно складывать и вычитать дроби только с одинаковыми знаменателями.

При сложении смешанных дробей отдельно складываются/вычитаются целые части, отдельно дробные, и опять же только при условии одинаковых знаменателей у дробных частей.

$5\frac27+3\frac17=(5+3)+(\frac27+\frac17)=8+\frac37=8\frac37$
$5\frac27-3\frac17=(5-3)+(\frac27-\frac17)=2+\frac17=2\frac17$

Если при вычитании смешанных дробей складывается такая ситуация, что числитель первой дробной части (уменьшаемое) меньше числителя второй (вычитаемого), то нужно взять единичку от целой части первого числа, представить ее в виде дроби с тем же знаменателем, что и у дробной части, и прибавить эту дробь к дробной части. Целая часть станет на единицу меньше, а дробная будет теперь представлять собой неправильную дробь (числитель больше знаменателя). Зато легко можно будет провести вычитание.

$5\frac17-3\frac27=\mathit4\mathit+\mathit1\mathit+\frac{\mathit1}{\mathit7}\mathit-\mathit3\frac{\mathit2}{\mathit7}\mathit=\mathit4\mathit+\frac{\mathit7}{\mathit7}\mathit+\frac{\mathit1}{\mathit7}\mathit-\mathit3\frac{\mathit2}{\mathit7}=4\frac87-3\frac27=(4-3)+(\frac87-\frac27)=1+\frac67=1\frac67$

Что же делать, если знаменатели разные? Разберемся. 1}{\cancel6_2}=\frac12$

Чтобы привести дроби к одинаковому знаменателю, принято находить наименьший общий знаменатель, а это то же самое, что наименьшее общее кратное (НОК) этих знаменателей. Вспомним, как находить НОК, статья по ссылке >>

$\frac59+\frac16=?$

9 | 3   6 | 2
3 | 3   3 | 3
1 |      1
НОК(6;9) = 3 * 3 * 2 = 18

$\frac59+\frac16=\frac{5\ast2}{9\ast2}+\frac{1\ast3}{6\ast3}=\frac{10}{18}+\frac3{18}=\frac{13}{18}$

Еще примеры:

Если в результате сложения или вычитания получается неправильная дробь, нужно перевести ее в смешанную. Если  получается сократимая дробь, результат необходимо сократить.

Вспоминаем: чтобы сократить дробь, нужно разделить ее числитель и знаменатель на одно и то же число — наибольший общий делитель (НОД). Статья о том, как найти НОД по ссылке >>

Для дробей, как и для натуральных чисел, выполняются переместительное и сочетательное свойства сложения:

$\frac ab+\frac cd=\frac cd+\frac ab$
$(\frac ab+\frac cd)+\frac pq=\frac ab+(\frac cd+\frac pq)$

Их нужно применять в заданиях на нахождение наиболее простого способа сложения нескольких дробей.

Пример. Вычислите значение выражения наиболее удобным способом:

Если все равно что-то в теме не поняли, задавайте вопросы в комментариях.

Fractions — сложение и вычитание дробей

Легко складывать и вычитать как дроби или дроби с одинаковым знаменателем. Ты просто сложите или вычтите числители и сохраните тот же знаменатель. Хитрый Часть получается, когда вы складываете или вычитаете дроби с разными знаменателями. Для этого нужно знать, как найти наименьший общий знаменатель. В На предыдущем уроке вы узнали, как упростить или уменьшить дробь, найдя эквивалентная или равная дробь, в которой числитель и знаменатель имеют общих факторов нет.Для этого вы разделили числитель и знаменатель на их самый большой общий фактор.

В этом уроке вы узнаете, что вы также можете умножить числитель и знаменатель на тот же коэффициент для получения эквивалентных дробей.

Пример 1

В этом примере так как 12, разделенное на 12, равняется единице, а любое число, умноженное на 1, равно самому себе, мы знаем, что 36/48 и 3/4 — эквивалентные дроби или дроби, которые имеют такое же значение.В общем, чтобы получить эквивалентную дробь, вы можете умножить или разделите числитель и знаменатель дроби на любое ненулевое число.

Так как только нравится дроби можно складывать или вычитать, сначала нужно преобразовать непохожие дроби в эквивалентные дроби. Мы хотим найти наименьшее или наименее распространенное знаменатель, потому что работа с меньшими числами упрощает наши вычисления. Наименьший общий знаменатель или ЖКД двух дробей — это наименьшее число. которое можно разделить на оба знаменателя.Есть два метода поиска наименьший общий знаменатель двух дробей:

Пример 2

Метод 1:
Запишите кратные обоих знаменателей, пока не найдете общее кратное.

Первый способ просто начать записывать все, кратные обоим знаменателям, начиная с с самими числами. Вот пример этого метода.Кратные 4 — это 4, 8, 12, 16 и т. Д. (Потому что 1 × 4 = 4, 2 × 4 = 8, 3 × 4 = 12, 4 × 4 = 16 и т. Д.). Кратные 6 равны 6, 12,… — это число, которое мы ищем, 12, потому что оно появляется первым в обоих списках кратных. Это наименьшее общее кратное, которое мы будем использовать как наш наименьший общий знаменатель.

Метод 2:
Используйте разложение на простые множители.

Для второго метод, мы используем разложение на простые множители, то есть мы записываем каждый знаменатель как произведение его основных факторов. Простые делители 4 равны 2 умноженным на 2. Простое число множители 6 умножаются на 2 умножить на 3. В качестве наименьшего общего знаменателя мы должны использовать каждый фактор, который появляется в любом числе. Поэтому нам нужны факторы 2 и 3, но мы должны использовать 2 дважды, так как оно используется дважды при факторизации для 4. Мы получаем тот же ответ для нашего наименьшего общего знаменателя, 12.

Пример 3

премьер факторизация 4 = 2 × 2
разложение на простые множители 6 = 2 × 3
ЖК-дисплей = 2 × 2 × 3 = 12

Теперь, когда мы имеют наименьший общий знаменатель, мы можем сделать эквивалентные дроби умножение числителя и знаменателя каждой дроби на коэффициент (ы) нужный.Умножаем 3/4 на 3/3, так как 3 умножить на 4 равно 12, а умножаем 1/6 на 2/2, так как 2 умножить на 6 равно 12. Это дает эквивалентные дроби 9/12 и 2/12. Теперь мы можем сложить числители 9 + 2, чтобы найти ответ 11/12.

Пример 4

назад наверх

Сложение и вычитание рациональных выражений

Сложение и вычитание рациональных выражений Вот шаги, необходимые для сложения и вычитания рациональных выражений:

Шаг 1 :	Разложите на множители знаменатель каждой дроби, чтобы найти ЖК-дисплей.
Шаг 2 :	Найдите наименьший общий знаменатель (ЖКД). Щелкните ссылку, если вам нужно просмотреть шаги по поиску ЖК-дисплея.
Шаг 3 :	Найдите новый числитель для каждой дроби. Чтобы найти новые числители для каждой дроби, сравните знаменатель каждой из исходных дробей с ЖК-дисплеем и запишите все отличия ЖК-дисплея в числитель этой дроби. Вам также следует подумать об использовании букв «LCD» в знаменателях вместо фактического ЖК-дисплея, потому что это сделает менее заманчивым сокращение дробей.
Шаг 4 :	Объедините дроби, добавляя или вычитая числители и сохраняя ЖК-дисплей. При вычитании обратите внимание, что знак вычитания перемещен в числитель, чтобы его можно было распределить позже, если это необходимо.
Шаг 5 :	Упростите числитель, распределив и комбинируя одинаковые термины.
Шаг 6 :	Разложите числитель на множители, если можете, и замените буквы «LCD» на фактический LCD.
Шаг 7 :	По возможности упростите или сократите рациональное выражение. Помните, что для сокращения рациональных выражений множители должны быть одинаковыми как в числителе, так и в знаменателе. Щелкните ссылку, если вам нужно просмотреть шаги по упрощению рациональных выражений.

Пример 1 — Упростить:

Пример 2 — Упростить:

Щелкните здесь для практических задач

Пример 3 — Упростить:

Щелкните здесь для практических задач

Пример 4 — Упростить:

Щелкните здесь для практических задач

Пример 5 — Упростить:

Щелкните здесь для практических задач

Пример 6 — Упростить:

Щелкните здесь для практических задач

Сравнение фракций | Помощь с математикой

Числитель тот же, знаменатель другой

В данном случае есть столько же разных вещей.В данном случае это трети и шестые. Убедитесь, что ваш ребенок понимает, что трети больше шестых. Правило сравнения здесь состоит в том, что дробь с меньшим знаменателем является наибольшей

.

Другой числитель, тот же знаменатель

Вот у нас другой номер одного и того же — семь восьмых и три восьмых. Семь больше трех. Правило сравнения заключается в том, что дробь с наибольшим числителем является наибольшей.

Числитель другой, знаменатель другой

Это более сложная задача из двух приведенных выше сравнений. В зависимости от уровня вашего ребенка, вы можете пропустить этот шаг и вернуться к нему позже.

Эти дроби сравниваются путем замены знаменателей на общее число. Это можно сделать, умножив верхнюю и нижнюю часть дроби на одно и то же число, так как это даст дробь с эквивалентным значением. Сделайте это, как показано ниже, для обеих дробей, чтобы получить общий знаменатель, а затем сравните их.

Итак, в приведенном выше примере, теперь, когда знаменатели равны, дробь с наибольшим числителем является наибольшей.

Некоторые учащиеся могут ответить на вопросы о том, какая дробь больше, сказав, что это зависит от размера целого, и, в зависимости от формулировки вопроса, они действительно могут быть правы! Поощряйте их мыслить категориями, которые составляют большую или меньшую долю, и быть точными в своих вопросах. например «какая самая большая дробь ?» а не просто «, какой самый большой ?»

Рабочие листы

Эквивалентные дроби
• e.грамм. 1/3 = 3/9
• Сравнение дробей (1 из 4) — две дроби — включает столбец дроби
• Сравнение дробей (2 из 4) — с использованием общих знаменателей
• Сравнение дробей (3 из 4) — упорядочивание наборов трех и четырех дробей
• Сравнение дробей (4 из 4) — порядок дробей, десятичных знаков и процентов

Попрактикуйтесь в сравнении дробей с таблицами выше.

Сложение и вычитание дробей с помощью пошагового решения математических задач

С самого начала изучения математики вы много раз сталкивались с дробями. Они встречаются в формулах и во многих повседневных практических задачах. Однако дроби в арифметике состоят строго из чисел. Теперь мы изучим операции над дробями, компоненты которых являются алгебраическими выражениями.

РЕШЕНИЕ УРАВНЕНИЙ С ЗАПИСАННЫМИ ЧИСЛАМИ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Разделите на множители числитель и знаменатель дроби.
2. Упростите алгебраические дроби.

Алгебраическая дробь — это указанное соотношение двух алгебраических выражений.

При изучении арифметики вас проинструктировали, что дробные ответы всегда следует оставлять в сокращенной или упрощенной форме. Для дроби, которую вы «уменьшили» до деления числителя и знаменателя на 4. Дробь не может быть уменьшена, потому что никакое число (кроме 1) не разделит числитель и знаменатель. Таким образом, упрощая дроби, вы использовали следующее определение.

Дробь представлена ​​в упрощенной (или сокращенной) форме , если числитель и знаменатель не содержат общего множителя (кроме 1).

Дробь, например, представлена ​​в упрощенной форме, поскольку числитель 2 и знаменатель 3 не имеют общего множителя, кроме единицы.

Для получения дроби в упрощенной форме примените следующее правило.

Для упрощения дроби полностью разложите числитель и знаменатель на множители, а затем разделите числитель и знаменатель на все общие множители.

Дробь, однако, представлена ​​не в упрощенной форме, поскольку числитель и знаменатель имеют общий множитель 2.

Затем разделите на общие множители, получив

.

Помните, коэффициент, деленный сам на себя, равен 1.

Теперь разделите на общий множитель (x + 2) в числителе и знаменателе, чтобы получить

.

Мы можем делить только общие множители, а не общие термины.

В таком выражении, как некоторые ученики хотят разделить на три.Обратите внимание, что это неправильное , поскольку это терминов , а не факторов.

Обратите внимание, что даже несмотря на то, что мы смогли разложить числитель и знаменатель на множители, мы все равно не можем разделить, поскольку нет общих факторов для обоих. Данная дробь уже находится в упрощенном виде.

Тот факт, что для данной дроби может потребоваться любой из изученных вами методов факторинга, еще раз подчеркивает важность владения факторингом.

Решение Здесь вы можете использовать «метод проб и ошибок» для числителя и «группировку» для знаменателя.

Здесь (x + 2) — общий множитель, поэтому числитель и знаменатель можно разделить.

Обратите внимание, что числитель 2x + 5 можно записать как (2x 4-5) * 1. Таким образом, когда множитель (2x + 5) делится, множитель 1 остается.

Решение Проблемы этого типа требуют особого внимания, поскольку они являются частой причиной ошибок. На первый взгляд, факторы могут быть ошибочно приняты за общие, а дробь — как уже упрощенная.Обратите внимание, что факторы нельзя разделить, так как знаки не позволяют им быть идентичными. Если, однако, отрицательная единица вычитается из одного из факторов, то есть подобные факторы, и деление может быть выполнено.

Любые множители в форме a — b и b — a отрицательны друг для друга, таким образом, 2x — 3 и 3 — 2x отрицательны друг для друга.

Все это эквивалентные формы одного и того же выражения.Предпочтительной формой будет та, в которой используется наименьшее количество письменных знаков. Всегда проверяйте свой ответ, чтобы убедиться, что он эквивалентен форме, приведенной в разделе ответов.

УМНОЖЕНИЕ АЛГЕБРАИЧЕСКИХ ФРАКЦИЙ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Числители множителей и знаменатели всех умножаемых дробей.
2. Определите и разделите по всем общим факторам.
3. Напишите продукт в простейшей форме.

Алгебраическая дробь — это указанное соотношение двух алгебраических выражений.

— это определение произведения двух дробей. На словах это говорит: «Умножьте числитель на числитель и знаменатель на знаменатель». Вы много раз использовали это правило в арифметике при умножении дробей.

Однако помните, что все дробные ответы должны быть в упрощенной форме. Мы могли бы следовать приведенному выше определению, а затем упростить ответ, как в предыдущем разделе.Но с алгебраическими дробями это может привести к очень сложным выражениям. Следующее правило позволяет нам упрощать умножение, поэтому ответ будет в упрощенной форме.

При умножении алгебраических дробей полностью разложите на множители все числители и знаменатели, затем разделите на все множители, общие для числителя и знаменателя, перед умножением.

Произведение оставшихся множителей числителя будет числителем ответа, а произведение оставшихся множителей знаменателя будет знаменателем ответа.

Опять же, помните, что общие факторы должны быть абсолютно одинаковыми.

Мы будем использовать точку * для обозначения умножения, поскольку использование X можно спутать с переменной x.

Обратите внимание, что (x + 2) и (2 + x) одинаковы, но (x — 4) и (4 — x) являются отрицательными по отношению друг к другу. Опять же, есть много возможных форм окончательных ответов. Приведенная здесь форма является предпочтительной, потому что она содержит наименьшее количество знаков.

В этой проблеме много факторов. Будь осторожен!

РАЗДЕЛЕНИЕ АЛГЕБРАИЧЕСКИХ ФРАКЦИЙ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Измените задачу деления на связанную задачу умножения.
2. Делим алгебраические дроби.

Деление дробей определяется умножением.

На делим умножаем на обратную величину делителя.

Чтобы разделить одно алгебраическое выражение на другое , инвертируйте делитель и измените операцию на умножение.

Делитель следует за знаком. Не переворачивайте неправильную дробь.

Если знаменатель не указан, подразумевается 1.

После того, как задача изменилась с задачи деления на задачу умножения, она будет завершена, как и в предыдущем разделе.

Опять же, обратите внимание, что инвертируется только дробь, следующая за знаком.

ПОИСК НАИМЕНЕЕ ОБЩЕГО ЗНАЧИТЕЛЯ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Полностью множите знаменатель дроби.
2. Найдите наименьший общий знаменатель двух или более дробей.

Правило сложения и вычитания дробей требует, чтобы объединяемые дроби имели один и тот же знаменатель. В качестве подготовки к выполнению этих операций мы теперь исследуем метод нахождения наименьшего общего знаменателя для любой группы дробей.

Общий знаменатель Лот из двух или более дробей — это выражение, которое содержит все множители знаменателя каждой дроби. Наименьший общий знаменатель содержит минимальное количество факторов, которые должны быть общим знаменателем.

Наименьший общий знаменатель набора дробей иногда называют наименьшим общим кратным знаменателей.

Мысленная арифметика позволит вам найти наименьший общий знаменатель для малых чисел. Если попросить сложить, легко прийти к наименьшему общему знаменателю 12. Если спросить, как мы пришли к 12, мы просто знаем, что 12 — это наименьшее число, делимое как на 4, так и на 6. Однако необходим более сложный метод. если числа больше или дроби являются алгебраическими дробями.

Пример 1 Найдите наименьший общий знаменатель для

Решение Эта проблема потребовала бы значительного количества догадок или возможностей тестирования, если бы у нас не было общего метода.

Мы могли бы получить общий знаменатель этих дробей, найдя произведение 12 X 14 X 15 X 18 = 45 360. Хотя это число является общим знаменателем, это не последний общий знаменатель.

Рассмотрим определение. Из него мы знаем, что общий знаменатель этих чисел должен содержать все множители каждого из них. Другими словами, мы ищем наименьшее число, делящееся на 12, 14, 15 и 18.
Сначала полностью разложите на множители каждое число.

Число, которое мы ищем, должно содержать (2) (2) (3), чтобы делиться на 12. Оно должно содержать (2) (7), чтобы делиться на 14, и так далее. Выполните следующие действия:
Напишите множители первого числа, 12.
(2) (2) (3)
Теперь посмотрите на множители следующего числа, 14, и увидите, что нам нужно (2) (7). Но поскольку у нас уже есть 2, нам нужен только множитель (7). Это дает
(2) (2) (3) (7).
Это число теперь делится на 12 и на 14. Множителями следующего числа, 15, являются (3) и (5).Поскольку у нас уже есть 3, нам нужен только множитель 5, что дает
(2) (2) (3) (7) (5).
Это число теперь делится на 12, 14 и 15. Множители следующего числа, 18, равны (2) (3) (3). У нас уже есть 2 и один 3. Значит, нам понадобится еще 3.
(2) (2) (3) (7) (5) (3) = 1,260
Это число, 1,260, является общим знаменателем 12, 14. , 15 и 18, потому что он содержит все множители каждого и поэтому делится на каждый. Это наименьший общий знаменатель, потому что он содержит только те множители, которые необходимы для деления его на 12, 14, 15 и 18.

Обратите внимание, что 1260 значительно меньше, чем число, полученное простым нахождением произведения всех знаменателей.

Предыдущее обсуждение дает начало правилу получения наименьшего общего знаменателя для любого количества дробей, будь то числа или алгебраические выражения.

Чтобы найти наименьший общий знаменатель для двух или более дробей:
1. Полностью разложите каждый знаменатель на множители.
2. Запишите знаменатель первой дроби в факторизованной форме в качестве предлагаемого общего знаменателя.
3. Путем проверки определите, какие множители второго знаменателя еще не входят в предложенный общий знаменатель, и включите их.
4. Повторите шаг три для каждой фракции.

После освоения эта пошаговая процедура значительно упростит вашу работу.

Обратите внимание, что при нахождении наименьшего общего знаменателя мы не обращаем внимания на числитель. Это знаменатель первой дроби.

При проверке второго знаменателя нам понадобится дополнительный множитель (x — 2). Наименьший общий знаменатель равен (3x — 4) (2x + l) (x — 2).

И снова числители не влияют на то, каким будет наименьший общий знаменатель. Иногда наименьший общий знаменатель сокращается до LCD.

Обратите внимание, что x 2 является множителем в знаменателе первой дроби, но не во второй дроби.

Здесь мы имеем три знаменателя.

Решение
Первый знаменатель: 3 (x + 2)
Второй знаменатель: 2 (2) (3)
Третий знаменатель: 2 (x + 3) (x + 2)
Предлагаемый общий знаменатель: 3 ( x + 2)
Изучив второй знаменатель, мы видим, что нам нужно включить множители (2) и (2). Теперь у нас есть 2 (2) (3) (x + 2). Посмотрев на третий знаменатель, мы видим, что нам нужен множитель (x + 3). Наименьший общий знаменатель равен 2 (2) (3) (x + 2) (x + 3) или 12 (x + 2) (x + 3).

ЭКВИВАЛЕНТНЫЕ ФРАКЦИИ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Поймите основной принцип дробей.
2. Заменить дробь на эквивалентную дробь.

При дальнейшей подготовке к сложению и вычитанию дробей мы должны иметь возможность изменить данную дробь на единицу с новым знаменателем без изменения значения исходной дроби.

называется фундаментальным принципом дробей .

Когда мы анализируем это утверждение, мы видим две эквивалентные дроби и замечаем, что числитель и знаменатель умножены на одно и то же ненулевое число a.

Чтобы преобразовать дробь в эквивалентную дробь , умножьте числитель и знаменатель на одно и то же ненулевое выражение.

Почему выражение должно быть ненулевым?

Вы можете представить себе этот процесс как процесс, обратный уменьшению дробей.

Решение Поскольку новый знаменатель представляет собой факторизованную форму, при осмотре мы видим, что исходный знаменатель (2x + 3) был умножен на множитель (x — 4).Следовательно, исходный числитель (x + 1) также нужно умножить на коэффициент (x — 4), получив

.

Обратите внимание, что в окончательной форме дроби мы умножили множители в числителе, но оставили знаменатель в факторизованной форме. Это предпочтительный способ написания ответа.

Решение Поскольку исходный знаменатель (x — 3) был умножен на (2) и (x + 1), исходный числитель (2x + 1) также должен быть умножен на (2) и (x + 1).

Опять же, обратите внимание на форму ответа.

ДОБАВЛЕНИЕ АЛГЕБРАИЧЕСКИХ ФРАКЦИЙ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Сложите дроби с одинаковым знаменателем.
2. Найдите наименьший общий знаменатель двух или более дробей.
3. Примените правило сложения дробей.

Теперь мы готовы сложить алгебраические дроби, используя методы, описанные в предыдущих двух разделах.Вы должны вспомнить следующее правило из арифметики.

Сумма двух или более дробей с одинаковым знаменателем — это сумма числителей над их общим знаменателем.

Обратите внимание, что это правило допускает только сумму дробей с одинаковым знаменателем. Другими словами, две или более дроби могут быть добавлены только в том случае, если у них есть общий знаменатель. Правило сложения любых двух или более дробей потребует навыков, полученных в последних двух разделах, в дополнение к знаниям комбинирования одинаковых терминов.

Чтобы сложить две или более дробей, выполните следующие действия:
Шаг 1 Найдите наименьший общий знаменатель (ЖКД) для всех участвующих дробей, используя метод, разработанный в разделе 9-4.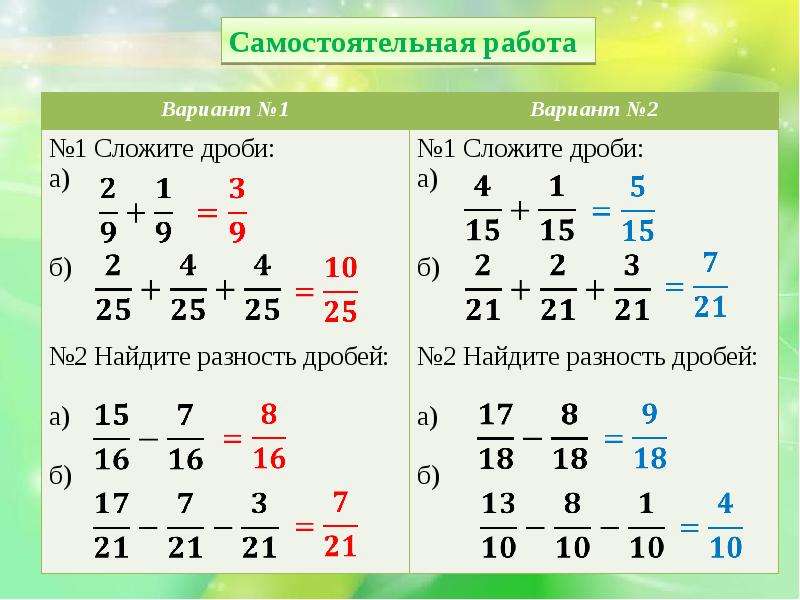
Шаг 2 Заменить каждую дробь на эквивалентную дробь с наименьшим общим знаменателем (раздел 9-5).
Шаг 3 Найдите сумму числителей и поместите эту сумму над наименьшим общим знаменателем.
Шаг 4 Упростите (или уменьшите) дробь, полученную на шаге 3.

Эти четыре шага следует использовать всякий раз, когда вы складываете дроби.

Не забудьте умножить числитель и знаменатель на одно и то же выражение.

Этот ответ дан в сокращенной форме.

Опять же, не забудьте умножить числитель на то же выражение, на которое вы умножили знаменатель.

Если знаменатели не имеют общих множителей, ЖК-дисплей является произведением знаменателей.

Здесь должна быть изменена только первая дробь.

Сумма

Обратите внимание, что числитель 3x — 15 можно разложить на множители как 3 (x — 5), а множитель (x — 5) совпадает с множителем в знаменателе.

Мы можем использовать меньше письменных шагов, если заметим, что «общий знаменатель» означает, что все дроби имеют один и тот же знаменатель, а если все имеют одинаковый знаменатель, то знаменатель необходимо записать только один раз.Чтобы проиллюстрировать это, мы переработаем предыдущий пример.

Этот ярлык подходит, если вы не забываете умножать числители на необходимые множители.

Опять же, знаменатели не имеют общих множителей, поэтому ЖК-дисплей является произведением всех трех знаменателей.

ВЫЧИТАНИЕ алгебраических дробей

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Вычтите дроби с одинаковым знаменателем.
2. Примените правило вычитания дробей с разными знаменателями.

Вычитание определяется в терминах сложения, поэтому метод вычитания алгебраических дробей будет таким же, как и сложение алгебраических дробей, описанных в предыдущем разделе. Скоро вы поймете, почему мы представили их отдельно.

Разница любых двух дробей с одинаковым знаменателем — это разница их числителей над общим знаменателем.

Обратите внимание, что это правило аналогично правилу сложения двух дробей с одинаковым знаменателем.

Таким образом, шаги вычитания дробей такие же, как и при сложении дробей.

Чтобы вычесть дроби:
Шаг 1 Найдите наименьший общий знаменатель двух дробей.
Шаг 2 Замените каждую дробь на эквивалентную дробь с наименьшим общим знаменателем.
Шаг 3 Найдите разность числителей и поместите результат над наименьшим общим знаменателем.
Шаг 4 Упростите (или уменьшите) дробь, полученную на шаге 3.

Возникает очевидный вопрос: «Если эти две операции одинаковы, зачем изучать их по отдельности?» Ответ заключается в том, что вычитание приводит к очень распространенной ошибке, которой ученик должен быть готов избежать.

Обратите внимание, мы вычитаем весь числитель второй дроби. Поэтому рекомендуется заключить весь числитель в круглые скобки со знаком вычитания перед ним.

Упомянутая ошибка часто возникает из-за того, что не осознается, что знак минус влияет на весь числитель второй дроби, а НЕ только на первый член.

Это произойдет, если вы не используете круглые скобки.

Стрелка указывает на ошибку, наиболее часто допускаемую при вычитании дробей. Лучший способ избежать этого — всегда использовать круглые скобки

.

, и вы вряд ли не сможете правильно поменять знак.

Обратите внимание, мы заключили в круглые скобки числитель второй дроби. Обратите внимание, что мы сначала умножили (x — 4) (2x — 1), а затем умножили (2×2 — 9x + 4) на -l.Умножать и менять знаки одновременно — значит допускать ошибку.

КОМПЛЕКСНЫЕ ФРАКЦИИ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Распознавать сложную дробь.
2. Упростите сложную дробь.

Дроби определяются как указанное частное двух выражений. В этом разделе мы представим метод упрощения дробей, в котором числитель или знаменатель или и то, и другое сами состоят из дробей.Такие фракции называются комплексными дробями .

Таким образом, если числитель и знаменатель сложной дроби состоят из отдельных дробей, это можно упростить, разделив числитель на знаменатель.

Как правило, более эффективный метод упрощения сложной дроби включает использование фундаментального принципа дроби. Мы умножаем числитель и знаменатель на общий знаменатель всех отдельных дробей комплексной дроби.

Напомним, что основной принцип дробей утверждает

Мы будем использовать основной принцип, чтобы снова упростить

ЖК-дисплей 3 и 4 равен 12. Таким образом,

Отдельные дроби:

Этот ответ можно записать как смешанное число

Убедитесь, что каждый член в числителе и знаменателе умножается на ЖК-дисплей.

Нам нужен ЖКИ отдельных дробей, y не дробь.

УРАВНЕНИЯ С АЛГЕБРАИЧЕСКИМИ ДОЛЯМИ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Примените метод решения дробных уравнений.
2. Определите, когда дробное уравнение не имеет решения.

В главе 2 мы встретили уравнения с дробями.Однако все эти дроби имели числовые знаменатели. Теперь мы обсудим уравнения, в которых дроби содержат переменные в знаменателях.

Метод решения этих уравнений будет следовать той же схеме, что и в главе 2, но есть некоторые дополнительные предостережения, к которым вы должны быть готовы.

Вы можете вернуться к некоторым примерам в главе 3, чтобы освежить свою память.

Чтобы освежить память, шаги для решения таких уравнений повторяются здесь.
Первое: исключите дроби, умножив каждый член уравнения на наименьший общий знаменатель всех дробей в уравнении.
Секунда: упростите, комбинируя одинаковые члены с каждой стороны уравнения.
Третий: сложите или вычтите необходимые количества, чтобы получить неизвестное количество с одной стороны и арифметические числа с другой.
Четвертое: разделить на коэффициент неизвестной величины.
Пятое: Проверьте свой ответ.

Основное различие в решении уравнений с арифметическими дробями и уравнениями с алгебраическими дробями заключается в проверке.Процесс проверки будет заключаться не только в поиске возможной ошибки, но и в определении того, имеет ли уравнение ответ.

Эта последняя возможность возникает из-за того, что с алгебраическими дробями мы умножаем на неизвестную величину. Эта неизвестная величина на самом деле может быть равна нулю, что сделает всю работу недействительной.

Помните, мы можем умножать каждую часть уравнения только на ненулевую величину.

Это означает, что ни (x — 1), ни (x + 1) не могут быть равны нулю. Если x = 1, то коэффициент (x — 1) равен нулю, и мы в беде!

Поскольку деление на ноль невозможно, мы должны сделать вывод, что x = 1 не является решением. И поскольку мы не допустили ошибок в вычислениях, мы должны сделать вывод, что это уравнение не имеет решения.
Правильный ответ — «нет решения».

Проверка необходима в алгебраических уравнениях. В противном случае вы могли бы проделать большую работу — не ошибиться — и все равно упустить проблемы. Другими словами, x = 1 не является решением, поскольку дает утверждение, не имеющее смысла.

Помните, проверка — чрезвычайно важный шаг, поскольку она определяет, есть ли решение или нет.

Обратите внимание, что в этих примерах, когда у нас есть x 2 членов, они сокращаются, и мы остаемся с линейным уравнением. Если бы они не сокращались, в уравнении был бы член x 2 .Этот тип уравнения (квадратного) будет рассмотрен в главе 11.

Таким образом, x = -5 — решение.

Следовательно, 11 — это величина, на которую был увеличен числитель.

РЕЗЮМЕ

Ключевые слова

• Алгебраическая дробь — это указанное соотношение двух алгебраических выражений.
• Дробь представлена ​​в упрощенной форме , если числитель и знаменатель не имеют общего делителя, кроме 1.
• Общий знаменатель для двух или более дробей — это выражение, которое содержит все множители знаменателей каждой дроби.
• Наименьший общий знаменатель содержит минимальное количество факторов, которые должны быть общим знаменателем.
• Основной принцип дробей —
  
• Сложные дроби — это дроби, у которых числитель или знаменатель (или оба) содержат дробь.

Процедуры

• Чтобы упростить или сократить дроби до наименьшего числа, множите числитель и знаменатель и делите на все одинаковые множители.
• Для умножения дробей множите все числители и знаменатели и делите на все одинаковые множители перед умножением.
• Чтобы разделить на дробь, переверните делитель, а затем умножьте.
• Чтобы найти наименьший общий знаменатель (LCD), сначала разложите на множители все знаменатели, затем найдите знаменатель, который содержит все множители каждого знаменателя, но не содержит никаких ненужных множителей.
• Чтобы преобразовать дробь в эквивалентную дробь, умножьте числитель и знаменатель на одно и то же ненулевое выражение.
• Чтобы сложить дроби, выполните следующие действия:
  1. Найдите наименьший общий знаменатель.
  2. Замените каждую дробь на эквивалентную дробь, указав в качестве знаменателя ЖК-дисплей.
  3. Сложите числители и поместите над ЖК-дисплеем.
  4. Упростите или сократите ответ.
• Чтобы вычесть дроби, действуйте так же, как сложение, но объедините числители путем вычитания.
• Сложные дроби можно упростить, умножив числитель и знаменатель комплексной дроби на ЖК-дисплей всех дробей в выражении.
• Для решения уравнений, содержащих дроби, сначала удалите все дроби, умножив все уравнение на ЖК-дисплей соответствующих дробей. Полученное уравнение затем решается, и решение необходимо проверить в исходном уравнении.

Как вычитать дроби с непохожими знаменателями

Как вычитать дроби с непохожими знаменателями

Чтобы вычесть дроби с разными знаменателями, выполните следующие действия:

1. Найдите наименьшее общее кратное знаменателей дробей.
2. Напишите эквивалентные дроби, у которых в качестве знаменателя используется наименьшее общее кратное.
3. Оставьте это наименьшее общее кратное в качестве знаменателя ответа.
4. Вычтите числители в вопросе, чтобы получить числитель ответа.

Самое важное правило при вычитании дробей — сначала составить общий знаменатель. Знаменатели дробей перед их вычитанием должны быть одинаковыми.

Например, здесь ⁴ / ₆ — ³ / ₈ .

Знаменатели — это числа внизу дроби. Знаменатели — 6 и 8 — разные. Чтобы вычесть дроби, нам нужно, чтобы знаменатели были одинаковыми.

Общий знаменатель — это число, кратное всем остальным знаменателям. Обычно его выбирают как первое число, которое появляется во всех таблицах умножения знаменателей. Например, для ⁴ / ₆ — ³ / ₈ общий знаменатель равен 24, потому что 24 — это первое число в таблицах умножения на 6 и 8.

Чтобы найти наименьший общий знаменатель, перечислите кратные каждого знаменателя и запишите первое число, которое появится в каждом списке. В качестве альтернативы общий знаменатель можно найти, умножив знаменатели вместе.

Кратные 6 равны 6, 12, 18, 24, а кратные 8 — 8, 16, 24. 24 — первое число, которое появляется в каждом списке, поэтому это наименьший общий знаменатель 6 и 8. Наименьшее общий знаменатель также широко известен как наименьший общий знаменатель.Это наименьший общий знаменатель, который можно найти.

Следующий шаг — найти эквивалентные дроби с наименьшим общим знаменателем.

Знаменатель первой дроби умножен на 4. Следовательно, нам нужно умножить числитель и на 4.

Вычисление знаменателя: 6 × 4 = 24. Вычисление числителя: 4 × 4 = 16. И числитель, и знаменатель умножаются на 4.

Знаменатель второй дроби был умножен на 3.Следовательно, нам нужно умножить числитель и на 3.

Вычисление знаменателя: 8 × 3 = 24. Вычисление числителя: 3 × 3 = 9. И числитель, и знаменатель умножаются на 3.

Теперь, когда дроби имеют общие знаменатели, можно производить вычитание. Знаменатель ответа такой же, как и общий знаменатель.

Наименьший общий знаменатель равен 24, поэтому знаменатель ответа также равен 24.

Чтобы найти числитель ответа, просто вычтите числители в вопросе.

16 — 9 = 7, поэтому числитель ответа равен 7.

⁴ / ₆ — ³ / ₈ = ⁷ / ₂₄ .

Вот еще один пример пошагового вычитания непохожих дробей.

У нас ¹ / ₂ — ¹ / ₅ .

Знаменатели разные, поэтому нам нужно найти эквивалентные дроби с общим знаменателем.

Кратное 2 равно 2, 4, 6, 8, 10, а кратное 5 равно 5 и 10.

Мы видим, что 10 — это первое число в обоих списках, и поэтому 10 — это наименьший общий знаменатель 2 и 5.

Запишем ¹ / ₂ как ⁵ / ₁₀ .

Запишем ¹ / ₅ как ² / ₁₀ .

Теперь, когда у нас есть общий знаменатель, мы можем вычесть дроби ⁵ / ₁₀ — ² / ₁₀ = ³ / ₁₀ .

Если оба знаменателя простые, наименьший общий знаменатель находится путем умножения знаменателей. Например, в ¹ / ₂ — ¹ / ₅ наименьший общий знаменатель равен 10, потому что 2 × 5 = 10.

Вычитание дробей по методу бабочки

Метод бабочки — это короткий метод, который можно использовать для сложения или вычитания двух дробей. Он включает в себя умножение числителя одной дроби на знаменатель другой с помощью пузырьков вокруг каждого умножения, нарисованных для создания изображения бабочки.

Чтобы вычесть дроби методом бабочки, выполните следующие действия:

1. Умножьте два знаменателя вместе, чтобы найти знаменатель ответа.
2. Умножьте первый числитель на второй знаменатель.
3. Умножьте второй числитель на первый знаменатель.
4. Запишите оба этих ответа в числитель, разделив их знаком вычитания.
5. Выполните вычитание, чтобы получить одно число в числителе.
6. По возможности упростите дробь.

Например, у нас есть ⁴ / ₅ — ² / ₃ .

На диаграмме ниже показано, как работает метод бабочки.

Сначала умножаем знаменатели 5 и 3.

5 × 3 = 15, поэтому знаменатель ответа равен 15.

Затем мы умножаем числитель первой дроби на знаменатель второй дроби.

4 × 3 = 12, поэтому запишем 12 в числителе дроби.

Затем мы умножаем числитель второй дроби на знаменатель первой дроби.

2 × 5 = 10, поэтому мы пишем 10 рядом с 12 со знаком вычитания между ними.

Для каждого умножения в методе бабочки нарисуйте кружок вокруг чисел. Это делает общий расчет похожим на бабочку и может помочь упростить запоминание и изучение метода.

Наконец, мы выполняем вычитание в числителе.

12 — 10 = 2, поэтому 2 — числитель.

Результат вычисления метода бабочки: ² / ₁₅

Метод бабочки — это простой способ решения сложения и вычитания двух дробей. Преимущества метода «бабочка» заключаются в том, что он сокращает время тренировки и его легче запомнить из-за симметричного рисунка «бабочка». Это полезный метод обучения, когда вы усвоили первоначальное понимание того, как складывать и вычитать дроби.

Основная проблема метода бабочки заключается в том, что он позволяет складывать и вычитать только две дроби. Не рекомендуется вводить сложение и вычитание дробей с помощью метода бабочки, потому что он не позволяет четко понять, почему метод работает, и его можно использовать только в определенных типах вопросов.

Вычитание в отличие от дробей Простые примеры

Вот несколько более простых примеров для практики. При обучении вычитанию дробей с разными номиналами полезно начинать с примеров, когда нужно изменить только одну дробь.

В этих примерах требуется изменить только одну дробь, чтобы найти общий знаменатель. Если знаменатель одной дроби кратен другой, нужно изменить только одну дробь.

Первый простой пример: ¹ / ₂ — ¹ / ₄ .

Мы видим, что знаменатель 4 кратен знаменателю 2.

Это означает, что мы можем просто удвоить значения в дроби ¹ / ₂ , чтобы получить общий знаменатель 4. ¹ / ₂ = ² / ₄ .

Записываем ¹ / ₂ — ¹ / ₄ как ² / ₄ — ¹ / ₄ .

2 — 1 = 1, поэтому числитель ответа равен 1. Знаменатель остается равным 4.

Ответ: ¹ / ₄ .

Вот еще один простой пример вычитания дробей с разными знаменателями.

У нас ¹¹ / ₁₂ — ³ / ₄ .

Мы видим, что 12 кратно 4, поэтому нужно изменить только одну дробь. 4 нужно умножить на 3, чтобы получить 12.

Записываем дробь ³ / ₄ как ⁹ / ₁₂ .

¹¹ / ₁₂ — ⁹ / ₁₂ = ² / ₁₂ .

Этот ответ можно упростить, уменьшив вдвое числитель и знаменатель.

² / ₁₂ упрощается до ¹ / ₆ .

Как вычесть смешанные числа с разными знаменателями

Чтобы вычесть смешанные числа с разными знаменателями, выполните следующие действия:

1. Запишите смешанные числа как неправильные дроби.
2. Найдите наименьший общий знаменатель.
3. Запишите неправильные дроби как эквивалентные дроби с наименьшим общим знаменателем.
4. Знаменатель ответа совпадает с наименьшим общим знаменателем.
5. Вычтите числители, чтобы найти числитель ответа.

Например, здесь 5 ¹ / ₄ -2 ² / ₃ .

Первый шаг — преобразовать смешанные числа в неправильные дроби.

Чтобы преобразовать смешанное число в неправильную дробь, умножьте целое число на знаменатель и добавьте числитель.Этот результат является новым числителем, а знаменатель совпадает со знаменателем смешанного числа.

5 × 4 = 20, а затем 20 + 1 = 21.

Смешанное число 5 ¹ / ₄ можно переписать как неправильную дробь как ²¹ / ₄ .

2 × 3 = 6, а затем 6 + 2 = 8.

Смешанное число 2 ² / ₃ можно переписать как неправильную дробь как ⁸ / ₃ .

Теперь, когда смешанные числа записаны как неправильные дроби, следующий шаг в вычитании — найти наименьший общий знаменатель.

Первое число в таблице умножения на 4 и 3 — 12. Наименьший общий знаменатель — 12.

Умножаем знаменатель и числитель первой дроби на 3, а второй дроби на 4.

²¹ / ₄ переписывается как ⁶³ / ₁₂ .

⁸ / ₃ переписывается как ³² / ₁₂ .

Теперь, когда смешанные числа были преобразованы в неправильные дроби, а неправильные дроби теперь имеют общие знаменатели, мы, наконец, можем выполнить вычитание.

Знаменатель остается прежним, и числители мы вычитаем.

⁶³ / ₁₂ — ³² / ₁₂ = ³¹ / ₁₂ .

Последний шаг — при необходимости записать неправильную дробь как смешанное число.

31 ÷ 12 = 2 остатка 7. Записываем целое число, а остаток записываем в числитель дроби.

Неправильная дробь ³¹ / ₁₂ записывается как смешанное число 2 ⁷ / ₁₂ .

Это окончательный ответ.

Вычитание смешанных чисел с разными знаменателями выполняется в несколько этапов. Проще говоря, чтобы вычесть смешанные непохожие дроби, сначала преобразуйте их в неправильные дроби, а затем преобразуйте их в эквивалентные дроби с общим знаменателем перед вычитанием.

Как разделить дроби с разными знаменателями

Обновлено 12 ноября 2018 г.

Лиза Мэлони

Когда вы складываете или вычитаете две дроби, обе дроби должны иметь одинаковые знаменатели. Но для умножения или деления дробей знаменатели не имеют значения. При умножении вы просто перебираете дробь, умножая все числители вместе, а затем все знаменатели вместе. Деление на дроби работает точно так же, с добавлением еще одного шага в начале.

TL; DR (слишком долго; не читал)

Чтобы разделить дроби, независимо от знаменателей, переверните вторую дробь (делитель) вверх ногами, а затем умножьте результат на первую дробь (делимое).

Итак, a / b ÷ c / d = a / b × d / c = ad / bc

Обзор: умножение дробей с разными знаменателями

Перед тем, как перейти к делению дробей, уделите время рассмотрению процесса умножения дробей.Вам также понадобится этот навык для решения задач разделения.

Если вы столкнулись с проблемой умножения вида

\ frac {a} {b} × \ frac {c} {d}

, то знаменатели не имеют значения. Все, что вам нужно сделать, это перемножить числители и записать их как числитель вашего ответа; затем умножьте знаменатели и умножьте их на знаменатель вашего ответа.

Пример 1: Вычислить

\ frac {2} {5} × \ frac {1} {3}

Помните, что для умножения не имеет значения, имеют ли ваши дроби одинаковые знаменатели.Все, что вам нужно сделать, это умножить прямо поперек, что дает:

\ frac {2 × 1} {5 × 3}

, что при упрощении дает:

\ frac {2} {15}

Если вы Вы можете упростить свой ответ, исключив множители как в числителе, так и в знаменателе. Но в данном случае дальнейшее упрощение невозможно, поэтому ваш полный ответ:

\ frac {2} {5} × \ frac {1} {3} = \ frac {2} {15}

Теперь о разделении Дроби

Теперь, когда вы рассмотрели, как умножать дроби, деление дробей работает почти так же — вам просто нужно добавить один дополнительный шаг.Переверните вторую дробь (также известную как делитель) вверх ногами, а затем измените операцию на умножение вместо деления.

Итак, если ваша исходная задача деления выглядит так:

\ frac {a} {b} ÷ \ frac {c} {d}

Первое, что вы делаете, это переворачиваете вторую дробь вверх дном, в результате чего получается d / c ; затем измените знак деления на знак умножения, что даст вам:

\ frac {a} {b} × \ frac {d} {c}

И поскольку вы практиковали умножение дробей, вы знаете, как решить эту проблему.Просто умножьте числители и знаменатели, и вы получите результат:

\ frac {a} {b} ÷ \ frac {c} {d} = \ frac {ad} {bc}

Два примера Деление дробей

Теперь, когда вы знаете процесс деления дробей, пора попрактиковаться на нескольких примерах.

Пример 2: Вычислить

\ frac {1} {3} ÷ \ frac {8} {9}

Помните, ваш первый шаг — перевернуть вторую дробь вверх ногами и изменить операцию на умножение.Это дает вам:

\ frac {1} {3} × \ frac {9} {8}

Теперь просто умножьте и упростите:

\ frac {1 × 9} {3 × 8} = \ frac {9} {24} = \ frac {3} {8}

\ frac {1} {3} ÷ \ frac {8} {9} = \ frac {3} {8}

Пример 3: Вычислить

\ frac {11} {10} ÷ \ frac {5} {7}

Обратите внимание, что одна из этих дробей неверна (ее числитель больше знаменателя). Но это не меняет процесса деления дробей, поэтому переверните эту вторую дробь вверх дном и измените операцию на умножение:

\ frac {11} {10} × \ frac {7} {5}

Как и раньше, умножьте и упростите, если можете:

\ frac {11 × 7} {10 × 5} = \ frac {77} {50}

77 и 50 не имеют общих факторов, поэтому вы не можете упростить дальше.Итак, ваш окончательный ответ:

\ frac {11} {10} ÷ \ frac {5} {7} = \ frac {77} {50}

Уловка для запоминания

Если вам сложно это запомнить , может быть полезно вспомнить, что умножение и деление являются взаимными операциями; то есть одно отменяет другое. Когда вы переворачиваете дробь вверх дном, это тоже называется обратным. Таким образом, d / c является обратной величиной c / d , и наоборот.

Это означает, что когда вы делите дробь, вы фактически выполняете обратную операцию над обратной дробью .Чтобы проблема разрешилась, должны быть обе эти противоположности. Если у вас есть только одна из них — скажем, если вы выполнили обратную операцию (умножение), не взяв сначала обратную величину этой второй дроби, — ваш ответ будет неправильным.

Как насчет деления смешанных чисел?

Если вас просят разделить смешанные числа, будьте осторожны — это ловушка! Прежде чем продолжить, вы должны преобразовать это смешанное число в неправильную дробь. Как только это будет сделано, вы будете следовать тому же процессу, который вы использовали бы для правильных дробей.См. Пример 3 выше, чтобы проиллюстрировать, как это работает. Он включает неправильную дробь 11/10, которую также можно записать как смешанное число 1 1/10.

Калькулятор сложения дробей

Этот калькулятор сложения дробей поможет вам вычислить сумму до пяти дробей в мгновение ока. Если вы хотите преобразовать дробь в проценты, вам может помочь этот калькулятор. В статье ниже вы не только узнаете, как складывать дроби, но и как работать с вычитанием.Вы боретесь с , складывая дроби с непохожими знаменателями ? Читайте дальше, чтобы больше никогда не столкнуться с этой проблемой! После того, как вы здесь закончите, сложение дробей больше никогда не будет ужасом!

Как складывать дроби?

Дробь — это число, образованное соотношением двух чисел ( A и B ). Эти числа обычно целые (целые числа), так что:

дробь = A / B .

Оказывается, любое десятичное число можно преобразовать в дробь.В результате вы можете складывать вместе столько десятичных знаков, сколько хотите, рассматривая их, как если бы они были дробями. Всякий раз, когда мы хотим сложить две дроби с общим знаменателем, скажем, 2 / 7 и 3 / 7 , нам нужно добавить числители, а знаменатель останется прежним :

2 / 7 + 3 / 7 = (2 + 3) / 7 = 5 / 7 .

Но как сложить дроби с разными знаменателями ?

Сложение дробей с разными знаменателями

Когда числа имеют разные знаменатели, сложение дробей немного сложнее, так как вы не можете просто сложить числители, как раньше. Хитрость заключается в использовании общего знаменателя . Посмотрим, как это работает. Допустим, мы хотим сложить 1 / 2 и 1 / 3 :

• 1 / 2 + 1 / 3 =…
• Найдите общий знаменатель.Для этого мы можем оценить наименьшее общее кратное (НОК) 2 и 3 . НОК (2,3) = 6
• Разверните каждую дробь так, чтобы знаменателем была эта НОК, в данном случае 6 : 1 / 2 = 3 / 6 , 1 / 3 = 2 / 6
• Поскольку мы знаем, как складывать дроби с одинаковым знаменателем, вы можете просто складывать эти дроби обычным образом: … = 3 / 6 + 2 / 6 = 5 / 6

Есть также другие эквивалентные дроби для этого результата, такие как 10 / 12 , 15 / 18 , и это лишь некоторые из них.Однако удобно представить результат в простейшем виде .

Сложение и вычитание дробей

Теперь мы знаем, как работает сложение дробей, даже при сложении дробей с разными знаменателями — круто! А как насчет вычитания? Это тоже так просто?

Вы также можете использовать этот калькулятор сложения дробей для вычитания дробей. Нам просто нужно помнить, что вычитание дроби аналогично сложению . Например, что такое 3 / 9 - 2 / 8 ?

• Измените вычитание на сложение: 3 / 9 - 2 / 8 = 3 / 9 + (-2 / 8 )
• Чтобы облегчить себе жизнь, максимально упростит дроби .Найдите наибольший общий множитель для каждой пары числителей и знаменателей: GCF (3,9) = 3 , GCF (2,8) = 2
• Перепишите выражение как: 1 / 3 + (-1 / 4 )
• Остальное как стандартное дополнение:
• Найдите общий знаменатель: НОК (3,4) = 12
• Разверните дроби и сложите их: 4 / 12 + (-3 / 12 ) = 1 / 12
• Что совпадает с: 1 / 3 - 1 / 4 = 1 / 12

Кроме того, в нашем калькуляторе нет разницы между -1 / 4 или 1 / -4 — наш калькулятор сложения дробей будет обрабатывать эти выражения одинаково!

Сложение дробей на практике — как пользоваться калькулятором сложения дробей?

Представьте себе историю — вы на вечеринке с друзьями.И вот оно — голод! Что еще хуже, вы только что поняли, что в холодильнике ничего не осталось.

Решение простое — вы собираетесь заказать пиццу, а то и две, а то и больше.