Как правильно вычитать обыкновенные дроби?
Оглавление
Время чтения: 5 минут
571
Дроби можно складывать, умножать, делить, а также вычитать. В этой статье мы рассмотрим вычисление разности таких дробей, которые имеют одинаковый или разный знаменатель. Также будет вычисление дроби из натурального числа и наоборот.
Вычитание дробей с одинаковыми знаменателями
Для нахождения разности дробей с одинаковыми знаменателями, необходимо вычесть один числитель из другого. Знаменатели не вычитаются.
Примеры
Найдите разность 4/8 – 3/8.
Решение:
Представьте, что у вас есть большая пицца, которая поделена на восемь частей. Вы взяли 4 куска, но съели лишь 3. Чтобы узнать, сколько осталось, нужно записать это так:
4/8 – 3/8 = 4-3/8 = 1/8
Выходит, что на тарелке остался 1 восьмой доли кусок пиццы. Из этого примера можно вывести формулу, которая подойдет для решения подобных примеров.
Рассмотрим ещё одно задание.
Пример 2:
Найдите разность 6/12 – 3/12.
Решение:
6/12 – 3/12 = 6-3/12 = 3/12 = 1/4 = 0.25
У этих дробей одинаковые знаменатели, поэтому нам нужно лишь вычесть 3 из 6. Мы получили 3/12 и сократили дробь делением на 3. Знак дроби означает деление, поэтому делим 1 на 4 и получаем 0.25.
Вычитание дробей с разными знаменателями
Если знаменатели разные, то нужно сделать так, чтобы они стали одинаковыми, т.е. привести дроби к общему знаменателю. После этого совершаем те же действия, что и выше.
Примеры
Пример 3:
Найдите разность 5/10 – 2/5.
Решение:
5/10 – 2/5 = 5/10 – 2•2/2•5 = 5/10 – 4/10 = 5-4/10 = 1/10 = 0.1
Чтобы найти общий знаменатель, нужно числитель и знаменатель второй дроби умножить на 2. Получим 4/10. Теперь можно находить разность как в прошлом примере.
Перейдем к следующему примеру.
Пример 4:
Найдите разность 52/24 – 14/12.
Решение:
52/24 – 14/12 = 52/24 – 2•14/2•12 = 52/24 – 28/24 = 52-28/24 = 24/24 = 1
Для того, чтобы привести к общему знаменателю, нужно умножить числитель и знаменатель второй дроби на 2. Будь в двух знаменателях 7 и 49, то мы бы умножали 7 не на 2, а на 7, чтобы получить в обоих знаменателях 49. Дальше все по формуле.
Будь в двух знаменателях 7 и 49, то мы бы умножали 7 не на 2, а на 7, чтобы получить в обоих знаменателях 49. Дальше все по формуле.
Вычитание натурального числа из обыкновенной дроби
Для того чтобы вычесть натуральное число из обыкновенной дроби, нужно представить натуральное число в виде обыкновенной дроби.
Рассмотрим на примере.
Примеры
Пример 5:
Найдите разность 288/36 – 6.
Решение:
288/36 – 6 = 288/36 – 6/1 = 288/36 – 36•6/36•1 = 288/36 – 216/36 = 288-216/36 = 72/36 = 2
Может показаться, что это сложно, но это не так. Число 6 можно представить в виде обыкновенной дроби: 6/1. Далее будем находить разность этих дробей. Приводим дроби к общему знаменателю, умножая знаменатель и числитель второй дроби на 36. Вычитаем, делим и получаем ответ.
Есть и второй вариант решения (для неправильных дробей, где числитель больше знаменателя) такого примера, более удобный и простой. Возьмем новые числа.
Пример 6:
Найдите разность 72/27 – 2.
Решение:
72/27 – 2 = 2 2/3 – 2 = 2/3
В этом случае не пришлось превращать натуральное число в дробь, 72/27 мы сделали смешанным числом, отняли двойки и получили ответ. Можно решать на основе прошлого примера, однако, это будет дольше и сложнее.
Понятия
- Смешанное число – это такая правильная дробь, в состав которой входит целое число.
- Неправильная дробь – это дробь, в которой числитель равен знаменателю или больше его.
- Правильная дробь – это дробь, в которой знаменатель больше числителя.
Для того, чтобы преобразовать неправильную дробь в смешанное число, необходимо поделить ее числитель на знаменатель. Неполное частное станет целой частью смешанной дроби, остаток будет числителем дробной части, а знаменатель неправильной дроби – знаменателем дробной части.
Вычитание обыкновенной дроби из натурального числа
Примеры
Сразу перейдем к примеру.
Пример 7:
Найдите разность 6 – 7/5.
Решение:
6 – 7/5 = 6/1 – 7/5 = 5•6/5•1 – 7/5 = 30/5 – 7/5 = 30-7/5 = 23/5 = 4 3/5 = 4.6
Все, как и ранее, натуральное число 6 представляем в виде дроби, приводим к общему знаменателю, а после
находим разность.
Есть ещё один способ. Он хорош в том случае, если приходится работать с большими числами.
Если вычитаемая дробь – правильная, то натуральное число необходимо предоставить как сумму двух чисел, где
одно из них равно 1. Последним действием является вычитание дроби из этой единицы. Рассмотрим на
примере.
Пример 8:
Найдите разность 1040 – 20/55.
Решение:
Отнимем от 1040 единицу и вычтем дробь:
1040 – 20/55 = (1039 + 1) – 20/55
Перейдем к поиску ответа. Для этого вспомним свойства вычитания, согласно которым можно записать получившееся
выражение как 1039 + (1 – 20/55). Просто так отнять единицу в виде натурального числа мы не можем, поэтому
предоставим ее как дробь 1/1.
А теперь можно находить разность:
1 – 20/55 = 1/1 – 20/55 = 55/55 – 20/55 = 35/55.
Но это не конец, ведь у нас ещё осталось число 1039. Здесь все легко, просто приписываем это число к нашей дроби и получаем ответ: 1039 35/55. Здесь можно сократить дробь и выйдет 1039 7/11.
Рассмотрим решение этого примера с помощью прошлого способа, чтобы определить то, какой из них более удобный:
1040 – 20/55 = 1040/1 – 20/55 = 55•1040/55•1 — 20/55 = 57200/55 = 11436•5/11•5 = 11436/11 = 1039 7/11.
Ответ одинаковый, но решение, очевидно, побольше.
Но что же делать с неправильной дробью? Нужно заменить ее смешанным числом, а далее все про инструкции.
Пример 9:
Найдите разность 378 – 35/6.
Решение:
Отделяем целую часть: 35/6 = 5 5/6
Теперь, как и ранее, совершаем следующие действия:
373 – 5/6 = (372 + 1) – 5/6 = 372 + (1 – 5/6) = 372 + 1/6 = 372 1/6.
Свойства, необходимые для вычитания дробей
Примеры
Свойства вычитания натуральных чисел действуют и на вычитание обыкновенных дробей.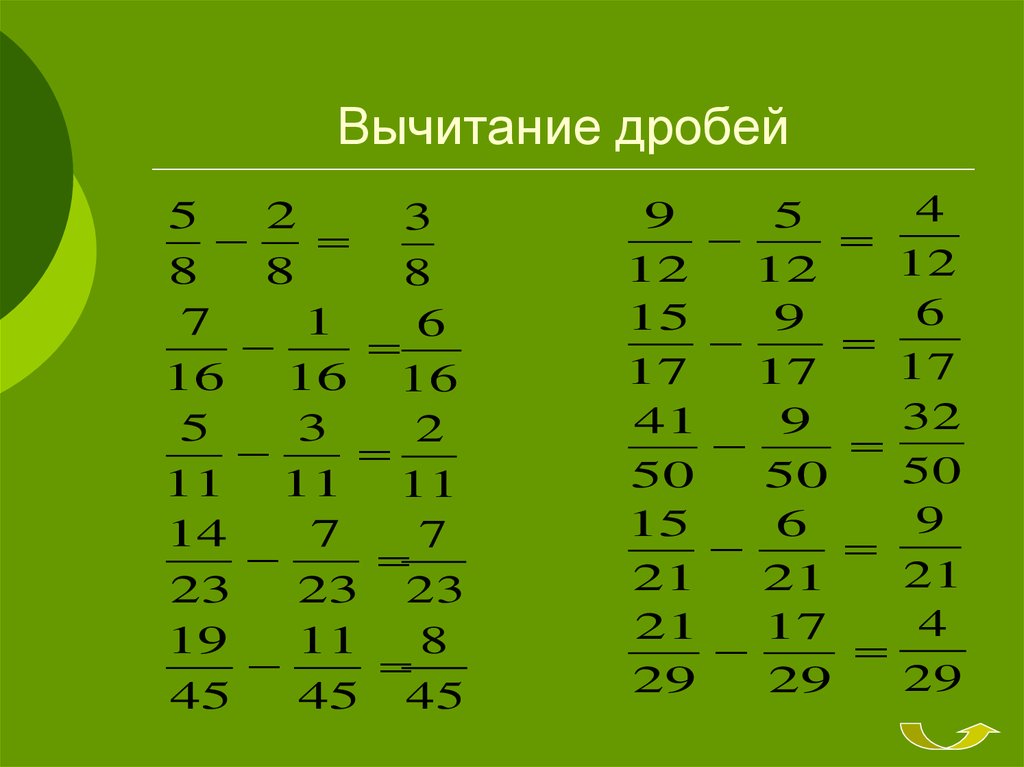
Пример 10:
Найдите разность 16/6 – 2/4 – 6/3.
Решение:
Сначала находим разность первых двух дробей, а после уже отнимаем и третью:
16/6 – 2/4 = 2•16/2•6 – 3•2/3•4 = 32/12 – 6/12 = 32-6/12 = 26/12 – 6/3 = 26/12 – 4•6/4•3 = 26/12 – 24/12 = 2/12 = 1/6
Когда необходимо работать с дробями и натуральными числами, то следует их распределять по типам в группы.
Пример 11:
Найдите разность (86 + 15/24) – (4 + 2/4).
Решение:
Сгруппируем числа.
(86 + 15/24) – (4 + 2/4) = 86 + 15/24 – 4 – 2/4 = (86 – 4) + (15/24 – 2/4)
Теперь можно решать дальше:
(86 – 4) + (15/24 – 2/4) = 82 + (15/24 – 12/24) = 82 + 3/24 = 82 + 1/8 = 82 1/8.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Задания для практики
Задание 1: Найдите разность 20/10 – 15/10.
Задание 2: Найдите разность 54/6 – 9/6.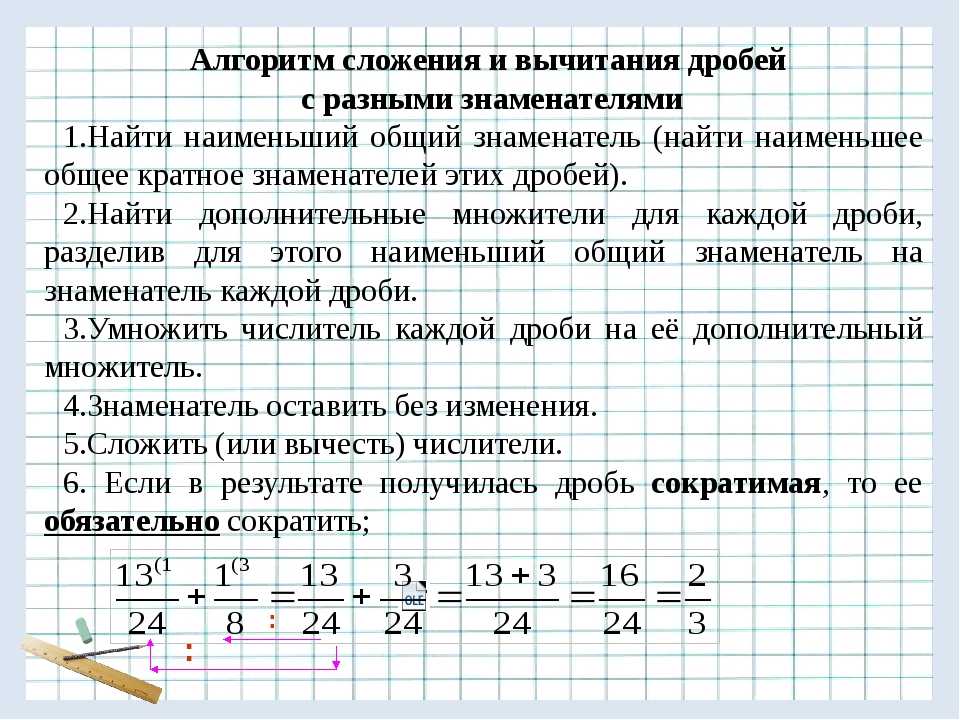
Задание 3: Выделите целую часть из неправильной дроби 7/3.
Задание 4: Выделите целую часть из неправильной дроби 9/5.
Задание 5: Найдите разность 63/2 – 42/8.
Задание 6: Найдите разность 101/25 – 4.
Задание 7: Найдите разность 1096 – 25/40.
Задание 8: Найдите разность 46/6 – 2/2 – 189/36.
Задание 9: Найдите разность (65 + 56/45) – (10 + 4/9).
Ответы
Решение задания 1: 20/10 – 5/10 = 20-15/10 = 5/10 = 1/2 = 0.5.
Решение задания 2: 54/6 – 9/6 = 54-9/6 = 45/6 = 15/2 = 7.5.
Решение задания 3: 7/3 = 7:3 = 2 (остаток 1) = 2 1/3.
Решение задания 4: 9/5 = 9:5 = 1 (остаток 4) = 1 4/5.
Решение задания 5: 63/2 – 42/8 = 4•63/4•2 – 42/8 = 252/8 – 42/8 = 252-42/8 = 210/8 = 26.25.
Решение задания 6: 101/25 – 4 = 101/25 – 4/1 = 101/25 – 100/25 = 101-100/25 = 1/25 = 0. 04.
04.
Решение задания 7: 1096 – 25/40 = (1095 + 1) – 25/40 = 1095 + (1 — 25/40) = 1/1 – 25/40 = 40/40 – 25/40 = 15/40 = 1095 15/40 = 1095 3/8 = 1095.375.
Решение задания 8: 46/6 – 2/2 – 189/36 = 46/6 – 2/2 = 46/6 – 3•2/3•2 = 46/6 – 6/6 = 46-6/6 = 40/6 – 189/36 = 6•40/6•6 – 189/36 = 240/36 – 189/36 = 240-189/36 = 51/36 = 1.416.
Решение задания 9: (65 + 56/45) – (10 + 4/9) = 65 + 56/45 – 10 – 4/9 = (65 – 10) + (56/45 – 4/9) = 55 + 36/45 = 55 + 4/5 = 55 4/5.
Оценить статью (55 оценок):
Поделиться
Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 3. ВЫЧИТАНИЕ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4.  СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ§ 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8.  УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН§ 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3.  СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ§ 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4.  § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2.  ФОРМУЛЫ СЛОЖЕНИЯ ФОРМУЛЫ СЛОЖЕНИЯ§ 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6.  ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ§ 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. ПРЕДЕЛ ФУНКЦИИ § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1.  ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ§ 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ ГЛАВА XXIV § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7.  ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕКонтрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Сложение и вычитание одинаковых дробей
Введение Мы узнали, что дробь — это число, представляющее часть целого. Целое может быть одним или группой объектов. Давайте теперь узнаем о сложении и вычитании одинаковых дробей. Но перед этим мы должны вспомнить, что мы понимаем под подобными дробями. Дроби, имеющие одинаковые знаменатели, называются подобными дробями. Например, дроби $\frac{4}{9}, \frac{13}{9}, \frac{1}{9} и \frac{5}{9}}$ подобны дробям, имеющим общий знаменатель 9.
Целое может быть одним или группой объектов. Давайте теперь узнаем о сложении и вычитании одинаковых дробей. Но перед этим мы должны вспомнить, что мы понимаем под подобными дробями. Дроби, имеющие одинаковые знаменатели, называются подобными дробями. Например, дроби $\frac{4}{9}, \frac{13}{9}, \frac{1}{9} и \frac{5}{9}}$ подобны дробям, имеющим общий знаменатель 9.
Мы знаем, что число вида $\frac{p}{q}$ или число, которое можно представить в виде $\frac{p}{ q}$, где p и q — целые числа, а q ≠ 0 называется рациональным числом. Так как же нам определить стандартную форму рационального числа?
Также важно помнить, что дробь называется стандартной, если знаменатель положительный и числители
не имеют общего делителя, отличного от 1.
Чтобы выразить заданную дробь в стандартной форме, необходимо выполнить следующие шаги –
Шаг 1 – Проверить, является ли данное число дробной формой.
Шаг 2 – Посмотрите, положительный знаменатель дроби или нет. Если оно отрицательное, умножьте или разделите числитель и знаменатель на -1, чтобы знаменатель стал положительным.
Если оно отрицательное, умножьте или разделите числитель и знаменатель на -1, чтобы знаменатель стал положительным.
Шаг 3 – Найдите наибольший общий делитель (НОД) абсолютных значений числителя и знаменателя.
Шаг 4 – Разделите числитель и знаменатель данной дроби на НОД (HCF), полученный в шаге III. Полученная дробь является стандартной формой данной дроби.
Это было важно понять, потому что после сложения или вычитания дробей нам нужно будет сводить их в простейшем виде.
Теперь давайте научимся складывать две или более одинаковые дроби.
Сложение одинаковых дробейЧтобы сложить две одинаковые дроби, выполните следующие действия:
- Получите числители двух данных дробей и их общий знаменатель
- Сложите числители, полученные на первом шаге.
- Запишите дробь, числитель которой равен сумме, полученной на втором шаге, а знаменатель — общий знаменатель данных дробей.

Давайте разберемся с этим на примере.
Пример
Предположим, мы хотим сложить дроби $\frac{3}{5}$ и $\frac{13}{5}$
Решение
Здесь мы видим, что обе дроби имеют один и тот же знаменатель, то есть 5.
Таким образом, мы идем по указанным выше шагам.
Проверяем числители обеих дробей. Это 3 и 13.
Затем складываем эти числители и получаем 3 + 13 = 16.
Теперь запишем сумму этих дробей в виде $\frac{16}{5}$
Следовательно, $\frac{3}{5} + \frac{13}{5} = \frac{16}{5}$
Чтобы яснее понять сложение одинаковых дробей, проверим графическое представление сложения подобных фракций.
Графическое представление сложения одинаковых дробей Прежде чем приступить к графическому изображению сложения одинаковых дробей, необходимо вспомнить, что мы понимаем под графическим представлением дроби. Рассмотрим дробь $\frac{3}{4}$. Эта дробь читается как «три четверти», что означает три части из четырех равных частей, на которые было разделено целое. Графически эту дробь можно представить как –
Эта дробь читается как «три четверти», что означает три части из четырех равных частей, на которые было разделено целое. Графически эту дробь можно представить как –
Теперь, когда мы вспомнили, как графически представлять дробь, давайте продолжим обсуждение графического представления сложения подобных дробей. Разберемся на примере.
Предположим, у нас есть дроби $\frac{2}{8}, \frac{3}{8} и \frac{1}{8}$, и мы хотим сложить эти дроби. Если мы пойдем по шагам, которые мы определили выше для сложения одинаковых дробей, мы увидим, что все три дроби имеют один и тот же знаменатель, то есть 8. Итак, чтобы сложить эти дроби, мы просто сложим их числители, то есть 2, 3 и 1. Получим 2 + 3 + 1 = 6. Следовательно,
$\frac{2}{8} + \frac{3}{8} + \frac{1}{8} = \frac{6}{8}$
Теперь представим каждую из этих дробей графически.
Дробь $\frac{2}{8}$ будет графически представлена как
Мы видим, что приведенная выше дробь имеет 2 заштрихованные части из 8 равных частей.
Дробь $\frac{3}{8}$ будет графически представлена как
Мы видим, что приведенная выше дробь имеет 3 заштрихованные части из 8 равных частей.
Дробь $\frac{1}{8}$ будет графически представлена как
Мы видим, что указанная выше дробь имеет 1 заштрихованную часть из 8 равных частей.
Если суммировать все заштрихованные части в трех дробях, то можно увидеть, что у нас будет 2 + 3 + 1 = 6 заштрихованных частей. Это будет представлено графически как –
Вышеупомянутая дробь будет записана как $\frac{6}{8}$, что является результатом, который мы получили после сложения трех приведенных выше дробей.
Теперь, когда мы поняли, как складывать одинаковые дроби как с помощью шагов, так и графически, давайте научимся находить разность двух или более одинаковых дробей.
Вычитание одинаковых дробейЧтобы сложить вычитание одинаковых дробей, выполните следующие действия:
- Получите числители двух данных дробей и их общий знаменатель
- Вычтите вычитаемый числитель из уменьшаемого числителя, полученного в первый шаг.
 Напомним, что вычитаемое число называется вычитаемое , а число, из которого вычитается вычитаемое, называется вычитаемое . Результат этого вычитания называется разностью .
Напомним, что вычитаемое число называется вычитаемое , а число, из которого вычитается вычитаемое, называется вычитаемое . Результат этого вычитания называется разностью . - Запишите дробь, числитель которой равен сумме, полученной на втором шаге, а знаменатель — общий знаменатель данных дробей.
Давайте разберемся с этим на примере.
Пример
Предположим, мы хотим найти разницу между дробями $\frac{3}{7} и \frac{1}{7}$
Решение
Здесь мы видим, что обе дроби имеют тот же знаменатель, то есть 7,
Таким образом, мы идем по указанным выше шагам.
Проверяем числители обеих дробей. Это 3 и 1.
Затем из 3 вычтем 1, получим 3 – 1 = 2
Теперь запишем разность этих дробей в виде $\frac{2}{7}$
Отсюда , $\frac{3}{7} -\frac{1}{7} = \frac{2}{7}$
Чтобы яснее понять вычитание одинаковых дробей, проверим графическое представление вычитания одинаковых дробей.
Предположим, у нас есть дроби $\frac{5}{8} и \frac{1}{8}$, и мы хотим найти разницу между этими дробями. Если мы пойдем по шагам, которые мы определили выше для вычитания одинаковых дробей, мы увидим, что две дроби имеют один и тот же знаменатель, то есть 8. Итак, чтобы вычесть эти дроби, мы просто вычтем числители, то есть 5 и 1. Получим 5 – 1 = 4 Следовательно,
$\frac{5}{8} – \frac{1}{8} = \frac{4}{8}$
Теперь представим каждую из этих дробей графически.
Дробь $\frac{5}{8}$ будет графически представлена как
Мы видим, что указанная выше дробь имеет 5 заштрихованных частей из 8 равных частей.
Дробь $\frac{1}{8}$ будет графически представлена как
Мы видим, что указанная выше дробь имеет 1 заштрихованную часть из 8 равных частей.
Если мы вычтем две заштрихованные части в этих дробях, мы увидим, что у нас будет 5 – 1 = 4 заштрихованных части. Это будет представлено графически как –
Это будет представлено графически как –
Приведенная выше дробь будет записана как $\frac{4}{8}$, что является результатом, полученным после вычитания двух приведенных выше дробей.
Решенные примерыПример 1 Мария закрасила 1/5 часть стены в своей комнате. Помог ее брат Ромиль, который покрасил 3/5 стены. Сколько они рисовали вместе? Какая часть комнаты осталась неокрашенной?
Решение Нам известно, что Мария закрасила 1/5 часть стены в своей комнате. Помог ее брат Ромиль, который покрасил 3/5 стены. От нас требуется выяснить –
- Сколько они нарисовали вместе?
- Какая часть комнаты осталась неокрашенной?
Давайте найдем вышеуказанную информацию одну за другой.
Прежде всего, нам нужно разобраться в данных нам дробях. У нас есть,
Доля площади стены, окрашенной Марией = 1/5
Доля площади стены, окрашенной Ромилем = 3/5
Хорошо видно, что обе дробные величины имеют одинаковый знаменатель. Поэтому первое, на что следует обратить внимание, это то, что они подобны дробям. Теперь, чтобы узнать, сколько они нарисовали вместе, нам нужно будет найти сумму этих дробей. Поскольку они похожи на дроби, нам просто нужно сложить числители дробей, как мы узнали выше. Поэтому имеем
Поэтому первое, на что следует обратить внимание, это то, что они подобны дробям. Теперь, чтобы узнать, сколько они нарисовали вместе, нам нужно будет найти сумму этих дробей. Поскольку они похожи на дроби, нам просто нужно сложить числители дробей, как мы узнали выше. Поэтому имеем
Площадь стены, окрашенная обоими = 1/5 + 3/5
= (1+3)/5 = 4/5
Следовательно, площадь стены, окрашенная ими вместе = 4/5, что является ответом на вопрос первая проблема.
Теперь давайте рассмотрим вторую задачу: какая часть комнаты осталась неокрашенной? Чтобы найти ответ на этот вопрос, нам нужно вычесть долю окрашенной стены из общего шага стены. У нас есть,
Здесь общее пространство стены будет равно 1, как единое целое.
Кроме того, мы уже выяснили, что площадь стены, закрашенная Марией и Ромилем вместе = 4/5
Следовательно,
Пространство стены, которое осталось покрасить = Общая площадь стены – Пространство стены, окрашенное
Получаем незакрашенное пространство = (5 – 4)/ 5 = 1/5
Следовательно, Мария и Ромил вместе покрасили 4/5 площади стены, а незакрашенная площадь комнаты составила 1/5.
Пример 2 Даниэль купил 2,5 кг сахара, а Сэм купил 3,5 кг сахара. Найдите общее количество сахара, купленного ими обоими.
Решение Нам известно, что Даниэль купил 2,5 кг сахара, а Сэм купил 3,5 кг сахара. Требуется найти общее количество сахара, купленного ими обоими.
Чтобы найти ответ на поставленную выше задачу, давайте сначала разберемся с данными нам значениями дробей.
Сахар, купленный Даниэлем = 2 ½ кг
Сахар, купленный Сэмом = 3 ½ кг
Можно ясно видеть, что обе дробные значения имеют один и тот же знаменатель, т.е. 2. Следовательно, первое, на что следует обратить внимание, это что они как дроби.
Теперь, чтобы найти стоимость всего купленного ими сахара, нам нужно сложить две дроби. Мы продолжим складывать эти дроби, добавляя числители, как мы узнали выше.
Но перед этим важно понимать, что данные дроби — смешанные дроби. Сначала нам нужно преобразовать их в неправильные дроби. Следовательно,
Следовательно,
2 ½ кг = 5/2 кг и 3 ½ кг = 7/2 кг
Итак, общее количество сахара, купленного ими обоими = Сахар, купленный Даниэлем + Сахар, купленный Сэмом
Теперь, сложив их числители, мы имеем 5 + 7 = 12
Следовательно, 5 / 2 + 7 / 2 = 12 / 2 = 6 кг
Следовательно, Дэниел и Сэм вместе купили 6 кг сахара.
Пример 3 Складываем дроби $\frac{5}{30} + \frac{7}{30}$
Решение Нам даны дроби $\frac{5}{30} и \frac{7}{30}$. требуется найти их сумму.
Хорошо видно, что обе дробные величины имеют один и тот же знаменатель, то есть 30. Поэтому первое, на что следует обратить внимание, это то, что они подобны дробям.
Первое, что нам нужно сделать, это сложить числители обеих дробей.
Получим, 5 + 7 = 12
Следовательно, $\frac{5}{30} + \frac{7}{30} = \frac{12}{30}$
Выше Ответ можно упростить, взглянув на числитель и знаменатель дроби. Мы видим, что числитель и знаменатель дроби делятся на 2 и 6. Однако мы всегда хотим, чтобы наибольший общий делитель уменьшал дробь до ее наименьшего члена.
Мы видим, что числитель и знаменатель дроби делятся на 2 и 6. Однако мы всегда хотим, чтобы наибольший общий делитель уменьшал дробь до ее наименьшего члена.
Следовательно, найдем наибольший общий делитель 12 и 30.
Мы знаем, что
12 = 2 x 2 x 3
30 = 2 x 3 x 5
Из приведенного выше видно, что наибольший общий делитель двух чисел, 12 и 30 = 6
Разделив числитель и знаменатель на 6, мы получим
$\frac{12}{30} = \frac{12 ÷6}{30 ÷ 6} = \frac{2}{5}$ , что является простейшей формой.
Следовательно, $\frac{5}{30} + \frac{7}{30} = \frac{2}{5}$
Пример 4 Вычесть дроби $\frac{10}{27} – \frac{4}{27}$
Решение Нам даны дроби $\frac{10}{27} и \ frac{4}{27}$, и нам нужно найти их разность.
Хорошо видно, что обе дробные величины имеют один и тот же знаменатель, то есть 27. Поэтому первое, на что следует обратить внимание, это то, что они подобны дробям. Итак, две дроби имеют одинаковые знаменатели, что означает, что мы должны легко вычесть их числители.
Итак, две дроби имеют одинаковые знаменатели, что означает, что мы должны легко вычесть их числители.
$\frac{10}{27} – \frac{4}{27} = \frac{10-4}{27} = \frac{6}{27}$
Приведенный выше ответ можно упростить. глядя на числитель и знаменатель дроби. Мы видим, что числитель и знаменатель дроби делятся на 3. Однако мы всегда хотим убедиться, что мы используем наибольший общий делитель, чтобы сократить дробь до ее наименьшего члена.
Итак, найдем наибольший общий делитель 6 и 27
Мы знаем, что
6 = 2 x 3
27 = 3 x 3 x 3
Из приведенного выше видно, что наибольший общий делитель двух чисел, 6 и 27 = 3
Разделив числитель и знаменатель на 3, мы получаем
$\frac{6}{27} = \frac{6 ÷3}{27 ÷3} = \frac{2}{9}$, что является простейшей формой.
Следовательно, $\frac{10}{27} – \frac{4}{27} = \frac{2}{9}$
Пример 5 Вычесть дроби $\frac{21}{ 81} и \frac{3}{81}$
Решение Поскольку знаменатели двух дробей равны, вычтите их числители и скопируйте общий знаменатель. Мы получим,
Мы получим,
$\frac{21}{81} – \frac{3}{81} = \frac{21-3}{81} = \frac{18}{81}$
Приведенный выше ответ можно упростить, взглянув на числитель и знаменатель дроби. Мы видим, что числитель и знаменатель дроби делятся на 3. Однако мы всегда хотим, чтобы наибольший общий делитель уменьшал дробь до ее наименьшего члена.
Следовательно, найдем наибольший общий делитель чисел 18 и 81
Мы знаем, что
18 = 3 x 2 x 3
81 = 3 x 3 x 3 x 3
Из приведенного выше видно, что наибольший общий делитель двух чисел, 18 и 81 = 9
Разделив числитель и знаменатель на 9, мы получим
$\frac{18}{81} = \frac{18 ÷9}{81 ÷9} = \frac{2}{9}$
Следовательно, $\frac{21}{81} – \frac{3}{81} = \frac{2}{9}$
Ключевые факты и Резюме- Дробь — это число, представляющее часть целого. Целое может быть одним или группой объектов.
- Дроби, имеющие одинаковые знаменатели, называются одинаковыми дробями.

- Говорят, что дробь имеет стандартную форму, если знаменатель положительный и числители не имеют общего делителя, кроме 1.
- Чтобы привести дробь к простейшей форме Найдите наибольший общий делитель (НОД) абсолютных значений числителя и знаменателя. Разделите числитель и знаменатель данной дроби на НОД (HCF), полученный на шаге III. Полученная дробь является стандартной формой данной дроби.
- Число, которое вычитается, называется вычитаемым, а число, из которого вычитается вычитаемое, называется уменьшаемым. Результат этого вычитания называется разностью.
Умножение и деление дробей (на тему Дня ветеранов) Рабочие листы по математике
Точечные диаграммы/линейные графики с дробными единицами (на тему закусок и напитков) Рабочие листы по математике
Сравнение одинаковых дробей Рабочие листы по математике
Мы тратим много времени на исследования и компиляцию информация на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Мы ценим вашу поддержку!
Сложение и вычитание дробей с одинаковыми знаменателями — Математика 3-го класса
На последних двух уроках вы узнали, как складывать и вычитать дроби , используя число строки .
Теперь давайте научимся складывать и вычитать дроби без числовой строки. 😺
Сложение и вычитание дробей Обзор
Когда сложение 2 дроби с одинаковыми или вроде того, знаменатель, мы добавить их числители .
При вычитании 2 дроби с одинаковыми знаменателями, мы вычитаем их числители .
Когда прибавляет или вычитает дроби с одинаковыми знаменателями, просто прибавляете или вычитаете числители и копируете те же самые знаменатели .
Сложение дробей Примеры
3/10 + 4/10 = ?
👉 Сложим числители, оставив прежний знаменатель.
Мы получили тот же результат! 😁
Попробуем другой пример.
5/12 + 5/12 = ?
👉 Сложите числители, затем оставьте тот же знаменатель.
 —М.: Просвещение, 1990.— 416 с.
—М.: Просвещение, 1990.— 416 с.

 Напомним, что вычитаемое число называется вычитаемое , а число, из которого вычитается вычитаемое, называется вычитаемое . Результат этого вычитания называется разностью .
Напомним, что вычитаемое число называется вычитаемое , а число, из которого вычитается вычитаемое, называется вычитаемое . Результат этого вычитания называется разностью .