Умножение десятичной дроби на натуральное число
Цель урока:
- В увлекательной форме ввести учащимся правило умножения десятичной дроби на натуральное число, на разрядную единицу и правило выражения десятичной дроби в процентах. Выработать умение применения полученных знаний при решении примеров и задач.
- Развивать и активизировать логическое мышление учащихся, умение выявлять закономерности и обобщать их, укреплять память, умение сотрудничать, оказывать помощь, оценивать свою работу и работу друг друга.
- Воспитывать интерес к математике, активность, мобильность, умение общаться.
Оборудование: интерактивная доска, плакат с цифрограммой, плакаты с высказываниями математиков.
Ход урока
- Организационный момент.
- Устный счёт – обобщение раннее изученного материала, подготовка к
изучению нового материала.

- Задание на дом.
- Математическая физкультминутка.
- Обобщение и систематизация полученных знаний в игровой форме при помощи компьютера.
- Выставление оценок.
2. Ребята, сегодня у нас урок будет несколько необычным, потому что я буду проводить его не одна, а со своим другом. И друг у меня тоже необычный, сейчас вы его увидите. (На экране появляется компьютер-мультяшка). У моего друга есть имя и он умеет разговаривать. Как тебя зовут, дружок? Компоша отвечает: “Меня зовут Компоша”. Ты сегодня готов помогать мне? ДА! Ну тогда давай начнём урок.
Мне сегодня пришла зашифрованная цифрограмма, ребята, которую мы должны
вместе решить и расшифровать. (На доске вывешивается плакат с устным счётом
на сложение и вычитание десятичных дробей, в результате решения которого ребята
получают следующий код 523914687. )
)
| 5 | 2 | 3 | 9 | 1 | 4 | 6 | 8 | 7 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Расшифровать полученный код помогает Компоша. В результате расшифровки получается слово УМНОЖЕНИЕ. Умножение – это ключевое слово темы сегодняшнего урока. На мониторе высвечивается тема урока: “Умножение десятичной дроби на натуральное число”
Ребята, мы знаем, как выполняется умножение натуральных чисел. Сегодня мы с
вами рассмотрим умножение десятичных чисел на натуральное число. Умножение
десятичной дроби на натуральное число можно рассматривать как сумму слагаемых,
каждое из которых равно этой десятичной дроби, а количество слагаемых равно
этому натуральному числу. Например: 5,21·3
= 5,21 + 5, 21 + 5,21 = 15,63 Значит, 5,21·3
= 15,63. Представив 5,21 в виде обыкновенной дроби на натуральное
число, получим
Сегодня мы с
вами рассмотрим умножение десятичных чисел на натуральное число. Умножение
десятичной дроби на натуральное число можно рассматривать как сумму слагаемых,
каждое из которых равно этой десятичной дроби, а количество слагаемых равно
этому натуральному числу. Например: 5,21·3
= 5,21 + 5, 21 + 5,21 = 15,63 Значит, 5,21·3
= 15,63. Представив 5,21 в виде обыкновенной дроби на натуральное
число, получим
И в этом случае получили тот же результат 15,63. Теперь, не обращая внимания
на запятую, возьмём вместо числа 5,21 число 521 и перемножим на данное
натуральное число. Здесь мы должны помнить, что в одном из множителей запятая
перенесена на два разряда вправо. При умножении чисел 5, 21 и3 получим
произведение равное 15,63. Теперь в этом примере запятую перенесём влево на два
разряда. Таким образом, во сколько раз один из множителей увеличили, во столько
раз уменьшили произведение . На основании сходных моментов этих способов,
сделаем вывод.
Чтобы умножить десятичную дробь на натуральное число, надо:
1) не обращая внимания на запятую, выполнить умножение натуральных чисел;
2) в полученном произведении отделить запятой справа столько знаков, сколько их
в десятичной дроби.
На мониторе высвечиваются следующие примеры, которые мы разбираем вместе с Компошей и ребятами: 5,21·3 = 15,63 и 7,624·15 = 114,34. После показываю умножение на круглое число 12,6·50 = 630. Далее перехожу на умножение десятичной дроби на разрядную единицу. Показываю следующие примеры: 7,423·100 = 742,3 и 5,2·1000 = 5200. Итак, ввожу правило умножения десятичной дроби на разрядную единицу:
Чтобы умножить десятичную дробь на разрядные единицы 10, 100, 1000 и т.д., надо в этой дроби перенести запятую вправо на столько знаков, сколько нулей в записи разрядной единицы.
Заканчиваю объяснение выражением десятичной дроби в процентах. Ввожу правило:
Ввожу правило:
Чтобы выразить десятичную дробь в процентах, надо её умножить на 100 и приписать знак %.
Привожу пример на компьютере 0,5·100 = 50 или 0,5 = 50%.
4. По окончании объяснения даю ребятам домашнее задание, которое тоже высвечивается на мониторе компьютера: № 1030, № 1034, № 1032.
5. Чтобы ребята немного отдохнули, на закрепление темы делаем вместе с Компошей математическую физкультминутку. Все встают, показываю классу решённые примеры и они должны ответить, правильно или не правильно решён пример. Если пример решён правильно, то они поднимают руки над головой и делают хлопок ладонями. Если же пример решён не верно, ребята вытягивают руки в стороны и разминают пальчики.
6. А теперь вы
немного отдохнули, можно и решить задания. Откройте учебник на странице 205,
№ 1029. в этом задании надо вычислить значение выражений:
в этом задании надо вычислить значение выражений:
Задания появляются на компьютере. По мере их решения, появляется картинка с изображением кораблика, который при полной сборке уплывает.
№ 1031 Вычисли:
Решая это задание на компьютере, постепенно складывается ракета, решив последний пример, ракета улетает. Учитель делает небольшую информацию учащимся: “ Каждый год с казахстанской земли с космодрома Байконур взлетают к звёздам космические корабли. Рядом с Байконуром Казахстан строит свой новый космодром “Байтерек”.
№ 1035. Задача.
Какое расстояние пройдёт легковая машина за 4 часа, если скорость легковой машины 74,8 км/ч.
Данная задача сопровождается звуковым оформлением и вынесением на монитор краткого условия задачи. Если задача решена, верно, то машина начинает двигаться вперёд до финишного флажка.
№ 1033. Запиши десятичные дроби в процентах.
Запиши десятичные дроби в процентах.
0,2 = 20%; 0,5 = 50%; 0,75 = 75%; 0,92 = 92%; 1,24 =1 24%; 3,5 = 350%; 5,61= 561%.
Решая каждый пример, при появлении ответа появляется буква, в результате чего появляется слово Молодцы.
Учитель спрашивает Компошу, к чему бы появилось это слово? Компоша отвечает: “Молодцы, ребята!” и прощается со всеми.
Учитель подводит итоги урока и выставляет оценки.
1.) как умножить десятичную дробь на 0,1 0,01 0,001 2.) на сколько цифр и в какую сторону надо перенести запятую при умножении на 0,001 ? 3.) сформулируйте правило умножения на десятичную дробь. 4.) что надо сделать при умножении на десятичную дробь, если в произведении меньше цифр, чем надо отделить запятой ?
Математика, 03.06.2019 19:20, прочитайслова
Ответ разместил: ygthjkujny
1 и 2) надо запятую перенести на столько цифр сколько нулей в десятичной дроби. 3) при умножении на десятичную дробь надо запятую перенести на столько цифр сколько нулей в десятичной дроби. 4) вопрос непонятный
4) вопрос непонятный
Спасибо
Ответ разместил: Гость
Если длина дороги 20 км , то 2/5 составит: 20/5*2=8 км
Ответ разместил: Гость
Раз диаметр равен 12см, то радиус 12/2 = 6, а дальше за формулой 2 умножить на 3.14 и умножить на 6 =37.68 см.
Другие вопросы по: Математика
Выберите правельный ответ: 1)первые государства образовались: а) 30 тысюлет назад б)5 тысяч лет назад в)тысячу лет назад…
Опубликовано: 28.02.2019 22:40
Ответов: 2
Мой том все чаще отворачивал от меня свой угасающий взгляд а вскоре и вовсе ушел и не вернулся.- как правильно поставить запятые?…
Опубликовано: 01.03.2019 00:10
Ответов: 3
На книгу, лежащую на столе, поставили стакан с водой массой 400г. сила давления книги на стол оказалась равной 12 н. какова масса книги?. ..
..
Опубликовано: 02.03.2019 00:40
Ответов: 2
Сарай имеющий форму прямугольного сеном. длина сарая 10 м, нирина 6м, высота 4 м. найдите массу сена в сарае, если масса 10м кубических сена равна 6ц…
Опубликовано: 02.03.2019 21:20
Ответов: 2
Пейзажные зарисовки 6-8 односоставных предложений о природе !…
Опубликовано: 02.03.2019 22:20
Ответов: 2
Напишиинтересный рассказ о школе , состоящий не менее чем из 5 фраз, в котором полностью отсуствует буква м….
Опубликовано: 03.03.2019 05:10
Ответов: 2
Знаешь правильный ответ?
1.) как умножить десятичную дробь на 0,1 0,01 0,001 2.) на сколько цифр и в какую сторону надо перен…
Популярные вопросы
. (Вкаких случаях ,состоящее в нахождении точки пересечения прямых, корректно, а в каких-нет? если корректно, то выполните его: а)y=15x+17 и y=15x+17 б)y=-3x+4 и y=2x-1 в)13x-8 и…
(Вкаких случаях ,состоящее в нахождении точки пересечения прямых, корректно, а в каких-нет? если корректно, то выполните его: а)y=15x+17 и y=15x+17 б)y=-3x+4 и y=2x-1 в)13x-8 и…
Опубликовано: 27.02.2019 06:30
Ответов: 3
Втрёх цехах фабрики работают 480 человек. число людей, работающих во втором цехе, составляет 36% числа людей первого цеха, а число людей, работающих в третьем цехе, составляет 2/3…
Опубликовано: 28.02.2019 07:50
Ответов: 3
.(На пошив пальто ушло в 4 раза больше ткани чем на юбку. сколько метров ткани ушло на пальто и юбку, если на юбку ушло на 2,55метров ткани меньше че на пальто?)….
Опубликовано: 28.02.2019 12:20
Ответов: 1
Втрех корзинах 96 кг черешни. в первой корзине 28 кг, во второй — третья часть всей черешни. сколько килограммов в третьей корзине?. ..
..
Опубликовано: 28.02.2019 22:50
Ответов: 1
При взаимодействии металлического натрия с 90г уксусной кислоты с учетом 10% потери водорода образуется водород объемом?…
Опубликовано: 01.03.2019 06:20
Ответов: 3
Каким членом предложения является слово- золотом? к какой части речи оно относится? на сверкающем золотом шпиле развевался флаг…
Опубликовано: 01.03.2019 16:30
Ответов: 1
Определите кокое количество теплоты потребуется для плавления 200г олова имеющего температуру 232 градусов цельсия….
Опубликовано: 01.03.2019 22:00
Ответов: 3
Туристическая фирма организует однодневные автобусные экскурсии. стоимость экскурсии для одного человека составляет 480 р. группам предоставляются скидки: группе от 3 до 10 челове…
группам предоставляются скидки: группе от 3 до 10 челове…
Опубликовано: 02.03.2019 06:30
Ответов: 1
Опубликовано: 02.03.2019 11:20
Ответов: 2
Какое растение можно считать символом россии? ? и почему?…
Опубликовано: 02.03.2019 18:30
Ответов: 1
Больше вопросов по предмету: Математика Случайные вопросы
Умножение десятичных дробей примеры. Дроби. Умножение десятичных дробей. Деление десятичной дроби на десятичную дробь
Вы уже знаете, что a *
10
= a + a + a + a + a + a + a + a + a + a.
Например, 0,2
* 10
= 0,2
+ 0,2
+ 0,2
+ 0,2
+ 0,2
+ 0,2
+ 0,2
+ 0,2
+ 0,2
+ 0,2
. Несложно догадаться, что эта сумма равна 2,
т.е. 0,2
* 10
= 2
.
Несложно догадаться, что эта сумма равна 2,
т.е. 0,2
* 10
= 2
.
Аналогично можно убедиться, что:
5,2 * 10 = 52 ;
0,27 * 10 = 2,7 ;
1,253 * 10 = 12,53 ;
64,95 * 10 = 649,5 .
Вы, наверное, догадались, что при умножении десятичной дроби на 10 надо в этой дроби перенести запятую вправо на одну цифру.
А как умножить десятичную дробь на 100 ?
Имеем: a * 100 = a * 10 * 10 . Тогда:
2,375 * 100 = 2,375 * 10 * 10 = 23,75 * 10 = 237,5 .
Рассуждая аналогично, получаем, что:
3,2 * 100 = 320 ;
28,431 * 100 = 2843,1 ;
0,57964 * 100 = 57,964 .
Умножим дробь 7,1212 на число 1 000 .
Имеем: 7,1212 * 1 000 = 7,1212 * 100 * 10 = 712,12 * 10 = 7121,2 .
Эти примеры иллюстрируют следующее правило.
Чтобы умножить десятичную дробь на 10, 100, 1 000 и т.д., надо в этой дроби перенести запятую вправо соответственно на 1, 2, 3 и т.д. цифры .
Итак, если запятую перенести вправо на 1,
2,
3
и т. д. цифры, то дробь увеличится соответственно в 10,
100,
1
000
и т.д. раз.
д. цифры, то дробь увеличится соответственно в 10,
100,
1
000
и т.д. раз.
Следовательно, если запятую перенести влево на 1, 2, 3 и т.д. цифры, то дробь уменьшится соответственно в 10, 100, 1 000 и т.д. раз .
Покажем, что десятичная форма записи дробей дет возможность умножать их, руководствуясь правилом умножения натуральных чисел.
Найдем, например, произведение 3,4 * 1,23 . Увеличим первый множитель в 10 раз, а второй − в 100 раз. Это означает, что мы увеличили произведение в 1 000 раз.
Следовательно, произведение натуральных чисел 34 и 123 в 1 000 раз больше искомого произведения.
Имеем: 34 * 123 = 4182 . Тогда для получения ответа надо число 4 182 уменьшить в 1 000 раз. Запишем: 4 182 = 4 182,0 . Перенося запятую в числе 4 182,0 на три цифры влево, получим число 4,182 , которое в 1 000 раз меньше числа 4 182 . Поэтому 3,4 * 1,23 = 4,182 .
Этот же результат можно получить, руководствуясь следующим правилом.
Чтобы перемножить две десятичные дроби, надо:
1 ) умножить их как натуральные числа, не обращая внимания на запятые;
2 ) в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
В тех случаях, когда произведение содержит меньше цифр, чем требуется отделить запятой, слева перед этим произведение дописывают необходимое количество нулей, а затем переносят запятую влево на нужное количество цифр.
Например, 2 * 3 = 6, тогда 0,2 * 3 = 0,006 ; 25 * 33 = 825, тогда 0,025 * 0,33 = 0,00825 .
В тех случаях, когда один из множителей равен 0,1 ; 0,01 ; 0,001 и т.д., удобно пользоваться следующим правилом.
Чтобы умножить десятичную дробь на 0,1 ; 0,01 ; 0,001 и т.д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т.д. цифры .
Например, 1,58 * 0,1 = 0,158 ; 324,7 * 0,01 = 3,247 .
Свойства умножения натуральных чисел выполняются и для дробных чисел:
ab = ba − переместительное свойство умножения,
(ab) с = a(b с) − сочетательное свойство умножения,
a(b +
с) = ab + ac −
распределительное свойство умножения относительно сложения.
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока:
- В увлекательной форме ввести учащимся правило умножения десятичной дроби на натуральное число, на разрядную единицу и правило выражения десятичной дроби в процентах. Выработать умение применения полученных знаний при решении примеров и задач.
- Развивать и активизировать логическое мышление учащихся, умение выявлять закономерности и обобщать их, укреплять память, умение сотрудничать, оказывать помощь, оценивать свою работу и работу друг друга.
- Воспитывать интерес к математике, активность, мобильность, умение общаться.
Оборудование: интерактивная доска, плакат с цифрограммой, плакаты с
высказываниями математиков.
Ход урока
- Организационный момент.
- Устный счёт – обобщение раннее изученного материала, подготовка к изучению нового материала.
- Объяснение нового материала.
- Задание на дом.
- Математическая физкультминутка.
- Обобщение и систематизация полученных знаний в игровой форме при помощи компьютера.
- Выставление оценок.
2. Ребята, сегодня у нас урок будет несколько необычным, потому что я буду проводить его не одна, а со своим другом. И друг у меня тоже необычный, сейчас вы его увидите. (На экране появляется компьютер-мультяшка). У моего друга есть имя и он умеет разговаривать. Как тебя зовут, дружок? Компоша отвечает: “Меня зовут Компоша”. Ты сегодня готов помогать мне? ДА! Ну тогда давай начнём урок.
Мне сегодня пришла зашифрованная цифрограмма, ребята, которую мы должны
вместе решить и расшифровать. (На доске вывешивается плакат с устным счётом
на сложение и вычитание десятичных дробей, в результате решения которого ребята
получают следующий код 523914687. )
)
| 5 | 2 | 3 | 9 | 1 | 4 | 6 | 8 | 7 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Расшифровать полученный код помогает Компоша. В результате расшифровки получается слово УМНОЖЕНИЕ. Умножение – это ключевое слово темы сегодняшнего урока. На мониторе высвечивается тема урока: “Умножение десятичной дроби на натуральное число”
Ребята, мы знаем, как выполняется умножение натуральных чисел. Сегодня мы с
вами рассмотрим умножение десятичных чисел на натуральное число. Умножение
десятичной дроби на натуральное число можно рассматривать как сумму слагаемых,
каждое из которых равно этой десятичной дроби, а количество слагаемых равно
этому натуральному числу. Например: 5,21·3
= 5,21 + 5, 21 + 5,21 = 15,63
Значит, 5,21·3
= 15,63.
Представив 5,21 в виде обыкновенной дроби на натуральное
число, получим
Умножение
десятичной дроби на натуральное число можно рассматривать как сумму слагаемых,
каждое из которых равно этой десятичной дроби, а количество слагаемых равно
этому натуральному числу. Например: 5,21·3
= 5,21 + 5, 21 + 5,21 = 15,63
Значит, 5,21·3
= 15,63.
Представив 5,21 в виде обыкновенной дроби на натуральное
число, получим
И в этом случае получили тот же результат 15,63. Теперь, не обращая внимания на запятую, возьмём вместо числа 5,21 число 521 и перемножим на данное натуральное число. Здесь мы должны помнить, что в одном из множителей запятая перенесена на два разряда вправо. При умножении чисел 5, 21 и3 получим произведение равное 15,63. Теперь в этом примере запятую перенесём влево на два разряда. Таким образом, во сколько раз один из множителей увеличили, во столько раз уменьшили произведение. На основании сходных моментов этих способов, сделаем вывод.
Чтобы умножить десятичную дробь на натуральное число, надо:
1) не обращая внимания на запятую, выполнить умножение натуральных чисел;
2) в полученном произведении отделить запятой справа столько знаков, сколько их
в десятичной дроби.
На мониторе высвечиваются следующие примеры, которые мы разбираем вместе с Компошей и ребятами: 5,21·3 = 15,63 и 7,624·15 = 114,34. После показываю умножение на круглое число 12,6·50 = 630 . Далее перехожу на умножение десятичной дроби на разрядную единицу. Показываю следующие примеры: 7,423·100 = 742,3 и 5,2·1000 = 5200. Итак, ввожу правило умножения десятичной дроби на разрядную единицу:
Чтобы умножить десятичную дробь на разрядные единицы 10, 100, 1000 и т.д., надо в этой дроби перенести запятую вправо на столько знаков, сколько нулей в записи разрядной единицы.
Заканчиваю объяснение выражением десятичной дроби в процентах. Ввожу правило:
Чтобы выразить десятичную дробь в процентах, надо её умножить на 100 и приписать знак %.
Привожу пример на компьютере 0,5·100 = 50 или 0,5 = 50% .
4. По окончании объяснения даю ребятам домашнее задание, которое тоже
высвечивается на мониторе компьютера: № 1030, № 1034, № 1032.
5. Чтобы ребята немного отдохнули, на закрепление темы делаем вместе с Компошей математическую физкультминутку. Все встают, показываю классу решённые примеры и они должны ответить, правильно или не правильно решён пример. Если пример решён правильно, то они поднимают руки над головой и делают хлопок ладонями. Если же пример решён не верно, ребята вытягивают руки в стороны и разминают пальчики.
6. А теперь вы немного отдохнули, можно и решить задания. Откройте учебник на странице 205, № 1029. в этом задании надо вычислить значение выражений:
Задания появляются на компьютере. По мере их решения, появляется картинка с изображением кораблика, который при полной сборке уплывает.
№ 1031 Вычисли:
Решая это задание на компьютере, постепенно складывается ракета, решив
последний пример, ракета улетает. Учитель делает небольшую информацию учащимся:
“ Каждый год с казахстанской земли с космодрома Байконур взлетают к звёздам
космические корабли.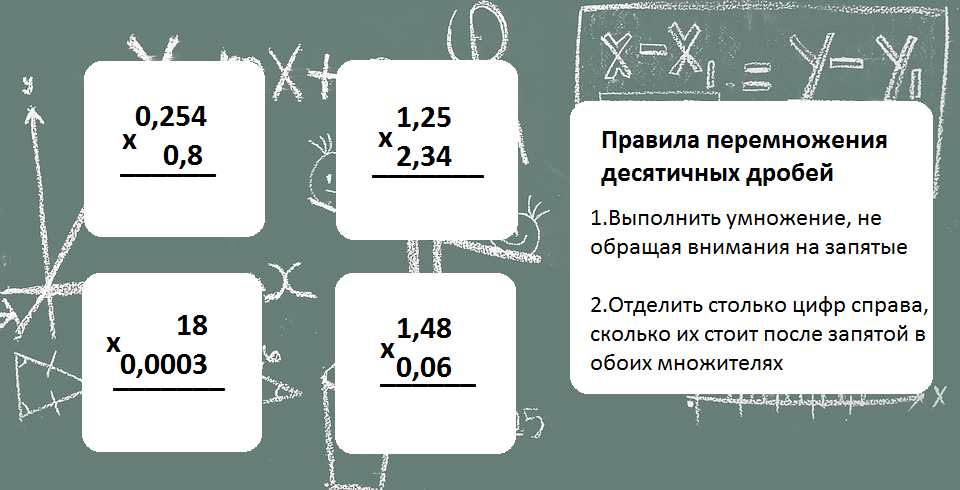 Рядом с Байконуром Казахстан строит свой новый космодром “Байтерек”.
Рядом с Байконуром Казахстан строит свой новый космодром “Байтерек”.
№ 1035. Задача.
Какое расстояние пройдёт легковая машина за 4 часа, если скорость легковой машины 74,8 км/ч.
Данная задача сопровождается звуковым оформлением и вынесением на монитор краткого условия задачи. Если задача решена, верно, то машина начинает двигаться вперёд до финишного флажка.
№ 1033. Запиши десятичные дроби в процентах.
0,2 = 20%; 0,5 = 50%; 0,75 = 75%; 0,92 = 92%; 1,24 =1 24%; 3,5 = 350%; 5,61= 561%.
Решая каждый пример, при появлении ответа появляется буква, в результате чего появляется слово Молодцы .
Учитель спрашивает Компошу, к чему бы появилось это слово? Компоша отвечает: “Молодцы, ребята!” и прощается со всеми.
Учитель подводит итоги урока и выставляет оценки.
В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Содержание урока
Сложение десятичных дробейКак мы знаем, десятичная дробь имеет целую и дробную часть. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой» .
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Начинаем складывать дробные части: 2 + 3= 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой» :
Получили ответ 8,5. Значит выражения 3,2 + 5,3 равно 8,5
На самом деле не всё так просто, как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Разряды в десятичных дробяхУ десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе некоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных
Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .
Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345
Видно, что сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345.
При сложении десятичных дробей соблюдаются те же принципы и правила, что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой» . Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
Пример 2. Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
3,51 + 1,22 = 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти . В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Записываем цифру 5 в целой части нашего ответа:
Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92
2,65 + 3,27 = 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3
9,5 + 2,8 = 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5 . Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:
Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:
Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:
Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Вычитание десятичных дробейПри вычитании десятичных дробей нужно соблюдать те же правила, что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
2,5 − 2,2 = 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
7,353 — 3,1 = 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
3,46−2,39=1,07
Пример 4 . Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,23 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
Умножение десятичных дробейУмножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:
Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75
2,5 × 1,5 = 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:
Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:
Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Умножение десятичной дроби на обычное числоИногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:
Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
2,54 × 2 = 5,08
Умножение десятичных дробей на 10, 100, 1000Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:
Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
2,88 × 10 = 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
2,88 × 10 = 28,8
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
2,88 × 100 = 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Умножение десятичных дробей на 0,1 0,01 и 0,001Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:
Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
3,25 × 0,1 = 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
3,25 × 0,1 = 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»
Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице» , то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
Получили ответ 0,5. Значит дробь равна 0,5
Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Пример 2. Найти значение выражения 4: 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.
Завершаем пример, умножив 8 на 5, и получив 40:
Получили ответ 0,8. Значит значение выражения 4: 5 равно 0,8
Пример 3. Найти значение выражения 5: 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:
Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0
Значит в частном опять записываем 0
Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:
Завершаем пример, умножив 4 на 125, и получив 500
Получили ответ 0,04. Значит значение выражения 5: 125 равно 0,04
Деление чисел без остатка
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
9: 5 = 1,8
Пример 2 . Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:
Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:
и завершаем пример, проверив есть ли еще остаток:
Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:
Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:
4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
8: 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:
Получили ответ 2,4. Значение выражения 4,8: 2 равно 2,4
Пример 2. Найти значение выражения 8,43: 3
Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:
Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:
24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Получили ответ 2,81. Значит значение выражения 8,43: 3 равно 2,81
Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение
Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9: 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2 ) : (3 × 2 ) = 18: 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17.
На самом деле внутри этого процесса происходило умножение на 10. Вот как это выглядело:
5,91 × 10 = 59,1
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и . Например, разделим 2,1 на 10. Решим этот пример уголком:
Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1: 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
2,1: 100 = 0,021
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1: 1000 = 0,0021
Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и . В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
Значит значение выражения 6,3: 0,1 равно 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3: 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
Переносим запятую вправо на одну цифру и получаем 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
6,3: 0,001 = 6300
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Как обычные числа.
2. Считаем число знаков после запятой у 1-ой десятичной дроби и у 2-ой. Их число складываем.
3. В итоговом результате отсчитываем справа налево такое число цифр, сколько получилось их в пункте выше, и ставим запятую.
Правила умножения десятичных дробей.
1. Умножить, не обращая внимания на запятую.
2. В произведении отделяем после запятой такое количество цифр, сколько их после запятых в обоих множителях вместе.
Умножая десятичную дробь на натуральное число, необходимо:
1. Умножить числа, не обращая внимания на запятую;
2. В результате ставим запятую так, чтобы справа от нее было столько цифр, сколько в десятичной дроби.
Умножение десятичных дробей столбиком.
Рассмотрим на примере:
Записываем десятичные дроби в столбик и умножаем их как натуральные числа , не обращая внимания на запятые. Т.е. 3,11 мы рассматриваем как 311, а 0,01 как 1.
Результатом является 311. Далее считаем число знаков (цифр) после запятой у обеих дробей. В 1-ой десятичной дроби 2 знака и во 2-рой — 2. Общее число цифр после запятых:
2 + 2 = 4
Отсчитываем справа налево четыре знака у результата. В итоговом результате цифр меньше, чем нужно отделить запятой. В этом случае необходимо слева дописать не хватающее количество нулей.
В нашем случае не достает 1-ой цифры, поэтому дописываем слева 1 ноль.
Обратите внимание:
Умножая любую десятичную дробь на 10, 100, 1000 и так далее, запятая в десятичной дроби переносится вправо на столько знаков, сколько нулей после единицы.
Например :
70,1 . 10 = 701
0,023 . 100 = 2,3
5,6 . 1 000 = 5 600
Обратите внимание:
Для умножения десятичной дроби на 0,1; 0,01; 0,001; и так далее, нужно в этой дроби перенести запятую влево на столько знаков, сколько нулей перед единицей.
Считаем и ноль целых!
Например:
12 . 0,1 = 1,2
0,05 . 0,1 = 0,005
1,256 . 0,01 = 0,012 56
Чтобы понять, как умножать десятичные дроби, рассмотрим конкретные примеры.
Правило умножения десятичных дробей
1) Умножаем, не обращая внимания на запятую.
2) В результате отделяем после запятой столько цифр, сколько их после запятых в обоих множителях вместе.
Примеры .
Найти произведение десятичных дробей:
Чтобы умножить десятичные дроби, умножаем, не обращая внимания на запятые. То есть мы умножаем не 6,8 и 3,4, а 68 и 34. В результате отделяем после запятой столько цифр, сколько их после запятых в обоих множителях вместе. В первом множителе после запятой одна цифра, во втором — тоже одна. Итого, отделяем после запятой две цифры.Таким образом, получили окончательный ответ: 6,8∙3,4=23,12.
В первом множителе после запятой одна цифра, во втором — тоже одна. Итого, отделяем после запятой две цифры.Таким образом, получили окончательный ответ: 6,8∙3,4=23,12.
Умножаем десятичные дроби, не принимая во внимание запятую. То есть фактически вместо умножения 36,85 на 1,14 мы умножаем 3685 на 14. Получаем 51590. Теперь в этом результате надо отделить запятой столько цифр, сколько их в обоих множителях вместе. В первом числе после запятой две цифры, во втором — одна. Итого, отделяем запятой три цифры. Поскольку в конце записи после запятой стоит нуль, в ответ мы его не пишем: 36,85∙1,4=51,59.
Чтобы умножить эти десятичные дроби, умножим числа, не обращая внимания на запятые. То есть умножаем натуральные числа 2315 и 7. Получаем 16205. В этом числе нужно отделить после запятой четыре цифры — столько, сколько их в обоих множителях вместе (в каждом — по два). Окончательный ответ: 23,15∙0,07=1,6205.
Умножение десятичной дроби на натуральное число выполняется аналогично. Умножаем числа, не обращая внимания на запятую, то есть 75 умножаем на 16. В полученном результате после запятой должно стоять столько же знаков, сколько их в обоих множителях вместе — один. Таким образом, 75∙1,6=120,0=120.
Умножаем числа, не обращая внимания на запятую, то есть 75 умножаем на 16. В полученном результате после запятой должно стоять столько же знаков, сколько их в обоих множителях вместе — один. Таким образом, 75∙1,6=120,0=120.
Умножение десятичных дробей начинаем с того, что умножаем натуральные числа, так как на запятые не обращаем внимания. После этого отделяем после запятой столько цифр, сколько их в обоих множителях вместе. В первом числе после запятой два знака, во втором — тоже два. Итого, в результате после запятой должно стоять четыре цифры: 4,72∙5,04=23,7888.
Умножение десятичных знаков | Математические подарки
Задача: два ученика умножили 0,2 на 0,4. Студент 1 нашел произведение 0,8, а студент 2 нашел произведение 0,08. Кто из учеников дал правильный ответ? Объяснять.
| Студент 1 | Студент 2 | |
Анализ: Преобразуем каждую десятичную дробь в дробь, чтобы решить эту задачу.
| Факторы | Продукт | ||||
| Дроби: | х | = | |||
| Десятичные числа: | 0,2 | х | 0,4 | = | 0,08 |
Если мы умножим две десятых на четыре десятых, мы получим произведение восьми сотых.
Ответ: Ученик 2 прав, так как 0,2 x 0,4 = 0,08.
В приведенной выше задаче произведение 0,08 меньше, чем каждый отдельный множитель. Это потому, что вы находите часть части: 0,2 из 0,4 равно 0,08. Таким образом, когда вы умножаете два десятичных множителя, каждый из которых меньше единицы, произведение будет меньше каждого отдельного множителя. Давайте рассмотрим еще несколько примеров умножения десятичных дробей.
Пример 1. Автомобиль Марины расходует по шоссе 44,8 мили на галлон. Если ее топливный бак вмещает 15,4 галлона, то как далеко она сможет проехать на одном полном баке бензина?
Если ее топливный бак вмещает 15,4 галлона, то как далеко она сможет проехать на одном полном баке бензина?
Анализ: Мы можем умножить 44,8 на 15,4, чтобы решить эту задачу.
Шаг 1: Оцените продукт.
Шаг 2: Умножьте, чтобы найти произведение.
Умножьте эти десятичные дроби, как если бы они были целыми числами. Не обращайте внимания на десятичную точку.
Компенсируйте, поставив десятичную точку в произведении.
Шаг 3: Сравните свою оценку с вашим продуктом, чтобы убедиться, что ваш ответ имеет смысл.
Наш ответ 689,92 имеет смысл, поскольку произведение 44,8 и 15,4 колеблется от 400 до 1000.
Ответ: Марина может проехать 689,92 мили с одним полным баком бензина.
При умножении десятичных дробей очень важно расположение десятичной точки. Поскольку в каждом факторе один десятичный разряд, в произведении должно быть два десятичных разряда. Это потому, что десятые доли х десятые = сотые доли. Оценка произведения позволяет нам убедиться, что десятичная точка расставлена правильно и что у нас есть разумный ответ. Например, если ваш продукт был 68,992 мили, тогда вы узнаете, что допустили ошибку умножения, сравнив ее со своей оценкой. Давайте рассмотрим еще несколько примеров умножения десятичных дробей.
Оценка произведения позволяет нам убедиться, что десятичная точка расставлена правильно и что у нас есть разумный ответ. Например, если ваш продукт был 68,992 мили, тогда вы узнаете, что допустили ошибку умножения, сравнив ее со своей оценкой. Давайте рассмотрим еще несколько примеров умножения десятичных дробей.
Пример 2. Умножение: 3,54 x 1,8
Анализ. В коэффициенте 3,54 две десятичные цифры, а в коэффициенте 1,8 — одна десятичная цифра.
Шаг 1: Оцените продукт.
Шаг 2: Умножьте, чтобы найти произведение.
Умножьте эти десятичные дроби, как если бы они были целыми числами. Не обращайте внимания на десятичную точку.
Компенсируйте, поставив десятичную точку в произведении.
Шаг 3: Сравните свою оценку с вашим продуктом, чтобы убедиться, что ваш ответ имеет смысл.
Наше произведение 6,372 имеет смысл, поскольку оно близко к нашей оценке 6.
Ответ: произведение 3,54 и 1,8 равно 6,372
в коэффициенте 1,8. Следовательно, в произведении должно быть три десятичных знака. Возможно, вам интересно, почему это так. Когда мы проигнорировали десятичную точку на шаге 2, мы действительно переместили ее на две позиции вправо для первого множителя (3,54 х 100 = 354) и на одну позицию вправо для второго множителя (1,8 х 10 = 18). Нам нужно компенсировать, чтобы получить правильный ответ. Для этого мы должны сложить общее количество знаков, на которые десятичная запятая была перемещена вправо. Затем, начиная справа от последней цифры произведения, мы должны передвинуть запятую на такое же количество знаков влево. Короче говоря, поскольку мы умножили на 10 в третьей степени, мы должны компенсировать это делением на 10 в третьей степени. Давайте посмотрим на другой пример.
Следовательно, в произведении должно быть три десятичных знака. Возможно, вам интересно, почему это так. Когда мы проигнорировали десятичную точку на шаге 2, мы действительно переместили ее на две позиции вправо для первого множителя (3,54 х 100 = 354) и на одну позицию вправо для второго множителя (1,8 х 10 = 18). Нам нужно компенсировать, чтобы получить правильный ответ. Для этого мы должны сложить общее количество знаков, на которые десятичная запятая была перемещена вправо. Затем, начиная справа от последней цифры произведения, мы должны передвинуть запятую на такое же количество знаков влево. Короче говоря, поскольку мы умножили на 10 в третьей степени, мы должны компенсировать это делением на 10 в третьей степени. Давайте посмотрим на другой пример.
Пример 3. Умножение: 0,121 x 0,02
Анализ. В коэффициенте 0,121 три десятичных знака, а в коэффициенте 0,02 — 2 десятичных знака.
Шаг 1: Оцените продукт.
Шаг 2: Умножьте, чтобы найти произведение.
Умножьте эти десятичные дроби, как если бы они были целыми числами. Не обращайте внимания на десятичную точку.
Компенсируйте, поставив десятичную точку в произведении.
Шаг 3: Сравните свою оценку с вашим продуктом, чтобы убедиться, что ваш ответ имеет смысл.
Наше произведение 0,00242 имеет смысл, поскольку оно близко к нашей оценке 0,00240
Ответ: Произведение 0,121 и 0,02 равно 0,00242.
В примере 3 коэффициент 0,121 состоит из трех десятичных цифр, а коэффициент 0,02 — из двух десятичных цифр. Следовательно, в произведении должно быть пять десятичных цифр. Когда мы проигнорировали десятичную точку на шаге 2, мы действительно переместили ее на три позиции вправо для первого множителя (0,121 x 1000 = 121) и на две позиции вправо для второго множителя (0,02 x 100 = 2). Нам нужно компенсировать, чтобы получить правильный ответ. Для этого мы должны сложить общее количество знаков, на которые десятичная запятая была перемещена вправо. Затем, начиная справа от последней цифры в произведении, мы должны передвинуть запятую на пять знаков влево. В продукте 242 всего 3 цифры. Таким образом, нам нужно написать два нуля слева от него, чтобы было достаточно мест для перемещения десятичной точки. Короче говоря, поскольку мы умножили на 10 в пятой степени, мы должны компенсировать это делением на 10 в пятой степени. Давайте посмотрим на другой пример.
Затем, начиная справа от последней цифры в произведении, мы должны передвинуть запятую на пять знаков влево. В продукте 242 всего 3 цифры. Таким образом, нам нужно написать два нуля слева от него, чтобы было достаточно мест для перемещения десятичной точки. Короче говоря, поскольку мы умножили на 10 в пятой степени, мы должны компенсировать это делением на 10 в пятой степени. Давайте посмотрим на другой пример.
Пример 4. Умножение: 5,27 x 0,01
Анализ. В каждом множителе две десятичные цифры.
Шаг 1: Оцените продукт.
Шаг 2: Умножьте, чтобы найти произведение.
Умножьте эти десятичные дроби, как если бы они были целыми числами. Не обращайте внимания на десятичную точку.
Компенсируйте, поставив десятичную точку в произведении.
Шаг 3: Сравните свою оценку с вашим продуктом, чтобы убедиться, что ваш ответ имеет смысл
Наше произведение 0,0527 имеет смысл, поскольку оно близко к нашей оценке 0,05.
Ответ: Произведение 5,27 и 0,01 равно 0,0527.
Обратите внимание, что в примере 4 в каждом множителе два десятичных знака, в результате чего в произведении четыре десятичных знака. Продукт 527 содержит только 3 цифры. Таким образом, нам нужно написать один ноль слева от него, чтобы было достаточно мест для перемещения десятичной точки. Давайте рассмотрим еще несколько примеров.
Пример 5. Умножение: 2,1 x 8,9
Анализ. В каждом множителе две десятичные цифры.
Шаг 1: Оцените продукт.
Можете ли вы оценить продукт, используя арифметику в уме?
Шаг 2: Умножьте, чтобы найти произведение.
Умножьте эти десятичные дроби, как если бы они были целыми числами. Не обращайте внимания на десятичную точку.
Компенсируйте, поставив десятичную точку в произведении.
Шаг 3: Сравните свою оценку с результатом, чтобы убедиться, что ваш ответ имеет смысл
Наш продукт 18,69 имеет смысл, поскольку он близок к нашей мысленной оценке 18,
Ответ: Произведение 2. 1 и 8.9 равно 18,69.
1 и 8.9 равно 18,69.
Обратите внимание, что в примере 5 в каждом факторе есть одна десятичная цифра, поэтому в произведении две десятичные цифры. Давайте рассмотрим еще один пример.
Пример 6: Сэм учился по 3,5 часа каждый день в течение 4,5 дней. Сколько часов он учился?
Анализ: мы умножим, чтобы решить эту задачу.
Ответ: Сэм учился 15,75 часов.
Резюме: при умножении десятичных дробей используется следующая процедура:
- Оценить продукт.
- Умножьте, чтобы найти произведение.
- Умножайте десятичные дроби, как если бы они были целыми числами. Не обращайте внимания на десятичную точку.
- Компенсируйте, поставив десятичную точку в произведении.
- Сравните свою оценку с вашим продуктом, чтобы убедиться, что ваш ответ имеет смысл.
Оценка произведения перед умножением позволяет нам убедиться, что десятичная точка расставлена правильно и что у нас есть разумный ответ. Когда мы игнорируем десятичную точку, мы действительно перемещаем ее справа от каждого множителя. Поскольку мы умножили каждый фактор на степень 10, нам нужно компенсировать, чтобы получить правильный ответ. Для этого мы должны сложить общее количество знаков, на которые десятичная запятая была перемещена вправо. Затем, начиная справа от последней цифры произведения, мы должны передвинуть запятую на такое же количество знаков влево.
Когда мы игнорируем десятичную точку, мы действительно перемещаем ее справа от каждого множителя. Поскольку мы умножили каждый фактор на степень 10, нам нужно компенсировать, чтобы получить правильный ответ. Для этого мы должны сложить общее количество знаков, на которые десятичная запятая была перемещена вправо. Затем, начиная справа от последней цифры произведения, мы должны передвинуть запятую на такое же количество знаков влево.
Упражнения
Указания: Прочтите каждый вопрос ниже. Вы можете использовать бумагу и карандаш, чтобы помочь вам умножить. Щелкните один раз в ПОЛЕ ОТВЕТА и введите свой ответ; затем нажмите ВВОД. После того, как вы нажмете ENTER, в ОКНЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, является ли ваш ответ правильным или неправильным. Чтобы начать сначала, нажмите ОЧИСТИТЬ.
| 1. | Умножение: 0,7 x 0,6 ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: |
2. | Умножить: 3,05 долл. США x 0,8 ЯЩИК ОТВЕТОВ: $ ЯЩИК РЕЗУЛЬТАТОВ: |
| 3. | Умножить: 0,46 x 8,61 ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: |
| 4. | Умножить: 9,7 x 0,001 ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: |
| 5. | Репетитор зарабатывает 41,50 доллара в час. Сколько он заработает, если будет работать 3,25 часа (округлив до цента)? ЯЩИК ОТВЕТОВ: $ ЯЩИК РЕЗУЛЬТАТОВ: |
Как складывать, вычитать, умножать и делить десятичные дроби
| База десяти – кратные десяти |
Наша система счисления основана на десятичной системе счисления, что означает, что она основана на десяти цифрах: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Одиннадцатая цифра — двузначная. число, начинающееся с единицы за один десять плюс ничего, 10, а двадцать первая цифра — это двузначное число, начинающееся с двух за два десятка, 20. Когда мы дойдем до десяти десятков, у нас получится трехзначное число 100. Это должно звучать очень похоже на обсуждение ранее о стоимости места.
Одиннадцатая цифра — двузначная. число, начинающееся с единицы за один десять плюс ничего, 10, а двадцать первая цифра — это двузначное число, начинающееся с двух за два десятка, 20. Когда мы дойдем до десяти десятков, у нас получится трехзначное число 100. Это должно звучать очень похоже на обсуждение ранее о стоимости места.
Одна тысяча, 1000, это 10 х 10 х 10. Таким образом, мы можем быстро увидеть, что, умножая еще на десять, мы получаем 10 000 и так далее.
Обратите внимание, что число, которое меньше единицы и не содержит целых чисел, обычно имеет ноль на месте целого числа слева от десятичной точки.
Существуют системы счисления, основанные на различном количестве цифр. Наиболее известной является двоичная система, которую используют многие компьютерные системы. Он основан на двух цифрах («би-» означает «два»), нуле (0) и единице (1). Этот курс охватывает только операции с основанием десять.
| Перемещение десятичной точки для умножения или деления на число, кратное десяти |
Любое число, не являющееся смешанным, можно легко разделить или умножить на 10, просто переместив десятичную точку в числе.
Все числа имеют десятичную точку, даже если вы ее не видите! Если это целое число или целое число, например 6, десятичная точка ставится после числа, например 6. Если это ровно 6, его можно записать как 6,0. Если бы вам нужно было умножить его на 10, вы бы переместили десятичную точку на один разряд вправо, потому что в 10 стоит один ноль. Таким образом, 10 x 6,0 будет 60,9.0003
Если бы вам нужно было умножить это число на 10 000, вы бы переместили десятичную цифру на четыре знака вправо, потому что 10 000 имеет четыре нуля, обозначающих, что это 10 х 10 х 10 х 10, поэтому вы должны умножить 6 на 10 х 10 х 10 х 10, что составляет 60 000.
Чтобы разделить на десять или кратное десяти, вы перемещаете десятичную точку влево на такое же количество знаков, сколько нулей или десятичных знаков в числе, на которое вы делите.
Если у вас есть число 475 и вам нужно разделить его на десять, вы можете использовать деление в длину, и это будет выглядеть так:
Однако вскоре после выполнения нескольких таких задач вы обнаружите, что при делении на десять вы просто переместили десятичную точку на один разряд влево. Вы также заметите, что если вы разделите на 1000, вы переместите десятичную точку на три знака влево. Таким образом, 67 823 разделить на 1000 получится 67,823.
Хотите узнать больше? Пройдите онлайн-курс по базовой математике.
Если в числе уже есть десятичная точка, начните с этой десятичной точки и переместите ее вправо при умножении и влево при делении.
| Преобразование дробей в десятичные и десятичных дробей |
В данном случае запятая выходила даже на тысячных. Для этого курса дроби будут четными десятичными, или вам скажут, сколько знаков нужно выразить. Вам нужно будет выработать десятичную дробь на один разряд больше, чтобы правильно округлить.
Для этого курса дроби будут четными десятичными, или вам скажут, сколько знаков нужно выразить. Вам нужно будет выработать десятичную дробь на один разряд больше, чтобы правильно округлить.
В приведенном выше примере вам могли бы предложить округлить до сотых. В этом случае вы бы доработали задачу до тысячных, где у вас 5. Поскольку это 5 или больше, вы округлили бы сотые до одного разряда и выразили ответ как 0,13. Если бы вас попросили выразить ответ с точностью до десятых, вы бы обработали его с точностью до сотых. Затем, поскольку сотые доли — это 2 (меньше 5), вы бы оставили это как 2 — даже если вы знаете, что следующим местом будет 5 или больше. Округлив до десятых: 0,1.
Ноль — это заполнитель справа от десятичной точки. Если бы мы не использовали ноль в качестве заполнителя, число было бы 0,625, что означало бы, что 16 входит в 10 шесть раз! Вместо этого он дошел до 100 шесть раз. Поэтому будьте осторожны, всегда используйте ноль в качестве заполнителя, если делитель не входит в делимое и вам нужно сбить еще одну цифру.
Сложение и вычитание десятичных знаков
Сложение и вычитание десятичных дробей не слишком отличается от сложения и вычитания любых чисел. Очень важно, чтобы вы записывали свои десятичные дроби так, чтобы десятичные точки совпадали, иначе вы обнаружите, что прибавляете десятые к единицам или вычитаете сотые из десятых.
Пока каждое из чисел, которые вы добавляете или вычитаете, имеет одинаковое количество знаков после запятой, сложение или вычитание довольно легко.
В первой задаче вам нужно будет поставить десятичную точку после пяти, а затем поставить нулевые заполнители в десятых и сотых местах. Очевидно, что тогда вам нужно будет одолжить одно целое из пяти, чтобы получить 10 десятых, а затем одолжить одну из десятых, чтобы получить 10 сотых, прежде чем вы сможете вычесть 5 сотых или 2 десятых.
Умножение и деление десятичных дробей |
При умножении десятичных дробей не выравнивайте десятичные точки. Просто выровняйте числа вдоль правой части задачи. Затем умножьте так же, как если бы все числа были целыми числами, и прибавьте в конце. После этого подсчитайте, сколько знаков после запятой имеют два множителя (начните с правого края каждого числа), а затем дайте ответ, сколько знаков после запятой.
Для деления десятичных дробей всегда используйте длинное деление. Если делитель имеет десятичную дробь, вам нужно будет переместить десятичную точку в делителе и делимое на количество знаков после запятой в делителе, чтобы делитель стал целым числом. Возможно, вам придется добавить нули в качестве заполнителей в делимом. Затем поместите десятичную запятую для частного непосредственно над последней десятичной запятой в делимом и будьте осторожны, чтобы выровнять все цифры в правильных значениях места при делении.
Возможно, вам придется добавить нули в качестве заполнителей в делимом. Затем поместите десятичную запятую для частного непосредственно над последней десятичной запятой в делимом и будьте осторожны, чтобы выровнять все цифры в правильных значениях места при делении.
Как умножать десятичные дроби? Определение, примеры, факты
Знакомство с умножением десятичных дробей
Умножение является важным жизненным навыком, который должен знать каждый. Умножение десятичных дробей — это более продвинутый навык умножения, повышающий навык по сравнению с простым умножением целых чисел. Знакомство детей с чем-то немного сложным, например, с десятичными умножениями, научит их использовать более сложные математические понятия.
Умножение десятичных дробей может показаться сложным и пугающим для юных умов. Как родитель или учитель, как вы можете преодолеть этот разрыв между неприязнью и жизненно важными математическими навыками? Растущий интерес и любопытство могут противостоять неприязни или страху перед предметом. SplashLearn — это платформа, созданная для помощи юным умам в понимании сложных математических концепций, соответствующих школьной программе, с помощью игр.
SplashLearn — это платформа, созданная для помощи юным умам в понимании сложных математических концепций, соответствующих школьной программе, с помощью игр.
Да, вы правильно прочитали. В конце концов, что может быть более заманчивым и интерактивным для детей, чем игры? Игры SplashLearn — это увлекательный и инновационный способ обучения детей теориям и концепциям, которые в противном случае были бы для них утомительным занятием.
Умножение десятичных чисел на целое число
Умножение десятичного числа на целое аналогично умножению целых чисел. Однако из-за десятичных знаков в одном из чисел это может показаться трудным. Итак, давайте посмотрим, как мы можем упростить этот процесс для вас.
Шаг 1: Забудьте о десятичных дробях. Да, они не играют никакой роли, пока вы выполняете реальную операцию. Теперь умножьте два числа, как если бы вы делали это с целыми числами.
Шаг 2: Подсчитайте количество цифр после запятой.
Шаг 3: Поставьте десятичную точку в произведении, оставив такое же количество цифр справа, как и десятичные разряды в коэффициенте.
Совет для профессионалов: Всегда помните, что произведение после умножения должно иметь такое же количество знаков после запятой, как и множители.
Теперь давайте посмотрим на примеры умножения десятичных дробей:
Пример: Найдите произведение 0,2$ \умножить на 3$
Шаг 1: Берем два числа без учета десятичной дроби, т.е. 2 и 3. Перемножаем их . Итак, мы получаем $2\times 3 = 6$.
Шаг 2: Считаем количество цифр после запятой. Здесь у нас есть только одна цифра после запятой.
Шаг 3: Ставим запятую в произведении, оставляя после себя одну цифру справа. Поскольку произведение равно 6, мы должны поставить десятичную дробь перед ним.
Значит, ответ будет 0,6.
Пример: Найдите произведение 0,4 доллара х 3 доллара
Аналогично, чтобы найти произведение 0,4 и 3, умножьте числа без десятичных знаков, т. е. 4 доллара х 3 = 12 долларов.
Теперь есть одна цифра после запятой, поэтому давайте поставим десятичную точку в произведении, оставив одну цифру справа: 1,2
Таким образом, $0,4 \ умножить на 3 = 1,2 $
Умножение двух десятичных чисел
При умножении двух десятичных чисел чисел, вы должны учитывать десятичные разряды обоих множителей.
Шаг 1: Сначала игнорируйте десятичные разряды. Выполните умножение данных чисел.
Шаг 2: Подсчитайте количество знаков после запятой в обоих множителях и рассчитайте их сумму.
Шаг 3: Поместите запятую с правого конца в соответствии с количеством знаков после запятой, которое вы подсчитали на шаге 2.
Пример: Найдите произведение 15,62 доллара США х 0,7 доллара
Шаг 1: игнорируем десятичные дроби и умножаем заданные числа.
$1562 \times 7 = 10934$
Шаг 2: Считаем количество знаков после запятой в обоих числах и вычисляем их сумму.
15,62 имеет 2 знака после запятой, а 0,72 имеет 1 знак после запятой. Следовательно, сумма десятичных множителей равна 3,9.0003
Шаг 3: Ставим десятичную дробь в произведении, оставляя после себя три цифры справа.
Итак, 15,62 доллара США \ умножить на 0,7 = 10,934 доллара
Умножение десятичных дробей на 10, 100 и 1000
Когда мы умножаем десятичное число на 10, десятичная дробь сдвигается вправо от числа на один разряд.
Например, $15,2705 \×10 = 152,705$
Здесь в решении происходит только одно изменение: десятичный сдвиг от его позиции в 15,2705 на один знак вправо. Итак, в качестве ответа мы получаем 152.705.
Когда мы умножаем десятичное число на 100, десятичная дробь сдвигается вправо от числа на два знака.
Например, $15,2705 \х100 = 1527,05$
Когда мы умножаем десятичное число на 1000, десятичное число сдвигается вправо от числа на три знака.
Например, 15,2705 долл. США \ умножить на 1000 = 15270,5 долл. США
Таким образом, когда нам нужно умножить десятичное число на 10, 100 или 1000, мы сдвигаем десятичное число справа от числа в соответствии с количеством нулей после 1. .
Let us consider a few examples:
- $53.5 \times 10 = 535$
- $469.127 \times 10 = 4691.27$
- $398.16 \times 100 = 39816$
- $826.3 \times 100 = 82630.0$
- $0.137 \ умножить на 100 = 13,7$
Решенные примеры
1) Найдите произведение 9,2$ \умножить на 0,08$ .
Решение :
Шаг 1: Мы игнорируем десятичные дроби и умножаем заданные числа.
92$ \умножить на 8 = 736$
Шаг 2: Заметим, что 9,2 имеет 1 десятичный знак, а 0,08 имеет 2 десятичных знака. Следовательно, сумма десятичных множителей равна 3.
Шаг 3: Подставляем десятичную дробь в произведение, оставляя после себя три цифры справа.
Итак, 9,2$ х 0,08 = 0,736$
2) Найдите произведение 20,1$ х 6,0$ .
Решение :
Шаг 1: Мы игнорируем десятичные дроби и умножаем заданные числа.
201$ \умножить на 60 = 12060$
Шаг 2: Заметим, что 20.1 имеет 1 десятичный разряд, а 6.0 имеет 1 десятичный разряд. Следовательно, сумма десятичных множителей равна 2.
Шаг 3: Подставляем десятичную дробь в произведение, оставляя две цифры справа.
Итак, 20,1$ х 6,0 = 120,60$
3) Найдите произведение 36$ х 0,5$ .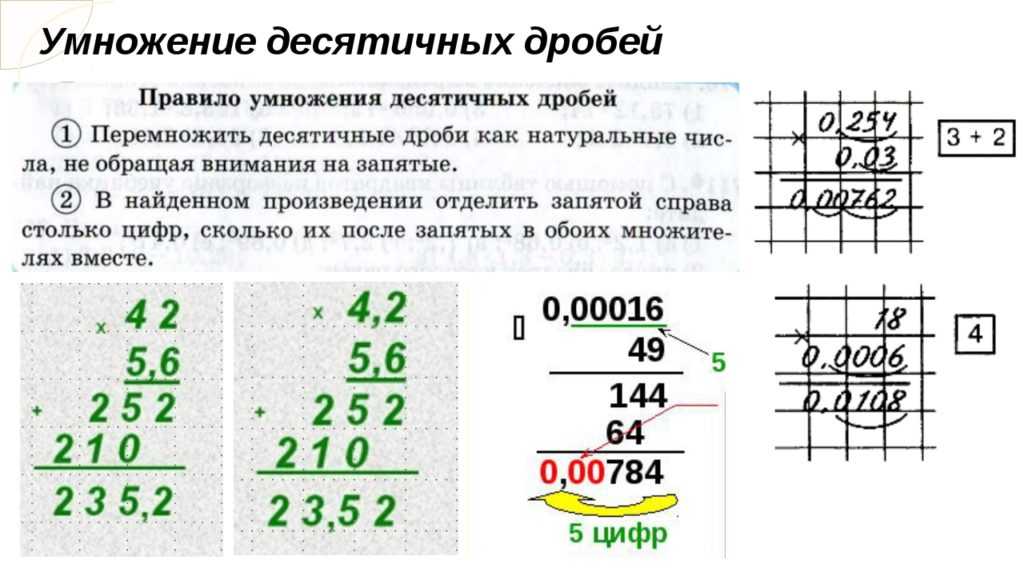
Решение :
Шаг 1: Мы игнорируем десятичные дроби и умножаем заданные числа.
36$ \умножить на 5 = 180$
Шаг 2: Заметим, что 0,5 имеет 1 десятичный знак.
Шаг 3: Ставим десятичную дробь в произведении, оставляя после себя одну цифру справа.
SO, $ 36 \ Times 0.5 = 18,0 $
Практические задачи
136632
1366,32
136,623
13363.2
Правильный ответ: 1366,32
11.
Получаем $34158 х 4 = 136632$
Поскольку $341,58$ имеет два десятичных знака, мы помещаем десятичную дробь в произведение, оставляя две цифры справа.
Итак, ответ $1366,32$.
531,2
351,2
53,12
5,312
Правильный ответ: 531,2
Мы игнорируем десятичные дроби и умножаем заданные числа.
Получаем $64 х 83 = 5312$
Поскольку $8,3$ имеет один десятичный знак, мы помещаем десятичную дробь в произведение, оставляя после себя одну цифру справа.
Итак, ответ $531,2$
2055,3
17,553
20,553
25,053
Правильный ответ: 20,553
Мы игнорируем десятичные дроби и умножаем заданные числа.
Получаем $527 х 39 = 20553$
Поскольку 5,27 имеет два десятичных знака, а 3,9 — один десятичный знак, мы помещаем десятичную дробь в произведение, оставляя после себя три цифры справа.
Итак, ответ равен $20,553$.
Часто задаваемые вопросы
Как умножить десятичные дроби на 10 и 100?
При умножении десятичного числа на 10 сдвиньте десятичное число вправо на один разряд. А при умножении десятичной дроби на 100 сдвиньте запятую на два знака.
Например, 4,89$ \х10 = 48,9$ и 3,4$\х100 = 340$
Каково правило умножения десятичных дробей?
Для десятичного умножения нет особого правила. Сначала умножьте данные числа, как если бы вы делали это с целыми числами. Затем подсчитайте сумму знаков после запятой в обоих факторах и примените то же самое к ответу.
