Математика 4 класс, деление многозначных чисел на 10, 100, 1000 с остатком, открытый урок математики в 4 классе

Тема: Деление многозначных чисел на 10, 100, 1000 с остатком.
Цели: — Учить делить с остатком многозначные числа на 10, 100, 1000.
— Отрабатывать вычислительные навыки.
— Закрепить умение решать текстовые задачи.
— Развивать умения анализировать, сравнивать, обобщать.
— Развивать внимание, речь, творческие способности, интерес к математике.

Ход урока.
1. Организационный момент.
— Я хочу заглянуть вам в глаза. Ведь недаром говорят: глаза – зеркало души. И я попробую догадаться, с каким настроением вы пришли на урок.
По-моему у вас хорошее, бодрое, задорное настроение. Я угадала?
— А кто сегодня пришёл не только с веселым, но и с рабочим, энергичным настроением?
— Так давайте сегодня поработаем так, чтобы передать свой заряд бодрости, поднять настроение нашим гостям. Постараемся? Тогда вперед!
2. Актуализация знаний.
— Начнем наш урок с тренировки внимания. Ведь так часто на уроках математики нам не хватает внимания.

— Внимательно посмотрите на фигуры, запомните (4 сек.) и зарисуйте в тетрадь.

Выполняем работу.
— Проверим. У кого выполнена работа верно?
— Молодцы! Я думаю, что теперь вы готовы к вычислительному тренингу.
Вычислительный тренинг (карточки раздаются каждому ученику).
— Возьмите карточку. На решение даются 2 мин.
I вариант.
30: 10= ————— 300: 10= ———— 3000: 10= ————— 30000: 10=
400: 100= ———— 4000: 100= ——— 40000: 100= ———- 400000: 100=
5000: 1000= ——— 50000: 1000= —— 500000: 1000= —— 5000000: 1000=
II вариант.
50: 10= —————- 500: 10= ———— 5000: 10= ————- 50000: 10=
600: 100= ————- 6000: 100= ——— 60000: 100= ——— 600000: 100=
7000: 1000= ——— 70000: 1000= ——- 700000: 1000= —— 7000000: 1000=
— Время вышло.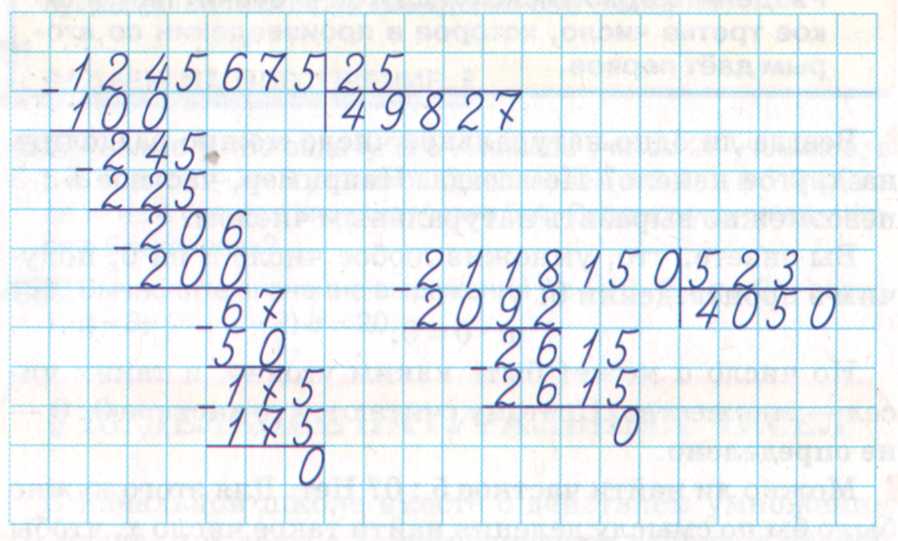

Проверим по вариантам. Назовите только ответы.
— У кого такие ответы?
— Внимательно посмотрите на строчки и столбцы. Что интересного заметили?
(Первая строка — деление на 10; вторая строка — деление на 100; третья строка — деление на 1000; делимое увеличивается в 10 раз, поэтому во всех строчках частное тоже увеличивается в 10 раз; в столбцах — частные однозначные, потом двузначные и т. д.).
— Сделайте вывод. Как разделить на 10, 100, 1000?
(При делении на 10, 100, 1000 и т. д. надо отбросить справа 1 нуль, 2 нуля, 3 нуля и т. д.).

3. Постановка проблемы.
— Внимание на доску.
630: 10= —————- 635: 10=
5300: 100= ————- 5384: 100=
81000: 1000= ———- 81325: 1000=
— Посмотрите на записи. Что между ними общего?
— Найдите значения выражений.
— Почему второй столбик вызвал у вас затруднения? Три знака вопроса.
(Числа не круглые, не делятся без остатка).

— Итак, у нас — проблема, встретились неизвестные случаи деления.
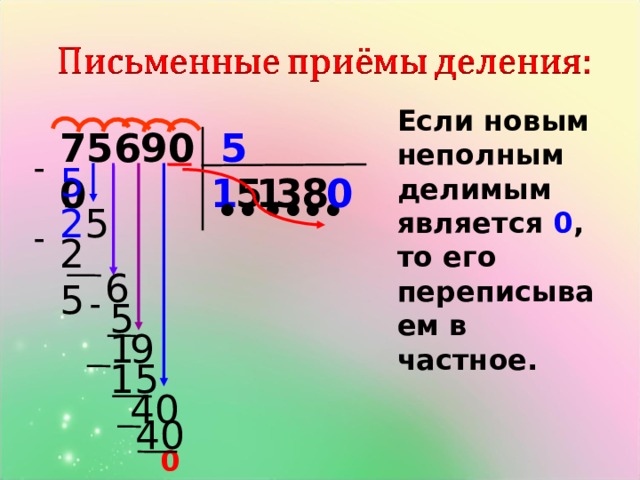
Цель нашего урока — учиться делить многозначные числа на 10, 100, 1000 с остатком.

4. «Открытие» детьми нового знания.
— Каким способом предлагаете делить многозначные числа?
— Выполним деление в столбик с комментирование на доске и в тетради.
635: 10
5384: 100
81325: 100
— Внимательно посмотрите на делимое, делитель, частное и остаток в каждом примере. Может, кто — то из вас заметил что — то интересное?
— Ребята, как считаете, есть ли необходимость выполнять деление
многозначных чисел на 10, 100, 1000 с остатком в столбик?
— Сделайте вывод, как разделить многозначные числа на 10, 100, 1000 с остатком?
Вывод: Чтобы разделить многозначные числа на 10, 100, 1000 с остатком, нужно в делимом отделить справа столько цифр, сколько нулей в делителе. Оставшееся число будет частным, а цифры, которые отделили, будут остатком.

— Ответим на наши знаки вопроса.
— Итак, проблема разрешена.

5. Физ. минутка (под музыку).
«Волшебный сон».

6. Первичное закрепление.
— Итак, какие же случаи деления мы рассмотрели?
— Потренируемся в решении примеров.
Учебник: стр. 47 № 4 (с комментированием по цепочке), стр. 47 № 5 (коллективно под а)
(в парах, взаимопроверка под б).
— Что ты замечаешь? Как перевести единицы в десятки и единицы, в сотни и единицы, в тысячи и единицы?
(Чтобы перевести единицы в десятки и единицы, нужно разделить на 10; в сотни и единицы — разделить на 100; в тысячи и единицы — разделить на 1000).
— Чему же мы научились?
— Сейчас небольшая самостоятельная работа. Каждый из вас сумеет себя проконтролировать.

7. Самостоятельная работа с самопроверкой в классе.

1вариант 2 вариант
5542: 10= ———— 5633: 10=
66381: 100= ————- 89311: 100=
70835: 1000= ————— 12672: 1000=
— Сравните свои ответы по образцу.
Если правильно +, все + — это «5».
— Кто выполнил все задания без ошибок и поставил себе «5»?
— Кто допустил ошибки?
— Две заполненные карточки положите в конец тетради.

8. Повторение.
— Молодцы! Поработали хорошо!
— Сейчас предлагаю решить задачу.
— Решим задачу № 12 стр. 48.
— Прочитаем задачу.
— № 9 стр. 48 — Дополнительное задание (решение уравнений).
— Кто сегодня будет анализировать задачу?
— Запишите решение задачи выражением.
(27 — 5*2 – 4*2): 3=3 (км/ч)…
— Кто уже может записать выражение на доске?
— У кого такое выражение?
— Итак, какова скорость туриста на последнем участке пути? Дайте ответ.

— Молодцы! С задачей справились хорошо.

9. Итог урока.
— Какова значимость нашего урока? Какое значение для вас имеет наш урок?
— Что можете сказать о работе своих одноклассников на уроке?
— Что можете сказать о своем личном вкладе в общую работу?
Отметки.
Д/з. 1) Математическое исследование
2) Творческое задание — составить и решить три примера на деление многозначного числа на 10, 100, 1000.
3) № 8 стр. 48 — найти значение выражения 1 гр. — а, б), 2 гр. — б)

Деление в столбик — Тур-инфо

Примеры деления в столбик по математике

Для деления чисел из двух и более цифр (знаков) применяют Деление в столбик.

По традиции, разбираться как делить столбиком будем на примере.

Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:

Их частное (результат) будем записывать под делителем. У нас это цифра « 8 ».

Начинаем делить « 512 » на « 8 » следующим образом:

Берём « 5 ». Цифра « 5 » меньше « 8 », значит нужно взять еще одну цифру из делимого.

Запомните!

Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.

Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас после « 51 » стоит только одно цифра « 2 ». Значит и добавляем в результат ещё одну точку.

Записываем « 48 » под « 51 ».

Запомните!

При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.

Между « 51 » и « 48 » слева поставим « − » (минус). Вычтем по правилам вычитания в столбик « 48 » и под чертой запишем результат.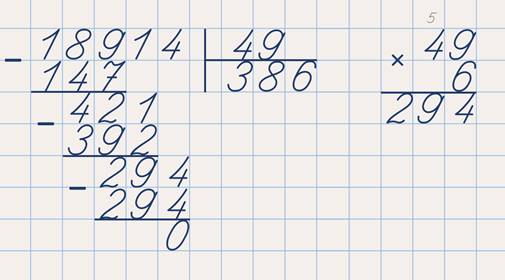

Запомните!

Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.

Спишем из делимого « 512 » цифру « 2 » к « 3 ».

Число « 32 » больше « 8 ». И опять по таблице умножения на « 8 », найдем ближайшее произведение.

Цифра 5 меньше 8 , значит нужно взять еще одну цифру из делимого.

Math-prosto. ru

17.09.2017 21:58:25

2017-09-17 21:58:25

Источники:

Https://math-prosto. ru/ru/pages/action-in-column/division-of-column/

Деление столбиком » /> » /> .keyword { color: red; }

Примеры деления в столбик по математике

Введите числа и калькулятор разделит числа столбиком и отобразит подробное решение.

Деление в столбик введение

Метод Деления столбиком, позволяет упростить деления чисел.

Рассмотрим как делить в столбик на примере нахождения частного двух чисел 6344 ÷ 61.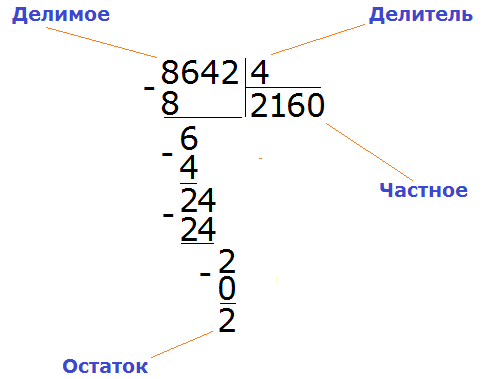

1 Запишем числа которые будем делить следующим образом: . Слева расположено делимое 6344, справа от черты делитель 61, ниже делителя будем записывать частное. 2 Найдем первую цифру частного, для этого сравниваем делитель 61 с числом состоящим из первый цифр делимого, пока не сформируем число большее или равное делителю. На первом шаге: 6 3 Добавляем следующую не использованную цифру равную 4 из делимого к 2, получаем 24 4 Добавляем следующую не использованную цифру равную 4 из делимого к 24, получаем 244 > 61, следовательно мы нашли третью цифру частного; записываем в частное 4=244 ÷ 61. Мы использовали все цифры и получили что число 61 делит на цело число 6344 а частное равно 104.

1 Запишем числа которые будем делить следующим образом: . Слева расположено делимое 6344, справа от черты делитель
61, ниже делителя будем записывать частное. 2 Найдем первую цифру частного, для этого сравниваем делитель 61 с числом состоящим из первый цифр делимого, пока не сформируем число большее или равное делителю. На первом шаге: 6 3 Добавляем следующую не использованную цифру равную 4 из делимого к 2, получаем 24 4 Добавляем следующую не использованную цифру равную 4 из делимого к 24, получаем 244 > 61, следовательно мы нашли третью цифру частного; записываем в частное 4=244 ÷ 61. Мы использовали все цифры и получили что число 61 делит на цело число 6344 а частное равно 104.

Деление в столбик введение

Метод деления столбиком, позволяет упростить деления чисел.

Calcs. su

26.06.2018 8:55:38

2018-06-26 08:55:38

Источники:

Https://calcs. su/%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0/%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5-%D1%81%D1%82%D0%BE%D0%BB%D0%B1%D0%B8%D0%BA%D0%BE%D0%BC. html

Деление в столбик ➗ примеры и правила, как научиться » /> » /> . keyword { color: red; }

Примеры деления в столбик по математике

Деление — это разбиение целого на равные части. Эта математическая операция пригодится не только на уроках математики, но и в повседневной жизни. В этой статье расскажем, как это делать самостоятельно. Для этого разберем примеры для 3 и 4 классов, где покажем деление двузначных и трехзначных чисел.

О чем эта статья:

3 класс, 4 класс

Деление с остатком

Прежде чем перейти к делению в столбик на двузначные и трехзначные числа, давайте вспомним, что значит «разделить с остатком». Если кратко, это такое деление, в результате которого получается остаток меньше делителя:

Например, делим 19 на 5. Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).

Еще пример: делим 29 на 6. Также определяем максимальное число, которое делится на 6 до 29. Подходит 24.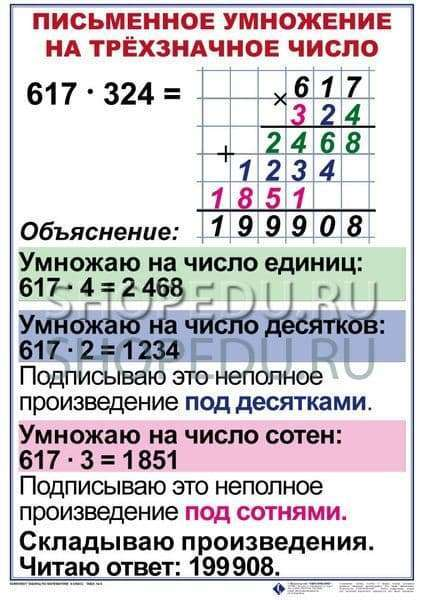 Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).

Как правильно делить в столбик

Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который потом будет срабатывать автоматически.

Деление трехзначного числа на однозначное

Рассмотрим пример деления трехзначного числа на однозначное в столбик — 322 : 7. Для начала определимся с терминами:

322 — делимое или то, что необходимо поделить; 7 — делитель или то, на что нужно поделить: частное — результат действия.

Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.

Шаг 2. Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.

Теперь нужно определить, сколько раз наш делитель 7 содержится в числе 32. Выполним деление с остатком. В результате деления 32 на 7 получили неполное частное 4 и остаток 4.

Результат вычитания должен быть меньше делителя. Если это не так, значит, есть ошибка в расчетах. Нужно увеличить выбранное число и выполнить действие еще раз.

Шаг 3. Запишем следующую цифру делимого справа от остатка 4. Говорят «сносим двойку». Получим следующее делимое — 42.

Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.

Мы закончили решать пример и в результате получили целое число 46.

Деление трехзначного числа на двузначное с примерами

Теперь разберем случаи деления трехзначных чисел на двузначные для 3 класса. Будьте внимательны: мы перешли к самому сложному.

Пример №1.

Разделим трехзначное число 324 на двузначное 81.

Шаг 1. В этом случае 324 будет делимым, его нужно поместить в уголок слева. 81 — это делитель, его вписываем справа.

Шаг 2. Чтобы понять, как делить в столбик на двузначное число, сначала нужно найти то, которое сможем разделить на 81. 3 и 32 не подходят — они меньше делителя. Поэтому придется искать частное к изначальному делимому методом подбора. Умножаем в столбик 81: сначала на 2, потом на 3 и на 4. 81*4=324. Подходит!

Шаг 3. Записываем 4 в столбик под делителем. Это и есть ответ.

Пример №2.

Продолжим разбираться, как делить столбиком многозначные числа, на следующем примере. В этот раз разделим 368 на 92.

Шаг №1. Здесь трехзначное число 368 будет делимым, а двузначное 92 — делителем. Расставляем их в столбике по своим местам.

Шаг №2. Теперь мы должны понять, какое наибольшее число в составе делимого можно нацело поделить на 92. 3 и 36 не подходят, придется снова подбирать частное. Для этого возьмем десятки и поделим их: 36:9=4. Проверим, подходит ли это число — умножим 92 на 4 столбиком.

Шаг №4. Подошло! Вписываем 4 в окошко для частного в столбике.

Как делить однозначные и многозначные числа в столбик с остатком

Как мы писали в начале, это такое же деление, только в результате получается неровное число. Теперь разберем те же примеры, только поделим в столбик.

Пример №1

Разделим двузначное число 19 на однозначное 5. В этом случае 19 будет делимым, а 5 — делителем.

Шаг 1. Рисуем уголок. Делимое 19 ставим слева, а делитель 5 — справа.

Шаг 2. Подбираем наибольшее число до 19, которое нацело делится на 5. Это 15. Проверяем, так ли это: 5*3=15. Теперь 3 можно записать в столбик под делителем, а 15 — под делимым.

Шаг 3. Вычитаем число, которое получили делением нацело, из делимого. 19-15=4. Это остаток.

Пример №2.

Разделим двузначное число 29 на однозначное 6. Теперь 29 будет делимым, а 6 — делителем.

Шаг 1. Располагаем числа в столбике. Как обычно, 29 ставим на место делимого справа, а делитель 6 — слева от уголка.

Шаг 2. Теперь найдем число до 29, которое можно целиком разделить на 6. Проверим, подходит ли 24: 6*4=24. Записываем 24 под делимым 29, а 4 — в свободном отсеке снизу уголка. Это будет целая часть в результате деления.

Шаг 3. Вычитаем из делимого 29 число, которое мы получили в шаге 2. 29-24=5. Это остаток от деления.

Примеры на деление в столбик для 3 класса

Давайте закрепим знания на практике. Ниже мы оставили примеры деления двузначных и трехзначных чисел для 3 класса. Решите их столбиком, а после проверьте полученные цифры — чур, не подглядывать! Обратите внимание: в сложном уровне есть деление многозначных чисел на двузначные, которые мы не разбирали в статье. Это задание со звездочкой.

322 делимое или то, что необходимо поделить;.

Skysmart. ru

20.02.2018 14:55:46

2018-02-20 14:55:46

Источники:

Https://skysmart. ru/articles/mathematic/delenie-v-stolbik

Как правильно делить числа в столбик? Как научить ребенка делить столбиком двузначные и трехзначные числа за 3 и 4 класс, как ему объяснить, как делить столбиком?

Алгоритм деления чисел в столбик, обучение ребёнка. Особенности деления многозначных чисел и многочленов.

Содержание статьи

• Как правильно делить числа в столбик: алгоритм деления
• Как объяснить ребенку деление и научить делить столбиком?
• Как письменно делить в столбик двузначное число на однозначное и двузначное: примеры, объяснение
• Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение
• Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение
• Как делить в столбик с остатком?
• Как делить столбиком десятичные дроби с запятой?
• Как делить столбиком меньшее число на большее?
• Как делить столбиком числа с нулями?
• Видео: как правильно делить числа в столбик?

Школа даёт ребёнку не только дисциплину, развитие талантов и навыков общения, но и знания по фундаментальным наукам.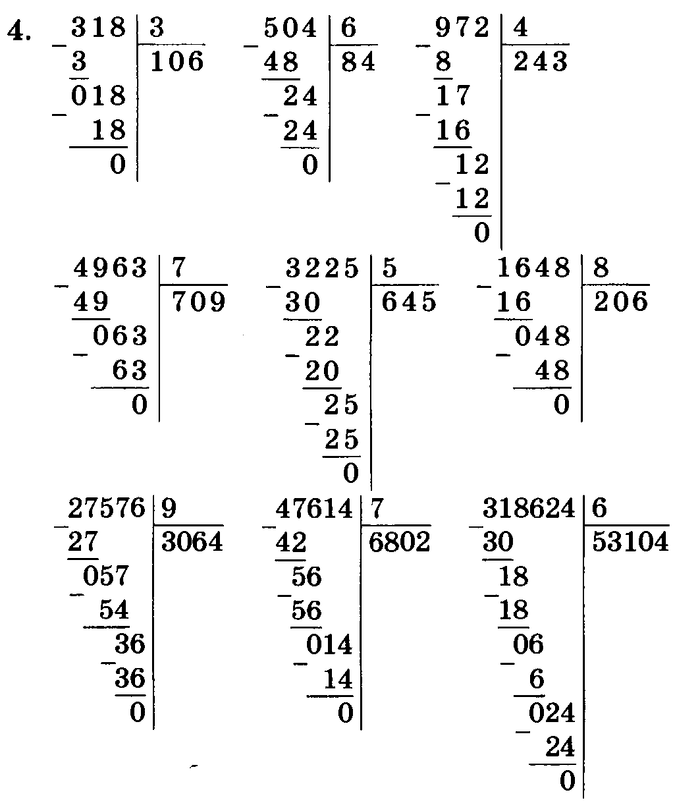 Одна из них — математика.

Хотя программа и нагрузка на учеников часто меняются, но деление в столбик чисел с разным количеством разрядов остаётся неприступной с первого захода вершиной для многих из них. Потому без тренировок дома с родителями часто не обойтись.

Дабы не упустить время и предотвратить образование кома непонятного у ребёнка в математике, освежите в памяти свои знания по делению чисел столбиком. Статья вам в этом поможет.

Как правильно делить числа в столбик: алгоритм деления

алгоритм деления чисел столбиком

Для деления чисел столбиком следуйте по таким шагам:

• правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
• разлинейте место между делимым и делителем.
  Вам поможет схема ниже.

схема и назнвания составных элементв действия деления чисел столбиком

• планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
• первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
• перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
• завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
• допишите следующую цифру делимого к остатку и продолжайте решение,
• последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя. Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.

Как объяснить ребенку деление и научить делить столбиком?

дети-школьники тренируются делить числа столбиком

Во-первых, учтите ряд вводных факторов:

• ребёнок знает таблицу умножения
• хорошо разбирается и умеет применять на практике действия вычитания и сложения
• понимает разницу между целым и его составными элементами

Дальше акценты в ваших действиях выглядят так:

• поиграйте с таблицей умножения. Положите её перед ребёнком и на примерах покажите удобство использования при делении,
• объясните расположение делимого, делителя, частного, остатка. Предложите ребёнку повторить эти категории,
• превратите процесс в игру, придумайте историю про цифры и действие деления,
• подготовьте наглядные предметы для обучения. Подойдут счётные палочки, яблоки, монеты, игрушки, очищенные сведение или апельсин. Предлагайте их распределить между разным количеством людей, например, между мамой, папой и ребенком,
• первым показывайте ребёнку действия с чётными числами, чтобы он видел результат деления, кратный двум.

Сам процесс освоения деления столбиком:

• запишите цифры, разделив их границами. Повторите с ребёнком расположение категорий деления,
• предложите ему проанализировать цифры делимого на предмет «больше-меньше» делителя. Помогайте вопросом — сколько раз одно число помещается во втором. В результате ребёнку следует выделить то число/числа, которые он будет применять для совершения первого действия,
• подскажите алгоритм определения разрядности частного. Её удобно изобразить точками, которые потом превратятся в цифры,
• помогите правильно определить и записать первое число в частное, совершите его умножение на делитель, запишите результат под делимым, выполните вычитание. Объясните, что результат вычитания всегда должен быть меньше делителя. В противном случае действие совершилось с ошибкой и его следует переделать,
• следующий шаг — анализ ситуации с добавлением второго числа от делимого и определения количества раз повторения делителя в нём,
• снова помогите с записью действия,
• продолжайте до момента, когда результат от разницы составит ноль. Это актуально только для деления чисел без остатка,
• закрепите знания у ребёнка еще несколькими примерами. Следите, чтобы он не устал, иначе дайте перерыв.

Как письменно делить в столбик двузначное число на однозначное и двузначное: примеры, объяснение

обучение ребёнка делению методом солнышка

Приступим к пошаговому разбору примеров на деление в столбик.

Осуществите действие над цифрами 25 и 2:

• запишите их рядом и разделите линиями границы,
• определите нужное количество цифр делимого для первого действия,
• запишите значение под делителем и результат умножения под делимым,
• выполните вычитание,
• допишите вторую цифру делимого и повторите действия на умножение и вычитание.

Частично выполненное задание на деление столбиком двузначного числа на однозначное смотрите ниже:

незаконченное решение примера на деление столбиком двузначного числа на однозначное

Учтите, что деление столбиком двухзначного числа на однозначное возможно и в одно действие.

Второй пример. Разделите 87 на 26 в столбик.

Алгоритм аналогичен рассмотренному выше с той лишь разницей, что учитывать нужно сразу 2 числа делителя при определении количества раз повторения в делимом.

Чтобы облегчить задачу ребёнку, который только осваивается азы деления, предложите ему ориентироваться на первые цифры у делимого и делителя.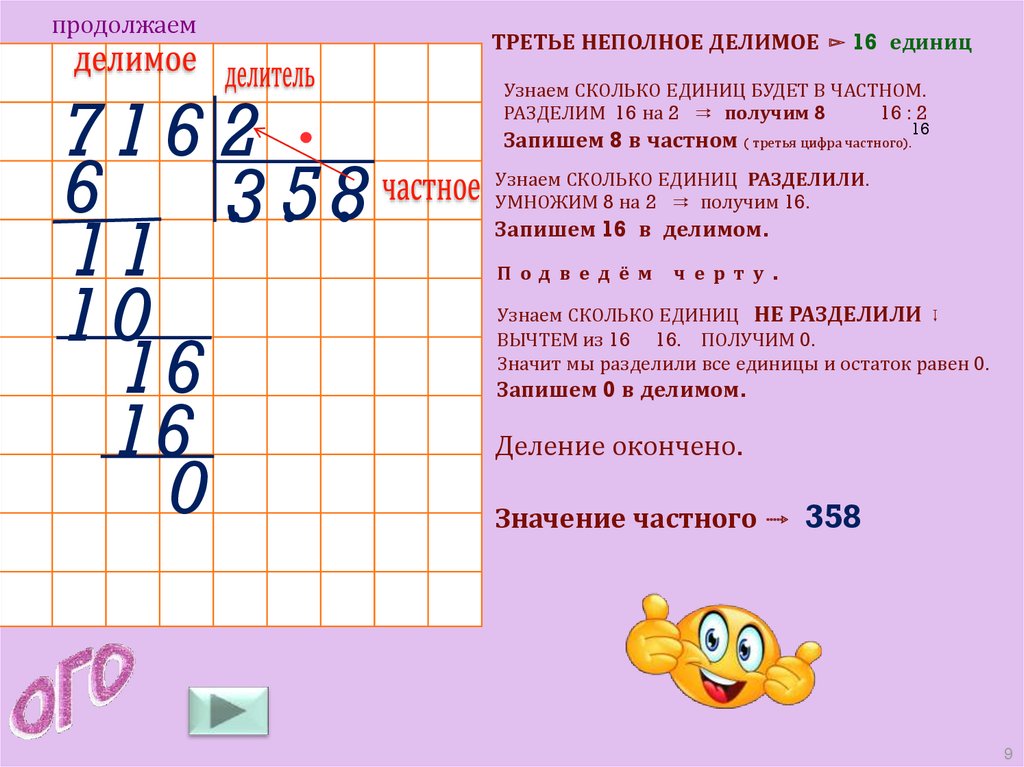 Например, 8:2=4. Пусть ребёнок подставит это число под черту и выполнит умножение. Ему нужно увидеть своими глазами, что 4 много и нужно попробовать с тройкой.

Ниже пример деления столбиком двузначного числа на двузначное с остатком.

пример деления столбиком двузначного числа на двузначное с остатком

Третий пример. Как разделить число в столбик с нулем в ответе.

Вначале делим 15 на 15, в остатке 0, в ответ 1. Сносим 6, а оно на 15 не делится, значит ставим в ответе 0. Далее, 15 умноженное на 0, будет ноль и его отнимаем от 6. Сносим ноль, что в конце числа, получаем 60, которое делится на 15 и в ответ ставим 4.

Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение

рисунок из презентации на тему деления трёхзначного числа столбиком

Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.

Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.

Схематически он выглядит так:

пример деления трехзначного числа на однозначное столбиком

В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.

Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.

Схема деления трехзначного на двузначное числа такая:

примеры деления столбиком трехзначных чисел на двузначные

Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.

Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.

Схема деления трёхзначного на трёхзначное числа.

пример деления в столбик трёхзначного числа на трёхзначное с остатком

Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение

на доске решены примеры на деление столбиком трёх- и более значных чисел

В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:

• определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
• появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
• проверку полученного результата посредством выполнения действия умножения. Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.

Ниже пример решения.

алгоритм деления столбиком четырёхзначного числа

пример деления столбиком четырёхзначного числа на двузначное

Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.

Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:

• количество знаков у частного, то есть результата
• цифры у делимого для первого действия
• правильность переноса остальных чисел

Примеры подробного решения ниже.

примеры деления столбиком многочленов

При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:

• у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
• для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
• совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов. Тогда их сократите и получится результат без остатка.

Ниже ряд подробных примеров с решениями.

примеры деления многочленов в столбик

Как делить в столбик с остатком?

слайд из презентации о делении чисел с остатком

Алгоритм деления в столбик с остатком аналогичен классическому. Разница лишь в появлении остатка, который меньше делителя. А значит первый остаётся без изменения.

Запишите его в ответе либо:

• как дробь, где в числителе остаток, а в знаменателе — делитель
• словами, например, 73 целых и 6 в остатке

Как делить столбиком десятичные дроби с запятой?

рисунок с алгоритмом действий при делении десятичной дроби столбиком

Существует несколько особенностей при подобном делении. Если вы совершаете действие с:

• десятичной дробью-делимым и целым числом-делителем, то действуйте по обычному алгоритму до тех пора, пока закончатся цифры у делимого перед запятой. Затем поставьте её в частном и продолжайте переносить цифры до окончания деления,
• числом, которое делится на 10, 100, 100 и т.д., то перенесите запятую в делимом влево на количество цифр, равное количеству нулей делителя. Например, 749,5:100=7,495,
• десятичными дробями одновременно и в делителе, и в делимом, то сначала избавьтесь от запятой у второго элемента. Для этого перенесите её вправо в обоих дробных числах на то количество знаков, которые отделены у делителя. Например, 416,788:5,3 преобразуйте в 4167,88:53 и совершите обычное деление в столбик.

Как делить столбиком меньшее число на большее?

девочка-школьница устала от решения примеров на деление столбиком

При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.

Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:

• первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
• поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
• когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка. В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.

Ниже пример.

примеры деления столбиком меньшего числа на большее

Как делить столбиком числа с нулями?

улыбчивая девочка у школьной доски

Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.

Из нюансов отметим:

• при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
• если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.

Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.

Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.

Практикуйте полученные знания и помогайте своему чаду осваивать математику.

Видео: как правильно делить числа в столбик?

NumberNut.com: Раздел: 2-значные числа

Не все подразделение сделано с числами меньше десяти (10). Когда вы узнаете больше о делении двузначных чисел, вы увидите шаблона, похожих на шаблоны, которые вы видели при умножении. Взгляните на эти примеры, прежде чем мы двинемся дальше. ..

25 = 5 х 5
25 ÷ 5 = 5

28 = 4 x 7
28 ÷ 7 = 4
28 ÷ 4 = 7

Мы думаем, что узоры очень интересные. Дивизия похожа на обратное умножения. В этом есть смысл, поскольку мы продолжаем говорить вам, что умножение — это объединение групп, а деление их разделяет. Если вы помните два множителя , которые использовались для создания исходного числа ( делимое ), проверка вашей работы должна быть легкой.

Пример:
Вы будете делить число двадцать четыре (24) на более мелкие части. Каковы возможные факторы?
Вы знаете, что:
3 x 8 = 24
4 x 6 = 24
6 x 4 = 24
8 x 3 = 24
Если вы столкнулись с проблемой 24 ÷ 4 = ? вы узнаете, что ответ равен 6, потому что 6 х 4 = 24.

Иногда ответы будут простыми, и вы получите единственное число в вашем частном . Эти простые задачи называются короткое деление .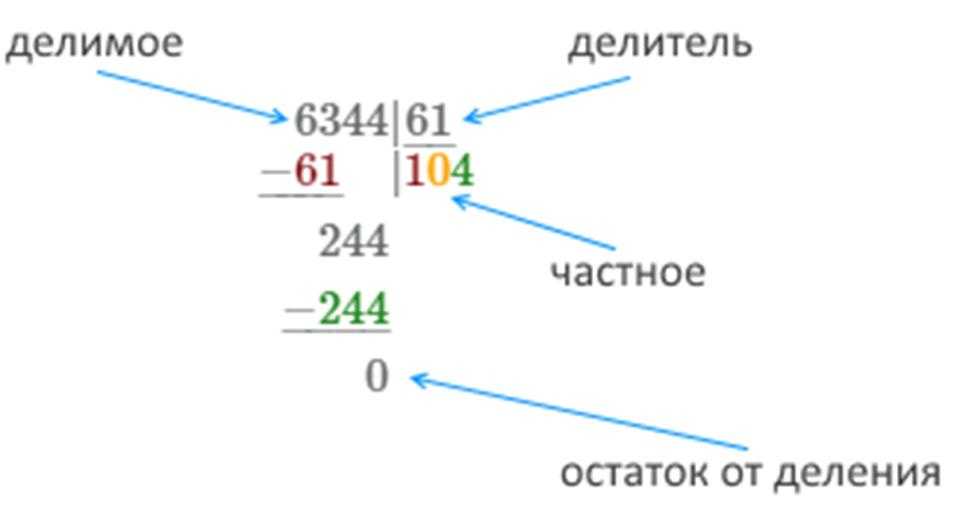 Число, которое вы делите, меньше чем в десять раз больше значения делителя . Примеры короткого деления включают…

28 ÷ 4 = 7
64 ÷ 8 = 8
54 ÷ 9 = 6
99 ÷ 11 = 9
— или —

9 11 ) 99 — 99 0

Это так же просто, как пирог. Однако иногда вы начнете с дивиденда, который более чем в десять раз превышает значение делителя. Затем пришло время для длинного деления . Вот несколько примеров, прежде чем мы покажем вам, как решать проблемы.

24 ÷ 2 = 12 (Посмотрите, как узнать, что частное больше 9?)
44 ÷ 4 = 11 (Четыре входит в число сорок четыре одиннадцать раз.)
63 ÷ 3 = 21 (Вы можете получить 21 группу, если разделите 63 на 3.)
80 ÷ 5 = 16 (В числе 80 16 групп по 5. В этой задаче тоже есть подлый остаток.)
— или —

16 5 ) 80 — 5     30 — 30   0

Родственные виды деятельности

Тест на одно- и двузначное деление (без остатка) — Игровая активность

Тест на одно- и двузначное деление (без остатка)  – Игровая активность

Ключ к решению этих проблем — увидеть, что число в столбце десятков делимого уже делится на делитель. В задаче 28 ÷ 2 = 12 «2» в числе 28 делится на два (один раз). Вы должны записать единицу (1) в качестве первого числа в вашем частном, а затем перейти к столбцу единиц и увидеть, что «8» делится на два (четыре раза). Затем вы пишете четыре (4) в следующем месте вашего ответа. Когда вы столкнетесь с этими типами задач на деление, разбейте их на кусочки размером с укус.

(1) У меня двузначное число для делителя?
• Если да, задайте вопрос 2.
• Если нет, выполните деление.

(2) Первое число делимого больше моего делителя?
• Если да, сначала выполните деление в столбце десятков, а затем перейдите к столбцу единиц.
• Если нет, вы можете разделить все делимое на делитель, и ваш ответ будет меньше десяти.

Да, при делении двузначных чисел получается остатка . Помните, что остаток будет никогда не будет больше вашего делителя. Неважно, будет ли ваш ответ десять или больше, остаток всегда будет меньше делителя.

Выполняя деление в длинное число, вы обнаружите остатки в середине задач на деление. Это не всегда будет красиво и ровно, как если бы вы разделили шестьдесят (62) на два (2). Это даже частное тридцати одного (31) просто повезло. Подумайте о числе пятьдесят четыре (54). Когда вы делите на два, 5 в столбце десятков делится на 2, но есть остаток от 1. В длинном делении вы держите этот остаток для деления в столбце единиц. Итак, у вас на самом деле есть две небольшие проблемы с делением.

Пример:
54 ÷ 2 = ?
Шаг 1: 5 ÷ 2 = 2 с остатком 1
Шаг 2: Объедините 1 со значением 4 из столбца единиц, чтобы получить 14.
Шаг 3: 14 ÷ 2 = 7
Шаг 4: соедините два значения вместе чтобы получить ответ 27.

Сейчас мы разобьем его на все этапы. Мы пропустили вычитание, чтобы упростить задачу. На самом деле вы будете делать эти шаги. Начните с первого числа делимого и подумайте, сколько раз его можно разделить на 2.

Шаг 1: 5 можно разделить только на 2 два (2) раза. 2 x 2 = 4
Шаг 2: 5 — 4 = 1. 1 — это остаток от деления в столбце десятков.
Шаг 3: Опустите 4 из столбца единиц в делимом и поместите его справа от остатка (1), так как столбец единиц находится справа от столбца десятков. Получается 14.
Шаг 4: 14 можно разделить на 2 семь (7) раз. 2 x 7 = 14
Шаг 5: 14 — 14 = 0. Поскольку разница равна 0, проблема решена.
— или —

27 2 ) 54 — 4     14 — 14   0

Возможно, вы начинаете замечать еще одно различие между умножением и делением. В своих задачах на умножение вы работали справа налево. Вы начали умножать единицы, затем десятки и двигались вверх по числам. В отделе мы работали слева направо. Мы начинаем наше деление с самых высоких значений дивиденда и двигаемся вниз. Это еще одна вещь, которую вы можете заметить, когда решаете все эти проблемы.

Чтобы научиться решать задачи на деление, вам нужна только практика, практика и еще раз практика. Это всегда один и тот же процесс.
(1) Сколько раз можно разделить одно число?
(2) Умножать и вычитать.
(3) Продолжайте перечислять все числа делимого.

Сопутствующая деятельность

Тест на одно- и двузначное деление (с остатками) — Игровая активность

Тест на одно- и двузначное деление (без остатка)  – Игровая активность

► СЛЕДУЮЩАЯ СТРАНИЦА ПО АРИФМЕТИКЕ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ

► Или выполните поиск на сайтах…

2.3: Деление целых чисел

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

48838

• Денни Бурзински и Уэйд Эллис-младший
• Колледж Южной Невады через OpenStax0X через OpenStax0X

  Цели обучения

  • уметь делить целое число на однозначный или многозначный делитель
  • уметь интерпретировать оператор калькулятора о том, что деление дает остаток

  Деление с однозначным делителем

  Наш опыт умножения целых чисел позволяет нам выполнять такие деления, как \(75 \div 5\). Мы выполняем деление, выполняя соответствующее умножение, \(5 \times Q = 75\). Каждое деление мы рассмотрели в [ссылка] имел однозначное частное. Теперь рассмотрим деления, в которых частное может состоять из двух и более цифр. Например, \(75 \дел 5\).

  Рассмотрим деление \(75 \div 5\). Нас просят определить, сколько пятерок содержится в числе 75. Мы подойдем к задаче следующим образом.

  1. Сделайте обоснованное предположение, основанное на опыте умножения.
  2. Найдите, насколько близка оценка, умножив оценку на 5.
  3. Если произведение, полученное на шаге 2, меньше 75, узнайте, насколько меньше, вычитая его из 75.
  4. Если произведение, полученное на шаге 2, больше 75, уменьшайте оценку до тех пор, пока произведение не станет меньше 75. Уменьшение оценки имеет смысл, поскольку мы не хотим превышать 75.

  Из этого обсуждения мы можем предположить, что процесс деления состоит из

  Четыре шага в делении

  1. обоснованного предположения
  2. умножение
  3. вычитание
  4. сбивание следующей цифры (при необходимости)

  Обоснованное предположение можно сделать, определив, сколько раз делитель содержится в делимом, используя только одну или две цифры делимого.

  Набор образцов A

  Найдите \(75 \div 5\).

  Решение

  \(5\overline{)75}\) Перепишите задачу, используя разделительную скобку.

  \(\begin{массив} {r} {10} \\ {5\overline{)75}} \end{массив}\)

  Сделайте обоснованное предположение, заметив, что одна 5 содержится в 75 не более 10 раз.
  Поскольку 7 — это цифра десятков, мы подсчитали, что 5 входит в число 75 не более 10 раз.

  \(\begin{array} {r} {10} \\ {5\overline{)75}} \\ {\underline{-50}} \\ {25} \end{array}\)

  Теперь определите, насколько близка оценка.
  10 пятерок — это \(10 \умножить на 5 = 50\). Вычтите 50 из 75.
  Оцените количество пятерок в числе 25.
  В числе 25 ровно 5 пятерок.

  Проверить:

  Таким образом, \(75 \div 5 = 15\).

  Обозначение в этом подразделе может быть сокращено письменно.

  \(\begin{array} {r} {15} \\ {5\overline{)75}} \\ {-5 \downarrow} \\ {\overline{\ \ 25}} \\ {-25 } \\ {\overline{\ \ \ \ 0}} \end{массив}\)

  \(\begin{cases} \text{Divide:} & \text{5 переходит в 7 не более 1 раза. } \\ \text{Умножение:} & 1 \times 5 = 5. \text{Запишите 5 под 7.} \\ \text{Вычтите:} & 7 — 5 = 2. \text{Запишите 5.} \ end{cases}\) \(\begin{cases} {\text{Divide:}} & {\text{5 входит в число 25 ровно 5 раз}} \\ {\text{Multiply:}} & {5 \times 5 = 25. \text{Напишите 25 под 25.}} \\ {\text{Вычитание:}} & {25 — 25 = 0} \end{case}\)

  Образец набора A

  Найдите \(4,944 \div 8\).

  Решение

  \(8\overline{)4944}\)

  Перепишите задачу, используя разделительную скобку.

  \(\begin{array} {r} {600} \\ {8\overline{)4944}} \\ {\underline{-4800}} \\ {144} \end{array}\)

  8 входит в число 49 не более 6 раз, а 9 находится в столбце сотен. Предположим, что 600.
  Тогда \(8 \х600 = 4800\).

  \(\begin{массив} {r} {10} \\ {600} \\ {8\overline{)4944}} \\ {\underline{-4800}} \\ {144} \\ {\ подчеркивание{-\ \ 80}} \\ {64} \end{массив}\)

  8 входит в число 14 не более 1 раза, а 4 находится в столбце десятков. Мы угадаем 10.

  \(\begin{array} {r} {8} \\ {10} \\ {600} \\ {8\overline{)4944}} \\ {\underline{-4800 }} \\ {144} \\ {\underline{-\ \ 80}} \\ {64} \\ {\underline{-64}} \\ {0} \end{массив}\)

  8 идет в 64 ровно 8 раз.
  600 восьмерок + 10 восьмерок + 8 восьмерок = 618 восьмерок.

  Проверить:

  Таким образом, \(4944 \div 8 = 618\).

  Как и в первой задаче, обозначения в этом делении можно сократить, убрав знаки вычитания и нули в каждом обоснованном предположении.

  \(\begin{cases} \text{Разделить:} & \text{8 входит в число 49 не более 6 раз.} \\ \text{Умножить:} & 6 \times 8 = 48. \text{ Запишите 48 под 49.} \\ \text{Вычтите:} & 49 — 48 = 1. \text{Вычтите 4.} \end{cases}\) \(\begin{cases} \text{Divide:} & \text{8 входит в 14 не более 1 раза.} \\ \text{Умножение:} & 1 \times 8 = 8. \text{Запишите 8 ниже 14.} \\ \text{Вычтите:} & 14 — 8 = 6. \text{Запишите 4.} \end{cases}\)

  \(\begin{cases} \text{Разделить:} & \text{8 входит в число 64 ровно 8 раз.} \\ \text{Умножить:} & 8 \times 8 = 64. \text{Запишите 64 под 64.} \\ \text{Вычесть:} & 64 — 64 = 0. \end{cases}\)

  Примечание

  Не все деления заканчиваются нулем. Мы рассмотрим такие деления в следующем подразделе.

  Тренировочный набор A

  Выполните следующие деления.

  \(126 \дел 7\)

  Ответить

  18

  Тренировочный набор A

  \(324 \дел 4\)

  Ответить

  81

  Тренировочный набор A

  \(2559 \дел 3\)

  Ответить

  853

  Тренировочный набор A

  \(5,645 \дел 5\)

  Ответить

  1 129

  Тренировочный набор A

  \(757 125 \дел 9\)

  Ответить

  84 125

  Деление с многозначным делителем

  Процесс деления также работает, когда делитель состоит из двух или более цифр. Теперь мы делаем обоснованные предположения, используя первую цифру делителя и одну или две цифры делимого.

  Набор образцов B

  Найти \(2,232 \div 36\).

  Решение

  \(36 \overline{)2232}\)

  Используйте первую цифру делителя и первые две цифры делимого, чтобы сделать обоснованное предположение.

  3 соответствует 22 не более 7 раз.

  Попробуйте 7: \(7 \times 36 = 252\), что больше 223. Уменьшите оценку.

  Попробуйте 6: \(6 \times 36 = 216\), что меньше 223.

  \(\begin{array} {ll} {\text{Multiply: }} & {6 \times 36 = 216. \text{Напишите 216 под 223.}} \\ {\text{Вычтите: }} & {223 — 216 = 7. \text{Опустите 2.}} \end{массив}\)

  Разделите 3 на 7, чтобы оценить, сколько раз 36 встречается в 72. 3 входит в 7 не более 2 раз.

  Попробуйте 2: \(2 \умножить на 36 = 72\).

  Проверить :

  Таким образом \(2,232 \дел 36 = 62\).

  Набор образцов B

  Найдите \(2 417 228 \div 802\).

  Решение

  \(802 \overline{)2417228}\)

  Первое предположение: \(24 \div 8 = 3\). Затем \(3 \times 802 = 2406\), что меньше 2417. Используйте 3 в качестве предположения. Так как \(3 х 802 = 2406\), а число 2406 состоит из четырех цифр, поместите 3 над четвертой цифрой делимого.

  Вычесть: 2417 — 2406 = 11.
  Опустить 2.

  Делитель 802 входит в число 112 не более 0 раз. Используйте 0.

  \(\begin{array} {ll} {\text{Multiply:}} & {0 \times 802 = 0.} \\ {\text{Вычитание:}} & {112 — 0 = 112.} \\ {\text{Выведите 2.}} & {} \end{массив}\)

  8 входит в 11 не более 1 раза, и \(1 \times 802 = 802\) , что меньше 1122. Попробуйте 1.

  Вычтите 1122 — 802 = 320
  Снизьте 8.

  8 входит в число 32 не более 4 раз.

  \(4 х 802 = 3208 ).

  Использовать 4.

  Проверить:

  Таким образом, \(2,417,228 \div 802 = 3,014\).

  Тренировочный набор B

  Выполните следующие деления.

  \(1,376 \дел 32\)

  Ответить

  43

  Практический набор B

  \(6 160 \дел 55\)

  Ответить

  112

  Практический набор B

  \(18 605 \дел 61\)

  Ответить

  305

  Практический набор B

  \(144 768 \дел 48\)

  Ответить

  3 016

  Деление с остатком

  Нам может быть интересно, сколько раз 4 содержится в 10. Повторное вычитание дает

  \(\begin{array} {r} {10} \\ {\underline{-\ \ 4}} \\ {6} \\ {\underline{-4}} \\ {2} \end{массив}\)

  Поскольку остаток меньше 4, останавливаем вычитание. Таким образом, 4 превращается в 10 два раза, и остается 2. Мы можем записать это как деление следующим образом.

  \(\begin{array} {r} {2} \\ {4 \overline{)10}} \\ {\underline{-\ \ 8}} \\ {2} \end{array}\)

  \(\begin{array} {ll} {\text{Divide:}} & {\text{4 переходит в 10 не более 2 раз.}} \\ {\text{Multiply:}} & {2 \ умножить на 4 = 8. \text{Запишите 8 под 0.}} \\ {\text{Вычитание:}} & {10 — 8 = 2.} \end{массив}\)

  \(\begin{array} {r} {\text{2R2}} \\ {4\overline{)\ \\ 10}} \\ {\underline{-8}} \\ {2} \end{ array}\) или \(10 \div 4 = \begin{matrix} \underbrace{\text{2R2}} \\ {\text{2 с остатком 2}} \end{matrix}\)

  Пример набора C

  Найти \(85 \дел 3\).

  Решение

  \(\begin{cases} \text{Divide:} & \text{3 входит в 8 не более 2 раз. } \\ \text{Multiply:} & 2 \times 3 = 6. \text{ Напишите 6 под 8.} \\ \text{Вычтите:} & 8 — 6 = 2. \text{ Уберите 5.} \end{cases}\) \(\begin{cases} \ text{Разделить:} & \text{3 входит в число 25 не более 8 раз.} \\ \text{Умножить:} & 3 \times 8 = 24. \text{ Записать 24 ниже 25.} \\ \text{Вычесть :} & 25 — 24 = 1 \end{case}\)

  Набор образцов C

  Найдите \(726 \div 23\).

  Решение

  Проверить: Умножить 31 на 23, затем добавить 13.

  Таким образом, \(726 \div 23 = 31R13\).

  Тренировочный набор C

  Выполните следующие деления.

  \(75 \дел 4\)

  Ответить

  18 Р3

  Тренировочный набор C

  \(346 \дел 8\)

  Ответ

  43 Р2

  Тренировочный набор C

  \(489 \дел 21\)

  Ответить

  23 Р6

  Тренировочный набор C

  \(5,016 \дел 82\)

  Ответить

  61 Р14

  Тренировочный набор C

  \(41 196 \дел 67\)

  Ответить

  614 Р58

  Калькуляторы

  Калькулятор может быть полезен для нахождения частных с однозначными и многозначными делителями. Однако если в результате деления должен получиться остаток, калькулятор не сможет предоставить нам конкретное значение остатка. Кроме того, некоторые калькуляторы (большинство ненаучных) не могут выполнять деление, в котором одно из чисел имеет более восьми цифр.

  Набор образцов D

  Используйте калькулятор для выполнения каждого деления.

  \(328 \дел 8\).

  Раствор

  Тип	328
  Пресс	\(\дел\)
  Тип	8
  Пресс	=

  Теперь на дисплее отображается 41.

  Набор образцов D

  \(53 136 \дел 82\).

  Решение

  Тип	53136
  Пресс	\(\дел\)
  Тип	82
  Пресс	=

  Теперь на дисплее отображается 648.

  Набор проб D

  \(730,019,001 \div 326\)

  Решение

  Сначала попробуем ввести 0, 01 7,001, но обнаружится, что мы можем ввести только 73001900. Если наш калькулятор имеет только восьмиразрядный дисплей (как в большинстве ненаучных калькуляторов), мы не сможем использовать калькулятор для выполнения этого деления.

  Набор образцов D

  \(3727 \div 49\).

  Раствор

  Тип	3727
  Пресс	\(\дел\)
  Тип	49
  Пресс	=

  Теперь на дисплее отображается 76.061224.

  Это число является примером десятичного числа (см. [ссылка] ). Когда десятичное число приводит к делению калькулятора, мы можем заключить, что деление дает остаток.

  Тренировочный набор D

  Используйте калькулятор для выполнения каждого деления.

  \(3330 \дел 74\)

  Ответ

  45

  Тренировочный набор D

  \(63 365 \дел 115\)

  Ответить

  551

  Тренировочный набор D

  \(21 996 385 287 \дел 53\)

  Ответить

  Поскольку делимое состоит из более чем восьми цифр, это деление невозможно выполнить на большинстве ненаучных калькуляторов. На других ответ 415 026 137,4

  Тренировочный набор D

  \(4,558 \дел 67\)

  Ответить

  В результате этого деления получается 68,02985075, десятичное число, и поэтому в настоящее время мы не можем найти значение остатка. Позже мы обсудим десятичные числа.

  Упражнения

  В следующих задачах выполните деление.

  Первые 38 задач можно проверить с помощью калькулятора, умножив делитель и частное, а затем прибавив остаток.

  Упражнение \(\PageIndex{1}\)

  \(52 \дел 4\)

  Ответить

  13

  Упражнение \(\PageIndex{2}\)

  \(776 \дел 8\)

  Упражнение \(\PageIndex{3}\)

  \(603 \дел 9\)

  Ответить

  67

  Упражнение \(\PageIndex{4}\)

  \(240 \дел 8\)

  Упражнение \(\PageIndex{5}\)

  \(208 \дел 4\)

  Ответить

  52

  Упражнение \(\PageIndex{6}\)

  \(576 \дел 6\)

  Упражнение \(\PageIndex{7}\)

  \(21 \дел 7\)

  Ответить

  3

  Упражнение \(\PageIndex{8}\)

  \(0 \дел 0\)

  Упражнение \(\PageIndex{9}\)

  \(140 \дел 2\)

  Ответить

  70

  Упражнение \(\PageIndex{10}\)

  \(528 \дел 8\)

  Упражнение \(\PageIndex{11}\)

  \(244 \дел 4\)

  Ответить

  61

  Упражнение \(\PageIndex{12}\)

  \(0 \дел 7\)

  Упражнение \(\PageIndex{13}\)

  \(177 \дел 3\)

  Ответ

  59

  Упражнение \(\PageIndex{14}\)

  \(96 \дел 8\)

  Упражнение \(\PageIndex{15}\)

  \(67 \дел 1\)

  Ответить

  67

  Упражнение \(\PageIndex{16}\)

  \(896 \дел 56\)

  Упражнение \(\PageIndex{17}\)

  \(1,044 \дел 12\)

  Ответить

  87

  Упражнение \(\PageIndex{18}\)

  \(988 \дел 19\)

  Упражнение \(\PageIndex{19}\)

  \(5,238 \дел 97\)

  Ответить

  54

  Упражнение \(\PageIndex{20}\)

  \(2530 \дел 55\)

  Упражнение \(\PageIndex{21}\)

  \(4,264 \дел 82\)

  Ответить

  52

  Упражнение \(\PageIndex{22}\)

  \(637 \дел 13\)

  Упражнение \(\PageIndex{23}\)

  \(3420 \дел 90\)

  Ответить

  38

  Упражнение \(\PageIndex{24}\)

  \(5,655 \дел 87\)

  Упражнение \(\PageIndex{25}\)

  \(2,115 \дел 47\)

  Ответить

  45

  Упражнение \(\PageIndex{26}\) ​​

  \(9,328 \дел 22\)

  Упражнение \(\PageIndex{27}\)

  \(55 167 \дел 71\)

  Ответить

  777

  Упражнение \(\PageIndex{28}\)

  \(68 356 \дел 92\)

  Упражнение \(\PageIndex{29}\)

  \(27 702 \дел 81\)

  Ответить

  342

  Упражнение \(\PageIndex{30}\)

  \(6,510 \дел 31\)

  Упражнение \(\PageIndex{31}\)

  \(60 536 \дел 94\)

  Ответить

  644

  Упражнение \(\PageIndex{32}\)

  \(31 844 \дел 38\)

  Упражнение \(\PageIndex{33}\)

  \(23 985 \дел 45\)

  Ответить

  533

  Упражнение \(\PageIndex{34}\)

  \(60,606 \дел 74\)

  Упражнение \(\PageIndex{35}\)

  \(2 975 400 \дел 285\)

  Ответить

  10 440

  Упражнение \(\PageIndex{36}\)

  \(1 389 660 \дел 795\)

  Упражнение \(\PageIndex{37}\)

  \(7 162 060 \дел 879\)

  Ответить

  8 147 остаток 847

  Упражнение \(\PageIndex{38}\)

  \(7 561 060 \дел 909\)

  Упражнение \(\PageIndex{39}\)

  \(38 \дел 9\)

  Ответить

  4 остаток 2

  Упражнение \(\PageIndex{40}\)

  \(97 \дел 4\)

  Упражнение \(\PageIndex{41}\)

  \(199 \дел 3\)

  Ответить

  66 остаток 1

  Упражнение \(\PageIndex{42}\)

  \(573 \дел 6\)

  Упражнение \(\PageIndex{43}\)

  \(10 701 \дел 13\)

  Ответить

  823 остаток 2

  Упражнение \(\PageIndex{44}\)

  \(13 521 \дел 53\)

  Упражнение \(\PageIndex{45}\)

  \(3628 \дел 90\)

  Ответить

  40 остаток 28

  Упражнение \(\PageIndex{46}\)

  \(10 592 \дел 43\)

  Упражнение \(\PageIndex{47}\)

  \(19 965 \дел 30\)

  Ответить

  665 остаток 15

  Упражнение \(\PageIndex{48}\)

  \(8,320 \дел 21\)

  Упражнение \(\PageIndex{49}\)

  \(61 282 \дел 64\)

  Ответить

  957 остаток 34

  Упражнение \(\PageIndex{50}\)

  \(1030 \дел 28\)

  Упражнение \(\PageIndex{51}\)

  \(7,319 \дел 11\)

  Ответить

  665 остаток 4

  Упражнение \(\PageIndex{52}\)

  \(3628 \дел 90\)

  Упражнение \(\PageIndex{53}\)

  \(35 279 \дел 77\)

  Ответить

  458 остаток 13

  Упражнение \(\PageIndex{54}\)

  \(52 196 \дел 68\)

  Упражнение \(\PageIndex{55}\)

  \(67 751 \дел 68\)

  Ответить

  996 остаток 23

  Для следующих 5 задач используйте калькулятор, чтобы найти частные.

  Упражнение \(\PageIndex{56}\)

  \(4,346 \дел 53\)

  Упражнение \(\PageIndex{57}\)

  \(3,234 \дел 77\)

  Ответить

  42

  Упражнение \(\PageIndex{58}\)

  \(6,771 \дел 37\)

  Упражнение \(\PageIndex{59}\)

  \(4 272 320 \дел 520\)

  Ответить

  8 216

  Упражнение \(\PageIndex{60}\)

  \(7 558 110 \дел 651\)

  Упражнение \(\PageIndex{61}\)

  Преподаватель математики в старшей школе получает 17 775 долларов за 9 месяцев. Сколько денег этот инструктор зарабатывает каждый месяц?

  Ответ

  1975 долларов в месяц

  Упражнение \(\PageIndex{62}\)

  Пара платит 4380 долларов в год за квартиру с одной спальней. Сколько эта пара ежемесячно платит за эту квартиру?

  Упражнение \(\PageIndex{63}\)

  Тридцать шесть человек вложили в одну акцию в общей сложности 17 460 долларов. Если каждый из них вложил одинаковую сумму, то сколько вложил каждый?

  Ответить

  $485 каждый вложил

  Упражнение \(\PageIndex{64}\)

  Каждый из 28 учеников класса математики покупает учебник. Если книжный магазин продает книг на 644 доллара, какова цена каждой книги?

  Упражнение \(\PageIndex{65}\)

  Холодильник определенной марки оснащен автоматическим генератором льда, который производит 336 кубиков льда за один день. Если льдогенератор производит кубики льда с постоянной скоростью, сколько кубиков льда он производит каждый час?

  Ответить

  14 кубов в час

  Упражнение \(\PageIndex{66}\)

  Производитель пива разливает в бутылки 52 380 унций пива каждый час. Если каждая бутылка содержит одинаковое количество унций пива, а производитель наполняет 4365 бутылок в час, сколько унций пива содержится в каждой бутылке?

  Упражнение \(\PageIndex{67}\)

  Компьютерная программа состоит из 68 112 бит. 68 112 бит равны 8 514 байтам. Сколько бит в одном байте?

  Ответить

  8 бит в каждом байте

  Упражнение \(\PageIndex{68}\)

  В 26-этажном здании в Сан-Франциско всего 416 офисов. Сколько этажей в этом здании, если на каждом этаже одинаковое количество офисов?

  Упражнение \(\PageIndex{69}\)

  В колледже 67 классных комнат и 2546 парт. Сколько парт в каждом классе, если в каждом классе одинаковое количество парт?

  Ответить

  38

  Упражнения для обзора

  Упражнение \(\PageIndex{70}\)

  Чему равно число 4 в числе 124 621?

  Упражнение \(\PageIndex{71}\)

  Округлите 604 092 до ближайших сотен тысяч.

  Ответить

  600 000

  Упражнение \(\PageIndex{72}\)

  Какое целое число является аддитивной идентичностью?

  Упражнение \(\PageIndex{73}\)

  Найти продукт. \(6 256 \умножить на 100\).

  Ответить

  625 600

  Упражнение \(\PageIndex{74}\)

  Найдите частное. \(0 \дел 11\)

  ---

  Эта страница под названием 2.3: Division of Whole Numbers распространяется по лицензии CC BY, автором, ремиксом и/или куратором являются Денни Бурзински и Уэйд Эллис-младший (OpenStax CNX).

  1. Наверх
  • Была ли эта статья полезной?

  1. Тип изделия

     Раздел или страница

     Автор

     Денни Бурзински и Уэйд Эллис-младший

     Лицензия

     СС BY

     Показать страницу TOC

     нет

  2. Метки

     1. Деление целых чисел

  Многозначное сложение | Как сделать, решить и примеры

  Что такое многозначное сложение?

  Сложение — одна из четырех основных операций арифметики. Обычно обозначается знаком плюс +. Результат каждого процесса сложения называется суммой, а складываемые числа называются слагаемыми. В двух словах, сложение — это процесс, в котором два или более числа объединяются вместе.

  Многозначное , от самого слова, это число, имеющее более одной цифры. Это означает, что многозначное сложение — это просто сложение любого числа, имеющего более одной цифры.

  При добавлении многозначных чисел обычно используется вертикальный метод и термины, как показано на рисунке:

  • Добавления — это числа, к которым будет применяться процесс сложения.
  • Сумма является результатом сложения слагаемых.
  • Перенос на — это однозначное число, которое перегруппировано из одного столбца цифр в столбец с более высоким разрядным значением.
  • Знак плюса — это символ, обозначающий процесс сложения.
  Как сделать многозначное сложение?

  В то время как однозначные числа могут быть легко добавлены, более крупные числа или многозначные числа требуют, чтобы мы разделили их на столбцы в соответствии с их соответствующими разрядами. Мы всегда начинаем сложение с правой стороны, в соответствии с позиционной системой.

  Добавление многозначных чисел без перегруппировки

  Чтобы добавить многозначные числа, выполните следующие действия.

• Сложите цифры вместо единиц.
• Сложите цифры десятков.
• Продолжайте выполнять эти шаги, пока не добавите все разрядные значения.

Пример №1 

Чему равна сумма 135 и 23?

Раствор

Процесс сложения	Пошаговое объяснение
	Расположите числа в виде столбца, выровняв разряды.
	Добавьте цифру единиц. Таким образом, 5 + 3 = 8. Затем запишите сумму единиц под чертой.
	Добавьте цифру десятков. Таким образом, 3 + 2 = 5. Затем запишите сумму десятков под чертой.
	Сократите число сотен в числе 135, так как 23 не содержит числа сотен.
	Следовательно, сумма 135 и 23 равна 158 .

Пример #2

Какова сумма 4381 и 418?

Решение

Процесс добавления	Пошаговый объяснение
	. Объясните номера в столбце с значениями.
	Добавьте цифру единиц. Таким образом, 1 + 8 = 9  . Затем запишите сумму цифр единиц под чертой.
	Добавьте цифру десятков. Следовательно, 8 + 1 = 9 Затем запишите сумму десятков цифр под чертой.
	Добавьте цифру сотен. Таким образом, 3 + 4 = 7  . Запишите сумму сотен цифр под чертой.
	Сократите число тысяч 4381, так как 418 не имеет разряда тысяч.
	Следовательно, сумма 4381 и 418 равна 4799 .

Example #3

Find the sum of 2048 and 2021.  

Solution

Addition Process	Step-by-Step Explanation
	Расположите числа в виде столбца, выровняв значения разрядов.
	Добавьте цифру единиц. Таким образом, 8 + 1 = 9 Затем запишите сумму единиц под чертой.
	Добавьте цифру десятков. Таким образом, 4 + 2 = 6  . Затем запишите сумму десятков под чертой.
	Поскольку разряд сотен равен 0, сумма всегда будет равна 0. Следовательно, 0 + 0 = 0. Затем запишите сумму цифр сотен под чертой.
	Получить сумму разряда тысяч. Следовательно, 2 + 2 = 4 Затем запишите сумму цифр сотен под чертой.
	Следовательно, сумма 2048 и 2021 равна 4069 .

Пример №4 

Каким будет результат 15 346 + 12 631?

Решение

Процесс добавления	Пошаговый объяснение
	. Объясните номера в столбце с значениями.
	Добавьте цифру единиц. Таким образом, 6 + 1 = 7  . Затем запишите сумму единиц под чертой.
	Добавьте цифру десятков. Таким образом, 4 + 3 = 7  . Затем запишите сумму десятков под чертой.
	Добавьте цифру сотен. Таким образом, 3 + 6 = 9  . Затем запишите сумму цифр сотен под чертой.
	Получите сумму тысяч. Следовательно, 5 + 2 = 7  . Затем запишите сумму цифр тысяч под чертой.
	Наконец, получите сумму разряда десяти тысяч. Таким образом, 1 + 1 = 2 Затем запишите сумму десяти тысяч под чертой.
	Следовательно, сумма 15 346 и 12 631 равна 27 977 .

Пример № 5

Определить сумму 194 765 и 304 212.

Решение

Процесс добавления
. 0003 Пошаговое объяснение
	Расположите числа в виде столбца, выровняв разряды.
	Добавьте цифру единиц. Таким образом, 5 + 2 = 7  . Затем запишите сумму единиц под чертой.
	Добавьте цифру десятков. Таким образом, 5 + 2 = 7  . Затем запишите сумму десятков под чертой.
	Добавьте цифру сотен. Таким образом, 7 + 2 = 9 Затем запишите сумму сотен под чертой.
	Получите сумму тысяч. Таким образом, 4 + 4 = 8  . Затем запишите сумму цифр тысяч под чертой.
	Любое число, добавленное к 0, всегда будет одинаковым. Таким образом, 9 + 0 = 9 Затем запишите сумму десяти тысяч под чертой.
	Получите сумму сотен тысяч цифр. Таким образом, 1 + 3 = 4  . Затем запишите сумму цифр сотен тысяч под чертой.
	Следовательно, сумма 194 765 и 304 212 равна 498 977 .

Добавление многозначных чисел с перегруппировкой

Чтобы добавить многозначные числа, требующие перегруппировки, выполните следующие действия.

• Сложите цифры вместо единиц. Если сумма больше 10, то цифра переносится на разряд десятков.
• Сложите цифры десятков. Если сумма больше 10, то цифра переносится на разряд сотен.
• Продолжайте выполнять эти шаги, пока не добавите все разрядные значения. Если есть необходимость перегруппироваться, перенесите на следующее более высокое место.

Пример №1 

Чему равна сумма 821 и 98? Пошаговое объяснение Получить сумму единиц. Следовательно, 1 + 8 = 9
Затем запишите сумму цифр единиц под чертой Добавьте цифру десятков. Таким образом, 2 + 9 = 11 
. Поскольку оно превышает 10, мы должны перенести 1 на следующее более высокое разрядное значение. В данном случае это разряд сотен. Добавьте перенос 1 к разряду сотен числа 821. Таким образом, 1 + 8 = 9
Затем запишите сумму под чертой.

Следовательно, сумма 821 и 98 это 919 .

Example #2

Determine the sum of 999 and 23. 

Solution

Addition Process	Step-by-Step Explanation
	Arrange the numbers в форме столбца с выровненными значениями мест.
	Получите сумму единиц. Таким образом, 9 + 3 = 12  . Поскольку сумма больше 10, то перенесите 1 на разряд десятков.
	Добавьте перенос к разряду десятков. Таким образом, 1 + 9 + 2 = 12  . Поскольку оно также больше 10, мы должны перенести 1 в разряд сотен.
	Получите сумму переноса и разряда сотен числа 999. Таким образом, 9 + 1 = 10 Поскольку оно равно 10, перенесите 1 на разряд тысяч.
	Снизьте перенос на том же разряде тысячного разряда.
	Следовательно, сумма 999 и 23 равна 1022 .

Пример №3

Каким будет результат 1995 + 345?

Решение

Процесс добавления	Пошаговый объяснение
	. Объясните номера в столбце с значениями.
	Добавьте цифру единиц. Следовательно, 5 + 5 = 10 Так как сумма равна 10, то 1 переносится на разряд десятков.
	Получите сумму переноса и цифры десятков. Таким образом, 1 + 9 + 4 = 14 . Поскольку сумма больше 10, напишите 4 под чертой и напишите перенос над разрядом сотен 1995 года.
	Добавьте перенос и цифры место сотни. Таким образом, 1 + 9 + 3 = 13  . Поскольку сумма превышает 10, напишите 3 под чертой и напишите перенос поверх разряда тысяч числа 19.95.
	Добавьте перенос и тысячную цифру 1995 года. Таким образом, 1 + 1 = 2 Затем запишите сумму под чертой.
	Следовательно, сумма 1995 и 345 равна 2340 .

Пример № 4

Определить сумму 4875 и 3249.

Решение

Степень

процесс добавления
	Степень		.0004
	Расположите числа в виде столбца, выровняв разряды.
	Сложите цифры единиц из двух чисел. Таким образом, 5 + 9 = 14  . Поскольку сумма равна 14, напишите 4 под чертой и поместите перенос 1 в тот же столбец разряда десятков.
	Добавьте перенос и разряд десятков двух чисел. Таким образом, 1 + 7 + 4 = 12  . Поскольку сумма равна 12, напишите 2 под чертой и поместите перенос 1 в тот же столбец разряда сотен.
	Получите сумму переноса и разряда сотен. Следовательно, 1 + 8 + 2 = 11  . Поскольку сумма равна 11, напишите 1 под чертой и поставьте перенос 1 на разряд тысяч.
	Добавьте все цифры тысяч и перенос. Таким образом, 1 + 4 + 3 = 8  . Затем запишите сумму под чертой.
	Следовательно, сумма 4875 и 3249 равна 8124 .

Пример #5

Чему равна сумма 23 765 и 87 845?

Решение

Процесс добавления	Пошаговый объяснение
	. Объясните номера в столбце с значениями.
	Добавьте цифру единиц. Следовательно, 5 + 5 = 10  . Поскольку сумма равна 10, напишите 0 под чертой и поместите перенос в столбец разряда десятков.
	Получите сумму переноса и цифр в столбце разряда десятков. Таким образом, 1 + 6 + 4 = 11  . Поскольку сумма равна 11, напишите 1 под чертой и поместите перенос в тот же столбец, что и сотни.
	Добавьте цифры сотен и перенос. Таким образом, 1 + 7 + 8 = 16  . Поскольку сумма равна 16, напишите 6 под чертой и поместите перенос в столбец разряда тысяч.
	Добавьте цифру тысяч и перенос. Таким образом, 1 + 3 + 7 = 11  . Поскольку сумма равна 11, напишите 1 под чертой и поместите перенос в столбец десятитысячного разряда.
	Получите сумму разряда десяти тысяч и переноса. Таким образом, 1 + 2 + 8 = 11 . Поскольку сумма равна 11, напишите 1 под чертой и поместите перенос в столбец стотысячного разряда.
	Снизьте перенос на стотысячный разряд.
	Следовательно, сумма 23 765 и 87 845 равна 111 610 .

Как решать задачи на сложение многозначных чисел?

Чтобы решить задачи на сложение нескольких цифр, выполните следующие действия: 

1. Перечислите всю информацию, указанную в задаче.
2. Проанализируйте проблему.
3. Применение правил сложения многозначных чисел.

Пример №1 

В цветочном магазине продаются только розы и подсолнухи. Судя по инвентаризации, у них 3546 роз и 4582 подсолнуха. Сколько цветов в цветочном магазине?

Решение

В задаче сказано, что есть 3546 роз и 4582 подсолнуха. Так как нас просят получить общее количество цветов в магазине, то воспользуемся операцией сложения.

Процесс добавления	Пошаговое объяснение
	Расположите числа в виде столбца, выровняв разряды.
	Получите сумму единиц. Таким образом, 2 + 6 = 8 Затем запишите сумму единиц под чертой.
	Добавьте цифру десятков. Следовательно, 8 + 4 = 12 . Поскольку сумма равна 12, напишите 2 под чертой и поместите перенос в тот же столбец, что и сотни.
	Получите сумму переноса и разряда сотен. Таким образом, 1 + 5 + 5 = 11 Поскольку сумма равна 11, напишите 1 под чертой и поместите перенос в тот же столбец, что и разряд тысяч.
	Добавьте перенос и цифру разряда тысяч. Таким образом, 1 + 4 + 3 = 8  . Затем запишите это число под чертой.
	Следовательно, в цветочном магазине 8128 цветов .

Пример №2 

Венера накопила 30 465 долларов за последние 4 года. В этом году она смогла сэкономить 2,9 доллара.75. Сколько всего сбережений Венеры?

Решение

В задаче указано, что Венера смогла накопить 30, 465 и 2975 долларов. Таким образом, используя правила многозначного сложения,

образуют столбец с числами, расположенными в строке

Процесс сложения	Пошаговое объяснение
	.
	Сложите разряд единиц двух чисел. Таким образом, 5 + 5 = 10 Так как сумма равна 10, напишите 0 под чертой и перенесите перенос на разряд десятков.
	Получите сумму десятков и переноса. Таким образом, 1 + 6 + 7 = 14  . Поскольку сумма равна 14, напишите 4 под чертой и поместите перенос в тот же столбец, что и разряд сотен.
	Добавьте разряд сотен и перенос. Следовательно, 1 + 4 + 9 = 14 . Поскольку сумма равна 14, напишите 4 под чертой и поместите перенос в столбец разряда тысяч.
	Получите сумму переноса и разряда тысяч. Таким образом, 1 + 0 + 2 = 3  . Затем запишите сумму под чертой.
	Наконец, выведите 3 в разряде десяти тысяч.
	Следовательно, Венера накопила $33 440 .

Пример №3 

Азиатский ресторан заработал на прошлой неделе 15 365 долларов. На этой неделе они заработали 23 499 долларов. Сколько они заработали за две недели?

Решение

Учитывая задачу, отметим, что за последние две недели азиат заработал $15 365 и $23 499. Таким образом, используя правила многозначного сложения,

образуют столбец с числами, расположенными в строке

Процесс сложения	Пошаговое объяснение
	.
	Сложите разряд единиц двух чисел. Таким образом, 5 + 9= 14 Поскольку сумма равна 14, перегруппируйте ее и напишите 4 под чертой, а перенос перенесите в столбец десятков.
	Получите сумму десятков и переноса. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт