Как делить в столбик: пошаговый алгоритм

Деление столбиком используют, когда нужно разделить простые или сложные многозначные числа. Оно помогает найти ответ за счёт разбивания решения на ряд более простых шагов. В статье объясним на примерах, как делить в столбик и дадим пошаговый алгоритм.

Какие арифметические действия используют при делении в столбик

При знакомстве с делением в столбик у школьника могут возникнуть трудности и недопонимания. Отчасти потому, что при сложении в столбик мы только складываем, а при вычитании только вычитаем. Когда же мы делим в столбик, то по очереди  выполняем: деление, умножение и вычитание. Кроме того, нужно знать таблицу умножения, уметь делить с остатком и аккуратно писать цифры, каждую в своей клетке, чтобы не ошибиться в расчётах.

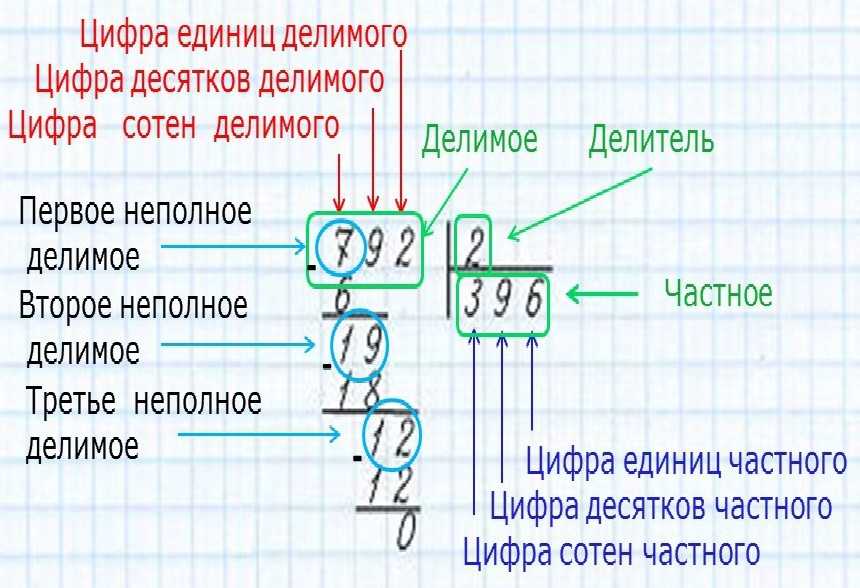
Термины «делимое», «делитель», «частное», «неполное делимое»

Деление двузначного числа на однозначное

Разделим 86 на 2

1. Для начала определим первое неполное делимое и узнаем, сколько будет цифр в частном. 8 можем разделить на 2, значит, 8 — первое неполное делимое, в частном будет первая цифра. После 8 есть ещё одна цифра, значит, и в частном будет ещё одна цифра — всего две цифры.

2. Разделим первое неполное делимое 8 на делитель 2, получим первую цифру частного — 4.

3. Умножим делитель 2 на цифру частного 4, получим ответ — 8. Этот результат записываем под первым неполным делимым.

4. Находим остаток 8 — 8 = 0. Остаток 0 меньше делителя 2, значит, продолжаем вычисления. Остаток 0 можно не писать.

5. Сносим (переписываем) цифру 6 — это новое неполное делимое.

6. Делим неполное делимое 6 на делитель 2, получаем — 3. Результат записываем в частное.

7. Умножаем делитель 2 на новую цифру частного 3, получаем 6. Результат записываем под вторым неполным делимым.

8. Записываем последний остаток 0. Больше мы не можем снести ни одной цифры, значит, неполных делимых не осталось. Деление в столбик закончено.

Деление трёхзначного числа на однозначное

Разделим 486 на 3

1. Сначала определим, сколько цифр в частном: первая цифра делимого — 4, мы можем разделить 4 на 3, значит, в частном будет первая цифра. После первого неполного делимого ещё две цифры, значит, и в частном будет ещё две цифры — всего три.

2. Затем разделим первое неполное делимое 4 на делитель 3. В результате получим 1.

3. Далее умножим делитель на полученную цифру частного: 3 · 1 =  3. Запишем 3 под первым неполным делителем.

4. Теперь нужно найти остаток при помощи вычитания.

5. Остаток 1 меньше делителя 3, значит, продолжаем вычисления. Рядом с цифрой остатка 1 пишем следующую цифру делимого — 8. Следующее неполное делимое — 18.

6. Разделим 18 на 3 и получим вторую цифру частного — 6.

7. Теперь умножим делитель на полученную цифру частного: 3 · 6 = 18 и найдём остаток — 0. Его можно не писать.

8. Сносим цифру 6 — это последнее неполное делимое. Делим 6 на 3 и получаем — 2. В частное пишем 2.

9. Далее умножим делитель на полученную цифру частного: 3 · 2 = 6 и найдём остаток — 0. Вычисления закончены.

Пример деления с нулём в частном, или сколько раз можно сносить цифру делимого, чтобы получить одно новое неполное делимое

Разделим 816 на 8

1. Первое неполное делимое 8, а за ним ещё две цифры. Значит, в частном будет 3 цифры.

2. Разделим первое неполное делимое 8 на делитель 4 и запишем в частное ответ — 2.

3. Умножим делитель 4 на цифру частного 2, получим 8. Запишем число под первым неполным делимым. 

4. Сносим цифру 1 — это новое неполное делимое. Остаток 0 не пишем.

5. Вспомним деление с остатком и разделим 1 на 4. В результате получим 0, остаток — 1. Цифру 0 записываем в частное.

6. Умножим делитель 4 на цифру частного 0, результат 0 запишем под вторым неполным делимым. Остаток 1. 

7. Сносим 6 и получаем новое неполное делимое 16. Делим 16 на 4, получаем цифру частного 4.

8. Умножаем делитель 4 на цифру частного 4

и пишем результат под неполным делимым.

9. Записываем последний остаток 0 — деление выполнено. 

Как можно сократить запись деления

Когда мы получили неполное делимое 1, которое меньше делителя 4, сносим вторую цифру делимого, чтобы новое неполное делимое было больше делителя. А в частное ставим 0. И далее выполняем деление в установленном порядке.

В этом примере мы дважды сносили цифру делимого, чтобы получить неполное делимое, которое больше делителя.

Надеемся, что теперь у вашего ребёнка не возникнет трудностей с делением в столбик. А если вдруг они есть, наши репетиторы с удовольствием готовы вам помочь!

Влюбляем в обучение на уроках в онлайн-школе Тетрика

Оставьте заявку и получите бесплатный вводный урок

Деление многозначного числа на однозначное (4 класс, математика)

4.2

Средняя оценка: 4.2

Всего получено оценок: 560.

4.2

Средняя оценка: 4.2

Всего получено оценок: 560.

Деление многозначных чисел на однозначные – это процесс утомительный, но в математике необходимый для развития навыков счета. Подобные умения необходимы на многих экзаменах

Однозначные и многозначные числа

Прежде чем перейти непосредственно к делению, давайте разберемся, какое число считается однозначным, а какое многозначным: двухзначным, трехзначным и так далее.

Дело в том, что в математике четко разделяют понятия цифры и числа. Цифры это обозначения от 0 до 9. Числа состоят из нескольких разрядов: единицы, десятки, сотни и так далее. Однозначное число содержит один разряд: единицы, а значит не может быть больше 9.

Такая система исчислений называется позиционной ,потому что значение каждой цифры зависит от позиции, которую она занимает в числе.

Двухзначное число содержит уже 2 разряда: единицы и десятки, следовательно, не может быть больше 99. Следуя той же логике трехзначные числа это числа от 100 до 999 и так далее

Деления

Деление это математическая операция, обратная операции умножения. Например выражение:

45:5=9 – показывает следующее: чтобы получить число 45 число 5 умножили на число 9.

Деление также имеет несколько интересных свойств.

Свойства деления

Свойства деления:

• Если любое число поделить на 1, то получится то же самое число
• Если ноль поделить на любое число, то получится ноль
• На ноль делить нельзя. Вообще-то можно, но получатся числа, с которыми в школьном курсе математики работать не учат ,поскольку это очень сложно. Поэтому правильнее будет сказать так: в школьном курсе математики делить на ноль нельзя.
• Если сумма делится на число, то можно каждое из слагаемых поделить на это число ,а потом сложить результат. То же касается и разности:

(а-в):с=а:с-в:с

• Если произведение делится на какое-то число, то можно любой из множителей разделить на число, а результат умножить на второй множитель:

(а*в):с=(а:с)*в

Деление в столбик

Столбик – это вертикальная линия, к середине которой проводится горизонтальная. Над горизонтальной чертой пишется делитель, с другой стороны вертикальной черты, рядом с делителем записывают делимое. Под горизонтальной чертой будет записываться результат.

Первым этапом нужно среди первых цифр числа 967 найти число, которое больше 23. Рассматриваем по порядку: 9 – меньше 23, а вот 96 уже больше. Значит первым шагом мы делим число 96 на число 23. Обязательно с остатком.

96:23=8, ост. 4 – в столбике под 96 записывается результат произведения 8*23=92. Число 92 подчеркивается и под ним записывается результат разности: 96-92=4. Рядом с 4 сносится цифра 7. Получается число 47, которое таким же образом делится на 23. А число 8 будет первой цирой в результате.

47:23=2, ост. 1 – цифра 2 будет второй цифрой результата.

Рядом с 1 можно снести 0 и считать уже дробную часть частного, но мы поделим число с остатком.

Результат: 967:23=82, ост.

Подобным образом можно поделить сколь угодно большое многозначное число на однозначное.

Что мы узнали?

Мы разобрались, чем отличается однозначное число от многозначного. Рассказали о том, что такое деление и выделили все свойства деления. Привели алгоритм деления многозначного числа на однозначное столбиком.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Оценка статьи

4. 2

Средняя оценка: 4.2

Всего получено оценок: 560.

---

А какая ваша оценка?

Многозначное сложение | Как сделать, решить и примеры

Что такое многозначное сложение?

Сложение — одна из четырех основных арифметических операций. Обычно обозначается знаком плюс +. Результат каждого процесса сложения называется суммой, а складываемые числа называются слагаемыми. В двух словах, сложение — это процесс, в котором два или более числа объединяются вместе.

Многозначное , от самого слова, это число, имеющее более одной цифры. Это означает, что многозначное сложение — это просто сложение любого числа, имеющего более одной цифры.

При добавлении многозначных чисел обычно используется вертикальный метод и термины, как показано на рисунке:

• Добавления — это числа, к которым будет применяться процесс сложения.
• Сумма является результатом сложения слагаемых.
• Перенос на — это однозначное число, которое перегруппировано из одного столбца цифр в столбец с более высоким разрядным значением.
• Знак плюс — это символ, обозначающий процесс сложения.

Как сделать многозначное сложение?

В то время как однозначные числа могут быть легко добавлены, более крупные числа или многозначные числа требуют, чтобы мы разделили их на столбцы в соответствии с их соответствующими разрядами. Мы всегда начинаем сложение с правой стороны, в соответствии с позиционной системой.

Добавление многозначных чисел без перегруппировки

Чтобы добавить многозначные числа, выполните следующие действия.

Сложите цифры вместо единиц.

Сложите цифры десятков.

Продолжайте выполнять эти шаги, пока не добавите все разрядные значения.

Пример №1 

Чему равна сумма 135 и 23?

Решение

Процесс добавления	Пошаговый объяснение
	Объедините количество в форме колонны со значениями.
	Добавьте цифру единиц. Таким образом, 5 + 3 = 8. Затем запишите сумму единиц под чертой.
	Добавьте цифру десятков. Таким образом, 3 + 2 = 5. Затем запишите сумму десятков под чертой.
	Сократите число сотен в числе 135, так как 23 не содержит числа сотен.
	Следовательно, сумма 135 и 23 равна 158 .

Пример #2

Сколько будет сумма 4381 и 418?

Решение

Процесс добавления	Пошаговый объяснение
	Объедините количество в форме колонны со значениями.
	Добавьте цифру единиц. Таким образом, 1 + 8 = 9  . Затем запишите сумму цифр единиц под чертой.
	Добавьте цифру десятков. Следовательно, 8 + 1 = 9 Затем запишите сумму десятков под чертой.
	Добавьте цифру сотен. Таким образом, 3 + 4 = 7  . Запишите сумму сотен цифр под чертой.
	Сократите число тысяч 4381, так как 418 не имеет разряда тысяч.
	Следовательно, сумма 4381 и 418 равна 4799 .

Example #3

Find the sum of 2048 and 2021. 

Solution

Addition Process	Step-by-Step Explanation
	Arrange the numbers in a форма столбца с выровненными значениями мест.
	Добавьте цифру единиц. Таким образом, 8 + 1 = 9  . Затем запишите сумму единиц под чертой.
	Добавьте цифру десятков. Таким образом, 4 + 2 = 6  . Затем запишите сумму десятков под чертой.
	Поскольку разряд сотен равен 0, сумма всегда будет равна 0. Следовательно, 0 + 0 = 0. Затем запишите сумму цифр сотен под чертой.
	Получить сумму разряда тысяч. Следовательно, 2 + 2 = 4  . Затем запишите сумму цифр сотен под чертой.
	Следовательно, сумма 2048 и 2021 равна 4069 .

Пример №4 

Каким будет результат 15 346 + 12 631?

Решение

Процесс добавления	Пошаговый объяснение
	Объедините количество в форме колонны со значениями.
	Добавьте цифру единиц. Таким образом, 6 + 1 = 7  . Затем запишите сумму единиц под чертой.
	Добавьте цифру десятков. Таким образом, 4 + 3 = 7  . Затем запишите сумму десятков под чертой.
	Добавьте цифру сотен. Таким образом, 3 + 6 = 9  . Затем запишите сумму цифр сотен под чертой.
	Получить сумму тысяч. Следовательно, 5 + 2 = 7  . Затем запишите сумму цифр тысяч под чертой.
	Наконец, получите сумму разряда десяти тысяч. Таким образом, 1 + 1 = 2 Затем запишите сумму десяти тысяч под чертой.
	Следовательно, сумма 15 346 и 12 631 равна 27 977 .

Example #5

Determine the sum of 194 765 and 304 212. 

Solution

Addition Process	Step-by-Step Explanation
	Расположите числа в виде столбца, выровняв разряды.
	Добавьте цифру единиц. Таким образом, 5 + 2 = 7  . Затем запишите сумму единиц под чертой.
	Добавьте цифру десятков. Таким образом, 5 + 2 = 7  . Затем запишите сумму десятков под чертой.
	Добавьте цифру сотен. Таким образом, 7 + 2 = 9  . Затем запишите сумму цифр сотен под чертой.
	Получить сумму тысяч. Таким образом, 4 + 4 = 8 Затем запишите сумму тысяч под чертой.
	Любое число, добавленное к 0, всегда будет одинаковым. Таким образом, 9 + 0 = 9 Затем запишите сумму цифр десяти тысяч под чертой.
	Получить сумму сотен тысяч цифр. Таким образом, 1 + 3 = 4  . Затем запишите сумму сотен тысяч цифр под чертой.
	Следовательно, сумма 194 765 и 304 212 равна 498 977 .

Добавление многозначных чисел с перегруппировкой

Чтобы добавить многозначные числа, которые необходимо перегруппировать, выполните следующие действия.

Сложите цифры вместо единиц. Если сумма больше 10, то цифра переносится на разряд десятков.

Сложите цифры десятков. Если сумма больше 10, то цифра переносится на разряд сотен.

Продолжайте выполнять эти шаги, пока не добавите все разрядные значения. Если есть необходимость перегруппироваться, перенесите на следующее более высокое место.

Пример №1 

Сколько будет сумма 821 и 98? Пошаговое объяснение Получите сумму единиц. Следовательно, 1 + 8 = 9
Затем запишите сумму цифр единиц под чертой Добавьте цифру десятков. Таким образом, 2 + 9= 11
Поскольку оно превышает 10, мы должны перенести 1 на следующее более высокое разрядное значение. В данном случае это разряд сотен. Добавьте перенос 1 к разряду сотен числа 821. Таким образом, 1 + 8 = 9
Затем запишите сумму под чертой.

Следовательно, сумма 821 и 98 равна 919 .

Пример №2

Определите сумму 999 и 23.  

Решение

Процесс сложения	Пошаговое объяснение
	Расположите числа в виде столбца, выровняв разряды.
	Получите сумму единиц. Таким образом, 9 + 3 = 12  . Поскольку сумма больше 10, то перенесите 1 на разряд десятков.
	Добавьте перенос к разряду десятков. Таким образом, 1 + 9 + 2 = 12  . Поскольку оно также больше 10, то мы должны перевести 1 в разряд сотен.
	Получите сумму переноса и разряда сотен числа 999. Таким образом, 9 + 1 = 10 Поскольку оно равно 10, перенесите 1 на разряд тысяч.
	Снизьте перенос на том же разряде тысячного разряда.
	Следовательно, сумма 999 и 23 равна 1022 .

Пример №3

Что получится в результате 1995 + 345?

Решение

Процесс добавления	Пошаговый объяснение
	Объедините количество в форме колонны со значениями.
	Добавьте цифру единиц. Следовательно, 5 + 5 = 10 . Так как сумма равна 10, то перенесите 1 на разряд десятков.
	Получите сумму переноса и цифры десятков. Таким образом, 1 + 9+ 4 = 14 Поскольку сумма больше 10, напишите 4 под чертой и напишите перенос поверх разряда сотен 1995 года. Таким образом, 1 + 9 + 3 = 13 . Поскольку сумма превышает 10, напишите 3 под чертой и напишите перенос поверх разряда тысяч 1995 года.
	Добавьте перенос и цифру тысяч. 1995 года. Таким образом, 1 + 1 = 2 Затем запишите сумму под чертой.
	Следовательно, сумма 1995 и 345 равна 2340 .

Пример № 4

Определите сумму 4875 и 3249.

Решение

	9003
	. Расположите числа в виде столбца, выровняв значения разрядов.
	Сложите цифры единиц двух чисел. Таким образом, 5 + 9= 14 Поскольку сумма равна 14, напишите 4 под чертой и поместите перенос 1 в тот же столбец разряда десятков.
	Добавьте перенос и разряд десятков двух чисел. Таким образом, 1 + 7 + 4 = 12  . Поскольку сумма равна 12, напишите 2 под чертой и поместите перенос 1 в тот же столбец разряда сотен.
	Получите сумму переноса и разряда сотен. Следовательно, 1 + 8 + 2 = 11  . Поскольку сумма равна 11, напишите 1 под чертой и поставьте перенос 1 на разряд тысяч.
	Добавьте все цифры тысяч и перенос. Таким образом, 1 + 4 + 3 = 8  . Затем запишите сумму под чертой.
	Следовательно, сумма 4875 и 3249 равна 8124 .

Пример #5

Чему равна сумма 23 765 и 87 845?

Решение

Процесс добавления	Пошаговое объяснение
	Расположите числа в виде столбца, выровняв разряды.
	Добавьте цифру единиц. Следовательно, 5 + 5 = 10  . Поскольку сумма равна 10, напишите 0 под чертой и поместите перенос в столбец разряда десятков.
	Получите сумму переноса и цифр в столбце разряда десятков. Таким образом, 1 + 6 + 4 = 11  . Поскольку сумма равна 11, напишите 1 под чертой и поместите перенос в тот же столбец, что и сотни.
	Добавьте цифры сотен и перенос. Таким образом, 1 + 7 + 8 = 16  . Поскольку сумма равна 16, напишите 6 под чертой и поместите перенос в столбец разряда тысяч.
	Добавьте цифру тысяч и перенос. Таким образом, 1 + 3 + 7 = 11  . Поскольку сумма равна 11, напишите 1 под чертой и поместите перенос в столбец десятитысячного разряда.
	Получите сумму разряда десяти тысяч и переноса. Таким образом, 1 + 2 + 8 = 11 Поскольку сумма равна 11, то напишите 1 под чертой и поместите перенос в столбец стотысячного разряда.
	Снизьте перенос на стотысячный разряд.
	Следовательно, сумма 23 765 и 87 845 равна 111 610 .

Как решать задачи на сложение многозначных чисел?

Чтобы решить задачи, связанные с многозначным сложением, выполните следующие действия: 

1. Перечислите всю информацию, указанную в задаче.
2. Проанализируйте проблему.
3. Применение правил сложения многозначных чисел.

Пример №1 

Цветочный магазин продает только розы и подсолнухи. Судя по инвентаризации, у них 3546 роз и 4582 подсолнуха. Сколько цветов в цветочном магазине?

Решение

В задаче сказано, что есть 3546 роз и 4582 подсолнуха. Так как нас просят получить общее количество цветов в магазине, то воспользуемся операцией сложения. 9Пошаговое объяснение Получите сумму единиц. Таким образом, 2 + 6 = 8 
. Затем запишите сумму единиц под чертой. Добавьте цифру десятков. Следовательно, 8 + 4 = 12
. Поскольку сумма равна 12, напишите 2 под чертой и поместите перенос в тот же столбец, что и разряд сотен. Получите сумму переноса и разряда сотен. Таким образом, 1 + 5 + 5 = 11 
. Поскольку сумма равна 11, напишите 1 под чертой и поместите перенос в тот же столбец, что и разряд тысяч. Добавьте перенос и цифру разряда тысяч. Таким образом, 1 + 4 + 3 = 8 
. Затем запишите это число под чертой. Следовательно, в цветочном магазине 8128 цветов .

Пример №2 

Венера накопила 30 465 долларов за последние 4 года. В этом году она смогла сэкономить 2975 долларов. Каковы общие сбережения Венеры?

Решение

В задаче указано, что Венера смогла накопить 30, 465 и 2975 долларов. Таким образом, используя правила многоразрядного сложения,0075 Расположите числа в виде столбца, выровняв разряды. Сложите разряд единиц двух чисел. Таким образом, 5 + 5 = 10 
. Поскольку сумма равна 10, напишите 0 под чертой и поставьте перенос в столбце десятков. Получите сумму десятков и переноса. Таким образом, 1 + 6 + 7 = 14 
. Поскольку сумма равна 14, напишите 4 под чертой и поместите перенос в тот же столбец, что и разряд сотен. Добавьте разряд сотен и перенос. Следовательно, 1 + 4 + 9 = 14

. Поскольку сумма равна 14, напишите 4 под чертой и поместите перенос в столбец разряда тысяч.

Получите сумму переноса и разряда тысяч. Таким образом, 1 + 0 + 2 = 3 
. Затем запишите сумму под чертой. Наконец, сбейте 3 в разряде десяти тысяч. Следовательно, Венера накопила $33 440 .

Пример №3

Азиатский ресторан заработал на прошлой неделе 15 365 долларов. На этой неделе они заработали 23 499 долларов. Сколько они заработали за две недели?

Решение

Учитывая задачу, отметим, что за последние две недели азиат заработал $15 365 и $23 499. Таким образом, используя правила многозначного сложения,

Процесс сложения	Пошаговое объяснение
	Расположите числа в виде столбца, выровняв разряды.
	Сложите разряд единиц двух чисел. Таким образом, 5 + 9 = 14  . Поскольку сумма равна 14, перегруппируйте ее и напишите 4 под чертой, а перенос перенесите в столбец десятков.
	Получите сумму десятков и переноса. Следовательно, 1 + 6 + 9 = 16 . Поскольку сумма равна 16, напишите 6 под чертой и поставьте перенос на разряд сотен.
	Добавьте перенос и цифру сотен. Таким образом, 1 + 3 + 4 = 8  . Затем запишите сумму под чертой.
	Добавьте разряд тысяч. Таким образом, 5 + 3 = 8 Затем запишите сумму под чертой.
	Сложите цифры в разряде десятков тысяч. Следовательно, 1 + 2 = 3 Затем запишите сумму под чертой.

Таким образом, азиатский ресторан заработал $38 864 за последние две недели.

https://helpingwithmath.com/worksheet/multiplication-of-multi-digit-numbers-world-oceans-day-themed-worksheets/
https://helpingwithmath.com/worksheet/addition-of-multi-digit -numbers-national-nutrition-month-themed-worksheets/
https://helpingwithmath.com/worksheet/subtraction-of-multi-digit-numbers-finances-themed-worksheets/

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

NumberNut.com: Раздел: 2-значные номера

Не все подразделение сделано с числами меньше десяти (10). Когда вы узнаете больше о делении двузначных чисел, вы увидите шаблона, похожих на шаблоны, которые вы видели при умножении. Взгляните на эти примеры, прежде чем мы двинемся дальше…

25 = 5 х 5
25 ÷ 5 = 5

28 = 4 x 7
28 ÷ 7 = 4
28 ÷ 4 = 7

Мы думаем, что узоры очень интересные. Дивизия похожа на обратное умножения. В этом есть смысл, поскольку мы продолжаем говорить вам, что умножение — это объединение групп, а деление их разделяет. Если вы помните два множителя , которые использовались для создания исходного числа ( делимое

), проверка вашей работы должна быть легкой.

Пример:
Вы будете делить число двадцать четыре (24) на более мелкие части. Каковы возможные факторы?
Вы знаете, что:
3 x 8 = 24
4 x 6 = 24
6 x 4 = 24
8 x 3 = 24
Если вы столкнулись с проблемой 24 ÷ 4 = ? вы узнаете, что ответ равен 6, потому что 6 х 4 = 24.

Иногда ответы будут простыми, и вы получите единственное число в вашем частном . Эти простые задачи называются короткое деление . Число, которое вы делите, меньше чем в десять раз больше значения делителя . Примеры короткого деления включают…

28 ÷ 4 = 7
64 ÷ 8 = 8
54 ÷ 9 = 6
99 ÷ 11 = 9
— или —

9 11 ) 99 — 99 0

Это так же просто, как пирог. Однако иногда вы начнете с дивиденда, который более чем в десять раз превышает значение делителя. Затем пришло время для длинного деления . Вот несколько примеров, прежде чем мы покажем вам, как решать проблемы.

24 ÷ 2 = 12 (Посмотрите, как узнать, что частное больше 9?)
44 ÷ 4 = 11 (Четыре входит в число сорок четыре одиннадцать раз.)
63 ÷ 3 = 21 (Вы можете получить 21 группу, если разделите 63 на 3.)
80 ÷ 5 = 16 (В числе 80 16 групп по 5. В этой задаче тоже есть подлый остаток.)
— или —

16 5 ) 80 — 5     30 — 30   0

Сопутствующая деятельность

Тест на одно- и двузначное деление (без остатка) — Игровая активность

Тест на одно- и двузначное деление (без остатка) — Игровая активность

Ключ к решению этих проблем — увидеть, что число в столбце десятков делимого уже делится на делитель. В задаче 28 ÷ 2 = 12 «2» в числе 28 делится на два (один раз). Вы должны записать единицу (1) в качестве первого числа в вашем частном, а затем перейти к столбцу единиц и увидеть, что «8» делится на два (четыре раза). Затем вы пишете четыре (4) в следующем месте вашего ответа. Когда вы столкнетесь с этими типами задач на деление, разбейте их на кусочки размером с укус.

(1) У меня двузначное число для делителя?
• Если да, задайте вопрос 2.
• Если нет, выполните деление.

(2) Первое число делимого больше моего делителя?
• Если да, сначала выполните деление в столбце десятков, а затем переходите к столбцу единиц.
• Если нет, вы можете разделить все делимое на делитель, и ваш ответ будет меньше десяти.

Да, при делении двузначных чисел получается остатка . Помните, что остаток будет никогда не будет больше вашего делителя. Неважно, будет ли ваш ответ десять или больше, остаток всегда будет меньше делителя.

Выполняя деление в длинное число, вы обнаружите остатки в середине задач на деление. Это не всегда будет красиво и ровно, как если бы вы разделили шестьдесят (62) на два (2). Это даже частное тридцати одного (31) просто повезло. Подумайте о числе пятьдесят четыре (54). Когда вы делите на два, 5 в столбце десятков делится на 2, но есть остаток от 1. В длинном делении вы держите этот остаток для деления в столбце единиц. Итак, у вас на самом деле есть две небольшие проблемы с делением.

Пример:
54 ÷ 2 = ?
Шаг 1: 5 ÷ 2 = 2 с остатком 1
Шаг 2: Объедините 1 со значением 4 из столбца единиц, чтобы получить 14.
Шаг 3: 14 ÷ 2 = 7
Шаг 4: соедините два значения вместе чтобы получить ответ 27.

Теперь мы собираемся разбить его на все этапы. Мы пропустили вычитание, чтобы упростить задачу. На самом деле вы будете делать эти шаги. Начните с первого числа делимого и подумайте, сколько раз его можно разделить на 2.

Шаг 1: 5 можно разделить только на 2 два (2) раза. 2 x 2 = 4
Шаг 2: 5 — 4 = 1. 1 — это остаток от деления в столбце десятков.
Шаг 3: Опустите 4 из столбца единиц в делимом и поместите его справа от остатка (1), так как столбец единиц находится справа от столбца десятков. Получается 14.
Шаг 4: 14 можно разделить на 2 семь (7) раз. 2 x 7 = 14
Шаг 5: 14 — 14 = 0. Поскольку разница равна 0, проблема решена.
— или —

27 2 ) 54 — 4 14 — 14 0

Возможно, вы начинаете замечать еще одно различие между умножением и делением. В своих задачах на умножение вы работали справа налево. Вы начали умножать единицы, затем десятки и двигались вверх по числам. В отделе мы работали слева направо. Мы начинаем наше деление с самых высоких значений дивиденда и двигаемся вниз. Это еще одна вещь, которую вы можете заметить, когда решаете все эти проблемы.