Деление дробей.

Деление дробей.

Навигация по странице:

• Деление дроби на натуральное число
• Деление натурального числа на дробь
• Деление обыкновенных дробей
• Деление смешанных чисел

Деление дроби на натуральное число.

Определение.

Чтобы разделить дробь на натуральное число, надо знаменатель дроби умножить на число, а числитель оставить тем же.

Примеры деления дроби на натуральное число

Пример 1.

Найти частное от деления дроби на натуральное число:

3	: 2	=	3	=	3
7			7 · 2		14

Пример 2.

Найти частное от деления дроби на натуральное число:

6	: 3	=	6	=	2 · 3	=	2
11			11 · 3		11 · 3		11

Определение.

Чтобы получить дробь, обратную данной, следует поменять местами числитель и знаменатель.

3	— дробь обратная	7
7		3

Деление натурального числа на дробь.

Определение.

Чтобы разделить натуральное число на дробь, следует число умножить на дробь обратную заданной.

Примеры деления натурального числа на дробь

Пример 3.

Найти частное от деления натурального числа на дробь:

2:	7	=	2·	2	=	4
	2			7		7

Пример 4.

Найти частное от деления натурального числа на дробь:

2:	4	=	2·	5	=	2 · 5	=	2 · 5	=	5	=	2 · 2 + 1	= 2	1
	5			4		4		2 · 2		2		2		2

Деление обыкновенных дробей.

Определение.

Чтобы разделить одну обыкновенную дробь на другую, надо умножить первую дробь на дробь, обратную второй.

Примеры деления обыкновенных дробей

Пример 5.

Найти частное от деления дробей:

3	:	4	=	3	·	5	=	3 · 5	=	15
7		5		7		4		7 · 4		28

Пример 6.

Найти частное от деления дробей:

6	:	4	=	6	·	7	=	6 · 7	=	3 · 2	=	3	=	2 + 1	= 1	1
7		7		7		4		7 · 4		2 · 2		2		2		2

Онлайн калькулятор дробей

Упражнения на тему деление двух обыкновенных дробей

Деление смешанных чисел.

Примеры деления смешанных чисел

Пример 7.

Найти частное от деления смешанных чисел:

112 : 223 = 1 · 2 + 12 : 2 · 3 + 23 = 32 : 83 = 32 · 38 = 3 · 32 · 8 = 916

Пример 8.

Найти частное от деления смешанного числа на дробь:

217 : 35 = 2 · 7 + 17 : 35 = 157 : 35 = 157 · 53 = 15 · 57 · 3 = 5 · 57 = 257 = 7 · 3 + 47 = 347

Онлайн калькулятор дробей

Упражнения на тему деление двух смешанных чисел

Дроби Виды дробей (обыкновенная правильная, неправильная, смешанная, десятичная) Основное свойство дроби Сокращение дроби Приведение дробей к общему знаменателю Преобразование неправильной дроби в смешанное число Преобразование смешанного числа в неправильную дробь Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичной дроби в обыкновенную дробь

Онлайн калькуляторы дробей

Онлайн упражнения с дробями

Действия с рациональными числами | СПАДИЛО

Что такое рациональные числа?

Рациональные числа – это числа, которые можно представить в виде обыкновенной дроби, где a – целое число, а b – натуральное.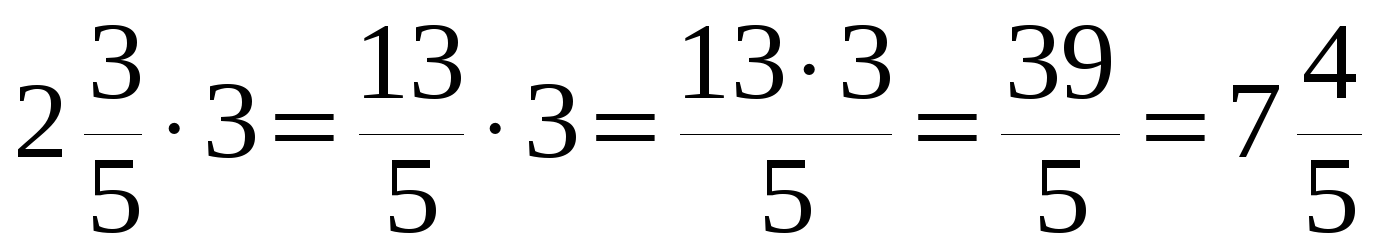

То есть все дробные и целые числа вместе образуют рациональные числа, так как любое целое можно представить в виде обыкновенной дроби, записав его в числитель, а в знаменателе надо написать 1.

Пример №1. Любые целые числа, например, 38, -24, 49 можно представить в виде обыкновенных дробей, их называют рациональными:

Действия с рациональными числами

Сложение (или вычитание) рационального числа и ноля

Для любого рационального числа применимо правило сложения (или вычитания): а + 0 = 0, a – 0 = a

Пример №2. –25,7 + 0 = –25,7 или 0+(–67)= –67

Аналогичное правило работает и для вычитания нуля.

Пример №3. 45 – 0=45 или – 67 – 0 = – 67

Как складывать отрицательные числа?

Чтобы сложить два отрицательных рациональных числа, складывают модули и перед полученным результатом ставят знак минус.

Модуль неотрицательного числа равен этому числу, модуль отрицательного числа равен числу, противоположному данному.

Пример №4. Складываем модули чисел –31 и –45, то есть модули чисел равны соответственно |–31|=31 и |–45|=45, значит, 31+45 = 76. Далее ставим минус в ответе. Запись самого решения выполняется без знака «модуля» следующим образом:

 – 31+(–45)= –(31+45)= –76

Как складывать числа с разными знаками?

При сложении чисел с разными знаками необходимо из числа, которое больше по модулю, вычесть число, которое меньше по модулю, а перед полученным результатом поставить знак того слагаемого, модуль которого больше.

Пример 5.

• 45+(–98) = – (98–45)= –53 здесь большее по модулю число – это 98, поэтому из него будем вычитать число 45 и ставить в ответе знак «минус».
• –43+81=81–43=38 здесь большее по модулю число это 81, поэтому из него вычитаем 43, соответственно результат будет положительный.

Правило вычитания рациональных чисел

Чтобы вычесть из одно числа другое, необходимо к уменьшаемому прибавить число, противоположное вычитаемому.

Пример №6.

• 10–18=10+(–18)= –8 здесь к уменьшаемому 10 прибавляем число противоположное 18, то есть прибавляем –18. Дальше работаем по известному правилу сложения чисел с разными знаками.
• –7–(–2)= –7+2= –5 здесь к уменьшаемому –7 прибавляем число противоположное –2, то есть 2. Далее опять работает правило сложения чисел с разными знаками.
• 15–(–12)=15+12=27 здесь к уменьшаемому 15 прибавляем число противоположное –12, то есть 12. Далее – получаем сложение положительных чисел.

Как умножать рациональные числа с разными знаками?

Правило умножения двух рациональных чисел, содержащих разные знаки, гласит: выполняем умножение модулей этих чисел и перед полученным результатом ставим знак минус. Другими словами, при умножении двух чисел с разными знаками всегда ставится минус  в ответе.

Пример №7.

• –6 80= –480
• 48 (–3)= –144

Как умножать отрицательные числа?Правило умножения двух отрицательных чисел: умножаем их модули; в ответ записываем полученное положительное число. Другими словами, при умножении двух отрицательных чисел всегда получается положительное число.

Пример №8.

• –25 (–4)=100
• –21,7 (–10)=217

Как делить рациональные числа?

Правило деления двух рациональных чисел аналогично правилу умножения: при делении двух чисел с разными знаками в ответе получается отрицательное число. При делении двух отрицательных чисел получается положительное число.

Пример №9.

• –215:5= –43
• –642:(–2)= 321

Умножение и деление рационального числа и нуля

1. При умножении рационального числа и нуля получается нуль.
2. При делении нуля на рациональное число получается нуль.
3. При делении рациональных чисел нужно помнить  правило о том, что на нуль делить нельзя!

Пример №10.

• –314×0=0
• 0×(–2,16)=0
• 0 : (–31)=0

Задание 6OM21R Найти значение выражения 4,9 – 9,4.

---

Выполним вычитание десятичных дробей, где 9,4 больше по модулю, значит, ответ будет отрицательным.

Итак, – (9,4 – 4,9)= – 4,5

Ответ: -4,5

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0806o

Найдите значение выражения:

---

В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=7² и 100=10². И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:   По аналогии извлекаем и 2-й корень: В итоге получаем:

Ответ: 70,7

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0606o Найдите значение выражения:

–0,3·(–10)⁴+4·(–10)²–59

---

Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.

–0,3·(–10)⁴+4·(–10)²–59 =

Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:

= –0,3·10000+4·100–59 =

Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:

= –3000+400–59 =

Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:

= –2600–59 =

Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:

= –(2600+59) = –2659

Ответ: -2659

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0605o Найдите значение выражения:

–13•(–9,3)–7,8

---

Это задание требует простого умения выполнять арифметические действия с десятичными дробями.

–13·(–9,3)–7,8 =

Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:

Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:

= 120,9–7,8 =

Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:

= 113,1

Ответ: 113,1

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0604o Найдите значение выражения:  ¼ + 0,07

---

К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.

Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:

0,25 + 0,07 = 0,32

Ответ: 0,32

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0602o Найдите значение выражения:

---

Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что   1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17  • 1/3, поэтому её можно легко вынести за скобку.

1/3 • (6 • (1/3)  — 17 )

Проведя вычисления в скобках, получим:

1/3 • ( 6 • (1/3)  — 17 ) = 1/3 • (6 /3  — 17 ) = 1/3 • ( 2  — 17 ) = 1/3 • ( -15 )

Теперь умножим полученное значение -15 на 1/3:

1/3 • ( -15 ) = -5

Ответ: -5

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0601o Найдите значение выражения:

---

Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.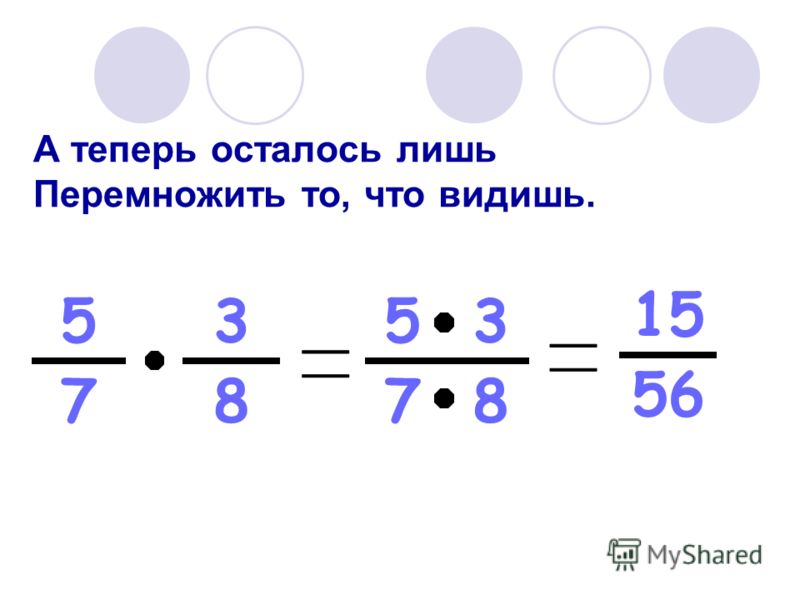

Вычислим значение знаменателя:

4,5 • 2,5

Можно произвести вычисления в столбик, тогда получим:

4,5 • 2,5 = 11,25

Либо перевести дробь к простому виду:

4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4

Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:

9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )

9 и 45 можно сократить на 9:

( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8

Ответ: 0,8

pазбирался: Даниил Романович | обсудить разбор | оценить

Даниил Романович | Просмотров: 5k

Просмотр размножения Фракционных образовательных ресурсов

Целые рабочие личные листы.

Результаты фильтрации

очистить все фильтры

By Grade

• Preschool
• Kindergarten
• 1st grade
• 2nd grade
• 3rd grade
• 4th grade
• 5th grade
• 6th grade
• 7th grade
• 8th grade

By Субъект

• Кодирование
•  Изобразительное искусство
•  иностранный язык

•  Математика

  •  Число. 0018
  •  Addition
  •  Subtraction
  •  Multiplication
  •  Division
  •  Mixed Operations

  •  Fractions

    •  Fraction Models
    •  Равные дроби
    •  Сравнение дробей
    • Смешанные числа и неправильные дроби
    •  Сложение и вычитание дробей

    •  Multiplying and Dividing Fractions

      •  Multiplying Fractions

      • Division with Unit Fractions
      • Dividing Fractions
  •  Decimals
  •  Percents, Ratios, and Скорости
  •  Алгебра
  •  Геометрия
  •  Измерение
  •  9009  Время
  0010 Money Math
  •  Data and Graphing
  •  Math Word Problems
  • Math Puzzles
•  Reading & Writing
•  Science
•  Social emotional
•  Социальные исследования
•  Typing

по теме

•  Праздники

Стандарт

.

0015  Common Core

Дроби 4



Учебный урок

Дроби углубляются в изучение 9

3 Учащиеся будут применять предыдущие знания о нахождении эквивалентных дробей и преобразовании между дробями и смешанными числами, чтобы работать с дробями более сложными способами. Студенты будут продолжать использовать визуальные модели для обучения и практики сложения, вычитания, умножения и деления дробей.

5-й класс

Математика



Урок с пошаговыми инструкциями

Поиск Умножение дробей Образовательные ресурсы

Умножение дробей — отличная отправная точка для изучения арифметики, если ваш ребенок только начинает изучать арифметику. Этому навыку обычно учат, начиная с четвертого класса, поэтому, если ваш ученик уже знаком с различными типами дробей, изучите наши ресурсы, чтобы помочь им освоить умножение дробей, прежде чем они перейдут к более сложным понятиям.

Узнайте больше об умножении дробей

Умножение дробей — одна из самых простых задач, потому что правил не так много. Ниже приведено пошаговое руководство по умножению правильных, неправильных и смешанных дробей.

Общие правила
Если обе дроби имеют числитель и знаменатель, правила очень просты:

1. Умножить числители (верхние числа)
2. Умножить знаменатели (нижние числа)
3. Упростить, если необходимо0018

Чтобы узнать, как умножать числа, посетите нашу страницу Умножение.

Дроби и целые числа
Если вы пытаетесь умножить дробь на целое число, преобразуйте целое число в дробь, присвоив ей знаменатель, равный 1 (3 станет ³ ⁄ ₁ ), и затем следуйте общим правилам умножения дробей.

Смешанные дроби
Чтобы умножать смешанные дроби, вы должны знать, как преобразовывать смешанную дробь в неправильную. Если вашему ребенку нужна помощь с этой концепцией, взгляните на «Основы дробей» в нижней части страницы «Дроби» и поработайте с некоторыми рабочими листами.

1. Преобразование смешанной дроби в неправильную
2. Умножение дробей по общим правилам
3. Преобразование произведения обратно в смешанную дробь

Используйте эти правила, чтобы работать с различными рабочими листами и упражнениями на этой странице, пока ваш ребенок не станет профессиональным умножителем дробей!

Калькулятор дробей

Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.

Правила выражений с дробями:

Дроби — для деления числителя на знаменатель используйте косую черту, т. е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.

Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .

Математические символы

Символ	Название символа	Символ Значение	Пример
+	plus sign	addition	1/2 + 1/3
—	minus sign	subtraction	1 1/2 — 2/3
*	asterisk	multiplication	2/3 * 3/4 ​​
×	times sign	multiplication	2/3 × 5/6
:	division sign	division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 ​​ • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций: PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание. BEDMAS — скобки, экспоненты, деление, умножение, сложение, вычитание BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание. GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание. MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS. Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо. Одна суббота Однажды субботним вечером в кинотеатре 40 девушек, 25 юношей, 18 женщин и 17 мужчин. Какую часть составляют девочки? Десятичная дробь Запишите дробь 3/22 в виде десятичной дроби. Кто-то Кто-то съел 1/10 торта, осталось только 9/10. Если вы съедите 2/3 оставшегося торта, сколько всего торта вы съедите? Ферма 6 На ферме 20 животных. Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме. Наименьшие члены 2 Мы можем записать выражение 4/12 в его наименьшем члене как 1/3. Чему равно 3/15 в наименьшем члене? Дробями Муравей поднимается на 2/5 шеста за первый час и на 1/4 шеста за следующий час. Какую часть шеста преодолевает муравей за два часа? Корзина для фруктов Если в корзине семь яблок и пять апельсинов, какая часть апельсинов в корзине с фруктами? Простейшая форма дроби Что такое 7/21 в простейшей форме? Дроби 80134 В школе 420 учеников. Двести пятьдесят два ученика переходят на 1-й уровень. Напишите в виде дроби, какая часть учеников идет в 1-й класс, а какая во 2-й класс. Сократите обе дроби до их основной формы. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт