Функция ЦЕЛОЕ — Служба поддержки Майкрософт

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции ЦЕЛОЕ в Microsoft Excel.

Описание

Округляет число до ближайшего меньшего целого.

Синтаксис

ЦЕЛОЕ(число)

Аргументы функции ЦЕЛОЕ описаны ниже.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
19,5
Формула	Описание	Результат
=ЦЕЛОЕ(8,9)	Округляет число 8,9 до ближайшего меньшего целого	8
=ЦЕЛОЕ(-8,9)	Округляет число -8,9 до ближайшего меньшего целого. При округлении отрицательного числа вниз оно округляется до ближайшего большего по модулю значения.	-9
=A2-ЦЕЛОЕ(A2)	Возвращает дробную часть положительного вещественного числа в ячейке A2	0,5

Корень (кубический, квадратный) в степени: решения, таблицы, примеры

Оглавление:

• Степень с натуральным показателем
• Степень с целым показателем
• org/ListItem»> Кубический корень
• Корень -ной степени
• Сравнение арифметических корней
• Как избавиться от иррациональности в знаменателе
• Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения

Степенью называется выражение вида .

Здесь  — основание степени,  — показатель степени.

к оглавлению ▴

Степень с натуральным показателем

Проще всего определяется степень с натуральным (то есть целым положительным) показателем.

По определению, .

Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.

.

Возвести число в куб — значит умножить его само на себя три раза.

.

Возвести число в натуральную степень  — значит умножить его само на себя раз:

к оглавлению ▴

Степень с целым показателем

Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.

По определению,

.

Это верно для . Выражение 0⁰ не определено.

Определим также, что такое степень с целым отрицательным показателем.

Конечно, все это верно для , поскольку на ноль делить нельзя.

Например,

Заметим, что при возведении в минус первую степень дробь переворачивается.

Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где  — целое,  — натуральное.

Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.

Определение.

Арифметический квадратный корень из числа  — это такое неотрицательное число, квадрат которого равен .

Согласно определению,

В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение    для нас сейчас имеет смысл только при .

Выражение всегда неотрицательно, т.е. . Например, .

Свойства арифметического квадратного корня:

 

Запомним важное правило:

По определению, .

к оглавлению ▴

Кубический корень

Аналогично, кубический корень из  — это такое число, которое при возведении в третью степень дает число .

Например, , так как ;

, так как ;

, так как .

Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.

Теперь мы можем дать определение корня -ной степени для любого целого .

к оглавлению ▴

Корень -ной степени

Корень -ной степени из числа  — это такое число, при возведении которого в -ную степень получается число .

Например,

Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.

Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.

Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.

По определению,

в общем случае .

Сразу договоримся, что основание степени больше 0.

Например,

Выражение по определению равно .

При этом также выполняется условие, что больше 0.

Например,

Запомним правила действий со степенями:

— при перемножении степеней показатели складываются;

— при делении степени на степень показатели вычитаются;

— при возведении степени в степень показатели перемножаются;

Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:

1.

Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.

2.

3.

Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при

Решение:

При получим

Ответ: -0,5.

5. Найдите значение выражения при

Решение:

При a = 12 получим

Мы воспользовались свойствами степеней.

Ответ: 144.

6. Найдите значение выражения при b = — 5.

Решение:

При b = — 5 получим:

Ответ: -125.

7. Расположите в порядке возрастания:

Решение:

Запишем выражения как степени с положительным показателем и сравним.

Так как то

Так как то

Сравним и для этого оценим их разность:

значит

Получим : поэтому

Ответ:

8. Представьте выражение в виде степени:

Решение:

Вынесем за скобку степень с меньшим показателем:

Ответ:

9. Упростите выражение:

Решение:

Приведем основания 6 и 12 к основаниям 2 и 3:

(выполним деление степеней с одинаковыми основаниями)

Ответ: 0,25.

10. Чему равно значение выражения при ?

Решение:

При получим

Ответ: 9.

к оглавлению ▴

Сравнение арифметических корней

11. Какое из чисел больше: или ?

Решение:

Возведем в квадрат оба числа (числа положительные):

Найдем разность полученных результатов:

так как

Значит, первое число больше второго.

Ответ:

к оглавлению ▴

Как избавиться от иррациональности в знаменателе

Если дана дробь вида то нужно умножить числитель и знаменатель дроби на :

Тогда знаменатель станет рациональным.

Если дана дробь вида или то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.

Сопряженные выражения — это выражения, отличающиеся только знаками. Например,

и и — сопряженные выражения.

Пример:

12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.

Пример 5.

13. Сравните и

1)

2) Сравним и 14.

то и а значит,

Ответ: меньше.

к оглавлению ▴

Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения

Покажем несколько примеров.

14. Упростите: выражения:

Пример 5.

т.к.

Пример 6.

Пример 7.

так как

Следующие несколько задач решаются с помощью формулы:

Решение:

Получим уравнение

Ответ:

19. Вычислите значение выражения:

Решение:

Ответ: 1.

20. Вычислите значение выражения:

Решение:

Ответ: 1.

21. Вычислите значение выражения: если

Решение.

Если то следовательно

Ответ: — 1.

22. Вычислите:

Решение:

Ответ: 1.

Рассмотрим уравнение вида где

Это равенство выполняется, только если

Подробно об таких уравнениях — в статье «Показательные уравнения».

При решении уравнений такого вида мы пользуемся монотонностью показательной функции.

23. Решите уравнение:

а)

б)

в)

Решение.

23. Решите уравнение:

Решение:

тогда

Ответ: -1.

24. Решите уравнение:

Решение:

Ответ: 4.

25. Решите уравнение:

Решение:

Значит,

Ответ: -0,2.

Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Корни и степени» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена: 08.01.2023

4.10: Сложение и вычитание смешанных чисел (часть 1)

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4996

• OpenStax
• OpenStax

Цели обучения

• Модель сложения смешанных чисел с общим знаменателем
• Сложить смешанные числа с общим знаменателем
• Модель вычитания смешанных чисел
• Вычитание смешанных чисел с общим знаменателем
• Сложение и вычитание смешанных чисел с разными знаменателями

будь готов!

Прежде чем приступить к работе, пройдите этот тест на готовность.

1. Нарисуйте фигуру в модели \(\dfrac{7}{3}\). Если вы пропустили эту проблему, просмотрите пример 4.1.6.
2. Заменить \(\dfrac{11}{4}\) на смешанное число. Если вы пропустили эту проблему, просмотрите пример 4.1.9.
3. Замените \(3 \dfrac{1}{2}\) на неправильную дробь. Если вы пропустили эту проблему, просмотрите пример 4.1.11.

Образец сложения смешанных чисел с общим знаменателем

До сих пор мы складывали и вычитали правильные и неправильные дроби, но не смешанные числа. Давайте начнем с размышлений о сложении смешанных чисел с помощью денег.

Если у Рона есть \(1\) доллар и \(1\) четвертак, у него есть \(1 \dfrac{1}{4}\) долларов. Если у Дона есть \(2\) долларов и \(1\) четвертак, у него есть \(2 \dfrac{1}{4}\) долларов. Что, если Рон и Дон соединит свои деньги? У них будет \(3\) долларов и \(2\) четвертаков. Они добавляют доллары и добавляют четвертак. Это составляет \(3 \dfrac{2}{4}\) долларов. Поскольку две четверти составляют полдоллара, у них будет \(3\) с половиной долларов или \(3 \dfrac{1}{2}\) долларов.

\[\begin{split} & 1 \dfrac{1}{4} \\ + & 2 \dfrac{1}{4} \\ \hline \\ & 3 \dfrac{2}{4} = 3 \dfrac{1}{2} \end{split} \nonumber \]

Когда вы добавляли доллары, а затем добавляли четверти, вы складывали целые числа, а затем добавляли дроби.

\[1 \dfrac{1}{4} + 2 \dfrac{1}{4} \nonumber \]

Мы можем использовать дробные круги для моделирования этого же примера:

Начните с \(1 \dfrac{1}{4}\).	одна целая и одна \(\dfrac{1}{4}\) штук		\(1 \dfrac{1}{4}\)
Добавьте \(2 \dfrac{1}{4}\) больше.	два целых и одна \(\dfrac{1}{4}\) штук		\(\begin{split}+ & 2 \dfrac{1}{4} \\ & \hline \end{split}\)
Сумма:	три целых и два \(\dfrac{1}{4}\)		\(3 \dfrac{2}{4} = 3 \dfrac{1}{2}\)

Пример \(\PageIndex{1}\): модель

Модель \(2 \dfrac{1}{3} + 1 \dfrac{2}{3}\) и введите сумму.

Решение

Мы будем использовать дробные круги, целые круги для целых чисел и \(\dfrac{1}{3}\) штук для дробей.

два целых и один \(\dfrac{1}{3}\)		\(2 \dfrac{1}{3}\)
плюс одно целое и два \(\dfrac{1}{3}\)s		\(\begin{split}+ & 1 \dfrac{2}{3} \\ & \hline \end{split}\)
сумма равна трем целым и трем \(\dfrac{1}{3}\)s		\(3 \dfrac{3}{3} = 4\)

Это то же самое, что и \(4\) целого. Итак, \(2 \dfrac{1}{3} + 1 \dfrac{2}{3} = 4\).

Упражнение \(\PageIndex{1}\)

Используйте модель, чтобы добавить следующее. Нарисуйте картинку, иллюстрирующую вашу модель. \(1 \dfrac{2}{5} + 3 \dfrac{3}{5}\)

Ответить

\(5\)

Упражнение \(\PageIndex{2}\)

Используйте модель, чтобы добавить следующее. Нарисуйте картинку, иллюстрирующую вашу модель. \(2 \dfrac{1}{6} + 2 \dfrac{5}{6}\)

Ответ

\(5\)

Пример \(\PageIndex{2}\): модель

Модель \(1 \dfrac{3}{5} + 2 \dfrac{3}{5}\) и представить сумму в виде смешанного числа.

Решение

Мы будем использовать дробные круги, целые круги для целых чисел и \(\dfrac{1}{5}\) штук для дробей.

одно целое и три \(\dfrac{1}{5}\)s		\(1 \dfrac{3}{5}\)
плюс два целых числа и три \(\dfrac{1}{5}\)s		\(\begin{split}+ & 2 \dfrac{3}{5} \\ & \hline \end{split}\)
сумма равна трем целым и шести \(\dfrac{1}{5}\)s		\(3 \dfrac{6}{5} = 4 \dfrac{1}{5}\)

Сложив целые круги и пятые части, мы получили сумму \(3 \dfrac{6}{5}\). Мы видим, что \(\dfrac{6}{5}\) эквивалентно \(1 \dfrac{1}{5}\), поэтому мы добавляем это к \(3\), чтобы получить \(4 \ dfrac{1}{5}\).

Упражнение \(\PageIndex{3}\)

Смоделируйте и задайте сумму в виде смешанного числа. Нарисуйте картинку, иллюстрирующую вашу модель. \(2 \dfrac{5}{6} + 1 \dfrac{5}{6}\)

Ответить

\(4\dfrac{2}{3}\)

Упражнение \(\PageIndex{4}\)

Смоделируйте и задайте сумму в виде смешанного числа. Нарисуйте картинку, иллюстрирующую вашу модель. \(1 \dfrac{5}{8} + 1 \dfrac{7}{8}\)

Ответ

\(3\dfrac{1}{2}\)

Добавление смешанных чисел

Моделирование с помощью дробных кругов помогает проиллюстрировать процесс сложения смешанных чисел: мы складываем целые числа и добавляем дроби, а затем, если возможно, упрощаем результат.

КАК: СЛОЖИТЬ СМЕШАННЫЕ ЧИСЛА С ОБЩИМ ЗНАМЕНАТЕЛЕМ

Шаг 1. Сложите целые числа.

Шаг 2. Сложите дроби.

Шаг 3. Упростите, если возможно.

Пример \(\PageIndex{3}\): добавить

Добавить: \(3 \dfrac{4}{9} + 2 \dfrac{2}{9}\).

Решение

Сложите целые числа.	\(\begin{split} & \textcolor{red}{3} \dfrac{4}{9} \\ + & \textcolor{red}{2} \dfrac{2}{9} \\ \hline \\ & \textcolor{red}{5} \end{split}\)
Сложите дроби.	\(\begin{split} & 3 \textcolor{red}{\dfrac{4}{9}} \\ + & 2 \textcolor{red}{\dfrac{2}{9}} \\ \hline \ \ & 5 \textcolor{red}{\dfrac{6}{9}} \end{split}\)
Упростите дробь.	\(\begin{split} & 3 \dfrac{4}{9} \\ + & 2 \dfrac{2}{9} \\ \hline \\ & \textcolor{red}{5 \dfrac{6} {9}} = 5 \dfrac{2}{3} \end{split}\)

Упражнение \(\PageIndex{5}\)

Найдите сумму: \(4 \dfrac{4}{7} + 1 \dfrac{2}{7}\).

Ответить

\(5\dfrac{6}{7}\)

Упражнение \(\PageIndex{6}\)

Найдите сумму: \(2 \dfrac{3}{11} + 5 \dfrac{6}{11}\).

Ответить

\(7\dfrac{9}{11}\)

В примере \(\PageIndex{3}\) сумма дробей была правильной дробью. Теперь рассмотрим пример, где сумма является неправильной дробью.

Пример \(\PageIndex{4}\): добавьте

Найдите сумму: \(9 \dfrac{5}{9} + 5 \dfrac{7}{9}\).

Решение

Сложите целые числа, а затем сложите дроби.	\(\begin{split} & 9 \dfrac{5}{9} \\ + & 5 \dfrac{7}{9} \\ \hline \\ & 14 \dfrac{12}{9} \end{ разделить}\)
Перепишите \(\dfrac{12}{9}\) как неправильную дробь.	\(14 + 1 \dfrac{3}{9}\)
Доп.	\(15 \dfrac{3}{9}\)
Упрощение.	\(15 \dfrac{1}{3}\)

Упражнение \(\PageIndex{7}\)

Найдите сумму: \(8 \dfrac{7}{8} + 7 \dfrac{5}{8}\).

Ответить

\(16\dfrac{1}{2}\)

Упражнение \(\PageIndex{8}\)

Найдите сумму: \(6 \dfrac{7}{9} + 8 \dfrac{5}{9}\).

Ответить

\(15\dfrac{1}{3}\)

Альтернативным методом сложения смешанных чисел является преобразование смешанных чисел в неправильные дроби и последующее сложение неправильных дробей. Этот метод обычно пишется горизонтально.

Пример \(\PageIndex{5}\): добавить

Сложить путем преобразования смешанных чисел в неправильные дроби: \(3 \dfrac{7}{8} + 4 \dfrac{3}{8}\).

Раствор

Преобразование в неправильные дроби.	\(\dfrac{31}{8} + \dfrac{35}{8}\)
Сложите дроби.	\(\dfrac{31 + 35}{8}\)
Упростите числитель.	\(\dfrac{66}{8}\)
Перепишите как смешанное число.	\(8 \dfrac{2}{8}\)
Упростите дробь.	\(8 \dfrac{1}{4}\)

Поскольку задача была задана в виде смешанного числа, запишем сумму в виде смешанного числа.

Упражнение \(\PageIndex{9}\)

Найдите сумму путем преобразования смешанных чисел в неправильные дроби: \(5 \dfrac{5}{9} + 3 \dfrac{7}{9}\)

Ответить

\(9\dfrac{1}{3}\)

Упражнение \(\PageIndex{10}\)

Найдите сумму, превратив смешанные числа в неправильные дроби: \(3 \dfrac{7}{10} + 2 \dfrac{9{10}\)

Ответ

\(6\dfrac{3}{5}\)

В таблице \(\PageIndex{1}\) сравниваются два метода сложения на примере выражения \(3 \dfrac{2}{5} + 6 \dfrac{4}{5}\). Какой путь вы предпочитаете?

Таблица \(\PageIndex{1}\)

Смешанные номера	Неправильные дроби
\(\begin{split} & 3 \dfrac{2}{5} \\ + & 6 \dfrac{4}{5} \\ \hline \\ & 9\dfrac{6}{5} \end{split}\)	\(3 \dfrac{2}{5} + 6 \dfrac{4}{5}\)
\(9 + \dfrac{6}{5}\)	\(\dfrac{17}{5} + \dfrac{34}{5}\)
\(9 + 1 \dfrac{1}{5}\)	\(\dfrac{51}{5}\)
\(10 \dfrac{1}{5}\)	\(10 \dfrac{1}{5}\)

Модель вычитания смешанных чисел

Давайте снова подумаем о пицце, чтобы смоделировать вычитание смешанных чисел с общим знаменателем. Предположим, вы только что испекли целую пиццу и хотите отдать половину пиццы своему брату. Что нужно сделать с пиццей, чтобы отдать ему половину? Вы должны разрезать его как минимум на две части. Тогда вы можете дать ему половину.

Мы будем использовать дробные круги (пиццы!), чтобы визуализировать процесс. Начните с одного целого.

Рисунок \(\PageIndex{1}\)

Алгебраически вы должны написать:

Пример \(\PageIndex{6}\): вычесть

\(Использовать модель для вычитания 1 — \dfrac{1}{3}\).

Решение

Упражнение \(\PageIndex{11}\)

Используйте модель для вычитания: \(1 − \dfrac{1}{4}\).

Ответ

\(\dfrac{3}{4}\)

Упражнение \(\PageIndex{12}\)

Используйте модель для вычитания: \(1 − \dfrac{1}{5}\).

Ответить

\(\dfrac{4}{5}\)

Что, если мы начнем с нескольких целых? Давайте узнаем.

Пример\(\PageIndex{7}\): вычесть

Используйте модель для вычитания: \(2 − \dfrac{3}{4}\).

Раствор

Упражнение \(\PageIndex{13}\)

Используйте модель для вычитания: \(2 − \dfrac{1}{5}\).

Ответить

\(\dfrac{9}{5}\)

Упражнение \(\PageIndex{14}\)

Используйте модель для вычитания: \(2 − \dfrac{1}{3}\).

Ответить

\(\dfrac{5}{3}\)

В следующем примере мы вычтем более одного целого.

Пример \(\PageIndex{8}\): вычесть

Используйте модель для вычитания: \(2 − 1 \dfrac{2}{5}\).

Решение

Упражнение \(\PageIndex{15}\)

Используйте модель для вычитания: \(2 − 1 \dfrac{1}{3}\).

Ответить

\(\dfrac{2}{3}\)

Упражнение \(\PageIndex{16}\)

Используйте модель для вычитания: \(2 − 1 \dfrac{1}{4}\).

Ответить

\(\dfrac{3}{4}\)

Что делать, если вы начинаете со смешанного числа и вам нужно вычесть дробь? Подумайте о такой ситуации: вам нужно поставить три четверти в парковочный счетчик, но у вас есть только счет \(\$1\) и одна четвертак. Что ты можешь сделать? Вы можете разменять долларовую купюру на \(4\) четвертаков. Стоимость \(4\) четвертаков такая же, как и одна долларовая купюра, но \(4\) четверти более полезны для парковочного счетчика. Теперь вместо счета \(\$1\) и одной четверти у вас есть \(5\) четвертаков и вы можете положить \(3\) четвертаков в счетчик.

Это моделирует то, что происходит, когда мы вычитаем дробь из смешанного числа. Мы вычли три четверти из одного доллара и одну четверть.

Мы также можем смоделировать это с помощью дробных кругов, как мы делали для сложения смешанных чисел.

Пример \(\PageIndex{9}\): вычесть

Использовать модель для вычитания: \(1 \dfrac{1}{4} − \dfrac{3}{4}\)

Решение

Переписать вертикально. Начните с одного целого и одной четверти.		\(\begin{split} & \textcolor{red}{1 \dfrac{1}{4}} \\ — & \dfrac{3}{4} \\ \hline \end{split}\)
Поскольку дроби имеют знаменатель 4, разрежьте целое на 4 части. Теперь у вас есть \(\dfrac{4}{4}\) и \(\dfrac{1}{4}\), что равно \(\dfrac{5}{4}\).		\(\begin{split} & \textcolor{red}{\dfrac{5}{4}} \\ — & \dfrac{3}{4} \\ \hline \end{split}\)
Заберите \(\dfrac{3}{4}\). Осталось \(\dfrac{1}{2}\).		\(\begin{split} & \dfrac{5}{4}\\\textcolor{red}{- & \dfrac}3}{4}}\\ \hline \\ & \dfrac{2}{4 } = \dfrac{1}{2} \end{split}\)

Упражнение \(\PageIndex{17}\)

Используйте модель для вычитания. Нарисуйте картинку, иллюстрирующую вашу модель. \(1 \dfrac{1}{3} − \dfrac{2}{3}\)

Ответ

Упражнение \(\PageIndex{18}\)

Используйте модель для вычитания. Нарисуйте картинку, иллюстрирующую вашу модель. \(1 \dfrac{1}{5} − \dfrac{4}{5}\)

Ответ

Авторы и авторство

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   На этой странице нет тегов.

Советы по обучению сложению и вычитанию дробей

3-й класс

Купить сейчас

4 класс

Купить сейчас

5-й класс

Купить сейчас

2-й класс

Купить сейчас

8 февраля 2021 г. Оставить комментарий

Пока мы продолжаем изучать дроби, пришло время складывать и вычитать. Опять же, моделирование является ключом к тому, чтобы помочь учащимся понять и объяснить процесс сложения и вычитания дробей. В таблице ниже показаны ожидания от сложения и вычитания дробей в 4-м и 5-м классах.

4 класс:

• Понимание сложения и вычитания дробей как соединения и разделения частей одного целого (4.NF.3a)
• Сложение и вычитание дробей с одинаковыми знаменателями (4.NF.3a)
• Разложить дробь на сумму дробей и записать с помощью уравнения (4.NF.3b)
• Сложение и вычитание смешанных чисел с одинаковыми знаменателями (4. NF.3c)
• Решайте текстовые задачи на сложение и вычитание дробей; использовать визуальные эффекты для моделирования (4.NF.3d)

5 класс:

• Сложение и вычитание дробей с разными знаменателями (включая смешанные числа) путем нахождения эквивалентных дробей (5.NF.1) 
• решать текстовые задачи, используя сложение и вычитание дробей с одинаковыми и разными знаменателями, относящимися к одному и тому же целому (5.NF.2)
• Используйте эталонные дроби и числовой смысл дробей, чтобы оценить в уме и решить, является ли ответ разумным (5.NF.2).

Начните с простого: 1 апельсин плюс 1 апельсин равно 2 апельсинам, так же как 1 треть плюс 1 треть равно 2 третям. Это помогает учащимся связать знаменатель с любой другой единицей измерения, такой как апельсины, мили, часы и т. д.  Это также может помочь понять, что, как нельзя просто сложить мили и футы, так нельзя сложить трети и четверти.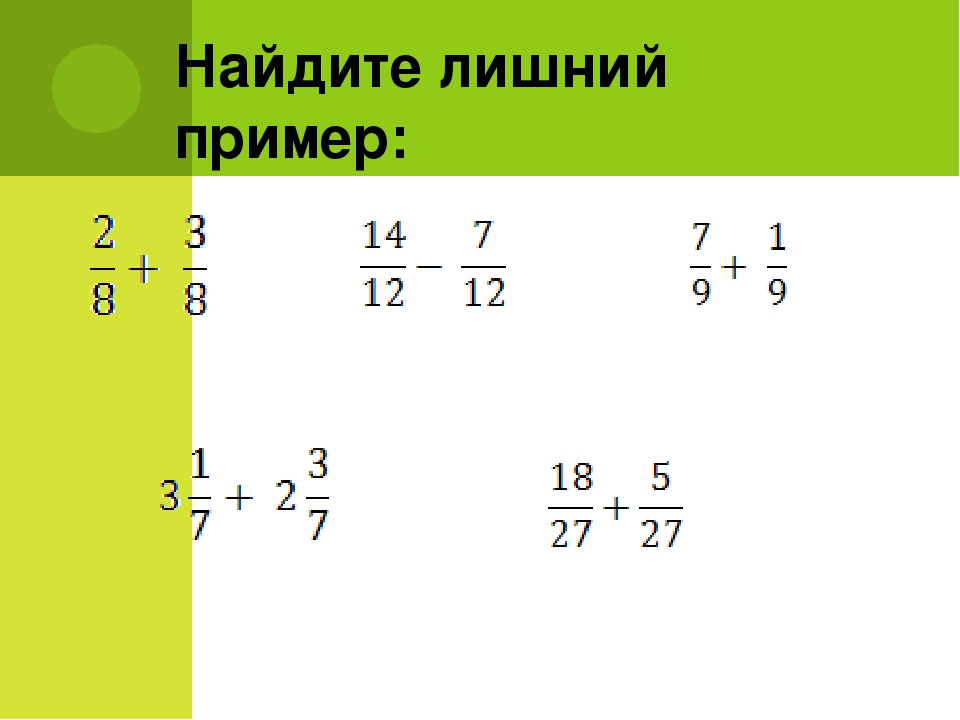 Но это может быть сделано!!

Смешанные числа

Попробуйте складывать и вычитать смешанные числа или неправильные дроби с помощью блоков шаблонов и числовых линий. Использование блоков шаблонов помогает учащимся физически складывать дроби или удалять дробные части при вычитании.

Вот пример использования числовой строки для сложения и вычитания чисел, превышающих одно целое. Числовые линии хороши тем, что они могут легко выходить за пределы одного или даже двух целых чисел.

Различные знаменатели

Сложение и вычитание с разными знаменателями требует дополнительного шага. Яичные коробки — отличный способ показать, как можно привести дроби к общему знаменателю, чтобы складывать и вычитать дроби, поскольку во всех коробках будет 12 яиц.

Задачи со словами

Хотя задачи со словами иногда могут быть более сложными для учащихся, работа в контексте реальной жизни может помочь учащимся действительно понять, зачем они изучают дроби. Когда учащиеся читают и работают над пониманием представленных проблем, они могут использовать некоторые из вышеперечисленных моделей или использовать бумагу с сеткой, чтобы нарисовать проблемы, чтобы смоделировать свое мышление.

Ресурсы для обучения учащихся сложению и вычитанию дробей

4 класс:

    

5-й класс:

    

Бесплатное сложение и вычитание дробей с помощью таблицы для яиц

Downloaded Under: Fractions & 04 Decimals

Занятия по математике для 3-го класса: распечатка и цифровая математика

Получите доступ к ТРЕМ печатным и цифровым математическим играм для повторения дробей!

Я хочу эту халяву!

Вам также могут понравиться эти публикации

Взаимодействие с читателями

Math Tech All Access

Получите мгновенный доступ ко всем ресурсам Math Tech Connections!

Вступай в клуб!

Интерактивные цифровые математические слайды

Все ресурсы

Здравствуйте, друзья!

Меня зовут Мариэла! Я преподаватель и основатель Math Tech Connections.