Как делить со скобками, что вперед: деление или умножение, как решить 36:3 (8–6) дробь 6, правильный ответ на пример — 17 января 2023

Сможете решить правильно?

Иллюстрация: Юрий Орлов / NGS.RU

Поделиться

Минимум неделю в интернете миллионы людей ломают копья из-за простенького, на первый взгляд, примера. NGS.RU решил задачку вместе с кандидатом физико-математических наук, доцентом и преподавателем Новосибирского государственного университета Ильей Марьясовым.

Вот этот пример: 36 : 3 (8 − 6) дробь 6.

Некоторые люди готовы спорить часами, как решить этот пример

Фото: Александра Бруня / NGS.RU

Поделиться

— Подвоха здесь особо никакого нет. У нас в математике есть соглашение о том, как у нас должны выполняться арифметические операции. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Когда нужно изменить порядок вычисления, чтобы сложение и вычитание выполнялись раньше, то используются скобки. И еще один момент — когда появляются дроби, а дробная черта — это деление, то в этом случае оно выполняется в последнюю очередь, — объяснил Илья Марьясов

Разбираемся с числителем. По очереди идут деление, умножение, вычитание — при этом последняя операция идет в скобках. Начинаем решать слева направо.

— Поскольку деление и умножение равноправны. Сначала 36 делим на 3 и получаем 12. Потом мы должны выполнить умножение, но поскольку вычитание стоит в скобках, то сначала делаем его. Из 8 вычитаем 6 и получаем 2. Теперь делаем умножение. Мы 12 умножаем на 2 и получаем 24. Теперь делим числитель на знаменатель. То есть 24 делим на 6 и получаем 4, — объяснил специалист.

Правильный ответ — 4.

— Как изучают математику в школе. В начальном звене вводят операции — сложение, вычитание, умножение и деление. Примерно до 6-го класса дети не знают, что существуют рациональные числа, которые записываются в виде дробной черты. Когда они вводятся, то выясняется, что операцию деления можно записать не в виде двух точек. И до самого вуза очень часто все выражения записываются, как дробное число и отдельная операция деления через две точки редко используется. Так умножение у людей фиксируется как приоритетная операция, — объяснил Илья Марьясов.

В итоге это приводит к ошибке в вычислениях.

— У людей возникает соблазн 3 умножить на 8 минус 6 (то есть на 2) и получается у них 6. Потом 36 делят на 6, получая 6. И в итоге 6 делят на 6 и выходит 1. Это неверный ответ в данном случае, — отметил математик.

Ранее в Высшей школе экономики подсчитали, что средний проходной балл ЕГЭ для поступления в вузы снизился впервые за 10 лет. Предлагаем вам ответить на несколько вопросов (разных лет) из того самого итогового среза знаний.

По теме

• 20 января 2023, 16:00

  Один и тот же пример в разных странах решают по-разному. Как это получается?

• 18 декабря 2022, 15:30

  «Любите ли вы сплетничать?» Журналист попытался обмануть детектор лжи, и вот что обнаружил полиграф

• 19 сентября 2022, 10:00

  Это точно русский? Проверьте, сможете ли вы написать правильно все эти слова

• 18 декабря 2022, 14:00

  Русский не родной? 10 простейших слов, которые все пишут с ошибками

Александра Бруня

Корреспондент

МатематикаРазборРешениеПример

• ЛАЙК13
• СМЕХ41
• УДИВЛЕНИЕ6
• ГНЕВ15
• ПЕЧАЛЬ7

Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter

КОММЕНТАРИИ215

Читать все комментарии

Гость

Войти

Новости РЎРњР?2

Новости РЎРњР?2

Комбинаторика: основные правила и формулы.

КОМБИНАТОРИКА

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и  принципы  комбинаторики  используются  в  теории  вероятностей для подсчета  вероятности  случайных  событий и,  соответственно, получения законов распределения случайных величин. Это,  в  свою  очередь,  позволяет  исследовать  закономерности массовых случайных явлений, что является весьма важным для правильного понимания  статистических  закономерностей, проявляющихся в природе и технике.

 

Правила сложения и умножения в комбинаторике

Правило суммы.  Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m  способами.

 

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Решение

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

 

Правило произведения.  Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k  способами, то все k действий вместе могут быть выполнены:

способами.

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Решение

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

 Сочетания без повторений. Сочетания с повторениями

 Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Решение

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

.

 Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

.

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

.

 Размещения без повторений. Размещения с повторениями

 Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

 

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Решение.

В  данной  задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким  образом,  задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

 

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог.

Сколько различных пятизначных номеров может составить мальчик?

Решение

Можно  считать,  что  опыт  состоит  в 5-кратном выборе  с возращением одной из 3 цифр (1, 3, 7). Таким образом,  число  пятизначных  номеров  определяется  числом  размещений с повторениями из 3 элементов по 5:

.

 Перестановки без повторений. Перестановки с повторениями

 Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Решение

Генеральной  совокупностью  являются 4  буквы слова  «брак» (б, р, а, к).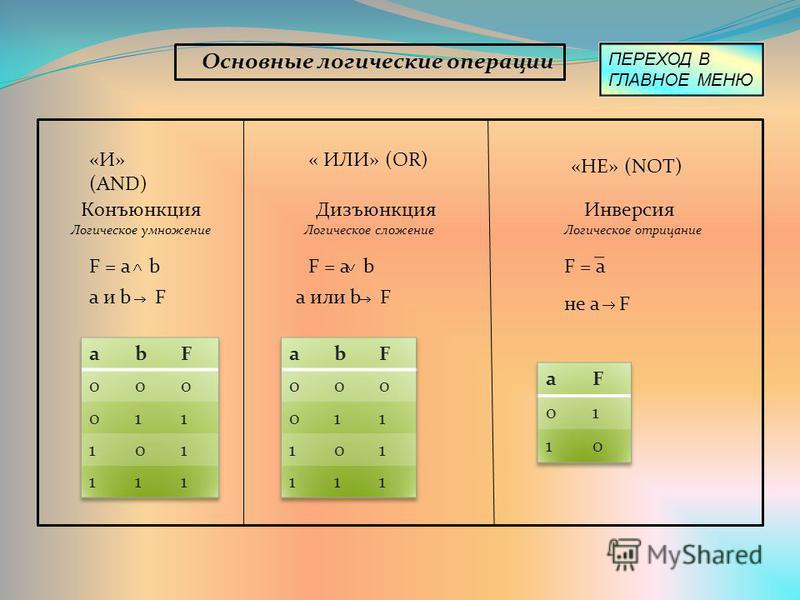 Число  «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Решение

Здесь 1 буква  «м», 4 буквы «и», 3 буквы «c» и 1 буква  «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

Купить

Документ без названия

Документ без названия

 

В регулярной алгебре мы можем комбинировать простые операции в более сложные операторы; например, мы можем написать выражение, которое включает в себя и сложение, и умножение: 4x+7, потому что у нас есть правила, которые говорят нам, что когда мы сталкиваемся с этим выражением, мы всегда сначала выполняем умножение, а затем сложение.

Теперь, когда мы узнали о четырех операциях над множествами: объединении, пересечении, разности и дополнении, мы хотим иметь возможность писать более сложные выражения, такие как, например, (A∪B′)∩A. Мы хотим иметь возможность рисовать диаграммы Венна для этих составных выражений, и мы хотим иметь возможность вычислять результат для этих составных выражений, если нам дано точное содержание каждого из задействованных наборов.

Дополнительная информация о рисовании диаграмм Венна:

Прежде чем мы пойдем дальше в изучении составных операций над множествами, нам нужно убедиться, что мы поняли некоторые важные моменты, касающиеся того, как рисовать диаграмму Венна.

Как нарисовать диаграмму Венна, содержащую два набора::

При построении диаграмм Венна мы должны быть осторожны, чтобы не делать предположений об отношениях между множествами, когда мы ничего не знаем о самих множествах. Если у нас есть два множества, то они могут быть связаны тремя возможными способами:

Назовем наши два набора A и B.

1. Один набор является подмножеством другого: (Здесь B является подмножеством A.)
   

2. Два набора не пересекаются:
   

3. Два набора пересекаются:
   

Когда мы ничего не знаем о наборах, с которыми работаем, мы всегда рисуем их так, как будто они перекрываются

:

Почему это работает? Мы на мгновение закрасим некоторые области разными цветами, чтобы объяснить, почему. На следующей диаграмме мы заштриховали множество A красным, а множество B синим; фиолетовый указывает, где были затенены и красный, и синий.

 

• Если два множества НЕ ПЕРЕСЕКАЮТСЯ, эта картина все еще работает, если мы предположим, что A ∩ B ПУСТО. Помните, что A ∩ B — это фиолетовая область в середине, где A и B перекрываются.

• Если A⊆B, то эта картина все еще работает, если мы предположим, что A-B ПУСТОЙ. Помните, что A-B — это просто красная область A слева (не включает фиолетовую область A, где она пересекается с B).

• Если B⊆A, то эта картина все еще работает, если мы предположим, что B-A ПУСТ. Помните, что B-A — это просто синяя область B справа (она не включает фиолетовую область B, где она пересекается с A).

Если вы рисуете диаграмму Венна, чтобы решить задачу, и не знаете, что это за наборы, обязательно нарисуйте диаграмму таким образом, чтобы два набора перекрывались.

Важно понимать, что мы никогда не можем предполагать, что произвольное множество не пусто.

Тот факт, что множество занимает место на диаграмме Венна, не означает, что оно обязательно содержит элементы. Например, если бы A на диаграмме Венна выше было пустым множеством, то это означало бы, что область, заштрихованная красным, и область, заштрихованная фиолетовым цветом (где также есть красное затенение) будут пустыми. Это означает, что хотя эти заштрихованные области на диаграмме занимают место, в них может ничего не быть.

Диаграммы Венна с 3 наборами:

Во всех примерах, которые мы будем рассматривать в этом разделе, мы часто будем работать с 3 или более множествами. Мы можем нарисовать диаграмму Венна с любым количеством множеств в ней. Общая диаграмма Венна для трех наборов будет выглядеть примерно так:

Важно всегда маркировать ваши диаграммы Венна. Всякий раз, когда вы используете диаграмму Венна для представления набора, вы должны поместить метку, указывающую, что затенение изображает выше или ниже диаграммы Венна. См. некоторые из примеров ниже:

Порядок операций на комплектах:

Иногда нам нужно объединить более двух наборов и более одной операции, чтобы создать более сложное выражение. Но для этого мы должны установить некоторый набор правил, чтобы мы знали, в каком порядке выполнять каждую операцию. Как и в случае с числами, мы используем круглые скобки, если хотим, чтобы операция была выполнена первой.

1. Как и в случае с числами, мы всегда сначала делаем что-то в скобках. Если имеется более одного набора скобок, мы работаем изнутри наружу.

2. Сначала делаем комплементы.

3. Операции объединения, пересечения и разности равны по порядку. Поэтому, если у нас есть более одной из них одновременно, мы должны использовать круглые скобки, чтобы указать, какая из этих операций должна быть выполнена первой. Например, выражение A∪B-C не имеет никакого смысла, потому что мы не знаем, какую операцию мы должны выполнить в первую очередь: взять сначала объединение, а затем разность, или сначала взять разность, а затем объединение ? Чтобы это было ясно, нам нужно писать либо (A∪B)-C, либо A∪(B-C).

Давайте рассмотрим несколько примеров. Для каждого из этих примеров пусть U={1,2,3,4,5,6,7,8,9}, A={1,2,3,4,5}, B={2,4, 6,8}, С={4,5,6}:

Итак, наша диаграмма Венна будет выглядеть следующим образом: (Каждый элемент я расставил по своим местам на диаграмме Венна. )

Пример 1:

(А∪В)-С

Сначала находим A∪B. В этом случае A∪B={1,2,3,4,5,6,8}. На диаграмме Венна для A∪B мы получили бы:

А∪В

Помните, что когда мы берем A∪B, мы игнорируем множество C. Не позволяйте тому факту, что существует множество C, отвлекать вас. Это не имеет ничего общего с операцией A ∪ B, поэтому пока мы ее игнорируем; мы будем использовать его на следующем шаге.

Далее находим (A∪B)-C. Поскольку A∪B={1,2,3,4,5,6,8} и C={4,5,6}, мы просто подставляем эти наборы вместо A∪B и C соответственно, чтобы получить:

(А∪В)-С={1,2,3,4,5,6,8}-{4,5,6}={1,2,3,8}

Чтобы создать диаграмму Венна для (A∪B)-C, мы должны сначала иметь диаграммы Венна для A∪B и для C, поэтому вот диаграмма Венна для C, где множество C заштриховано синим цветом:

С

Теперь мы поместим обе эти штриховки для A∪B и C вместе на одну и ту же диаграмму Венна, и мы получим следующую картину; набор C показан синим цветом, набор A∪B красным, а область, где они пересекаются, становится фиолетовой:

A∪B красного цвета, C синего цвета

Теперь, чтобы взять (A∪B)-C, мы просто убираем все, что было заштриховано синим цветом (включая фиолетовую часть), потому что мы хотим сохранить все, что есть в множестве A∪B, но избавиться от всего, что есть в наборе. C. То, что осталось, это диаграмма Венна для (A∪B)-C:

А∪В

Обратите внимание, что именно то, что осталось в заштрихованной красным области, — это множество {1,2,3,8}, именно то, что мы получили выше, когда вычисляли это, используя только множества без диаграмм!

Пример 2:

А∪(В∩С′)

Сначала находим C′, потому что сначала делаем то, что в скобках; в скобках у нас есть две операции: пересечение и дополнение, и порядок операций говорит нам, что сначала нужно выполнить дополнение.

В данном случае C={4,5,6}. Итак, C′={4,5,6}′={1,2,3,7,8,9}.

Чтобы найти диаграмму Венна для C′, мы должны сначала нарисовать диаграмму Венна для C: (Здесь C заштриховано синим цветом.)

С

Теперь, чтобы найти C’, мы заштрихуем любую часть, которая была белой на диаграмме для C, чтобы получить следующую диаграмму C’, где C’ закрашено красным:

С’

Теперь, когда у нас есть C′, теперь мы хотим найти B∩C′. Поскольку B={2,4,6,8} и C′={1,2,3,7,8,9}, подставляя эти множества в B∩C′, мы получаем:

B∩C′={2,4,6,8}∩{1,2,3,7,8,9}={2,8}

Чтобы построить диаграмму Венна для B∩C′, нам сначала нужны диаграмма Венна для B и диаграмма Венна для C′. На нашей диаграмме Венна для B мы заштриховали B синим цветом:

.

Б

Теперь мы сложим наши диаграммы Венна для B и для C’ вместе; мы заштриховываем C’ красным, а B синим, чтобы область, где B и C’ перекрываются, была фиолетовой. Обратите внимание, что эта фиолетовая область находится там, где пересекаются C′ и B, поэтому числа, заштрихованные фиолетовым, в точности являются элементами множества {2,8}!

C’ красного цвета, B синего цвета

Итак, мы берем только фиолетовую область, где B и C’ пересекаются, и рисуем нашу диаграмму Венна для B∩C’ следующим образом:

Б∩С’

Теперь мы можем взять A∪(B∩C′). Поскольку теперь мы знаем, что B∩C′={2,8}, а A={1,2,3,4,5}, мы можем подставить эти множества в A∪(B∩C′), чтобы получить:

А∪(В∩С′)={1,2,3,4,5}∪{2,8}={1,2,3,4,5,8}.

Будьте осторожны! Помните, что когда мы берем СОЮЗ, мы складываем ВСЕ элементы обоих наборов вместе. Это ПРОТИВОПОЛОЖНО взятию ПЕРЕСЕЧЕНИЯ, когда мы берем только элементы, которые находятся в ОБОИХ наборах одновременно! Будьте осторожны, не перепутайте объединение с пересечением.

Чтобы получить диаграмму Венна для A∪(B∩C′), нам нужны диаграммы Венна для A и для B∩C′. Мы рисуем диаграмму Венна для A, заштриховав A желтым цветом:

.

А

Итак, теперь мы соединим нашу штриховку для A с нашей штриховкой для B ∩ C ‘, так что A будет закрашено желтым, а B ∩ C ‘заштриховано фиолетовым на той же диаграмме Венна. Там, где желтый набор A и фиолетовый набор (B ∩ C′) перекрываются, мы получаем что-то вроде сине-зеленого, так что картина выглядит так:0005

 

A желтого цвета, B∩C′ фиолетового цвета

Поскольку мы хотим взять ОБЪЕДИНЕНИЕ желтого множества A и фиолетового множества B∩C′, мы берем всю заштрихованную область, где есть желтый и фиолетовый, и где желтый и фиолетовый перекрываются, чтобы получить сине-зеленый. . Чтобы сделать нашу окончательную диаграмму Венна ясной, мы закрасим всю область одним цветом (здесь мы выбрали оранжевый):

.

А∪(В∩С′)

Обратите внимание, что наша последняя заштрихованная область — это множество {1,2,3,4,5,8}, точно такой же ответ, который мы получили для A∪(B∩C′) выше!

 

Когда следует использовать диаграммы Венна?

Для любых данных наборов и операций мы можем выполнять операции, либо рисуя несколько диаграмм Венна шаг за шагом, либо мы можем просто работать с элементами самих наборов. Обратите внимание на инструкции, чтобы решить, какой из этих методов вас просят использовать.

Как правило, если мы знаем, что такое множества, мы просто вычисляем ответ, но если мы не знаем, что это за множества, мы рисуем диаграммы Венна, потому что Диаграммы Венна — единственный способ представления абстрактных множеств, о которых мы ничего не знаем!

Использование диаграмм Венна для доказательства равенства двух выражений:

Мы также можем использовать диаграммы Венна, чтобы доказать равенство двух выражений. Если мы хотим показать, что два выражения, включающие множества и операции над множествами, на самом деле равны независимо от того, что представляют собой множества, все, что нам нужно сделать, это нарисовать диаграмму Венна для каждого выражения и показать, что две диаграммы Венна идентичны.

Например, когда мы узнали определения дополнения и различия, мы поняли, что A’ и U-A — это одно и то же. Таким образом, мы можем написать A′=U-A. Лучший способ доказать, что два выражения одинаковы, — нарисовать их диаграммы Венна и показать, что они имеют точно такую ​​же заштрихованную площадь.

Мы знаем, что A’ имеет следующую диаграмму Венна:

А’

Теперь нарисуем диаграмму Венна U-A. Сначала у нас должна быть диаграмма Венна для U и диаграмма Венна для A.

У

Здесь множество U заштриховано красным цветом. Обратите внимание, что это вся диаграмма Венна, потому что универсальное множество всегда включает все.

А

Здесь множество A закрашено желтым цветом.

Теперь мы помещаем U и A вместе на одну и ту же диаграмму Венна так, чтобы A была закрашена желтым цветом, а U — красным, так что места, где красный и желтый перекрываются, были оранжевыми:

А желтый, У красный

Чтобы взять разность U-A, мы должны начать с U, части, заштрихованной красным, и удалить все части, которые были в A или были закрашены желтым цветом. Поскольку оранжевая часть этой диаграммы была закрашена желтым, мы должны удалить ее из диаграммы, чтобы получить диаграмму для UA:

U-A

Обратите внимание, что диаграмма Венна для A′ и диаграмма Венна для U-A идентичны! Это доказывает, что A′=U=A, что бы ни содержали множества U и A!

Будьте осторожны — Вы НЕ МОЖЕТЕ доказать, что два выражения всегда равны, приведя ПРИМЕРЫ определенных множеств, которые сделали бы выражения равными; вы можете сделать это, только показав, что их диаграммы Венна равны. Это очень важное понятие в математике: ПРИМЕР: НЕ ДОКАЗАТЕЛЬСТВО! Убедитесь, что вы знаете разницу между примером и доказательством!

Чтобы проиллюстрировать эту идею, давайте приведем пример и доказательство для нескольких разных задач:

Пример:

А-В=(А’∪В)’

Сначала давайте придумаем пример. Если мы сделаем A={15,20,25} и B={20,30}, и U={5,10,15,20,25,30}, тогда:

А-Б={15,20,25}-{20,30}={15,25}

Чтобы найти (A′∪B)′, нам нужно сначала найти A′, потому что оно находится внутри круглых скобок, а дополнения идут первыми. Здесь А’={5,10,30}.

Далее мы можем найти A′∪B={5,10,30}∪{20,30}={5,10,20,30}.

Тогда мы можем найти (A′∪B)′={5,10,20,30}′={15,25}.

Поскольку AB={15,25} и (A′∪B)′={15,25}, мы можем сказать, что AB=(A′∪B)′.

Но это только ПРИМЕР! Это показывает только, что AB=(A′∪B)′, когда A={15,20,25} и B={20,30}, и U={5,10,15,20,25,30}.

Мы не можем сказать, верно ли A-B=(A′∪B)′ для ВСЕХ ВОЗМОЖНЫХ НАБОРОВ A и B! Так что это НЕ доказательство!

Доказательство:

Теперь попробуем доказательство. Единственный способ доказать, что AB = (A′∪B)′ для всех возможных множеств A и B, — это показать, что диаграмма Венна для AB такая же, как диаграмма Венна для (A′∪B)′.

Сначала напомним, что диаграмма Венна AB выглядит так:

А-Б

Теперь нам нужно шаг за шагом построить диаграмму Венна для (A′∪B)′, чтобы показать, что она точно такая же, как и выше.

Чтобы сделать это, мы должны сначала нарисовать A′ (что мы уже сделали в предыдущем примере, поэтому мы просто воспользуемся этой диаграммой здесь), потому что мы должны сначала сделать то, что указано в скобках, а дополнение идет перед каждой другой операцией. .

Диаграмма Венна для A’:

А’

 

Теперь возьмем диаграмму Венна для B:

Б

Будьте осторожны. Обратите внимание, что у нас есть овал, обозначающий множество B на диаграмме Венна для A′, и овал, обозначающий множество A на диаграмме Венна для B, что в общем случае не обязательно.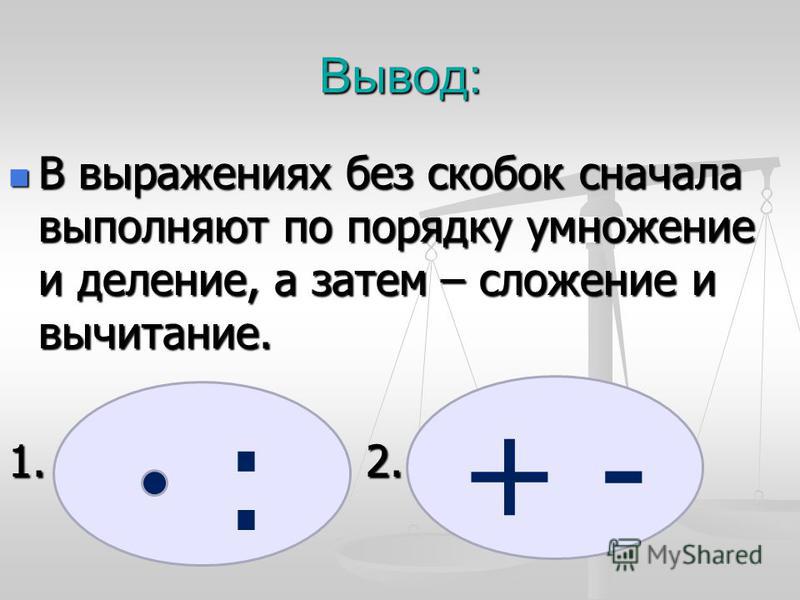 ОДНАКО, поскольку в этом случае нам нужны эти диаграммы Венна только как шаг для создания диаграммы Венна для (A′∪B)′, а ЭТО ОКОНЧАТЕЛЬНОЕ ВЫРАЖЕНИЕ содержит ОБА множества A и B, то ОБА овал, обозначающий множество A, И овал, указывающий, что множество B должен быть на КАЖДОЙ диаграмме Венна, которую мы делаем, ведущую к нашей диаграмме Венна для (A′∪B)′. Если бы на диаграмме Венна для A’ отсутствовал овал, указывающий на множество B, или на диаграмме Венна для B отсутствовал овал, указывающий на множество A, то мы не смогли бы поместить их вместе на одной диаграмме Венна, чтобы получить объединение .

Теперь закрасим B желтым, а A′ синим на той же диаграмме Венна, чтобы найти A′∪B. Области на диаграмме Венна, где желтая B и синяя A’ перекрываются, становятся зелеными:

A’ синего цвета, B желтого цвета

Мы хотим взять объединение желтого множества B и синего множества A′, поэтому мы берем все, что было закрашено желтым или синим (или зеленым, где желтый и синий перекрываются). Чтобы сделать нашу диаграмму более ясной, мы перерисовываем ее, чтобы она была полностью окрашена в один цвет, поэтому диаграмма Венна, которую мы получаем для A′∪B, будет следующей:

А’∪В

 

Теперь нам нужно найти (A′∪B)′ . Итак, мы хотим взять дополнение заштрихованной красным областью выше, которая представляет множество A′∪B. Напомним, что дополнение — это все, что есть в универсальном множестве, но не в A′∪B. Область, которая находится в U, но не в A′∪B, — это точно белая область на диаграмме Венна. Таким образом, чтобы закрасить (A′∪B)′ , все, что нам нужно сделать, это закрасить область, которая была белой на приведенной выше диаграмме Венна, вот так:

(А’∪В)’

Это то же самое, что и диаграмма Венна для AB! Итак, мы ДОКАЗАЛИ, что A-B=(A′∪B)′!

Это доказательство, потому что все диаграммы Венна являются общими и не требуют от нас знания, что такое А и В.

С помощью диаграмм Венна мы показали, что A-B=(A′∪B)′ для ВСЕХ множеств A, B и U. A, B и U могут быть НИЧЕГО, и A-B=(A′∪B )′ все равно будет правдой!

Использование диаграмм Венна для доказательства того, что два множества не равны:

Если мы хотим доказать, что два множества НЕ равны, все, что нам нужно сделать, это показать, что их диаграммы Венна не совпадают:

. Рассмотрим A∪B=A∩B. Всегда ли это так? Иногда правда? Или никогда не правда?

Чтобы проверить, верно ли это в общем случае, нарисуем диаграммы Венна:

Мы помним из предыдущих примеров, что A∪B имеет диаграмму Венна:

А∪В

Мы также помним из предыдущих примеров, что A∩B имеет диаграмму Венна:

А∩В

Эти две диаграммы НЕ совпадают! Это означает, что НЕВЕРНО, что A∪B=A∩B для ВСЕХ ВОЗМОЖНЫХ МНОЖЕСТВ A и B.

Однако могут существовать наборы, для которых A∪B=A∩B.

Ясно, что если A={1,2,3} и B={2,4,6}, A∪B={1,2,3,4,6} и A∩B={2}. Очевидно {1,2,3,4,6}≠{2}.

Но если A={1,2,3} и B={1,2,3}, то A∪B={1,2,3} и A∩B={1,2,3}, поэтому в этом случай А∪В=А∩В.

Итак, A∪B=A∩B верно ИНОГДА, но НЕ ВСЕГДА.

Если вы посмотрите внимательно, то заметите, что A∪B=A∩B будет истинным только тогда, когда A=B. Чтобы убедиться в этом, посмотрите на диаграммы Венна выше. Единственный способ сделать область, заштрихованную красным, и область, заштрихованную желтым цветом, одинаковыми, — это объединить наборы A и B в один набор, чтобы они были точно одним и тем же набором.

Законы ДеМоргана:

Когда можно заменить одно составное выражение, содержащее множества, другим?

Прямо сейчас мы сделаем еще один пример, показывающий, как мы можем доказать эквивалентность двух составных выражений, содержащих множества. Этот пример на самом деле является одним из двух хорошо известных правил теории множеств, называемых законами Де Моргана (по имени математика, открывшего их).

Когда была изобретена теория множеств, и у нас появились составные выражения, включающие множества и множественные операции, становится естественным спросить, равны ли на самом деле два разных составных выражения. Например, в обычной алгебре, использующей числа и операции над числами, такие как сложение, вычитание, умножение и деление, существуют правила, гласящие, что вы можете переписать 3(4 x +2) как 12 x +6 путем распределения умножения над сложением. Верен ли тот же процесс для множеств?

Например, могу ли я написать (A∪B)′ как A′∪B′? Другими словами, могу ли я распределить дополнение множества по объединению множеств? Единственный способ сказать это — нарисовать диаграмму Венна для (A∪B)′ и диаграмму Венна для A′∪B′ и посмотреть, идентичны ли две диаграммы Венна:

Начнем с рисования диаграммы Венна для (A∪B)′:

Мы помним из предыдущей задачи, что диаграмма Венна для A ∪ B выглядит так: (помните, что, поскольку объединение находится внутри скобок, мы должны сделать это до того, как возьмем дополнение, которое находится вне скобок)

А∪В

Теперь, чтобы взять дополнение к A∪B, мы возьмем только белую область на предыдущей диаграмме Венна, чтобы получить:

(А∪В)’

Теперь нарисуем диаграмму Венна для A′∪B′. Начнем с диаграмм Венна для A′ и B′, которые мы помним из предыдущих примеров:

А’

Б’

Теперь нам нужно поместить A′ и B′ на одну и ту же диаграмму Венна. Поскольку A’ — синий, а B’ — красный, область, где они перекрываются, будет фиолетовой:

.

A’ — синий, B’ — красный

Поскольку мы берем объединение, мы сохраняем все, что было заштриховано синим или красным (или фиолетовым, потому что фиолетовый происходит от красного и синего затенения). Чтобы сделать нашу диаграмму более четкой, мы решили заштриховать все одним цветом, так что это диаграмма A′∪B′:

.

А’∪В’

Это явно , а не то же самое, что и диаграмма Венна для (A∪B)′! Таким образом, мы можем заключить, что в общем случае (A∪B)′ нельзя заменить на A′∪B′ без изменения результирующего множества!

Будьте осторожны! Вы можете НИКОГДА не заменять (A∪B)′ на A′∪B′, потому что эти два множества НЕ (вообще) равны! Если вас попросят нарисовать диаграмму Венна для (A∪B)′, например, убедитесь, что вы следуете порядку операций — НИКОГДА начните с дополнения A и B, потому что это ВНЕ круглых скобок ! Точно так же вы НЕ МОЖЕТЕ заменить (A∩B)′ на A′∩B′, потому что эти два набора НЕ (вообще) равны! (Чтобы убедиться в этом, попробуйте нарисовать диаграмму Венна для каждой стороны и сравнить их. )

Законы ДеМоргана:

Оказывается, на самом деле существует своего рода искаженное правило распределения, которое позволяет вам «распределять» дополнение множества по объединению множеств (или пересечению)

Оказывается, следующие два правила ВСЕГДА верны для ЛЮБЫХ двух множеств A и B:

1) А′∪В′=(А∩В)′

2) А′∩В′=(А∪В)′

Эти правила называются ЗАКОНЫ ДЕМОРГАНА .

Откуда мы знаем, что эти два правила всегда будут верны?

Начнем с первого правила: откуда мы знаем, что A′∪B′ всегда будет равно (A∩B)′, какими бы ни были множества A и B? Мы рисуем диаграммы Венна для каждой части этого уравнения и показываем, что они совпадают.

Сначала мы рисуем диаграмму Венна для A′∪B′; поскольку мы только что сделали это в предыдущем примере, мы можем просто использовать ту же диаграмму здесь:

А’∪В’

Теперь построим диаграмму Венна для (A∩B)′:

Поскольку мы всегда сначала делаем то, что указано в скобках, мы сначала рисуем диаграмму Венна для A ∩ B, которая у нас есть из предыдущего примера:

А∩В

Теперь мы берем дополнение, заштриховав белую область на диаграмме выше (помните, что дополнением является все, что НЕ находится в A ∩ B!):

Таким образом, мы получаем следующую диаграмму Венна для (A∩B)′:

(А∩В)′

Это та же самая диаграмма Венна, которую мы получили для A′∪B′.

Итак, мы доказали первый закон Де Моргана: A′∪B′=(A∩B)′, потому что диаграммы Венна каждой части уравнения идентичны.

Рисование диаграмм Венна нулевого и универсального множеств

Иногда вам может понадобиться нарисовать диаграммы Венна нулевого множества Ø или универсального множества U. Чтобы нарисовать диаграмму Венна нулевого множества, нам нужно только нарисовать любую диаграмму Венна без какой-либо штриховки . Ниже приведены несколько примеров различных диаграмм Венна нулевого набора:

Ø

Ø

Ø

Ø

Чтобы нарисовать диаграмму Венна Универсального набора, заштриховываем все . Ниже приведены несколько различных примеров диаграмм Венна универсального набора:

U

U

U

U

 

 

Ключевые слова для изменения порядка

Обратные слова указывают на изменение порядка исходной английской фразы. Обычно вы используете ключевые слова одним из двух способов:

• Переведите слова напрямую в том порядке, в котором они даны.

• Распознайте ведущие ключевые слова и найдите соответствующие И, ДО, ПО или ОТ, которые подскажут вам, как перевести уравнение.

Чтобы вам было легче понять оборотные слова, подумайте об указаниях на коробке смеси для торта. Если в инструкции написано «три яйца добавлены в смесь», что вы кладете в миску первым? Сначала вы кладете смесь в миску, а затем добавляете яйца. Слово TO является одним из основных оборотных слов, обсуждаемых в следующем разделе, и чтобы помочь вам не забыть перевернуть выражение, вы заключаете это слово в рамку.

Основные оборотные слова

Определенные ключевые слова указывают на изменение порядка перевода. Все ключевые слова, указывающие на изменение порядка, содержат следующие слова:

• К

• ИЗ

• ЧЕМ

Дополнительные оборотные слова

Дополнительные ключевые слова, указывающие на поворот,

• ДОБАВИТЬ _____ К _____

• _____ ДОБАВЛЕНО К _____

• _____ БОЛЕЕ _____

Пример 1: Переведите следующее: двенадцать прибавить к минус четырем

Чтобы помочь вам перевести эту задачу, поставьте оборотное слово в рамку.

Замените каждое слово алгебраическими символами и переверните выражение.

Выражение переводится как -4 + 12.

Пример 2: Переведите следующее: прибавьте минус три к пяти

В примере 2 используются оборотное слово и ведущее ключевое слово, и оно переводится следующим образом:

1. Поскольку первое слово в выражении, ADD, указывает на операцию, ADD является ведущим ключевым словом. ДОБАВИТЬ определяет ТО, поэтому подчеркните слова до и после ТО: «минус три» и «пять».

• добавить минус три к пяти

2. Обведите ведущее ключевое слово и укажите соответствующий ТО, который оно определяет; поле оборотное слово, ТО.

3. Переведите каждое подчеркнутое выражение, замените TO знаком плюс и переверните выражение.

• Выражение переводится как 5 + −3.

Люди иногда утверждают, что оборотное слово не является необходимым при сложении из-за коммутативного свойства сложения; , то есть как -3 + 5, так и 5 + -3 приводят к одному и тому же ответу для Примера 2 (+2) при упрощенном . Однако последнее (5 + −3) показывает понимание порядка, указанного ключевым словом. У вас есть две причины научиться переводить выражения в правильном порядке:

• Формируются хорошие привычки для правильного перевода выражений вычитания и деления, которые не являются коммутативными.

• Точно так же, как производители смеси для кекса хотят, чтобы вы сначала положили смесь для кекса в миску, а потом добавили яйца, автор задачи хочет, чтобы вы выполняли добавление в предписанном порядке.

Вычитание оборотных слов

Ключевые слова вычитания, указывающие на поворот:

• ВЫЧИТАТЬ _____ ИЗ _____

• _____ ВЫЧЕТ ИЗ _____

• _____ МЕНЕЕ _____

Пример 3: Переведите следующее: число меньше семи

Чтобы помочь вам решить эту проблему, поставьте в рамку оборотное слово THAN.

Замените каждое слово алгебраическими символами и переверните выражение.

• Выражение переводится как 7 − x .

Пример 4: Переведите следующее: вычесть семнадцать из пятидесяти четырех

1. Поскольку слово ВЫЧИТАТЬ является ведущим ключевым словом, которое определяет ОТ, подчеркните слова до и после ОТ: «семнадцать» и «пятьдесят четыре».

• из пятидесяти четырех вычесть семнадцать

2. Обведите ведущее ключевое слово и укажите соответствующее ОТ, которое оно определяет; вставьте оборотное слово, ОТ.

3. Переведите каждое подчеркнутое выражение, замените FROM знаком минус и переверните выражение.

• Выражение переводится как 54 − 17.

Обратные слова умножения

Ни одно из ключевых слов умножения не указывает на поворот. Все выражения умножения могут быть переведены с использованием стратегии прямого перевода или ведущих ключевых слов.

Произведение числа и 8 можно перевести как n × 8, но чаще всего выражение записывается как 8 × n или 8 n , потому что математики установили стандарт, что коэффициент пишется перед переменной. (В этом примере число 8 является коэффициентом.)

Примечание: Выражение 8 n использует подразумеваемое умножение . Умножение подразумевается, когда число помещается рядом с переменной или когда число помещается рядом с выражением, заключенным в круглые скобки. Хотя знак умножения не показан, его использование подразумевается.

Обратные слова дивизии

Ключевые слова отдела

, указывающие на изменение ситуации:

• РАЗДЕЛИТЬ _____ НА _____

• _____ ДЕЛИТСЯ НА _____

Обратите внимание, что TO, основное слово оборота, включено в слово INTO и указывает на оборот.

Пример 5: Переведите следующее: разделить пять на 125

Решите пример 5 следующим образом:

1.