Как разделить число на дробь. Как разделить число на дробь правило. Целое число разделить на дробь пример.
- Альфашкола
- Статьи
- Как разделить число на дробь
Деление числа на дробь происходит по правилу: дробь меняет местами числитель и знаменатель, далее умножаем на число по правилу умножению числа на дробь : https://myalfaschool.ru/articles/kak-umnozhit-chislo-na-drob.
Пример 1. Разделите \(5:\frac{5}{12}\).
Решение:
Здесь мы сократили дробь на \(5\) и получили \(12\).
Ответ: \(12.\)
Пример 2. Разделите \(8:\frac{4}{5}\).
Решение:
Ответ: \(10\)
Пример 3. Разделите \(27:\frac{9}{5}\).
Разделите \(27:\frac{9}{5}\).
Решение:
Ответ: \(15.\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Эвелина Евгеньевна Мурзакова
Репетитор по математике
Стаж (лет)
Образование:
Санкт-Петербургский Горный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии 8-11 классы.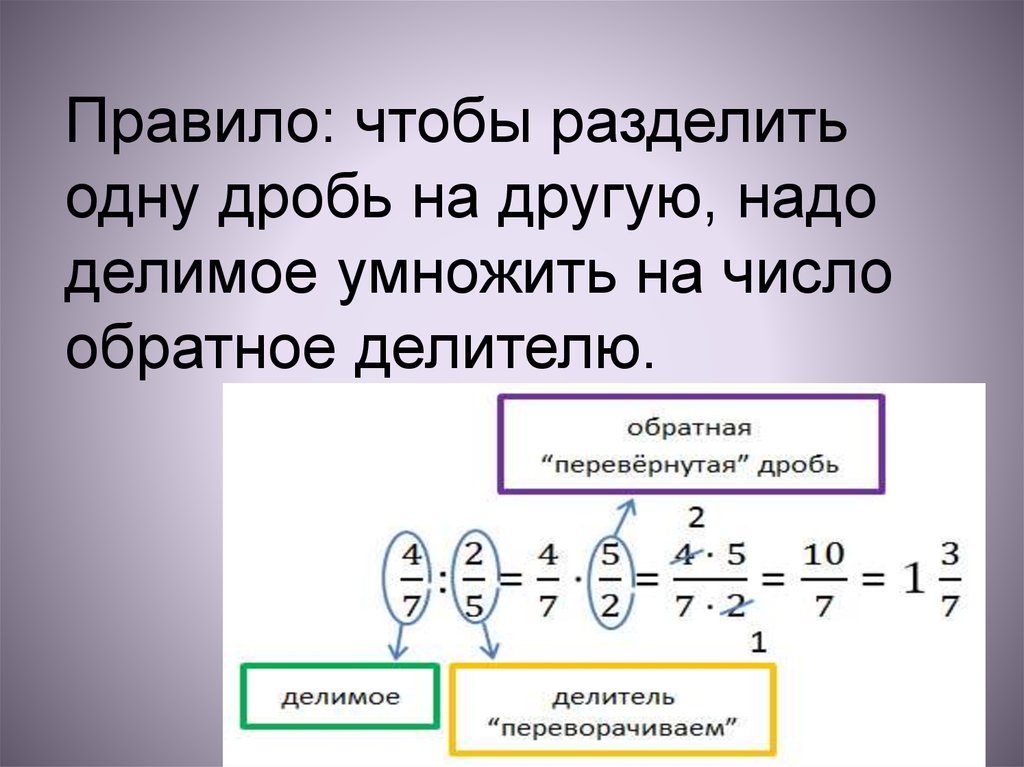 Подготовка к ОГЭ/ЕГЭ. Люблю химию за то, что ее можно понять, а не только принять, как данность. Эта наука дает возможность найти подход, подъезд, подлет, если угодно, главное — попробовать, и никогда — не прогибает под себя. Учит думать и смотреть, ведь зачастую обратить внимание — это все, что требуется, чтобы попасть в суть ответа на вопрос
Подготовка к ОГЭ/ЕГЭ. Люблю химию за то, что ее можно понять, а не только принять, как данность. Эта наука дает возможность найти подход, подъезд, подлет, если угодно, главное — попробовать, и никогда — не прогибает под себя. Учит думать и смотреть, ведь зачастую обратить внимание — это все, что требуется, чтобы попасть в суть ответа на вопрос
Гузель Ильдаровна Сафиуллина
Репетитор по математике
Стаж (лет)
Образование:
Казанский федеральный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по английскому языку для 1-7 классов и по французскому языку для 4-11классов. Обучаю прекрасному французскому языку с нуля и помогаю совершенствовать его всем желающим (от 1 до 11 класса). Также могу помочь сдать ‘экзамен DELF. Будем прорабатывать все языковые навыки и речевые умения. На занятиях не исключён билингвизм (двуязычие — французский + английский). Доступны уроки и английского языка в 1-7 классах. Опыт работы — более 2193 часов.
Обучаю прекрасному французскому языку с нуля и помогаю совершенствовать его всем желающим (от 1 до 11 класса). Также могу помочь сдать ‘экзамен DELF. Будем прорабатывать все языковые навыки и речевые умения. На занятиях не исключён билингвизм (двуязычие — французский + английский). Доступны уроки и английского языка в 1-7 классах. Опыт работы — более 2193 часов.
Николай Иванович Мельченко
Репетитор по математике
Стаж (лет)
Образование:
Новосибирский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по биологии для 8-11 классов, ОГЭ, ЕГЭ и по химии для 7-9 классов, ОГЭ. Мне нравятся естественные науки, потому что они позволяют лучше понять мир. В наше время биология стремительно развивается, появляются новые дисциплины связанные с ней, которых еще не было лет пятнадцать назад. Сейчас человек, знающий биологию, может стать генетиком, биоинформатиком, биоинженером и быть многопрофильным специалистом, основной задачей которого остается работа с живыми организмами. Если вы интересуетесь биологией и химией, буду рад объяснить сложные темы и подготовить к экзаменам.
Мне нравятся естественные науки, потому что они позволяют лучше понять мир. В наше время биология стремительно развивается, появляются новые дисциплины связанные с ней, которых еще не было лет пятнадцать назад. Сейчас человек, знающий биологию, может стать генетиком, биоинформатиком, биоинженером и быть многопрофильным специалистом, основной задачей которого остается работа с живыми организмами. Если вы интересуетесь биологией и химией, буду рад объяснить сложные темы и подготовить к экзаменам.
Похожие статьи
- Движение в противоположных направлениях
- Как построить график гиперболы?
- НИУ ВШЭ (Компьютерная безопасность): проходной балл, отзывы, расписание
- Как вычислить площадь квадрата стороны которого лежат на прямых
- ЕГЭ по математике, базовый уровень.
 Планиметрия. Прямоугольный треугольник (вариант 2)
Планиметрия. Прямоугольный треугольник (вариант 2) - Престижные премии по математике
- Полезные физические упражнения для тех, кто долго сидит за учебниками: зарядка для спины
- Как организовать режим школьника на каникулах, чтобы потом было легче снова идти в школу
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
№1 Умножение дробей ПРАВИЛО ОБРАЗЕЦ ЗАДАНИЯ Чтобы умножить дробь
Математика
Чтобы умножить дробь на дробь надо:
1.Числители перемножить и записать в числитель.
2.Знаменатели перемножить и записать в знаменатель. Пример №1.
3 = =
Пример №2.
* 3 = =
Пример №3
* = =
№1.
а) * 2 б) *5 в) *14
г) 25 * д) 32* е) 15 *
№2.
а) * б) * в) *
г) * д) * е) *
ж) * з) * и) *
к) * л) * м) *
н) *
№2 Деление дробей
ПРАВИЛО ОБРАЗЕЦ ЗАДАНИЯ
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй
Чтобы разделить дробь на число, нужно это число умножить на знаменатель и записать в знаменатель
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Пример №1.
: = * = = 2
Пример №2
: 6 = =
Пример №3.
7: = 7 * = =
№1.
а) : б) : в) :
г) : д) : е) :
№2
а) : 2 б) : 3 в) : 2
№3
а)8 : б) 15 : в) 21 :
Пошаговое объяснение:низнаю
1) 4/27*9/16=1/27*9/4=1/3*1/4=1/12
2) 5 3/5=18/5, 1 4/21=25/21 18/5*25/21=6*5/7=30/7=4 2/7
3)13/16*32=26
Вика купила 56 тетрадей, из них 4/7 составили тетради в клетку. Сколько тетрадей в клетку купила Вика?
(3-15/28 х 1 1/6) х 2 2/19
Решение:
(3-15/28*7/6)*21/19=(3-5/8)*21/19=19/8*21/19=21/8=2 5/8=2,625
Высота прямоугольного параллелепипеда равна 6 2/3 см, его длина в 2 1/4 раза больше высоты, а ширина составляет 20% длины. Вычислите объём параллелепипеда.
Решение:
Длина =9/4*20/3=15
ширина =1/5*15=3
Объем=20/3*3*15=300 см кубических
1 1/2 х 2 10/13 +2 3/4 х 2 10/13 — 2 10/13 х 3 1/6
Решение :
(3/2+11/4-19/6)*36/13=(17/4-19/6)*36/13=((51-38)/12)*36/13=3
Яблони составляют 7/24 деревьев, растущих в саду, вишни — 9/17 оставшихся деревьев, а остальные деревья — груши. Каких деревьев в саду растёт больше всего?
Каких деревьев в саду растёт больше всего?
Не яблони составляют 17/24 всех деревьев. Вишни 9/24=3/8 всех деревьев
Груши 1 -7/24-9/24=8/24=1/3.
Сравнивать удобнее 7/24 9/24 и 8/24.
за четко написанные условия!)
1)Сократить если можно, или числитель умножать на числитель, и знаменатель на знаменатель. 2) нужно числитель дроби умножать на это число, а знаменатель оставить без изменений
1) в
2) б
3) а
4) г
5) г
Пошаговое объяснение:
надеюсь правильно
1) нет, но если задумал одинаковые, то может
2)то же самое
3)420
4)180
5)60
6)100
7)111,1
8)18%
2.
Задание 1
1.-
2.-
3.+
4.+
5.-
6.+
7.-
8.-
9.+
10.-
3.
А) 2
Б)?
В)?
4. Задание 2
0,87=87% (+ ) 57%=0,57 ( +)
1,7=17% ( -) 8%=80 (- )
2=20% ( -) 240%=2,4 (+ )
3,01=301% ( +) 30%=0,3 (-)
1,1=110% (+ ) 482%=48,2 ( -)
0,08=0,8% (+ ) 3%=300 (- ).
Ответы:
Показать ответы
Математика, 28.02.2019 08:50, лунтик73
2х+у+3z=1 2у+3z+t=2 х+у+z+t=3 2х+2z+t=1
Ответы:
Показать ответы
Математика, 03.03.2019 00:10, lolkek3023
Если отрезок на местности в соответствующего отрезка на карте, то карта сделана в одна
Ответы:
Показать ответы
Математика, 03.03.2019 09:00, kisa1756
1)торт массой 2,5 кг разрезали на 12 одинаковых кусков. найдите массу каждого куска выразив её в граммах. 2)в коробке 27 белых и синих шаров. число белых к синим шарикам равно 4: 5. сколько в коробке белых шариков?
Ответы:
Показать ответы
Русский язык, 09.10.2022 20:19
Вставить пропущенный мягкий в слова на фото…
Алгебра, 09.10.2022 16:17
Вычесление лагорифмов по фото все примеры…
Алгебра, 09.10.2022 04:01
1){3х-2у=7 {2х+2у=8 . 2) {7х-0,4у=-15 {4х-0,4у=10. 3){5х-0,6у=-6 {2х-0,3у=16….
Другие предметы, 08. 10.2022 21:13
10.2022 21:13
создать дизайн обложки книги или журнала как сделать подскажите пожалуйста…
Химия, 08.10.2022 10:55
Лаллслаоо это 7 в первом нужно выбрать картинку с помощью в первом письме не в…
Информатика, 01.12.2020 10:46
Определить произведение двух чисел, если b положительное и частное (a/b) в противном случае. Записать решение задачи на алгоритмическом языке и в виде блок-схемы пипец как надо…
Математика, 01.12.2020 10:46
А) 14 мин 20 с – 9 мин 25 с =б) 35 ц 2 кг + 15 т 48 кг = решите столбиком…
Математика, 01.12.2020 10:46
Исследовать данную функцию на непрерывность и построить ее график.
Українська мова, 01.12.2020 10:46
чи можна вважати вірш мені однаково чи буду ліричною сповіддю поета. відповідь повинна бути аргументованна…
Физика, 01.12.2020 10:46
какое количество теплоты необходимо затратить для плавления 6 кг золота, взятого при температуре 30°?…
Lebih banyak pertanyaan tentang hal ini: Математика Вопросы без ответов
Умножение смешанных дробей — правило и примеры решения » Kupuk.
 net
netИзучение математических отношений важно для дальнейшего понимания алгебры. Это тема не из простых, но проявив усердие и внимание, понять её сможет каждый учащийся. С дробными числами можно делать любые операции, например, деление, сложение, вычитание и умножение. Смешанные дроби позволяют упростить расчёт, избавиться от неправильного вида выражений, поэтому нужно обязательно научиться выполнять с ними действия, особенно на практических заданиях.
Общие сведения
По своей сути, дробь представляет собой какое-либо отношение, то есть разделение. Например, имеется торт, который разделён на 3 равные части. Все куски составляют одно целое — пирог. Но если из него взять один кусок, целостность будет нарушена. В математике такое действие записывают дробным отношением. В частности, для рассматриваемого случая алгебраическое выражение будет выглядеть как 1/3.
Здесь чёрточка обозначает деление. Число сверху над ней называют числителем (делимое), а снизу — знаменателем (делитель). Читается запись — «одна третья» или «одна третьей доли». Такого вида дроби принято считать обыкновенными. В них знаменатель показывает, на какое количество одинаковых частей что-либо можно поделить. Числитель же обозначает, какая часть была взята.
Читается запись — «одна третья» или «одна третьей доли». Такого вида дроби принято считать обыкновенными. В них знаменатель показывает, на какое количество одинаковых частей что-либо можно поделить. Числитель же обозначает, какая часть была взята.
Обыкновенные отношения разделяют на 3 вида:
С простыми дробями можно выполнять любые действия. При сложении или вычитании суть операции сводится к нахождению общего знаменателя, то есть наименьшего общего кратного и выполнения действия в числителе с учётом дополнительного множителя. Например, 1/15 + 2/15 = 3/15; 2/33 — 1/33 = (2 — 1) / 33 = 1/33.
При умножении нужно числитель одного выражения умножить на делимое второго. Также поступить и со знаменателями — перемножить их.
При делении в дроби, на которую уменьшают, нужно поменять местами верхнее число дроби с нижним, а после выполнить перемножение с первым отношением. Например, 2/3 * 3/6 = (2 * 3)/(3 * 6) = 6/18; 1/7: 1/7 = 1/7 * 7/1 = 7/7.
Операции сами по себе несложные. Но часто на практике приходится иметь дело с неправильными и смешанными дробями. Правило умножения при работе с ними немного изменяется. Следует знать, что смешанную дробь всегда можно представить как неправильную. Это важное замечание, именно на него и опирается закон произведения смешанных чисел. Кроме того, при выполнении действий используют основное свойство дроби — делитель и делимое можно умножить на одно и то же любое натуральное число без изменения конечного результата.
Преобразование смешанных чисел
Умножение на обыкновенную дробь смешанного выражения невозможно без предварительных преобразований. Чтобы понять, как их делать, нужно чётко понимать, что собой представляет смешанное число. Состоит такая запись из двух частей:
Чтобы понять, как их делать, нужно чётко понимать, что собой представляет смешанное число. Состоит такая запись из двух частей:
- целой — натуральное число;
- дробной — простое отношение.
Например, 3 1/3; 12 24/78; 1 ½. Другими словами, смешанная дробь — это запись числа, которая представляет сумму целой и дробной части. То есть справедливо будет записать равенство: 6 12/45 = 6 + 12/45. Это выражение всегда можно привести к неправильному виду. Для этого нужно выполнить всего два действия:
Формулой эту операцию можно записать в следующем виде: a b/c = (a * c + b)/c.
Например, нужно перевести смешанное число 3 27/34 в неправильную дробь. Используя алгоритм, знаменатель оставляют без изменения, а числитель умножают на делимое и складывают с целым: 3 27/34 = 3 + 27/34 = (3 * 34)/34 + 27/34 = (3*34 + 27)/34 = 129/34. Полученное выражение пробуют упростить, то есть разделить без остатка на одно и то же число.
Полученное выражение пробуют упростить, то есть разделить без остатка на одно и то же число.
Вот немного сложнее задание. Следующее выражение нужно перевести в неправильную дробь: 3 — 27/34. Существует одна хитрость: если целая часть не содержит единицу, её приводят к такому виду, чтобы она содержала единичный член. Так, задание можно преобразовать к равенству: 2 + 1 — 27/34. Единицу в выражении можно заменить отношением, согласно свойству дробей, то есть представить её как 34/34. Теперь задание примет вид: 2 + 34/34 — 27/34.
Используя правило вычитания дробей с одинаковым знаменателем довольно просто выполнить действие: 2 + ((34−27) / 34) = 2 + 7/34 = 2 7/34. Полученное число уже без затруднений можно привести к виду неправильной записи: 2 7/34 = (2 * 34 + 7)/34 = (64 + 7)/34 = 75/34. При этом всегда можно выполнить и обратную операцию. Отсюда следует не менее важное правило, что натуральное число разрешено представлять как обыкновенную дробь с единичным знаменателем. Например, 33 = 33/1; 564 = 564/1.
Например, 33 = 33/1; 564 = 564/1.
Решение примеров
После изучения теории для её закрепления необходимо перейти к решению практических заданий. Начинать нужно с простых примеров, а после их освоения переходить к более сложным примерам. Существует набор типовых задач, после самостоятельного решения которых можно утверждать о понимании материала. Вот один из сборников, содержащий типовые задачи:

Для решения сложных заданий необходимо уметь комбинировать различные действия. Вот пример одного из таких заданий: (2/34 + 5 7/8) * 2 12/5 * 4 * 2/3. При решении такой задачи в первую очередь следует выполнить сложение в скобке: (2/34 + 5 7/8) = 5 + 2/34 + 7/8 = 5 + 8/136 +119/136 = 5 + (8 + 119)/136 = 5 + (127/136) = 5 127/136. Вторым действием будет приведение смешанных чисел к неправильным дробям: 2 12/5 = 2 + 12/5 = 2 + (2 * 5 + 2)/5 + 2/5 = 4 2/5.
Теперь можно перемножить первый член со вторым, а третий с четвёртым: 5 127/136 * 4 2/5 = ((5 * 136) + 127)/136) * (4 * 5 + 2)/5) = 807/136 * 22/5 = (807/ 2 * 68) * (2 * 11/5) = (807 * 11)/(68 * 5) = 8877/340 = (37 + (26 * 340))/340 = 26 37/340; 4 * 2/3 = 4/1 + 2/3 = (4 * 2) / (1 * 3) = 8/3 = (2 + 2 * 3)/3 = 2 2/3.
youtube.com/embed/mMbRFy9hx9A»/>Последнее действие заключается в перемножении полученных членов: (26 37/340) * (2 2/3) = ((26 * 340 + 37)/340) * (2 * 3 + 2)/3) = (8877/340) * (8/3) = (3 * 2959)/(4 * 85) * (4 * 2/3) = (2959/85) * (2 /1) = 5918/85. Это и есть ответ на поставленную задачу. Но так как в ответе стоит неправильная дробь, её желательно преобразовать в смешанную: 5918/85 = (53 + 69 * 85) / 85 = 69 53/85. Пример решён.
Использование онлайн-калькулятора
На обычном калькуляторе выполнить умножение смешанных чисел возможно только путём переведения их в десятичные., то есть нужно будет представить члены выражения в виде неправильных дробей, затем разделить и найти произведение. Но если есть подключение к интернету, удобно использовать так называемые математические онлайн-калькуляторы.
Это сайты, специализирующиеся на вычислениях. Чтобы ими воспользоваться, не нужно особой подготовки. Достаточно загрузить сервис и в предлагаемую форму ввести условия примера. После нажать кнопку «Рассчитать» и через одну-две секунды, зависит от сложности задания, получить ответ. Для этого, конечно же, понадобится подключение к интернету и гаджет, на котором установлен веб-браузер с поддержкой Flash-плеера.
После нажать кнопку «Рассчитать» и через одну-две секунды, зависит от сложности задания, получить ответ. Для этого, конечно же, понадобится подключение к интернету и гаджет, на котором установлен веб-браузер с поддержкой Flash-плеера.
Из множества сайтов, существующих в русскоязычном секторе интернета, можно выделить:
- onlinemschool;
- webmath;
- naobumium;
- 0oq;
- allcalc.
Эти сервисы предлагают свои услуги бесплатно и даже не требуют регистрации или указания каких либо своих данных. Удобство их использования ещё и в том, что кроме автоматического подсчёта правильного произведения, сайты предоставляют пошаговое решение. Это удобно в процессе обучения. Можно не только проверить самостоятельно полученный ответ, но и проследить все этапы выполнения действий.
Для новичков на сервисах предусмотрен краткий теоретический материал, так что даже неподготовленному пользователю будет понятно, как получается то или иное преобразование.
А примеры с комментариями помогут понять алгоритм вычисления задач с дробями и закрепить пройденный на уроках материал.
Онлайн-калькуляторы — это отличное подспорье учащимся при освоении материала. К тому же они будут полезны студентам и инженерам. Всё дело в том, что расчёт с их помощью занимает несколько секунд и практически исключена ошибка. В то же время самостоятельные вычисления не только требуют повышенной внимательности, но и занимают намного больше времени.
Умножение дробей на целые числа Чтение материала
1%
Обработка, подождите…
Обработано успешно!
ЧТО ТАКОЕ УМНОЖЕНИЕ ДРОБЕЙ НА ЦЕЛЫЕ ЧИСЛА?
Повторное сложение дробей учащиеся связывают с умножением дробей на целые числа. Изучив примеры во многих различных контекстах, где дробь умножается на целое число, они разработали следующее правило: умножьте целое число на числитель дроби и сохраните знаменатель дроби.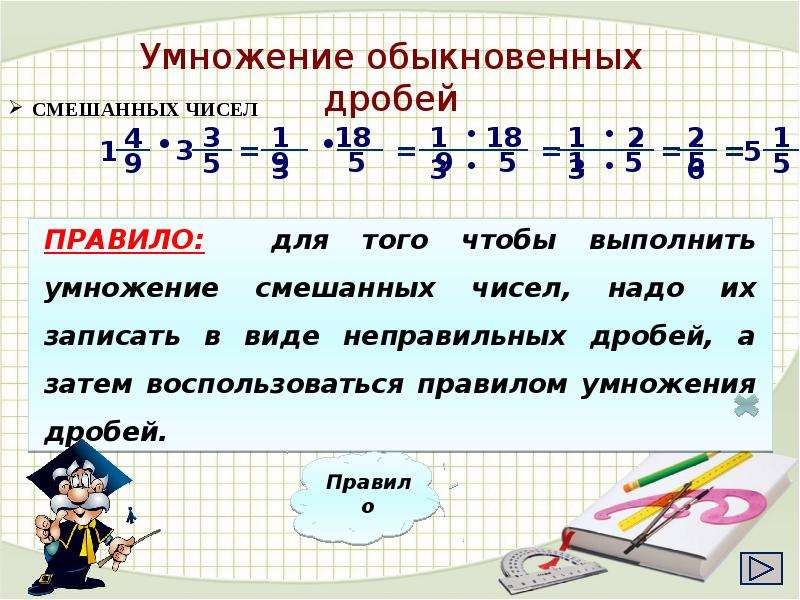
Чтобы лучше понять умножение дробей на целые числа…
ЧТО ТАКОЕ УМНОЖЕНИЕ Дробей НА ЦЕЛЫЕ ЧИСЛА?. Повторное сложение дробей учащиеся связывают с умножением дробей на целые числа. Изучив примеры во многих различных контекстах, где дробь умножается на целое число, они разработали следующее правило: умножьте целое число на числитель дроби и сохраните знаменатель дроби. Чтобы лучше понять умножение дробей на целые числа…
ДАВАЙТЕ РАЗЪЯСНИМ!
Планирование пиццерии на 8 человек
Умножение дробей на целые числа поможет вам определить, сколько пицц нужно заказать для пиццерии. Допустим, вы пригласили 7 друзей на вечеринку с пиццей, и вы тоже хотите поесть. Сколько пирогов вам нужно заказать, если каждый получит по одному кусочку? Мы можем понять это, представив кусок пиццы как дробь. Поскольку пицца разрезается на 8 частей, один кусок пиццы может быть представлен дробью [ggfrac]1/8[/ggfrac]. Поскольку нам нужно 8 таких фракций, мы можем представить это как [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1 /8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] что равно [ggfrac]8/8[/ggfrac]. Дробь [ggfrac]8/8[/ggfrac] совпадает с целым числом 1. Мы также можем представить это повторяющееся сложение как 8 × [ggfrac]1/8[/ggfrac], что по-прежнему равно [ggfrac]8. /8[/ggfrac] (одна пицца). Помните, что умножение — это просто многократное сложение. Попробуйте сами: Допустим, на вечеринке будет всего 24 человека, и каждый получит по одному кусочку. Сколько пицц вам нужно заказать в этом случае?
Дробь [ggfrac]8/8[/ggfrac] совпадает с целым числом 1. Мы также можем представить это повторяющееся сложение как 8 × [ggfrac]1/8[/ggfrac], что по-прежнему равно [ggfrac]8. /8[/ggfrac] (одна пицца). Помните, что умножение — это просто многократное сложение. Попробуйте сами: Допустим, на вечеринке будет всего 24 человека, и каждый получит по одному кусочку. Сколько пицц вам нужно заказать в этом случае?
Планирование пиццерии на 8 человек Умножение дробей на целые числа поможет вам определить, сколько пицц нужно заказать для пиццерии. Допустим, вы пригласили 7 друзей на вечеринку с пиццей, и вы тоже хотите поесть. Сколько пирогов вам нужно заказать, если каждый получит по одному кусочку? Мы можем понять это, представив кусок пиццы как дробь. Поскольку пицца разрезается на 8 частей, один кусок пиццы может быть представлен дробью [ggfrac]1/8[/ggfrac]. Поскольку нам нужно 8 таких фракций, мы можем представить это как [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1 /8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] + [ggfrac]1/8[/ggfrac] что равно [ggfrac]8/8[/ggfrac].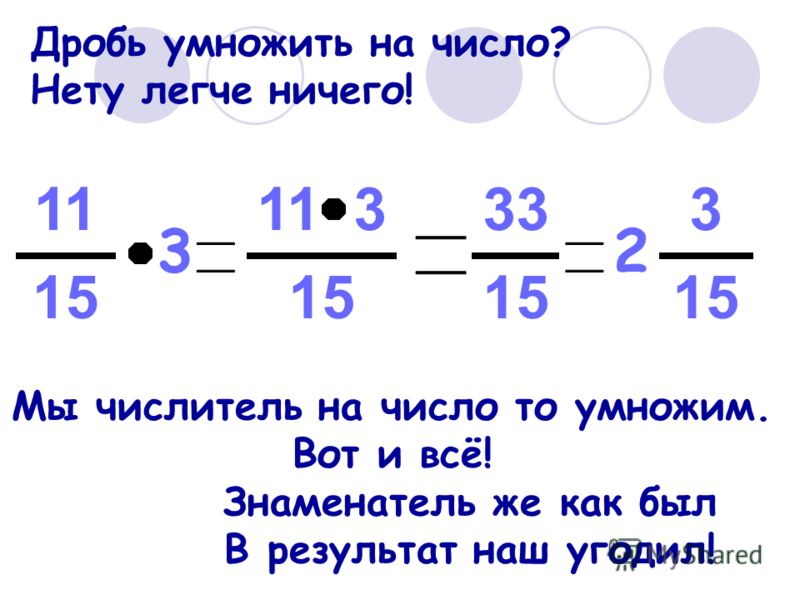 Дробь [ggfrac]8/8[/ggfrac] совпадает с целым числом 1. Мы также можем представить это повторяющееся сложение как 8 × [ggfrac]1/8[/ggfrac], что по-прежнему равно [ggfrac]8. /8[/ggfrac] (одна пицца). Помните, что умножение — это просто многократное сложение. Попробуйте сами: допустим, на вечеринке будет всего 24 человека, и каждый получит по одному кусочку. Сколько пицц вам нужно заказать в этом случае?
Дробь [ggfrac]8/8[/ggfrac] совпадает с целым числом 1. Мы также можем представить это повторяющееся сложение как 8 × [ggfrac]1/8[/ggfrac], что по-прежнему равно [ggfrac]8. /8[/ggfrac] (одна пицца). Помните, что умножение — это просто многократное сложение. Попробуйте сами: допустим, на вечеринке будет всего 24 человека, и каждый получит по одному кусочку. Сколько пицц вам нужно заказать в этом случае?
Планирование вечеринки с пиццей на 32 человека
Допустим, вы хотите устроить очень большую вечеринку с пиццей на 32 человека. Сколько пицц вам нужно заказать, если каждый получит по одному кусочку? Поскольку пицца разрезается на 8 частей, один кусок пиццы может быть представлен дробью [ggfrac]1/8[/ggfrac]. Для нашей партии нам нужно 32 таких дроби. Мы можем представить это, написав выражение, в котором [ggfrac]1/8[/ggfrac] встречается 32 раза. Это много нужно написать. Более простой способ представить это с помощью умножения: 32 × [ggfrac]1/8[/ggfrac]. Мы должны умножить 32 × 1, чтобы получить числитель и сохранить 8 в знаменателе. 32 × [ggfrac]1/8[/ggfrac] = [ggfrac]32/8[/ggfrac]. Теперь мы, вероятно, не хотим звонить в пиццерию и говорить, что хотим пиццу [ggfrac]32/8[/ggfrac]. Итак, нам нужно упростить дробь [ggfrac]32/8[/ggfrac]. Поскольку 8 четыре раза равно 32, [ggfrac]32/8[/ggfrac] равно [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac]. И [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] = 1 + 1 + 1 + 1 = 4. Теперь мы знаем, что на 32 гостей нам нужно 4 пиццы. Попробуйте сами: Допустим, на вечеринке будет всего 48 человек, и каждый получит по одному кусочку. Сколько пицц вам нужно заказать в этом случае?
32 × [ggfrac]1/8[/ggfrac] = [ggfrac]32/8[/ggfrac]. Теперь мы, вероятно, не хотим звонить в пиццерию и говорить, что хотим пиццу [ggfrac]32/8[/ggfrac]. Итак, нам нужно упростить дробь [ggfrac]32/8[/ggfrac]. Поскольку 8 четыре раза равно 32, [ggfrac]32/8[/ggfrac] равно [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac]. И [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] = 1 + 1 + 1 + 1 = 4. Теперь мы знаем, что на 32 гостей нам нужно 4 пиццы. Попробуйте сами: Допустим, на вечеринке будет всего 48 человек, и каждый получит по одному кусочку. Сколько пицц вам нужно заказать в этом случае?
Планирование вечеринки с пиццей на 32 человека Предположим, вы хотите устроить очень большую вечеринку с пиццей на 32 человека. Сколько пицц вам нужно заказать, если каждый получит по одному кусочку? Поскольку пицца разрезается на 8 частей, один кусок пиццы может быть представлен дробью [ggfrac]1/8[/ggfrac]. Для нашей партии нам нужно 32 таких дроби. Мы можем представить это, написав выражение, в котором [ggfrac]1/8[/ggfrac] встречается 32 раза. Это много нужно написать. Более простой способ представить это с помощью умножения: 32 × [ggfrac]1/8[/ggfrac]. Мы должны умножить 32 × 1, чтобы получить числитель и сохранить 8 в знаменателе. 32 × [ggfrac]1/8[/ggfrac] = [ggfrac]32/8[/ggfrac]. Теперь мы, вероятно, не хотим звонить в пиццерию и говорить, что хотим пиццу [ggfrac]32/8[/ggfrac]. Итак, нам нужно упростить дробь [ggfrac]32/8[/ggfrac]. Поскольку 8 четыре раза равно 32, [ggfrac]32/8[/ggfrac] равно [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac]. И [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] = 1 + 1 + 1 + 1 = 4. Теперь мы знаем, что на 32 гостей нам нужно 4 пиццы. Попробуйте сами: допустим, на вечеринке будет всего 48 человек, и каждый получит по одному кусочку. Сколько пицц вам нужно заказать в этом случае?
Для нашей партии нам нужно 32 таких дроби. Мы можем представить это, написав выражение, в котором [ggfrac]1/8[/ggfrac] встречается 32 раза. Это много нужно написать. Более простой способ представить это с помощью умножения: 32 × [ggfrac]1/8[/ggfrac]. Мы должны умножить 32 × 1, чтобы получить числитель и сохранить 8 в знаменателе. 32 × [ggfrac]1/8[/ggfrac] = [ggfrac]32/8[/ggfrac]. Теперь мы, вероятно, не хотим звонить в пиццерию и говорить, что хотим пиццу [ggfrac]32/8[/ggfrac]. Итак, нам нужно упростить дробь [ggfrac]32/8[/ggfrac]. Поскольку 8 четыре раза равно 32, [ggfrac]32/8[/ggfrac] равно [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac]. И [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] + [ggfrac]8/8[/ggfrac] = 1 + 1 + 1 + 1 = 4. Теперь мы знаем, что на 32 гостей нам нужно 4 пиццы. Попробуйте сами: допустим, на вечеринке будет всего 48 человек, и каждый получит по одному кусочку. Сколько пицц вам нужно заказать в этом случае?
Партии печенья
Допустим, у вас есть рецепт печенья, который требует [ggfrac]2/3[/ggfrac] стакана муки для одной партии печенья. Вы решаете, что хотите испечь четыре порции печенья, и хотите узнать, сколько муки вам понадобится. Итак, вам нужно найти [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac]. Это то же самое, что 4 × [ggfrac]2/3[/ggfrac]. Мы можем умножить 4 × 2, чтобы получить числитель ответа, и оставить 3 в качестве знаменателя. 4 × [ggfrac]2/3[/ggfrac] = [ggfrac]8/3[/ggfrac]. Нам нужно [ggfrac]8/3[/ggfrac] чашки. С этим числом будет намного проще работать, если мы его упростим. [ggfrac]8/3[/ggfrac] можно разбить на [ggfrac]3/3[/ggfrac] + [ggfrac]3/3[/ggfrac] + [ggfrac]2/3[/ggfrac]. Поскольку [ggfrac]3/3[/ggfrac] равно единице, это дает нам 1 + 1 + [ggfrac]2/3[/ggfrac] = 2 [ggfrac]2/3[/ggfrac]. Вам понадобится 2 [ggfrac]2/3[/ggfrac] стакана муки. Попробуйте сами: Сколько муки вам понадобится, чтобы испечь 7 маленьких лепешек, если вам нужно [ggfrac]3/4[/ggfrac] стакана муки, чтобы испечь 1 лепешку.
Вы решаете, что хотите испечь четыре порции печенья, и хотите узнать, сколько муки вам понадобится. Итак, вам нужно найти [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac]. Это то же самое, что 4 × [ggfrac]2/3[/ggfrac]. Мы можем умножить 4 × 2, чтобы получить числитель ответа, и оставить 3 в качестве знаменателя. 4 × [ggfrac]2/3[/ggfrac] = [ggfrac]8/3[/ggfrac]. Нам нужно [ggfrac]8/3[/ggfrac] чашки. С этим числом будет намного проще работать, если мы его упростим. [ggfrac]8/3[/ggfrac] можно разбить на [ggfrac]3/3[/ggfrac] + [ggfrac]3/3[/ggfrac] + [ggfrac]2/3[/ggfrac]. Поскольку [ggfrac]3/3[/ggfrac] равно единице, это дает нам 1 + 1 + [ggfrac]2/3[/ggfrac] = 2 [ggfrac]2/3[/ggfrac]. Вам понадобится 2 [ggfrac]2/3[/ggfrac] стакана муки. Попробуйте сами: Сколько муки вам понадобится, чтобы испечь 7 маленьких лепешек, если вам нужно [ggfrac]3/4[/ggfrac] стакана муки, чтобы испечь 1 лепешку.
Партии печенья Допустим, у вас есть рецепт печенья, который требует [ggfrac]2/3[/ggfrac] стакана муки для одной партии печенья. Вы решаете, что хотите испечь четыре порции печенья, и хотите узнать, сколько муки вам понадобится. Итак, вам нужно найти [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac]. Это то же самое, что 4 × [ggfrac]2/3[/ggfrac]. Мы можем умножить 4 × 2, чтобы получить числитель ответа, и оставить 3 в качестве знаменателя. 4 × [ggfrac]2/3[/ggfrac] = [ggfrac]8/3[/ggfrac]. Нам нужно [ggfrac]8/3[/ggfrac] чашки. С этим числом будет намного проще работать, если мы его упростим. [ggfrac]8/3[/ggfrac] можно разбить на [ggfrac]3/3[/ggfrac] + [ggfrac]3/3[/ggfrac] + [ggfrac]2/3[/ggfrac]. Поскольку [ggfrac]3/3[/ggfrac] равно единице, это дает нам 1 + 1 + [ggfrac]2/3[/ggfrac] = 2 [ggfrac]2/3[/ggfrac]. Вам понадобится 2 [ggfrac]2/3[/ggfrac] стакана муки. Попробуйте сами: сколько муки вам понадобится, чтобы испечь 7 маленьких лепешек, если вам нужно [ggfrac]3/4[/ggfrac] стакана муки, чтобы испечь 1 лепешку.
Вы решаете, что хотите испечь четыре порции печенья, и хотите узнать, сколько муки вам понадобится. Итак, вам нужно найти [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac] + [ggfrac]2/3[/ggfrac]. Это то же самое, что 4 × [ggfrac]2/3[/ggfrac]. Мы можем умножить 4 × 2, чтобы получить числитель ответа, и оставить 3 в качестве знаменателя. 4 × [ggfrac]2/3[/ggfrac] = [ggfrac]8/3[/ggfrac]. Нам нужно [ggfrac]8/3[/ggfrac] чашки. С этим числом будет намного проще работать, если мы его упростим. [ggfrac]8/3[/ggfrac] можно разбить на [ggfrac]3/3[/ggfrac] + [ggfrac]3/3[/ggfrac] + [ggfrac]2/3[/ggfrac]. Поскольку [ggfrac]3/3[/ggfrac] равно единице, это дает нам 1 + 1 + [ggfrac]2/3[/ggfrac] = 2 [ggfrac]2/3[/ggfrac]. Вам понадобится 2 [ggfrac]2/3[/ggfrac] стакана муки. Попробуйте сами: сколько муки вам понадобится, чтобы испечь 7 маленьких лепешек, если вам нужно [ggfrac]3/4[/ggfrac] стакана муки, чтобы испечь 1 лепешку.
Более длинный самолет
Допустим, у вас есть модель самолета длиной 2 [ggfrac]1/2[/ggfrac] фута.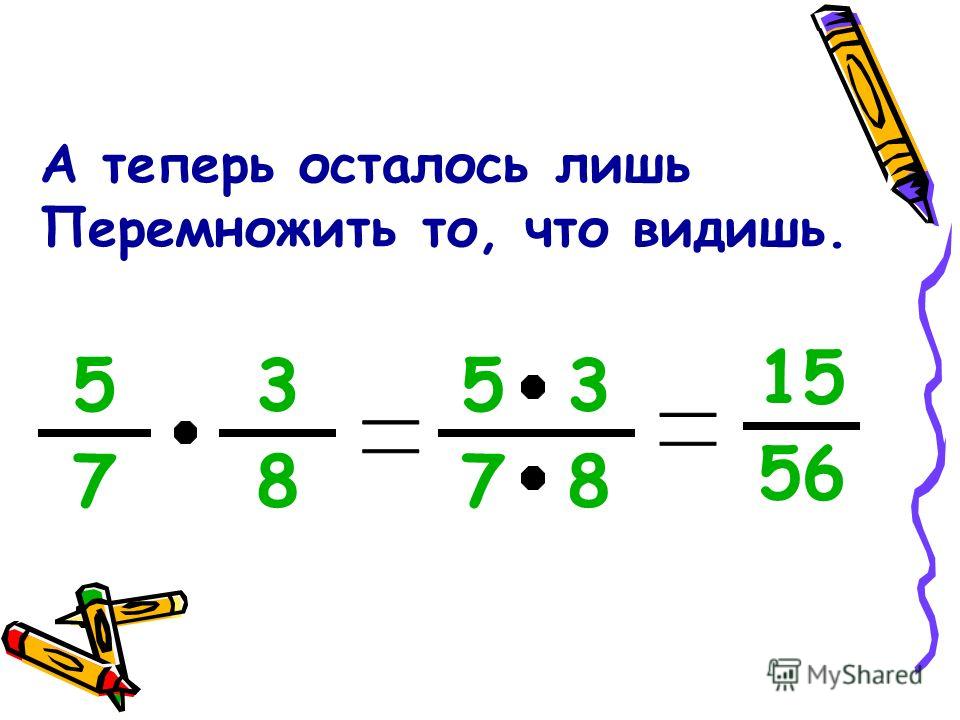 Вы хотите построить модель, которая в 3 раза длиннее. Чтобы найти длину новой модели самолета, вам нужно умножить 3 × 2 [ggfrac]1/2[/ggfrac]. 2 [ggfrac]1/2[/ggfrac] — смешанное число, и его можно записать в виде дроби, большей 1. 2 [ggfrac]1/2[/ggfrac] = [ggfrac]2/2[/ggfrac] + [ggfrac]2/2[/ggfrac] + [ggfrac]1/2[/ggfrac] = [ggfrac]5/2[/ggfrac]. Теперь вы можете записать задачу на умножение как 3 × [ggfrac]5/2[/ggfrac]. Чтобы найти 3 × [ggfrac]5/2[/ggfrac], вы умножаете 3 × 5, чтобы получить числитель и оставить тот же знаменатель: 2. 3 × [ggfrac]5/2[/ggfrac] = [ggfrac]15 /2[/ggfrac] = 7 [ggfrac]1/2[/ggfrac] футов. Новая модель будет иметь длину 7 [ggfrac]1/2[/ggfrac] футов. Попробуйте сами: Допустим, у вас есть модель автомобиля длиной 1 [ggfrac]3/4[/ggfrac] дюйма, и вы делаете новую модель автомобиля, длина которой в 5 раз больше. Как долго новая модель автомобиля?
Вы хотите построить модель, которая в 3 раза длиннее. Чтобы найти длину новой модели самолета, вам нужно умножить 3 × 2 [ggfrac]1/2[/ggfrac]. 2 [ggfrac]1/2[/ggfrac] — смешанное число, и его можно записать в виде дроби, большей 1. 2 [ggfrac]1/2[/ggfrac] = [ggfrac]2/2[/ggfrac] + [ggfrac]2/2[/ggfrac] + [ggfrac]1/2[/ggfrac] = [ggfrac]5/2[/ggfrac]. Теперь вы можете записать задачу на умножение как 3 × [ggfrac]5/2[/ggfrac]. Чтобы найти 3 × [ggfrac]5/2[/ggfrac], вы умножаете 3 × 5, чтобы получить числитель и оставить тот же знаменатель: 2. 3 × [ggfrac]5/2[/ggfrac] = [ggfrac]15 /2[/ggfrac] = 7 [ggfrac]1/2[/ggfrac] футов. Новая модель будет иметь длину 7 [ggfrac]1/2[/ggfrac] футов. Попробуйте сами: Допустим, у вас есть модель автомобиля длиной 1 [ggfrac]3/4[/ggfrac] дюйма, и вы делаете новую модель автомобиля, длина которой в 5 раз больше. Как долго новая модель автомобиля?
Более длинный самолет
Допустим, у вас есть модель самолета длиной 2 [ggfrac]1/2[/ggfrac] футов. Вы хотите построить модель, которая в 3 раза длиннее. Чтобы найти длину новой модели самолета, вам нужно умножить 3 × 2 [ggfrac]1/2[/ggfrac]. 2 [ggfrac]1/2[/ggfrac] — смешанное число, и его можно записать в виде дроби, большей 1. 2 [ggfrac]1/2[/ggfrac] = [ggfrac]2/2[/ggfrac] + [ggfrac]2/2[/ggfrac] + [ggfrac]1/2[/ggfrac] = [ggfrac]5/2[/ggfrac]. Теперь вы можете записать задачу на умножение как 3 × [ggfrac]5/2[/ggfrac]. Чтобы найти 3 × [ggfrac]5/2[/ggfrac], вы умножаете 3 × 5, чтобы получить числитель и оставить тот же знаменатель: 2. 3 × [ggfrac]5/2[/ggfrac] = [ggfrac]15 /2[/ggfrac] = 7 [ggfrac]1/2[/ggfrac] футов. Новая модель будет иметь длину 7 [ggfrac]1/2[/ggfrac] футов. Попробуйте сами: допустим, у вас есть модель автомобиля длиной 1 [ggfrac]3/4[/ggfrac] дюйма, и вы делаете новую модель автомобиля, длина которой в 5 раз больше. Как долго новая модель автомобиля?
Вы хотите построить модель, которая в 3 раза длиннее. Чтобы найти длину новой модели самолета, вам нужно умножить 3 × 2 [ggfrac]1/2[/ggfrac]. 2 [ggfrac]1/2[/ggfrac] — смешанное число, и его можно записать в виде дроби, большей 1. 2 [ggfrac]1/2[/ggfrac] = [ggfrac]2/2[/ggfrac] + [ggfrac]2/2[/ggfrac] + [ggfrac]1/2[/ggfrac] = [ggfrac]5/2[/ggfrac]. Теперь вы можете записать задачу на умножение как 3 × [ggfrac]5/2[/ggfrac]. Чтобы найти 3 × [ggfrac]5/2[/ggfrac], вы умножаете 3 × 5, чтобы получить числитель и оставить тот же знаменатель: 2. 3 × [ggfrac]5/2[/ggfrac] = [ggfrac]15 /2[/ggfrac] = 7 [ggfrac]1/2[/ggfrac] футов. Новая модель будет иметь длину 7 [ggfrac]1/2[/ggfrac] футов. Попробуйте сами: допустим, у вас есть модель автомобиля длиной 1 [ggfrac]3/4[/ggfrac] дюйма, и вы делаете новую модель автомобиля, длина которой в 5 раз больше. Как долго новая модель автомобиля?
УМНОЖЕНИЕ ДРОБЕЙ НА ЦЕЛЫЕ ЧИСЛА СЛОВАРЬ
Дробь
Дробь представляет собой часть целого.
Знаменатель
Знаменатель дроби — это число под чертой. Знаменатель показывает общее количество равных частей в целом.
Числитель
Числитель дроби — это число над чертой. Числитель показывает, сколько равных частей целого представляет дробь.
Единица Доля
Дробь, у которой числитель равен 1.
Дробь больше 1
Дробь больше 1 — это дробь, у которой числитель больше знаменателя. Дробь больше 1 представляет количество больше одного целого.
Смешанное число
Смешанное число — это число, которое включает в себя как целое число, так и дробь.
Целое
Целое равно 1 чему-то, например, 1 кругу или 1 единице на числовой прямой.
Равные части
Равные части — это части одинакового размера, на которые делится целое.
УМНОЖЕНИЕ ДРОБЕЙ НА ЦЕЛЫЕ ЧИСЛА ВОПРОСЫ ДЛЯ ОБСУЖДЕНИЯ
Как бы вы написали [ggfrac]3/4[/ggfrac]+ [ggfrac]3/4[/ggfrac] + [ggfrac]3/4[/ggfrac] + [ggfrac]3/4[/ggfrac] + [ggfrac]3/4[/ggfrac] как задача на умножение?
5 x [ggfrac]3/4[/ggfrac]
Будет ли добавление [ggfrac]2/9[/ggfrac] двадцать раз таким же, как 20 x [ggfrac]2/9[/ggfrac]? Какой метод вы бы использовали для решения задачи? Почему?
Да будет то же самое. Пример ответа: я бы умножил 20 x [ggfrac]2/9[/ggfrac], потому что думаю, что это займет меньше времени, чем сложение.
Пример ответа: я бы умножил 20 x [ggfrac]2/9[/ggfrac], потому что думаю, что это займет меньше времени, чем сложение.
Гита сказала, что 4 x [ggfrac]2/5[/ggfrac] = [ggfrac]8/20[/ggfrac]. Гита права? Объяснять.
Гита ошибается. Она умножила и числитель, и знаменатель дроби на 4. Она должна была просто умножить числитель на 4 и оставить знаменатель прежним.
Хусам говорит, что ответ на 6 x [ggfrac]1/3[/ggfrac] меньше 1, потому что [ggfrac]1/3[/ggfrac] меньше 1. Прав ли Хусам? Объяснять.
Хусам ошибается. 6 x [ggfrac]1/3[/ggfrac] равно [ggfrac]6/3[/ggfrac] или 2 и 2 не меньше 1.
На что можно умножить [ggfrac]1/3[/ggfrac] чтобы получить ответ меньше 1? Чтобы получить ответ, равный целому числу? Чтобы получить ответ, который на дробь больше единицы и не равен целому числу?
Пример ответа: 2; 9; 10
Вернуться к уроку
Калькулятор дробей
Этот калькулятор дробей выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .
е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 |
| — | minus sign | subtraction | 1 1/2 — 2/3 |
| * | asterisk | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2/3 × 5/6 |
| : | division sign | division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
Дроби | SkillsYouNeedКак и десятичные дроби, дроби описывают части целого. Понимание того, как работают дроби, как ими манипулировать и как выполнять с ними вычисления, — это навыки, которые пригодятся в удивительном количестве повседневных ситуаций. Вот несколько примеров:
Что такое дроби?На нашей странице «Числа и введение» объясняется, что дроби выражаются в виде деления, когда одно число делится на другое. Они также обычно выражаются как одно число над другим. Половина, например, записывается как ½. Один, разделенный на два, или часто говорят как «один на два». Дроби, как и десятичные дроби, это всего лишь числа. Некоторые основные термины и правила дробей
Сложение и вычитание дробейСм. наши страницы Сложение и Вычитание для более общей помощи. Проще всего складывать или вычитать дроби с одинаковым знаменателем. Вы просто добавляете или вычитаете два числителя и кладете их на один и тот же знаменатель. Например: 3 / 8 + 2 / 8 = 5 / 8 Alase Alase, то же самое, когда Subtracting .0482 7 / 8 – 5 / 8 = 2 / 8 . Это можно еще упростить до 1 / 4 Однако это немного сложнее, когда два числа не имеют общего знаменателя. В таких случаях нужно найти наименьший общий знаменатель или ЖК. Это может быть просто; например, если вы добавляете 1 / 4 and 1 / 2 , then 4 divides by 2, and the lowest common denominator is therefore 4. So 1 / 4 + 2 / 4 = 3 / 4 . Иногда не так просто определить наименьший общий знаменатель. Самый простой способ сделать это, особенно если знаменатели большие, обычно состоит в том, чтобы умножить два знаменателя вместе, а затем уменьшить, если это необходимо. Как только вы нашли наименьший общий знаменатель, вам нужно умножить числители, чтобы получить совпадение. Так же, как мы уменьшали дроби в предыдущем разделе, теперь вам нужно их умножить. Пока вы всегда умножаете или делите верхние и нижние части дроби на одно и то же число, дробь остается той же . Таким образом, вы умножаете числитель на то, на что вы умножали знаменатель, чтобы получить ЖК-дисплей . Пример 1 3 / 5 + 1 / 6 Наименьшее число, которое делится на оба знаменателя (5 и 6), равно 30. Когда вы умножаете 5 на 6, вы также должны умножить 3 на 6, чтобы получить 18 / 30 . Вам нужно было умножить 6 на 5, поэтому теперь вам нужно умножить 1 на 5, чтобы получить 5 / 30 . Важным правилом здесь является «все, что вы делаете на дне, вы должны делать и наверху». В первой дроби вы умножаете знаменатель на 6, поэтому вы также должны умножить числитель на 6. Точно так же во второй дроби вы умножаете знаменатель на 6, поэтому вы также должны умножать числитель на 6. Теперь у вас есть вычисление, которое выглядит следующим образом, где оба знаменателя одинаковы: 18 / 30 + 5 / 30 Затем вы можете сложить вместе два числителя + 5 = 23. Таким образом, ответ будет 23 / 30 . Пример 2 3 / 8 + 1 / 4 И 8, и 4 являются коэффициентами 8, поэтому ЖК-дисплей равен 8. Вы ни на что не умножали 8, поэтому и 3 менять не нужно. Вы умножили 4 на 2, поэтому вам также нужно умножить 1 на 2, чтобы получить 2. Теперь ваш расчет выглядит следующим образом: ответ. поэтому. 5 / 8 . Пример 3 3 / 4 — 1 / 2 ЖК-дисплей равен 4, потому что 4 делится на 2. Число 1 / 2 , выраженное в четвертях, равно 2 / 4 . Ваш расчет можно записать как 3 / 4 — 2 / 4 Таким образом, ответ будет 1 / 4 . Умножение дробейСм. нашу страницу Умножение для более общей помощи. При умножении дробей вы записываете две дроби рядом. Умножьте два числителя, чтобы найти числитель в вашем ответе, и умножьте два знаменателя, чтобы найти знаменатель. Наконец, сократите дробь до простейшей формы. Деление дробейСм. нашу страницу, Раздел для более общей помощи. Чтобы разделить одну дробь на другую, переверните делитель дроби (той, на которую вы делите) вверх дном и затем умножьте (как указано выше). Если это не имеет смысла, помните, что умножение на 1 / 2 равносильно делению на 2. 2 можно записать в виде дроби 2 / 1 , так что все, что вы сделали, это перевернул дробь вверх ногами. Дальнейшее чтение из книги «Навыки, которые вам нужны» Пропорции отношению к другим числам. Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас. Примечание о соотношенияхСоотношения — это еще один способ выражения дробей и десятичных дробей. Отношение 1 к 5 равно дроби 1/5 или, выраженное в виде десятичной дроби, 0,2. Все это способы сказать одну часть из пяти. Соотношение обычно пишется с двоеточием посередине, то есть 1:5, 1:2 и так далее. Ставки и математика «Коэффициенты» для ставок на скачки и вообще на что-либо еще обычно выражаются в виде коэффициентов. Поэтому вы увидите шансы 2-1, 11-7 и так далее. В этом случае второе число — это то, что вы ставите, а первое — то, что вы выигрываете. При коэффициенте 2-1, если вы поставите 1 фунт стерлингов, вы выиграете 2 фунта стерлингов. Вы также можете увидеть шансы 1-2 и даже. Шансы 1-2 означают, что вы ставите 2 фунта стерлингов и выигрываете 1 фунт стерлингов. Конечно, вы также получите свою ставку обратно! Коэффициенты иногда воспринимаются букмекерами как оценка того, насколько вероятно, что это событие произойдет. Однако это не обязательно так. Букмекеры, будучи бизнесменами и женщинами, не хотят терять деньги. Низкие коэффициенты обычно означают, что многие люди сделали ставку на это событие, будь то конкретная лошадь, которая выиграет, или пол королевского ребенка. Букмекеры не хотят терять деньги, поэтому уменьшили возможную выплату. Иногда, если слишком много людей делают ставки, букмекеры вообще закрывают книгу. В заключениеНа первый взгляд дроби могут показаться не очень полезными. Однако, когда вы думаете о том, чтобы разделить торт внутри группы или даже сделать ставку, вы можете увидеть, что дроби жизненно важны в повседневной жизни. |
 Планиметрия. Прямоугольный треугольник (вариант 2)
Планиметрия. Прямоугольный треугольник (вариант 2)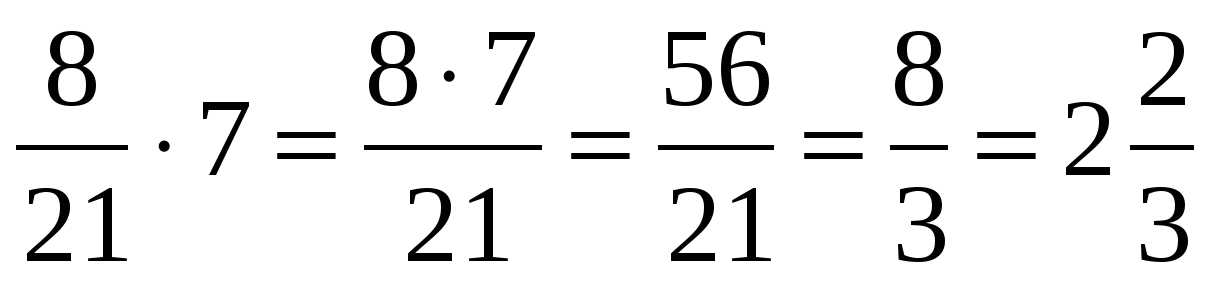 При делении в дроби, на которую уменьшают, нужно поменять местами верхнее число дроби с нижним, а после выполнить перемножение с первым отношением. Например, 2/3 * 3/6 = (2 * 3)/(3 * 6) = 6/18; 1/7: 1/7 = 1/7 * 7/1 = 7/7.
При делении в дроби, на которую уменьшают, нужно поменять местами верхнее число дроби с нижним, а после выполнить перемножение с первым отношением. Например, 2/3 * 3/6 = (2 * 3)/(3 * 6) = 6/18; 1/7: 1/7 = 1/7 * 7/1 = 7/7. А примеры с комментариями помогут понять алгоритм вычисления задач с дробями и закрепить пройденный на уроках материал.
А примеры с комментариями помогут понять алгоритм вычисления задач с дробями и закрепить пройденный на уроках материал. Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Использовала 1/3 яйца. Какая часть яиц использовалась?
Использовала 1/3 яйца. Какая часть яиц использовалась? .. все математические калькуляторы
.. все математические калькуляторы
 Они соответствуют правилам. Хотя правила для дробей могут показаться немного более сложными, при небольшой практике их относительно легко понять.
Они соответствуют правилам. Хотя правила для дробей могут показаться немного более сложными, при небольшой практике их относительно легко понять.  Другими словами, если нижнее число делится на верхнее число, делите его в меньшую сторону ( уменьшите ), пока вы больше не сможете этого делать.
Другими словами, если нижнее число делится на верхнее число, делите его в меньшую сторону ( уменьшите ), пока вы больше не сможете этого делать.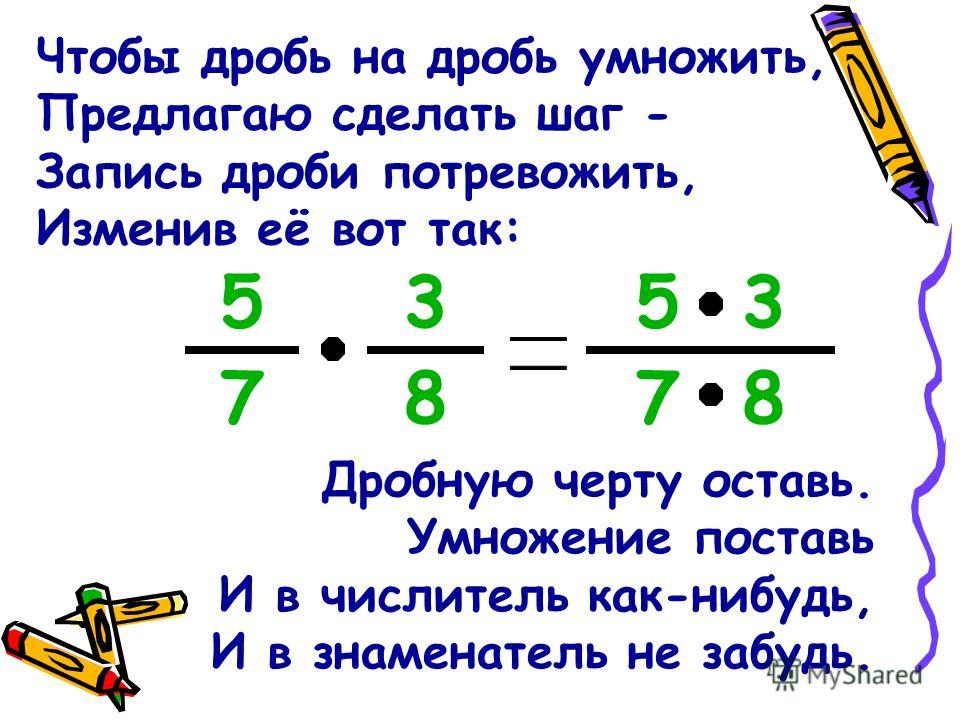 То есть наименьшее число, которое делится на оба знаменателя.
То есть наименьшее число, которое делится на оба знаменателя.


 В книге рассматриваются дроби и десятичные дроби, отношения и проценты с рабочими примерами, чтобы вы могли попробовать и развить свои навыки.
В книге рассматриваются дроби и десятичные дроби, отношения и проценты с рабочими примерами, чтобы вы могли попробовать и развить свои навыки. Эвенс означает, что два числа одинаковы. С точки зрения ставок, вы выиграете то, что поставили.
Эвенс означает, что два числа одинаковы. С точки зрения ставок, вы выиграете то, что поставили.