1.13. Как складываются и умножаются понятия?. Логика. Учебное пособие
1.13. Как складываются и умножаются понятия?
Помимо ограничения, обобщения, определения и деления понятий существуют еще две логические операции – сложение и умножение понятий.
Сложение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник и спортсмен образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой:
Умножение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий.
Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения (школьник и спортсмен). В других случаях отношений между понятиями результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. Читатель без труда сможет определить их для всех случаев отношений между понятиями с помощью круговых схем. Так, если два понятия находятся в отношении подчинения, например, карась и рыба, то результатом их сложения является родовое понятие рыба (т. е. логической суммой понятий карась и рыба будет множество всех рыб):
Результатом умножения понятий карась и рыба, находящихся в отношении родовидового подчинения, будет видовое понятие карась (т. е. логическим произведением понятий карась и рыба является множество всех карасей):
е. логическим произведением понятий карась и рыба является множество всех карасей):
Так же, если два понятия находятся в отношении соподчинения, например, береза и сосна, то результат их сложения – это два объема данных понятий (т. е. логической суммой понятий береза и сосна будет как множество всех берез, так и множество всех сосен):
Результатом умножения соподчиненных понятий береза и сосна является нулевое понятие (т. е. логическое произведение понятий береза и сосна представляет собой пустое множество – не существует ни одной березы, которая могла бы быть сосной и наоборот):
Точно так же устанавливаются результаты сложения и умножения объемов двух понятий, которые находятся в отношениях равнозначности, противоположности и противоречия (см. 1.5.). Так, например, нетрудно догадаться, что если два понятия находятся в отношении равнозначности, то результат их сложения будет полностью совпадать с результатом их умножения (логическая сумма равнозначных понятий равна их логическому произведению). Так же понятно, что результатом умножения противоположных и противоречащих понятий является нулевое понятие и т. п.
Так же понятно, что результатом умножения противоположных и противоречащих понятий является нулевое понятие и т. п.
Как правило, в естественном языке (т. е. том, на котором мы общаемся) результат сложения понятий выражается союзом или, а умножения – союзом и. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является или
школьником, или спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является и школьником, и спортсменом одновременно.Относительно употребления союзов или и и в естественном языке в качестве выражения результатов логических операций сложения и умножения понятий удачный пример приводит в своем учебнике по логике известный отечественный автор В. И. Свинцов (Логика. Элементарный курс для гуманитарных специальностей. М. : Скорина, 1998. С. 60–61), отрывок из которого приводится ниже. «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом:
: Скорина, 1998. С. 60–61), отрывок из которого приводится ниже. «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: 
Здесь следует отметить неоднозначность разделительного союза или, который может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании: Можно изучать английский язык или немецкий союз или употребляется в нестрогом значении, т. к. можно изучать и тот, и другой язык одновременно, одно другое не исключает. В данном случае разделительный союз или очень близок к соединительному союзу и. С другой стороны, в высказывании: Он родился в 1987 году или в 1989 году союз или употребляется в строгом значении, т. к. если он родился в 1987 году, то – никак не в 1989 году и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза или мы еще будем говорить далее). Если в рассмотренное выше правило пользования городским транспортом поставить союз или вместо союза и, как предлагает В. И. Свинцов, то получится следующее: «Безбилетный проезд или бесплатный провоз багажа наказываются штрафом»
 В данном случае союз или, являющийся показателем логического сложения, надо воспринимать в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации.
В данном случае союз или, являющийся показателем логического сложения, надо воспринимать в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации.В силу всего сказанного надо отметить, что употребление союза или всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется. Понятно, что без этого комментария вполне возможны разночтения, которые нередко приводят к различным и существенным недоразумениям.
Данный текст является ознакомительным фрагментом.
ПРОБЛЕМА ПОНЯТИЯ
ПРОБЛЕМА ПОНЯТИЯ ПОНЯТИЕ В ЯЗЫКЕ Исходным пунктом кассиреровских рассуждений о лингвистическом образовании понятий послужило учение Гумбольдта о «внутренней форме», выявляющей специфический закон этого образования в различных языках. По Гумбольдту, «внутренняя
Что такое понятия?
Что такое понятия? Почему, на взгляд Макдауэлла, овладение комплексом понятий приводит к пониманию мира? Почему благодаря пребыванию в концептуальной сфере опыт делает возможной открытость миру? Здесь важную роль играет пассивность опыта — тот факт, что мы не
Ключевые понятия
Ключевые понятия
Задавшись экстремальной целью – свести общий язык к одному слову – можно было бы уверенно сказать: это слово ориентирование.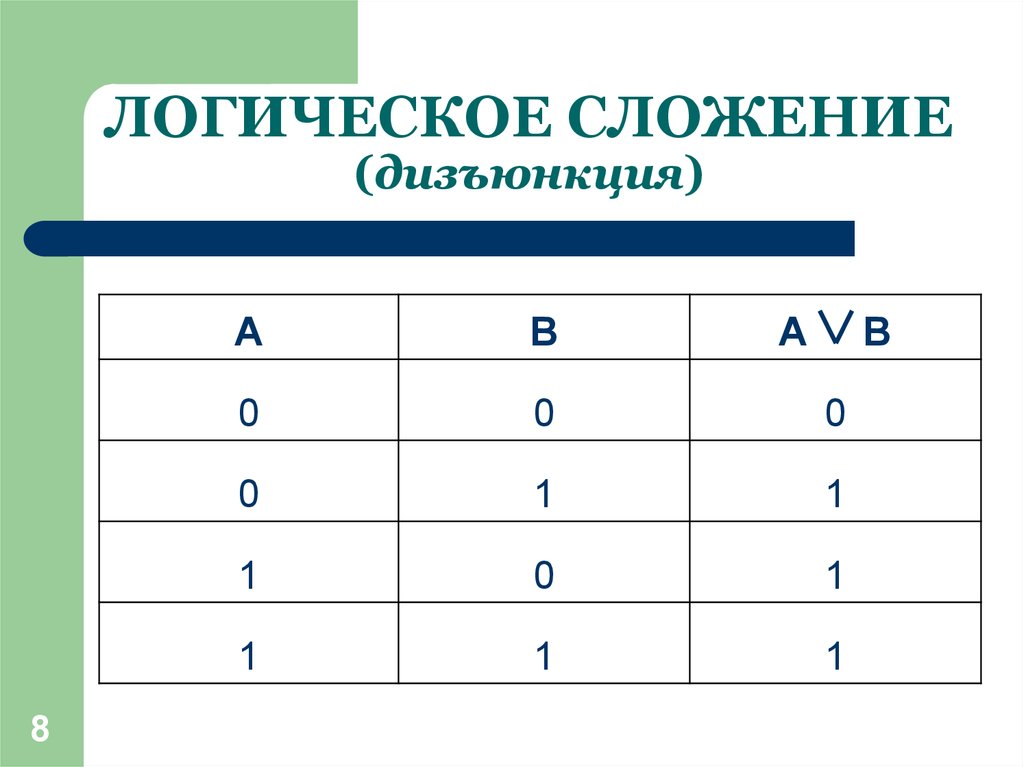 Поэтому ничего удивительного в том, что другие главные понятия минимального общего языка, которые мы хотим определить, тесно
Поэтому ничего удивительного в том, что другие главные понятия минимального общего языка, которые мы хотим определить, тесно
1.9. Определение понятия
1.9. Определение понятия Одной из важных логических операций с понятиями, которая постоянно используется как в научном, так и в повседневном мышлении, является операция определения понятия. В жизни мы часто встречаемся с такими выражениями, как «начнем с определения…»,
1.11. Деление понятия
1.11. Деление понятия Еще одной важной логической операцией с понятиями, наряду с определением, является деление. Определение понятия, как мы уже знаем, раскрывает его содержание, а деление понятия – это логическая операция, которая раскрывает его объем.Деление понятия§3. Понятия
§3. Понятия
«Объект» и «Предмет», «Содержание» и «Сущность»,«Объективности» и «Реальность» .Для того чтобы далее перейти к тому, что можно было бы назвать алгоритмом диалектического метода, нам необходимо уточнить ряд понятий. Что мы будем подразумевать под:- объектом и
Понятия
«Объект» и «Предмет», «Содержание» и «Сущность»,«Объективности» и «Реальность» .Для того чтобы далее перейти к тому, что можно было бы назвать алгоритмом диалектического метода, нам необходимо уточнить ряд понятий. Что мы будем подразумевать под:- объектом и
2. Понятия и смыслы
2. Понятия и смыслы Ноосфера – последнее из многих состояний эволюции биосферы в геологической истории – состояние наших дней. Ход этого процесса только начинает нам выясняться из изучения ее геологического прошлого в некоторых аспектах [663] . В.И. Вернадский 2.1.
5. Два понятия сознания
5. Два понятия сознания Исходя из того, что очень многие ментальные термины имеют двойную природу, не удивительным будет узнать, что даже термин «сознание» имеет как феноменальный, так и психологический смысл. До сих пор я говорил о сознании в феноменальном смысле,
15.
 Совместимые понятия
Совместимые понятия15. Совместимые понятия Отношения совместимости могут быть трех видов. Сюда входят равнозначность, перекрещивание и подчинение.Равнозначность. Отношение равнозначности иначе называется тождеством понятий. Оно возникает между понятиями, содержащими один и тот же
16. Несовместимые понятия
16. Несовместимые понятия Несовместимыми являются понятия, объемы которых не совпадают ни полностью, ни частично. Это происходит в результате того, что в содержании данных понятий присутствуют признаки, которые полностью исключают совпадение их объемов.Отношения
2. Совместимые понятия
2. Совместимые понятия
Отношения совместимости могут быть трех видов. Сюда входят равнозначность, перекрещивание и подчинение.Равнозначность. Отношение равнозначности иначе называется тождеством понятий. Оно возникает между понятиями, содержащими один и тот же
Оно возникает между понятиями, содержащими один и тот же
3. Несовместимые понятия
3. Несовместимые понятия Несовместимыми являются понятия, объемы которых не совпадают ни полностью, ни частично. Это происходит в результате того, что в содержании данных понятий присутствуют признаки, которые полностью исключают совпадение их объемов.Отношения
Два понятия системы[89]
Два понятия системы[89] Когда сейчас характеризуют «систему» (будь то содержание понятия или объект), говорят обычно, что это сложное единство, в котором могут быть выделены составные части, или элементы, а также схема связей и отношений между ними; иногда к этому добавляют
1. Понятия и категории
1. Понятия и категории
Каждая наука имеет свой терминологический лексикон. Услышав слова «электрон» или «квант», любой грамотный человек понимает, что речь идет о физике. Когда произносят слово «молекула» – речь о химии, а аббревиатуру ДНК – о биологии. Некоторое
Услышав слова «электрон» или «квант», любой грамотный человек понимает, что речь идет о физике. Когда произносят слово «молекула» – речь о химии, а аббревиатуру ДНК – о биологии. Некоторое
НЕТОЧНЫЕ ПОНЯТИЯ
НЕТОЧНЫЕ ПОНЯТИЯ Имена можно классифицировать, исходя из самых разных соображений. Несколько ранее они были подразделены, например, на единичные, общие и пустые. Затем разделены на собственные и не являющиеся собственными.Имена принято делить также на конкретные
НЕЯСНЫЕ ПОНЯТИЯ
НЕЯСНЫЕ ПОНЯТИЯ До сих пор речь шла о неточных понятиях.Граница множества вещей, подпадающих под неточное понятие, является размытой и неопределенной. Относительно тех из них, которые лежат на этой границе, нельзя с уверенностью и без колебаний сказать ни то, что им
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 5 из 19Следующая ⇒
В предыдущих параграфах мы говорили о логических операциях ограничения, обобщения, определения и деления понятий. Теперь рассмотрим еще две логические операции – сложение и умножение понятий. Сложение понятий– это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник и спортсмен образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой,на схеме Эйлера изображается штриховкой:
Умножение понятий– это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий.
Выше были приведены примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения (школьник и спортсмен). В других случаях отношений между понятиями (о которых речь шла в § 1.3) результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. В приводимой ниже таблице штриховкой показаны результаты сложения и умножения понятий во всех видах отношений между ними.
Как видим, результаты сложения и умножения понятий полностью совпадают только в случае равнозначности между ними, частично совпадают в пересечении и подчинении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трех случаях результатом умножения является нулевое или пустое понятие). Как правило, в естественном языке (то есть том, на котором мы общаемся) результат сложения понятий выражается союзом или, а умножения – союзом и. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является или школьником, или спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является и школьником, и спортсменом одновременно. Относительно употребления союзов или и и в естественном языке в качестве выражения результатов логических операций сложения и умножения понятий удачный пример приводит В.И. Свинцов в уже упоминавшемся нами учебнике по логике (Свинцов В.И. Логика. Элементарный курс для гуманитарных специальностей. – М.: Скорина, 1998. – С. 60 – 61), отрывок из которого приводится ниже. «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Однако следует отметить, что и в данном случае могут возникнуть недоразумения. Дело в том, что разделительный союз или может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем).
Глава 2. СУЖДЕНИЕ
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1865; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Когда сложение и умножение одинаковы
Когда сложение и умножение одинаковыЭто еще одно небольшое эссе — упражнение в математических развлечениях; Надеюсь, вы найдете это забавным!
Когда сложение совпадает с умножением? Другими словами, когда верно следующее?
х + у = х * у
Немного подумав, вы поймете, что {x,y} = {2,2} и {0,0} есть два решения проблемы, потому что:
2 + 2 = 2 * 2 = 4 0 + 0 = 0 * 0 = 0
Но есть ли другие решения? Чтобы это выяснить, нам нужно решить уравнение, используя небольшую алгебру:
х + у = ху 0 = ху - х - у 0 = (x-1)(y-1) - 1 (Запутался? См. Постскриптум ниже) 1 = (х-1)(у-1) 1/(х-1) = у-1 у = 1/(х-1) + 1
Итак, существует бесконечное количество решений для действительных чисел; найти
заданный y, просто вычислите y = 1/(x-1)+1
(пока x не равен 1; в этом случае нет действительного числового решения). Например, пара {1.5,3} работает, потому что:
92
+1 или -1 = х-1
х = 0 или 2
Например, пара {1.5,3} работает, потому что:
92
+1 или -1 = х-1
х = 0 или 2
Теперь вместо того, чтобы ограничиваться x=y, допустим любое значение x и y, но только если они оба являются целыми числами. Учитывая этот вариант, существуют ли какие-либо другие решения для целочисленных пар? Короткий ответ — нет — если вы ограничитесь целыми числами, 0 и 2 все что возможно. Вот почему. Поскольку целые числа являются подмножеством действительных чисел, уравнение приведенное выше применяется:
у = 1/(х-1)+1Итак, чтобы y было целым числом, 1/(x-1) должно быть целым числом. Чтобы дробь давала целое число, когда единица находится сверху, его знаменатель должен иметь абсолютное значение меньше единицы, поэтому:
|х-1|
Это верно только для x = {0,1,2}. х не может быть 1, потому что
потребует, чтобы y был бесконечен.
Таким образом, 0 и 2 также являются единственными целочисленными решениями.
Итог: существует бесконечное количество пар действительных чисел, где
сложение и умножение пары даст тот же ответ. Но если вам требуется, чтобы пара имела одинаковое значение или оба
быть целыми числами, есть только два ответа: {0,0} и {2,2}.
Но если вам требуется, чтобы пара имела одинаковое значение или оба
быть целыми числами, есть только два ответа: {0,0} и {2,2}.
К сожалению, некоторые люди прислали мне сообщения,
просят меня объяснить, почему:
ху - х - у
такой же как:
(х-1)(у-1) - 1
Тск, тск! Пожалуйтесь своим учителям алгебры, они
пропустил важный материал.
Оказывается, это нетрудно показать;
просто начните с "(x-1)(y-1)" и умножьте его.
Это два тривиальных выражения; можно просто умножить
их так же, как вы перемножаете многозначные числа:
х - 1
* у - 1
===============
-х + 1
ху-у
===============
ху-х-у + 1
Итак, (x-1)(y-1) равно почти то же, что xy-x-y, за исключением того, что
у него есть дополнительный «+1». Нет проблем, просто вычтите единицу, и она у вас есть.
Что означает, что:
ху - х - у = (х-1)(у-1) - 1
Вот, если честно, я сразу же узнал "ху-ху-у" так же легко
переписано как «(x-1)(y-1)-1»; Мне не пришлось «разбираться». Но если вы не видели этого раньше, надеюсь, это вас убедит.
Но если вы не видели этого раньше, надеюсь, это вас убедит.
Если вам понравилась эта статья, вам могут понравиться мои статьи о
Задача четыре четверки или
странные базы.
Не стесняйтесь видеть мой
домашняя страница на dwheeler.com.
Дэвид А. Уилер, 10 сентября 2002 г.
Это Copyright (C) 2002-2005 Дэвид А. Уилер.
Идентификационные числа для сложения и умножения — Криста Кинг Математика
Что такое идентификационные номера?
Идентификационные номера — это числа, которые не изменяют «идентификацию» исходного значения.
Идентификатор для дополнение это ???0???.
Идентичность для умножения равна ???1???.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Причина в том, что
Можно добавить ???0??? на любое число, и это не меняет исходное значение.
Вы можете умножить любое число на ???1??? и это не меняет исходное значение.
Как идентификационные номера не меняют личность
Пройти курс
Хотите узнать больше о Pre-Algebra? У меня есть пошаговый курс для этого. 🙂
Учить больше
Идентификационные числа для сложения и умножения
Пример
Что такое ???17+0????
Даже не думая об этом с точки зрения идентификационных номеров, мы уже должны знать, что ???17+0=17???, потому что если у вас есть ???17??? и вы ничего не добавляете к нему, у вас все еще есть ???17???.
Если мы подумаем об этом более технически с точки зрения идентификационных номеров, мы знаем, что ???0??? является идентификационным номером для добавления. Так как мы добавляем ???0???, и потому что ???0??? это идентификационный номер для добавления, мы знаем, что добавление ???0??? до ???17??? не изменит личность ???17???, поэтому ???17+0??? будет просто ???17???.

 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
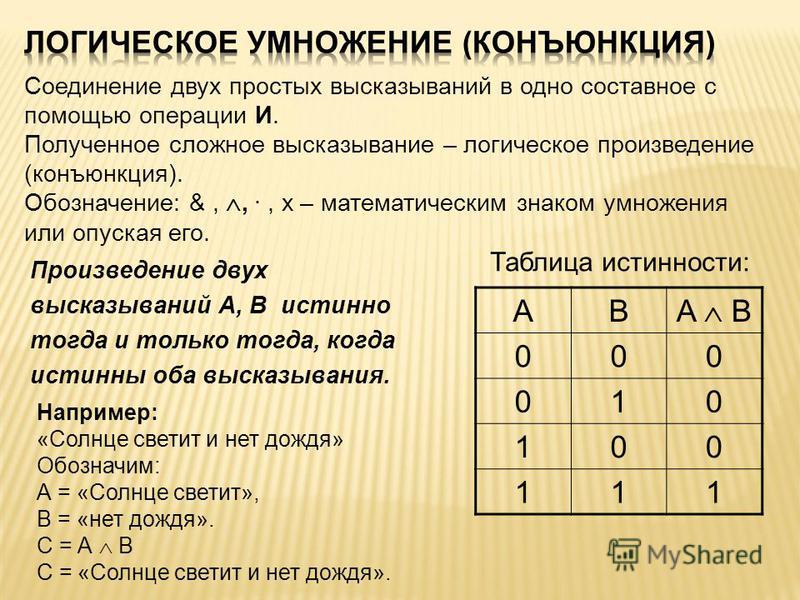 Например, при умножении понятий школьник и спортсмен образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением,на схеме Эйлера изображается штриховкой (так же, как и результат сложения):
Например, при умножении понятий школьник и спортсмен образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением,на схеме Эйлера изображается штриховкой (так же, как и результат сложения): В отношении подчинения результатом сложения является родовое понятие, а умножения – видовое.
В отношении подчинения результатом сложения является родовое понятие, а умножения – видовое. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: «Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза «или» здесь следует признать предпочтительным».
Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: «Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза «или» здесь следует признать предпочтительным». Например, в высказывании: Можно изучать английский язык или немецкий союз или употребляется в нестрогом значении, так как можно изучать и тот, и другой язык одновременно, одно другое не исключает. В данном случае разделительный союз или очень близок к соединительному союзу и. С другой стороны, в высказывании: Он родился в 1987 году или в 1989 году союз или употребляется в строгом значении, так как если он родился в 1987 году, то – никак не в 1989 году, и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза или мы еще будем говорить в § 2.6, посвященном видам сложных суждений.) Если в рассмотренное выше правило пользования городским транспортом поставить союз или вместо союза и, как предлагает В.И. Свинцов, то получится следующее: «Безбилетный проезд или бесплатный провоз багажа наказываются штрафом». В данном случае союз или, являясь показателем логического сложения, должен восприниматься в его нестрогом, неисключающем значении.
Например, в высказывании: Можно изучать английский язык или немецкий союз или употребляется в нестрогом значении, так как можно изучать и тот, и другой язык одновременно, одно другое не исключает. В данном случае разделительный союз или очень близок к соединительному союзу и. С другой стороны, в высказывании: Он родился в 1987 году или в 1989 году союз или употребляется в строгом значении, так как если он родился в 1987 году, то – никак не в 1989 году, и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза или мы еще будем говорить в § 2.6, посвященном видам сложных суждений.) Если в рассмотренное выше правило пользования городским транспортом поставить союз или вместо союза и, как предлагает В.И. Свинцов, то получится следующее: «Безбилетный проезд или бесплатный провоз багажа наказываются штрафом». В данном случае союз или, являясь показателем логического сложения, должен восприниматься в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации. В силу всего сказанного надо отметить, что употребление союза или всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется.
Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации. В силу всего сказанного надо отметить, что употребление союза или всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.) Но если вам требуется, чтобы пара имела одинаковое значение или оба
быть целыми числами, есть только два ответа: {0,0} и {2,2}.
Но если вам требуется, чтобы пара имела одинаковое значение или оба
быть целыми числами, есть только два ответа: {0,0} и {2,2}.
 Но если вы не видели этого раньше, надеюсь, это вас убедит.
Но если вы не видели этого раньше, надеюсь, это вас убедит.