Головоломка пифагора схемы: 5 знаменитых геометрических игр-головоломок, которые можно сделать своими руками | Реальные Игры | Головоломки

Содержание

Танграм, Пифагор, Листик и другие обитатели нашего холодильника.

Оригинал взят у lidavetta в Танграм, Пифагор, Листик и другие обитатели нашего холодильника.

Мне так понравилась игра Пентамино на магнитах, которую я сделала пару дней назад, что

Остапа

меня понесло дальше! Ну, а что — магнит простаивает без дела! Теперь я знаю, на сколько хватает рулона 100*100 см — на 5 магнитных музыкальных инструментов, размером с альбомный лист, а еще на громадное Пентамино, огромный Танграм, и не менее громадные Пифагор, Листик, Монгольскую и Вьетнамскую игру, Колубово яйцо и букву Т.

И после этого кусок чуть больше формата А4 еще остался. Я бы сделала еще и Стомахион и Магический круг, но вдруг выяснилось, что магнит этот не примагничивается к поверхностям с обратной стороны. Это минус,конечно. За счет этого несимметричные кусочки головоломок трудно использовать,ведь все их можно переворачивать по правилам. На столе собирать — сколько угодно, а вот как магниты — уже сложно. Придется, кстати, ту же Пентамино дополнять дубляминесимметричных фигур в зеркальном отражении, их ровно половина из набора.

Но зато, благодаря этому свойству магнита я узнала, что Саня очень хорошо может собирать фигуры в зеркальном отражении,без проблем. Собирал он из головоломки «Листик» уточку по схеме. А там нужно использовать несимметричный четырехугольник, и у нас он повернут не в ту сторону, которая на схеме. Я предложила Сане собрать фигуру в обратную сторону ,и он тут же взял и все переложил зеркально, даже не задумавшись. Сама бы я до такого хода не додумалась, а так — получилось хорошо и полезно. Правда, параллелограмм тоже оказался не в ту сторону, но его мы взяли из другой головоломки, поэтому он другого цвета. Получилось вот так:

Утка на схеме — первоначальный вариант, а с синей шеей — он собрал сам. Он вообще все фигуры, которые я сфотографировала, собрал сам, причем очень быстро, без «черновиков», так сказать.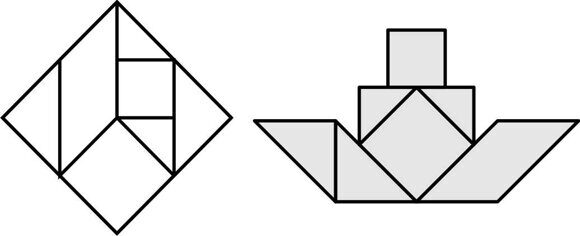 Это еще один момент, которому я его никогда не учила, но который он всегда умел — собирать по схемам.

Вот сам «Листик» — форма как у листа сирени:

Саня собирал, серьезный такой:

Это фигура из этой же головоломки.

Краб, как мне кажется. Параллелограмм пришлось тоже взять из другого набора:

Больше всего Сане почему-то понравилась «Монгольская игра», хотя фигуры у нее самые простые:

Вот схемы к ней:

Собирает:

Вот какой большой жираф!

И еще по схемам:

Танграм. Классика жанра. Я сделала цветной. И похожий на него — Пифагор, немного по-другому разрезан и у нас — одноцветный:

Схемы для Танграма:

В сборке:

Колумбово яйцо:

Схемы для него:

Зайчик:

Лисичка:

Глаза и носы добавили, потому что на схемах есть. Кстати, другие магниты к этому с обратной стороны очень даже магнитятся.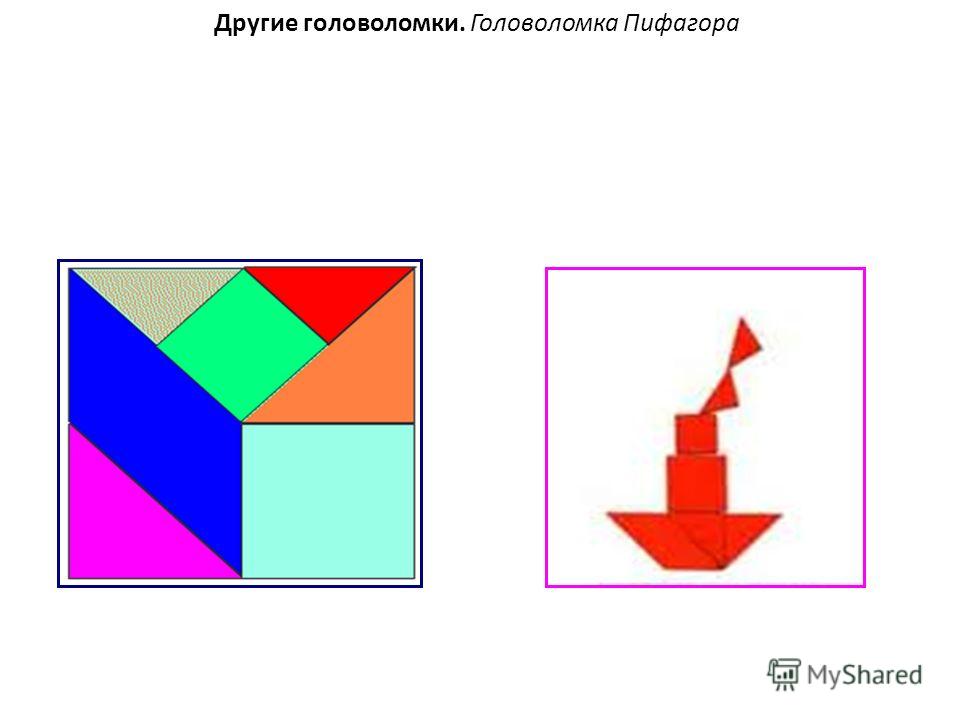 Колумбово яйцо имеет несколько нессиметричных деталей, которые не заменишь деталями из другого набора, поэтому я их продублирую. Я уже решила, что не буду дублировать целиком головоломку, сделаю только нессиметричные детали в зеральном отражении, и по правилам можно будет использовать только одну подобную деталь, они разноцветные, так что думаю, это будет вполне удобно. Ну, или, как мы сделали с уточкой- отзеркаливать фигуры, тоже вариант, а кое-что хорошо дублируется деталями из других наборов.

А это — Вьетнамская игра:

Вот она несимметрична почти вся, кроме двух маленьких деталей, поэтому у нее дубль почти полный:

Но ее я сделала в двойном варианте, потому что мало деталей, а вот такие, как Стомахион, где почти все детали несимметричны, и их не 5 штук — я делать на магните не буду.
Схемы ко Вьетнамской игре:

Попугай:

А это самая необычная головоломка, которую я видела — буква Т:

Всего-то 4 детали, но зато сколько возможностей! Другой ее название — 100 фигур, и даже есть задания, по которым эти фигуры можно собрать. Это не схемы — поэтому не так-то просто это сделать, Сане однозначно трудно. Да даже нам, взрослым, трудно!

Эта игра вообще оказалась не так проста, как кажется на первый взгляд — начиная с ее длительной истории и заканчивая пропорциями. Оказалось, что ее надо разрезать очень даже с умом, чтобы все вышло, как надо. Но про эту головоломку я, пожалуй, сделаю как-нибудь отдельный пост.

Вот такие игры у нас теперь есть в дополнение к нашему и так немаленькому арсеналу)))

Новый: Игры

Вы любите играть?

Сегодня увлечение настольными играми принимает тотальный характер. Ведь современные настольные игры – это не только «бродилки», но и стратегические, экономические, детективные, логические игры.

В мире существует уже до 10 тысяч настольных игр разной тематики. Конечно, за всеми новшествами не угнаться, а некоторые игры слишком дорого стоят. Но ведь игру можно сделать и своими руками

Вот несколько игр.

Танграм

Игры-головоломки, на воссоздание из геометрических фигур образных изображений используются для совершенствования зрительного восприятия, и анализа, зрительной памяти, комбинаторики. Наборы фигур представляют собой части разрезанной определенным образом фигуры: квадрата, прямоугольника, круга или овала. Они интересны детям. Детей увлекал результат — составить увиденное на образце или задуманное.

Успешность освоения игры у детей зависит от сенсорного развития детей. Дети называли геометрические фигуры, их свойства, их отличительные признаки, свободно перемещать фигуры. У детей развивается умение анализировать изображения, выделять геометрические формы, видоизменять фигуры путем разрезания и составлять их из частей.

Существуют различные игры- головоломки, на воссоздание из геометрических фигур плоскостных изображений предметов, животных, птиц, домов, кораблей такие как: «Танграм», «Пифагор», «Сфинкс», «Волшебный круг», «Колумбово яйцо», «Листик», «Вьетнамская игра», «Пентамино».

Но мы сейчас рассмотрим только одну из них — «Танграм».

Появление этой китайской головоломки связано с красивой легендой. Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по летам. Одно беспокоило старого императора Мальчику доставляло большое удовольствие целый день забавляться игрушками. Император призвал к себе трех мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей.

Три мудреца придумали «Ши-Чао-Тю» — квадрат, разрезаннный на семь частей.

Говорят, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, «упражняя свое терпение и находчивость»

Суть игры заключается в том, чтобы на плоскости из семи частей квадрата создавать самые разнообразные фигуры, силуэты предметов по образцу или замыслу. В коммерческих наборах обычно прилагаются карточки с заданиями.

1 вариант: Самый простой. Если ребенок маленький предложите ему составить фигуру путём наложения элементов на образец разделенными на составные части.

2 вариант: Если с первым разобрались ,то можно составлять фигуры по примеру, то есть картинка перед вами а элементы составляете уже смотря на фигуры разделённую на части.

3 вариант: Для детей постарше, можно оставлять в фигуре только контуры.

4 вариант: Собственно творческие задания — самому придумать и сложить фигуру.

Малыши тоже могут приобщаться к головоломке. Для них можно придумать совсем простенькие задания. Например, сложить из двух треугольников или из двух прямоугольников — квадратики, из треугольников — большой треугольник или параллелограмм. Таким методом можно изучить основные геометрические фигуры.

Сделать танграм можно самому. Это очень просто. Вам понадобятся шаблон головоломки. Распечатайте Танграм или нарисуйте сами по образцу. Можно использовать разноцветные элементы, если ребёнок маленький — заодно вспомните цвета, да и интереснее работать — играть с красочным
материалом.

При решении головоломки требуется соблюдать два правила: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны перекрываться друг другом. Взяв на вооружение математическую науку – комбинаторику, было получено более 5000 возможных вариантов сложенных фигурок.

Примеры сборки :

«ПИФАГОР»

Головоломка Пифагор очень похожая на старый добрый Танграм.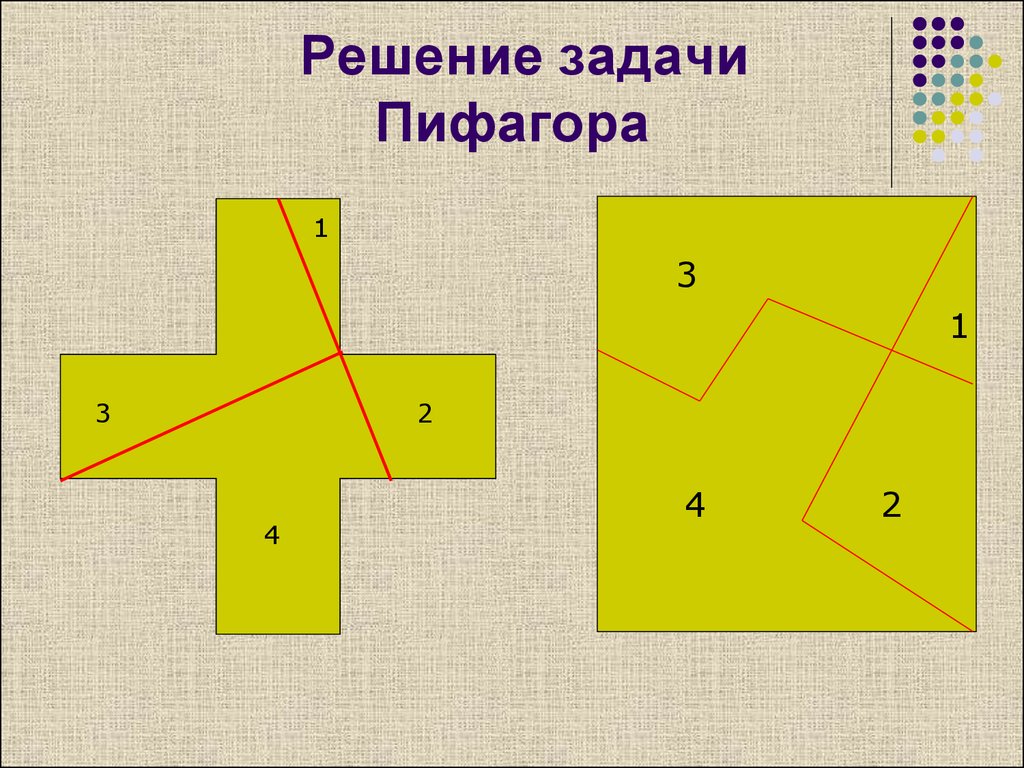

Головоломка имеет форму квадрата, разрезанного на 7 частей, комбинируя которые, можно создать огромное количество геометрических фигур, силуэтов животных, людей, разных предметов и т.п. Все детали разного размера, в этом и заключается сложность, поэтому сложить фигуру из них достаточно сложно.

В инструкции к

головоломке предлагаются 15 разных заданий.
Головоломку Пифагор можно использовать на занятиях по математике, дома или в школе, ведь она отлично способствует развитию воображения, логики, внимания, пространственного мышления, математических и творческих способностей. Вы можете сделать из картона или вырезать из пластика головоломку Пифагор и Вашей семье гарантированы положительные эмоции и хорошее нестроение.

ВОЛШЕБНЫЙ КВАДРАТ

Геометрическая головоломка Волшебный квадрат относится ко второму уровню сложности и подходит для детей в возрасте от 4 лет. Занимаясь с головоломкой, ребенок познакомится с простыми геометрическими фигурами: треугольником, трапецией, квадратом.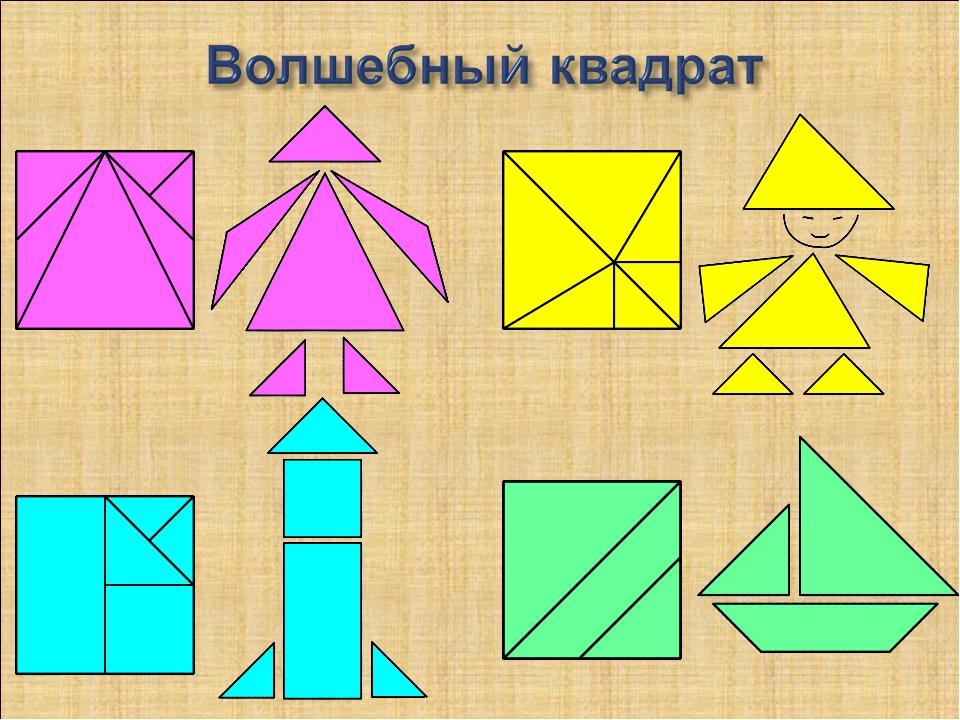

Головоломка “Монгольская игра”

Разновидность геометрической головоломки, на подобии “Танграма” или “Квадрата Пифагора”.

Головоломка представляет собой квадрат разрезанный на 11 частей: 2 квадрата, один большой прямоугольник, 4 маленьких прямоугольника, 4 треугольника. Лучше всего изготовить такую головоломку из двустороннего картона или пластика.

Суть игры — собирать фигурки из данных элементов по принципу мозаики.

Как можно играть:

Составлять геометрические фигуры по образцу. В интернете можно найти готовые задания с ответами,, а можно придумать задания для своего ребенка и самим.
Для того, чтобы нарисовать фигуры Вам потребуется лист в клетку. Можно взять обычный лист из школьной бумаги. Элементы из которых состоит “Монгольская игра” очень просты, и вам не составит большого труда составить из них композиции.

Вот, для примера, несколько фигур, составленных их элементов головоломки.

Если ребенок маленький, то можно составлять фигуры по примеру, то есть фигурам, разделенными на составные части.

Для детей постарше, можно оставлять в фигуре только контуры.

Головоломка «СФИНКС»

Головоломка «Сфинкс» состоит из разнообразных геометрических фигур: из
4 треугольников и 3 четырехугольников с разным соотношением сторон. Из
элементов можно собрать силуэты птиц, человека, животных, развивая
наблюдательность и геометрическое воображение.

Инструкция содержит
схемы для построения более двух десятков фигур:

Игры — головоломки развивают пространственное воображение, комбинаторные способности, сообразительность, смекалку, находчивость.

Простые в понимании, но достаточно трудные в решении, головоломки находятся на тонкой грани, соединяющей увлекательную игру и интеллектуальное развитие.

Головоломки от Алексея Шамшина

И ещё одна

Головоломка Архимеда СТОМАХИОН

Предлагаемая головоломка Архимедова игра — уникальный геометрический конструктор, в который играли еще в глубокой древности. Ее иное название «Стомахион».

Элементы игры получаются путем произвольного деления прямоугольника на 14 частей. Из получившихся деталей конструируют на плоскости разнообразные предметные силуэты, например, сидящей собаки, бегущего человека, разнообразных цветов, птиц. Можно сложить и многофигурные композиции. Знакомить ребенка с игрой необходимо постепенно.

Поупражняйте малыша в различении геометрических фигур. Можно предложить ребенку сосчитать стороны, углы, сгруппировать фигуры по форме, размеру, назвать их. Затем попробуйте конструировать простейшие изображения.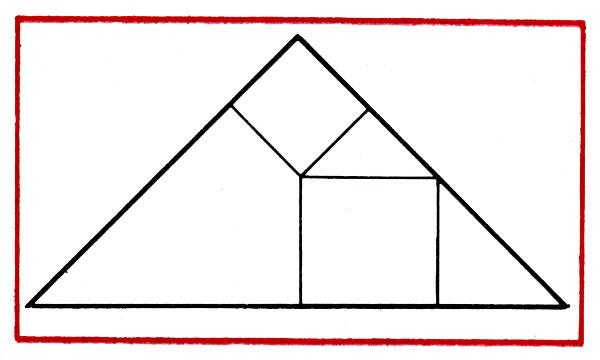

Для облегчения головоломки Архимедова игра, предлагается сначала выкладывать фигуры по прилагаемым схемам.

Головоломка «ЛИСТИК»

Геометрическая головоломка-мозаика Листик разработана для детей в возрасте от 4 лет Фигура, напоминающая лист сирени. Этот лист сирени выложен из других фигур: треугольников, квадратов, трапеций.

Работа с головоломкой развивает глазомер ребенка, восприятие им формы, зрительно-моторную координацию, пространственное мышление и воображение. Способствует развитию произвольности (умения играть по правилам и выполнять инструкции), познавательной активности, мелкой моторики, воображения, сформированности сенсорных эталонов цвета, величины и формы, комбинаторных способностей, абстрактного мышления.

«Волшебный круг»

Круг разрезается на 10 частей. Правила игры те же, что и в других подобных играх: использовать для составления силуэта все 10 частей, не накладывая одну не другую. Разрезанный круг должен быть окрашен одинаково, с двух сторон.

ВЬЕТНАМСКАЯ ИГРА

В состав «Вьетнамской игры» входит разделенный на семь частей круг и рамка, в которую укладываются элементы. Все детали головоломки имеют обтекаемую форму, некоторые из них одинаковы по размеру. Предложите малышу сконструировать из замысловатых деталей силуэт какого-нибудь животного или птицы. Сначала можно задействовать не все элементы, затем постепенно усложнять задания.

Можно конструировать по схемам, а можно выдумывать свои сюжетные композиции.

Конструируя простые образные фигуры, дети учатся восприятию формы, способности выделять, фигуру из фона, выделению основных признаков объекта. Головоломка развивает глазомер, аналитико-синтетические функции, воображение (репродуктивное и творческое), зрительно-моторную координацию, умение работать по правилам. Игра предназначена для детей от 4 лет

КОЛУМБОВО ЯЙЦО

Существует рассказ — может быть, и вымышленный.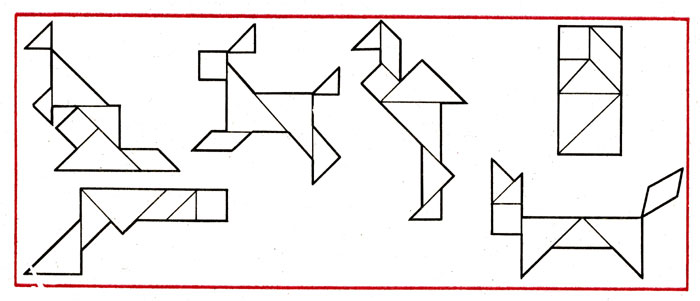 Открыватель Америки Колумб был приглашен к всемогущему кардиналу Мендозе. За столом, по просьбе гостей, он начал рассказывать, как именно был им открыт Новый Свет (который, впрочем, он считал Индией). Кто-то из присутствующих, человек ограниченный, но самоуверенный, пожав плечами, сказал: «Так просто всё?»

Колумб взглянул на него и протянул ему лежавшее на блюде куриное яйцо: «Сделайте так, чтобы оно стояло на своем носке». Разумеется, попытки установить яйцо успехом не увенчались. «Это немыслимо…» — сказал обескураженный собеседник Колумба. «Это очень просто!» — с усмешкой ответил мореплаватель и, разбив о стол носок яйца, без труда заставил его стоять.

Выражение «колумбово яйцо» — стало воплощением остроумного и неожиданного выхода из затруднения, синонимом простого разрешения трудных вопросов.

Знакомимся с увлекательной головоломкой Колумбово яйцо, которая отлично скрасит время в дороге, ожиданиt в поликлинике и конечно же, разовьет логику и мышление ребенка.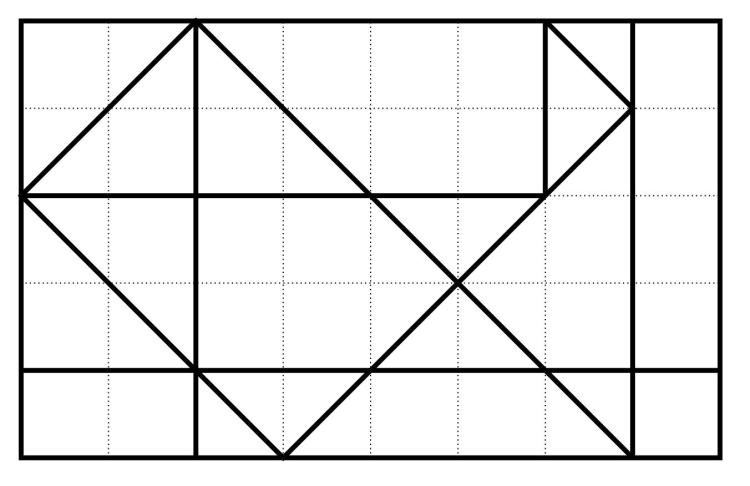 Принцип игры прост. Разрезаем по линиям фигурку яйца на мелкие детали. Задача ребенка – собрать фигурку по образцу. Но иногда можно пофантазировать и придумать свои варианты, разглядеть в фигуре знакомый образ.

Вот фигуры с заданиями

Пентамино

Известная логическая игра-головоломка. Именно эта игра вдохновила Алексея Пажитнова на создание популярной компьютерной игры тетриса.

Пентамино — очень популярная логическая игра и головоломка одновременно. Элементы в игре — плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов. Всего существуют 12 элементов пентамино, обозначаемых латинскими буквами, форму которых они напоминают

Можно изготовить пентамино из кубиков, но тогда Вам нужно будет склеить и обклеить цветной пленкой 60 кубиков — трудновато.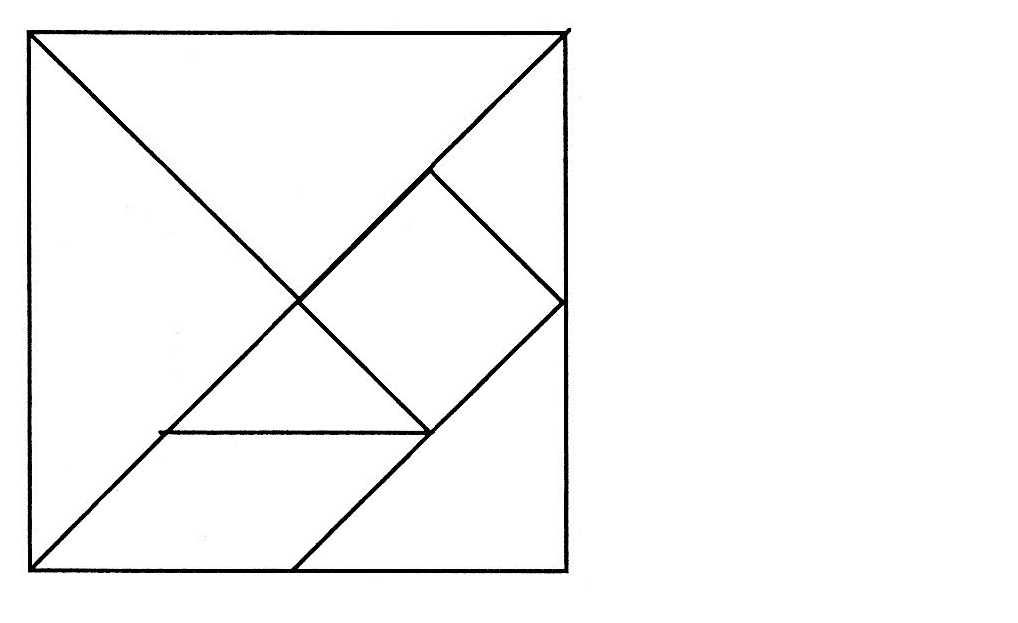 Предлагаем сделать элементы их плотного картона.

Рисуем каждый элемент на твердом картоне, вырезаем, проверяем, чтобы элемент входил в элемент “U”. Подрезаем , если надо лишнее. Мы рисовали детали из квадратиков 2,5х2,5 см.

Обводим готовый картонный элемент на сложенной вдвое цветной бумаге и вырезаем сразу две цветные детали. Лучше цветные детали делать меньше, чем картонные, и приклеиваются лучше, и углы поровнее будут.

Клеим клеем-карандашом цветную бумагу с двух сторон картонки.

Находим коробочку для хранения деталей, куда потом будем складывать также схемы и задания к игре.

Сложи прямоугольник.

Самая распространённая задача о пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20.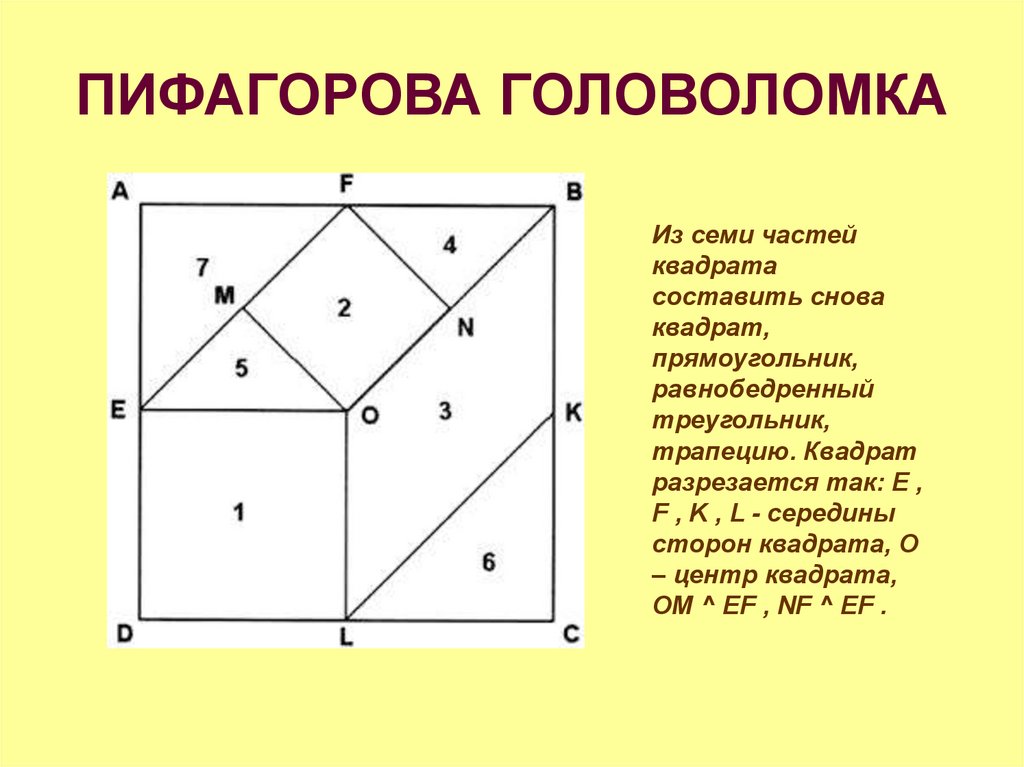
Существует ровно 2339 различных укладок пентамино в прямоугольник 6×10, а вот вариантов прямоугольника 3х20 всего 2.

Один из двух способов складывания прямоугольника 3х20

Честно скажу, пыталась весь вечер сложить — не получилось, поэтому ребенку такую задачу лучше не предлагать.

Детям лучше тренироваться на маленьких прямоугольниках из нескольких деталей.
Вот нарисовали варианты складывания прямоугольников из трех деталей.

Сложи фигуру

Их элементов можно складывать различные фигуры, симметричные узоры, буква алфавита, цифры.
Для маленьких детей, лучше фигуры складывать по образцу, как мозаику.
Фигурки можно распечатать или перерисовать на листочек в клеточку

Ответы

ГЕКСАМИНО

Гексамино — это развивающая геометрическая головоломка-мозаика. На поле головоломки из отдельных деталей собрана причудливая геометрическая фигура. Все детали отличаются друг от друга по форме. Головоломка имеет четвертый уровень сложности и предназначена для детей в возрасте от 6 лет.

ГЕКСАТРИОН

ТЕТРИС

Классический Тетрис — случайные фигурки падают сверху, в игре игрок может переворачивать фигурки, двигать их горизонтально и ускорять движение вниз. Фигурка двигается пока не соприкоснется с другой фигуркой или не упадет на самый низ.

Если в игре заполняется ряд, то ряд исчезает и все что выше этого ряда опускается на одну клетку вниз. Игра постепенно наращивает темп. Если одновременно фигурки заполняют 4 ряда — это Тетрис, от этого и происходит название игры. В игре игрок получает очки за каждую фигурку и за каждый исчезнувший ряд. Игра Тетрис заканчивается когда верхняя фигурка касается верхней границы экрана.

Одна из самых классических игр, игра Тетрис (Tetris) обладает воистину магической притязательностью, сколько в неё не играешь, а хочется всё больше и больше.

В игру Тетрис (Tetris) смогут играть не только взрослые, но и маленькие исследователи этого загадочного мира, игра тетрис всегда выручит и взбодрит скучными зимними вечерами. Итак, правила в игре такие же классические как и сама игра, складываем фигурки, так чтобы получилась одна сплошная линия.

Тетрис — это одна из первых электронных игр, которая появилась еще тогда, когда ни у кого не было домашних компьютеров.
Это самая современная и красочная версия тетриса. Дизайн и управление тут на высоте, кроме того добавлены некоторые интересные фишки. Цель игры — расставить падающие сверху фигурки таким образом, чтобы они заняли всё пространство по горизонтали, в этом случае они испарятся и дадут вам игровые очки.

Головоломка с теоремой Пифагора — Преподавание математики

Рубрика: Алгебра, Геогебра, Геометрия

Опубликовано автором

Математические головоломки — отличное занятие для изучения математики. Ниже приведен пример Тачиавасэ. Тачиавасэ — популярная в Японии головоломка, в которой геометрическая фигура разрезается на несколько частей, а затем объединяется из них в другую геометрическую фигуру. Загадка ниже принадлежит Хикодате Накане (1743 г.). Это была одна из головоломок, раздававшихся на стенде Японского общества математического образования во время ICME 12 в Сеуле в этом году.

Создайте фигуру из двух квадратов разного размера , разделив их на три части, а затем соедините их в один квадрат . [Переформулированная версия: сделайте два разреза в приведенных ниже фигурах, чтобы получились фигуры, которые можно сложить в больший квадрат.]

Вот как я разгадал загадку: я знаю, что она должна иметь какое-то отношение к теореме Пифагора, потому что она просит составить из двух меньших квадратов больший. Но где я должен сделать разрез? Я смог понять это только после того, как изменил условие головоломки на два квадрата с одинаковыми размерами. Это значительно уменьшило сложность. Это натолкнуло меня на мысль, где я мог бы сделать разрез для стороны квадрата, которую я буду формировать. Решение этой головоломки также дало мне представление о том, как преподавать теорему Пифагора.

Я сделал следующий математик GeoGebra (динамический математический апплет), основанный на решении головоломки. Я думаю, что математическая головоломка с двумя квадратами немного сложна для начала урока, поэтому я предлагаю начать урок с этой математики, а затем дать головоломку позже. Как всегда, ключом к любому уроку являются вопросы, которые вы задаете. Для приведенного ниже апплета предлагается следующая последовательность вопросов:

Какова площадь каждого из квадратов на рисунке? Укажите не менее двух способов нахождения площади.
Как связаны их области? Перетащите F, чтобы узнать, работает ли ваша гипотеза для любого размера квадратов.
Можете ли вы придумать другие способы доказательства соотношений между тремя квадратами без использования мер сторон?
Если два меньших квадрата BEDN и GFNH имеют стороны p и q, то как выразите площадь самого большого квадрата LEJG через площади меньших?
Выразите длину сторон LEJG через стороны BEDN и GFNH.

[iframe https://math5teaching.com/wp-content/uploads/2012/08/Pythagorean.html 550 450]

После этого урока по пифагорову соотношению вы можете дать головоломку. Как только у них будут правильные фигуры, попросите учеников переместить фигуры, используя трансформацию, за наименьшее количество возможных ходов. Они должны быть в состоянии сделать это за три движения, используя вращение. Щелкните здесь, чтобы загрузить апплет. Примечание. Если вы не видите апплет, включите Java в своем браузере. Если вам понравился этот пост, поделитесь им в своей сети. Спасибо.

Метки: GeoGebra деятельность, головоломка, теорема Пифагора, вращение, квадраты, обучение пифагору, преобразование

Пифагор 1: Математика дома

Подготовка

Распечатайте этот лист с кусочками пазла.
Печать на тонкой карточке была бы чудесной, но если нет, то подойдет и бумага.
Аккуратно вырежьте детали пазла. Найдите конверт или запечатанный пакет для их хранения.
Найдите линейку и карандаш. Они понадобятся вам позже в упражнении.
Распечатайте эту бумагу с квадратными линиями.
Напишите название задачи и сегодняшнюю дату на новой странице своего математического журнала.

Начало работы

Вам нужны все фигуры, кроме треугольника и квадрата.
Оставьте этих двоих в конверте.
Вы используете четыре (4) конгруэнтных четырехугольника.
Как вы думаете, что означает четырехугольник?
Как вы думаете, что означает конгруэнтность?
Ответ в вашем журнале.
Соедините четыре части вместе, чтобы получился квадрат.
Его площадь будет равна 4 четырехугольникам.
Нарисуйте, как соединяются детали.
Соедините четыре части вместе, чтобы получился квадрат с пустым пространством посередине.
Нарисуйте, как соединяются детали.
Вы что-нибудь заметили в пустом пространстве?

Следующее испытание

Теперь вы знаете, что можете сделать квадрат из четырех частей и квадрат из пяти (5) частей.

Откройте стартер Pythagoras 1.
Вы можете прочитать это на экране или распечатать.
Теперь вы добавите треугольник и квадрат к четырем четырехугольникам.
Прочтите рассказ и ответьте на вопросы 1, 2 и 3.
Пока не выполняйте задание на стартере.
Делайте заметки и диаграммы, связанные с тем, что вы записали ранее.

Получайте удовольствие от изучения Пифагора 1

Математик по имени Генри Перигал открыл, как разрезать квадрат среднего размера на четыре четырехугольника и использовать их для демонстрации теоремы Пифагора. Он не был профессиональным математиком вроде университетского профессора или программиста. Математика была его хобби. Он делал это в свободное время, потому что ему нравились вызовы. Но он известен благодаря своему открытию.

В вопросах 1, 2 и 3 вы использовали перигал для доказательства теоремы Пифагора для одного треугольника. Вы показали, что квадрат из четырех частей вместе с малым квадратом имеет такую же площадь, как квадрат, построенный на гипотенузе прямоугольного треугольника.

Но доказательство того, что Пифагор работает для одного треугольника, не доказывает, что оно работает для всех треугольников.
Это может сработать только для этого. Мы должны попробовать еще хотя бы один.
Вернуться к испытанию на Стартере.
Он просит вас создать свой собственный треугольник и его квадраты.
Используйте их, чтобы снова ответить на вопросы 1, 2 и 3.

Вам нужно будет выяснить, как Генри Перигал знал, где провести
линии разреза, чтобы сделать четыре части квадрата среднего размера.

Подсказки

Как было предложено в Starter, используйте свои фигуры в качестве модели.
Есть ли что-нибудь особенное в том, где пересекаются линии разреза?
Сможете ли вы найти на чертеже другую фигуру?

Теперь вы доказали, что Пифагор работает для двух треугольников.
Но что произойдет, если треугольник равнобедренный?
Тогда два квадрата будут одинакового размера.
Будут ли они складываться в квадрат гипотенузы?

Расследовать.

Вы проверили доказательство теоремы Пифагора Перигала для трех различных треугольников. Это заняло много времени, и до сих пор не доказано, что это работает для каждого прямоугольного треугольника. Перигаль доказал это для каждых прямоугольных треугольников. Это то, что нам не нужно делать прямо сейчас, но, по крайней мере, мы знаем, что он не делал этого по одному треугольнику за раз. Так что есть еще чему поучиться.

Математик также должен был бы проверить, что происходит, если треугольник не имеет прямого угла.

Игра с Перигал

Мы знаем, что четыре четырехугольника могут составить четыре квадрата или пять квадратов с пробелом в центре. В этих головоломках вы научитесь делать их с помощью вращения. Однако лучше, если ваши четырехугольники имеют некоторую толщину, за которую можно держаться. Приклейте их к листу картона и аккуратно обрежьте.

Превращение квадрата в квадрат
В этой головоломке все равно что работать с игрушкой-трансформером.

Сделайте пять частей с пробелом посередине.
Это возможно использовать вращение только для преобразования пяти частей с зазором в четыре части.