Тема: «Танграм – геометрическая головоломка». Внеурочное занятие . | План-конспект занятия по математике (2 класс) на тему:

Внеурочное занятие

Тема: «Танграм – геометрическая головоломка».

Подготовила и провела учитель

Русакова Н.А.

Молодежное

2016год

Тема: «Танграм – геометрическая головоломка».

Цели: создать условия для знакомства  с понятием «танграм» ; учебе играм, связанным с танграмом.

Предметные результаты: познакомиться  с понятием «танграм» и их типами; научиться играм, связанным с танграмом.

Формирование УУД:

Регулятивные УУД: контроль в форме сличения способа действия и его результата с заданным эталоном.

Познавательные УУД: логические – анализ объекта с выделением существенных и несущественных признаков, синтез как составление целого из частей и с восстановлением недостающих.

Коммуникативные УУД: учитывать разные мнения, стремиться к координации различных позиций в сотрудничестве.

I. Вступительное слово учителя.  
Здравствуйте, ребята! Как ваше настроение? Настроены ли вы на занятие? Садитесь!
Я услышала о старинной китайской игре — головоломке танграм. Меня очень заинтересовала  эта игра. Мне захотелось, как можно больше узнать о танграме. Я решила подробно изучить историю возникновения этой головоломки и исследовать возможности этой игры, применение ее в форме игры. Поэтому, целью данного занятия является: изучить историю возникновения игры – головоломки «Танграм» и исследовать ее применение.
Головоломки – игрушки на все времена. До появления компьютерных и бурного развития настольных игр, одним из основных развлечений для большинства людей была игра — головоломка «Танграм». В наше время очень много людей увлекаются головоломками. Они любимы не только детьми, но и взрослыми. Игра помогает развивать логическое мышление, геометрическую интуицию. Это способ отвлечения от повседневных проблем и направлен на развитие различных мыслительных процессов — сопоставление, обобщение, установление последовательности, определение отношений «целое» — «часть». Все эти умения необходимы будущим математикам.

Что такое танграм?

Тангирам  — головоломка, которую придумали в Китае. В переводе с китайского, обозначает 7 дощечек мастерства. Состоит танграм из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.).

 Легенды  появления танграм

II. Выступления учащихся:
Танграм  — очень древняя  игра – головоломка. Она появилась в Китае более
4000 лет назад. Существует целый ряд версий и гипотез возникновения игры “Танграм”.
Легенда первая: версия про разбитую плитку. 
Более 4000 тысяч лет назад у одного человека из рук выпала фарфоровая плитка и разбилась на семь частей. Расстроенный, он в спешке старался ее сложить, но каждый раз получал все новые интересные изображения. Это занятие оказалось настолько увлекательным, что впоследствии квадрат, составленный из семи геометрических фигур, назвали Доской Мудрости.

Легенда вторая: три мудреца придумали «Ши-Чао-Тю». 
Появление этой китайской головоломки связано с красивой легендой. Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по летам. Одно беспокоило старого императора: его сын, будущий властелин огромной страны, не хотел учиться. Мальчику доставляло большее удовольствие целый день забавляться игрушками. Император призвал к себе трех мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали «Ши-Чао-Тю»- квадрат, разрезанный на семь частей.

Из истории танграма

Хотя танграм часто считают изобретением древности, первое печатное упоминание о нем встречается в китайской книге, созданной в 1813году и написанной, очевидно, в правление император Цзяцина.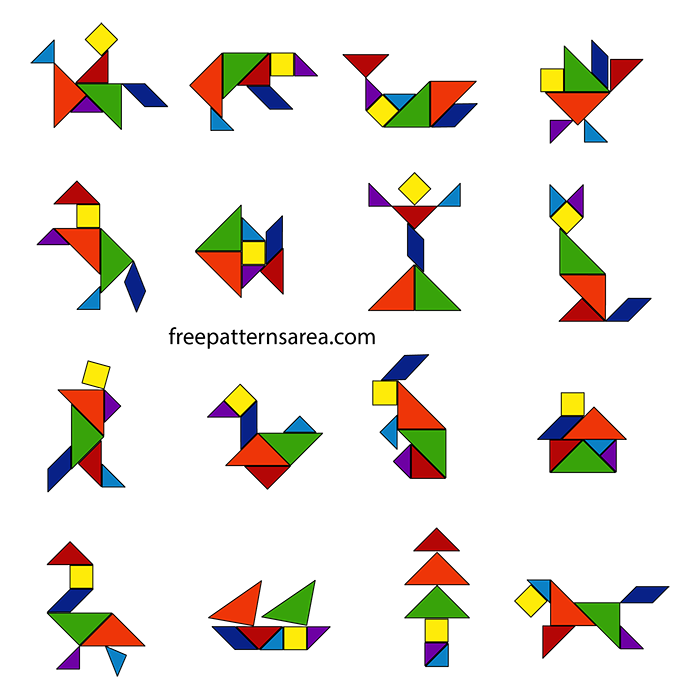

Появление танграма  на западе относят не     ранее чем к началу 19 столетия, когда эти       головоломки попали в Америку  на китайских и американских судах. Старейший такой экземпляр, подаренный сыну американского судовладельца в 1802 году, сделан из слоновой кости и хранится в шёлковом футляр

Название «танграм» впервые было использовано в 1848 году Томасом Хиллом, в дальнейшем президентом Гарвардского университета, в его брошюре «Головоломки для обучения геометрии»

Популярность танграма

Льюис Кэрролл
Все мы хорошо знаем книгу “Алиса в стране чудес” Л.Кэрролла (Чарльз Лютвидж Доджсон). Однако это его не единственное произведение. В книге “Модная китайская головоломка” он пишет, что танграм был любимой игрой Наполеона Бонапарта, который, лишившись трона, в изгнании на Острове Святой Елены проводил долгие часы за этой забавой, “упражняя свое терпение и находчивость”. 
Нас заинтересовала головоломка «Танграм», как игра, так как можно творчески провести время. Увлекает то, что из простых геометрических фигур можно сделать более сложные композиции. 
Суть игры заключается в конструировании на плоскости разнообразных предметных силуэтов, напоминающих животных, людей, предметы быта, транспорт, буквы, цифры, цветы и т.д. Всего насчитывают более 7 000 различных комбинаций. Самые распространенные из них — фигуры животных, птиц и человека.
Правила игры: 
В каждую собранную фигуру должны входить все семь элементов.¬
При составлении фигур элементы не должны налегать друг на друга.¬
Элементы фигур должны примыкать один к другому.¬
Начинать нужно с того, чтобы найти место самого большого треугольника.¬
В результате игры получается плоскостное силуэтное изображение. Оно условно, схематично, но образ легко угадывается по основным характерным признакам предмета: его строению, пропорциональному соотношению частей и форме. 
Типы задач, решаемых танграмом.   
1. Нужно сложить фигуру по контурному рисунку.
2. Нужно сложить фигуру по рисунку со сплошной заливкой, при котором не видно границ элементов.          
Затем можно попрактиковаться самостоятельно, создавая свои — простейшие изображения. Тем самым развивается собственная фантазия.

Применение танграма

1. Танграм может применяться на уроках математики для получение начальных сведений о геометрии. Знакомство с простейшими геометрическими фигурами: квадрат, треугольник, ромб, знакомство с углами. Сравнение фигур по форме, размеру, площади.

Составление из нескольких фигур новой геометрической фигуры: из двух треугольников – ромб, большой треугольник, квадрат, из трёх – треугольник, 
трапецию, параллелограмм  и т.д.

Играя, мы запоминаем названия геометрических фигур, их свойства, отличительные признаки, обследуем формы зрительным и осязательно-двигательным путем, свободно перемещаем их с целью получения новой фигуры. У нас развивается умение анализировать простые изображения, выделять в них и в окружающих предметах геометрические формы, практически видоизменять фигуры путем разрезания и составлять их из частей.

2. Танграм во всех его проявлениях можно встретить начиная от дизайна одежды, заканчивая архитектурой и ландшафтным дизайном.

IV.Работа в парах.

Сегодня я предлагаю составить фигуру семью танами одного танграма, на каждой парте конверт с танграмом.

Заключение
Что интересного было на занятии? 
Что особенно запомнилось?
Какой композиции вы бы отдали предпочтение, и почему?

Закончить о танграмах можно словами М. Гарднера: «Очарование танграма состоит в простоте материала и в кажущейся его непригодности для создания фигурок, обладающих эстетической привлекательностью»

Геометрические танграмы в категории «Подарки, хобби, книги»

Набор деревянных геометрических фигур Djeco Танграм Геоврум Ze Geo Vroom DJ06436

Заканчивается

Доставка по Украине

860 грн

Купить

Геометрическая интеллектуальная головоломка Танграм Разноцветная

На складе в г. Буча

Доставка по Украине

65 грн

Купить

Развивающий набор для детей Монтессори геометрические Деревянные пазлы танграм (86 шт) от Obetty

На складе

Доставка по Украине

462 грн

429 грн

Купить

Детский развивающий набор деревянные геометрические фигуры Танграм с карточками от Obetty

На складе

Доставка по Украине

303 грн

264 грн

Купить

Развивающий набор танграм Геометрическая мозаика с шаблонами от Obetty

На складе

Доставка по Украине

424 грн

Купить

Танграм геометрические фигуры Dodo

Доставка по Украине

200 грн

Купить

Доска магнитная с геометрическим конструктором Танграм 91334 (4820098991334)

Доставка по Украине

160 грн

Купить

Развивающая игра танграм DoDo Toys Магнитные геометрические фигуры 200212 GR, код: 7522654

Доставка по Украине

340 грн

234. 98 грн

Купить

Развивающая игра танграм DoDo Toys Магнитные геометрические фигуры 200212 SK, код: 7522654

Доставка по Украине

340 грн

234.98 грн

Купить

Развивающая игра танграм DoDo Toys Магнитные геометрические фигуры 200212 SC, код: 7522654

Доставка по Украине

340 грн

234.98 грн

Купить

Развивающая игра танграм DoDo Toys Магнитные геометрические фигуры 200212 GM, код: 7522654

Доставка по Украине

340 грн

234.98 грн

Купить

Развивающая игра танграм DoDo Toys Магнитные геометрические фигуры 200212 ML, код: 7522654

Доставка по Украине

340 грн

234.98 грн

Купить

Развивающая игра танграм DoDo Toys Магнитные геометрические фигуры 200212 EM, код: 7522654

Доставка по Украине

340 грн

234.98 грн

Купить

Геометрическая мозаика танграм с шаблонами

На складе

Доставка по Украине

269 грн

Купить

Геометрическая деревянная головоломка Танграм 22х22см

Доставка по Украине

335 грн

Купить

Смотрите также

Развивающая игра танграм DoDo Toys Магнитные геометрические фигуры 200212 ZK, код: 7522654

Доставка по Украине

340 грн

234. 98 грн

Купить

Развивающая игра танграм DoDo Toys Магнитные геометрические фигуры 200212 TS, код: 7522654

Доставка по Украине

340 грн

234.98 грн

Купить

Деревянная игра С 49875 «Танграм», магнитный планшет, 7 геометрических фигур, книжечка с заданиями

Доставка из г. Одесса

121.18 — 181.18 грн

от 2 продавцов

181.18 грн

Купить

Развивающая игра танграм DoDo Toys Магнитные геометрические фигуры 200212 CS, код: 7522654

Доставка по Украине

340 грн

234.98 грн

Купить

Развивающая игра танграм DoDo Toys Магнитные геометрические фигуры 200212 BS, код: 7522654

Доставка по Украине

340 грн

234.98 грн

Купить

Деревянная игра С 49875 «Танграм», магнитный планшет, 7 геометрических фигур, книжечка с заданиями, в кульке

Доставка по Украине

179 грн

Купить

Развивающая игра танграм «Магнитные геометрические фигуры» DoDo Toys 200212

Доставка по Украине

215. 1 — 239.7 грн

от 2 продавцов

239 грн

215.10 грн

Купить

Деревянная игра С 49875 «Танграм», магнитный планшет, 7 геометрических фигур, книжечка с заданиями, в пакете

Доставка по Украине

150 — 155 грн

от 2 продавцов

155 грн

Купить

Танграм деревянная геометрическая головоломка 17Х17см

Доставка по Украине

254 грн

Купить

Деревянная игра С 49875 (80) «Танграм», магнитный планшет, 7 геометрических фигур, книжечка с заданиями, в

Доставка из г. Одесса

164 грн

Купить

Деревянная игра С 49875 (80) «Танграм», магнитный планшет, 7 геометрических фигур, книжечка с заданиями, в

На складе в г. Киев

Доставка по Украине

121.18 — 145 грн

от 5 продавцов

145 грн

Купить

Танграм деревянный арт. MD 2239 | 155 деталей, 24 карточки | Limo Toy

На складе

Доставка по Украине

259 грн

Купить

Деревянный танграм мозаика с карточками-заданиями, деревянные геометрические пазлы

Доставка по Украине

326 грн

Купить

Танграм деревянный арт.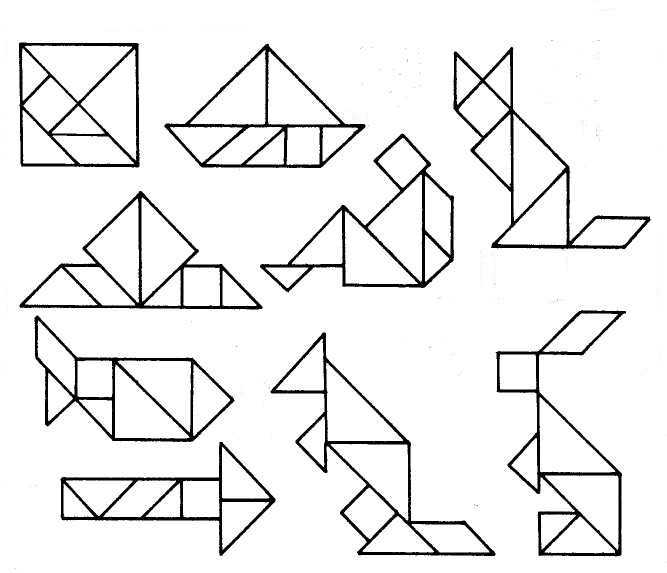 MD 2239 | 155 деталей, 24 карточки | Limo Toy

На складе

Доставка по Украине

259 грн

Купить

Tangrams: геометрические практические математические манипуляции

Toggle Nav

Знакомство с танграмами

Танграм представляет собой обманчиво простой набор семи геометрических фигур, состоящий из пяти треугольников (два маленьких треугольника, один средний треугольник и два больших треугольника), квадрат и параллелограмм. Когда части расположены вместе, они предлагают удивительное разнообразие форм, воплощая множество числовых и геометрических концепций. Части танграма широко используются для решения головоломок, требующих создания определенной формы из всех семи частей. Наборы Tangram бывают четырех цветов: красного, зеленого, синего и желтого. Все три треугольника Танграма разного размера подобны прямоугольным равнобедренным треугольникам. Таким образом, все треугольники имеют углы 45°, 45° и 9°.0°, и соответствующие стороны этих треугольников пропорциональны.

Еще одним интересным аспектом набора Tangram является то, что все части Tangram могут быть полностью покрыты маленькими треугольниками Tangram.

Отсюда легко увидеть, что все углы фигур Танграма кратны 45, то есть 45°, 90° или 135°, и что малый треугольник Танграма является единицей измерения, которая может можно использовать для сравнения площадей частей Танграма. Поскольку средний треугольник, квадрат и параллелограмм состоят из двух маленьких треугольников Танграма, каждый из них имеет площадь, вдвое превышающую площадь маленького треугольника. Большой треугольник состоит из четырех маленьких треугольников Танграма и, таким образом, имеет площадь в четыре раза больше, чем у маленького треугольника, и в два раза больше, чем у других частей Танграма.

Еще одна особенность частей состоит в том, что все семь частей соединяются вместе, образуя квадрат.

Некоторых учащихся очень утомляет создание фигур Танграма, особенно если они привыкли выполнять математические операции, следуя правилам и алгоритмам. Для таких студентов вы можете снизить уровень разочарования, дав несколько подсказок. Например, вы можете отложить первую часть или нарисовать линии на схеме, чтобы показать, как можно разместить части. Тем не менее, важно найти правильный уровень сложности, чтобы ученики могли получать удовольствие от каждого исследования Танграма. Иногда неправильное размещение некоторых фрагментов Танграма, а затем моделирование исследовательского подхода, такого как следующий, может помочь учащимся почувствовать себя более комфортно: «Интересно, смогу ли я расположить этот фрагмент Танграма таким образом? Наверное, нет, потому что тогда здесь больше ничего не подходит. Итак, Я лучше попробую по-другому…»

Танграммы — хороший инструмент для развития пространственного мышления и изучения дробей и различных геометрических понятий, включая размер, форму, конгруэнтность, сходство, площадь, периметр и свойства многоугольников. Танграмы особенно подходят для самостоятельной работы студентов, так как каждому студенту можно дать набор, за который он отвечает. Однако, поскольку учащиеся сильно различаются по своим пространственным способностям и языку, следует также выделить время для групповой работы, и большинству учащихся требуется достаточно времени, чтобы свободно экспериментировать с танграмами, прежде чем они приступят к более серьезным исследованиям.

Юные ученики поначалу воспринимают фигуры Танграма буквально. С опытом они увидят общие черты и начнут развивать абстрактный язык для аспектов паттернов в своих формах. Например, учащиеся могут сначала составить квадрат просто из двух маленьких треугольников. Однако со временем у них может развиться абстрактный мысленный образ квадрата, разделенного диагональю на два треугольника, что позволит им строить квадраты других размеров из двух треугольников.

Танграммы также могут предоставить визуальный образ, необходимый для понимания алгоритмов дробей. Многие учащиеся учатся делать такие примеры, как ¹ ⁄2 =  ^? ⁄8 или ¹ ⁄4 + ¹ ⁄8 +  ¹ ⁄16 = ? на чисто символическом уровне, так что если они забудут о процедуре, то проиграют. Студенты, у которых было много досимволических опытов, решали такие задачи, как «Найдите, сколько маленьких треугольников заполняет большие треугольники» или «Какая часть полного квадрата покрыта маленьким, средним и большим треугольниками?» будет иметь прочную интуитивную основу, на которой можно построить эти базовые навыки и на которые можно будет опереться, если память их подводит.

У юных учеников изначально есть склонность работать с другими и копировать работы друг друга. Тем не менее, даже копирование чужой формы Танграма может расширить опыт ученика, развить способность распознавать сходства и различия и обеспечить контекст для развития языка, связанного с геометрическими идеями. На протяжении всего исследования учащимся следует предлагать рассказывать о своих построениях, чтобы прояснить и расширить свое мышление. Например, учащиеся разовьют интуитивное чувство углов, соединяя углы частей Танграма вместе, и их можно побудить подумать о том, почему одни части поместятся в заданном пространстве, а другие нет. Учащиеся могут начать развивать восприятие симметрии, когда они по очереди зеркально отображают фрагменты Танграма по линии, расположенной между ними на коврике, а также могут начать испытывать гордость за свое совместное произведение.

Учащиеся любого возраста, которые раньше не видели Танграм, скорее всего, сначала изучают формы, собирая объекты, похожие на объекты — например, бабочку, ракету, лицо или букву алфавита. Учащиеся с более богатым геометрическим образованием, вероятно, наложат интересные ограничения на свои конструкции, выбрав, например, построение заполненного многоугольника, такого как квадрат или шестиугольник, или симметричного узора.

Использование Tangrams дает прекрасную возможность для достоверной оценки. Наблюдая за тем, как студенты работают с произведениями Танграма, вы понимаете, как они подходят к математической задаче.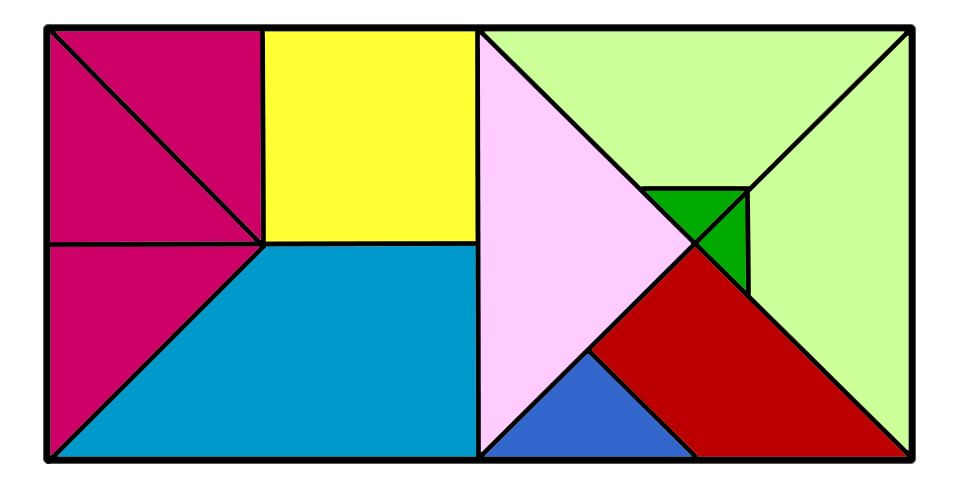 Их мышление можно «увидеть», поскольку это мышление выражается в расположении фрагментов Танграма, и когда класс разбивается на небольшие рабочие группы, вы можете циркулировать, слушать и задавать вопросы, все время сосредотачиваясь на том, как думают люди.

Чтобы убедиться, что учащиеся знают не только, как выполнять определенную операцию, но и как она соотносится с моделью, оценивание должно включать не только символические задания с карандашом и бумагой, такие как «Найти  ¹ ⁄2 +  ¹ ⁄ 8», но и задания на выполнение, такие как «Покажи, почему твой ответ правильный, используя кусочки Танграма».

Когда учащиеся описывают свои творения и делятся своими стратегиями и размышлениями со всем классом, это дает вам еще одну возможность для оценивания через наблюдение. Кроме того, поскольку пространственное мышление играет важную роль в интеллектуальном развитии учащихся, включите в свою общую оценку некоторое внимание к пространственным задачам.

Уроки

Геометрические приложения Tangram многочисленны.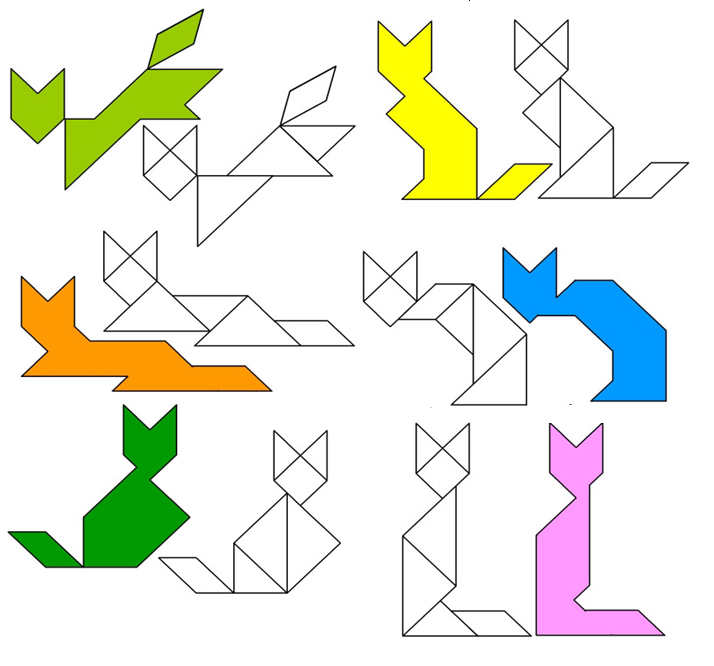 Помимо создания фигур, младшие дети могут работать над тем, чтобы складывать кусочки Танграма в фигуры на карточках-пазлах. Дети могут познакомиться с геометрическими фигурами, развивая способности пространственного мышления. Некоторым детям могут быть трудны пространственные задачи, но с опытом они улучшатся.

Вот два упражнения для знакомства с танграмами и начала их использования для изучения и понимания математики, которую они представляют.

Деятельность	Направления учебной программы	Темы
Собери и считай В этой игре для двух игроков дети размещают кусочки Танграма на сетке из точек, стараясь покрыть как можно больше точек.	Измерение Число Геометрия	Подсчет Сложение Конгруэнтность Стратегии игры
Изготовление стеганого одеяла Дети делают бумажные лоскутные одеяла на основе шаблонов стеганых квадратов, которые они создают с помощью треугольников Танграма.	Геометрия Узоры	Пространственная визуализация Поиск закономерностей Трансформационная геометрия Конгруэнтность

Промежуточные классы могут использовать детали Tangram для создания квадратов, треугольников, параллелограммов, прямоугольников и трапеций. Учащиеся могут не только исследовать и создавать фигуры, но и узнавать об отношениях между фигурами.

Вот два упражнения для знакомства с танграмами и начала их использования для изучения и понимания математики, которую они представляют.

Деятельность	Направления учебной программы	Темы
Дробное вращение Учащиеся определяют фрагмент Танграма как дробную часть целой фигуры. Затем они строят целое.	Геометрия Номер	Пространственная визуализация Дроби Счет Сравнение
Парад многоугольников Учащиеся строят многоугольники, используя разное количество кусочков Танграма. Они записывают свои результаты на диаграмме формы.	Геометрия	Пространственная визуализация Сравнение Классификация

Танграмы помогают учащимся средних классов развивать навыки пространственной визуализации и вводить или закреплять геометрические понятия, такие как конгруэнтность, сходство, симметрия и т. д. Учащиеся используют их для вычисления площади многоугольников, или же танграмы можно использовать для ознакомления с термины «конгруэнтный» и «подобный».

Вот два упражнения для знакомства с танграмами и начала их использования для изучения и понимания математики, которую они представляют.

Деятельность	Направления учебной программы	Темы
Сокрытие квадрата Учащиеся закрывают сетку кусочками Танграма и находят процент покрытия сетки.	Номер Измерение	Проценты Оценка Площадь
Чем больше, тем лучше Учащиеся ищут все выпуклые фигуры Танграма, которые можно составить из разного количества частей, представляющих одну и ту же дробную часть квадрата Танграма, состоящего из семи частей.	Геометрия Номер	Сравнение Классификация Многоугольники Дробная эквивалентность Пространственная визуализация

Приобретенные навыки

• Анализ данных
• Уголки
• Район
• Шанс
• Круговые диаграммы и центральные углы
• Классификация
• Комбинации
• Сравнение
• Конгруэнтность
• Эквивалентные дроби
• Оценка
• Экспериментальная вероятность
• Следуя указаниям
• Дробный эквивалент
• Игровые стратегии
• Геометрические узоры
• Графические свойства полигонов
• Язык математики
• В поисках закономерностей
• Меры центральной тенденции
• Нестандартное измерение
• Номер
• Шаблоны/Функции
• Периметр
• Перестановки
• Полигоны
• Свойства углов
• Свойства геометрических фигур
• Свойства полигонов
• Свойства треугольников
• Пропорция
• Четырехугольники
• Соотношение
• Чертежи в масштабе
• Фасонный фитинг
• Похожие полигоны
• Подобие
• Пространственная визуализация
• Стандартные размеры
• Симметрия
• Теоретическая вероятность
• Трансформационная геометрия

Преподаваемые предметы

• Дополнение
• Подсчет
• Подразделение
• Фракции
• Геометрия
• Логика
• Измерение
• Деньги
• Умножение
• Проценты
• Вероятность и статистика

Геометрия и 2D-фигуры с помощью Tangram

В сегодняшней статье мы поговорим о геометрии и 2D-фигурах. Чтобы помочь нам, мы собираемся использовать старую китайскую игру Танграм.

Танграм  – это головоломка, состоящая из 7 частей: параллелограмма (ромба), квадрата и 5 треугольников. Цель этой игры состоит в том, чтобы создавать фигуры, используя 7 частей. Кусочки должны соприкасаться, но не перекрываться.

Работа с Танграмом, помимо стимуляции творчества и развития пространственного зрения, углубляет знания в различных областях математики, в частности в геометрии. Его можно использовать для ознакомления с понятиями двумерной геометрии.

Давайте посмотрим на формы, которые мы используем в Tangram:

Треугольник:  Многоугольник с тремя сторонами и тремя углами.

Квадрат:  Многоугольник с четырьмя равными сторонами и четырьмя прямыми углами.

Параллелограмм: Многоугольник с четырьмя сторонами, который имеет два набора равных сторон и два набора равных углов.

В Smartick мы делаем еще один шаг вперед и вводим больше форм, поэтому мы можем делать почти все, что можем себе представить. Давайте посмотрим, из каких двухмерных геометрических фигур состоит Smartick Rooster:

Smartick Rooster содержит 1 квадрат:

Если вы рассчитываете, вы обнаружите, что Smartick Proost

Живот Smartick Rooster сделан из пятиугольника.  Пятиугольник  – это двумерная геометрическая фигура с пятью сторонами и пятью равными углами.

Его ножки сделаны из прямоугольника.       Прямоугольник — это параллелограмм, у которого два набора равных сторон и четыре прямых угла.

Ножки сделаны из овала.  Овал  – это сплющенный круг, представляющий яйцевидную или эллиптическую форму.

Вы можете сделать свой собственный Танграм со всеми этими 2D фигурками!!

Есть много других 2D-фигур, которые вы можете найти, если будете исследовать. .. Взгляните на наши предыдущие посты, чтобы узнать, сможете ли вы найти больше фигур, чем те, которые мы видели сегодня:

• Геометрические плоские формы
• Откройте для себя геометрические фигуры, найденные в нашей среде
• Геометрическая форма: свойства квадрата
• Геометрическая форма: круг

Если вы хотите продолжать изучать начальную математику, зарегистрируйтесь в Smartick и попробуйте ее бесплатно.

Узнать больше:

• Откройте для себя геометрические фигуры, найденные в нашей среде
• Геометрические фигуры с примерами
• Треугольники: характеристики, виды и классификация
• Геометрические плоские формы: круги, треугольники, прямоугольники, квадраты и трапеции
• Геометрические фигуры и прямые линии
• Автор
• Последние сообщения

Smartick

Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.