Математика. Краткосрочный план урока № 31 для 4 класса по теме :Переместительное и сочетательное свойства объединения и пересечения множеств при решении задач. Здоровье – жизненная ценность.

1.Актуализация жизненного опыта.

(К) Математический диктант:

1. Запишите числа, в которых 7 сот. 8 дес. 2 ед.; 1 сот. 4 дес. 9 ед.; 5 сот. 1 ед.; 4 сот. 3 дес.; 5 дес. Зед.

2. Запишите числа, в которых 2 ед. ΙΙΙ разряда, 7 ед. ΙΙ разряда и 5 ед. Ι разряда;

9 ед. ΙΙΙ разряда и 4 ед. ΙΙ разряда;

1 ед. ΙΙΙ разряда и 9 ед. Ι разряда;

4ед. ΙΙΙ разряда, 9 ед. ΙΙ разряда и 7 ед. Ι разряда.

3. Запишите числа 348, 209, 880, 402, 927, 700, 1000.

4. Сколько сотен нужно прибавить к 400, чтобы получить 1000?

2. Вводное задание на подготовку к изучению нового.

-Назови множества, имеющие общие элементы.

А = 1; 2; 3; 4

В = 3; 4; 5

С = 4; 7; 8

D = 9; 10; 11

3. Постановка цели (проблемная ситуация). Вводное задание на подготовку к изучению нового.

(И) Самостоятельная работа.

• Изобрази при помощи диаграммы пересечение множеств А и В.

• Пересечение множеств В и А.

• Изобрази при помощи диаграммы пересечение множеств А. В и С.

4.Работа по теме урока. Открытие нового.

(Г) Работа в группе.

• Изобрази при помощи диаграммы объединение множеств А и В.

• Объединение множеств В и А.

• Изобрази при помощи диаграммы объединение множеств А,В и С.

(К) Физминутка.

Раз, два, три, четыре, пять –

Все умеем мы считать.

Раз! Подняться, потянуться.

Два! Согнуться, разогнуться.

Три! В ладоши три хлопка,

Головою три кивка.

На четыре – руки шире.

Пять – руками помахать.

Шесть — за парту мы присели.

Значит, хватит отдыхать!

5.Первичное закрепление с проговариванием.

(Г) Работа в паре.

Допиши равенства, выражающие переместительное и сочетательное свойства операции пересечения множеств:

6. Закрепление с проговариванием.

(И) Самостоятельная работа.

Запиши равенства, выражающие переместительное и сочетательное свойства операции объединения множеств М. К и Т.

(И) Математика в жизни.

— Выполни действия с остатком и сделай проверку.

(К) Пальчиковая гимнастика.

Рак.

— Как хватает рыбу рак?

— Да клешней своей — вот так!

— Манит он своей клешнею:

— «Пощипаемся с тобою!»

(Двумя пальчиками изображается движение клешни рака. )

(И) Самостоятельная работа.

Вычисли.

180 240 : 6

421 022 : 2

(К) Математика в жизни.

Длина беговой дорожки на стадионе — 400 метров Атлету нужно пробежать 2 км. Сколько кругов он должен пробежать? Спортсмен бежит со скоростью 200 м/мин. Сколько времени ему потребуется для преодоления дистанции?

(К) Творческая работа.

При помощи кругов Эйлера изобрази отношения множеств «Скрипачи» и «Музыканты», «Девочки» и «Мальчики».

(Г) Работа в группе.

а) Расстояние от города до посёлка — 30 км. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со средней скоростью б км/ч?

6) Самолёт летел 4 часа со средней скоростью 600 км/ч. Какое расстояние он пролетел?

(К) Исследуй.

В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом — 15 учеников, метро и троллейбусом — 13 учеников, троллейбусом и автобусом — 9 учеников. Сколько учеников пользуются только одним видом транспорта?

(И) Самостоятельная работа.

Реши задачу.

В сутки автомобиль способен выбросить в воздух пример­но 20 кг выхлопных газов. Сколько килограммов выхлопных газов могут выбросить в воздух 8 автомобилей за 10 суток?

Свойства пересечения и объединения множеств

Из школьного курса математики известно, что операция, при помощи которой находят сумму чисел, называется сложе­нием. Над числами выполняют и другие операции, например умножение, вычитание, деление; при этом результат умноже­ния чисел называют произведением, деления — частным, т. е. для операций над числами и результатов этих операций суще­ствуют разные термины. Для рассмотренных операций над множествами ситуация иная: операции, при помощи которых находят пересечение и объединение множеств, называются соответственно пересечением и объединением.

Из школьного курса математики нам также известно, что операции над числами обладают рядом свойств. Например, сложение действительных чисел обладает переместительным и сочетательным свойствами: для любых действительных чисел а и Ь справедливо равенство а + b = b + а, а для любых чисел a, b и с — равенство (а + b)+ с = а + b+ с).

Аналогичными свойствами обладает умножение действи­тельных чисел. Кроме того, для сложения и умножения выпол­няется распределительное свойство: для любых действительных чисел а, b и с справедливо равенство: (а+b) · с = а · с + b ·с.

Выясним, обладают ли «похожими» свойствами пересече­ние и объединение множеств.

Если обратиться к определениям пересечения и объедине­ния множеств, то можно увидеть, что в них не фиксируется порядок оперирования множествами. Например, выполняя объединение, можно к элементам одного множества присоединить элементы другого, а можно поступить наоборот: к элементам второго множества присоединить элементы перво­го. (При этом надо только помнить, что в новом множестве не должно быть повторяющихся элементов.) Аналогичная си­туация и в случае, когда выполняется пересечение множеств. Это означает, что пересечение и объединение множеств обла­дают переместительным, или, как говорят в математике, ком­мутативным свойством: для любых множеств А и В выпол­няются равенства: А В = В A и A B = B A.

Пересечение и объединение множеств обладают также со­четательным, или ассоциативным, свойством: для любых множеств А, В и С выполняются равенства:

(А В) С = А (В С и (А В) С = А (В С).

Заметим, что назначение скобок в этих записях то же, что и в записях операций над числами.

Свойство ассоциативности для пересечения и объединения множеств не столь очевидно, как свойство коммутативности, и поэтому нуждается в доказательстве.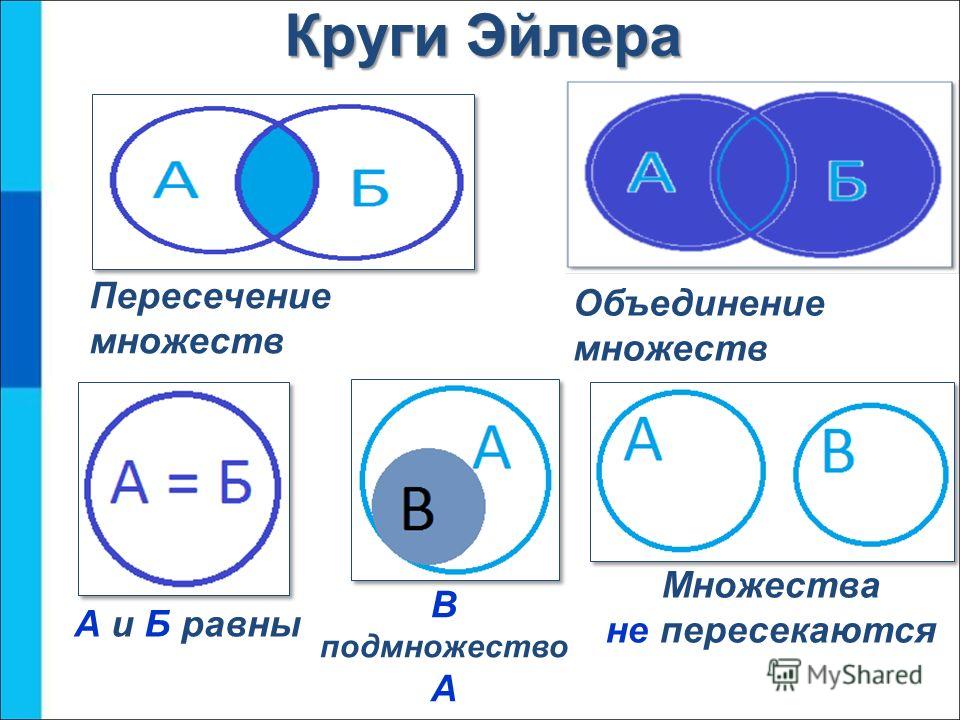 Но прежде можно эти свойства проиллюстрировать при помощи кругов Эйлера. Рассмотрим, например, ассоциативное свойство пересечения множеств. Изобразим множества А, В и С в виде трех попарно пересекающихся кругов (рис. 9).

В выражении (А В) С скобки определяют следующий порядок действий: сначала выполняется пересечение множеств А и В — оно показано на рисунке 9а вертикальной штрихов­кой, а затем находят пересечение полученного множества и множества С. Если выделить множество С горизонтальной штриховкой, то область, заштрихованная дважды, будет изо­бражать множество (А В) С.

Представим теперь наглядно множество А (В С). В соответствии с указанным порядком действий сначала

 

надо найти пересечение множеств В и С — на рисунке 96 оно показано вертикальной штриховкой, а затем выполнить пересечение множества А с полученным множеством. Если отметить множество А горизонтальной штриховкой, то область, заштрихованная дважды, и будет изображать множество А (В С).

Видим, что области, представляющие на рисунке 9 множества (А В) С и А (В С), одинаковы, что и подтверждает справедливость свойства ассоциативности для пересечения множеств.

Аналогично можно проиллюстрировать свойство ассоциативности и для объединения множеств.

В чем важность ассоциативного свойства пересечения и объединения множеств? Во-первых, можно находить пересечение и объединение трех множеств, зная, как это делать для двух. Во-вторых, на основании этого свойства в выражениях А (В С), (А В) С, А (В С), (А В) С можно опускать скобки и писать А В С или А В С, что облегчает запись.

Рассмотрим строгое доказательство свойства ассоциативности одной из операций над множествами, например объединения, т.е. докажем, что для любых множеств А,В и С справедливо равенство (А B) C = А (B С).

Чтобы доказать равенство двух множеств, надо убедиться в том, что каждый элемент множества (А В) С содержится в множестве А (В С), и наоборот.

1. Пусть х — любой элемент множества (А В) С. Тогда, по определению объединения, х А В или х С.

Если х А В, то, по определению объединения, х А или х В. В том случае, когда х А, то, также по определению объединения, х А (В С).

Если х В, то имеем, что х В С, а значит, х А (В С). Случай, когда х А и х В, сводится к рассмотренным. Таким образом, из того, что х А В, следует, что х А (В С).

Если х С, то, по определению объединения, х В С, и следовательно, х А (В С).

Случай, когда х А В и х С, сводится к рассмотренным выше.

Итак, мы показали, что каждый элемент множества (А В) С содержится и в множестве А (В С), т.е. (А В) С А (В С).

2. Пусть y — любой элемент множества А (В С). Тогда, по определению объединения, у А или у В С.

Если y А, то, по определению объединения, у А В и, следовательно, у А и (В С).

Если y В С, то у В или у C.

B том случае, когда у В, то у А В и, значит, у (А В) и С. Когда же у С, то у (А B) C. Случай, когда у В и у С, сводится к уже рассмотренным.

Итак, мы показали, что каждый элемент множества А (B С) содержится в множестве (A В) С, т.е. А (В С) (А В) С.

Согласно определению равных множеств заключаем, что (А В) С = А (В С), что и требовалось доказать.

Аналогично доказывается и ассоциативное свойство пересечения множеств.

Взаимосвязь пересечения и объединения множеств отражается в распределительных, или дистрибутивных, свойствах этих операций. Таких свойств два:

1. Пересечение дистрибутивно относительно объединения множеств, т.е. для любых множеств А, В к С выполняется равенство

(А В) С = (А С) (В С).

2. Объединение дистрибутивно относительно пересечения множеств, т.е. для любых множеств А, В и С выполняется равенство

(А В) С = (А С) (В С).

Заметим, что если в выражении есть знаки пересечения и объединения множеств и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение. В связи со сказанным запись дистрибутивного свойства пересечения относительно объединения можно упростить, опустив скобки в правой части равенства.

Убедиться в справедливости сформулированных свойств можно путем доказательства, которое аналогично доказательству свойства ассоциативности объединения.

Проиллюстрировать свойства дистрибутивности можно, используя круги Эйлера.

Если провести аналогию с действиями над числами, то можно увидеть, что дистрибутивное свойство пересечения относительно объединения сопоставимо с распределительным свойством умножения относительно сложения, при условии, что в качестве операции, аналогичной пересечению, рассматривать умножение, а для объединения — сложение.

Но для дистрибутивного свойства объединения множеств относительно пересечения аналогичного свойства над числами нет.

Действительно, наличие такого свойства означало бы, что для всех чисел выполняется равенство а • b + с = (а + с) • (b + с), что невозможно. Подмеченное отличие говорит о том, что наряду с тем, что пересечение и объединение множеств обладают рядом свойств, аналогичных свойствам сложения и умножения чисел, операции над множествами обладают свойствами, которых нет у операций над числами.

Завершая рассмотрение свойств пересечения и объединения множеств, отметим еще следующее.

Понятие пересечения и объединения множеств можно обобщить на любое конечное число множеств:

А₁ А₂ … А_n = {х | х А₁ и х А₂ и… и х А_n},

А₁ А₂ … А_n = {х | х А₁ или х А₂ или … или х А_n},

Аналогично можно поступить и по отношению к рассмотренным свойствам данных операций.

 

---

Дата добавления: 2017-02-13; просмотров: 15952; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

---

4.3: Объединения и пересечения — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

24953

• Харрис Квонг
• Государственный университет Нью-Йорка во Фредонии через OpenSUNY

Мы можем сформировать новый набор из существующих наборов, выполнив операцию набора.

Определение: \(A \cap B\)

Для двух множеств \(A\) и \(B\), определите их пересечение как множество

\[A \cap B = \{ x\in{\cal U} \mid x \in A \wedge x \in B \}\]

Грубо говоря, \(A \cap B\) содержит элементы, общие как для \(A\), так и для \( Б\).

Определение: \(A \чашка B\)

Союз из \(A\) и \(B\) определяется как

\[A \cup B = \{ x\in{\cal U} \mid x \in A \vee x \in B \}\]

Таким образом, \(A \cup B\), как следует из названия, представляет собой множество, объединяющее все элементы из \(A\) и \(B\).

ПЕРЕКРЕСТОК

        СОЕДИНЕНИЕ

 

Определение: \(A-B\)

Разность наборов \(AB\), иногда записываемая как \(A \setminus B\), определяется как

\[A-B = \{ x\ in{\cal U} \mid x \in A \клин x \not\in B \}\] 9c\), определяется как

\[\overline{A} = \{ x\in{\cal U} \mid x \notin A \}\]

Определение: \(A \bigtriangleup B\)

Симметричная разность   \(A \bigtriangleup B\), определяется как

\[A \bigtriangleup B = (A — B) \cup (B — А)\] 

Определение: непересекающиеся

Два множества являются непересекающимися , если их пересечение пусто.

Например, рассмотрим \(S=\{1,3,5\}\) и \(T=\{2,8,10,14\}\).

\(S \cap T = \emptyset\), поэтому \(S\) и \(T\) не пересекаются.

Примечание

Напоминаем читателям, что авторы нередко принимают разные обозначения для одного и того же математического понятия. Точно так же одно и то же обозначение может означать что-то другое в другом учебнике или даже в другой области математики. Важно выработать привычку исследовать контекст и убедиться, что вы понимаете значение обозначений, когда начинаете читать математическое изложение.

Пример \(\PageIndex{1}\label{eg:unionint-01}\)

Пусть \({\cal U}=\{1,2,3,4,5\}\), \(A =\{1,2,3\}\) и \(B=\{3,4\}\). Найдите \(A\cap B\), \(A\cup B\), \(A-B\), \(BA\), \(A\bigtriangleup B\), \(\overline{A}\), и \(\overline{B}\).

Раствор

Имеем \[\begin{aligned} A\cap B &=& \{3\}, \\ A\cup B &=& \{1,2,3,4\}, \\ A — B & =& \{1,2\}, \\ B \bigtriangleup A &=& \{1,2,4\}. \end{aligned}\] Мы также находим \(\overline{A} = \{4,5\}\) и \(\overline{B} = \{1,2,5\}\).

практическое упражнение \(\PageIndex{1}\label{he:unionint-01}\)

Пусть \({\cal U} = \{\mbox{Джон}, \mbox{Мэри}, \mbox {Дэйв}, \mbox{Люси}, \mbox{Питер}, \mbox{Ларри}\}\), \[A = \{\mbox{Джон}, \mbox{Мэри}, \mbox{Дэйв}\ }, \qquad\mbox{и}\qquad B = \{\mbox{Джон}, \mbox{Ларри}, \mbox{Люси}\}.\] Найдите \(A\cap B\), \(A \cup B\), \(AB\), \(BA\), \(\overline{A}\) и \(\overline{B}\).

практическое упражнение \(\PageIndex{2}\label{he:unionint-02}\)

Если \(A\subseteq B\), что будет \(A-B\)?

Пример \(\PageIndex{2}\label{eg:unionint-02}\)

Набор целых чисел может быть записан как \[\mathbb{Z} = \{-1,-2,-3, \ldots\} \cup \{0\} \cup \{1,2,3,\ldots\}.\] Можем ли мы заменить \(\{0\}\) на 0? Объяснять.

практическое упражнение \(\PageIndex{3}\label{he:unionint-03}\)

Объясните, почему следующие выражения синтаксически неверны.

• \(\mathbb{Z} = \{-1,-2,-3,\ldots\} \cup \;0\; \cup \{1,2,3,\ldots\}\).
• \(\mathbb{Z} = \ldots,-3,-2,-1 \;\cup\; 0 \;\cup\; 1,2,3,\ldots\,\) 9+\)

Как бы вы исправили ошибки в этих выражениях?

Пример \(\PageIndex{3}\label{eg:unionint-03}\)

Для любого набора \(A\), что такое \(A\cap\emptyset\), \(A\cup\emptyset \), \(A-\emptyset\), \(\emptyset-A\) и \(\overline{\overline{A}}\)?

Ответить

Ясно, что \[A\cap\emptyset = \emptyset, \qquad A\cup\emptyset = A, \qquad\mbox{and}\qquad A-\emptyset = A.\] Из определения разности множеств , находим \(\emptyset-A = \emptyset\). Наконец, \(\overline{\overline{A}} = A\).

Пример \(\PageIndex{4}\label{eg:unionint-04}\)

Запишите в интервальной нотации \([5,8)\cup(6,9]\) и \([5, 8)\шапка(6,9]\).

Ответить

Ответы: \[[5,8)\cup(6,9] = [5,9], \qquad\mbox{and}\qquad [5,8)\cap(6,9] = (6, 8). \] Они получаются сравнением расположения двух интервалов на прямой с действительными числами.

практическое упражнение \(\PageIndex{4}\label{he:unionint-04}\)

Запишите в интервальной записи \((0,3)\cup[-1,2)\) и \((0,3)\cap[-1,2)\).

Пример \(\PageIndex{5}\label{eg:unionint-05}\)

Теперь мы можем описать следующий набор \[\{x\in\mathbb{R} \mid (x<5) \vee (x>7)\}\] в интервальной нотации. Его можно записать как \((-\infty,5)\cup(7,\infty)\) или, используя дополнение, \(\mathbb{R}-[5,7\,]\). Следовательно, сказать \(x\notin[5,7\,]\) то же самое, что сказать \(x\in(-\infty,5) \cup(7,\infty)\) или, что то же самое, \( x\in\mathbb{R}-[5,7\,]\).

Чтобы доказать, что набор пуст

Чтобы доказать, что набор пуст , используйте доказательство от противного со следующими шагами:

(1) Предположим, что нет. То есть предполагается, что \(\ldots\) не пусто.

(2) Это означает, что есть элемент \(\ldots\) по определению пустого множества.

(3) Пусть \(x \in \ldots \).

(4) Прийти к противоречию и завершить доказательство.

 

Пример \(\PageIndex{6}\)

Докажите: \(\forall A \in {\cal U}, A \cap \emptyset = \emptyset.\)

Доказательство:  Предположим, что нет. То есть предположим, что для некоторого набора \(A,\)  \(A \cap \emptyset \neq \emptyset.\)
По определению пустого набора это означает, что в \(A \cap \emptyset . \)

Пусть \(x \in A \cap \emptyset .\)

\(x \in A \wedge x\in \emptyset\) по определению пересечения.

Здесь написано \(x \in \emptyset \), но в пустом множестве нет элементов! Это противоречие!

Таким образом, наше предположение неверно, а исходное утверждение верно.
\(\forall A \in {\cal U}, A \cap \emptyset = \emptyset.\)

 

Установить свойства

Примечания:

(a) Эти свойства должны быть понятны вам, и вы должны быть в состоянии доказать их. Однако вы не должны использовать их в качестве доводов в доказательстве. Скорее ваши обоснования шагов в доказательстве должны исходить непосредственно из определений. Исключением являются законы ДеМоргана, на которые вы можете ссылаться в качестве причины в доказательстве.

(b) Вам не нужно запоминать эти свойства или их названия. Однако вы должны знать значения: коммутативного, ассоциативного и дистрибутивного. Кроме того, вы должны знать законы ДеМоргана по названию и содержанию.

Следующие свойства выполняются для любых множеств \(A\), \(B\) и \(C\) в универсальном множестве \({\cal U}\).

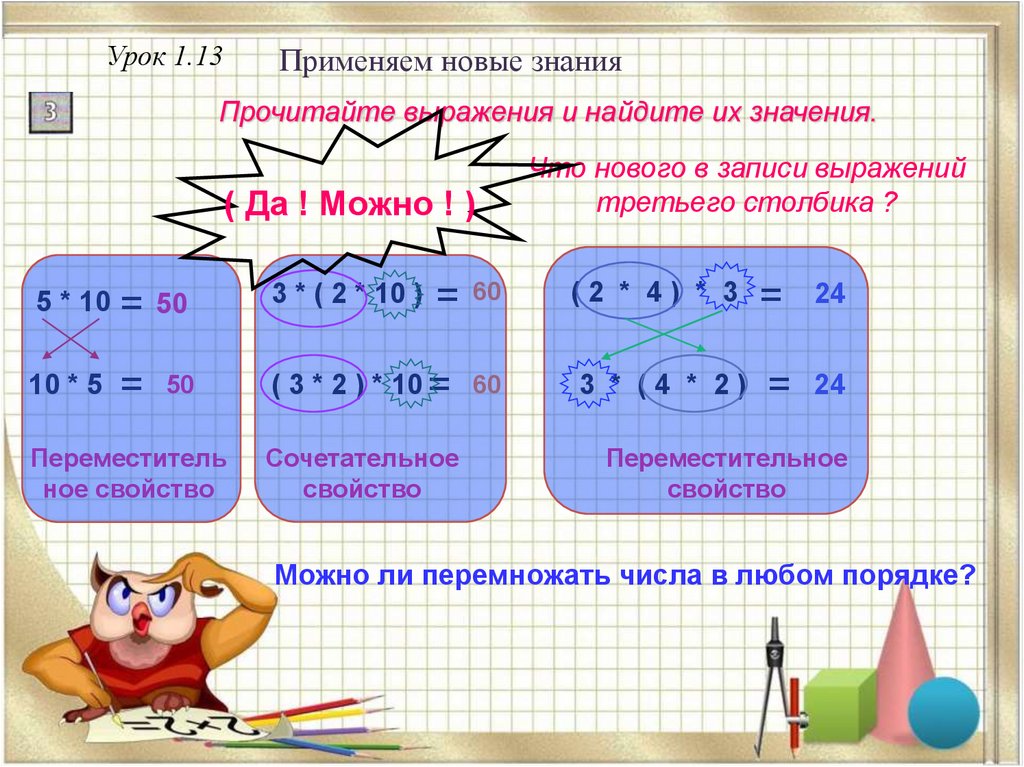
1. Коммутативные свойства : \(\begin{array}[t]{l} A \cup B = B \cup A, \\ A \cap B = B \cap A. \end{array} \)
2. Ассоциативные свойства : \(\begin{array}[t]{l} (A \cup B) \cup C = A \cup (B \cup C), \\ (A \cap B) \ крышка C = A \cap (B \cap C).\end{массив}\)
3. Распределительные законы : \(\begin{array}[t]{l} A \cup (B \cap C) = (A \cup B) \cap (A \cup C), \\ A \ крышка (B \чашка C) = (A \крышка B) \чашка (A \крышка C). \end{array}\)
4. Законы идемпотента : \(\begin{array}[t]{l} A \cup A = A, \\ A \cap A = A. \end{array}\)
5. Законы Де Моргана : \(\begin{array}[t]{l} \mbox{  (a)  } \overline{A \cup B} = \overline{A} \cap \overline{B} , \\ \mbox{  (b)  }  \overline{A \cap B} = \overline{A} \cup \overline{B}. \end{array}\)
6. Законы исключенного третьего , или обратные законы : \(\begin{array}[t]{l} A \cup \overline{A} = {\cal U}, \\ A \cap \overline{A} = \emptyset.\end{массив}\)

В качестве иллюстрации докажем распределительный закон \[A \cup (B \cap C) = (A \cup B) \cap (A \cup C).\] 

Нужно показать, что \[A \cup (B \cap C) \subseteq (A \cup B) \cap (A \cup C), \qquad\mbox{and}\qquad (A \cup B) \cap (A \cup C) \subseteq A \cup (B \cap C).\]

Доказательство дистрибутивного закона \(A \cup (B \cap C) = (A \cup B) \крышка (А\чашка С)\).

Доказательство
 

Сначала мы покажем \(A \cup (B \cap C) \subseteq (A \cup B) \cap (A \cup C).\)
Пусть \(x\in A\cup(B\cap C) )\).
\(x\in A\vee x \in B\cap C\) по определению объединения.

Случай 1: \(x \in A.\)
Так как \(x \in A\),  \(x \in A \cup B,\) по определению объединения и \(x \in A \cup C ,\) по определению объединения.
\(\следовательно x \in (A \cup B) \cap (A \cup C)\), по определению пересечения.

Случай 2: \(x \in B\cap C.\)
\(x \in B\клин x\in C,\) по определению пересечения.
\(x \in A \cup B,\) по определению объединения и \(x \in A \cup C,\) по определению объединения.
\(\следовательно x \in (A \cup B) \cap (A \cup C)\), по определению пересечения.

Мы показали, если \(x\in A\cup(B\cap C)\), то \(x \in (A \cup B) \cap (A \cup C)\).
Итак, по определению подмножества, \(A \cup (B \cap C) \subseteq (A \cup B) \cap (A \cup C).\)

Далее мы покажем \((A \ чашка B) \крышка (A \чашка C)\subseteq A \чашка (B \чашка C). \)
Пусть \(x \in (A \чашка B) \крышка (A \чашка C).\)
\(x\in (A\cup B) \клин x \in (A\cup C)\) по определению пересечения.
Случай 1: \(x \in A.\)
Так как \(x \in A,\) мы имеем \(x\in A\cup(B\cap C)\) по определению объединения.

Случай 2: \(x \notin A.\)
Поскольку \(x\in (A\cup B), \) \(x \in A \vee x \in B\) по определению объединения, поэтому \(x\) должен быть элементом \(B.\)
Кроме того, поскольку \(x\in (A\cup C),\) \(x \in A \vee x \in C\) по определению объединения, поэтому \(x\) должен быть элементом \(C.\)
. по определению перекрестка.
Итак,  \(x\in A\cup(B\cap C)\). по определению союз.

В обоих случаях, если \(x \in (A \cup B) \cap (A \cup C),\), то \(x\in A\cup(B\cap C.)\)
Итак, по определению подмножества, \((A \cup B) \cap (A \cup C) \subseteq A \cup (B \cap C.)\)

Отсюда следует, что \(A \cup (B \cap C) = (A\cup B) \cap (A\cup C)\), по определению равенства множеств.

практическое упражнение \(\PageIndex{5}\label{he:unionint-05}\)

Докажите, что \(A\cap(B\cup C) = (A\cap B)\cup(A\ шапка С)\).

практическое упражнение \(\PageIndex{6}\label{he:unionint-06}\)

Докажите, что если \(A\subseteq B\) и \(A\subseteq C\), то \(A \subseteq B\cap C\).

Обсуждение

Начнем с черновика. Утверждение, которое мы хотим доказать, принимает форму \[(A\subseteq B) \wedge (A\subseteq C) \Rightarrow A\subseteq B\cap C.\] Следовательно, что мы предполагаем и что мы хотим доказывать?

Предположим:

Хочу доказать:

Вы записали, что мы предполагаем \(A\subseteq B\) и \(A\subseteq C\), и мы хотим доказать \(A\subseteq B\cap C\)? Большой! Теперь, что означает \(A\subseteq B\)? Как насчет \(A\subseteq C\)? Что означает \(A\subseteq B\cap C\)?

\(A\subseteq B\) означает: Для любого \(x\in{\cal U}\), если \(x\in A\), то и \(x\in B\) .

\(A\subseteq C\) означает:

\(A\subseteq B\cap C\) означает:

Как вы можете использовать первые две части информации, чтобы получить то, что нам нужно установить?

Теперь пришло время собрать все воедино и отполировать до финальной версии. Помните три вещи:

• план доказательства,
• причина на каждом шаге главного аргумента и
• введение и заключение.

Поместите полное доказательство в поле ниже.

Вот два результата с дополнениями.

Теорема \(\PageIndex{1}\label{thm:subsetsbar}\)

Для любых двух множеств \(A\) и \(B\) имеем \(A \subseteq B \Leftrightarrow \overline{B } \subseteq \overline{A}\).

Теорема \(\PageIndex{2}\label{thm:genDeMor}\)

Для любых множеств \(A\), \(B\) и \(C\),  

(a) \(A- (B \чашка C)=(A-B) \cap (A-C)\)

(b) \(A-(B \cap C)=(A-B) \cup (A-C)\)

Резюме и обзор

• Запомните определения пересечения, объединения и разности множеств. Мы полагаемся на них, чтобы доказать или получить новые результаты.
• Пересечение двух множеств \(A\) и \(B\), обозначаемое как \(A\cap B\), есть множество элементов, общих как для \(A\), так и для \(B\). В символах \(\ forall x \ in {\ cal U} \, \ big [x \ in A \ cap B \ Leftrightarrow (x \ in A \ клин x \ in B) \ big] \).
• Объединение двух множеств \(A\) и \(B\), обозначаемое как \(A\cup B\), представляет собой множество, объединяющее все элементы в \(A\) и \(B\). В символах \(\forall x\in{\cal U}\,\big[x\in A\cup B \Leftrightarrow (x\in A\vee x\in B)\big]\).
• Разность множеств между двумя множествами \(A\) и \(B\), обозначаемая \(A-B\), представляет собой множество элементов, которые можно найти только в \(A\), но не в \(B\ ). В символах это означает \(\forall x\in{\cal U}\, \big[x\in AB \Leftrightarrow (x\in A \wedge x\notin B)\big]\).
• Симметричная разность между двумя множествами \(A\) и \(B\), обозначаемая как \(A \bigtriangleup B\), представляет собой множество элементов, которые можно найти в \(A\) и в \(B \), но не в обоих \(A\) и \(B\). В символах это означает \(\forall x\in{\cal U}\, \big[x\in A \bigtriangleup B \Leftrightarrow x\in AB  \vee x\in BA)\big]\).

Упражнения 

Упражнение \(\PageIndex{1}\label{ex:unionint-01}\)

Напишите каждый из следующих наборов, явно перечислив его элементы. 9-\)

(f) \((4,5)\cap\mathbb{Z}\)
 

Ответ

(а) \(\{-4,-3,-2,-1,0,1,2,3,4\}\)

(б) \(\{-3,-2,-1,0,1,2,3,4\}\)

(с) \(\{-3,-2,-1,0,1,2,3,\ldots\}\)

Упражнение \(\PageIndex{2}\label{ex:unionint-02}\)

Предположим, \({\cal U} = \mathbb{Z}\), и пусть

\(A=\ {\ldots, -6,-4,-2,0,2,4,6, \ldots \} = 2\mathbb{Z},\)

\(B=\{\ldots, -9,-6,-3,0,3,6,9, \ldots\} = 3\mathbb{Z},\)

\(C=\{\ldots, -12,-8,-4,0 ,4,8,12, \ldots\} = 4\mathbb{Z}.\)

 Опишите следующие множества, явно перечислив их элементы.

(a) \(A\cap B\)

(b) \(C-A\)

(c) \(A-B\)

(d) \(A\cap\overline{B}\)

(e) \(B-A\)

(f) \(B\чашка C\)

(g) \((A\чашка B)\крышка C\)

(h) \((A \cup B)-C\)

Упражнение \(\PageIndex{3}\label{ex:unionint-03}\)

Верны эти утверждения или нет?

(a) \([1,2]\cap[2,3] = \emptyset\)

(b) \([1,2)\cup(2,3] = [2,3]\ )

Ответить

(а) неверно (б) неверно

Упражнение \(\PageIndex{4}\label{ex:unionint-04}\)

Пусть универсальное множество \({\cal U}\) будет множеством людей, проголосовавших на президентских выборах в США в 2012 г. . Определим подмножества \(D\), \(B\) и \(W\) из \({\cal U}\) следующим образом: \[\begin{aligned} D &=& \{x\in {\cal U} \mid x \mbox{ зарегистрирован как демократ}\}, \\ B &=& \{x\in{\cal U} \mid x \mbox{ проголосовал за Барака Обаму}\}, \ \ W &=& \{x\in{\cal U} \mid x \mbox{ принадлежит объединению}\}. \end{aligned}\] Выразите следующие подмножества \({\cal U}\) через \(D\), \(B\) и \(W\).

(а) Люди, которые не голосовали за Барака Обаму.

(b) Члены профсоюза, проголосовавшие за Барака Обаму.

(c) Зарегистрированные демократы, которые голосовали за Барака Обаму, но не состояли в профсоюзе.

(d) Члены Союза, которые либо не были зарегистрированы как демократы, либо голосовали за Барака Обаму.

(e) Люди, которые голосовали за Барака Обаму, но не были зарегистрированы как демократы и не были членами профсоюза.

(f) Люди, которые либо были зарегистрированы как демократы и были членами профсоюза, либо не голосовали за Барака Обаму.

Упражнение \(\PageIndex{5}\label{ex:unionint-05}\)

Страховая компания классифицирует свой набор \({\cal U}\) держателей полисов по следующим наборам: \[\ begin{align} A &=& \{x\mid x\mbox{ водит малолитражный автомобиль}\}, \\ B &=& \{x\mid x\mbox{ водит автомобиль старше 5 лет}\} , \\ C &=& \{x\mid x\mbox{ женат}\}, \\ D &=& \{x\mid x\mbox{ старше 21 года}\}, \\ E & =& \{x\mid x\mbox{ мужчина}\}. \end{aligned}\] Опишите каждое из следующих подмножеств \({\cal U}\) в терминах \(A\), \(B\), \(C\), \(D\), и \(Е\).

(a) Страхователи мужского пола старше 21 года.

(b) Страхователи женского пола или водители автомобилей старше 5 лет.

(c) Страхователи женского пола старше 21 года, которые водят малолитражные автомобили.

(d) Мужчины, состоящие в браке или старше 21 года и не водящие малолитражные автомобили.

Ответить

(a) \(E\cap D\) (b) \(\overline{E}\cup B\)

Упражнение \(\PageIndex{6}\label{ex:unionint-06}\)

Пусть \(A\) и \(B\) — произвольные множества. Дополните следующие утверждения.

(a) \(A\subseteq B \Leftrightarrow A\cap B = \)        ___________________

(b) \(A\subseteq B \Leftrightarrow A\cup B = \)        ___________________

(c) \(A \subseteq B \Leftrightarrow A — B = \)           ___________________

(d) \(A\subset B \Leftrightarrow (A-B= \)  ___________________\(\wedge\,B-A\neq\) ___________________ \()\)

(e) \(A\subset B \Leftrightarrow (A\cap B=\)  ___________________\(\wedge\,A\cap B\neq\) ___________________  \()\)

(f) \(A — B = B — A \Leftrightarrow \)           ___________________

Упражнение \(\PageIndex{7}\label{ex:unionint-07}\)

Приведите примеры множеств \(A \) и \(B\) такие, что \(A\in B\) и \(A\subset B\).

Ответить

Например, возьмите \(A=\{x\}\) и \(B=\{\{x\},x\}\).

Упражнение \(\PageIndex{8}\label{ex:unionint-08}\)

(a) Докажите закон де Моргана, (a) .

(b) Докажите закон Де Моргана, (b) .

Упражнение \(\PageIndex{9}\label{ex:unionint-09}\)

Пусть \(A\), \(B\) и \(C\) — любые три множества. Докажите, что если \(A\subseteq C\) и \(B\subseteq C\), то \(A\cup B\subseteq C\).

Ответить

Предположим, \(A\subseteq C\) и \(B\subseteq C\), мы хотим показать, что \(A\cup B \subseteq C\).

Пусть \(x\в A\чашке B\). мы также хотим показать, что \(x\in C\).

Так как \(x\in A\cup B\), то либо \(x\in A\), либо \(x\in B\) по определению объединения.

Случай 1: Если \(x\in A\), то \(A\subseteq C\) подразумевает, что \(x\in C\) по определению подмножества.

Случай 2: если \(x\in B\), то \(B\subseteq C\) подразумевает, что \(x\in C\) по определению подмножества.

 

В обоих случаях мы находим \(x\in C\). Итак, если \(x\в A\чашке B\), то \(x\в C\).

Это доказывает, что \(A\cup B\subseteq C\) по определению подмножества.

\(\следовательно\) Для любых множеств \(A\), \(B\) и \(C\), если \(A\subseteq C\) и \(B\subseteq C\), то \( A\чашка B\subseteq C\).

Упражнение \(\PageIndex{10}\label{ex:unionint-10}\)

Докажите теорему 4.3.1

Упражнение \(\PageIndex{11}\label{ex:unionint-11}\ )

(a) Докажите теорему 4.3.2, часть (a)

(b) Докажите теорему 4.3.2, часть (b)

Упражнение \(\PageIndex{12}\label{ex:unionint-12}\ )

Пусть \(A\), \(B\) и \(C\) — любые три множества. Докажите, что

(a) \(A-B=A\cap\overline{B}\)

(b) \(A=(A-B)\cup(A\cap B)\)

(c) \( A-(B-C) = A\cap(\overline{B}\cup C)\)

(d) \((A-B)-C = A-(B\cup C)\)

Упражнение \( \PageIndex{13}\label{ex:unionint-13}\)

Прокомментируйте следующие утверждения. Являются ли они синтаксически правильными?

(a) \(x\in A \cap x\in B \equiv x\in A\cap B\)

(b) \(x\in A\клин B \Rightarrow x\in A\cap Б\)

Ответить

(a) Обозначение \(\cap\) используется для соединения двух множеств, но «\(x\in A\)» и «\(x\in B\)» являются логическими утверждениями. Мы также должны использовать \(\Leftrightarrow\) вместо \(\equiv\). Оператор должен был быть записан как «\(x\in A \,\wedge\, x\in B \Leftrightarrow x\in A\cap B\)».

(b) Если мы прочитаем это вслух, то получится идеально: \[\mbox{Если $x$ принадлежит $A$ и $B$, то $x$ принадлежит $A\cap B$}.\] проблема в том, что каждое обозначение имеет свое значение и конкретное использование. В этом случае \(\клин\) не является заменой английского слова «и». Вместо этого это обозначение соединения двух логических утверждений для образования конъюнкции. Перед \(\wedge\) стоит «\(x\in A\)», что является логическим утверждением. Но после \(\wedge\) у нас есть «\(B\)», которое является набором, а не логическим выражением. Он должен быть записан как «\(x\in A\,\wedge\,x\in B \Rightarrow x\in A\cap B\)».

Упражнение \(\PageIndex{14}\label{ex:unionint-14}\)

Докажите или опровергните каждое из следующих утверждений о произвольных множествах \(A\) и \(B\). Если вы думаете, что утверждение верно, докажите это; если вы считаете, что это неверно, приведите контрпример.

(а) \(\mathscr{P}(A\cap B) = \mathscr{P}(A)\cap\mathscr{P}(B)\)

(b) \(\mathscr{P }(A\cup B) = \mathscr{P}(A)\cup\mathscr{P}(B)\)

(c) \(\mathscr{P}(A — B) = \mathscr{P }(A) — \mathscr{P}(B)\)

Примечание

Чтобы показать, что два множества \(U\) и \(V\) равны, мы обычно хотим доказать, что \(U \subseteq V\) и \(V \subseteq U\). Для отношения подмножества мы начинаем с let \(x\in U \). В этой задаче элемент \(x\) на самом деле является множеством. Поскольку мы обычно используем заглавные буквы для обозначения множеств, для (а) мы должны начать доказательство отношения подмножества «Пусть \(S\in\mathscr{P}(A\cap B)\)»,  используя заглавную букву для подчеркните, что элементы \(\mathscr{P}(A\cap B)\) являются множествами. Эти замечания относятся также к пунктам (b) и (c).

Упражнение \(\PageIndex{15}\)

Пусть \({\cal U}=\{1,2,3,4,5,6,7,8\}\), \(A=\ {2,4,6,8\}\), \(B=\{3,5\}\), \(C=\{1,2,3,4\}\) и \(D=\ {6,8\}\). Найти

(a) \(A\cap C\)                   (b) \(A\cap B\)                    (c) \(\emptyset \cup B\)   

(d) \(\emptyset \cap B\ )                          (e) \(A-(B \cup C)\)              (f) \(C-B\)                                             

(g) \(A\bigtriangleup C\)                (h) \(A \cup} \)                  (i)  \(A\cap D\)                         

(j) \(A\cup D\)                 (k) \(B\cap D\)                      (l) \(B\bigtriangleup C\)   

(m)  \(A \cap {\cal U} \)                 (n) \(\overline{A}\)                      (o) \(\overline{B}\).

(p) \(D \cup (B \cap C)\)        (q) \(\overline{A \cup C}\)            (r) \(\overline{A} \cup \overline{C} \)

(s) Какие пары множеств не пересекаются?

Ответ    

(a) \(\{2,4\}\)            (b) \(\emptyset \)       (c) \(B\)               (d)  \(\emptyset\)    

Упражнение \(\PageIndex{16}\)

Докажите:

Если \(A \subseteq B\), то \(A-B= \emptyset. \)

---

Эта страница под заголовком 4.3: Unions and Intersections используется в соответствии с лицензией CC BY-NC-SA, ее автор, ремикс и/или куратор — Харрис Квонг (OpenSUNY) .

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Харрис Квонг

   Лицензия

   CC BY-NC-SA

   Показать страницу TOC

   да

2. Теги

   1. Законы Де Моргана
   2. Законы идемпотента
   3. Перекресток
   4. Союз

2.

5: Свойства множеств — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• Идентификатор страницы

  4873

• Pamini Thangarajah
• Mount Royal University

Пусть \(A, B,\) и \(C\) — множества, а \(U\) — универсальное множество. Тогда:

Закон перестановочности

Теорема \(\PageIndex{1}\): Закон перестановочности

Для всех множеств \(A\) и \(B\), \(A \cup B =B \cup A \) и \ (A \крышка B= B \крышка A \)

Доказательство

Пусть \(x \in A \cup B\). Тогда \(x \in A\) или \(x \in B\). Что подразумевает \(x \in B\) или \(x \in A\). Отсюда \(x \in B \cup A\). Таким образом, \(A \cup B \subseteq B \cup A \). Точно так же мы можем показать, что \(B \cup A \subseteq A \cup B \). Следовательно, \(A \cup B =B \cup A \).

Пусть \(x \in A \cap B\). Тогда \(x \in A\) и \(x \in B\). Отсюда следует \(x \in B\) и \(x \in A\). Отсюда \(x \in B \cap A\). Таким образом, \(A \cap B \subseteq B \cap A \). Точно так же мы можем показать, что \(B \cap A \subseteq A \cap B \). Следовательно, \(A \cap B =B \cap A \).

Распределительный закон

Теорема \(\PageIndex{2}\): Распределительный закон

Для всех множеств \(A,B\) и \(C\), \(A \cap (B \cup C) = (A \крышка B) \чашка (A \крышка C)\) и \(A \чашка (B \крышка C) = (A \чашка B) \крышка (A \чашка C).\)

Доказательство

Пусть \( x \in A \cap (B \cup C) \).

Затем \(x \in A\) и \( x \in B \cup C\).

Таким образом, \(x \in A\) и \( x \in B \) или \(x \in C\).

Что означает \(x \in A\) и \( x \in B \) или \(x \in A\) и \( x \in C \).

Отсюда \( x \in (A \cap B) \cup (A \cap C)\). Таким образом, \(A \cap (B \cup C) \subseteq (A \cap B) \cup (A \cap C)\). Аналогично можно показать, что \((A \cap B) \cup (A \cap C) \subseteq A \cap (B \cup C) \). Следовательно, \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\).

Мы проиллюстрировали это с помощью диаграммы Венна:

Законы Де Моргана

Теорема \(\PageIndex{3}\): Закон Де Моргана 9c \)

Мы проиллюстрировали с помощью диаграммы Венна:

 

Относительные дополнения

Теорема \(\PageIndex{4}\): Относительные дополнения

\(A \setminus (B \cup C) = (A \setminus B) \cap (A \setminus C)\) и \(A \setminus (B \cap C) = (A \setminus B) \cup (A \setminus C).\)

Мы проиллюстрировали это диаграммой Венна:

Идемпотенты

Теорема \(\ PageIndex{5}\): Идемпотенты

9c=\пустой набор\).

 

---

Эта страница под названием 2.