Сложение и вычитание десятичных дробей – методическая разработка для учителей, Камалова Джамиля Джолдасовна
Цели обучения: | 5.1.2.27 выполнять сложение и вычитание десятичных дробей. | ||||||||||||||||||
Цели урока: | отработать навыки сложения и вычитания десятичных дробей, углубить полученные знания и навыки при решении примеров, уравнений и задач; развить логическое мышление, математическую речь. | ||||||||||||||||||
Критерии успеха: | Научится: самостоятельно складывать и вычитать десятичные дроби; выполнять действия в сотрудничестве с учителем по предложенному плану; самостоятельно выстраивать план действий по решению учебной задачи изученного вида; контролировать и оценивать по эталону свои работы и работы товарищей; получит возможность адекватно воспринимать оценку своей работы учителем, товарищами. | ||||||||||||||||||
Привитие ценностей: | Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни. | ||||||||||||||||||
Языковые цели: | Ученики: — могут объяснить алгоритм операций над десятичными дробями. Учащиеся будут: — комментировать выполнение сравнения дробей и нахождение суммы и разности десятичных дробей; — устно формулировать алгоритм сложения и вычитания десятичных дробей; — устно формулировать вопросы для проверки понимания темы сложения и вычитания десятичных дробей. Предметная лексика и терминология:
— целая часть, дробная часть; — десятичная дробь; — количество знаков, отделяемых запятой; — количество знаков после запятой; — десятая, сотая, тысячная части и т.д. | ||||||||||||||||||
Межпредметные связи: | Алгебра, физика, экономика | ||||||||||||||||||
Навыки использования ИКТ: | На данном уроке используется презентация и ресурсы с сайта BilimLand.kz и Itest.kz | ||||||||||||||||||
Предварительные знания: | Учащиеся могут сравнивать десятичные дроби, умеют правильно читать и записывать десятичные дроби. |
Ход урока
Этапы урока | Запланированная деятельность на уроке | Ресурсы | ||||||||||||||||||
Начало урока 7 мин | Приветствие. Создание коллаборативной среды. Круг радости. Игра «Я люблю свою родину, потому что…». Деление на группы. На доске прикреплены стикеры, на которых написаны примеры на сложение, вычитание, сравнение и изображение на координатном луче. Учащийся выбирает стикер и садится за тот стол, запись с примером которого подходит к названию группы. На столах лежат слова на казахском русском и английском языках. Нужно найти соответствие и закрепить на постере терминологию:
Логическая минутка. По порядку нумерации расшифровать девиз к уроку, слова которого принадлежат нашему Президенту страны Назарбаеву Н.А. Девиз нашего урока: Біздің құатымыз – бірлікте! Проблемный вопрос: Вставьте пропущенные цифры в клеточки, выполняя сложение и вычитание. Учитель: «Как вы думаете, какова тема нашего урока? А какие цели мы ставим перед собой на этот урок? Правильно!» | Презентация Слайд 1-4
Стикеры
Стикеры
Карточки с сайта BilimLand.
Стикеры | ||||||||||||||||||
Критерии успеха | Учащиеся расшифровывают девиз к уроку. Ученики самостоятельно называют тему урока и ставят цели на уроке. |
| ||||||||||||||||||
Середина урока 25 мин | Мотивация изучения материала. Групповые работы. Метод «Джиг-со»: в группе учащиеся делятся на 1, 2, 3, 4 и собираются в новые группы по своей нумерации. 1 за 1 стол. 2 за 2 стол и т.д. Учащимся включают видеоуроки с пунктами:
Для самостоятельного изучения и исследования учащимся предоставляются ноутбуки с подключением к интернету.
Групповые работы. Взаимопроверка по слайду с готовыми ответами. Взаимооценивание по методу «Карусель».
Работа с учебником № 625. | Учебник Видеоролики с сайта BilimLand.kz https://bilimland.kz/ru/courses/math-ru/arifmetika/raczionalnye-chisla/desyatichnye-drobi/lesson/slozhenie-i-vychitanie-desyatichnyx-drobei
Карточки с ресурсами из сайта BilimLand.kz Презентация слайда 5 — 8 Стикеры
| ||||||||||||||||||
Критерии успеха | Умеют осуществлять самооценку на основе критерия успешности учебной деятельности. |
| ||||||||||||||||||
Конец урока 8 мин | Физминутка: «Пальчики»
Самостоятельная работа. Тест. Проверим результаты. Формативное оценивание по критериям: 3 правильных ответа – 100% — высокий уровень 2 правильных ответа – 66% — средний уровень 1 правильный ответ – 33% — низкий уровень Подведение итогов. Подсчет стикеров в группах. Наибольшее количество стикеров у группы победителей. Награждаются победители. Домашнее задание: № 520, 521 Рефлексия «Микрофон». Учащимся предлагается в микрофон ответить на следующие вопросы: Что было понятно? Какую тему мы сегодня прошли? Достиг ли ты цели? Что было легко? Трудно? Что бы хотелось повторить?
Закончить урок хотелось мне следующими строчками: Мой Казахстан! Люблю тебя я За красоту твою, широкие просторы. Мой Казахстан! Велик ты и могуч, Певуч язык твой, величавы горы! Пусть солнце льется на твои просторы В богатстве недр и в золоте зерна. Пусть высится, как снеговые горы,
Спасибо за урок! До свидания!!! | Видеозарядка Карточки с тестом с сайта Itest.kz
Презентация правильных ответов. Слайд 9
Слайд 10 Слайд 11-12 | ||||||||||||||||||
Критерии успеха | Анализируют работу на уроке через оценку себя |
kz
Дифференциация Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание Как Вы планируете проверить уровень усвоения материала учащимися? Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока. | Здоровье и соблюдение техники безопасности |
Раздаточный материал:
Сложение и вычитание десятичных дробей / Десятичные дроби / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Десятичные дроби
- Сложение и вычитание десятичных дробей
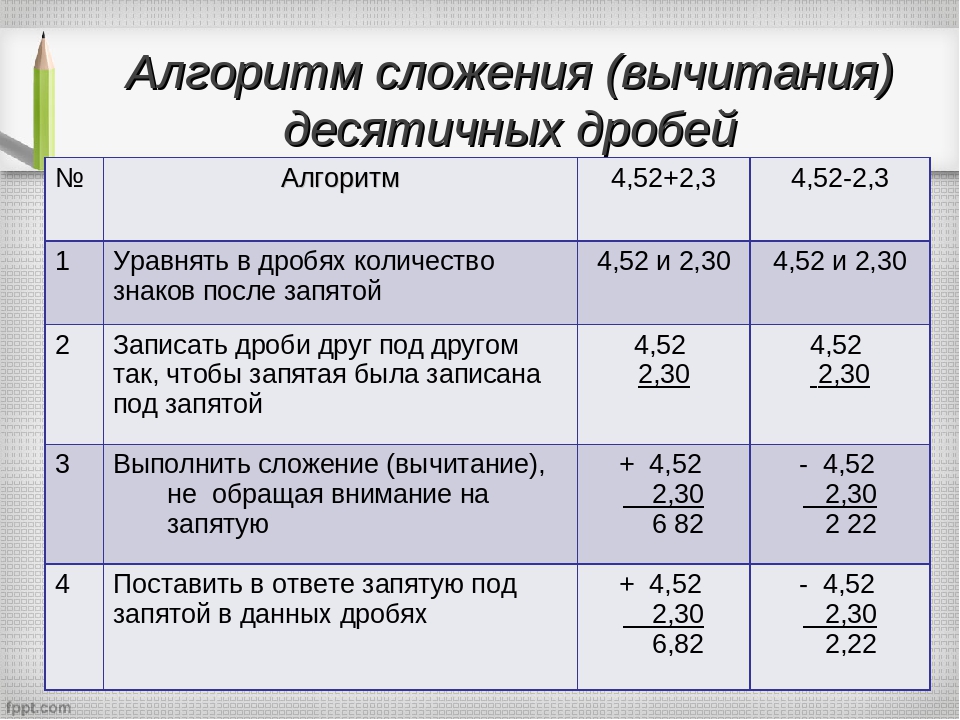
Здесь мы рассмотрим, как складывать и вычитать десятичные дроби.
Чтобы сложить или вычесть десятичные дроби, нужно записать числа столбиком так, чтобы запятая стояла под запятой. Затем выполнить действие не обращая внимание на запятую, а в ответе поставить запятую под запятой.
Пример: 1) Сложение и вычитание дробей, если одинаковое количество цифр после запятой
| + | 1 | 7 | , | 6 |
| 9 | , | 7 | ||
| 2 | 7 | , | 3 |
| — | 1 | 7 | , | 6 |
| 9 | , | 7 | ||
| 7 | , | 9 |
2) Вычитание дробей, если разное количество цифр после запятой.
Дроби 147,33 — 89,7. Сначала нужно уровнять количество цифр после запятой, для этого мы добавим справа в конце один ноль, затем выполним действие столбиком.
| + | 1 | 4 | 7 | , | 3 | 3 |
| 8 | 9 | , | 7 | 0 | ||
| 2 | 3 | 7 | , | 0 | 3 |
| — | 1 | 4 | 7 | , | 3 | 3 |
| 8 | 9 | , | 7 | 0 | ||
| 5 | 7 | , | 6 | 3 |
Советуем посмотреть:
Десятичная запись дробных чисел
Сравнение десятичных дробей
Приближенные значения чисел.
Округление чисел
Умножение десятичных дробей
Деление десятичных дробей
Среднее арифметическое
Десятичные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 1262, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1266, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1270, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1348, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1383, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1396, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1590, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1779, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 4, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Номер 994, Мерзляк, Полонский, Якир, Учебник
Номер 1010, Мерзляк, Полонский, Якир, Учебник
Номер 1032, Мерзляк, Полонский, Якир, Учебник
Задание 423, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 471, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 495, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 548, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 994, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1055, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1421, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 138, Мерзляк, Полонский, Якир, Учебник
Номер 149, Мерзляк, Полонский, Якир, Учебник
Номер 290, Мерзляк, Полонский, Якир, Учебник
Номер 430, Мерзляк, Полонский, Якир, Учебник
Номер 480, Мерзляк, Полонский, Якир, Учебник
Номер 545, Мерзляк, Полонский, Якир, Учебник
Номер 874, Мерзляк, Полонский, Якир, Учебник
Номер 1059, Мерзляк, Полонский, Якир, Учебник
Номер 1139, Мерзляк, Полонский, Якир, Учебник
Номер 1172, Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 92, Мерзляк, Полонский, Якир, Учебник
Номер 10, Мерзляк, Полонский, Якир, Учебник
Номер 222, Мерзляк, Полонский, Якир, Учебник
Номер 225, Мерзляк, Полонский, Якир, Учебник
Номер 226, Мерзляк, Полонский, Якир, Учебник
Номер 242, Мерзляк, Полонский, Якир, Учебник
Номер 266, Мерзляк, Полонский, Якир, Учебник
Номер 269, Мерзляк, Полонский, Якир, Учебник
Номер 303, Мерзляк, Полонский, Якир, Учебник
Номер 309, Мерзляк, Полонский, Якир, Учебник
Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробейСложение и вычитание десятичных дробей
Назад на страницу с десятичными дробями Назад к математике 187A страница Назад к математике Страница отдела электронная почта Вопросы и предложения
|
Напомним, что десятичные дроби
просто дроби. Мы складываем дроби, складывая целые части числа и
дробные части отдельно, перенося 1 из дробной части, если
необходимо для целой части числа. Для десятичных дробей мы выстраиваем
десятичных знаков так, чтобы целые части числа совпадали, а десятичные части
расстановка. Затем добавьте каждый.
Мы линии
поднимите десятичные дроби по вертикали, прикрепите лишние нули справа и вычтите
вниз. В частности, выполните следующие действия: 
2 1 4 
Сколько стоит ваш общий счет?Сложение и вычитание десятичных дробей.
Обзор математики (видео) мальчишки появляются часто на протяжении всей нашей повседневной жизни.Например, товар в магазине может стоить 2,75 доллара, а ваш любимый баскетболист может стоить в среднем 19 долларов.0,7 очка за игру. Вы можете взять кредит под 4,45% годовых, или победитель эстафеты на 100 метров может завершить гонку за 12,67 секунды.
Чтобы эффективно использовать десятичные дроби, важно уметь использовать десятичные дроби и манипулировать ими в математических выражениях.
Сегодня мы рассмотрим основы — сложение и вычитание.
Сложение десятичных знаков
Мы начнем с простого примера сложения десятичных знаков, так что давайте попробуем:
\(32,61+11,54\)
Первым шагом, как вы видите, является выстраивание двух десятичных знаков следующим образом:
| \(32,61\) | |
| \ (+\) | \(11,54\) |
Обратите внимание, что из-за коммутативного свойства сложения не имеет значения, какой десятичный знак ставится первым (однако это будет иметь значение при вычитании).
Убедитесь, что десятичные точки в каждом числе выровнены точно. Если ваши десятичные дроби выстроены неправильно, вы получите неправильный ответ.
Как только вы выстроите два десятичных знака в ряд, вы начнете решать задачу так же, как и любую задачу на сложение.
Во-первых, мы добавляем два числа в сотых долей , \(1\) и \(4\), что дает нам \(5\) в сотых долях. Затем мы добавляем \(6\) и \(5\), которые находятся в десятых разрядах, и это дает нам 11, поэтому мы переносим 1. Уменьшаем нашу десятичную дробь, и теперь у нас есть \(2+1+ \) этот другой \(1\), так что это \(3\), \(4\). А теперь складываем \(3\) и \(1\) и получаем \(4\). Итак, наш окончательный ответ: \(44,15\).
| \(32,61\) | |
| \(+\) | \(11,54\) |
| 903 22 \(44.15\) |
Вычитание десятичных дробей
Давайте двигаться к вычитанию. Начнем с простой задачи:
\(7,5-2,8\)
Как и в случае сложения, первым шагом является выстраивание чисел с запятой в одном месте.
Ваше выражение должно выглядеть так: 9
Начните вычитать, как в любой задаче на вычитание. Начиная с десятого столбца, вам нужно сначала заимствовать из нашего столбца, потому что \(5-8\) не получается. Итак, возьмите \(1\), сделайте это \(6\), а затем перенесите его. Итак, теперь у нас есть \(8\), вычитаемое из \(15\), что дает нам \(7\). Сократите нашу десятичную дробь, и теперь у нас есть \(2\), вычитаемое из \(6\), что дает нам \(4\). Итак, наш окончательный ответ: \(4.7\).
| \(7.5\) | |
| \(–\) | \(2.8\) |
| \( 4.7\) |
Наконец, сделаем еще одно вычитание задача:
\(10,53-4,274\)
Еще раз выстраиваем два числа, убедившись, что наши десятичные точки находятся в одном положении. Ваше выражение должно выглядеть так:
| \(10.53 \phantom{0}\) | |
| \(–\) | \(4,274\) |
Вы можете добавить нули, чтобы сбалансировать, так что это выглядит, просто чувствуется, что там полно, и это нормально.
Их можно не добавлять, и это тоже нормально.
| \(10,530\) | |
| \(–\) | \(4,274\) |
И снова в этой задаче нам нужно начать с заимствования с нашего сотого места . Итак, мы делаем это \(2\) и переносим наш \(1\), так что теперь у нас есть \(4\), вычитаемый из \(10\), что дает нам \(6\). Затем из \(2\) вычитается \(7\), что не работает, поэтому нам нужно снова брать взаймы. Это становится \(4\), переносим \(1\), чтобы получить \(12\), так что \(7\) вычитается из \(12\), что дает нам \(5\). Теперь у нас есть \(2\), вычитаемое из \(4\), что дает нам \(2\). Уменьшите нашу десятичную точку, у нас есть \(4\), вычитаемое из \(0\), что, как мы знаем, не работает, так что это становится \(0\). Нести наш \(1\), и у нас есть \(10-4\), что дает нам \(6\). Итак, наш окончательный ответ: \(6,256\).
| \(10,530\) | |
| \(–\) | \(4,274\) |
| 90 322 \(6. |
256\)
Теперь у вас должно быть четкое понимание как складывать и вычитать десятичные дроби. Не забывайте всегда выстраивать числа и следить за тем, чтобы десятичные дроби каждого числа стояли на одном месте!
Спасибо за просмотр и до встречи в следующий раз!
Часто задаваемые вопросы
Q
Каковы шаги для сложения и вычитания десятичных знаков?
A
Чтобы сложить или вычесть десятичные числа, настройте числа как обычно для сложения или вычитания по вертикали, выровняв числа по десятичным точкам. При необходимости добавьте дополнительные нули после запятой. Сложите или вычтите как обычно, сохраняя десятичную дробь в той же позиции.
Пример. 243,5 + 1,279 =
243,5 + 1,279 = 244,779
Q
Чем полезна оценка при сложении и вычитании десятичных дробей?
A
Оценка полезна при сложении и вычитании десятичных знаков, поскольку она помогает узнать, близок ли ваш ответ к правильному ответу или нет.
Например, вы сложили 12,4 + 2,73 и получили 3,97. Округление каждого числа до ближайшего целого числа даст вам 12 + 3, что равняется 15. 3,97 и близко не соответствует этому значению, поэтому вы понимаете, что где-то допустили ошибку. Вы возвращаетесь к исходной работе и замечаете, что забыли выровнять десятичные точки. Теперь вы можете исправить свою проблему и получить правильный ответ 15.13.
Q
Почему важно выстраивать десятичные дроби при сложении?
A
При сложении важно выровнять десятичные дроби, поскольку это гарантирует, что вы добавляете правильные разряды.
Q
Как вычесть десятичные дроби из целых чисел?
A
Вычитание десятичных чисел из целых чисел путем преобразования целого числа в десятичное путем добавления десятичной точки и необходимого количества нулей. Затем вычтите как обычно.
Пр. 12 – 8.13
Q
Как вычитать отрицательные десятичные дроби?
A
Вычитание отрицательного числа похоже на сложение этого числа.
Таким образом, вычитание отрицательного десятичного числа добавляет это отрицательное десятичное число.
Пример. -2,3 – (-7,4) = -2,3 + 7,4 = 5,1
Q
Как вычесть повторяющиеся десятичные дроби?
A
Вычитание повторяющихся десятичных дробей путем преобразования их в дроби и вычитания дробей или путем округления повторяющихся десятичных дробей и вычитания.
Пр. \(0.\overline{6}-0.\overline{3}\)
\(0.\overline{6}=\frac{2}{3}\) и \(0.\overline{3} =\frac{1}{3}\)
\(\frac{2}{3}-\frac{1}{3}=\frac{1}{3}\)
ИЛИ
\(0.\ overline{6}≈0,67\) и \(0.\overline{3}≈0,33\)
\(0,67-0,33=0,34\)
Практические вопросы
Вопрос № 1:
\ (4 +17.31=\)
17.35
57.31
17.71
21.31
Показать ответ
Ответ:
Правильный ответ: 21.
31. Чтобы добавить десятичные знаки, выровняйте десятичные точки друг над другом, добавьте нули, где необходимо, в качестве заполнителей и добавьте как обычно. Помните, если десятичной точки нет, она стоит в конце числа.
Скрыть ответ
Вопрос №2:
\(16,17+2,421=\)
40,38
18,591
4.083
1.85
Показать ответ
Ответ:
Правильный ответ: 18,591. Чтобы добавить десятичные знаки, выровняйте десятичные точки друг над другом, добавьте 0, где необходимо, в качестве заполнителей и добавьте, как обычно.
Скрыть ответ
Вопрос №3:
\(78,179-1,23=\)
70,056
7,69
76.949
7.06
Показать ответ
Ответ:
Правильный ответ ответ 76,949.
Чтобы вычесть десятичные дроби, выровняйте десятичные точки друг над другом, добавьте 0, где необходимо, в качестве заполнителей и вычтите как обычно.
Скрыть ответ
Вопрос №4:
Сьюзи печет булочки с корицей, ей нужно 0,63 ч.л. корицы для теста, 3,71 ч.л. корицы для начинки и 0,12 ч.л. ложки корицы для глазури. Сколько всего чайных ложек корицы ей нужно?
3.19 ч.л.
4.46 ч.л.
5.63 ч.л.
6.21 ч.л. 0008
Правильный ответ: 4,46 ч. л. При решении задач со словами ищите слова-подсказки, которые помогут вам понять, о чем идет речь. Ключевое слово в этой задаче — «всего», которое говорит нам, что нам нужно сложить наши значения.
Скрыть ответ
Вопрос № 5:
Джонатан получает 45 долларов на свой день рождения. Он тратит 29,73 доллара на видеоигру, 1,12 доллара на упаковку жевательной резинки и 2,81 доллара на газировку.
Сколько денег у него осталось?
$11,34
$12,73
$11,17
$12,12
Показать ответ
Ответ:
900 09 Правильный ответ: 11,34 доллара. Когда словесная задача спрашивает, сколько осталось, она часто включает вычитание. Джонатан начинает с 45 долларов, а затем использует эти деньги для трех разных целей. Вычтите цену каждого предмета из его начальной стоимости, чтобы определить, сколько денег у него осталось. Сначала вычтите 29 долларов.0,73 для видеоигры.Затем вычтите 1,12 доллара за упаковку жевательной резинки.
Наконец, вычтите 2,81 доллара за газировку.
У Джонатана осталось 11,34 доллара.
Скрыть ответ
Вопрос № 6:
Зола покупает 22,31 унции леденцов и 16,58 унций жевательных конфет. Какое общее количество конфет купил Золя?
3,889 унции
38,89 унции
388,9 унции
3889 унции
Показать ответ
Ответ:
Правильный ответ B: 38,89 унции.