Сложение и вычитание десятичных дробей – правило (5 класс, математика)
4.3
Средняя оценка: 4.3
Всего получено оценок: 106.
4.3
Средняя оценка: 4.3
Всего получено оценок: 106.
Сложение и вычитание десятичных дробей не самая сложная тема в курсе математики 5 класса. Но особую сложность представляет правильный перенос запятой. Чтобы ни у кого не возникало проблем с этой операцией, рассмотрим алгоритм сложения и вычитания дробей.
Десятичная дробь и ее знаменатель
Дробь в общем случае это незаконченная операция деления. Что это значит? Очень часто в вычислении не получится вычислить деление в точности до последнего знака. Поэтому для повышения точности в математике придумали заменять деление на дробь. Так получаются обычные дроби.
Но обычные дроби хорошо подходят для математических вычислений. В сложных вычислениях, которые применяются, к примеру, в бухгалтерском учете, использовать такие дроби слишком сложно.
Почему?
Обратите внимание, знаменатель должен быть кратным 10. А это не только число 10, но и 100, 1000 и так далее. Количество нулей в десятичной дроби равняется количеству знаков после запятой.
Именно на количестве знаков после запятой и прячется основная доля ошибок. Дело в том, что для правильного сложения дробей нужно знак запятой перенести ,чтобы превратить дробь в обычное число. После выполнения операции запятая переносится обратно. При обратном перенесении запятой очень важно не ошибиться с количеством знаков после запятой, иначе получится ошибка. Но обо всем по порядку.
Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей выполняется с помощью переноса запятой. Для того, чтобы правильно перенести запятую, нужно посмотреть на число с наибольшим количеством знаков после запятой.
В числе значащей цифрой называют все цифры, кроме нуля. Значащие цифры иногда подсчитывают по порядку слева направо.
В нашем случае это должна быть первая и единственная значащая цифра. Приведем пример использования правила сложения и вычитания десятичных дробей:
30,0598=300598*0,0001 – в этом примере искомым числом будет 0,0001. Как видно, количество знаков после запятой равняется количеству знаков после запятой в изначальном числе. Благодаря вынесению множителя мы смогли передвинуть запятую.
Теперь, нужно вспомнить распределительное свойство умножения и воспользоваться им. Распределительное свойство выглядит так:
а*(в+с)=а*в+а*с – только свойством мы воспользуемся наоборот.
Решим пример: 30,0598+0,783 – обратите внимание, что количество знаков после запятой у каждого числа разное, поэтому нужно выбирать число, у которого знаков после запятой больше.
Вынесем множитель:
30,0598+0,783=0,0001*(300598+…. – здесь очень интересный момент. Дело в том, что знаков после запятой в числе 0,783 меньше. Значит, для того, чтобы понять, какое число получится после вынесения множителя, нужно решить небольшое уравнение:
0,783=0,0001*х
$$Х={0,783\over{0,0001}}=0,783*10000 = 7830$$ – обратите внимание, что мы просто перенесли запятую вправо на то же количество знаков, какое содержится в общем множителе. Поэтому в условиях урока не нужно решать уравнение, достаточно просто переносить запятую нужным образом.
В итоге мы получим следующий пример:
30,0598+0,783=0,0001*(300598+7830)=0,0001*308428=30,8428 – вот и весь пример.
После выработки навыка все дополнительные операции будут выполняться сами собой в уме. Нужно просто запастись терпением и решать как можно больше примеров.
Что мы узнали?
Мы узнали, что такое десятичные дроби и как с ними работать.
Обучились базовым навыкам сложения и вычитания десятичных дробей. Разбили эти операции на отдельные шаги, чтобы никогда не допускать досадных ошибок по неправильному перенесению запятой.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Руслан Лунин
10/10
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 106.
А какая ваша оценка?
Сложение и вычитание десятичных дробей
Дополнительные файлы
-
Презентация
-
Урок
Размер файла: 18 КБ Кол-во скачиваний: 277
Учитель: Логвиненко Л.
А., МБОУ «СОШ № 18 п. Теплоозерск»
Тема урока: «Сложение и вычитание десятичных дробей»
Тип урока: изучение и первичное закрепление новых знаний.
(Учебник: математика 6 кл, автор Г.В. Дорофеев, И. Ф. Шарыгин)
Цель урока: изучить правило сложения(вычитания) десятичных дробей и научиться им пользоваться при решении примеров и задач.
Задачи урока:
Образовательные:
Развивающие:
Воспитывающие:
- воспитывать интерес к математике;
- прививать навык самостоятельности в работе, умение выслушивать других.
В соответствии с поставленными целями и содержанием материала урок строится по следующим этапам:
1.Математики — древности ( к неделе математики)-презентация
2. Повторение правил прочтения, записи и сравнения дробей. (3 мин)
3. Диктант (с взаимопроверкой) — 4 мин
4. Актуализация знаний — расположить десятичные дроби по возрастанию
(4 мин)
5.
Постановка учебных целей и задач. (2 мин)
Предложения ребят: понять правило сложения(вычитания) десятичных дробей, научиться складывать (вычитать) десятичные дроби. Уметь работать в группе и в парах.
6.Открытие детьми нового знания (5 мин) — с.67
Запись темы «Сложение десятичных дробей»
8.Первичное закрепление — образец решения
9.Решение примеров: № 290,291,296
10.Подведение итогов урока (2 мин)
11.Рефлексия учебной деятельности на уроке (1мин) — поднять кружки: зеленый — всё понятно ; желтый — понятно многое, но не всё ; красный- много не понятно.
Этапы урока:
1 этап. Самоопределение к деятельности
Цель первого этапа– организация мотивации к учебно – познавательной деятельности.
(Учитель приветствует детей, проверяет готовность к уроку, настраивает детей на деловой ритм)
Учитель: Здравствуйте ребята! Мы начинаем урок. Девизом нашего урока будут такие слова: (слайд №2)
Думать — коллективно!
Решать – оперативно!
Отвечать – доказательно!
И всё будет у нас — замечательно!
2 этап.
Повторение правил прочтения, записи и сравнения дробей. ( Работа в парах)
3 этап.
Диктант (с взаимопроверкой) (слайд № 3, слайд №4)
Слайд № 5 поможет сделать логический переход к новой теме.
4 этап. Расположить десятичные дроби по возрастанию (данное задание поможет определить тему урока) (сдайд № 6)
5 этап. Постановка учебных целей и задач. (2 мин)
Предложения ребят: понять правило сложения(вычитания) десятичных дробей, научиться складывать(вычитать) десятичные дроби. Уметь работать в группе и в парах.
6 этап. Открытие детьми нового знания (5 мин) — с.67,68 учебника (получение информации)
Запись темы «Сложение десятичных дробей» и рассмотрение правила.
(слайд № 7)
7 этап. Физминутка (3 мин) — игра «Назови разряды» — каждой группе нужно десятичную дробь составить с помощью разрядов, используя таблички с названием разрядов: тысячи, сотни, десятки, единицы, десятые, сотые,…)
(слайд № 8)
8 этап.
9 этап. Решение примеров: № 290 (уст.), 291.
10 этап Подведение итогов: оценить работу группы (ответственный в группе анализирует работу группы)
11 этап Рефлексия: поднять кружки: зеленый — всё понятно ; желтый — понятно многое, но не всё ; красный- много не понятно. (общий от группы)
Каждый ученик оценивает свою работу на уроке, заполнив таблицу:
Этапы урока | Оценка деятельности |
1. Повторение правил | |
2. Диктант | |
3. Разгадывание темы | |
4. игра «Назови разряды» | |
5. решение примеров |
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно.
Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.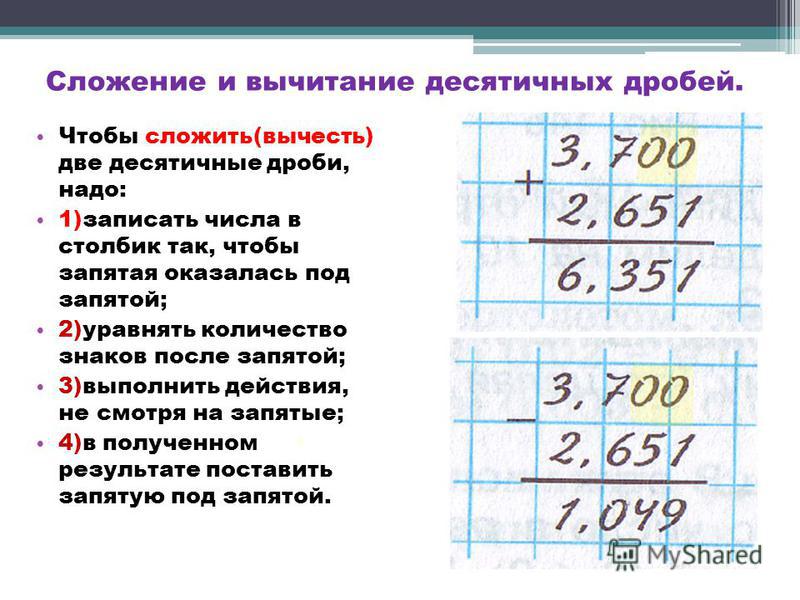
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Операции с дробями и десятичными знаками Add/Sub/Mult/Div
Правила умножения
- Поместите все СМЕШАННЫЕ ЧИСЛА в НЕПРАВИЛЬНУЮ ФОРМУ.
- Уменьшить все дроби перед умножением
- Умножьте числитель на числитель и знаменатель на знаменатель.
Для умножения десятичных чисел:
Смотреть видео: Основы арифметики: умножение десятичных дробей Патрика ДжМТ
|
Правила раздела
- ЗАМЕНИТЬ знак деления на знак умножения.
- Напишите ОБРАТНУЮ ЧИСЛО от делителя (число 2 и ).
- Соблюдайте правила умножения.
К РАЗДЕЛИТЬ десятичных чисел:
Смотреть видео: Основы арифметики: Деление десятичных дробей от Патрика ДжМТ
| |
Смотреть видео: дроби — умножение и деление Патрика ДжМТ
|
Правила сложения и вычитания
- Должен иметь общий знаменатель
- Складывать или вычитать только числители
- Знаменатель остается прежним
- Сократить до минимума
- При сложении или вычитании смешанных чисел
а. Сложение или вычитание целых чисел
b.
При сложении и вычитании может потребоваться дополнительный шаг (перенос или заимствование)
в. Ответы всегда должны быть в наименьшем выражении.
Вычтите следующие числа: 10,8–3,52
Сопоставьте элементы.
Задача состоит в том, чтобы сопоставить элементы с буквами и элементами с правильными номерами. Ниже показан список обозначенных буквами элементов. Далее следует список пронумерованных элементов. За каждым пронумерованным элементом следует раскрывающийся список. Выберите букву в раскрывающемся списке, которая лучше всего соответствует пронумерованному элементу с буквенными альтернативами.
| а. | |
| б. 4,37 | |
в. |