Деление умножение вычитание сложение столбиком: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком

Содержание

§ Сложение в столбик. Как складывать в столбик

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Геометрия: начальная школа
Действия в столбик
Деление с остатком
Законы арифметики
Периметр
Порядок действий
Разряды и классы. Разрядные слагаемые
Счет в пределах 10 и 20

Математика 5 класс

Взаимно обратные числа и дроби
Десятичные дроби
Натуральные числа
Нахождение НОД и НОК
Обыкновенные дроби
Округление чисел
Перевод обыкновенной дроби в десятичную

Площадь
Проценты
Свойства сложения, вычитания, умножения и деления
Среднее арифметическое
Упрощение выражений
Уравнения 5 класс
Числовые и буквенные выражения

Математика 6 класс

Масштаб
Модуль числа
Окружность. Площадь круга
Отношение чисел
Отрицательные и положительные числа
Периодическая дробь
Признаки делимости
Пропорции
Рациональные числа
Система координат
Целые числа

Алгебра 7 класс

Алгебраические дроби
Как применять формулы сокращённого умножения
Многочлены
Одночлены
Системы уравнений
Степени
Уравнения
Формулы сокращённого умножения
Функция в математике

Геометрия 7 класс

Точка, прямая и отрезок
Что такое аксиома и теорема

Алгебра 8 класс

Квадратичная функция. Парабола
Квадратные неравенства
Квадратные уравнения
Квадратный корень
Неравенства
Системы неравенств
Стандартный вид числа
Теорема Виета

Алгебра 9 класс

Возрастание и убывание функции
Нули функции
Область определения функции
Отрицательная степень
Среднее
геометрическое

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Теоретически между теорией и практикой разницы практически нет.

Но практика показывает, что она есть. Йоги Бера

на главную

Введите тему

Русский язык Поддержать сайт

Сложение в столбик Вычитание в столбик Умножение в столбик Деление в столбик

Чтобы складывать большие числа, которые имеют более двух цифр (знаков), используют сложение столбиком. Такой способ сложения поможет быстрее решить пример и не сделать ошибок.

Итак, рассмотрим пример:

Складываем по одной цифре (знаку) справа налево. Результат записываем под чертой.
8 + 1 = 9

Теперь складываем «4» с восьмеркой.
4 + 8 = 12
У нас получилось число большее «10», поэтому под цифрами записываем только последнюю цифру полученного числа «12». Это «2».
Но и про десяток не забудем. Поставим над соседом слева от «4» (над «7») единичку.

Напомним, что означает единица над «7». Единица означает, что к «7» надо прибавить «1» и уже потом складывать с «3».
7 + 1 = 8
Полученную восьмерку складываем с «3».
8 + 3 = 11
Снова получилось число большее «10», поэтому поступаем также как и ранее. Теперь и над «6» появится единичка.
В итоге получаем:

После всех действий в столбик не забудьте записать ответ в исходный пример.

Проверить свои вычисления вы можете на нашем сайте с помощью калькулятора сложение в столбик онлайн.

Сложение в столбик Вычитание в столбик Умножение в столбик Деление в столбик

вычислительные навыки в начальной школе

Продолжаем тему «основные содержательные линии курса математики начальной школы». В предыдущей статье мы рассмотрели такие линии, как «нумерации» и «величины». Продолжим далее по списку, представленному в предыдущей статье, и рассмотрим освоение учениками начальной школы вычислительных навыков.

Сложение и вычитание

В первом классе начальной школы дети осваивают сложение и вычитание в пределах 10, а также в пределах 100 без перехода через десяток.

Во втором классе сложение и вычитание осваивается уже сначала в пределах 20 с переходом через десяток, затем в пределах 100, также с переходом через десяток. Также осваивается письменное вычисление двухзначных чисел «в столбик».

В третьем классе осваивается сложение с переходом через разряд в пределах 10000, а также вычитание с переходом через разряд в пределах 1000. Дети устно складывают и вычитают круглые числа в пределах 1000, письменно – трехзначные числа.

В четвертом классе осваивается сложение и вычитание многозначных чисел, уже в пределах 1000000. Устно складывают и вычитают круглые числа, такие как тысячи и миллионы, а письменно – многозначные числа в пределах миллиона.

На нашем сайте Вы можете посмотреть видеоуроки сложение и вычитание.

Умножение и деление

Освоение таких вычислительных навыков, как умножение и деление начинается со второго класса, здесь осваивается таблица умножения, а также соответствующие случаи деления.

В третьем классе осваивается умножение трехзначных чисел на однозначное число, а также деление с остатком. Деление осуществляется трехзначных чисел на однозначное число, берутся простые случаи. Устно осуществляется внетабличное умножение двухзначных чисел на однозначные, умножение и деление на 10 и на 100, а также умножение и деление десятков на однозначное число. Письменно умножаются и делятся трехзначные числа на однозначные.

В четвертом классе осваивается умножение и деление многозначных чисел на двухзначные и трехзначные числа в пределах миллиона. Устно вычисляются круглые числа, а именно умножение и деление на двузначное число в пределах 100.

Письменно умножаются и делятся многозначные числа на двузначные и трехзначные числа.

О том, что такое умножение и деление Вы можете прочитать на нашем сайте, а также здесь Вы можете найти информацию о том как выучить таблицу умножения.

На этом мы прервем наши исследования и продолжим их в следующей статье “найти значение выражения“.

Если вы хотите получать информацию о новых статьях и проектах нашего сайта, то подпишитесь на рассылку новостей сайта. Всего вам наилучшего и успехов. Спасибо.

Понравилась статья — поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

‎Набор альтернативных алгоритмов деления, умножения, сложения и вычитания в App Store

В этом комплекте 10 математических приложений iDevBooks. Сэкономьте 62 % по сравнению с покупкой приложений по отдельности.

Решеточное умножение

Решеточное умножение алгоритмически эквивалентно длинному умножению. Решетка (сетка) направляет расчет. Все умножения выполняются сначала, а затем сложения. Этот метод был представлен Европе в 1202 году в Liber Abaci Фибоначчи.

В этой новаторской книге Фибоначчи представил множество алгоритмов для работы с арабскими цифрами. Древние индийцы и китайцы изначально изобрели некоторые алгоритмы. Фибоначчи представил как текущее стандартное длинное умножение, так и первоначально индийский метод, называемый решетчатым умножением, который быстрее и компактнее для работы с большими числами.

Умножение сетки

Метод умножения сетки представляет собой двухэтапный процесс. В примере 39 х 24 числа сначала разбиваются на 30 + 9.и 20 + 4, и написано на сетке. Умножение заголовков строк и столбцов затем решает каждую ячейку сетки. В конце концов частичные произведения 600, 180, 120 и 36 складываются.

Египетское умножение

Древние египтяне могли умножать любые два числа, используя только способность умножать на 2 и складывать.

Русский Умножение

В этом методе единственные факты умножения, которые нам нужно знать, это как удвоить и как взять половину числа.

Деление по столбцам

Метод деления по столбцам представляет собой простую вариацию традиционного метода деления по столбцам. Линии рисуются для разделения цифр делителя. Каждый столбец разрядных значений решается слева направо.

Ежедневное добавление столбцов

Метод ежедневного добавления столбцов был разработан первоклассником. Метод имеет два этапа. На первом этапе цифры добавляются по одному столбцу за раз в каждом столбце. После первого этапа некоторые столбцы могут иметь двузначные номера. На втором этапе выполняются переносы для получения результата.

Вычитание частичных разностей

Метод вычитания частичных разностей представляет собой двухэтапный процесс. В примере 936–580 каждое разрядное значение сначала вычитается отдельно слева направо. Частичные разности складываются, и 400 — 50 + 6 дает ответ 356.

Wired.com: «Приложения Эсы Хелттулы отлично подходят для изучения и практики математики и не перегружены мини-играми, поощрениями или надоедливой музыкой. ».

Вычитание по программе Trade-First

Метод вычитания по принципу trade-first подобен традиционному методу вычитания по столбцу. Метод имеет два этапа. Вся «торговля» или «заимствование» выполняется в первую очередь. Затем решаются вычитания. Это дало методу название «торговля в первую очередь».

Равное сложение и вычитание

Метод основан на идее, что прибавление одинаковой суммы к двум числам не повлияет на разницу между двумя числами. Процесс можно представить так:
— Работа столбец за столбцом справа налево
— Когда цифра первого числа меньше соответствующей цифры второго числа, прибавить десять к цифре первого числа и единицу к цифре второго числа в следующем столбце слева.

Метод вычитания с равным сложением также называется методом «одолжить и вернуть» или методом вычитания с равным сложением. Сегодня метод используется в Австралии и Латинской Америке. Равное сложение было очень популярным методом вычитания в США до середины 20 века.

Вычитание слева направо

Метод вычитания слева направо представляет собой двухэтапный процесс. В примере 936 — 581 вычитаемое число сначала записывается в развернутом виде: 500+80+1. Каждая из частей затем вычитается из начального числа. В нашем примере 936-500=436, 436-80=356 и, наконец, 356-1=355.

Конфиденциальность

В приложениях нет рекламы или встроенных покупок, и они не передают никаких данных во время работы приложения. Приложения также не содержат ссылок на другие приложения или Интернет.

Видео

Десятки видео этих и других приложений можно найти на idevbooks.com.

Двоичное сложение, умножение, вычитание и деление | by Malay Biswas

Основные математические операции с двоичными числами аналогичны десятичной системе. Однако есть несколько правил, специфичных для двоичной системы. Мы рассмотрим каждый из них в отдельности.

Сложение

Существует 3 основных правила сложения двоичных чисел:

0). Таким образом, мы сохраняем 0 в столбце 1 и сдвигаем (переносим) 1 в столбец 2.

Другие правила такие же, как и в десятичной системе, т. е. мы добавляем справа налево, а перенос получаем, добавляемый к цифрам в следующем столбце.

Теперь давайте попробуем добавить 11 к 13. Двоичный код для 11 равен 1011, а для 13 — 1101. 1 к 2 цв.

2-й столбец = 1 + 0 + 1 (перенос) = (1 + 0) + 1 = 1 + 1 = 10. Снова мы сохраняем 0 в 2-м столбце и переносим 1-й на 4-й столбец. 90 = 16 + 8 + 0 + 0 + 0 = 24 = 11 + 13.

Умножение

Умножение в двоичном формате точно такое же, как и в десятичном, т. е. умножение чисел справа налево и умножение каждой цифры одного числа на каждую цифру другого числа, они суммируют их. 3 основных правила двоичного умножения также аналогичны десятичному.

1 * 1 = 1
1 * 0 = 0 * 1 = 0
0 * 0 = 0

Кроме того, помните, что к каждому сдвигу влево цифры множителя необходимо добавлять лишний ноль к продукту. Это также похоже на десятичную систему.

1011

x 1101

1011 * 1 (COL Multiplier 1) = 1011
1011 * 0 (Multiplier 2 Col) = 00000 (один нулевой приложенный в конце)
1011 * 1 (Умножение 4 -е col). = 101100 (два нуля в конце)
1011 * 1 (множитель 8) = 1011000 (три нуля в конце)
Суммируем. 1011 + 00000 + 101100 + 1011000 = ((1011 + 00000) + 101100) + 1011000 = (01011 + 101100) + 1011000 = 110111 + 1011000 = 10001111

Вычитание

Прежде чем пытаться вычитать, нам нужно понять, как отрицательные числа представлены в двоичном виде. Какая бы система ни использовалась (например, 4-битная, 8-битная, 16-битная и т. д.), все числа со знаком должны иметь одинаковое количество битов. 0 используются для заполнения пустых битов. Мы будем использовать 8-бит для этого урока. Существует 3 основных стандарта записи отрицательных чисел.

Величина со знаком

В этой записи дополнительный бит добавляется слева от числа для обозначения его знака. 0 указывает +ve, а 1 указывает -ve. Используя 8 бит, +13 соответствует 00001101, а +11 соответствует 00001011. -13 соответствует 10001101 и -11 соответствует 10001011.

Дополнение до единиц

В этой записи положительные числа представляются точно так же, как обычные двоичные числа. Таким образом, 13 будет 00001101, а 11 будет 00001011. Отрицательные числа представляются простым переворачиванием бита, т.е. 0 становится 1, а 1 становится 0. Таким образом, -13 будет 11110010, а -11 будет 11110100.

Вычитание с использованием дополнения к единице

В этом методе вычитаемое число должно быть инвертировано с использованием дополнения до 1, а затем добавлено (не вычтено) к другому числу. Поскольку все числа со знаком должны иметь одинаковое количество битов, любой бит «переполнения» должен быть добавлен обратно к остальной части результата.

Если мы хотим сделать 13–11, это по существу 13 + (-11) или 00001101 + 11110100. Сложение их даст 100000001. Обратите внимание, что это не 9 бит, поэтому мы сохраняем самые правые 8 бит 00000001 и добавляем ‘ переносим в него 9-й бит (в данном случае 1), что дает нам 00000010 = 2 = 13–11.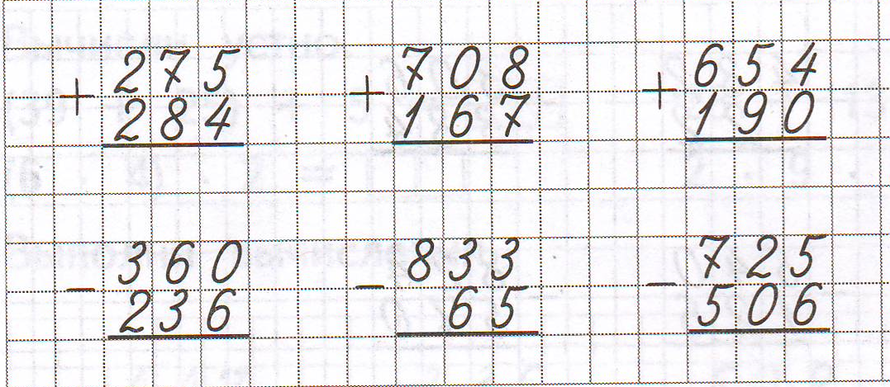

Теперь давайте попробуем 11–13 или 11 + (-13) = 00001011 + 11110010 = 11111101. Слева от него стоит 1, что указывает на его отрицательное значение. Используя дополнение до 1, мы можем вычислить абсолютное (положительное) число, которое равно 00000010 или 2. Таким образом, результат равен -2. 9n или проще говоря, результат вычитания числа из 2n. В этом методе отрицательное число обозначается сначала определением дополнения до 1 положительного числа, а затем добавлением к нему 1. Таким образом, 8-битное -13 будет 11110010 (дополнение до 1) + 1 = 11110011; -11 будет 11110101.

При сложении или вычитании двоичных чисел в дополнении до 2 все лишние (переносные) биты отбрасываются.

Теперь давайте попробуем те же примеры, что и в дополнении 1.

13–11 = 13 + (-11) = 00001101 + 11110101 = 100000010. Отбрасывание остатка 9й бит слева мы получаем результат как 00000010 = 2.

11–13 = 11 + (-13) = 00001011 + 11110011 = 11111110. 1 в крайнем левом бите означает отрицательное число. Так как это в дополнении до 2, мы вычитаем из него 1, чтобы получить нотацию дополнения до 1 11111101. Переворачивая биты, мы получаем 00000010 или 2, что означает, что наш результат равен -2 в нотации дополнения до 2.

При выполнении двоичных операций важно знать используемое соглашение, чтобы выполнить операцию в соответствии с применимыми правилами.

Деление

Двоичное деление аналогично десятичному. Единственное отличие состоит в том, что в десятичной системе, поскольку мы делим традиционные числа, делимое (или его часть) может быть 0, 1 или более чем в 1 раз больше делителя. Однако в двоичном формате это может быть только 0 или 1 раз, то есть делимое (или его часть) >= или < делителя.

Давайте попробуем разделить 6 на 3. Двоичное число 6 равно 110, а это или 3 равно 11. Следуя соглашению о десятичном делении

Мы проверяем часть дивиденда слева от него, которая >= делителя.
Затем мы вычитаем кратное делителю, которое равно <= части делимого.

РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7