Умножение и деление десятичных дробей

Умножение

Умножение десятичных дробей сводится к умножению соответствующих натуральных чисел, и правильному определению места запятой в полученном результате.

Пример. Найти произведение чисел  2,13  и  1,2.

Решение: можно перемножить числа  2,13  и  1,2,  заменив их обыкновенными дробями:

2,13 · 1,2	=	2	13	·	1	2	=	213	·	12	=
			100			10		100		10

=	213 · 12	=	2556	= 2,556.
	100 · 10		1000

Можно сказать, что мы перемножили натуральные числа, которые получатся если у данных десятичных дробей отбросить запятые. Так как знаменатели тоже перемножаются, то в знаменателе вышло число с тремя нулями, а в соответствующей десятичной дроби — три цифры после запятой. Значит в результате умножения двух десятичных дробей, ответ будет содержать столько знаков после запятой, сколько их было в обоих множителях вместе.

Данное произведение можно посчитать и столбиком, заменив дроби на натуральные числа:

Из рассмотренного примера можно сделать вывод, что:

Чтобы перемножить две десятичные дроби, достаточно перемножить их как натуральные числа, и в полученном произведении отделить справа запятой столько знаков, сколько их было в множимом и множителе вместе.

Данное правило работает и для умножения десятичной дроби на натуральное число. Только в случае, когда один из множителей — натуральное число, количество десятичных знаков в результате будет равно количеству знаков дробного множителя.

Пример.

Найти произведение чисел  4,324  и  11:

Решение:

4,324 · 11 = 47,564.

Деление

Чтобы разделить десятичную дробь на целое число, нужно сначала разделить целую часть (если она есть), затем поставить запятую в неполном частном и приступить к делению дробной части:

В этом примере мы сначала разделили  13  на  4  и записали в частное  3,  затем мы поставили в частном запятую, так как у нас в остатке осталась единица, которую на  4  мы уже поделить не могли, затем мы продолжили делить дробную часть. Особенность этого примера заключается в том, что когда мы получили в частном  9  сотых, то обнаружили остаток, равный  2  сотым, мы раздробили этот остаток на тысячные доли, получили  20  тысячных и довели деление до конца.

Чтобы разделить десятичную дробь (или целое число) на десятичную дробь, нужно в делимом и в делителе перенести запятую на столько цифр вправо, сколько их после запятой в делителе, после чего выполнить деление по правилу деления на целое число.

В качестве примера разделим  72,9  на  0,09:

Также можно осуществить деление десятичной дроби (или целого числа) на десятичную дробь, представив оба числа в виде обыкновенных дробей:

Таким образом, частное двух десятичных дробей всегда можно записать в виде обыкновенной дроби.

Математика, Умножение и деление столбиком — образование детей онлайн

Умножение и деление в столбик

Ребёнок испытывает трудности при умножении и делении больших чисел в уме, поэтому, гораздо удобнее выполнять эти действия особенным способом – делением и умножением в столбик. У этого метода есть свои правила написания и последовательность.

Для начала, нужно запомнить, как называется каждое число при делении и умножении.  

Компоненты при делении называются: 

• a — «делимое» (число, которое нужно разделить),
• b — «делитель» (число, на которое нужно разделить) и c — «частное» (ответ, который получается при делении делимого на делитель) A : B=C

Компоненты при умножении называются: умножаемые друг на друга числа называются «множителями» (A х B), а ответ при умножении называется «произведением» (=C).

Чтобы ребёнок усвоил тему деления, предложите ему поиграть в игру. Попросите ребёнка разделить конфеты поровну на каждого члена семьи, или между друзьями. Он запомнит, что делить нужно таким образом, чтобы всем досталось одинаковое количество конфет.

Напишите пример деления в столбик на листе бумаги. Покажите, как именно он должен быть записан. Сначала в одной строке слева направо записываются делимое и делитель, после чего между ними нужно провести черту.

Умножение

Для записи примера на умножение в столбик нужно записать друг под другом. Наибольшее число всегда нужно записывать наверху, а меньшее – под ним. Слева сбоку между числами всегда ставим знак умножения «х», и снизу подводим числа прямой чертой, под которую записываем ответ – произведение.

Например: 315х5=1575

Умножаем поочерёдно каждую цифру верхнего компонента на последнюю цифру нижнего – с права налево. То есть, 5 на 5, затем 5 на 1, и 5 на 3. Если при умножении каждого компонента получается большое число, то под чертой мы записываем только последнюю его цифру.

Например, 5х5=25 Под чертой записываем 5, а двойку запоминаем, или записываем над примером, чтобы не забыть. При умножении 5 на 1, получаем ответ – 5. Прибавляем к нему двойку от предыдущего ответа, и получаем 7. Записываем 7 под черту. 5х3=15. Ответ – 1575

Освоив умножение и деление столбиком, ребёнку будет  легче проверять свои ответы обратным путём. Если он проверяет ответ при делении, ему необходимо умножить частное на делитель, и если ответ равен делимому, значит, решение верное. Так же он может проверить результат умножения. Разделив произведение на один из множителей, чтобы получить ответ равный второму множителю.

Умножение и деление в столбик

Описание

Примеры на умножение и деление в столбик решать просто. Но они требуют концентрации и внимания, особенно для очень торопливых детей. Практика счета таких примеров поможет развить внимательность и закрепить навыки счета больших чисел, а также добиться автоматизированного счета.

Программа представляет собой тренажер для счета. Она имеет внутренние настройки, изменяя которые можно создать примеры на умножение и деление в столбик  для детей разного возраста и уровня подготовки:

• Умножение на однозначное, двузначное или  трехзначное число,
• Деление на однозначное, двузначное или трехзначное число.

Поэтому программа будет полезна как для учеников начальной школы 3-4 классов, так и для более старших классов.

Программа счета написана в Excel с помощью макросов. Формируются примеры на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. При записи примеров разряды чисел формируются друг под другом, что позволяет легко ориентироваться в примерах.

В конце карточки формируются ответы на примеры, которые после печати карточки можно отрезать. Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.

Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.

Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы.
Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.

Другие программы, которые помогут закрепить навыки счета:

 Также есть программы, в которых можно выбрать уровень сложности. В них можно начать с решения легких примеров, а затем перейти к более сложным.

На сайте представлен каталог программ, в котором все программы распределены по группам с указанием различий в программах внутри каждой группы. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Калькулятор умножение в столбик онлайн

Не секрет, что знакомство с математикой начинается с важнейшей науки о числах — арифметики. Как утверждал великий ученый М. В. Ломоносов, с арифметикой мы входим «во врата учености», именно с нее начинается нелегкий, но заманчивый путь познания мира. Эта наука изучает числа и действия над ними. Одним из таких действий над цифрами является умножение столбиком. Без ясного понимания последовательности действий при совершении умножения двух чисел в математике нельзя двигаться дальше. Следует знать, что числа, которые умножаются, называются множителями, а полученный результат — произведением. В числах имеются разряды, самый маленький — единицы, затем десятки, после них сотни и т. д. Если вы умножаете в столбик, расположите оба множителя друг над другом, чтобы совпадали разряды чисел. Большее число расположите в верхней строке, меньшее — в нижней. Если оба множителя или один из них имеют на концах нули, то числа располагают так, чтобы цифры наименьшего разряда (кроме 0) находились в одном столбике. Нули в поле поэтапных операций не заносятся, они переносятся под черту в конечный результат. Это делается потому, что при умножении любого числа на 0, все равно получается 0.

Слева от множителей ставим «х». Умножение в столбик — поразрядное умножение. Это значит, что каждый разряд 1-го множителя, начиная с последней цифры, умножается на последнюю цифру 2-го множителя. Следующей строкой будет результат умножения верхнего числа (1-го множителя) на следующую цифру нижнего числа (2-го множителя). Следует помнить, что полученный после умножения на вторую цифру результат, следует размещать под второй цифрой полученного результата от первого умножения. Поэтапные произведения (разрядные) складываются по разрядам, результат заносится под черту, начиная с самой правой стороны. Слева от полученных произведений, которые складываются, ставим «+».

Онлайн калькулятор поможет вам быстро и правильно выполнить умножение столбиком.

Урок математики на тему «Умножение и деление столбиком 102*3, 306:3 » 3 класс

1. Краткосрочный план урока 133.

2. ІІІ четверть 4А Письменное умножение и деление

3. Математика 3 класс. Учебник А. Б. Акпаева, Л. А. Лебедева, М. Ж. Мынжасарова,

4. Т. В. Лихобабенко. Издательство Алматыкiтапбаспасы 2018

Предмет: математика

Класс: 3 Д

Школа:

КГУ «Школа-лицей №7 им. Н.Марабаева»

Дата: 05.04.2019 г.

Тема урока: Умножение и деление столбиком 102 3, 306 :3

В контексте сквозных тем «Вода – источник жизни», «Культура отдыха. Праздники»

ФИО учителя: Литовка И.П.

Количество присутствующих:

Количество отсутствующих:

Цели обучения (ЦО) из долгосрочного плана

3. 1.2.13 применять алгоритм деления трехзначного числа на однозначное, когда в одном из разрядов частного есть нуль и алгоритм обратного действия — умножение

Цели урока

Применять алгоритм деления трехзначного числа на однозначное, когда в одном из разрядов частного есть нуль и алгоритм обратного действия — умножение

Критерий оценивания

Учащиеся применяют алгоритм деления трехзначного числа на однозначное, когда в одном из разрядов частного есть нуль и алгоритм обратного действия — умножение

Академический язык

Предметная лексика и терминология: произведение, частное

Полезные слова и сочетания для диалога и записи:

— Что значит цифра 0 в разряде?

— результат произведения любого числа и 0 – это…

— если 0 разделить на любое число, получится….

Формирование ценностей

Задачи по формированию ценностей:

ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни

Межпредметные связи

Естествознание, познание мира

Навыки использования ИКТ

Возможно применение демонстрации в виде презентации

Предыдущие знания

Алгоритм письменного умножения и деления

Ход урока

Запланирован-ные периоды урока

Деятельность учащихся на уроке

Ресурсы

Начало урока

0 — 9

Канва урока «Значение воды для растений».

Актуализация имеющихся знаний.

Геометрическая задача

Каждая пара получает иллюстрацию задачи. Задание: решить задачу по указанному на интерактивной доске алгоритму выполнения, представить решение. ФО «Аплодисменты».

Ребята, у вас на столах лежат листы с геометрическими задачами: изображения прямоугольника и квадрата. Предлагаю вам выполнить практическую работу в парах, план работы на экране (слайд 2)

1. Измерьте стороны фигур и найдите площади.

Площадь какой фигуры больше и на сколько?

Контролирует выполнение работы. Оцените себя и работу в паре.

Открытие нового знания.

Учитель:

— Отчего зацвел цветок? —

Мальчик спрашивает мать.

— Оттого, что мы цветок

Не ленились поливать.

Ф. Троицкий

Беседа: — Какое значение имеет вода в жизни растений?

Проблемная ситуация.

Задача: Для полива клумбы нужно каждый день 104 литра воды. Сколько воды нужно для полива клумбы на два дня.

Ребята объясняют свой вариант алгоритма умножения. Работы сравниваются, коллективно объясняется способ умножения. ФО «Аплодисменты».

Определения темы урока и цели, которые необходимо достичь в процессе работы.

Карточки с заданием

Алгоритм на доске.

Слайд 2.

Слайд 3.

Слайд 4.

Задача на слайде 6.

Объяснить решение. Слайд 7.

Слайд 8.

Середина урока

10 –19

20 – 22

23– 37

Работа по учебнику стр. 9 – 11.

К. Анализ способа умножения и деления — коллективно. Учитель обращает внимание учеников на применение сокращенной записи при делении числа, в записи которого есть ноль (если первое неполное делимое разделено без остатка).

П. Задание 3. Ученики выполняют вычисления в парах с комментированием. Проверка ответов по цепочке.

Самооценивание по критериям:

Всё верно:

Одна неточность:

Нужна помощь:

Физминутка

Вместе по лесу идём,

Не спешим, не отстаём.

Вот выходим мы на луг.

(Ходьба на месте.)

Тысяча цветов вокруг!

(Потягивания — руки в стороны.)

Вот ромашка, василёк,

Медуница, кашка, клевер.

Расстилается ковёр

И направо, и налево.

(Наклониться и коснуться левой ступни правой рукой, потом наоборот — правой ступни левой рукой.)

К небу ручки протянули,

Позвоночник растянули.

(Потягивания -руки вверх.)

Отдохнуть мы все успели

И за парты снова сели.

(Дети садятся за парты.)

Г. Задание 4 (а). Работа в группах – учащиеся анализируют задачу, записывают решение без выполнения краткой записи на ламинированных листах. Группа, которая выполнит решение, поднимает свой лист. В случае разногласий, проводится коллективный разбор.

Проверка:

а) 7 100 = 700 тонн воды

б) 120 5 = 600 литров воды

в) 900 : 3 = 300 литров воды.

К.Задание 5.Математика в жизни. Коллективное решение задачи.

Ход рассуждения: чтобы узнать расход воды, надо узнать количество кочанов капусты. Для этого нужно узнать площадь части огорода (грядки с капустой).

Исходя из плана участка, находим сторону грядки квадратной формы – 2 м.

Решение задачи:

1. 2 2 = 4 – S грядки

2. 4 2 = 8 кочанов капусты

3. 8 101 = 808 (л)

Ответ: 808 литров воды.

П.Задание – исследование 6. Ученики в парах проводят анализ одной задачи на выбор, определяют лишние для решения задачи данные, выполняют решение. Затем пары меняются работами для проверки и взаимооценки.

ФО «Звёздочка».

Дополнительные задания.

И.Самостоятельная работа. Дифференциация.

(1,2 уровень парами, 3 уровень – самостоятельно).

К. Дополнительные задания.

Слайд 9.

Критерии самооценивания.

Школа

физминуток

В.И. Ковалько

http://rabuny.edu.minskregion.by/gallery/123/fizkultmin.pdf

Ламинированные листы, маркеры

тетради

Листы А3, маркеры.

Конец урока

38 — 40

Рефлексия урока. Полянка успеха.

Усвоил, тема понятна – желтый

Тема понятна, но требует закрепления – оранжевый

Не усвоил тему — красный

Домашнее задание. Стр. 11 № 8. Учащимся уровня 3 дополнительное задание стр. 10 № 4 (б,в).

На доске зеленая полянка.

Стикеры цветов разного цвета для рефлексии

Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?

Здоровье и соблюдение техники безопасности

Дифференциация:

1. Выполнение дополнительных заданий (самостоятельная работа по карточкам трёх уровней).

2. Домашняя работа.

На уроке – ФО работы групп, пар.

Диагностировать степень усвоения учебного материала поможет проверка дифференцированных заданий, анализ учителем рефлексии.

Соблюдение ТБ. Физминутка

Деление столбиком и умножение столбиком worksheet

Advanced search

Content:

Language: AfarAbkhazAvestanAfrikaansAkanAmharicAragoneseArabicAssameseAsturianuAvaricAymaraAzerbaijaniBashkirBelarusianBulgarianBihariBislamaBambaraBengali, BanglaTibetan Standard, Tibetan, CentralBretonBosnianCatalanChechenChamorroCorsicanCreeCzechOld Church Slavonic, Church Slavonic,Old BulgarianChuvashWelshDanishGermanDivehi, Dhivehi, MaldivianDzongkhaEweGreek (modern)EnglishEsperantoSpanishEstonianBasquePersian (Farsi)Fula, Fulah, Pulaar, PularFinnishFijianFaroeseFrenchWestern FrisianIrishScottish Gaelic, GaelicGalicianGuaraníGujaratiManxHausaHebrew (modern)HindiHiri MotuCroatianHaitian, Haitian CreoleHungarianArmenianHereroInterlinguaIndonesianInterlingueIgboNuosuInupiaqIdoIcelandicItalianInuktitutJapaneseJavaneseGeorgianKongoKikuyu, GikuyuKwanyama, KuanyamaKazakhKalaallisut, GreenlandicKhmerKannadaKoreanKanuriKashmiriKurdishKomiCornishKyrgyzLatinLuxembourgish, LetzeburgeschGandaLimburgish, Limburgan, LimburgerLingalaLaoLithuanianLuba-KatangaLatvianMalagasyMarshalleseMāoriMacedonianMalayalamMongolianMarathi (Marāṭhī)MalayMalteseBurmeseNauruanNorwegian BokmålNorthern NdebeleNepaliNdongaDutchNorwegian NynorskNorwegianSouthern NdebeleNavajo, NavahoChichewa, Chewa, NyanjaOccitanOjibwe, OjibwaOromoOriyaOssetian, OsseticEastern Punjabi, Eastern PanjabiPāliPolishPashto, PushtoPortugueseQuechuaRomanshKirundiRomanianRussianKinyarwandaSanskrit (Saṁskṛta)SardinianSindhiNorthern SamiSangoSinhalese, SinhalaSlovakSloveneSamoanShonaSomaliAlbanianSerbianSwatiSouthern SothoSundaneseSwedishSwahiliTamilTeluguTajikThaiTigrinyaTurkmenTagalogTswanaTonga (Tonga Islands)TurkishTsongaTatarTwiTahitianUyghurUkrainianUrduUzbekValencianVendaVietnameseVolapükWalloonWolofXhosaYiddishYorubaZhuang, ChuangChineseZulu    Subject:   

Grade/level:    Age: 3456789101112131415161718+

Search: All worksheetsOnly my followed usersOnly my favourite worksheetsOnly my own worksheets

Решение примера столбиком 64 6.

Деление столбиком. Игра «Быстрое сложение»

Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?

Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.

Я уже писала о том, Эта статья может стать для вас полезной.

Осваиваем операцию разделения (деления) на части в игровой форме

На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.

Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.

Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.

Умножаем и делим, используя таблицу умножения

Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.

Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.

Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.

Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!

По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.

Делим столбиком – приведем пример

Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.

Объясняем наглядно

Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.

Шаг 1 . Записываем числа, разделив их «уголком».

Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.

Шаг 3. Переходим к оформлению деления столбиком:

Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.

Записываем результат.

Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.

Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.

Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.

Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.

Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.

Как научить ребенка делению – закрепляем навык

Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.

1. «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
2. «Деление. Уровень 4. Рабочая тетрадь» от Kumon
3. «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров

Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.

Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.

Для того чтобы легко научить ребёнка операции деления нужно:

• Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
• Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.

Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.

Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт

Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:

Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.

После прохождения курса ребенок сможет:

1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Для деления чисел из двух и более цифр (знаков) применяют деление в столбик .

По традиции, разбираться как делить столбиком будем на примере.

Вычислить:

Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:

Их частное (результат) будем записывать под делителем. У нас это цифра «8 ».

Начинаем делить «512 » на «8 » следующим образом:

1. Определяем неполное частное . Для этого слева направо сравниваем цифры делимого и делитель.

   Берём «5 ». Цифра «5 » меньше «8 », значит нужно взять еще одну цифру из делимого.

2. «51 » больше «8 ». Значит это неполное частное. Ставим точку в частном (под уголком делителя).

   Запомните!

   Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.

   Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас после «51 » стоит только одно цифра «2 ». Значит и добавляем в результат ещё одну точку.

3. Приступаем к делению. Вспоминая таблицу умножения на «8 », находим ближайшее к «51 » произведение.
   «6 · 8 = 48 »
   Записываем цифру «6 » в частное.

   Записываем «48 » под «51 ».

   Запомните!

   При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.

   Между «51 » и «48 » слева поставим «− » (минус). Вычтем по правилам вычитания в столбик «48 » и под чертой запишем результат.

4. В остатке получилось «3 ». Сравним остаток с делителем. «3 » меньше «8 ».

Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .

Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:

За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:

Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:

Под делимым будут записываться промежуточные вычисления:

Полностью форма записи деления столбиком выглядит следующим образом:

Как делить столбиком

Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:

В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.

К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.

Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.

Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:

Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:

Деление столбиком с остатком

Пусть нам требуется разделить 1340 на 23.

Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:

Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:

Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:

1340: 23 = 58 (остаток 6)

Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:

3: 10 = 0 (остаток 3)

Калькулятор деления столбиком

Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.

Как научить многозначному умножению и длинному делению

Узнайте, как лучше всего научить многозначному умножению и делению в столбик. Эта дифференцированная стратегия помогает учащимся 3-го, 4-го, 5-го и специального образования.

Если вы ищете лучшие стратегии для обучения многозначному умножению и делению в столбик, вы нашли отличное место для начала. Это самых простых методов обучения студентов. Лучше всего они работают с учениками 4-го класса, учениками 5-го класса, учащимися из групп риска, борцами и учащимися специального образования — ВСЕ УЧАЩИЕСЯ !

Этот визуальный метод действительно работает почти для каждого студента!

Несколько лет назад обучение алгоритмам умножения и деления в столбик имело для меня ОГРОМНЫЙ ФАКТОР УЖАСОВ.Традиционные методы, которые я использовал, просто не работали.

Мои ученики забыли ступеньки. Они запутались, они не могли выровнять свои числа и — они не могли даже прочитать свои собственные письма!

Стратегии умножения и деления в столбик Shape Math ™

Я знал, что должен быть способ получше. Короче говоря, я не мог найти лучшего способа. Итак, я разработал собственную стратегию, и я назвал ее Shape Math ™.

Я обучал этой стратегии многозначного умножения и длинного деления в своем классе в течение многих лет, и я получил ФАНТАСТИЧЕСКИЕ отзывы от других учителей об их успехах в использовании!

Рабочий лист умножения с помощью органайзера двузначного умножения

Об организаторах

Методы Shape Multiplication ™ и Shape Division ™ используют форм и цветов , чтобы помочь учащимся запомнить последовательность шагов.

Формы и цвета помогают студентам решать задачи до тех пор, пока они не освоятся с процессом. В конце концов, органайзер им больше не понадобится. Это очень визуальный процесс , который работает для многих студентов, в том числе для тех, кто борется!

Органайзеры для умножения выглядят так:

А вот органайзер для задач с длинным делением:

Как я Явно Обучаю этим стратегиям

Для сложных типов уроков я обычно использую SmartBoard перед классом, за которым следует помощь в небольших группах или индивидуальная помощь.

Инструкция для всей группы

Я представляю органайзер и предлагаю своим ученикам обратить внимание на разные формы и цвета. Мы говорим о том, как разные формы и цвета помогают нам при решении длинных математических задач.

Я начинаю анализировать то, с чем студенты уже знакомы, например, решение задачи с двумя цифрами на одну цифру, составленную в этом стиле. После беглого обзора я перехожу к подробному обучению тому, как решать задачу многоэтапного умножения с помощью органайзера.

Я прямо объясняю свои мысли вслух, чтобы студенты могли их услышать. Я говорю что-то вроде: «Мне нужно умножить 5 в треугольнике единиц на 3 в круге». Я не забываю указывать на формы и заполнять органайзер, когда говорю.

Студенты наблюдают за процессом несколько раз, пока я начинаю задавать вопросы о последовательности шагов.

Круги переходят в круги; Квадраты сочетаются с квадратами

На фотографии ниже вы можете видеть, что любая цифра, умноженная на 3 в красном кружке, дает продукты, указанные в красных кружках под цифрой 3.Вот почему я постоянно повторяю: «Круги идут с кругами».

Цифры, умноженные на 2 в синем квадрате, дают продукты, указанные в синих квадратах на органайзере. Вот почему я снова и снова повторяю: «Квадраты идут с квадратами».

Это более старая фотография — в органайзерах больше не используются треугольники

Во время обучения я звучу как зарезанная пластинка, постоянно повторяю: «Круги идут кругами; квадраты идут с квадратами ». Это работает, даже если вы дифференцируете, удаляя цвета и используя органайзер черно-белых фигур.

Многоразовые пластиковые рукава привлекают студентов и экономят бумагу!

Групповое / индивидуальное обучение

Пока я нахожусь у Smartboard, ученики вместе со своими организаторами следят за ними на своих местах. Студенты с удовольствием используют органайзеры, помещенные в прозрачные пластиковые рукава с маркерами для сухого стирания.

Затем мы переходим от обучения в группе к студентам, работающим над заданием самостоятельно.

Пока ученики работают, я быстро прогуливаюсь по классу и замечаю, что ученики выглядят сбитыми с толку.Вот когда я обычно либо собираю студентов в небольшую группу за задним столиком, либо предлагаю индивидуальную помощь.

Многоразовые прозрачные пластиковые рукава

Мне нравится использовать эти потрясающие рукава для сухого стирания ( Щелкните здесь, чтобы увидеть похожие рукава для сухого стирания на Amazon ). Мне они очень нравятся, и я использую их почти каждый день по-разному для разных предметов.

Shape Math ™ использует цвета и формы для различения

С помощью органайзеров и рабочих листов, включенных в наборы Shape Math, вы сможете легко отличить друг от друга.Универсальность действительно позволяет подобрать необходимый уровень помощи для уникальных потребностей каждого учащегося.

Как отличить друг от друга с помощью органайзеров

Увеличьте объем помощи для учащихся, нуждающихся в максимальной поддержке, используя как цвета, так и формы. По мере того, как учащиеся улучшают свои навыки, уменьшайте поддержку, удаляя цвета и вводя заранее подготовленные рабочие листы.

В конце концов, вы можете исключить как формы, так и цвета и использовать прилагаемые листы миллиметровой бумаги.Когда придет время, студенты могут перейти к базовому алгоритму умножения или деления без цветов, форм или миллиметровой бумаги.

Варианты строительных лесов, предлагаемые в этих пакетах, повышают уверенность и вовлеченность учащихся. Уверенность и заинтересованность вызывают азарт, гордость и желание учиться!

Органайзеры разного размера с разными цветами и формами легко отличить друг от друга.

Наборы умножения и деления включают в себя органайзеры разных размеров.Предварительно разработанные рабочие листы позволяют вам выбрать подходящее время для ознакомления с более сложными навыками.

Типовые леса

Прогресс обычно включает:

• Устранение цвета на органайзерах
• Устранение форм, которое устраняет органайзеры
• Переход на миллиметровую бумагу
• Переход от миллиметровой бумаги к независимости.

Добавление или удаление цвета форм обеспечивает различные уровни строительных лесов

На картинке выше я изначально убрал цвета для этого ученика.Я заметил, что ему очень трудно без цветов, поэтому я использовал маркеры, чтобы снова добавить цвета для него. Есть много способов помочь вашим ученикам оказать помощь нужного уровня.

Вы выбираете подходящее время, чтобы убрать цвета с органайзеров с конечной целью полностью устранить организатора. Затем учащиеся могут перейти на рабочие листы с миллиметровой бумагой, прежде чем они перейдут к самостоятельности без органайзеров или миллиметровой бумаги.

Якорные диаграммы в классе

Я ОБОЖАЮ якорные диаграммы — их легко сделать, и ЗАМЕТНЫЕ справочные инструменты! Ниже приведена таблица привязки умножения, которую я использую и показываю своим ученикам в качестве справочника.

Схема привязки 2-значного умножения Якорная диаграмма с помощью визуального органайзера с цветами и формами

Диаграмма якоря длинной секции

Я начал использовать это мнемоническое устройство с хорошим оле ‘ McDonald’s:

• (разделить)
• McDonald’s (умножить),
• подать (вычесть),
• сыр (проверить),
• бургеры (подавить
• ), (повторить и начать заново).

Раньше я хранил в своей комнате схему привязки Division Family (на фото ниже) в качестве ориентира, чтобы напоминать студентам о шагах. Но семьи могут выглядеть по-разному, поэтому я перешел на мнемоническое устройство McDonald’s.

• Папа , (Разделить)
• Мамочка (Умножить),
• Сестра (Вычесть),
• Brother (Bring Down),
• Rover (Повторить и начать сначала).

Иногда в начале урока математики у меня возникает задача, например, утренняя работа.

Как только учащиеся усваивают правила деления в столбик, я меняю числа на стикерах. Я изо всех сил стараюсь, чтобы он соответствовал цвету, но, ну, жизнь случается! Наличие диаграммы привязки Sticky-Note делает изменение проблем более простым и увлекательным. В стикерах есть что-то, что нравится студентам.

И последняя мысль о таблицах привязок с липкими заметками. Студентам нравится, когда их поручают менять числа.Им нравится руководить этой работой.

Мне бы хотелось услышать, как вы используете стикеры в классе!

статей о многозначном умножении:

Статьи о длинном дивизионе:

• Дифференцированные рабочие листы с длинным разделением БЕСПЛАТНО — Получите эти дифференцированные рабочие листы с длинным разделением БЕСПЛАТНО и значительно повысьте успехи учащихся и ваши успехи в преподавании!
• Миллиметровая бумага Math Intervention — В этой статье блога объясняется, как использовать миллиметровую бумагу в качестве быстрого и легкого ресурса для вмешательства с вашими учениками.Он включает ссылки на бесплатную печатную миллиметровку и идеи о том, как использовать ее в классе.

Длинный дивизион Ресурсы:

Если вы нашли эту статью полезной, подпишитесь на меня в моем Teachers Pay Teachers Store , Pinterest и Facebook ! Я был бы рад услышать от вас!

Связанные

Стандартный алгоритм | CoolMath5Kids

Первое, что мы делаем, это меняем способ написания задачи. ..

Первый математический шаг — посмотреть на первое число парня, на которого мы делим … это 6. Это шаг деления!

Умножьте 3 и 2 и поместите ответ прямо под 6:

Вот третий шаг … Это шаг вычитания!

Выполните вычитание … Это 6-6 = 0

Эй, мы только что закончили первый этап шагов! И это было не так уж и плохо!

Деление, затем умножение, затем вычитание.
Назовем это петлей DMS!
Эй, эти буквы идут по алфавиту !! Вы можете использовать это, чтобы запомнить это!

Хорошо, теперь мы сделаем то же самое, но с другим номером …

Первое: Перетащите 8 вниз.

Теперь вернемся к нашему циклу деления, умножения и вычитания с использованием восьмерки!

Отдел: Мы хотим увидеть, сколько раз 2 превратится в 8… 2 переходит в 8 четыре раза … Итак, мы помещаем это 4 прямо над 8:

Умножение: Умножьте 4 и 2 и поместите ответ прямо под 8:

Вычитание: Это 8-8 = 0

Угадайте, что? Мы сделали! (Ни за что.) СПОСОБ!

Мы использовали 6 и 8 . .. и закончили с 0 внизу … Который я превратил в «счастливое лицо «, потому что я был так счастлив, что все готово! Ответ — 34.

Итак, мы выполняем наш цикл DMS (деление-умножение-вычитание) до тех пор, пока мы не используем все числа в парне, на которое мы делимся (этот тип официально называется делимым).

У нас есть два способа проверить правильность нашего ответа:

1)	Возьмите калькулятор и разделите 68 на 2.
2)	Используйте умножение! Помните, что деление и умножение идут рука об руку … Они уничтожают друг друга! Итак, 34 x 2 должно = 68! Это отличная практика для вас.

Давайте сделаем еще много… Перейдите на следующую страницу, чтобы сделать еще одну!

Песня Numberock’s Long Division | Разделить, умножить, вычесть, сбить

Песня с длинным делением решает проблему с однозначным делителем и трехзначным дивидендом и выходит с остатком. В анимации есть очень запоминающаяся песня, которая понравится детям и, что еще более важно, запомнится. Разделить, умножить, вычесть, сбить. Вот как находится частное. Добро пожаловать в разделение на длинные позиции, которое стало проще, поскольку мы шаг за шагом проходим процесс.

Текст песни:

Пять групп по пять штук — 29
Их произведение — 25
Поместите 5 над линией
Сверху за чертой
Затем нарисуйте знак вычитания
и напишите 25
Разница — четыре, и есть еще один шаг
Принесите восьмерку Вниз рядом с четырьмя

Разделить, умножить, вычесть, сбить
Вот как находится коэффициент

Разделите 48 на группы по пять
Вы обнаружите, что их девять.
Поставьте девять над линией
и умножьте девять на пять
Затем нарисуйте знак вычитания
и напишите 45
Осталось три
Итак, напишите наши три
Вот как легко может быть деление

Разделить, умножить, вычесть, сбить
Вот как находится коэффициент

Делить, умножать, вычитать, сбрасывать
Вот как находится коэффициент!

И когда есть остаток,
Напишите R, за которым следует то, что осталось больше
Вот как находится коэффициент!

Узнать больше

Эта песня ориентирована на стандарты обучения TEKS и Common Core как для 4-х, так и для 5-х классов. Ознакомьтесь с соответствующими стандартами здесь или более подробно о делении на длинные позиции здесь.

Если вы заинтересованы в том, чтобы получить идеи о том, как спланировать надежный урок, связанный со стандартами, мы рекомендуем ознакомиться с рекомендациями Instructure по общим базовым стандартам 4.NBT.6 и 5.NBT.6. Эти страницы помогают разбить стандартный язык, определить соответствующий классу уровень строгости для каждой концепции и предлагают различные предложения по занятиям (семенам уроков), которые помогают учащимся достичь своих учебных целей.

Чтобы продолжить просмотр библиотеки материалов по математике Numberock, щелкните здесь. Чтобы получить доступ к растущей библиотеке премиум-контента Numberock, щелкните здесь.

Урок шестого класса Большое умножение и длинное деление

Я расскажу ученикам, что со временем учителя и ученики разработали разные способы запоминания алгоритма деления. Я разработал свой собственный метод на основе анимационных сериалов «Симпсоны», которыми я поделюсь. Большинство студентов знают о семье Симпсонов, поэтому я начну с опроса студентов об их знаниях.

Кто такой Гомер Симпсон? Кто такая Мардж Симпсон? Кто такая Лиза Симпсон? Кто такой Барт Симпсон? У них есть собака?

Вопросы вызовут некоторое волнение на предстоящем уроке. Кроме того, опрос гарантирует, что все учащиеся хотя бы знакомы с персонажами шоу. Студенты знают, что имя собаки не Ровер, но я объясню, что мы будем использовать более легкое имя для запоминания.

Я буду моделировать пример с семьей Симпсонов, указывающей нам, что делать.Я покажу направления на доске. (см. Подразделение Симпсонов)

Пример 1: 9632/4

Папа, Гомер, говорит нам: сначала разделите . Сколько раз можно разделить 4 на 9?

Мама, Мардж, говорит нам: умножить на . Что такое произведение 4 на 2?

Сестра, Лиза, говорит нам: вычесть чисел.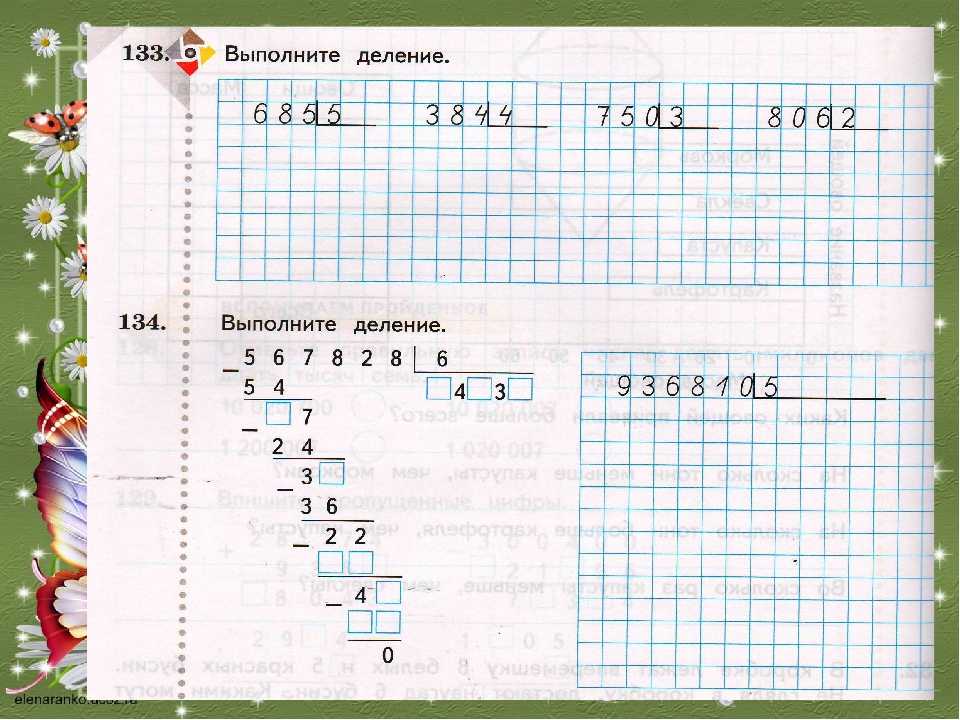 В чем разница между 9 и 8?

Брат, брат, говорит нам, что нужно понизить до следующего числа в дивиденде.

Ровер говорит нам повторить процесс. Если в дивиденде больше нет чисел, Ровер сообщает нам, что у нас есть остаток.

Доделаю задачу классом.

Какими различными способами мы можем проверить частное, наш ответ?

Важно отметить, что даже студенты, которые привыкли к своим таблицам умножения, совершают ошибки, потому что их работа с длинным делением не организована.Я буду поощрять студентов организовывать свою работу, используя столбцы для разделения значений мест.

Освоение математики в 5-м классе — Том 4

• Учитесь с помощью , решая проблемы шаг за шагом.
• Быстро улучшайте навыки и повышайте на оценки.
• Прочтите о нашей гарантии возврата денег!

Этот курс доступен для загрузки

Цена загрузки: $ 14.99

Урок 1: Порядок операций
Урок 2: Написание и интерпретация выражений
Урок 3: Шаблоны и упорядоченные пары
Урок 4: Десятичный разряд
Урок 5: Умножение на 10
Урок 6: Разделите на 10 разрядов
Урок 7: Сравнение десятичных знаков
Урок 8: Округление десятичных дробей

Урок 9: Умножение целых чисел
Проблемные слова урока Целые числа
Урок 11: Разделите на однозначный делитель
Урок 12: Разделите на двухзначный делитель
Урок 13: Задачи со словами — деление целых чисел

---

Попробуй курс!

Просмотрите урок № 1 ниже, затем загрузите рабочие листы для этого урока

Практика навыков! — Загрузите рабочий лист этого урока

(Ответы на все листы, включенные в курс)

---

Подробное описание

Освойте математику в 5-м классе с пошаговыми видео-уроками! Математика — сложная тема для большинства студентов, но обычно это происходит потому, что большинство студентов не имеют хорошей базы в фундаментальном материале.Самый простой способ овладеть мастерством — это не только практика, но и пошаговые инструкции.

В этой серии видео ученик выучит каждую тему с помощью пошаговых видеоуроков, которые проводит Джейсон Гибсон, который помог тысячам учеников овладеть математикой на всех уровнях. Секрет в том, чтобы никогда не пропускать никаких шагов при обучении ученика любой концепции — даже самой элементарной.

Джейсон проводит студента по материалу с многочисленными примерами задач, объясняя каждый шаг на этом пути.Каждая последующая задача сложнее предыдущей, и быстро ученик увидит, что каждая концепция полностью понятна. Обладая такой уверенностью, ученик добьется успеха.

Последней частью головоломки является то, что учащемуся также предоставляются рабочие листы для проверки мастерства по каждой теме. Эта комбинация пошагового обучения и практических заданий — самый быстрый и простой способ для любого ученика овладеть математикой!

Приглашаем вас прочитать наши отзывы!

ПОЧЕМУ РАБОТАЕТ ДОЛГОСРОЧНОЕ ПОДРАЗДЕЛЕНИЕ?

Введение

Студенты сначала знакомятся с концепцией умножения с помощью таблиц умножения, затем задают прямые вопросы и задачи.Позже их учат концепции разделения, которую они опровергают.

В конце концов, когда обе концепции объединяются, они путаются.

Деление в столбик — один из таких методов, в котором используются концепции деления, умножения и вычитания. Когда эти многие базовые концепции интегрированы, они обязательно столкнутся с некоторыми трудностями при их изучении.

Вместо того, чтобы просто изучать деление, учащиеся должны понимать использование деления, значение делителей, дивидендов и кратных.

В этой статье мы покажем вам, почему работает метод деления в столбик и как умножение дополняет этот процесс.

---

ПОЧЕМУ РАБОТАЕТ ДОЛГОСРОЧНОЕ ПОДРАЗДЕЛЕНИЕ?

Длинное деление — это стандартный алгоритм деления, подходящий для деления многозначных чисел, который достаточно просто выполнить вручную. Он разбивает задачу разделения на ряд более простых шагов.

ПОЧЕМУ РАБОТАЕТ ДОЛГОСРОЧНОЕ ПОДРАЗДЕЛЕНИЕ? упоминается ниже в загружаемом PDF-файле.

📥

ПОЧЕМУ РАБОТАЕТ ДОЛГОСРОЧНОЕ ПОДРАЗДЕЛЕНИЕ?

Загрузить

---

Что такое деление?

Деление — это повторное вычитание.Это процесс деления числа (делимого) на другое число с таким же или меньшим значением (делитель) для нахождения частного и остатка. Этот остаток равен 0, если делитель является множителем делимого, и ненулевым, если делитель не является множителем.

Если впоследствии частное умножить на делитель, мы получим дивиденд.

---

Почему работает длинное разделение?

• Чтобы понять, почему работает метод деления в столбик, давайте рассмотрим пример.Допустим, нужно упаковать 960 конфет. В каждой коробке может быть только 4 сладости, сколько коробок нам понадобится?
  
• Теперь нам не нужно непрерывно вычитать 4 из 960, чтобы прийти к ответу.
  
• Метод длинного деления поможет нам найти ответ. Так как 9 находится в разряде сотен в 960, мы считаем 400 вместо 4, так что 4 также находится в разряде сотен.
  
• 400 пошло бы дважды в 960. Будет проще, если мы проверим «Сколько раз 4 уйдет в 9?» Ответ на этот вопрос будет 2.
  
• Это первая цифра частного.
  
• Когда мы вычитаем 800 из 960, мы получаем первый остаток как 160.

• Следующим шагом будет определение того, как 400 делит 160. Это невозможно, поскольку 400 больше 160, и поэтому мы рассматриваем 40.
  
• 40 пошло бы 4 раза из 160.
  
• Таким образом, вторая цифра частного будет 4.
  
• 160 целиком делится на 40 и не оставляет остатка.

В конце концов, 4 переходит в 0 раз в 0, и именно так мы получаем последнюю цифру частного. Частное, полученное из этого расчета, составляет 240, как показано на правой стороне изображения выше.

Итак, вы знаете, ПОЧЕМУ работает метод длинного деления. Не думаете ли вы, что теперь вы лучше подготовлены, чтобы помочь своим ученикам?

---

Заключение

Мини-урок, посвященный увлекательной концепции деления в столбик.Математическое путешествие по делению в столбик начинается с того, что ученик уже знает, и переходит к творческому созданию новой концепции в молодых умах. Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат.

О компании Cuemath

Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-классы для преподавателей и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей, развивающее несколько навыков.Ознакомьтесь со структурой Cuemath Fee и подпишитесь на бесплатную пробную версию.

---

Часто задаваемые вопросы (FAQ)

Что означает DMSB?

DMSB (Папа, Мать, Сестра, Брат) — мнемоника для запоминания шагов деления в столбик: это означает D ivide, M ultiply, S ubtract, B ring Down.

Какие 5 шагов деления в столбик?

---

Внешние ссылки

Чтобы узнать больше о длинном делении, посетите эти блоги:

Калькулятор длинного деления

— с шагами для решения

Введите делитель и делимое ниже, чтобы вычислить частное и остаток с использованием длинного деления.Результаты и шаги по ее решению показаны ниже.

Результат:

Полный ответ:	18 R 3
Частное:	18
остаток:	3

Решение:

---

---

Как сделать длинное деление с остатками

Изучение деления в столбик — важнейшая веха в освоении основных математических навыков и обряд перехода к окончанию начальной школы.Это внушает страх как ученикам начальной школы, так и их родителям.

Недавнее исследование показало, что понимание деления в столбик и дробей в начальной школе напрямую связано со способностью ученика изучать и понимать алгебру позже в школе. ^[1]

Не бойся!

Выучить деление в столбик может быть легко, и всего за несколько простых шагов вы сможете решить любую задачу. Продолжайте, пока мы разбираем это, но сначала нам нужно охватить анатомию проблемы деления на столбик.

Части задачи о длинном делении

Как показано на изображении выше, проблема длинного деления состоит из нескольких частей.

Дивиденд — это число справа и под линией деления, которое является делимым числом.

Делитель — это число слева от линии деления и число, на которое делится.

Частное является решением и отображается над делимым над разделительной линией.Часто при длинном делении частное — это целая числовая часть решения.

Остаток — это оставшаяся часть решения, или то, что осталось, что неравномерно не входит в частное.

Шаги к решению задачи длинного деления

Есть несколько основных шагов к решению проблемы длинного деления: деление, умножение, вычитание, уменьшение числа и повторение процесса.

Шаг первый: составьте уравнение

Первым шагом в решении задачи деления в столбик является составление уравнения, которое необходимо решить.Если проблема уже связана с длинным разделением, переходите к шагу два.

Если это не так, вот как нарисовать задачу о делении в столбик.

Начните с рисования вертикальной черты для разделения делимого и делимого и верхней черты для разделения делимого и частного.

Разместите дивиденд справа от вертикальной полосы под полосой сверху. Разместите делитель слева от вертикальной черты.

Например, , чтобы разделить 75 на 4, задача длинного деления должна выглядеть так:

Шаг второй: разделить

Решив задачу деления в столбик, начните с деления первой цифры делимого на делитель.

Вы также можете думать об этом как о подсчете того, сколько раз делитель уместится в цифру в делимом.

Отбросьте остаток или десятичную часть результата и запишите целую числовую часть результата в частном над верхней чертой непосредственно над цифрой в делимом.

Например, , делитель «4» переходит в первую цифру делимого «7» два раза, поэтому к частному можно прибавить «1».

Шаг третий: умножить

Следующим шагом будет умножение делителя на цифру, добавленную к частному.Напишите результат под цифрой делимого.

Этот шаг формирует следующую часть уравнения для следующего шага.

Умножение делителя «4» на «1», которое мы нашли на предыдущем шаге, дает «4». Итак, добавьте «4» под первой цифрой делимого.

Шаг четвертый: вычесть

Теперь добавьте знак минус «-» перед числом, добавленным на предыдущем шаге, и проведите линию под ним, чтобы сформировать уравнение вычитания.

Продолжая приведенный выше пример, добавьте «-» перед «4» и линию вычитания под ним.

Теперь, когда у вас есть задача на вычитание, пора ее решить.

Чтобы решить, вычтите «7» минус «4», что равно «3», поэтому запишите «3» в уравнение.

Если в задаче с делением в столбик делимое состоит из одной цифры, то ура, готово! Оставшееся число, которое является результатом задачи вычитания, является остатком, а число над делимым является решенным частным.

Если в дивиденде осталось больше цифр, переходите к следующему шагу.

Шаг пятый: потяните вниз следующее число

На этом этапе пора работать со следующим числом в дивиденде. Для этого потяните вниз следующую цифру в делимом и поместите ее прямо справа от результата задачи вычитания выше.

Следующая цифра делимого — «5». Итак, потяните «5» вниз и запишите его рядом с «3», найденным на предыдущем шаге.

Шаг шестой: повторите

На этом этапе вам может быть интересно, куда идти дальше.Повторите шаги со второго по пятый, пока все цифры делимого не будут убраны, разделены, умножены и вычтены.

При делении используйте результат задачи на вычитание в сочетании с опущенной цифрой в качестве делимого и разделите на него делитель.

Продолжая приведенные выше примеры, разделите результат задачи на вычитание и уменьшенную цифру на делитель. Таким образом, следующий шаг — разделить 35 на 4. Результатом будет «8», поэтому прибавьте «8» к частному.

Затем умножьте цифру частного «8» на делитель «4», который равен 32. Добавьте «32» к задаче деления в столбик.

Затем повторите процесс вычитания, вычтя 32 из 35, что равно 3. Добавьте «3» под линией вычитания.