10 трюков, упрощающих математические операции
9 декабря 2014Советы
Не так давно на Лайфхакере вышла рецензия на книгу «Магия чисел», в которой содержится огромное количество математических трюков. Книга не оставила нас равнодушными, и мы выбрали из неё 10 самых интересных советов по упрощению математических операций.
Поделиться
0Недавно, прочитав книгу «Магия чисел», я почерпнул огромное количество информации. В книге рассказывается о десятках трюков, которые упрощают привычные математические операции. Оказалось, что умножение и деление в столбик — это прошлый век, и непонятно, почему этому до сих пор учат в школах.
Я выбрал 10 самых интересных и полезных трюков и хочу поделиться ими с вами.
Умножение «3 на 1» в уме
Умножение трёхзначных чисел на однозначные — это очень простая операция. Всё, что нужно сделать, — это разбить большую задачу на несколько маленьких.
Пример: 320 × 7
- Разбиваем число 320 на два более простых числа: 300 и 20.
 2
2- Умножаем 7 на 8 и получаем 56.
- Добавляем к числу 25 и получаем 5 625.
Деление на однозначное число
Деление в уме — это достаточно полезный навык. Задумайтесь о том, как часто мы делим числа каждый день. К примеру, счёт в ресторане.
Пример: 675 : 8
- Найдём приближенные ответы, умножив 8 на удобные числа, которые дают крайние результаты (8 × 80 = 640, 8 × 90 = 720). Наш ответ — 80 с хвостиком.
- Вычтем 640 из 675. Получив число 35, нужно разделить его на 8 и получить 4 с остатком 3.
- Наш финальный ответ — 84,3.
Мы получаем не максимально точный ответ (правильный ответ — 84,375), но согласитесь, что даже такого ответа будет более чем достаточно.
Простое получение 15%
Чтобы быстро узнать 15% от любого числа, нужно сначала посчитать 10% от него (перенеся запятую на один знак влево), затем поделить получившееся число на 2 и прибавить его к 10%.
Пример: 15% от 650
- Находим 10% — 65.

- Находим половину от 65 — это 32,5.
- Прибавляем 32,5 к 65 и получаем 97,5.
Банальный трюк
Пожалуй, все мы натыкались на такой трюк:
Задумайте любое число. Умножьте его на 2. Прибавьте 12. Разделите сумму на 2. Вычтите из неё исходное число.
Вы получили 6, верно? Что бы вы ни загадали, вы всё равно получите 6. И вот почему:
- 2x (удвоить число).
- 2x + 12 (прибавить 12).
- (2x + 12) : 2 = x + 6 (разделить на 2).
- x + 6 − x (вычесть исходное число).
Этот трюк построен на элементарных правилах алгебры. Поэтому, если вы когда-нибудь услышите, что кто-то его загадывает, натяните свою самую надменную усмешку, сделайте презрительный взгляд и расскажите всем разгадку. 🙂
Магия числа 1 089
Этот трюк существует не одно столетие.
Запишите любое трёхзначное число, цифры которого идут в порядке уменьшения (к примеру, 765 или 974). Теперь запишите его в обратном порядке и вычтите его из исходного числа.
 К полученному ответу добавьте его же, только в обратном порядке.
К полученному ответу добавьте его же, только в обратном порядке.Какое бы число вы ни выбрали, в результате получите 1 089.
Быстрые кубические корни
Для того чтобы быстро считать кубический корень из любого числа, понадобится запомнить кубы чисел от 1 до 10:
1 2 3 4 5 6 7 8 9 10 1 8 27 64 125 216 343 512 729 1 000 »
Как только вы запомните эти значения, находить кубический корень из любого числа будет элементарно просто.Пример: кубический корень из 19 683
- Берём величину тысяч (19) и смотрим, между какими числами она находится (8 и 27).
 3. Следовательно, последняя цифра ответа — 7.
3. Следовательно, последняя цифра ответа — 7. - Ответ — 27.
Примечание: трюк работает только тогда, когда исходное число является кубом целого числа.
Правило 70
Чтобы найти число лет, необходимых для удвоения ваших денег, нужно разделить число 70 на годовую процентную ставку.
Пример: число лет, необходимое для удвоения денег с годовой процентной ставкой 20%.
70 : 20 = 3,5 года
Правило 110
Чтобы найти число лет, необходимых для утроения денег, нужно разделить число 110 на годовую процентную ставку.
Пример: число лет, необходимое для утроения денег с годовой процентной ставкой 12%.
110 : 12 = 9 лет
Математика — волшебная наука. Я даже немного смущён тем, что такие простые трюки смогли меня удивить, и даже не представляю, сколько ещё математических фокусов можно узнать.
По материалам книги «Магия чисел»
Электронная книга Купить на amazon
Электронная книга на английском языкеДеление натуральных чисел столбиком, примеры, решения.
 Деление в столбик Как разделить на двузначное число столбиком
Деление в столбик Как разделить на двузначное число столбикомДеление столбиком (также можно встретить название деление уголком) — стандартная процедура в арифметике, предназначенная для деления простых или сложных многозначных чисел за счёт разбивания деления на ряд более простых шагов. Как и во всех задачах на деление, одно число, называемое делимым , делится на другое, называемое делителем , производя результат, называемый частным .
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи при делении столбиком.
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой — так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида .

Например , если делимым является число 6105, а делителем 55, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком. Как делить в столбик лучше всего объяснить на примере. Вычислить :512:8=?
Для начала запишем делимое и делитель в столбик.
 Выглядеть это будет так:
Выглядеть это будет так:Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит. это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
3. Теперь, вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48 → записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).

Внимание! При записи под неполным частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения .
4. Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.

Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в скобках (например, 64(2)).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично. При этом, в первое «промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Например , 1976 разделим на 26.
- Число 1 в старшем разряде меньше 26, поэтому рассмотрим число, составленное из цифр двух старших разрядов — 19.
- Число 19 также меньше 26, поэтому рассмотрим число, составленное из цифр трех старших разрядов — 197.
- Число 197 больше 26, делим 197 десятков на 26: 197: 26 = 7 (15 десятков осталось).
- Переводим 15 десятков в единицы, добавляем 6 единиц из разряда единиц, получаем 156.

- 156 делим на 26, получаем 6.
Значит, 1976: 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить поразрядное деление и получить в частном десятичную дробь.
Например , 64 разделим на 5.
- 6 десятков делим на 5, получаем 1 десяток и 1 десяток в остатке.
- Оставшийся десяток переводим в единицы, добавляем 4 из разряда единиц, получаем 14.
- 14 единиц делим на 5, получаем 2 единицы и 4 единицы в остатке.
- 4 единицы переводим в десятые, получаем 40 десятых.
- 40 десятых делим на 5, получаем 8 десятых.
Значит, 64: 5 = 12,8
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего, меньшего разряда и продолжать деление.

Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.

Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.

Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.

Столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок .
Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.
Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.
 е. без остатка. Потренируйтесь на разных примерах.
е. без остатка. Потренируйтесь на разных примерах.Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобнопоказать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
Как объяснить ребенку деление двузначного числа на однозначное не в столбик?
3 — делитель;
4 — частное (результат деления).
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.

Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).
213:3
213 — делимое
3 — делитель- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя.
 Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.- Повторить действия, пока в остатке не окажется 0.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ.
 Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Давайте сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5. Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим . Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном.
Значение частного чисел 265 и 53 — 5. Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.

Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 — это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим . А 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим . Мы видим, что цифра 8 подходит. Можем ее записать в частном.
Значение частного чисел 184 и 23 — 8.
Рассмотрим более сложные случаи деления. Найдем значение частного чисел 768 и 24.
Первое неполное делимое — 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 — это пробная цифра частного.
 Сначала проверим, подойдет ли она. Умножим . . Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного.
Сначала проверим, подойдет ли она. Умножим . . Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного.Продолжим деление. Следующее неполное делимое — 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим . Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного.
Значение частного чисел 768 и 24 — 32.
Найдем значение частного чисел 15 344 и 56.
Первое неполное делимое — 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 — это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она.
 Умножим . А 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим . А . Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Умножим . А 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим . А . Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.Образуем следующее неполное делимое. Это 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. . . Помните: 8 — это пробная цифра. Проверим ее. . А 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. . Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Продолжим деление. Следующее неполное делимое — 224 единицы. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 — это пробная цифра, проверим ее, подойдет ли она. . И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном.

Значение частного чисел 15 344 и 56 — 274.
Мы сегодня учились делить письменно на двузначное число.
Список литературы
- Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова — М.: Просвещение, 2010.
- Узорова О.В., Нефедова Е.А. Большой задачник по математике. 4 класс. — М.: 2013. — 256 с.
- Математика: учеб. для 4-го кл. общеобразоват. учреждений с рус. яз. обучения. В 2 ч. Ч. 1 / Т.М. Чеботаревская, В.Л. Дрозд, А.А. Столяр; пер. с бел. яз. Л.А. Бондаревой. — 3-е изд., перераб. — Минск: Нар. асвета, 2008. — 134 с.: ил.
- Математика. 4 класс. Учебник. В 2 ч./Гейдман Б.П. и др. — 2010. — 120 с., 128 с.
- Ppt4web.ru ().
- Myshared.ru ().
- Viki.rdf.ru ().
Домашнее задание
Выполните деление
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей.
 Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке.
 Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.

Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5.
 А именно, результатом умножения.
А именно, результатом умножения. - Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример.
 Число 5 два раза входит в число 10.
Число 5 два раза входит в число 10. - В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8.
 Запишите в столбик задачу.
Запишите в столбик задачу. - Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5.
 То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.

Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
Деление в столбик — Математика и Английский
Как правильно делить в столбик 4 класс по математике
Деление — это разбиение целого на равные части. Эта математическая операция пригодится не только на уроках математики, но и в повседневной жизни. В этой статье расскажем, как это делать самостоятельно.
О чем эта статья:
3 класс, 4 класс
Деление с остатком
Прежде чем перейти к делению в столбик, давайте вспомним, что значит Деление с остатком. Это такое деление, в результате которого получается остаток меньше делителя:
Например, делим 19 на 5. Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).
Еще пример: делим 29 на 6. Также определяем максимальное число, которое делится на 6 до 29.
 Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).
Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.
Рассмотрим пример деления трехзначного числа на однозначное 322 : 7. Для начала определимся с терминами:
- 322 — делимое или то, что необходимо поделить; 7 — делитель или то, на что нужно поделить: частное — результат действия.
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.
Теперь нужно определить, сколько раз наш делитель 7 содержится в числе 32. Выполним деление с остатком. В результате деления 32 на 7 получили неполное частное 4 и остаток 4.

Результат вычитания должен быть меньше делителя. Если это не так, значит, есть ошибка в расчетах. Нужно увеличить выбранное число и выполнить действие еще раз.
Шаг 3. Запишем следующую цифру делимого справа от остатка 4. Говорят «сносим двойку». Получим следующее делимое — 42.
Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Как выглядит деление в столбик с остатком
Это такое же деление, только в результате получается неровное число, как получилось в примере выше.
- Например, делим 19 на 5. Наибольшее число, делящееся на 5 до 19 это 15. Проверяем 5*3=15, 19-15=4. Ответ: 3 и остаток 4. Записываем так: 19:5=3(4). Еще пример: делим 29 на 6.
 Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5).
Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5).Примеры на деление в столбик
Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!
Частное результат действия.
Skysmart. ru
16.10.2018 20:22:04
2018-10-16 20:22:04
Источники:
Https://skysmart. ru/articles/mathematic/delenie-v-stolbik
Алгоритм деления на однозначное число столбиком » /> » /> .keyword { color: red; }
Как правильно делить в столбик 4 класс по математике
Многим детям сложно делить в столбик из-за неотработанного до автоматизма приема вычитания и деления в столбик, а также недоученной назубок таблицы умножения.
Все остальное – тренировка!
Еще очень важно показать, где можно применить полученные знания в жизни.
Для деления в столбик используют алгоритм.
 Разберем деление в столбик на примере деления трехзначного числа на однозначное по алгоритму.
Разберем деление в столбик на примере деления трехзначного числа на однозначное по алгоритму.Алгоритм деления трёхзначного числа на однозначное в столбик (уголком)
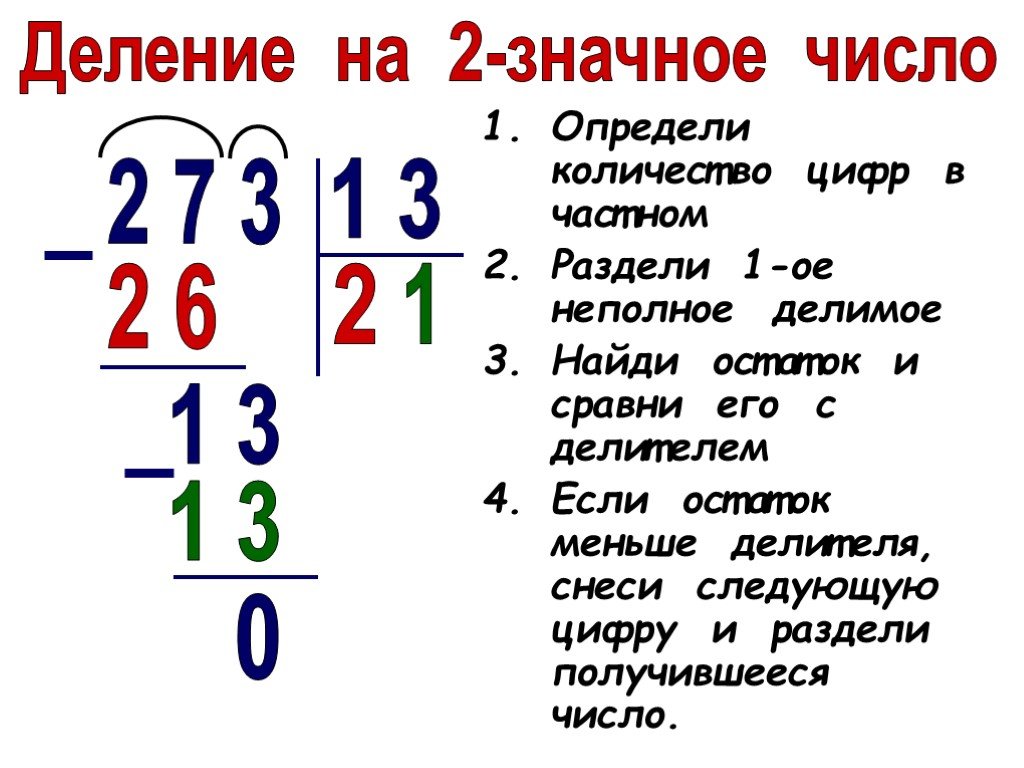
Записывают деление с помощью уголка. Нахожу первое неполное делимое и определяю количество цифр в частном. Делю сотни. Подбираю первую цифру в частном. Узнаю сколько сотен разделили, умножая делитель на первую цифру в частном. Вычитаю из первого неполного делимого число сотен, которое разделили. Получившийся остаток сравниваю с делителем. Остаток должен быть меньше делителя. Делю десятки… Делю единицы… Читаю ответ…
Пример:
1. Записываю деление 968 на 4 уголком.
2. Определяю Неполное частное. Для этого слева направо сравниваю цифры делимого и делителя. Первое неполное делимое – 9 сотен, потому что оно больше делителя «4». Ставлю первую точку под уголком. В делимом осталось еще 2 цифры. Значит в частном будет число, состоящее из сотен, десятков и единиц – трехзначное число.
 Ставлю 3 точки под уголком.
Ставлю 3 точки под уголком.Чтобы избежать ошибок, не забывайте определять количество цифр в частном.
3. Делю сотни и вспоминаю таблицу на 4: 9 делю на 4, получается 2. Записываю в частное первую цифру — 2 сотни. Умножаю 4 на 2, получается 8. Разделили 8 сотен. Вычитаю из 9 число 8, получается 1. Осталось разделить 1 сотню. Сравниваю остаток с делителем: 1
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
4. Делю десятки. Образуется второе неполное делимое: 1 сотни и 6 десятков – это 16 десятков. Делю 16 на 4, получается 4. В частном будет 4 десятка. Умножаю 4 на 4, получается 16. Разделили 16 десятков. Вычитаю: 16 – 16 = 0. Остатка нет. Десятки разделили все.
5. Делю единицы. 8 разделить на 4, получится 2. В частном будет 2 единицы. Умножаю 4 на 2, получается 8. Разделили 8 единиц. Вычитаю: 8 — 8 = 0. Остатка нет. Единицы разделили нацело.

Чтобы избежать ошибок, не забывайте определять количество цифр в частном.
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
Алгоритм деления трёхзначного числа на однозначное в столбик уголком.
Koncpekt. ru
27.10.2018 23:38:43
2018-10-27 23:38:43
Источники:
Https://koncpekt. ru/nachalnye-klassy/konspekty-urokov/matematika-3klass/4487-algoritm-deleniya-v-stolbik-ugolkom. html
Деление столбиком. Онлайн калькулятор | Математика » /> » /> .keyword { color: red; }
Как правильно делить в столбик 4 класс по математике
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют Деление уголком.
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно.
 Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:Это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет Неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78.
 Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули.
 Допустим нам нужно разделить 9027 на 9.
Допустим нам нужно разделить 9027 на 9.Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями.
 Пусть нам требуется разделить 3000 на 6.
Пусть нам требуется разделить 3000 на 6.Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134.
 Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340 : 23 = 58 (остаток 6).
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3 : 10 = 0 (остаток 3).
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
В результате выполнения деления столбиком мы нашли частное оно записано под делителем.

Izamorfix. ru
08.08.2018 18:01:49
2018-08-08 18:01:49
Источники:
Https://izamorfix. ru/matematika/arifmetika/delenie_stolbikom. html
Учебная программа по математике для 5 класса: примеры и шаблоны
- Домашняя страница
- Математика
- Учебная программа по математике для 5 класса
Это ресурсная страница для родителей, которые хотят научить своего ребенка математике в шестом классе. Он охватывает содержание средней учебной программы 6 класса. Прочитайте разделы и загрузите предоставленные рабочие тетради. Не забывайте, что тренировки должны быть веселыми и сложными, и ваш ребенок будет процветать!
Соскучились по математике в 4 классе? Посетите нашу страницу ресурсов по математике для 4 класса. Мы также любим писать веселые и находчивые блоги об обучении. Посмотрите наш блог о 6 бесплатных занятиях по математике в школе, чтобы перейти на следующий уровень.
Добавьте заголовок, чтобы начать создание оглавления
Введение в математическое образование
Как и в строительстве здания, в изучении математики нет коротких путей.
 Вся новая математика основана на существующих математических концепциях. Сэр Исаак Ньютон, знаменитый ученый и математик, однажды написал: «Если я и видел дальше, то потому, что стоял на плечах гигантов». Это означает, что мы открываем истину, опираясь на предыдущие открытия. Поэтому важно, чтобы мы изучили основу как можно лучше. Это откроет математику, которую нам еще предстоит изучить. Без прочного фундамента нам будет трудно следовать за классом в последующие годы. Подобно строительству дома, мы должны стремиться к максимально полному фундаменту. Трещины должны быть устранены, прежде чем строительство может быть продолжено.
Вся новая математика основана на существующих математических концепциях. Сэр Исаак Ньютон, знаменитый ученый и математик, однажды написал: «Если я и видел дальше, то потому, что стоял на плечах гигантов». Это означает, что мы открываем истину, опираясь на предыдущие открытия. Поэтому важно, чтобы мы изучили основу как можно лучше. Это откроет математику, которую нам еще предстоит изучить. Без прочного фундамента нам будет трудно следовать за классом в последующие годы. Подобно строительству дома, мы должны стремиться к максимально полному фундаменту. Трещины должны быть устранены, прежде чем строительство может быть продолжено.Эти 2 пирамиды представляют собой образовательное обучение, в основе которого лежит математика в начальной школе. Pinnacle является pHD. Пробел в знаниях в основе прорывается к вершине.
Учебный план по математике для 5 класса
Для родителей очень важно знать, что их ребенок изучает в школе. Ваша школа получает указания от руководящего органа.
 Школьный совет издает учебную программу (или математический стандарт), которой должны следовать школы. Учебная программа варьируется по всему миру. Например. в России таблица умножения начинается с 1 класса, а в Онтарио — с 3 класса. Это означает, что учебная программа вашей школы отличается от той, которую вы можете найти в Интернете. В этой статье мы рассмотрим оценку того, что вы можете ожидать от учебной программы вашей школы.
Школьный совет издает учебную программу (или математический стандарт), которой должны следовать школы. Учебная программа варьируется по всему миру. Например. в России таблица умножения начинается с 1 класса, а в Онтарио — с 3 класса. Это означает, что учебная программа вашей школы отличается от той, которую вы можете найти в Интернете. В этой статье мы рассмотрим оценку того, что вы можете ожидать от учебной программы вашей школы.- Десятичный разряд: 5 класс
- Добавить десятичные знаки: 5-й класс
- Вычитание десятичных дробей: 5 класс
- Сложение и вычитание дробей: 5 класс
- Многозначное умножение и деление: 5 класс
- Умножить дроби: 5 класс
- Разделить дроби: 5 класс
- Умножение десятичных дробей: 5 класс
- Разделить десятичные дроби: 5 класс
- Степени десяти: 5-й класс
- Том: 5 класс
- Координатная плоскость: 5 класс
- Алгебраическое мышление: 5 класс
- Преобразование единиц измерения: 5 класс
- Линейные участки: 5 класс
- Свойства форм: 5 класс
Найдите репетитора по математике онлайн уже сегодня!
Бесплатный поиск репетиторов!
Примеры учебных программ по математике для 5 класса
Десятичный разряд
Мы используем «арабские цифры».
 Числа работают так, что каждая цифра имеет позицию. Есть 1 позиция. Есть 10-е место. Есть позиция 100. Это полезно, потому что позволяет числу представлять что-то очень большое. Подумайте о числе 973. 9 представляет 9 сотен, 7 представляет 7 десятков, а 3 представляет 3 единицы. Сложите все это вместе, и вы получите (9 х 100) + (7 х 10) + (3 х 1) = 973. Вот как вы представляете большие вещи. На самом деле вы можете продолжать подниматься вверх вечно! Точно так же число позволяет представлять что-то очень маленькое. Посмотрим, как.
Числа работают так, что каждая цифра имеет позицию. Есть 1 позиция. Есть 10-е место. Есть позиция 100. Это полезно, потому что позволяет числу представлять что-то очень большое. Подумайте о числе 973. 9 представляет 9 сотен, 7 представляет 7 десятков, а 3 представляет 3 единицы. Сложите все это вместе, и вы получите (9 х 100) + (7 х 10) + (3 х 1) = 973. Вот как вы представляете большие вещи. На самом деле вы можете продолжать подниматься вверх вечно! Точно так же число позволяет представлять что-то очень маленькое. Посмотрим, как.Когда вы пишете число, вы можете думать о том, что каждая цифра умножается на коэффициент разряда для каждой позиции. Что, если этот коэффициент ценности места был равен 0,1? Так можно записать 1 десятую часть числа. Например, 1,1 = (1 х 1) + (1 х 0,1). 2,2 = (2 х 1) + (2 х 0,1). Видите, как это работает так же, как когда число большое? Подумайте о числе 0,973. 9 представляет 9 десятых, 7 представляет 7 сотых, 3 представляет 3 тысячи. Сложите все это вместе, и вы получите (9 x 0,1) + (7 x 0,01) + (3 x 0,001).
 Вот как вы можете представлять маленькие вещи. На самом деле вы можете продолжать снижаться в значении места навсегда!
Вот как вы можете представлять маленькие вещи. На самом деле вы можете продолжать снижаться в значении места навсегда!Обыкновенные дроби в десятичной форме
В математике есть много форм одних и тех же вещей. В большинстве случаев вы можете переписать дробь в десятичной форме. Выполнение вычисления одним способом может быть настолько сложным, что было бы проще преобразовать это число во что-то другое, чтобы упростить вычисление.
Дроби можно преобразовать в десятичную форму, если вы найдете правильный коэффициент для их умножения. Например, дробь 1/5 можно преобразовать в 0,2, умножив числитель и знаменатель на 2. Тогда, когда дробь будет записана как 2/10, вы можете понять, что это то же самое, что иметь 2 на десятых местах в десятичная форма. Таким образом, вы можете написать 2/10 = 0,2.
Другой пример — переписать дробь 1/4 как 0,25. Сначала попробуйте придумать число, которое при умножении превратит 4 в 100. Число 25 сделает это. Умножьте числитель и знаменатель на 25, чтобы получить 25/100.
 Теперь поймите, что это то же самое, что иметь 2 в десятых и 5 в сотых, поэтому 25/100 = 0,25
Теперь поймите, что это то же самое, что иметь 2 в десятых и 5 в сотых, поэтому 25/100 = 0,25Сложение десятичных знаков
Сложение десятичных знаков почти такое же, как сложение целых чисел. Ключ состоит в том, чтобы добавить одно и то же значение, удерживая цифры вместе. При сложении чисел 8 и 2 оба числа имеют одинаковую разрядность 1. Таким образом, можно сказать, что 8 + 2 = 10. При сложении чисел 0,8 и 0,2 оба числа имеют одинаковую разрядность 0,1. Таким образом, вы можете сказать 0,8 + 0,2 = 1,0. Перенос всегда происходит, когда вы достигаете 10 от этой стоимости места. Вот как это работает для сложения однозначных чисел.
Для добавления нескольких цифр повторите тот же процесс, что и для добавления одной цифры. Начните с наименьшего разряда и продвигайтесь вверх. Например, добавляя 8,8 и 2,2, начните с добавления 0,8 и 0,2, что равно 1,0. Теперь перенесите 1 на следующее разрядное значение. Таким образом, у вас будет 8 и 3. 8 + 3 = 11. Итак, вы знаете, что 8,8 + 2,2 = 13.
 Практика делает совершенным!
Практика делает совершенным!Сложение по вертикали
Одним из способов добавления номера является использование вертикального метода. Вы ставите два числа друг на друга. Затем, начиная с самых маленьких цифр, складывайте их. Переносите 1 каждый раз, когда две цифры больше 10. Это отлично работает для десятичных чисел или целых чисел. Этот метод требует много шагов, но добавляет только два 0-9цифры. Тем не менее, требуется много часов практики, чтобы научиться делать это быстро. Лучший способ учиться — это делать.
Вертикальный метод вычитания с десятичными дробями
Вертикальный метод, показанный ранее, можно использовать для вычитания двух чисел. Разница лишь в том, что перенос происходит в обратном порядке. Когда цифра, из которой вы вычитаете, меньше, перенесите 1 из следующего по величине разряда и «разбейте» ее на 10. Это сделает число, из которого вы вычитаете, достаточно большим. Разница будет положительной. Десятичные числа работают так же, как и числа, мы просто помним, что они намного меньше разрядного значения.

Многозначное умножение
Самое удивительное в умножении то, что порядок, в котором вы это делаете, не имеет значения. Точно так же, как результат чистки зубов, а затем чистки зубной нитью такой же, как и результат чистки зубной нитью, а затем чистки: вы получаете чистые зубы! То же самое и с цифрами. Таким образом, 2 x 3 равно 3 x 2. Это означает, что вы можете упростить расчеты, изменив порядок! Когда нам нужно умножить много цифр, таких как 234 x 321, это сложно. Как всегда есть подвох. Признайте, что 234 = 2 x 100 + 3 x 10 + 4 и что 321 = 3 x 100 + 2 x 20 + 1. Таким образом, 234 x 321 равно ((2 x 100) + (3 x 10) + 4) x (3). х 100 + 2 х 10 + 1). Переставляя, мы имеем 2 х 3 х 100 + 3 х 2 х 10 + 4 + 1. Мы знаем, что 2 х 3 = 6 и, следовательно, 3 х 2. Тогда мы имеем 6 х 100 + 6 х 10 + 14, что равно 600 + 60. + 14. Упростите, и ваш ответ будет 674.
Мы также можем сделать вертикальный метод!
Многозначный раздел
При делении двух больших чисел мы можем использовать вертикальный метод, но вместо того, чтобы начинать с наименьшего разрядного значения, мы начинаем с наибольшего разрядного значения. Мы разбиваем задачу на более простые задачи, спрашивая, сколько раз делитель может содержаться в цифре. Затем мы вычитаем общее количество, чтобы получить остаток. Мы делим этот остаток на следующую наименьшую цифру-заполнитель. Мы повторяем этот процесс до тех пор, пока у нас не останется цифр для деления.
Мы разбиваем задачу на более простые задачи, спрашивая, сколько раз делитель может содержаться в цифре. Затем мы вычитаем общее количество, чтобы получить остаток. Мы делим этот остаток на следующую наименьшую цифру-заполнитель. Мы повторяем этот процесс до тех пор, пока у нас не останется цифр для деления.Умножение дробей
При умножении двух или более дробей просто перемножайте числители (верхние числа) и знаменатели (нижние числа). Вы также должны поставить дробь в самых низких условиях общего пользования. Например, если числитель и знаменатель являются четными числами, разделите их оба на 2, чтобы разделить их пополам. Продолжайте, пока дробь не примет простейшую форму.
Деление дробей
Вы должны понять, что дроби и деление — это одно и то же. Это означает, что деление дроби равносильно умножению на дробь. Предположим, мы хотим разделить 5/3 на 3. Затем мы умножим 5/3 x 1/3. Используя технику умножения дробей, мы имеем 5/3 х 1/3 = 5/9. Это означает, что 5/3 делится на три равные части 5/9.
 В этом видео показано, как делить дроби и чем это похоже на умножение обратной.
В этом видео показано, как делить дроби и чем это похоже на умножение обратной.Рабочие листы с задачами по математике для пятого класса
Вы ищете что-нибудь, что можно передать своему второкласснику, чтобы он начал учиться? Ознакомьтесь с нашими бесплатными загружаемыми таблицами по математике для 5-го класса или попробуйте наш генератор математических задач, чтобы учиться онлайн. Вы можете сделать копию, скачать и распечатать эти задачи. Сделайте это увлекательной игрой и начните изучать математику для 6 класса уже сегодня! Если у вас нет принтера, откройте его с помощью iPad и играйте онлайн.
Ссылки на избранные сайты
- Академия Хана
- Учебная программа по математике Онтарио
Откройте для себя торговую площадку TutorOcean с потрясающими и доступными онлайн-репетиторами по математике
Найдите онлайн-репетитора по математике
Длинное деление (стандартный алгоритм деления) Math Video
ЧТО ТАКОЕ СТАНДАРТНЫЙ АЛГОРИТМ ДЛЯ ДЛИННОГО ДЕЛЕНИЯ?
Стандартный алгоритм деления в длинное число обеспечивает быстрый и эффективный процесс деления любых двух чисел.
 Процесс одинаков независимо от того, какие числа вы используете.
Процесс одинаков независимо от того, какие числа вы используете.Чтобы лучше понять деление в длинное число…
КАКОЙ СТАНДАРТНЫЙ АЛГОРИТМ ДЛЯ ДЕЛЕНИЯ В ДЛИННОЕ?. Стандартный алгоритм деления в длинное дает быстрый и эффективный процесс деления любых двух чисел. Процесс одинаков независимо от того, какие числа вы используете. Чтобы лучше понять деление в длину…
ДАВАЙТЕ РАЗЪЯСНИМ!
Разделите трехзначное число на однозначное число
Для партии зубной пасты для слонов требуется 936 миллиграммов перекиси водорода, поровну разделенных на 4 контейнера. Разделить 936 ÷ 4, чтобы найти, сколько миллиграммов содержится в каждом контейнере. Стандартный алгоритм длинного деления представляет собой серию шагов, повторяющихся в таком порядке: разделить, умножить, вычесть, опустить. По стандартному алгоритму мы решаем задачи деления по одному разряду за раз. Начните с 9 в числе 938. Умножьте: какое число, кратное 4, ближе всего к (но меньше) 9? 4 × 2 = 8.
 Запишите 2 в разряде сотен над 9. Вычтите: 9 -8 = 1. Опусти вниз: следующая цифра 938 — 3. Напиши ее рядом с 1, чтобы получилось 13. Повтори все шаги. 4 × 3 = 12, что ближе всего к 13. Напишите цифру 3 в разряде десятков над чертой. Вычтите 13 – 12, чтобы получить 1. Сократите последнюю цифру, 6, чтобы получить 16. Повторите шаги еще раз. 4 × 4 = 16. Напишите 4 над разрядом единиц. 16 – 16 = 0. Не осталось цифр, которые нужно сбить, так что все готово! Число над строкой равно 234, а последнее вычитание дало 0,9.36 ÷ 4 = 234. Попробуйте сами: что такое 875 ÷ 7?
Запишите 2 в разряде сотен над 9. Вычтите: 9 -8 = 1. Опусти вниз: следующая цифра 938 — 3. Напиши ее рядом с 1, чтобы получилось 13. Повтори все шаги. 4 × 3 = 12, что ближе всего к 13. Напишите цифру 3 в разряде десятков над чертой. Вычтите 13 – 12, чтобы получить 1. Сократите последнюю цифру, 6, чтобы получить 16. Повторите шаги еще раз. 4 × 4 = 16. Напишите 4 над разрядом единиц. 16 – 16 = 0. Не осталось цифр, которые нужно сбить, так что все готово! Число над строкой равно 234, а последнее вычитание дало 0,9.36 ÷ 4 = 234. Попробуйте сами: что такое 875 ÷ 7? Разделите трехзначное число на однозначное. Для партии зубной пасты для слонов требуется 936 миллиграммов перекиси водорода, поровну разделенных на 4 контейнера. Разделите 936 ÷ 4, чтобы узнать, сколько миллиграммов содержится в каждом контейнере. Стандартный алгоритм длинного деления представляет собой серию шагов, повторяющихся в таком порядке: разделить, умножить, вычесть, опустить. По стандартному алгоритму мы решаем задачи деления по одному разряду за раз.
 Начните с 9в 938. Умножение: какое число, кратное 4, ближе всего к (но меньше) 9? 4 × 2 = 8. Запишите 2 в разряде сотен над 9. Вычтите: 9 -8 = 1. Опусти вниз: следующая цифра 938 — 3. Напиши ее рядом с 1, чтобы получилось 13. Повтори все шаги. 4 × 3 = 12, что ближе всего к 13. Напишите цифру 3 в разряде десятков над чертой. Вычтите 13 – 12, чтобы получить 1. Сократите последнюю цифру, 6, чтобы получить 16. Повторите шаги еще раз. 4 × 4 = 16. Напишите 4 над разрядом единиц. 16 – 16 = 0. Не осталось цифр, которые нужно сбить, так что все готово! Число над строкой равно 234, а последнее вычитание дало 0,9.36 ÷ 4 = 234. Попробуйте сами: что такое 875 ÷ 7?
Начните с 9в 938. Умножение: какое число, кратное 4, ближе всего к (но меньше) 9? 4 × 2 = 8. Запишите 2 в разряде сотен над 9. Вычтите: 9 -8 = 1. Опусти вниз: следующая цифра 938 — 3. Напиши ее рядом с 1, чтобы получилось 13. Повтори все шаги. 4 × 3 = 12, что ближе всего к 13. Напишите цифру 3 в разряде десятков над чертой. Вычтите 13 – 12, чтобы получить 1. Сократите последнюю цифру, 6, чтобы получить 16. Повторите шаги еще раз. 4 × 4 = 16. Напишите 4 над разрядом единиц. 16 – 16 = 0. Не осталось цифр, которые нужно сбить, так что все готово! Число над строкой равно 234, а последнее вычитание дало 0,9.36 ÷ 4 = 234. Попробуйте сами: что такое 875 ÷ 7?Разделить 4-значное число на 1-значное число
Вы хотите проехать 1421 милю за 6 дней. Разделите 1421 : 6, чтобы узнать, сколько миль вы должны проезжать каждый день. Чтобы разделить по стандартному алгоритму, напишите 1421 под знаком деления и 6 слева. Используйте шаги умножения, вычитания и сокращения, чтобы найти частное.
 Какое число, кратное 6, ближе всего к 14? 6 × 2 = 12. Напишите 2 в разряде сотен. Вычтите: 14 – 12 = 2. Сократите следующую цифру, 2, чтобы получить 22. Какое число, кратное 6, ближе всего к 22? 6 × 3 = 18. Напишите 3 в разряде десятков. Вычтите: 22 – 18 = 4. Сократите следующую цифру, 1, чтобы получить 41. Какое число, кратное 6, ближе всего к 41? 6 × 6 = 36. Напишите 6 над единицами. Вычтите: 41 – 36 = 5. Больше нет цифр, которые нужно сводить. 5 меньше 6, поэтому 5 нельзя разделить на 6 групп. 1421 ÷ 6 = 236 с остатком 5. Каждый день вам нужно проезжать чуть больше 236 миль. Попробуйте сами: Разделить 2576 ÷ 8.
Какое число, кратное 6, ближе всего к 14? 6 × 2 = 12. Напишите 2 в разряде сотен. Вычтите: 14 – 12 = 2. Сократите следующую цифру, 2, чтобы получить 22. Какое число, кратное 6, ближе всего к 22? 6 × 3 = 18. Напишите 3 в разряде десятков. Вычтите: 22 – 18 = 4. Сократите следующую цифру, 1, чтобы получить 41. Какое число, кратное 6, ближе всего к 41? 6 × 6 = 36. Напишите 6 над единицами. Вычтите: 41 – 36 = 5. Больше нет цифр, которые нужно сводить. 5 меньше 6, поэтому 5 нельзя разделить на 6 групп. 1421 ÷ 6 = 236 с остатком 5. Каждый день вам нужно проезжать чуть больше 236 миль. Попробуйте сами: Разделить 2576 ÷ 8. Разделить 4-значное число на 1-значное Вы хотите проехать 1421 милю за 6 дней. Разделите 1421 : 6, чтобы узнать, сколько миль вы должны проезжать каждый день. Чтобы разделить по стандартному алгоритму, напишите 1421 под знаком деления и 6 слева. Используйте шаги умножения, вычитания и сокращения, чтобы найти частное. Какое число, кратное 6, ближе всего к 14? 6 × 2 = 12.
 Напишите 2 в разряде сотен. Вычтите: 14 – 12 = 2. Сократите следующую цифру, 2, чтобы получить 22. Какое число, кратное 6, ближе всего к 22? 6 × 3 = 18. Напишите 3 в разряде десятков. Вычтите: 22 – 18 = 4. Сократите следующую цифру, 1, чтобы получить 41. Какое число, кратное 6, ближе всего к 41? 6 × 6 = 36. Напишите 6 над единицами. Вычтите: 41 – 36 = 5. Больше нет цифр, которые нужно сводить. 5 меньше 6, поэтому 5 нельзя разделить на 6 групп. 1421 ÷ 6 = 236 с остатком 5. Каждый день вам нужно проезжать чуть больше 236 миль. Попробуйте сами: разделите 2576 ÷ 8,9.0011
Напишите 2 в разряде сотен. Вычтите: 14 – 12 = 2. Сократите следующую цифру, 2, чтобы получить 22. Какое число, кратное 6, ближе всего к 22? 6 × 3 = 18. Напишите 3 в разряде десятков. Вычтите: 22 – 18 = 4. Сократите следующую цифру, 1, чтобы получить 41. Какое число, кратное 6, ближе всего к 41? 6 × 6 = 36. Напишите 6 над единицами. Вычтите: 41 – 36 = 5. Больше нет цифр, которые нужно сводить. 5 меньше 6, поэтому 5 нельзя разделить на 6 групп. 1421 ÷ 6 = 236 с остатком 5. Каждый день вам нужно проезжать чуть больше 236 миль. Попробуйте сами: разделите 2576 ÷ 8,9.0011Разделить трехзначное число на двузначное число
Вы хотите разделить партию из 384 печенья между 12 учителями средней школы. Решите 384 ÷ 12, используя стандартный алгоритм деления в большую сторону. Один и тот же процесс работает независимо от того, сколько цифр в делителе или делимом. Начните с вопроса, какое число, кратное 12, меньше или равно 38? 12 × 3 = 36, поэтому запишите 3 в разряде десятков и вычтите, чтобы найти остаток: 38 – 36 = 2.
 Сократите 4, чтобы получить 24. Какое число, кратное 12, ближе всего к 24? 12 × 2 = 24, поэтому запишите 2 в позиции единиц и вычтите, чтобы найти остаток 24 – 24 = 0. Больше нет цифр, которые нужно записывать. 384 ÷ 12 = 32. Вы можете дать каждому учителю по 32 печенья. Ням! Попробуйте сами: Что такое 224 ÷ 32?
Сократите 4, чтобы получить 24. Какое число, кратное 12, ближе всего к 24? 12 × 2 = 24, поэтому запишите 2 в позиции единиц и вычтите, чтобы найти остаток 24 – 24 = 0. Больше нет цифр, которые нужно записывать. 384 ÷ 12 = 32. Вы можете дать каждому учителю по 32 печенья. Ням! Попробуйте сами: Что такое 224 ÷ 32? Разделить трехзначное число на двузначное Вы хотите разделить партию из 384 печенья между 12 учителями средней школы. Решите 384 ÷ 12, используя стандартный алгоритм деления в большую сторону. Один и тот же процесс работает независимо от того, сколько цифр в делителе или делимом. Начните с вопроса, какое число, кратное 12, меньше или равно 38? 12 × 3 = 36, поэтому запишите 3 в разряде десятков и вычтите, чтобы найти остаток: 38 – 36 = 2. Сократите 4, чтобы получить 24. Какое число, кратное 12, ближе всего к 24? 12 × 2 = 24, поэтому запишите 2 в позиции единиц и вычтите, чтобы найти остаток 24 – 24 = 0. Больше нет цифр, которые нужно записывать. 384 ÷ 12 = 32. Вы можете дать каждому учителю по 32 печенья.
 Ням! Попробуйте сами: что такое 224 ÷ 32?
Ням! Попробуйте сами: что такое 224 ÷ 32?Разделить большое многозначное число на многозначное число
Для опыления одной яблони требуется 23 пчелы. Если у нас всего 31 359 пчел, сколько яблонь они смогут опылить? Решите 31 359 ÷ 23, используя стандартный алгоритм деления в большую сторону. Рассмотрим первые две цифры числа 31 359. Какое число, кратное 23, ближе всего к 31? 23 × 1 = 23, поэтому запишите 1 в разряде тысяч и вычтите, чтобы найти разницу: 31 – 23 = 8. Сократите 3, чтобы получить 83. 23 × 3 = 69, поэтому запишите 3 в разряде сотен и вычтите найти разницу: 83 – 69= 14. Сократите 5, чтобы получить 145. 23×6=138, поэтому напишите 6 в разряде десятков и вычтите 145-138 =7. Сократите 9, чтобы получить 79. 23×3=69, поэтому напишите 3 вместо единиц и вычтите 79-69=10. Больше нет цифр, которые нужно записывать, а 10 нельзя разделить на 23 равные группы. 31 359 ÷ 23 = 1 363 с остатком 10. Пчелы могут опылить 1 363 яблони. Попробуйте сами: Сколько будет 53 922 ÷ 43?
Разделить большое многозначное число на многозначное число Для опыления одной яблони требуется 23 пчелы.
 Если у нас есть в общей сложности 31 359пчелы, сколько яблонь они могут опылить? Решите 31 359 ÷ 23, используя стандартный алгоритм деления в большую сторону. Рассмотрим первые две цифры числа 31 359. Какое число, кратное 23, ближе всего к 31? 23 × 1 = 23, поэтому запишите 1 в разряде тысяч и вычтите, чтобы найти разницу: 31 – 23 = 8. Сократите 3, чтобы получить 83. 23 × 3 = 69, поэтому запишите 3 в разряде сотен и вычтите чтобы найти разницу: 83 – 69 = 14. Уменьшите 5, чтобы получить 145. 23 × 6 = 138, поэтому запишите 6 в разряде десятков и вычтите 145-138 = 7. Сбить 9чтобы получить 79. 23 × 3 = 69, поэтому напишите 3 вместо единиц и вычтите 79-69 = 10. Больше нет цифр, которые нужно записывать, а 10 нельзя разделить на 23 равные группы. 31 359 ÷ 23 = 1 363 с остатком 10. Пчелы могут опылить 1 363 яблони. Попробуйте сами: чему равно 53 922 ÷ 43?
Если у нас есть в общей сложности 31 359пчелы, сколько яблонь они могут опылить? Решите 31 359 ÷ 23, используя стандартный алгоритм деления в большую сторону. Рассмотрим первые две цифры числа 31 359. Какое число, кратное 23, ближе всего к 31? 23 × 1 = 23, поэтому запишите 1 в разряде тысяч и вычтите, чтобы найти разницу: 31 – 23 = 8. Сократите 3, чтобы получить 83. 23 × 3 = 69, поэтому запишите 3 в разряде сотен и вычтите чтобы найти разницу: 83 – 69 = 14. Уменьшите 5, чтобы получить 145. 23 × 6 = 138, поэтому запишите 6 в разряде десятков и вычтите 145-138 = 7. Сбить 9чтобы получить 79. 23 × 3 = 69, поэтому напишите 3 вместо единиц и вычтите 79-69 = 10. Больше нет цифр, которые нужно записывать, а 10 нельзя разделить на 23 равные группы. 31 359 ÷ 23 = 1 363 с остатком 10. Пчелы могут опылить 1 363 яблони. Попробуйте сами: чему равно 53 922 ÷ 43?ДЛИННЫЙ СЛОВАРЬ ДЕЛЕНИЯ
Модель площади
Прямоугольная диаграмма или модель, используемая для задач на умножение и деление, в которой множители или частное и делитель определяют длину и ширину прямоугольника.
 Также называется методом коробки.
Также называется методом коробки.Частичные частные
Стратегия деления, при которой мы вычитаем множители делителя из делимого, пока не получим 0 или как можно ближе к 0.
Алгоритм
Процедура в математике или описание набора шагов, которые мы можем использовать для решения математических вычислений.
Длинное деление
Процесс деления числа, состоящего как минимум из трех цифр, на число, состоящее из двух или более цифр, иногда с сохранением остатка.
Стандартный алгоритм деления
Серия повторяющихся шагов для решения задач на деление. Шаги по порядку: разделить, умножить, вычесть, опустить.
Разделение
Разделение на равные части.
Дивиденд
При делении сумма или число, подлежащее делению.
Делитель
При делении — число, которое делится на другое число полностью или с остатком.
ДЛИННОЕ РАЗДЕЛЕНИЕ ВОПРОСЫ ДЛЯ ОБСУЖДЕНИЯ
Каковы четыре повторяющихся шага стандартного алгоритма деления в большую сторону?
Деление, умножение, вычитание, уменьшение
Как умножение помогает делить?
Когда я делю, я могу посмотреть на множители делителя, чтобы найти делимое.

Как узнать, что вы справились с задачей на деление?
Когда больше нет цифр, которые нужно записать, и остаток равен 0, или когда больше нет цифр, которые нужно записать, и остаток меньше делителя.
Зачем использовать стандартный алгоритм деления?
Стандартный алгоритм — очень эффективный способ деления.
Как с помощью стандартного алгоритма найти 4564 ÷ 7?
Я могу начать с составления списка кратных 7. 4 меньше 7, поэтому рассмотрим кратные 7 близкие к 45. Умножьте: 7 × 6 = 42. Вычтите: 45 – 42 = 3. Уменьшите 6 до сделать 36. Найдите числа, кратные 7, близкие к 36. Умножьте: 7 × 5 = 35. Вычтите: 36 – 35 = 1. Сократите 4, чтобы получить 14. Найдите кратные 7, близкие к 14. Умножьте: 7 × 2 = 14 Вычтите: 14 – 14 = 0. Не осталось чисел, которые нужно сбить, и остаток равен 0, 4 564 ÷ 7 = 652, 9.0011
Вернуться к уроку
Решения для 6 распространенных причин, по которым у детей возникают проблемы с делением
Многие дети испытывают трудности с делением.
 Их трудности часто связаны с одной из этих 6 причин. Используйте этот инструмент, чтобы узнать, относятся ли какие-либо из этих ситуаций к вашему ребенку. Затем получите решения, которые помогут вашему ребенку стать суперзвездой дивизиона!
Их трудности часто связаны с одной из этих 6 причин. Используйте этот инструмент, чтобы узнать, относятся ли какие-либо из этих ситуаций к вашему ребенку. Затем получите решения, которые помогут вашему ребенку стать суперзвездой дивизиона!Во-первых, давайте освежим наш математический словарный запас. Делимое – это число, которое делится. Делитель — это количество групп, входящих в делимое, а частное показывает, сколько единиц в каждой группе.
делимое ÷ делитель = частное
или
частное ÷ делитель = делимое
Делитель и частное можно поменять местами, и уравнение останется верным. 12÷2=6 и 12÷6=2. 12 может иметь две группы по шесть или шесть групп по два.
Причина #1 Ребёнок борется с Отделом . Многие дети не понимают, что на самом деле означает деление. Это означает создание равных групп. Если взять 12 яблок и составить одну группу из 6 яблок, одну группу из 1 яблока и одну группу из 5 яблок, то яблоки не будут делиться.
 вот еще один способ думать об этом: делимое — это целое, а делимое — это части. Некоторые люди называют это «разложением дивиденда» на множители. В Mathnasium мы предпочитаем называть это «целое и части». Мы также говорим о разделении: «Сколько их в этом?» Например: 12 ÷ 6 = означает «Сколько шестёрок в числе 12?» Точно так же 4 ÷ 1/2 = означает «Сколько 1/2 в 4?»
вот еще один способ думать об этом: делимое — это целое, а делимое — это части. Некоторые люди называют это «разложением дивиденда» на множители. В Mathnasium мы предпочитаем называть это «целое и части». Мы также говорим о разделении: «Сколько их в этом?» Например: 12 ÷ 6 = означает «Сколько шестёрок в числе 12?» Точно так же 4 ÷ 1/2 = означает «Сколько 1/2 в 4?»Решение: Объясните, что, как и умножение, деление должно иметь равные группы. Затем дайте ребенку много возможностей поработать с реальными предметами и разделите их на равные группы. Пусть ребенок напишет уравнение деления, которое он только что представил с помощью предметов.
Причина #2 У детей проблемы с подразделением . Дети часто забывают шаги для длинного деления. Это происходит, когда они не понимают, почему это работает. Они полагаются на запоминание серии шагов, алгоритма, которые кажутся им бессмысленными. Память — плохая замена пониманию, потому что на нее тоже нельзя положиться.

Решения: Предложите ребенку придумать другой метод решения задач на деление с несколькими цифрами. Метод, который они придумают, может иметь для них больше смысла, чем тот, который они изучают в школе. Если ваш ребенок понимает, почему работает длинное деление, он, скорее всего, запомнит каждый шаг. Длинное и короткое деление — это просто разные алгоритмы решения задачи деления. В школах США
чаще всего преподается метод длинного деления. Подумайте о том, чтобы привести своего ребенка в наш центр Mathnasium of Littleton. Мы специализируемся на том, чтобы сделать математику понятной.
Посмотрите, как в мире учат делению. Возможно, бразильская система обозначений покажется вашему ребенку более понятной.
Попросите ребенка попробовать деление на короткое вместо длинного. Это может быть отличным инструментом для решения задач деления, когда длинное деление делает его слишком сложным. Хотя он традиционно не входит в школьную программу США, это полезный инструмент.
 Если вам интересно узнать больше о том, как сделать короткое деление, вот два ресурса. Один представляет собой видео, а другой представляет собой письменное объяснение, чтобы узнать больше о коротком делении. Имейте в виду, что ребенок должен иметь четкое представление о простых понятиях умножения и деления, прежде чем изучать краткое или длинное деление.
Если вам интересно узнать больше о том, как сделать короткое деление, вот два ресурса. Один представляет собой видео, а другой представляет собой письменное объяснение, чтобы узнать больше о коротком делении. Имейте в виду, что ребенок должен иметь четкое представление о простых понятиях умножения и деления, прежде чем изучать краткое или длинное деление.Причина № 3 Дети находят дивизион сложным . У них всегда были проблемы с математикой. Это всего лишь последняя концепция, которая вызывает у них трудности.
Решение: Иногда нужно вернуться назад, чтобы идти вперед. Ребенку, у которого отсутствует базовый навык, будет трудно разделить, потому что оно связано с предыдущими понятиями. Деление — это многократное вычитание и противоположное умножению. Это связано со счетом, целыми и частями, пропорциональным мышлением.
Прочитайте некоторые из наших предыдущих статей об изучении математики, в том числе:
- Есть ли у вашего ребенка какие-либо из 4 предупредительных признаков неизбежных математических трудностей?
- Математика требует времени, чтобы победить
- Почему Mathnasium of Littleton фокусируется на базовых навыках?
- Подготовьте ребенка к математическим вычислениям, начиная со второго класса
- Ваш ребенок K-6 находится на уровне по математике?
- Какой тип математики у вашего ребенка?
Позвоните Сьюзи по телефону 303-979-9077, чтобы назначить оценку, и мы проверим, отсутствуют ли у вашего ребенка навыки из предыдущих классов.

Причина № 4 Детям тяжело с Подразделением . Они никогда не развивали беглость умножения. Дети могут использовать многократное вычитание и обратный счет для решения задачи на деление, но это трудоемкий процесс. Дети, использующие эти методы, будут склонны к ошибкам. Поскольку деление является обратным умножению, ребенок с беглостью умножения сможет выполнять деление быстро и точно.
Решение : Запишите своего ребенка в нашу программу обучения беглому умножению или в нашу программу New! Учебный лагерь умножения.
Ваш ребенок станет настолько хорош в умножении, делению станет намного легче.Причина № 5 Дети борются с подразделением . Они не понимают остатков, как они пишутся и что они означают. Остатки — это упрощенный метод выражения частного. Они используются, когда делитель не делится на делимое с использованием только целых чисел. 47÷3=15,66666… или 47÷3=15 2/3. Это работает, если вы делите объекты, которые можно бесконечно разбивать на более мелкие части.
 Некоторые предметы нелегко разбить. Если у вас есть 47 шаров, которые вы собираетесь разделить на 3 части, у вас получится 3 группы по 15 шаров, а затем останется два шара. Таким образом, 47 ÷ 3 = 15 остаток 2. Педагоги часто говорят детям в 3-5 классах использовать частное с остатком, а не дроби или десятичные дроби. Эта тенденция усугубляет замешательство детей в отношении значения остатка.
Некоторые предметы нелегко разбить. Если у вас есть 47 шаров, которые вы собираетесь разделить на 3 части, у вас получится 3 группы по 15 шаров, а затем останется два шара. Таким образом, 47 ÷ 3 = 15 остаток 2. Педагоги часто говорят детям в 3-5 классах использовать частное с остатком, а не дроби или десятичные дроби. Эта тенденция усугубляет замешательство детей в отношении значения остатка.Решение: Используйте деньги, единицы измерения, пиццу и другие предметы, чтобы узнать, как делятся разные вещи. Обсудите ситуации, когда частное не имеет смысла иметь остаток, например, деление машин, людей или мячей. Также обсудите ситуации, когда для частного имеет смысл использовать обыкновенную или десятичную дробь, например, при расчете ставки. Если задача на деление не является частью реальной жизненной ситуации или задачи со словами, невозможно узнать, как должно быть выражено частное.
Причина № 6 Дети находят деление сложным . Дети путаются с символами, потому что деление может быть записано в разных форматах.

Решение: Признайте, что разные способы написания деления могут сбивать с толку. Поговорите о том, как чтение имеет некоторые из тех же проблем. Звуки (фонемы) могут образовываться с помощью различных комбинаций букв (например, /x/ и /cks/ или /ew/ и /oo/). Убедите вашего ребенка, что если он научился читать, то вскоре усвоит различные способы деления письма. Это требует практики. Помогите им создать шпаргалку, показывающую одну простую задачу на деление тремя способами.
12÷4 = 3 12/4= 3
Если ваш ребенок испытывает трудности с делением по другой причине, позвоните нам. Мы хотели бы услышать об этом и посмотреть, сможем ли мы помочь. Обычно мы можем. 303-979-9077 или нажмите кнопку ниже для получения дополнительной информации.
Он защищен авторским правом. Mathnasium of Littleton имеет разрешение на его использование. В других местах Mathnasium следует связаться с Хизер по адресу [email protected], прежде чем использовать его.

 2
2
 К полученному ответу добавьте его же, только в обратном порядке.
К полученному ответу добавьте его же, только в обратном порядке. 3. Следовательно, последняя цифра ответа — 7.
3. Следовательно, последняя цифра ответа — 7. Деление в столбик Как разделить на двузначное число столбиком
Деление в столбик Как разделить на двузначное число столбиком.gif)
 Выглядеть это будет так:
Выглядеть это будет так:

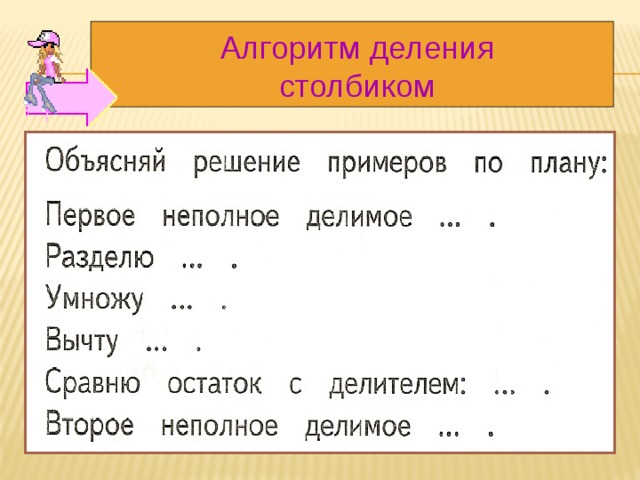

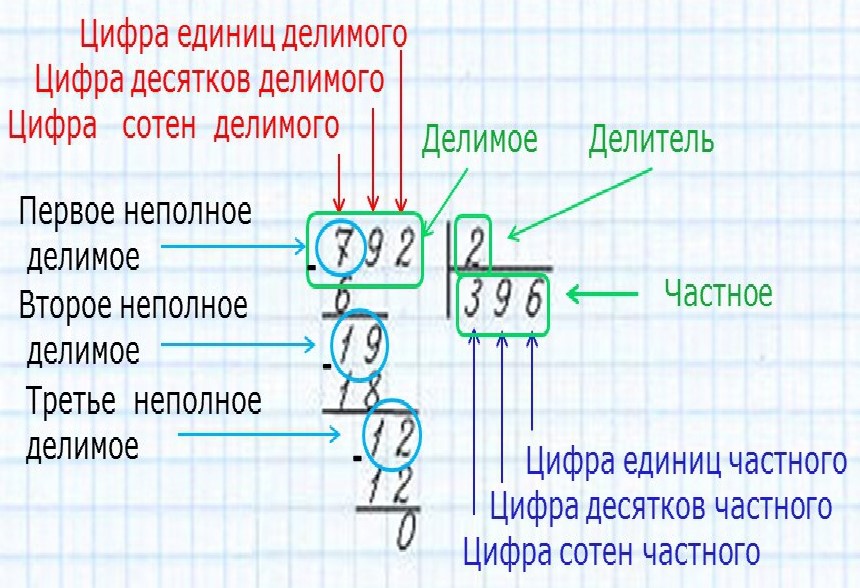


 е. без остатка. Потренируйтесь на разных примерах.
е. без остатка. Потренируйтесь на разных примерах.

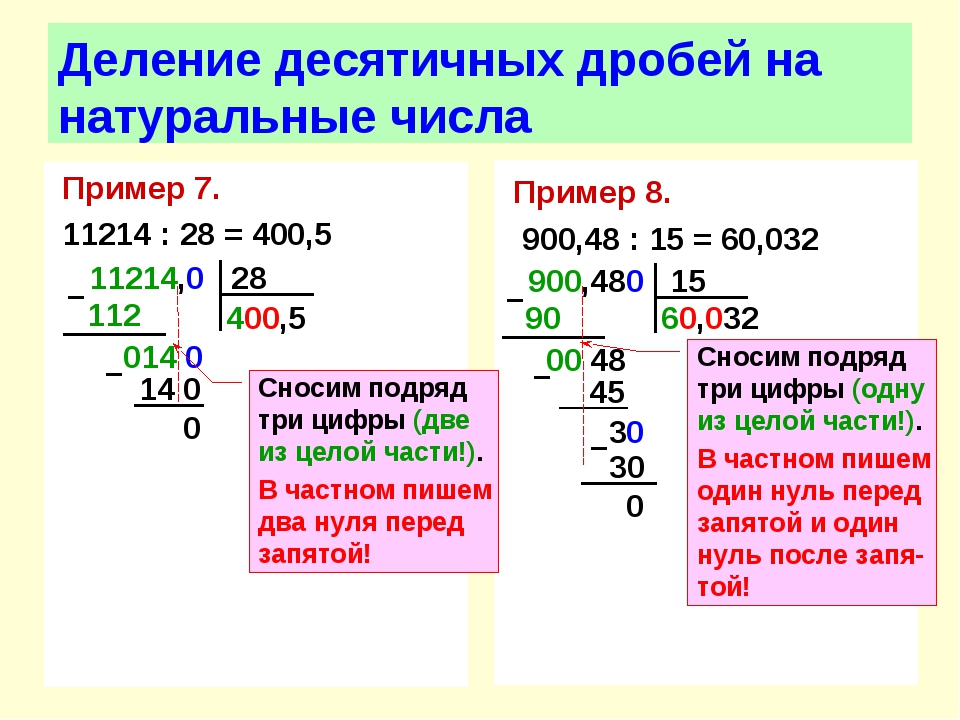 Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз. А у нас 84! Не подходит.
А у нас 84! Не подходит.  Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
 Сначала проверим, подойдет ли она. Умножим . . Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного.
Сначала проверим, подойдет ли она. Умножим . . Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. Умножим . А 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим . А . Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Умножим . А 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим . А . Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.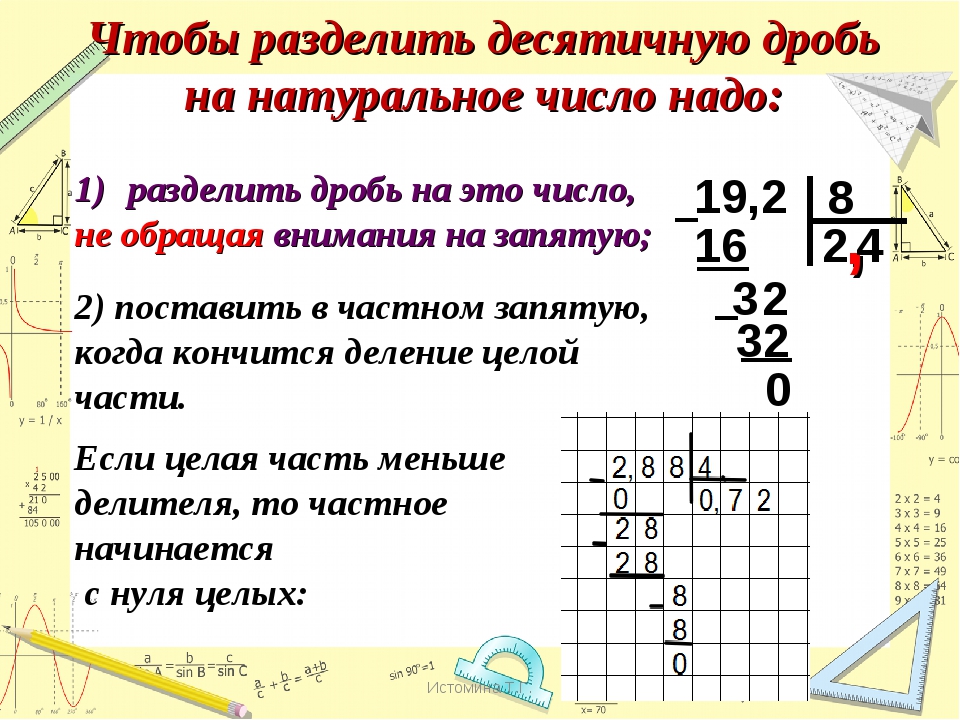
 Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
 А именно, результатом умножения.
А именно, результатом умножения. Число 5 два раза входит в число 10.
Число 5 два раза входит в число 10.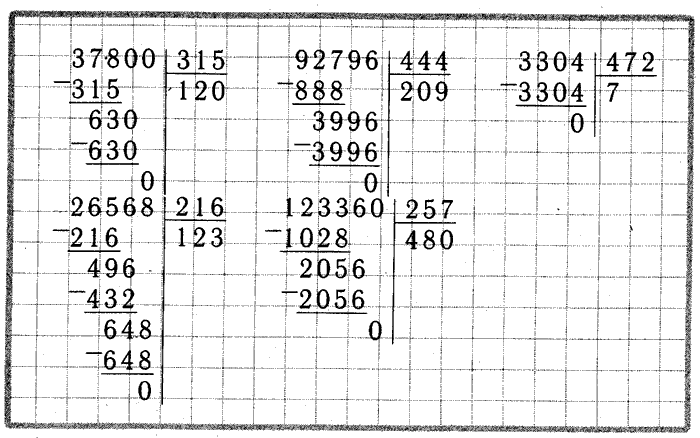 Запишите в столбик задачу.
Запишите в столбик задачу. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
 Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).
Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).
 Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5).
Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5). Разберем деление в столбик на примере деления трехзначного числа на однозначное по алгоритму.
Разберем деление в столбик на примере деления трехзначного числа на однозначное по алгоритму. Ставлю 3 точки под уголком.
Ставлю 3 точки под уголком.
 Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого: Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6: Допустим нам нужно разделить 9027 на 9.
Допустим нам нужно разделить 9027 на 9.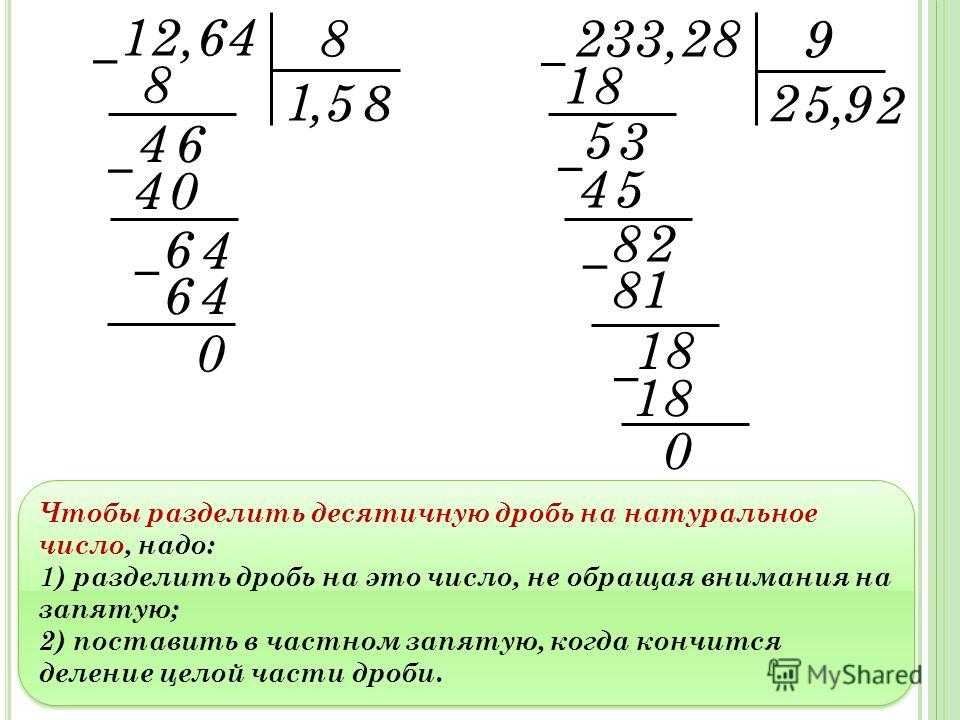 Пусть нам требуется разделить 3000 на 6.
Пусть нам требуется разделить 3000 на 6. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
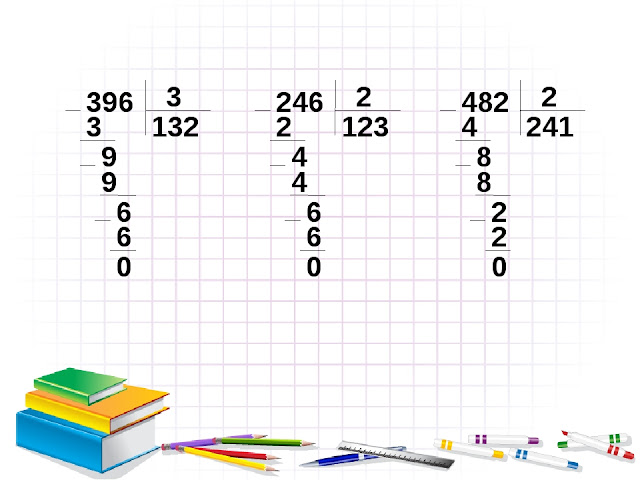 Вся новая математика основана на существующих математических концепциях. Сэр Исаак Ньютон, знаменитый ученый и математик, однажды написал: «Если я и видел дальше, то потому, что стоял на плечах гигантов». Это означает, что мы открываем истину, опираясь на предыдущие открытия. Поэтому важно, чтобы мы изучили основу как можно лучше. Это откроет математику, которую нам еще предстоит изучить. Без прочного фундамента нам будет трудно следовать за классом в последующие годы. Подобно строительству дома, мы должны стремиться к максимально полному фундаменту. Трещины должны быть устранены, прежде чем строительство может быть продолжено.
Вся новая математика основана на существующих математических концепциях. Сэр Исаак Ньютон, знаменитый ученый и математик, однажды написал: «Если я и видел дальше, то потому, что стоял на плечах гигантов». Это означает, что мы открываем истину, опираясь на предыдущие открытия. Поэтому важно, чтобы мы изучили основу как можно лучше. Это откроет математику, которую нам еще предстоит изучить. Без прочного фундамента нам будет трудно следовать за классом в последующие годы. Подобно строительству дома, мы должны стремиться к максимально полному фундаменту. Трещины должны быть устранены, прежде чем строительство может быть продолжено. Школьный совет издает учебную программу (или математический стандарт), которой должны следовать школы. Учебная программа варьируется по всему миру. Например. в России таблица умножения начинается с 1 класса, а в Онтарио — с 3 класса. Это означает, что учебная программа вашей школы отличается от той, которую вы можете найти в Интернете. В этой статье мы рассмотрим оценку того, что вы можете ожидать от учебной программы вашей школы.
Школьный совет издает учебную программу (или математический стандарт), которой должны следовать школы. Учебная программа варьируется по всему миру. Например. в России таблица умножения начинается с 1 класса, а в Онтарио — с 3 класса. Это означает, что учебная программа вашей школы отличается от той, которую вы можете найти в Интернете. В этой статье мы рассмотрим оценку того, что вы можете ожидать от учебной программы вашей школы.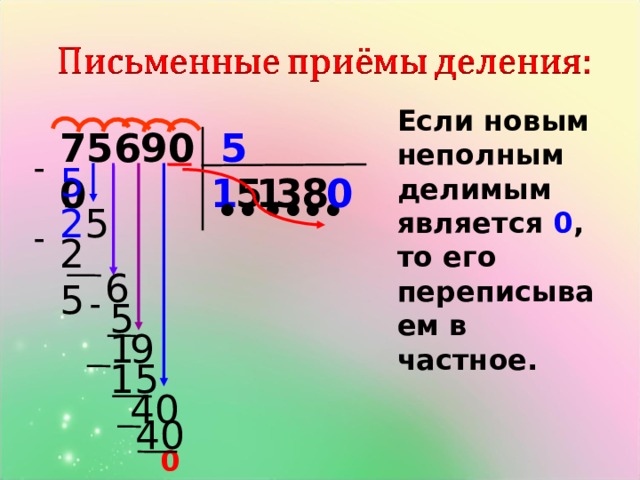 Числа работают так, что каждая цифра имеет позицию. Есть 1 позиция. Есть 10-е место. Есть позиция 100. Это полезно, потому что позволяет числу представлять что-то очень большое. Подумайте о числе 973. 9 представляет 9 сотен, 7 представляет 7 десятков, а 3 представляет 3 единицы. Сложите все это вместе, и вы получите (9 х 100) + (7 х 10) + (3 х 1) = 973. Вот как вы представляете большие вещи. На самом деле вы можете продолжать подниматься вверх вечно! Точно так же число позволяет представлять что-то очень маленькое. Посмотрим, как.
Числа работают так, что каждая цифра имеет позицию. Есть 1 позиция. Есть 10-е место. Есть позиция 100. Это полезно, потому что позволяет числу представлять что-то очень большое. Подумайте о числе 973. 9 представляет 9 сотен, 7 представляет 7 десятков, а 3 представляет 3 единицы. Сложите все это вместе, и вы получите (9 х 100) + (7 х 10) + (3 х 1) = 973. Вот как вы представляете большие вещи. На самом деле вы можете продолжать подниматься вверх вечно! Точно так же число позволяет представлять что-то очень маленькое. Посмотрим, как. Вот как вы можете представлять маленькие вещи. На самом деле вы можете продолжать снижаться в значении места навсегда!
Вот как вы можете представлять маленькие вещи. На самом деле вы можете продолжать снижаться в значении места навсегда! Теперь поймите, что это то же самое, что иметь 2 в десятых и 5 в сотых, поэтому 25/100 = 0,25
Теперь поймите, что это то же самое, что иметь 2 в десятых и 5 в сотых, поэтому 25/100 = 0,25 Практика делает совершенным!
Практика делает совершенным!
 Мы разбиваем задачу на более простые задачи, спрашивая, сколько раз делитель может содержаться в цифре. Затем мы вычитаем общее количество, чтобы получить остаток. Мы делим этот остаток на следующую наименьшую цифру-заполнитель. Мы повторяем этот процесс до тех пор, пока у нас не останется цифр для деления.
Мы разбиваем задачу на более простые задачи, спрашивая, сколько раз делитель может содержаться в цифре. Затем мы вычитаем общее количество, чтобы получить остаток. Мы делим этот остаток на следующую наименьшую цифру-заполнитель. Мы повторяем этот процесс до тех пор, пока у нас не останется цифр для деления. В этом видео показано, как делить дроби и чем это похоже на умножение обратной.
В этом видео показано, как делить дроби и чем это похоже на умножение обратной. Процесс одинаков независимо от того, какие числа вы используете.
Процесс одинаков независимо от того, какие числа вы используете. Запишите 2 в разряде сотен над 9. Вычтите: 9 -8 = 1. Опусти вниз: следующая цифра 938 — 3. Напиши ее рядом с 1, чтобы получилось 13. Повтори все шаги. 4 × 3 = 12, что ближе всего к 13. Напишите цифру 3 в разряде десятков над чертой. Вычтите 13 – 12, чтобы получить 1. Сократите последнюю цифру, 6, чтобы получить 16. Повторите шаги еще раз. 4 × 4 = 16. Напишите 4 над разрядом единиц. 16 – 16 = 0. Не осталось цифр, которые нужно сбить, так что все готово! Число над строкой равно 234, а последнее вычитание дало 0,9.36 ÷ 4 = 234. Попробуйте сами: что такое 875 ÷ 7?
Запишите 2 в разряде сотен над 9. Вычтите: 9 -8 = 1. Опусти вниз: следующая цифра 938 — 3. Напиши ее рядом с 1, чтобы получилось 13. Повтори все шаги. 4 × 3 = 12, что ближе всего к 13. Напишите цифру 3 в разряде десятков над чертой. Вычтите 13 – 12, чтобы получить 1. Сократите последнюю цифру, 6, чтобы получить 16. Повторите шаги еще раз. 4 × 4 = 16. Напишите 4 над разрядом единиц. 16 – 16 = 0. Не осталось цифр, которые нужно сбить, так что все готово! Число над строкой равно 234, а последнее вычитание дало 0,9.36 ÷ 4 = 234. Попробуйте сами: что такое 875 ÷ 7?  Начните с 9в 938. Умножение: какое число, кратное 4, ближе всего к (но меньше) 9? 4 × 2 = 8. Запишите 2 в разряде сотен над 9. Вычтите: 9 -8 = 1. Опусти вниз: следующая цифра 938 — 3. Напиши ее рядом с 1, чтобы получилось 13. Повтори все шаги. 4 × 3 = 12, что ближе всего к 13. Напишите цифру 3 в разряде десятков над чертой. Вычтите 13 – 12, чтобы получить 1. Сократите последнюю цифру, 6, чтобы получить 16. Повторите шаги еще раз. 4 × 4 = 16. Напишите 4 над разрядом единиц. 16 – 16 = 0. Не осталось цифр, которые нужно сбить, так что все готово! Число над строкой равно 234, а последнее вычитание дало 0,9.36 ÷ 4 = 234. Попробуйте сами: что такое 875 ÷ 7?
Начните с 9в 938. Умножение: какое число, кратное 4, ближе всего к (но меньше) 9? 4 × 2 = 8. Запишите 2 в разряде сотен над 9. Вычтите: 9 -8 = 1. Опусти вниз: следующая цифра 938 — 3. Напиши ее рядом с 1, чтобы получилось 13. Повтори все шаги. 4 × 3 = 12, что ближе всего к 13. Напишите цифру 3 в разряде десятков над чертой. Вычтите 13 – 12, чтобы получить 1. Сократите последнюю цифру, 6, чтобы получить 16. Повторите шаги еще раз. 4 × 4 = 16. Напишите 4 над разрядом единиц. 16 – 16 = 0. Не осталось цифр, которые нужно сбить, так что все готово! Число над строкой равно 234, а последнее вычитание дало 0,9.36 ÷ 4 = 234. Попробуйте сами: что такое 875 ÷ 7? Какое число, кратное 6, ближе всего к 14? 6 × 2 = 12. Напишите 2 в разряде сотен. Вычтите: 14 – 12 = 2. Сократите следующую цифру, 2, чтобы получить 22. Какое число, кратное 6, ближе всего к 22? 6 × 3 = 18. Напишите 3 в разряде десятков. Вычтите: 22 – 18 = 4. Сократите следующую цифру, 1, чтобы получить 41. Какое число, кратное 6, ближе всего к 41? 6 × 6 = 36. Напишите 6 над единицами. Вычтите: 41 – 36 = 5. Больше нет цифр, которые нужно сводить. 5 меньше 6, поэтому 5 нельзя разделить на 6 групп. 1421 ÷ 6 = 236 с остатком 5. Каждый день вам нужно проезжать чуть больше 236 миль. Попробуйте сами: Разделить 2576 ÷ 8.
Какое число, кратное 6, ближе всего к 14? 6 × 2 = 12. Напишите 2 в разряде сотен. Вычтите: 14 – 12 = 2. Сократите следующую цифру, 2, чтобы получить 22. Какое число, кратное 6, ближе всего к 22? 6 × 3 = 18. Напишите 3 в разряде десятков. Вычтите: 22 – 18 = 4. Сократите следующую цифру, 1, чтобы получить 41. Какое число, кратное 6, ближе всего к 41? 6 × 6 = 36. Напишите 6 над единицами. Вычтите: 41 – 36 = 5. Больше нет цифр, которые нужно сводить. 5 меньше 6, поэтому 5 нельзя разделить на 6 групп. 1421 ÷ 6 = 236 с остатком 5. Каждый день вам нужно проезжать чуть больше 236 миль. Попробуйте сами: Разделить 2576 ÷ 8. 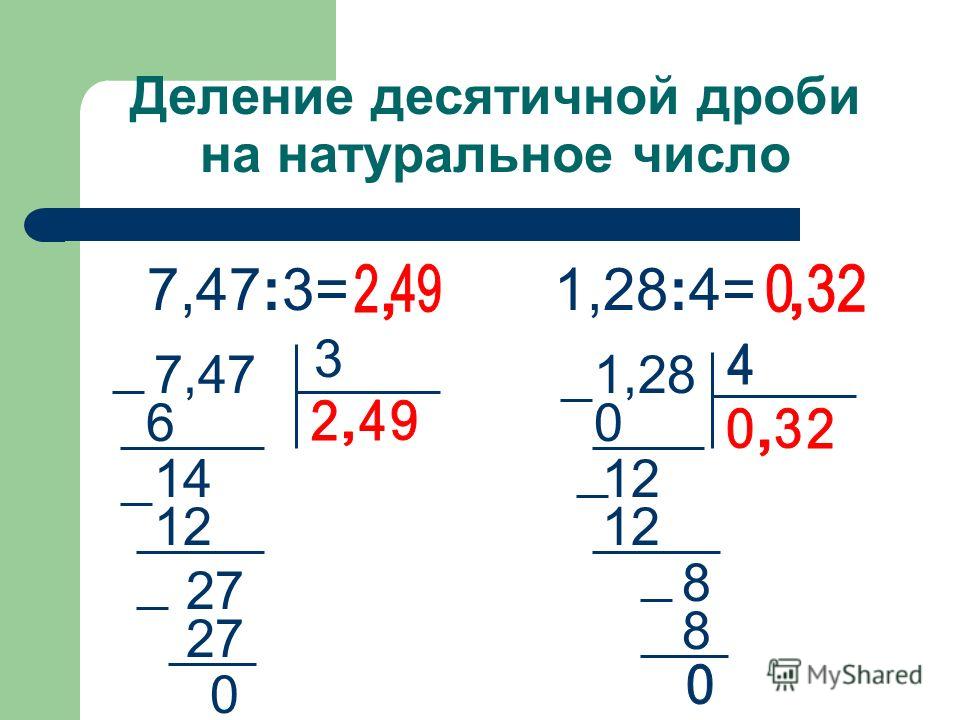 Напишите 2 в разряде сотен. Вычтите: 14 – 12 = 2. Сократите следующую цифру, 2, чтобы получить 22. Какое число, кратное 6, ближе всего к 22? 6 × 3 = 18. Напишите 3 в разряде десятков. Вычтите: 22 – 18 = 4. Сократите следующую цифру, 1, чтобы получить 41. Какое число, кратное 6, ближе всего к 41? 6 × 6 = 36. Напишите 6 над единицами. Вычтите: 41 – 36 = 5. Больше нет цифр, которые нужно сводить. 5 меньше 6, поэтому 5 нельзя разделить на 6 групп. 1421 ÷ 6 = 236 с остатком 5. Каждый день вам нужно проезжать чуть больше 236 миль. Попробуйте сами: разделите 2576 ÷ 8,9.0011
Напишите 2 в разряде сотен. Вычтите: 14 – 12 = 2. Сократите следующую цифру, 2, чтобы получить 22. Какое число, кратное 6, ближе всего к 22? 6 × 3 = 18. Напишите 3 в разряде десятков. Вычтите: 22 – 18 = 4. Сократите следующую цифру, 1, чтобы получить 41. Какое число, кратное 6, ближе всего к 41? 6 × 6 = 36. Напишите 6 над единицами. Вычтите: 41 – 36 = 5. Больше нет цифр, которые нужно сводить. 5 меньше 6, поэтому 5 нельзя разделить на 6 групп. 1421 ÷ 6 = 236 с остатком 5. Каждый день вам нужно проезжать чуть больше 236 миль. Попробуйте сами: разделите 2576 ÷ 8,9.0011 Сократите 4, чтобы получить 24. Какое число, кратное 12, ближе всего к 24? 12 × 2 = 24, поэтому запишите 2 в позиции единиц и вычтите, чтобы найти остаток 24 – 24 = 0. Больше нет цифр, которые нужно записывать. 384 ÷ 12 = 32. Вы можете дать каждому учителю по 32 печенья. Ням! Попробуйте сами: Что такое 224 ÷ 32?
Сократите 4, чтобы получить 24. Какое число, кратное 12, ближе всего к 24? 12 × 2 = 24, поэтому запишите 2 в позиции единиц и вычтите, чтобы найти остаток 24 – 24 = 0. Больше нет цифр, которые нужно записывать. 384 ÷ 12 = 32. Вы можете дать каждому учителю по 32 печенья. Ням! Попробуйте сами: Что такое 224 ÷ 32?  Ням! Попробуйте сами: что такое 224 ÷ 32?
Ням! Попробуйте сами: что такое 224 ÷ 32? Если у нас есть в общей сложности 31 359пчелы, сколько яблонь они могут опылить? Решите 31 359 ÷ 23, используя стандартный алгоритм деления в большую сторону. Рассмотрим первые две цифры числа 31 359. Какое число, кратное 23, ближе всего к 31? 23 × 1 = 23, поэтому запишите 1 в разряде тысяч и вычтите, чтобы найти разницу: 31 – 23 = 8. Сократите 3, чтобы получить 83. 23 × 3 = 69, поэтому запишите 3 в разряде сотен и вычтите чтобы найти разницу: 83 – 69 = 14. Уменьшите 5, чтобы получить 145. 23 × 6 = 138, поэтому запишите 6 в разряде десятков и вычтите 145-138 = 7. Сбить 9чтобы получить 79. 23 × 3 = 69, поэтому напишите 3 вместо единиц и вычтите 79-69 = 10. Больше нет цифр, которые нужно записывать, а 10 нельзя разделить на 23 равные группы. 31 359 ÷ 23 = 1 363 с остатком 10. Пчелы могут опылить 1 363 яблони. Попробуйте сами: чему равно 53 922 ÷ 43?
Если у нас есть в общей сложности 31 359пчелы, сколько яблонь они могут опылить? Решите 31 359 ÷ 23, используя стандартный алгоритм деления в большую сторону. Рассмотрим первые две цифры числа 31 359. Какое число, кратное 23, ближе всего к 31? 23 × 1 = 23, поэтому запишите 1 в разряде тысяч и вычтите, чтобы найти разницу: 31 – 23 = 8. Сократите 3, чтобы получить 83. 23 × 3 = 69, поэтому запишите 3 в разряде сотен и вычтите чтобы найти разницу: 83 – 69 = 14. Уменьшите 5, чтобы получить 145. 23 × 6 = 138, поэтому запишите 6 в разряде десятков и вычтите 145-138 = 7. Сбить 9чтобы получить 79. 23 × 3 = 69, поэтому напишите 3 вместо единиц и вычтите 79-69 = 10. Больше нет цифр, которые нужно записывать, а 10 нельзя разделить на 23 равные группы. 31 359 ÷ 23 = 1 363 с остатком 10. Пчелы могут опылить 1 363 яблони. Попробуйте сами: чему равно 53 922 ÷ 43? Также называется методом коробки.
Также называется методом коробки.
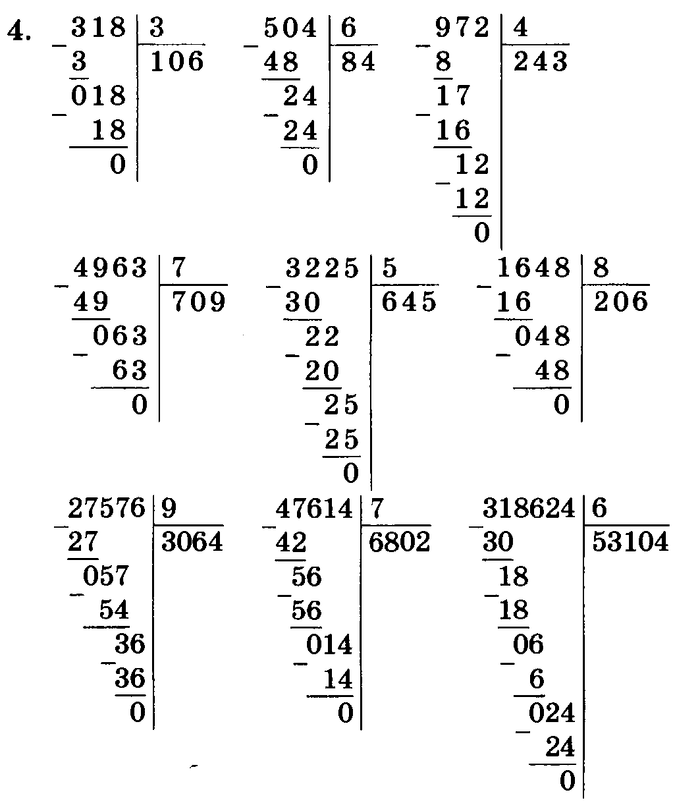 Их трудности часто связаны с одной из этих 6 причин. Используйте этот инструмент, чтобы узнать, относятся ли какие-либо из этих ситуаций к вашему ребенку. Затем получите решения, которые помогут вашему ребенку стать суперзвездой дивизиона!
Их трудности часто связаны с одной из этих 6 причин. Используйте этот инструмент, чтобы узнать, относятся ли какие-либо из этих ситуаций к вашему ребенку. Затем получите решения, которые помогут вашему ребенку стать суперзвездой дивизиона! вот еще один способ думать об этом: делимое — это целое, а делимое — это части. Некоторые люди называют это «разложением дивиденда» на множители. В Mathnasium мы предпочитаем называть это «целое и части». Мы также говорим о разделении: «Сколько их в этом?» Например: 12 ÷ 6 = означает «Сколько шестёрок в числе 12?» Точно так же 4 ÷ 1/2 = означает «Сколько 1/2 в 4?»
вот еще один способ думать об этом: делимое — это целое, а делимое — это части. Некоторые люди называют это «разложением дивиденда» на множители. В Mathnasium мы предпочитаем называть это «целое и части». Мы также говорим о разделении: «Сколько их в этом?» Например: 12 ÷ 6 = означает «Сколько шестёрок в числе 12?» Точно так же 4 ÷ 1/2 = означает «Сколько 1/2 в 4?»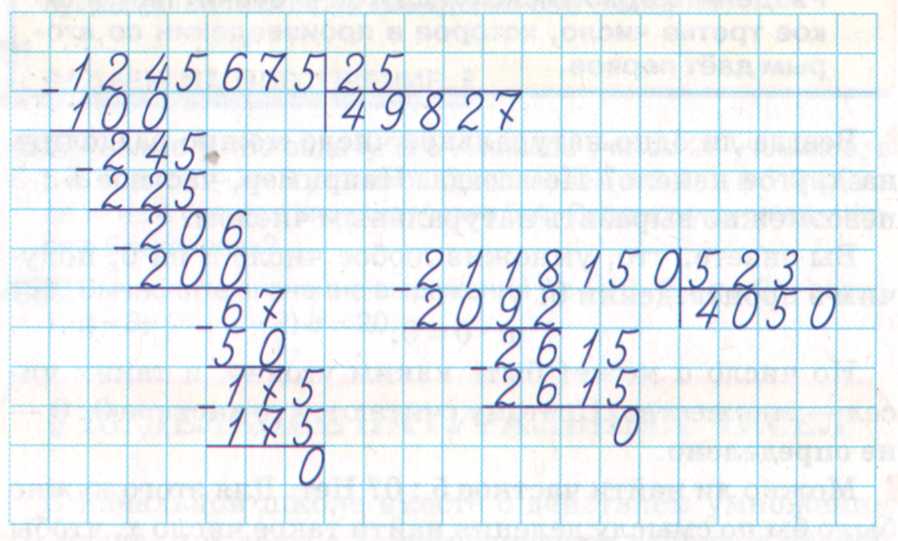
 Если вам интересно узнать больше о том, как сделать короткое деление, вот два ресурса. Один представляет собой видео, а другой представляет собой письменное объяснение, чтобы узнать больше о коротком делении. Имейте в виду, что ребенок должен иметь четкое представление о простых понятиях умножения и деления, прежде чем изучать краткое или длинное деление.
Если вам интересно узнать больше о том, как сделать короткое деление, вот два ресурса. Один представляет собой видео, а другой представляет собой письменное объяснение, чтобы узнать больше о коротком делении. Имейте в виду, что ребенок должен иметь четкое представление о простых понятиях умножения и деления, прежде чем изучать краткое или длинное деление.
 Некоторые предметы нелегко разбить. Если у вас есть 47 шаров, которые вы собираетесь разделить на 3 части, у вас получится 3 группы по 15 шаров, а затем останется два шара. Таким образом, 47 ÷ 3 = 15 остаток 2. Педагоги часто говорят детям в 3-5 классах использовать частное с остатком, а не дроби или десятичные дроби. Эта тенденция усугубляет замешательство детей в отношении значения остатка.
Некоторые предметы нелегко разбить. Если у вас есть 47 шаров, которые вы собираетесь разделить на 3 части, у вас получится 3 группы по 15 шаров, а затем останется два шара. Таким образом, 47 ÷ 3 = 15 остаток 2. Педагоги часто говорят детям в 3-5 классах использовать частное с остатком, а не дроби или десятичные дроби. Эта тенденция усугубляет замешательство детей в отношении значения остатка.