Двоичная арифметика – примеры чисел

4.5

Средняя оценка: 4.5

Всего получено оценок: 274.

4.5

Средняя оценка: 4.5

Всего получено оценок: 274.

Операции сложения, вычитания, умножения и деления в двоичной системе – это двоичная арифметика. Некоторые примеры двоичной арифметики рассмотрены в данной статье.

Двоичная арифметика

Все арифметические действия, которые применимы к двоичным числам, выполняются аналогично как в десятичной системе. Удобнее всего двоичные числа складывать, вычитать, умножать и делить столбиком.

Числа записываются друг под другом с учетом разрядов. При необходимости производится перенос в старший разряд или заем из старшего разряда.

При сложении двоичных чисел следует помнить, что в числовом двоичном ряду после 1 идет 10. Это означает, что 1 + 1 = 10, а 11 + 1= 100.

Изучению двоичной системы много времени посвятил В. Лейбниц. По его просьбе была отчеканена медаль в честь двоичной системы, на которой отображались простейшие арифметические действия с двоичными числами.

Рис. 1. Медаль в честь двоичной системы счисления

Сложение

Вычисление суммы двоичных чисел производится следующим образом: числа записываются в столбик. Затем производится поразрядное суммирование цифр, начиная с младшего разряда, как в десятичной системе. Если сумма цифр текущего разряда превышает его размер, то происходит перенос единицы в старший разряд.

Правила сложения двоичных чисел:

0 + 0 = 0

0 + 1 = 1

1 + 1 =10

Например, сумма двоичных чисел 1000111 + 110011 = 1111010

Первое слагаемое	1	0	0	0	1	1	1
Второе слагаемое		1	1	0	0	1	1
Сумма	1	1	1	1	0	1	0

На примере видно, как происходит перенос в старший разряд.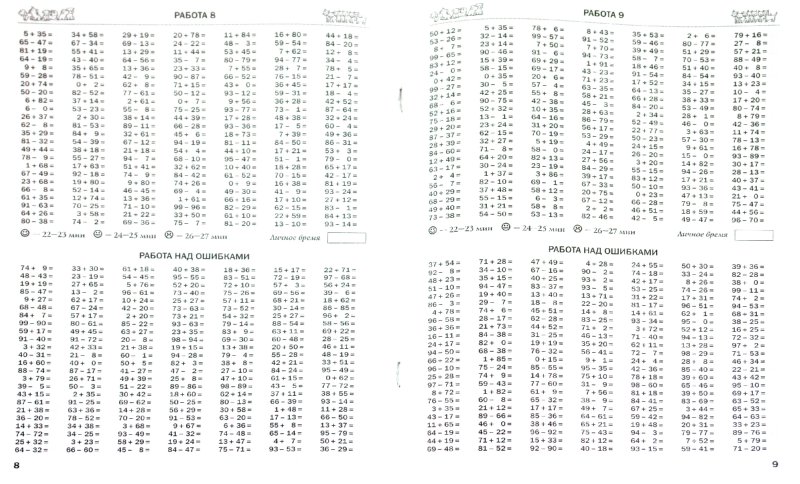 При сложении единиц самого младшего разряда получается 10. Ноль остается на своем месте, а единица переносится в старший разряд слева, где уже складываются две единицы. Получается 11. И снова, младшую единицу оставляют, а старшую переносят влево.

Вычитание

Действие разности следует также выполнять столбиком. Вычитание производится поразрядно. Если возникает ситуация, что приходится вычитать из нуля единицу, то происходит заем из старшего разряда.

Все как в десятичной системе. Только следует помнить, что в двоичной системе 10 – 1 = 1.

Например, разность чисел: 1000111 – 110011 = 10100

Уменьшаемое	1	0	0	0	1	1	1
Вычитаемое		1	1	0	0	1	1
Разность			1	0	1	0	0

На примере видно, как производится заем в старшем разряде. В пятом справа разряде производится вычитание 0 – 1. Здесь следует занять единицу из ближайшего старшего разряда слева.

Умножение

Умножать следует столбиком с учетом правил умножения:

0 * 0 = 0

0 * 1 = 0

1 * 1 = 1

Произведение выполняется также поразрядно, каждый разряд второго числа умножается на каждую цифру первого числа, результат суммируется

Произведение двоичных чисел 1101 * 11 = 100111

Первый множитель			1	1	0	1
Второй множитель					1	1
			1	1	0	1
		1	1	0	1
Итог (произведение)	1	0	0	1	1	1

Деление

Операция деления выполняется столбиком, аналогично как в десятичной системе счисления.

Рис. 2. Деление двоичных чисел

Всегда можно проверить результаты двоичной арифметики с помощью калькулятора. Считать можно и в двоичном формате. Электронный калькулятор в группе стандартных приложений операционной системы MS Windows имеет такой режим работы.

Рис. 3. Режим Программист электронного калькулятора ОС Windows

Что мы узнали?

Над двоичными числами можно выполнять арифметические операции сложения, умножения, вычитания, деления. Удобнее всего это делать столбиком. Числа следует располагать с учетом разрядов и помнить об особенностях двоичной системы.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Алексей Беляев

  5/5

Оценка статьи

4.5

Средняя оценка: 4.5

Всего получено оценок: 274.

---

А какая ваша оценка?

Как умножать в столбик | BeginPC.ru

Все мы изучали в школе методы выполнения арифметических операций над числами.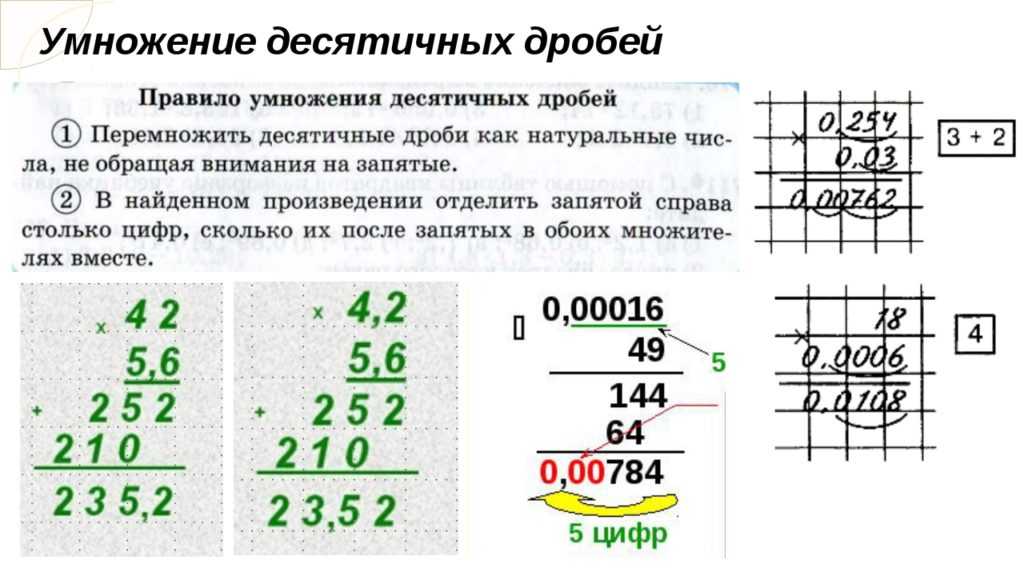 Чтобы облегчить процесс счета и ускорить его в разные времена для этого применялись различные устройства. Старшее поколение возможно еще помнит счеты и логарифмическую линейку, в то время как молодым известен только электронный калькулятор в различных его проявлениях.

Тем не менее, есть еще один универсальный способ выполнения арифметических операций без использования вспомогательных устройств известный всем с детства, это выполнения операций в столбик на листе бумаги. Мы уже рассматривали ранее сложение, вычитание и деление, а сейчас давай освежим нашу память и вспомним, как выполняется умножение в столбик.

Чтобы перемножить два числа в столбик (например 381 на 29), их нужно записать одно под другим, удобнее большее число располагается над меньшим. Кроме того необходимо разместить числа так, чтобы их разряды оказались друг над другом, то есть единицы над единицами, десятки над десятками, сотни над сотнями и так далее. Все точно также как и в случае сложения в столбик. После этого проводим под ними горизонтальную черту и пишем слева от них знак умножения «×».

Подготовительные операции выполнены, теперь переходим непосредственно к процессу перемножения. Счет идет справа налево, берем разряд единиц двух множителей в данном примере 1 и 9 и перемножаем их воспользовавшись знанием таблицы умножения. У нас получается 9, поскольку получившееся число меньше 10, то оно просто записывается под чертой в разряде единиц.

Теперь нам нужно перемножить цифру из разряда единиц нижнего числа на цифру из разряда десятков верхнего, то есть 9 на 8. В результате получается число 72, но поскольку оно больше 9, то оно разбивается на две части. Разряд единиц записывается под чертой левее ранее записанной цифры, то есть в разряде десятков, а 7 пишем над нашим столбиком, но со смещением на одну позицию вправо, над сотнями.

Следующим шагом нужно перемножить разряд единиц нижнего числа с разрядом сотен верхнего 9 на 3. Таблица умножения подсказывает, что в результате получится 27, но наверху над сотнями у нас еще записана цифра 7, значит ее нужно прибавить к 27 и в результате получится 34. Снова результат получился больше 9, значит записываем 4 под чертой в разряде сотен, но поскольку больше цифр в верхнем числе нет, то записываем 3 под чертой со смещение на одну позицию влево.

Половину дела мы сделали, перемножили 9 из нижнего множителя со всеми цифрами из верхнего. Теперь нужно сделать то же самое со второй цифрой из нижнего числа. Для этого считаем 2×1=2. Результат меньше 9, значит просто записываем его под чертой в столбце десятков, но уже на строчку ниже.

Следуя алгоритму, находим произведение чисел 2 и 8, в результате получается 16. Поскольку он больше 9, то он разбивается на две части, 6 записываем в столбце сотен под чертой, а 1 наверху столбика. Поскольку там уже есть 7 от предыдущего шага вычислений, то зачеркиваем ее, чтобы не запутаться.

Остался последний шаг, вычисляем 2×3=6 и наверху есть цифра 1, значит 6+1=7. Поскольку 7 меньше 10, то записываем ее под чертой левее предыдущей. В итоге под чертой у нас оказались два числа, как результат выполнения следующих операций 381×9=3427 и 381×2=762. Остался сущий пустяк, сложить эти два числа между собой способом сложения в столбик. Единственное что нужно отметить это то, что в позиции ниже 9 и правее 2 находится 0, который мы не записали.

В результате мы нашли произведение двух чисел методом умножения в столбик и получили результат 11049. Кажется все очень сложно, но на самом деле долго объяснять, а когда дело доходит до практических вычислений все оказывается довольно быстро.

Фактически данный способ сводится к разбиению одного из множителей на составляющие его цифры, перемножение этих чисел с другим множителем и умножении получившегося числа на соответствующий разряд, а затем сложение получившихся чисел.

Предыдущий пример выглядит следующим образом, 9×381=3429 и поскольку 9 из разряда единиц, то 3429×1=3429. Идем дальше 2×381=762, поскольку 2 это десятки, то 762×10=7620. Осталось сложить 3429+7620=11049. Таким образом 29×381=11049.

С тем же успехом можно было сделать наоборот, 1×29×1=29, 8×29×10=2320, 3×29×100=8700. Теперь считаем 29+2320+8700=11049, результат тот же, надеюсь это никого не удивляет.

Умение выполнять арифметические операции без помощи калькулятора может сослужить хорошую службу даже в наш век повсеместного использования компьютеров. Впрочем, пересчитывать единицы информации все таки гораздо проще в онлайн-конвертере.

Сложение, вычитание, умножение и деление Рабочие листы

Сложение, вычитание, умножение и деление — это основные математические операции, которые учащиеся должны освоить в раннем возрасте. Этот набор дифференцированных рабочих листов включает многозначные целые числа и содержит вопросы с несколькими вариантами ответов и открытые вопросы.

Рабочие листы на сложение и вычитание предполагают перегруппировку и не перегруппировывают.

Рабочие листы умножения включают умножение с использованием моделей площадей, частичных произведений и стандартного алгоритма.

Рабочие листы деления включают деление с использованием моделей площадей, частичное частное и длинное деление.

Вы можете использовать эти неподготовительные листы для повторения вместе с учащимися или для проверки их понимания сложения, вычитания, умножения и деления с использованием различных стратегий. Рабочие листы можно использовать для утренней работы, домашних заданий, разминки и многого другого.

*** Приобретая этот пакет, вы можете сэкономить $$ (30%) ***

 

*** Моя платежная платформа не получает платеж в

ДОЛЛАРЫ СОЕДИНЕННЫХ ШТАТОВ (США)    долларов США . Используйте конвертер валют справа, чтобы изменить валюту на GHANA CEDI    GHS  перед оформлением заказа. ***

 

 

Этот комплект содержит 15 продуктов . Каждый продукт состоит из двух версий для печати .

1.   Рабочие листы со стандартами (4.NBT.B.4, 4.NBT.B.5 или 4.NBT.B.6) в списке
2.   Версия рабочих листов без перечисленных стандартов

 

Каждая версия содержит два набора рабочих листов .

• Набор A: Вопросы с несколькими вариантами ответов – обведите правильный ответ (A, B, C или D)
• Набор B: Открытые вопросы – Решите/покажите свою работу

Средства отслеживания данных и ключи ответов в комплекте

 

Покрываемые навыки

• Сложение и вычитание без перегруппировки
• Сложение и вычитание с перегруппировкой
• Умножение 2 цифр на 1 цифру с использованием различных стратегий
• Умножение 3 цифр на 1 цифру с использованием различных стратегий
• Умножение 4 цифр на 1 цифру с использованием различных стратегий
• Умножение двух цифр на две цифры с использованием различных стратегий
• 2-значное деление на 1-значное длинное деление
• 3-значное на 1-значное длинное деление
• 4-значное деление на 1-значное длинное деление
• 2-значное на 1-значное деление модели области
• 3-значное на 1-значное деление модели области
• 4-значное на 1-значное деление модели области
• 2-значное деление на 1-значное частичное частное
• Разделение частичных частных на 3 цифры на 1 цифру
• 4-разрядное деление на 1-значное частичное частное

 

Вы также можете приобрести этот товар в других моих магазинах.

TPT Store

Сделано Teachers Store

Длинный мультипликационный калькулятор

, созданный WOJCIECH SAS, PHD

Обзор STEVEVING

: содержание:

• Как вы умножаете десятичные дроби?
• Как сделать длинное умножение?
• Длинное умножение с десятичными дробями
• Как умножать большие числа? Алгоритм умножения на практике
• Как (и когда) использовать калькулятор длинного умножения?

Добро пожаловать в калькулятор длинного умножения — отличный инструмент, который поможет вам самостоятельно решить задачу умножения. Если вы когда-нибудь спрашивали себя: Как вы умножаете десятичные дроби? или Как умножать большие числа? , вот правильное место, чтобы найти ответ.

Знание основного алгоритма умножения позволяет решать более сложные задачи, такие как умножение дробей или матриц. Кроме того, если вы научитесь выполнять умножение в длину, а также потренируетесь с калькулятором деления в длину, это сделает математические упражнения с операциями над числами такими простыми, как никогда раньше!

Если вы хотите попробовать альтернативный подход к умножению больших чисел, воспользуйтесь калькулятором частичных произведений Omni!

Как умножать десятичные дроби?

Начнем с основ — умножение — это компактный способ записи сложения повторяющихся чисел. Если мы хотим решить такую ​​задачу, как 6×2 , это будет то же самое, как если бы мы должны были сложить 2 шесть раз, 2+2+2+2+2+2 . В этом смысле умножение чрезвычайно полезно, особенно для больших чисел.

Математики называют первое число в умножении множителем , а второе число множимым . Результат умножения — произведение .

💡 Умножение коммутативно . Это означает, что мы можем изменить множитель и множимое местами , и результат не изменится.

С самого начала обучения мы все учимся умножать числа от одного до десяти — кошмар большинства школьников, не так ли? Но на самом деле это все, что вам нужно знать о том, как умножать большие числа или как долго работает умножение с десятичными дробями!

Итак, как умножать десятичные дроби? Короче говоря, забудьте о десятичной точке и выполняйте умножение с целыми числами. Далее складываем десятичные разряды в множителе и множимом . Сумма – это количество знаков после запятой в произведении. Мы подробно опишем весь процесс в специальном разделе ниже.

Как сделать длинное умножение?

Алгоритм длинного умножения можно описать в несколько шагов:

1. Поставить оба числа одно под другим и выровняйте их по правому краю так, чтобы первые значащие цифры были первыми справа.

🙋 Хорошей практикой является установка большего числа как множителя, а меньшего как множимого. Это не меняет произведение, но уменьшает количество шагов .

2. Начните умножать множитель на первую цифру (справа) множимого, цифра за цифрой. Каждый раз, когда вы заканчиваете с числом больше 9, запишите цифру единиц, а перенесите цифру десятков на следующий шаг

   (например, 7×5=35 , поэтому напишите 5 и перенесите 3 ).

3. Повторить для остальных цифр множителя. Всякий раз, когда вы носите число, добавьте его к продукту (например, 1×5 и 3 , перенесенные из предыдущего шага, дают нам 8 ).

4. Когда вы закончите с первой цифрой множимого, вы получите первые промежуточный продукт .

5. Повторите ту же процедуру для остальных цифр множимого, каждый раз начиная с одной позиции справа от (при умножении на десятки, сотни и т. д.). Вы также можете написать конечные нули, если хотите.

🙋 Если в множимом встречаются какие-либо 0 цифры, то можно пропустить шаг , так как произведение нуля и любого другого числа всегда равно нулю.

6. Когда вы закончите со всеми промежуточными продуктами, сложите их .

7. Результат – ваш конечный продукт. Теперь вы знаете, как делать длинное умножение!

Длинное умножение с десятичными дробями

Давайте перейдем на следующий уровень и узнаем, как умножать десятичные дроби, используя метод длинного умножения. Например, умножим 4,37 на 8,5 . Оказывается, мы можем рассматривать ее как задачу на умножение трех и двух цифр. Чтобы получить ответ, мы можем выполнить следующие шаги:

1. Подсчитайте количество десятичных цифр в обоих числах . В первом два десятичных знака, во втором один десятичный.

2. Сумма десятичных цифр в множителе и множимом равна трем ( 2+1 ). У нас также будет с тремя десятичными знаками в произведении .

3. На этом этапе мы можем забыть о десятичных точках и выполнить умножение 437 × 85 .

4. Продукт 437 и 5 равен 2185 .

5. Продукт 437 и 8 равен 3496 . Не забудьте начать писать на одно место справа. В качестве альтернативы вы можете добавить один 0 в конце, чтобы продукт стал 34960 , и тогда оба числа были выровнены по правому краю.

6. Оцените сумму этих двух промежуточных продуктов. 2185 + 34960 = 37145 .

7. Наконец, применяет десятичную точку к произведению . Мы знаем, что должно быть три десятичных цифры , поэтому наш результат равен 37,145 .

Если вы сомневаетесь, заблудились в какой-то момент или просто хотите проверить ответ, вы всегда можете воспользоваться нашим калькулятором длинного умножения!

Как умножать большие числа? Алгоритм умножения на практике

Преимущество длинного умножения в том, что оно не усложняет задачу для больших чисел. Что имеет значение длина чисел , а не сами значения. Более того, умножать большие числа может быть еще проще, если какое-либо из них (или оба) оканчивается несколькими нулями в конце. Почему?

Мы можем просто пропустить конечные нули для умножения , так как любые промежуточные продукты будут равны нулю. Мы можем добавить конечные нули как из множителя, так и из множимого и записать их рядом с произведением . Процедура очень похожа на процедуру с десятичными дробями.

Давайте применим алгоритм длинного умножения для двух больших чисел, скажем, 34000 и 2870 :

1. Подсчитать количество нулей в конце в обоих случаях . Их три в первом числе и один ноль во втором.

2. Теперь наши новые значения равны 34 и 287 соответственно. Обратите внимание, что в данном случае первое число короче второго (в отличие от исходных чисел). мы можем поменять местами и выполнить умножение 287 на 34 .

3. Первый промежуточный продукт — 1148 , а второй — 861 (помните о смещении этого числа на одну цифру влево). Суммируя их, получаем 9758 .

4. Пришло время применить недостающие нули в конце к продукту . Всего у нас их четыре.

5. Окончательный результат длинного умножения равен 97 580 000 . Мы даже можем записать это как 9,758 × 10⁷ , используя экспоненциальную запись.

Как (и когда) использовать калькулятор длинного умножения?

Вы когда-нибудь пробовали складывать или вычитать дроби? Если да, то вы, вероятно, знакомы с концепцией нахождения наименьшего общего знаменателя. Проще говоря, все дело в нахождении наименьшего общего кратного двух (или кратных) чисел. Процесс предполагает определенный навык умножения.