Признак делимости на 3: примеры, доказательство

Приступим к рассмотрению темы «Признак делимости на 3». Начнем с формулировки признака, приведем доказательство теоремы.  Затем рассмотрим основные подходы к установлению делимости на 3 чисел, значение которых задано некоторым выражением. В разделе приведен разбор решения основных типов задач, основанных на применении признака делимости на 3.

Признак делимости на 3, примеры

Формулируется признак делимости на 3 просто: целое число будет делиться на 3 без остатка, если сумма входящих в его состав цифр делится на 3. Если суммарное значение всех цифр, которые входят в состав целого числа, на 3 не делится, то и само исходное число на 3 не делится. Получить сумму всех входящих в целое число цифр можно с помощью сложения натуральных чисел.

Теперь рассмотрим примеры применения признака делимости на 3.

Пример 1

Делится ли на 3 число -42?

Решение

Для того, чтобы ответить на этот вопрос, сложим все цифры, входящие в состав числа -42: 4+2=6.

Ответ: согласно признаку делимости, раз сумма цифр, входящих с восстав исходного числа, делится на три, то и само исходное число делится на 3.

Для того, чтобы ответить на вопрос о том, делится ли на 3 число 0, нам понадобится свойство делимости, согласно которому нуль делится на любое целое число. Получается, что нуль делится на три.

Существуют задачи, для решения которых прибегать в признаку делимости на 3 необходимо несколько раз.

Пример 2

Покажите, что число 907 444 812 делится на 3.

Решение

Найдем сумму всех цифр, которые образуют запись исходного числа: 9+0+7+4+4+4+8+1+2=39. Теперь нам нужно определить, делится ли на 3 число 39. Еще раз складываем цифры, входящие в состав этого числа: 3+9=12. Нам осталось провести сложение цифр еще раз для того, чтобы получить окончательный ответ: 1+2=3. Число 3 делится на 3

Ответ: исходное число 907 444 812 также делится на 3.

Пример 3

Делится ли на 3 число −543 205?

Решение

Посчитаем сумму цифр, входящих в состав исходного числа:

5+4+3+2+0+5=19. Теперь посчитаем сумму цифр полученного числа: 1+9=10. Для того, чтобы получить окончательный ответ, найдем результат еще одного сложения: 1+0=1.
Ответ: единица на 3 не делится, значит и исходное число на 3 не делится.

Для того, чтобы определить, делится ли данное число на 3 без остатка, мы можем провести деление данного числа на 3. Если разделить число −543 205из рассмотренного выше примера столбиком на три, то в ответе мы не получим целого числа. Это точно также значит, что −543 205на 3 без остатка не делится.

Доказательство признака делимости на 3

Здесь нам понадобятся следующие навыки: разложение числа по разрядам и правило умножения на 10, 100 и т.д. Для того, чтобы провести доказательство, нам необходимо получить представление числа a вида a=an·10n+an-1·10n-1+…+a2·102+a1·10+a0, где an, an−1, …, a0 – это цифры, которые располагаются слева направо в записи числа.

Приведем пример с использованием конкретного числа: 528=500+20+8=5·100+2·10+8.

Запишем ряд равенств: 10=9+1=3·3+1, 100=99+1=33·3+1, 1 000=999+1=333·3+1 и проч.

А теперь подставим эти равенства вместо 10, 100 и 1000 в равенства, приведенные ранее a=an·10n+an-1·10n-1+…+a2·102+a1·10+a0.

Так мы пришли к равенству:

a=an·10n+…+a2·100+a1·10+a0==an·33….3·3+1+…+a2·33·3+1+a1·3·3+1+a0

А теперь применим свойства сложения и свойства умножения натуральных чисел для того, чтобы переписать полученное равенство следующим образом:

a=an·33…3·3+1+…++a2·33·3+1+a1·3·3+1+a0==3·33…3·an+an+…++3·33·a2+a2+3·3·a1+a1+a0==3·33…3·an+…++3·33·a2+3·3·a1++an+…+a2+a1+a0==3·33…3·an+…+33·a2+3·a1++an+…+a2+a1+a0

Выражение an+…+a2+a1+a0 — это сумма цифр исходного числа a. Введем для нее новое краткое обозначение А. Получаем: A=an+…+a2+a1+a0.

В этом случае представление числа a=3·33…3·an+…+33·a2+3·a1+A  принимает такой вид, который нам будет удобно использовать для доказательства признака делимости на 3.

Определение 1

Теперь вспомним следующие свойства делимости: 

• необходимым и достаточным условием для того, чтобы целое число a делилось на целое число
  ​​​​​​b, является условие, по которому модуль числа a делится на модуль числа b;
• если в равенстве a=s+t все члены, кроме какого-то одного, делятся на некоторое целое число b, то и этот один член делится на b.

Мы заложили основу для того, чтобы провести доказательство признака делимости на 3. Теперь же сформулируем этот признак в виде теоремы и докажем ее.

Теорема 1

Для того, чтобы утверждать, что целое число a делится на 3, нам необходимо и достаточно, чтобы сумма цифр, которая образует запись числа a, делилась на 3.

Доказательство 1

Если взять значение a=0, то теорема очевидна.

Если ы возьмем число a, отличное от нуля, то модуль числа a будет натуральным числом. Это позволяет нам записать следующее равенство:

a=3·33…3·an+…+33·a2+3·a1+A , где A=an+. ..+a2+a1+a0 — сумма цифр числа a.

Так как сумма и произведение целых чисел есть целое число, то 
33…3·an+…+33·a2+3·a1 — целое число, тогда по определению делимости произведение 3·33…3·an+…+33·a2+3·a1  делится на 3 при любых a0, a1, …, an.

Если сумма цифр числа a делится на 3, то есть, A делится на 3, то в силу свойства делимости, указанного перед теоремой, a  делится на 3, следовательно, a делится на 3. Так доказана достаточность.

Если a делится на 3, то и a  делится на 3, тогда в силу того же свойства делимости число

A делится на 3, то есть, сумма цифр числа a делится на 3. Так доказана необходимость.

Другие случаи делимости на

3

Целые числа могут быть заданы как значение некоторого выражения, которое содержит переменную, при определенном значении этой переменной. Так, при некотором натуральном n значение выражения  4n+3n-1 является натуральным числом. В этом случае непосредственное деление на 3 не может дать нам ответ на вопрос, делится ли число на 3. Применение признака делимости на 3 также может быть затруднено. Рассмотрим примеры таких задач и разберем методы их решения.

Для решения таких задач может быть применено несколько подходов. Суть одного из них заключается в следующем:

• представляем исходное выражение как произведение нескольких множителей;
• выясняем, может ли хотя бы один из множителей делиться на 3;
• на основе свойства делимости делаем вывод о том, что все произведение делится на 3.

В ходе решения часто приходится прибегать к использованию формулы бинома Ньютона.

Пример 4

Делится ли значение выражения 4n+3n-1 на 3 при любом натуральном n?

Решение

Запишем равенство 4n+3n-4=(3+1)n+3n-4. Применим формулу бинома Ньютона бинома Ньютона:

4n+3n-4=(3+1)n+3n-4==(Cn0·3n+Cn1·3n-1·1+…++Cnn-2·32·1n-2+Cnn-1·3·1n-1+Cnn·1n)++3n-4==3n+Cn1·3n-1·1+. ..+Cnn-2·32+n·3+1++3n-4==3n+Cn1·3n-1·1+…+Cnn-2·32+6n-3

Теперь вынесем 3 за скобки:3·3n-1+Cn1·3n-2+…+Cnn-2·3+2n-1. Полученное произведение содержит множитель 3, а значение выражения в скобках при натуральных n представляет собой натуральное число. Это позволяет нам утверждать, что полученное произведение и исходное выражение 4n+3n-1 делится на 3.

Ответ: Да.

Также мы можем применить метод математической индукции.

Пример 5

Докажите с использованием метода математической индукции, что при любом натуральном
n значение выраженияn·n2+5 делится на 3.

Решение

Найдем значение выражения n·n2+5 при n=1: 1·12+5=6. 6 делится на 3.

Теперь предположим, что значение выражения n·n2+5 при  n=k делится на 3. Фактически, нам придется работать с выражением k·k2+5 , которое, как мы ожидаем, будет делиться на 3.

Учитывая, что k·k2+5 делится на 3, покажем, что значение выражения n·n2+5 при n=k+1 делится на 3, то есть, покажем, что k+1·k+12+5 делится на 3.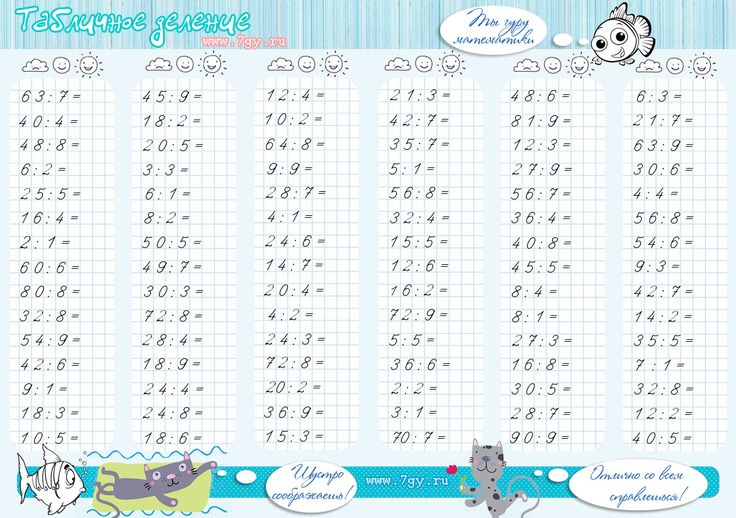

Выполним преобразования:

k+1·k+12+5==(k+1)·(k2+2k+6)==k·(k2+2k+6)+k2+2k+6==k·(k2+5+2k+1)+k2+2k+6==k·(k2+5)+k·2k+1+k2+2k+6==k·(k2+5)+3k2+3k+6==k·(k2+5)+3·k2+k+2

Выражение k·(k2+5) делится на 3 и выражение 3·k2+k+2 делится на 3, поэтому их сумма делится на 3.

Так мы доказали, что значение выражения n·(n2+5) делится на 3 при любом натуральном n.

Теперь разберем подход к доказательству делимости на 3, которых основан на следующем алгоритме действий:

• показываем, что значение данного выражения с переменной n при n=3·m, n=3·m+1 и n=3·m+2, где m – произвольное целое число, делится на 3;
• делаем вывод о том, что выражение будет делиться на 3 при любом целом n.

Для того, чтобы не отвлекать внимание от второстепенных деталей, применим данный алгоритм к решению предыдущего примера.

Пример 6

Покажите, что n·(n2+5)  делится на 3 при любом натуральном n.

Решение

Предположим, что n=3·m.

Тогда: n·n2+5=3m·3m2+5=3m·9m2+5 . Произведение, которое мы получили, содержит множитель 3, следовательно само произведение делится на 3.

Предположим, что n=3·m+1. Тогда:

n·n2+5=3m·3m2+5=(3m+1)·9m2+6m+6==3m+1·3·(2m2+2m+2)

Произведение, которое мы получили, делится на 3.

Предположим, что n=3·m+2. Тогда:

n·n2+5=3m+1·3m+22+5=3m+2·9m2+12m+9==3m+2·3·3m2+4m+3

Это произведение также делится на 3.

Ответ: Так мы доказали, что выражение n·n2+5 делится на 3 при любом натуральном n.

Пример 7

Делится ли на 3 значение выражения 103n+102n+1  при некотором натуральном n.

Решение

Предположим что n=1. Получаем:

103n+102n+1=103+102+1=1000+100+1=1104

Если посчитать сумму цифр полученного числа, то получим 3. Это позволяет нам утверждать, что полученное число делится на 3.

Предположим, что

n=2. Получаем:

103n+102n+1=106+104+1=1000 000+10000+1=1010001

Если посчитать сумму цифр этого числа, то мы снова получаем три. Это позволяет нам утверждать, что полученное число делится на 3.

Так мы можем сделать вывод, что при любом натуральном n мы будем получать числа, которые делятся на 3. Это значит, что 103n+102n+1 при любом натуральном n делится на 3.

Ответ: Да

Деление двузначного числа на однозначное 3 класс, примеры с ответами

Автор: admin

Категория: Математика

Опубликовано: 28 сентября 2021

Тема по математике 3 класс «Деление двузначного числа на однозначное». Дан алгоритм решения и карточка с примерами и ответами.

Решая такие примеры по предложенному алгоритму, объясните ребенку что необходимо вслух проговаривать этот алгоритм. Так быстрее запомнится решение. То есть ребенок должен научится рассуждать, как удобнее будет ему решить этот пример.
Используя алгоритм решения деление двузначного числа на однозначное (он дан в первой таблице), решите примеры из карточки (вторая таблица).

Начинайте решение, представив в голове, как удобнее разложить число на сумму разрядных слагаемых.

Решать примеры можно прямо в распечатанной таблице.

1 таблица алгоритм решения:

2 таблица карточка с примерами:

Ответы: 1-13, 2-14, 3-13, 4-21, 5-13, 6-12, 7-36, 8-41, 9-14, 10-16, 11-15, 12-28, 13-31, 14-12, 15-22, 16-23, 17-11, 18-19, 19-7, 20-8.

Сохраните материал в вашей социальной сети, чтобы легко найти его:

Ответы на домашние задания:

• Как записать цифры в порядке убывания, таблица.
• Виды феминизма и их различие
• Запущен телескоп ‘GOTO’ для обнаружения оптических сигналов от гравитационных волн
• Как найти арифметическую прогрессию формула по математике 9 класс
• org/Article»>Характеристики капитализма
• Что такое ион в химии? (Катионы и анионы. Электрохимия. Энтальпия и энтропия связи)
• Математика в футболе
• Где на карте мира расположена Албания
• Сленговые слова в английском языке с переводом
• Таблица растворимости кислот оснований и солей в воде по химии
• Что такое юснатурализм
• Важность робототехники для детей в школе
• Тренажеры вычисления
• Значение планетария в образовании
• Что такое поведение в биологии

• Назад
• Вперед

Деление однозначных, двухзначных и трехзначных чисел (определение, типы и примеры)

Содержание

• Что такое деление?
• Что такое дивиденд, делитель, частное и остаток?
• Деление на однозначные числа
• Деление трехзначных чисел на двузначные числа
• Деление четырехзначного числа на двузначное число
• Решаемые примеры
• Часто задаваемые вопросы

Что такое деление?

В математике есть четыре основных действия: сложение, вычитание, умножение и деление. Деление — это процесс деления чисел на равные части или равные доли. Предположим, 25 студентов нужно разделить на баскетбольные команды по 5 игроков в каждой. Чтобы найти количество баскетбольных команд, мы делим 25 на 5 = 5. Это означает, что учеников можно разделить на 5 команд поровну. Здесь 25 известно как делимое, 5 известно как делитель, а результат 5 известен как частное.

Что такое делимое, делитель, частное и остаток?

Общая форма деления: \(\text{Дивиденд}\div \text{Дивизор}=\text{Частное}\)

Деление также может быть записано как \(\frac{\text{Дивиденд}} {\text{Делитель}}=\text{Частное}\)

Делимое — это число, которое делится в операции деления. Делитель — это число, на которое делится делимое. Частное есть результат операции деления.

 

Во многих случаях делитель не может полностью делить делимое. В таких случаях мы получаем остаток после операции деления. Остаток — это остаточное значение, которое мы получаем после операции деления.

 

 

 

Предположим, вы хотите раздать 15 файлов cookie поровну между 4 друзьями. Вы можете раздать своим друзьям только 12 файлов cookie, если хотите, чтобы каждый из них получил одинаковую долю. Оставшиеся 3 файла cookie представляют остаток. Результат операции деления можно записать как 3 R 3, где 3 — частное, а 3 — остаток.

Если есть остаток, то

 

\(\text{Дивиденд}=\text{Делитель}\times \text{Частное}+\text{Остаток}\)

 

Пример остатка:

 

Важно отметить, что делитель не может быть равен 0. В таких случаях операция деления не определена. То есть мы не можем выполнить деление, а значит, и результата не получим.

Деление на однозначные числа

Деление на однозначные числа можно выполнить с помощью длинной таблицы деления. Предположим, вы хотите разделить \(2048\div 5\).

Выполните следующие действия.

Сначала находим оценку \(2000\дел 5=400\)

 

 

Здесь делимое равно 2048, делитель равен 5, частное равно 409, а остаток равен

. проверить результат, мы можем умножить частное на делитель, добавить остаток и сравнить его с делимым. Если оба значения равны, это означает, что операция деления выполнена правильно.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=5\times 409+3 \)

\ (= 2045+3 \)

\ (= 2048 \)

\ (= \ text {dividend} \)

Следовательно, операция деления проверяется

Отдел 3- digit Числа на двузначные числа

Деление трехзначных чисел на двузначные числа аналогично делению, которое мы выполняли ранее с однозначными числами. В этом случае единственное отличие состоит в том, что делимое будет трехзначным числом, а делитель — двузначным числом.

Давайте посмотрим, как мы можем разделить

\(369\дел 12\).

Сначала найдем оценку, так что \(300\div 10=30\)

В этом случае делимое равно 369, делитель равен 12, частное равно 30, а остаток равен 9. 

 

Чтобы проверить результат, мы можем умножить частное на делитель, добавить остаток и сравнить его с делимым. Если оба значения равны, это означает, что операция деления выполнена правильно.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=12\times 30+9\)

\ (= 360+9 \)

\ (= 369 \)

\ (= Dividend \)

Операция деления проверяется.

Деление четырехзначного числа на двузначное

Деление четырехзначного числа на двузначное также аналогично операциям деления, которые мы выполняли ранее. Разделим 4156 на 41,9.0005

Сначала мы находим оценку так \(4000\times 40=100\)

В этом примере делимое равно 4156, делитель равен 41, частное равно 101, а остаток равен 15. 

Проверить результат, мы можем умножить частное на делитель, добавить остаток и сравнить его с делимым. Если оба значения равны, это означает, что операция деления выполнена правильно.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=41\times 101+15\)

\ (= 4141+15 \)

\ (= 4156 \)

\ (= Dividend \)

Операция деления проверяется.

Решенные примеры

Пример 1: Разделите 418 ÷ 4 и проверьте результат.

 

Решение:

Найдем оценку \(400\дел 4=100\)

 

Мы можем проверить ответ, используя следующее уравнение.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=4{\times} 104+2=416+2=418=\text{Дивиденд}\)

 

Пример 2: Уильям разделил \(2149\div 7\) и получил частное как 306, а остаток как 6. Разумен ли этот ответ?

 

Решение:

Если операция деления верна, она должна удовлетворять следующему условию.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=\text{Дивиденд}\)

 

В этом случае делимое равно 2149, делитель равен 7, частное равно 306, а остаток равен 6.

Подставьте значения в уравнение:

\(7\times 306+6=2142+6=2148\)

\(2148\neq 2149\)

Следовательно, мы можем сделать вывод, что Вильям допустил ошибку в операции деления.

 

Пример 3: Две недели называются двумя неделями. Сколько двухнедель в году? (1 год = 365 дней)

 

Решение:  

1 год = 365 дней

1 две недели = 14 дней

Чтобы найти количество двух недель в году, нужно разделить количество дней в году на количество дней. через две недели. Это означает, что нам нужно найти \(300\div 10=30\).

Сначала находим оценку \(300\дел 10=30\)

 

Итак, в году 26 полных двухнедельников. Дополнительный 1, который мы получили в качестве остатка, можно считать дополнительным днем. Следовательно, в году 26 двухнедельников и один дополнительный день.

Здесь делимое равно 365, делитель равен 14, частное равно 26, а остаток равен 1. Чтобы проверить ответ, мы можем использовать следующее уравнение.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=\text{Дивиденд}\)

 

\(14\times 26+1=364+1=365 = Дивиденд\)

Следовательно, операция деления проверена

 

Пример 4: Франклин владеет кукурузным полем, и на нем работают 14 рабочих. Он передал 6200 долларов Куперу, который также работает на ферме. Франклин попросил Купера разделить деньги поровну и выплатить заработную плату всем рабочим. Если после деления заработной платы поровну останутся деньги, Франклин хочет, чтобы Купер купил всем закуски. Какова дневная заработная плата каждого рабочего? Сколько денег осталось на покупку напитков?

 

Решение:  

Общая заработная плата = $6200

Количество рабочих = 14

Чтобы найти дневную заработную плату каждого рабочего, нужно найти \(6200\div 14\). Сумма денег на угощение будет получена как оставшаяся часть этой операции разделения.

 

Сначала найдем оценку \(6000\дел 15=400\)

 

Здесь делимое равно 6200, делитель 14, частное 442, а остаток 9 1.0005

 

Это означает, что работники фермы получат по 442 доллара каждый, и у них есть 12 долларов на покупку напитков.

Часто задаваемые вопросы

Что осталось?

Остаток — это остаточное значение, которое мы получаем после выполнения операции деления. Во многих случаях делимое не может полностью делить делитель. Получаем остаток в таких операциях деления.

Как проверить результат операции деления?

Чтобы операция деления была корректной, она должна удовлетворять следующему условию.

 

\(\text{Делитель}\times \text{Частное}+\text{Остаток}=\text{Дивиденд}\)

 

Если мы не получим дивиденд при добавлении остатка к произведение делителя и частного, значит, операция деления пошла не так.

Почему результат операции деления можно проверить умножением?

Мы можем проверить результат операции деления с помощью умножения, потому что операция умножения обратна операции деления. Например, разделим 1 на 2.

\(1\div 2=\frac{1}{2}\)

Теперь умножим результат на 2.

\(\frac{1}{2 }{\times}2 =1\)

Выполнив умножение того же числа, мы получили исходное число. Это потому, что умножение обратно делению. Мы используем ту же логику для проверки результата длинной операции деления.

 

Где мы используем деление в реальной жизни?

Мы используем разделение в нашей повседневной жизни для различных целей. Разделение используется при разделении счета в ресторане, поровну делящихся закусками между друзьями, выделении времени для изучения разных предметов и т.д.

Ознакомьтесь с другими нашими курсами

Математика и точные науки: деление дробей на дроби с использованием визуальных моделей

Деление дробей — одна из тех тем, которые мне нужно время от времени освежать. Для меня это определенно одна из тех ситуаций «не используй, потеряешь». Итак, этот пост пришел от меня, чтобы освежить мою память о дробном делении. Но почему сейчас? Этот твит:

После того, как я поделился твитом Хоуи Хуа в нашей группе Visual Math на Facebook, я вспомнил о делении дробей. И полное раскрытие, я никогда не рассматривал разделение как вещь. Мне 42 года, я имею степень магистра математики для преподавания, и это никогда не приходило мне в голову. Я обычно не слишком беспокоюсь о том, как я веду себя, но я был признателен другим учителям в группе за то, что они тоже никогда не думали об этом. Это позволило нам всем узнать что-то новое вместе, и я люблю, когда это происходит.

В одном выпускном классе нам пришлось писать статьи о различных алгоритмах, изучаемых в математике, и о том, почему они работают. Деление на дроби было одним из таких алгоритмов, и после более чем нескольких «повторений», написанных в верхней части моей работы, я наконец сдал работу, которую действительно можно было оценить. Излишне говорить, что это был облагающий налогом класс.

Хранить, менять, переворачивать. Почему? Я надеюсь ответить на это с помощью 3 примеров в этом посте.

Пример 1: (2/3)÷(1/2)

Подразделение спрашивает: «Сколько из них подходит к этому?» Например, при делении 10 на 2 мы спрашиваем: «Сколько двойок вписывается в 10?» Мы задаем тот же вопрос, когда делим дроби, просто его немного сложнее увидеть.

В нашем первом примере (2/3)÷(1/2) мы спрашиваем: «Сколько 1/2 укладывается в 2/3?» Было бы легче ответить на этот вопрос, если бы наши дроби были разбиты на одинаковое количество частей. Создав общий знаменатель, будет легче увидеть, сколько из них подойдет.

Создав общий знаменатель 6, мы увидим, что все 3 наших зеленых столбца поместятся в пространство, занимаемое нашими синими столбцами. Есть даже место для еще одного! Таким образом, все зеленые столбцы (1 целиком) могут поместиться в синее пространство и еще 1 столбец из 3 (1/3). Итак, (2/3)÷(1/2) = 1 и 1/3.

Вот видео с объяснением:

Связь с «Keep-Change-Flip»

кхм, умножение на обратное) стандартный алгоритм. Как и везде в математике, есть несколько хороших способов установить связь. Мне лично нравится возвращать его к целым числам:

Если 10 разделить на 2, будет 5,

Тогда половина 10 будет 5. .

Если вы хотите напрямую связать алгоритм с этим примером дроби, вот как это можно сделать:

Мы видим, что числитель второй дроби становится знаменателем нашего ответа. Это потому, что мы спрашиваем: «Сколько числителя второй дроби (столбиков) мы можем поместить в числитель первой дроби [после того, как мы создадим общий знаменатель]?»

Пример 2: (1/2)÷(2/3)

Этот пример точно такой же, как и в примере 1, мы просто поменяли местами дроби, что забавно, потому что оно усиливает правильность деления. не коммутативный.

Во втором примере (1/2)÷(2/3) мы спрашиваем: «Сколько 2/3 вписывается в 1/2?» Создав общий знаменатель, мы легко увидим, что 3 из 4 синих полос поместятся в пространство, занимаемое зелеными полосами. Итак, (1/2)÷(2/3)=(3/4).

Вот видео:

Пример 3: (4/5)÷(2/3)  

Иногда создание общего знаменателя только с столбцами было бы слишком запутанным, чтобы быть полезным, поэтому вместо этого мы можем создать сетку, чтобы показать его. Мы всегда можем сделать это, я просто предпочитаю столбцы, когда есть возможность их использовать, потому что я чувствую, что их легче увидеть.

С (4/5)÷(2/3) наш общий знаменатель равен 15, поэтому мы можем создать сетку из 15 пробелов. 4/5 занимает 12 из этих ячеек, а 2/3 занимает 10 из этих ячеек. Таким образом, все наши 2/3 могут вписаться в 4/5 плюс дополнительные 2. Тогда мы можем увидеть, что (4/5)÷(2/3) = 1 и 2/10.

Вот видео, объясняющее этот пример:

Резюме:

Все три примера деления на дроби из этого поста в этом видео:

Эти ссылки на умножение и деление дробей включены в мою стену слов по математике 6-го класса — печатную и цифровую.

Я также только что создал этот набор карточек с заданиями на разделение фракций, чтобы сопровождать этот пост. Карточки можно заламинировать и использовать с маркером для сухого стирания, чтобы их можно было использовать повторно.

Деление дробей с использованием моделей задач

И для забавного обзора, эта дробь обзор цифровой математики квест.