Деление многозначного числа на однозначное (4 класс, математика)

4.2

Средняя оценка: 4.2

Всего получено оценок: 493.

4.2

Средняя оценка: 4.2

Всего получено оценок: 493.

Деление многозначных чисел на однозначные – это процесс утомительный, но в математике необходимый для развития навыков счета. Подобные умения необходимы на многих экзаменах

Однозначные и многозначные числа

Прежде чем перейти непосредственно к делению, давайте разберемся, какое число считается однозначным, а какое многозначным: двухзначным, трехзначным и так далее.

Дело в том, что в математике четко разделяют понятия цифры и числа. Цифры это обозначения от 0 до 9. Числа состоят из нескольких разрядов: единицы, десятки, сотни и так далее. Однозначное число содержит один разряд: единицы, а значит не может быть больше 9.

Такая система исчислений называется позиционной ,потому что значение каждой цифры зависит от позиции, которую она занимает в числе.

Двухзначное число содержит уже 2 разряда: единицы и десятки, следовательно, не может быть больше 99. Следуя той же логике трехзначные числа это числа от 100 до 999 и так далее

Деления

Деление это математическая операция, обратная операции умножения. Например выражение:

45:5=9 – показывает следующее: чтобы получить число 45 число 5 умножили на число 9.

Деление также имеет несколько интересных свойств.

Свойства деления

Свойства деления:

• Если любое число поделить на 1, то получится то же самое число
• Если ноль поделить на любое число, то получится ноль
• На ноль делить нельзя. Вообще-то можно, но получатся числа, с которыми в школьном курсе математики работать не учат ,поскольку это очень сложно. Поэтому правильнее будет сказать так: в школьном курсе математики делить на ноль нельзя.
• Если сумма делится на число, то можно каждое из слагаемых поделить на это число ,а потом сложить результат.
  То же касается и разности:

(а-в):с=а:с-в:с

• Если произведение делится на какое-то число, то можно любой из множителей разделить на число, а результат умножить на второй множитель:

(а*в):с=(а:с)*в

Деление в столбик

Столбик – это вертикальная линия, к середине которой проводится горизонтальная. Над горизонтальной чертой пишется делитель, с другой стороны вертикальной черты, рядом с делителем записывают делимое. Под горизонтальной чертой будет записываться результат.

Первым этапом нужно среди первых цифр числа 967 найти число, которое больше 23. Рассматриваем по порядку: 9 – меньше 23, а вот 96 уже больше. Значит первым шагом мы делим число 96 на число 23. Обязательно с остатком.

96:23=8, ост. 4 – в столбике под 96 записывается результат произведения 8*23=92. Число 92 подчеркивается и под ним записывается результат разности: 96-92=4. Рядом с 4 сносится цифра 7. Получается число 47, которое таким же образом делится на 23. А число 8 будет первой цирой в результате.

47:23=2, ост. 1 – цифра 2 будет второй цифрой результата.

Рядом с 1 можно снести 0 и считать уже дробную часть частного, но мы поделим число с остатком.

Результат: 967:23=82, ост.

Подобным образом можно поделить сколь угодно большое многозначное число на однозначное.

Что мы узнали?

Мы разобрались, чем отличается однозначное число от многозначного. Рассказали о том, что такое деление и выделили все свойства деления. Привели алгоритм деления многозначного числа на однозначное столбиком.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Оценка статьи

4.2

Средняя оценка: 4.2

Всего получено оценок: 493.

---

А какая ваша оценка?

6.2.4. Умножение многозначных чисел

Умножение также происходит аналогично умножению в столбик. Первый множитель последовательно умножается на отдельные 32-битовые слова второго множителя, а результаты умножения, сдвинутые на соответствующее число разрядов, складываются.

Для умножения используется команда mul, которая позволяет не потерять результат умножения, если его длина превышает 32 бита, записывая произведение в регистрыEDX:EAX.

6.2.5. Деление многозначных чисел

Деление числа произвольного размера на число произвольного размера выполнить с помощью команды divвыполнить невозможно. Используется деление в столбик с помощью последовательных вычитаний делителя (сдвинутого влево на соответствующее число разрядов) из делимого, увеличивая соответствующий разряд частного на 1 при каждом вычитании, пока не останется число меньшее делителя.

Если выполняется деление числа произвольного размера на число длиной не больше 32 бит, то можно использовать более простой и быстрый алгоритм, использующий команду div.

6.3. Особенности реализации симметричных алгоритмов

6.3.1. Дополнение сообщений

Блочные алгоритмы обрабатывают блоки фиксированного размера, например, 8 байт, но длина открытого текста часто не кратна 8. С этой целью производится дополнение последнего неполного блока нулевыми байтами. Затем добавляется еще один блок, в котором все байты кроме первого нулевые, а первый байт содержит количество байтов в последнем неполном блоке. Этот блок также шифруется и добавляется в конец зашифрованного текста. Он необходим, чтобы при дешифрации открытый текст не содержал лишних нулей в конце. Эта процедура дополнения используется и в том случае, когда длина открытого текста кратна 8. При этом длина зашифрованного текста на 16 байт больше, чем длина открытого.

6.3.2. Таблицы подстановки для алгоритма шифрования гост 28147-89

Согласно стандарту таблицы подстановок служат дополнительным ключом и должны держаться в секрете [2]. Этот долговременный ключ является общим для всех пользователей сети связи и поставляется в установленном порядке. Стандарт объясняет это тем, что стойкость данного алгоритма критически зависит от качества используемых таблиц подстановок. При правильном выборе даже в случае известных таблиц подстановки стандарт обеспечивает высокую стойкость. Однако критерии выбора таблиц подстановки для этого шифра не приводятся в официальных документах.

Такой подход имеет серьезные недостатки.

1. Требования секретности таблиц подстановок не согласуется с общепринятым принципом Керхкоффа, поскольку данные элементы относятся скорее к алгоритму шифрования, а не к легко сменяемому секретному ключу.

2. При уходе хотя бы одного пользователя из коллектива, в котором используются секретные таблицы подстановки, требуется смена таблиц подстановки.

Учитывая данные замечания, было решено генерировать таблицы подстановок случайным образом. Конечно, такой подход может привести к резкому снижению стойкости алгоритма, но в данном случае основной задачей было только продемонстрировать учащимся принцип работы данного шифра.

6.3.3. Подключи и таблицы подстановки для алгоритма Blowfish

Подключи и таблицы подстановки для Blowfishгенерируются следующим образом [3].

1. В порядке возрастания номера элемента заполнить массив подключей, а затем таблицы подстановки строкой, состоящей из 16-ричных цифр записи числа .

2. Произвести операцию исключающего ИЛИ с K₁и первыми 32 битами ключа и результат занести вK₁, повторить ту же операцию сK₂и вторыми 32 битами ключа. Повторять эти действия для всехK_i.

3. Зашифровать строку из 64 нулевых бит алгоритмом Blowfish, используя подключи, сгенерированные на шаге 1 и 2.

4. Заменить K₁иK₂

   результатом шифрования на шаге 3.

5. Зашифровать результат шага 3, используя алгоритм Blowfishс модифицированными подключами.

6. Заменить K₃иK₄результатом шага 5.

7. Продолжать эти процедуры шифрования, последовательно заполняя подключи и таблицы подстановки результатами работы постоянно изменяющегося алгоритма Blowfish.

Такой алгоритм позволяет создать подключи и таблицы подстановки, которые сильно зависят от ключа. Использование числа упрощает реализацию алгоритма, т.к. в противном случае пришлось бы отдельно определять значения для инициализации.

Поскольку в обучающей программе необязательно строго следовать стандартам, подключи и таблицы подстановки заполняются псевдослучайными значениями. Чтобы одному и тому же ключу всегда соответствовали одни и те же таблицы, перед заполнением генератор случайных чисел инициализируется значением секретного ключа.

Умножение многозначных чисел | Как?, Определение, Примеры, Метод

Введение

Умножение — одна из четырех основных математических операций, а остальные три — это сложение, вычитание и деление. Прежде чем мы перейдем к изучению того, как умножать многозначные числа, давайте вспомним, что мы подразумеваем под умножением.

Как определить умножение?

Умножение определяется как процесс нахождения произведения двух или более чисел. Полученный таким образом результат называется продукт . Предположим, вы купили 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.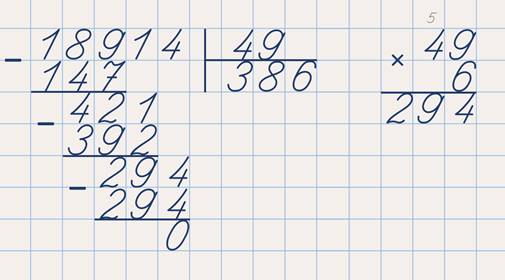

Это также можно записать как 2 x 6 = 12

Не тот символ, который используется для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)  

Символ умножения

Обратите внимание на символ, используемый в приведенном выше примере для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)  

Теперь давайте рассмотрим некоторые важные термины, которые используются при умножении двух чисел.

Важные термины при умножении

Некоторые важные термины, используемые при умножении: –

Множимое – Число, которое нужно умножить, называется множимым.

Множитель — Число, на которое мы умножаем, называется множителем.

Произведение – Результат, полученный после умножения множителя на множимое, называется произведением.

Связь между множителем, множимым и произведением может быть выражена как –

Множитель ×  Множитель = Произведение

Давайте разберемся с этим на примере.

Предположим, у нас есть два числа 9 и 5. Мы хотим умножить 9 на 5.

Итак, мы выражаем это как 9 x 5, что дает нам 45.

Следовательно, 9 x 5 = 45

Здесь 9 равно множимое, 5 — множитель, 45 — произведение.

Теперь, когда мы поняли, что мы подразумеваем под умножением и терминами, связанными с ним, давайте перейдем к изучению умножения однозначных чисел.

Теперь давайте разберемся, как выполнять умножение, когда у нас есть многозначные числа.

Как умножать многозначные числа?

Прежде чем мы приступим к пониманию умножения многозначных чисел, важно вспомнить, что подразумевается под многозначными числами?

Напомним, что каждая цифра числа имеет разрядное значение. Например, число 5 — это однозначное число, где 5 стоит на месте единицы. Точно так же в числе 27 цифра 2 стоит на месте десятков, а цифра 7 — на месте единиц. Итак, как мы определяем многозначные числа? Многозначные числа — это числа, состоящие из более чем 1 цифры. Например, числа 535 и 678 являются многозначными числами.

Теперь давайте перейдем к изучению умножения многозначных чисел. Когда дело доходит до умножения многозначных чисел, есть два метода умножения чисел. Этими методами являются метод расширенной записи и метод столбца. Давайте разберемся в обоих методах.

Метод расширенной записи

В методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.

Например, умножьте 1235 на 40

Решение

Мы решим это шаг за шагом.

Шаг 1 – Запишите число (множимое) в развернутом виде.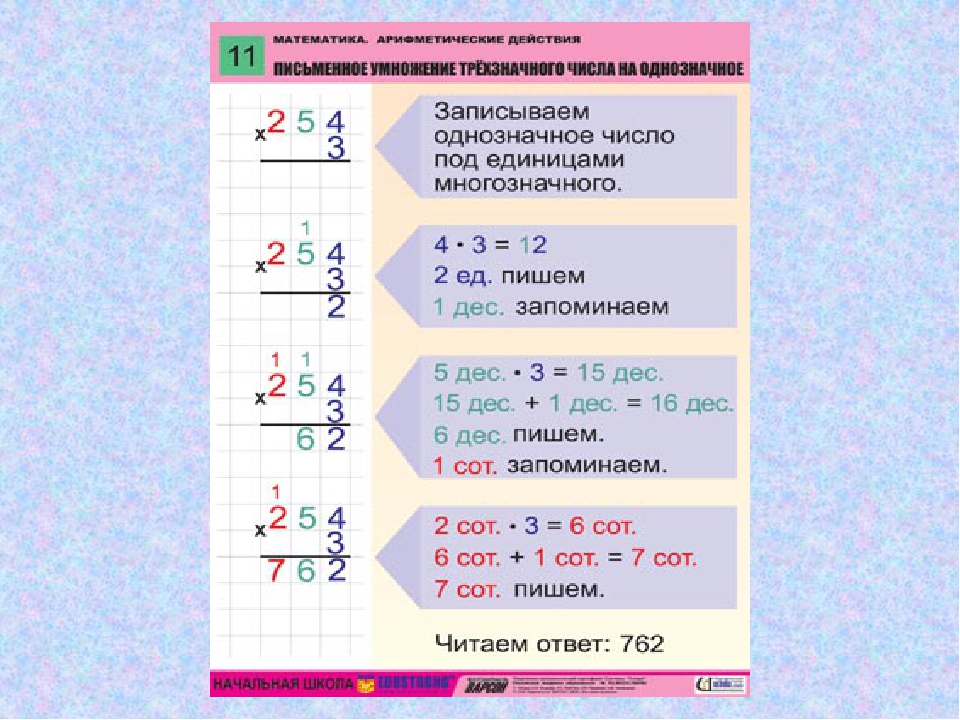 Получаем,

1235 = 1000 + 200 + 30 + 5

Шаг 2 — Умножаем каждое число на заданное число (множитель) по одному. Получаем,

1000 х 40 + 200 х 40 + 30 х 40 + 5 х 40

= 40000 + 8000 + 1200 + 200

Шаг 3 – Складываем полученные результаты. Получаем,

40000 + 8000 + 1200 + 200 = 49400

Следовательно, 1235 x 40 = 49400

Этот метод, хотя и прост, может не подходить для больших чисел. Но он используется для понимания основных понятий умножения.

Метод столбца

В этом методе мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим. Есть два сценария использования этого метода.

Разберем их по порядку

Умножение без перегруппировки

Этот метод вступает в силу, когда у нас есть меньшие числа, которые не требуют переноса каких-либо чисел к цифре на следующем разряде. Давайте разберемся на примере.

Например, умножьте 1021 на 32

 Решение

Чтобы получить результат, выполните следующие действия.

Шаг 1. Сначала мы записываем множимое и множитель в столбцах. Здесь у нас есть 1021 как множимое и 32 как множитель.

Шаг 2. Теперь умножаем число, стоящее на месте множимого, т. е. 1, на число, стоящее на месте множителя, которое в данном случае равно 2. Получаем

. Шаг 3. Теперь умножаем число в десятом разряде множимого на 2. Получаем

Шаг 4 – Далее умножаем число в сотенном разряде множимого на 2. Получаем

Шаг 5 – Наконец, умножаем число в тысячный разряд множимого на 2. Получаем

Шаг 6. Теперь нам нужно поместить 0 на место единиц в следующей строке в качестве заполнителя. Мы получим

. Шаг 7. Так как мы завершили умножение множимого на первую цифру множителя, мы выполняем те же действия, что и выше для умножения множимого на следующее число множителя, а затем пишем результатом будет строка напротив 0, которую мы поместили в качестве заполнителя на предыдущем шаге. Получим –

Шаг 8 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали.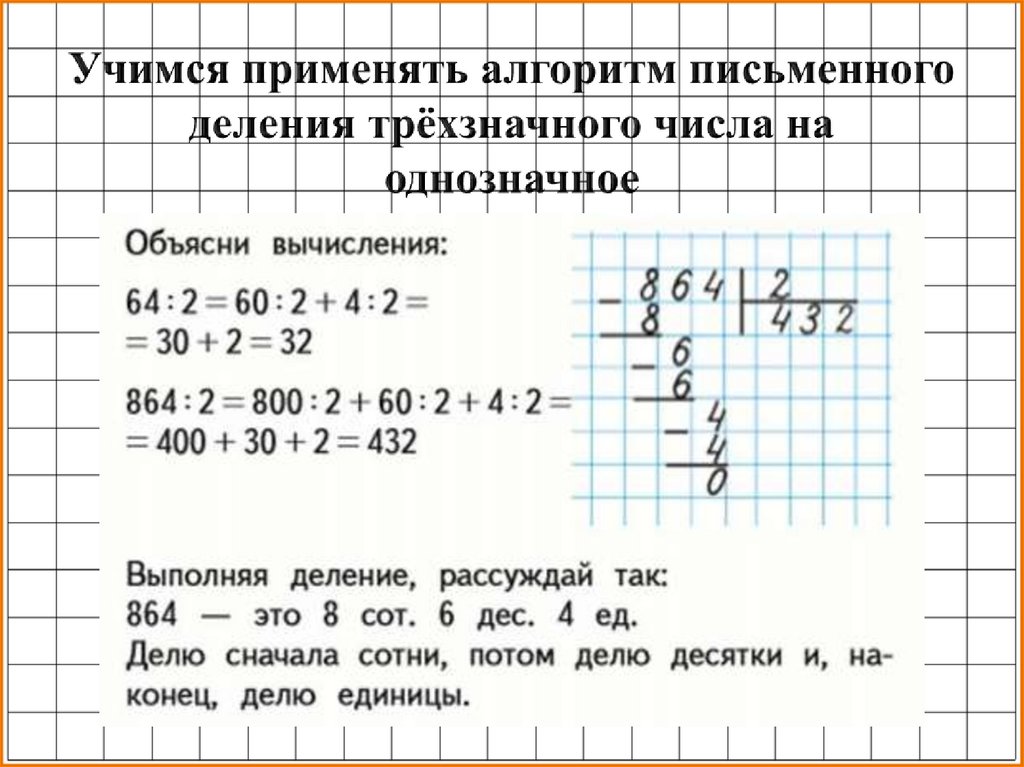 Получим –

Полученный таким образом результат является нашим ответом. Следовательно, 1021 x 32 = 32672

Умножение с перегруппировкой

В приведенном выше случае мы имеем небольшие умножения, которые ни на одном шаге не требуют двузначных результатов. Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.

Например, умножить 1025 на 34

Решение

Мы будем использовать следующие шаги, чтобы получить наш результат.

Шаг 1. Сначала мы записываем множимое и множитель в столбцах.

Шаг 2. Умножьте цифру единицы множимого на 4. У нас есть 4 x 5 = 20. Запишите 0 в столбце единиц и перенесите 2 в столбец десятков.

Шаг 3. Умножаем десятый разряд множимого на 4. Получаем 2 x 4 = 8. Прибавляем к нему перенесенные 2, получаем 8 + 2 = 10. Теперь запишем 0 в столбце десятков и перенесем 1 в сто столбик.

Шаг 4. Умножаем стозначную цифру множимого на 4. Получаем 0 x 4 = 0. Добавляем к ней перенесенную 1, чтобы получить 0 + 1 = 1. Теперь запишем 5 в столбце сотен.

Шаг 5. Умножьте цифры тысячного разряда множимого на 4. Получаем 4 x 1 = 4. Запишите 4 в столбце тысяч, чтобы получить – 

Шаг 6. Теперь нам нужно поставить 0 вместо единиц. поместите в следующую строку в качестве заполнителя. Мы получим

. Шаг 7 — Далее мы повторяем описанные выше шаги, чтобы умножить все цифры множимого на цифру в десятом разряде множителя. мы получим

Шаг 8 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. Мы получим –

Следовательно, 1025 x 34 = 34850

Вышеприведенные шаги можно обобщить для определения умножения, которое обычно известно как длинное умножение. Определим эти шаги.

Длинное умножение

Длинное умножение похоже на метод столбца, за исключением того факта, что здесь мы умножаем большие числа. Этот метод используется, когда множимое больше 9, то есть множимое больше однозначного числа. Этот метод включает следующие шаги: 

1. Сначала мы записываем множимое и множитель в столбцах.
2. Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
3. Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.
4. Теперь перейдите к следующей строке.
5. Поставьте 0 на месте единицы в этой строке.
6. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0.
7. Снова переходите на следующую строку.
8. Поставьте 0 на месте единиц и десятков в этой строке.
9. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.
10. Продолжайте в том же духе, добавляя дополнительный ноль в каждую строку, пока не дойдете до конца множителя 
11. Сложите числа по вертикали в соответствии с их разрядами.
12. Полученное таким образом число и есть ваш результат.

Разберем это на примере

Например, Умножьте 132 на 13

Решение

1. Сначала мы запишем множимое и множитель в столбцах.

2. Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.

3. Поставьте 0 на месте единицы следующей строки

4. Теперь найдите цифру на месте десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.

5. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.

6. Окончательный ответ: 1716. Следовательно, 132 x 13 = 1716

Давайте посмотрим на другой пример, где мы 3 цифры в множимом.

Например, Умножить 364 на 123

Решение

1. Сначала запишем множимое и множитель в столбцы

2. все числа множимого и запишем их горизонтально.

3. Поставьте 0 на месте единиц следующей строки

4. Теперь найдите цифру на десятом месте множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0007

5. Поставьте 0 вместо единиц и десятков в следующей строке.

6. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.

7. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.

8. Следовательно, конечный продукт равен 44 772. Мы можем сказать, что 364 х 123 = 44772

Умножение на 100 и 1000

• Чтобы умножить число на 100, нужно поставить два нуля справа от числа. Например, 435 х 100 = 43500
• Чтобы умножить число на 1000, поставьте справа от числа три нуля. Например, 435 x 1000 = 435000
• Чтобы умножить число на произведение 100 и 1000 на счетные числа, умножьте числа на ненулевые числа, а затем добавьте к результату количество нулей. Например, умножьте 45 на 200. Чтобы решить это, мы сначала умножим 45 на 200. Получаем 45 х 2 = 90. Теперь прибавляем 2 нуля (поскольку у 200 было 2 нуля) справа от 90. Получаем 9000. Следовательно, 45 x 200 = 9000

Решенные примеры

Пример 1 Шинный завод производит

6348 шин в день. Сколько шин произведет завод за 460 дней?

Решение Нам известно, что шинный завод производит 6348 шин в день. Нам нужно найти, сколько шин завод произведет за 460 дней. Обобщим эту информацию как – 

Шины, произведенные заводом за один день = 6348

Количество шин, которые завод произведет за 460 дней = ?

Чтобы получить это значение, нам нужно будет умножить 6348 на 460. Мы будем использовать длинные шаги умножения, определенные выше, чтобы найти значение. Получим – 

Следовательно, количество шин, которые будут произведены за 460 дней, будет 2920080.

Пример 2 World Tour Travels берет 80563 фунтов стерлингов за 7-дневную поездку в США с одного пассажира. Если 790 пассажиров совершили эту поездку за год, сколько туристическое агентство заработало за этот год? Кроме того, за год эту поездку совершают 790 пассажиров. Нам необходимо найти доходы от World Tour Travels в этом году. Подытожим имеющуюся у нас информацию.

Общая сумма, взимаемая World Tour Travels за 7-дневную поездку в США на одного пассажира = £80563

Количество пассажиров, совершающих эту поездку в год = 790

Общий доход от поездок в рамках мирового турне в этом году = ?

Чтобы найти общий доход от World Tour Travels в этом году, мы должны найти, умножив 80563 на 790. Мы получим

Следовательно, доход от World Tour Travels в год, когда он взимал 80563 фунтов стерлингов за 7-дневная поездка в США на одного пассажира и 790 пассажиров, совершающих эту поездку за год, составила 6 364 4770 фунтов стерлингов.

Основные факты и резюме

1. Умножение определяется как процесс нахождения произведения двух или более чисел.
2. Число, которое нужно умножить, называется множимым.
3. Число, на которое мы умножаем, называется множителем.
4. Результат, полученный после умножения множителя и множимого, называется произведением.
5. Многозначные числа — это числа, состоящие из более чем 1 цифры.
6. В методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ.
7. В методе столбца мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим.

Умножение двузначных чисел (на тему путешествий и туров) Рабочие листы
Свойства умножения (на тему недвижимости) Рабочие листы
Умножение смешанных чисел (на тему Дня отца) Рабочие листы

Просмотреть все рабочие листы

900 времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

Видео с вопросами: Решение текстовых задач с использованием деления многозначных чисел на трехзначные числа

Стенограмма видео

Партия сахара весом 9504 кг разделена на 528 упаковок. Какова масса сахара в каждой упаковке?

Первая часть информации, которую мы получаем в этой задаче, — это вес партии сахара. Это 9504 килограмма. Следующая часть информации, которую нам сообщают, — это то, что с ней происходит. Он разделен. На что оно разделено? 528 упаковок. Затем нас спрашивают, какой вес сахара в каждой упаковке. Итак, чтобы найти ответ, нам нужно разделить 9504 на 528. И чтобы сделать это, нам нужно будет использовать длинное деление.

Сколько партий из 528 содержится в числе 9504. В девяти и даже в 95 партиях по 528 нет. Итак, для начала нам нужно посмотреть на первые три цифры нашего числа. Сколько партий из 528 в 950? Вместо того, чтобы пробовать каждое число, кратное 528, мы можем использовать оценку здесь, чтобы помочь нам. Мы можем думать о 528 как о примерно равном 500. Итак, сколько лотов по 500 мы ожидаем получить от 950? Что ж, два лота по 500 — это 1000. Итак, мы знаем, что только один лот из 500 в 950. А поскольку 528 больше 500, мы знаем, что в этом числе будет только одна партия из 528. Таким образом, мы можем написать один наверху.

Одна партия из 528 равна 528. И если мы вычтем это из 950, мы сможем узнать, что у нас есть в остатке. Мы не можем вычесть восемь единиц из нуля. Значит, нам нужно произвести обмен. Возьмем одну десятку. Итак, пять десятков, теперь у нас есть четыре десятки, и мы обменяем их на 10 единиц. Теперь мы можем вычесть наши восемь единиц. 10 единиц убирают восемь единиц, оставляя нам две единицы. В столбце десятков четыре десятка вычитают два десятка, и у нас остается два десятка. И в столбце сотен 900 убираем 500, остается 400. Теперь можно продолжить деление.

Сколько партий из 528 в 422? 422 слишком мало. Нам нужно будет добавить еще одну цифру. И место, откуда мы собираемся получить нашу цифру, — это верхнее число. Итак, мы собираемся записать следующую цифру, то есть последнюю цифру в нашем номере. Это четверка. И это превратит наше число 422 в 4224. Сколько партий из 528 в этом числе? Что мы будем делать, начнем с одного лота из 528 и продолжим считать? Нет, давайте снова воспользуемся нашими навыками оценки.

4224 примерно равно 4000. И как мы уже говорили, 528 примерно равно 500. Мы знаем, что в 1000 два лота по 500. Итак, в 4000 должно быть восемь лотов по 500. Итак давайте прикинем, что в этом числе будет около восьми лотов по 528 штук. Есть только один способ узнать. Умножим 528 на восемь. Восемь единиц умножить на восемь равно 64. Итак, мы напишем четыре на месте единиц и заменим 60 единиц на шесть десятков. Два десятка умножить на восемь равно 16 десяткам. У нас уже есть шесть десятков, которые мы обменяли. Итак, это приводит нас к 22 десяткам.