Натуральные числа | Порядок выполнения действий

Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.

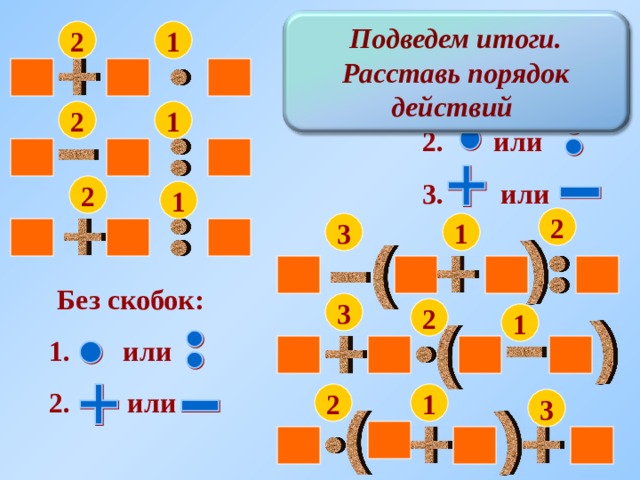
Порядок выполнения действий при нахождении значений выражений определяется следующими правилами.

1. Если в выражении нет скобок, и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.

2. Если выражение содержит действия первой и второй ступени, и в нем нет скобок, то сначала выполняют действия второй ступени, потом – действия первой ступени

3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).

Пример 1. Найдем значение выражения:

800 — 625 + 331 + 87 — 119.

Это выражение не имеет скобок и содержит действия только первой ступени, поэтому следует выполнять действия по порядку слева направо: 800 — 625 = 175, 175 + 331 = 506, 506 + 87 = 593, 593 — 119 = 474.

Итак, значение выражения равно 474.

Пример 2. Найдем значение выражения:

780 : 39 • 212 : 106 • 13.

Это выражение не содержит скобок, и в нем имеются действия только второй ступени, поэтому их следует выполнять по порядку слева направо:

780 : 39 = 20, 20 • 212 = 4240, 4240 : 106 = 40, 40 • 13 = 520.

Итак, значение выражения равно 520.

Пример 3. Найдем значение выражения:

5781 — 28 •75 : 25 + 156 : 12.

Это выражение не содержит скобок, и в нем есть действия первой и второй ступени. Поэтому вначале выполним действия второй ступени: 23 • 75 = 2100, 2100 : 25 = 84, 156 : 12 = 13, а потом действия первой ступени: 5781 — 84 = 5697, 5697 + 13 = 5710.

Значение выражения равно 5710.

Пример 4. Найдем значение выражения:

36000 : (62 + 14 • 2) – 23 • 5.

Это выражение содержит скобки. Поэтому выполним сначала действия в скобках: 62+14 • 2 = = 62 + 28 = 90.

Подставив это значение, получим: 36 000 : 90 — 23 • 5.

Вычислив значение последнего выражения, получим 285.

В выражениях, содержащих скобки, можно эти скобки не писать, если при этом порядок действий не изменяется.

Пример 5. Вместо (53 — 12) + 14 можно написать 53 — 12 + 14, так как в обоих случаях порядок действий одинаков:

53 — 12 = 41, 41 + 14 = 55.

Изменять порядок действий можно на основе свойств сложения, вычитания и умножения.

Каждое выражение задает программу своего вычисления. Она состоит из команд.

Например, программе вычисления выражения

(814 + 36 • 27) : (101 — 2052 : 38) состоит из следующих команд.

1. Перемножить числа 36 и 27.

2. Сложить 814 с результатом команды 1.

3. Разделить 2052 на 38.

4. Вычесть из 101 результат команды 3.

5. Разделить результат команды 2 на результат команды 4.

Эту программу вычислений можно изобразить в виде схемы (рис. 57).

Рис. 57. Схема программы вычисления выражения: (814 + 36 • 27) : (101 — 2052 : 38)

Последовательно выполнив действия и заполнив при этом пустые клетки, получим в нижней клетке ответ.

Порядок выполнения действий: правило, примеры

Содержание

При решении небольших примеров не возникает проблем с порядком выполнения действий. В подобных задачах в основном только одно действие, например умножение или сложение. Но в выражениях, где есть сразу несколько действий, нужно уже грамотно подбирать порядок действий. Именно поэтому необходимо знать, какие действия следует выполнять в первую очередь, а какие — в последнюю.

Правила соблюдения порядка

Сложение и вычитание чисел называют действиями первой ступени. Умножение и деление чисел — действиями второй ступени.

Рисунок 1. Действия первой и второй ступени

В выражениях, которые содержат скобки, можно эти скобки не писать, если при этом порядок действий не изменяется.

Изменять порядок действий можно на основе свойств сложения, вычитания и умножения

Правильный порядок выполнения действий выглядит так:

1. Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
2. В выражении, которое содержит действия первой и второй ступени и в нем нет скобок, нужно сначала выполнить действия второй ступени, и только потом действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках, при этом учитывая правила 1 и 2.

{"questions":[{"content":"Расставь правильный порядок действий[[sorter-1]]","widgets":{"sorter-1":{"type":"sorter","items":["Действия второй ступени в скобках","Действия первой ступени в скобках","Действие второй ступени за скобками","Действие первой ступени за скобками"]}}}]}

Рисунок 2

Примеры выражений

Давайте рассмотрим несколько примеров, в которых мы правильно расставим порядок выполнения действий.

1-ый пример: $80-62+32+87-19$

Так как тут нет скобок, а все действия в выражении только первой ступени, то действия следует выполнять слева направо. Таким образом решение будет выглядеть так:

$$80-62=18$$

$$18+32=50$$

$$50+87=137$$

$$137-19=118$$

Следовательно, ответом данного выражения станет $118$.

2-ой пример: $70:10\cdot4:2\cdot3$

Итак, данном выражении нет скобок, при этом все действия только второй ступени. Здесь действия также будут выполняться по порядку слева направо. В нашем случае решение будет таким: $$70:10=7$$

$$7\cdot4=28$$

$$28:2=14$$

$$14\cdot3=42$$

Ответом выражения является $42$.

3-ий пример: $36-1\cdot8:4+16:4$

Здесь мы видим, что помимо действий первой ступени, тут есть действия второй ступени, но скобок тут нет. Поэтому, сначала нам нужно вычислить действия второй ступени:

$$1\cdot8=8$$

$$8:4=2$$

$$16:4=4$$

Затем следует посчитать действия первой ступени:

$$36-2=34$$

$$34+4=38$$

В конечном итоге мы получили результат всего выражения — $38$.

4-ый пример: $100:(8+2\cdot1)-3\cdot3$

Это выражение имеет и скобки, и действия первой и второй ступени. В данном случае нужно выполнить действия в скобках второй ступени, затем первой:

$$2\cdot1=2$$

$$8+2=10$$

Следующим шагом нужно сделать действия второй ступени за скобками:

$$100:10=10$$

$$3\cdot3=9$$

Последним этапом станет выполнение действий первой ступени:

$$10-9=1$$

Именно $1$ и станет ответом данного примера.

{"questions":[{"content":"Реши пример: $$110-60+(15\\cdot4-40:2)-10\\cdot3$$ [[input-1]]","widgets":{"input-1":{"type":"input","answer":"60"}},"hints":["Сначала выполни действия второй ступени в скобках.","Затем посчитай действия первой ступени в скобках.","Дальше нужно посчитать действия второй ступени за скобками.","Последним шагом следует посчитать действия первой ступени за скобками."]}]}

Схема порядка действий

Для каждого выражения можно выстроить свою схему порядка действий. Такую схему называют программой вычисления, которая состоит из команд. Давайте разберем на основе одного примеров:

$$(30+7\cdot2):(12-20:2)$$

Данную программу вычисления выражения мы можем разбить на команды:

Рисунок 3. Порядок действий
1. Перемножить числа $7$ и $2$.
2. Сложить $30$ с результатом выполнения команды $1$.
3. Разделить $20$ на $2$.
4. Вычесть из $12$ результат выполнения команды $3$.
5. Разделить результат команды $2$ на результат команды $4$.

5

Оценить урок

Поделиться уроком →

Войдите, чтобы оценивать уроки

Что нужно исправить?




Спасибо, что помогаете нам стать лучше!

Комментарии

Умножение и деление целых чисел – методы и примеры

В математике арифметические операции с целыми числами включают вычитание, сложение, деление и умножение всех типов действительных чисел. В частности, целые числа — это числа, включающие положительные, отрицательные и нулевые числа. Умножение и деление целых чисел регулируются аналогичными правилами.

Как умножать целые числа?

Умножение определяется как многократное сложение целых чисел. Умножение целых чисел включает три случая:

• Умножение двух положительных целых чисел
• Умножение двух отрицательных целых чисел
• Умножение положительного и отрицательного целых чисел.

Умножение двух целых чисел с одинаковыми знаками всегда дает положительный результат. Это означает, что произведение двух положительных или двух отрицательных целых чисел положительно. С другой стороны, целые числа произведений с разными знаками всегда будут отрицательными.

Многие учащиеся сталкиваются с проблемой запоминания приведенных выше правил умножения целых чисел. В этой статье есть сценарий, который поможет вам избежать путаницы. В этом сценарии положительный знак (+) использовался для обозначения ‘ GOOD », а знак минус символизирует фразу BAD . «Давайте посмотрим на эти мнемоники.

• Если хорошие (+) вещи случаются с хорошими (+) людьми, то это хорошо (+)
• Если хорошие (+) вещи случаются с плохими (-) людьми, то это плохо (-)
• Если плохие (-) вещи случаются с хорошими (+) людьми, тогда это плохо (-)
• Если плохие (-) вещи случаются с плохими (-) людьми, то это хорошо (+)

Чтобы умножить целые числа, просто умножьте числовые числа без знака и поставьте знак на продукте, вспомнив вышеприведенные правила.

Пример 1

• 7 x 5 = 35
• 7 × (-6) = -42
• (-9) × 5 = -45
(
• -5-) = -4) 20

Если число отрицательных множимых в предложении умножения нечетное, произведение будет отрицательным числом.

Пример 2

(-2) × (−4) × (−3) = -24; здесь количество множимых = 3 (нечетное число)

Когда количество отрицательных множимых четно в предложении умножения, произведение будет положительным.

Пример 3

(−4) × (−3) = 12; Здесь число множимых равно 2 (четным)

Как делить целые числа?

В то время как умножение является суммированием целых чисел, деление, с другой стороны, является распределением целых чисел. Мы можем просто сказать, что деление обратно умножению. Правила деления целых чисел аналогичны правилам умножения. Единственная разница в делении состоит в том, что частное не обязательно должно быть целым числом.

Давайте также посмотрим на правила деления:

• Частное натурального числа всегда положительно. Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3
• Частное двух отрицательных чисел всегда положительно. Это означает, что если делимое и делитель оба отрицательны, то частное всегда положительно. Например;
  (- 9) ÷ (- 3) = + 3
  Следовательно, при делении двух целых чисел с одинаковыми знаками мы делим числа без знака и ставим перед результатом знак плюс.
• Деление положительного и отрицательного целых чисел дает отрицательный ответ. Например; (+ 16) ÷ (- 4) = – 4

Таким образом, чтобы разделить целые числа с разными знаками, мы делим числовые значения без знаков и ставим к результату знак минус.

 

Упрощенная процедура для больших чисел

Целые числа: Умножение: Упрощенная процедура для больших чисел


  математика > целые числа

Умножение: упрощенная процедура для больших чисел

    что вы узнаете. ..

обзор

Умножение в первых принципах объяснялось как многократное повторение множимого, множителя. Этот метод переработан для двузначных чисел и установлен, что требуется перегруппировка единиц, десятков и т. д. Это устанавливает упрощенную процедуру: умножение на разрядное значение с перегруппировкой.


перегруппировка

Рассмотрим умножение 1212 на 33.

Это выполняется так: соедините 1212 33 раза и подсчитайте объединенное количество.

Учитывая умножение 12×312×3.

Комбинирование 1212 33 раза показано на рисунке. Есть 3 десятка и 6 единиц, которые вместе образуют число 36.

Учитывая умножение 12×3. На рисунке число 12 указано в разрядном формате.

Визуализируется повторное сложение и выполняется умножение, как показано на рисунке.

Разряд единиц умножается как 2×3=6, а разряд десятков умножается как 1×3=3. Результат умножения равен 36.

Рассмотрим умножение 26×2. То есть 26 повторяется дважды, как показано на рисунке. Если сложить эти две величины вместе, получится 4 десятка и 12 единиц. Суммарное значение равно 52.

Учитывая умножение 26×2. То есть 26 повторяется дважды и комбинируется, как показано на рисунке.
Обратите внимание, что 10 единиц перегруппированы вместе, чтобы сформировать 1 десяток. Таким образом, результат умножения равен 52.

Учитывая умножение 26×2. На рисунке число 26 дано в разрядном формате.

Упрощенная процедура Умножение на разрядное значение с перегруппировкой представлена ​​на рисунке.

В разряде единиц 6 и 2 умножаются на 12. Единица 10 преобразуется в 1 десяток и перемещается в разряд десятков. Эта перегруппировка 10 с более низким разрядным значением в 1 с непосредственным более высоким разрядным значением переносится. Остальные агрегаты 2 сохраняются.

В разряде десятков 2 и 2 умножаются на 4, и к этому прибавляется перенос. Итак, разряд десятков результата равен 4+1=5.

Результат 52.

упростить

Рассмотрим умножение: 34×4. Один 34 показан на рисунке.

Для умножения количество 34 можно повторить 4 раза или можно использовать упрощенную процедуру «умножение на разрядное значение с перегруппировкой».

С учетом умножения: 34×4. Значение 34 повторяется 4 раза и комбинируется, как показано на рисунке. Суммарное количество составляет 12 десятков и 16 единиц.

10 десятков перегруппированы в 1 сотню. 10 единиц перегруппированы в 1 десяток. Затем количество сотен, десятков и единиц подсчитывается до результата 136.

С учетом умножения: 34×4. Цифры даны в разряде на рисунке.

Упрощенная процедура Умножение на разрядное значение представлена ​​на рисунке.

Цифра в разряде единиц умножается на множитель. Образовавшиеся десятки переносятся на позицию десятков,
Затем цифра в разряде десятков умножается на множитель. Сформированные сотни переносятся на позицию сотен.